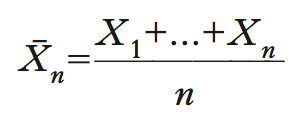grandi numeri, legge dei

grandi numeri, legge dei

Uno dei risultati fondamentali del calcolo delle probabilità, che descrive il comportamento della media di una successione di variabili aleatorie all’aumentare del loro numero. Tale legge è talvolta chiamata legge empirica del caso o teorema di Bernoulli, dal nome del matematico J. Bernoulli che per primo ne ha data una formulazione. Nella formulazione originaria di Bernoulli, la frequenza relativa di ‘testa’ in una sequenza di lanci di monete tende a essere sempre più vicina alla probabilità di ottenere testa in un singolo lancio. Un risultato simile è vero più in generale.

Per enunciare la legge dei g. n. nella sua forma più semplice, si consideri una successione di variabili aleatorie indipendenti e identicamente distribuite, tutte con media

per ogni n-upla.

La legge dei g. n. assicura che al crescere di n, la variabile aleatoria _n converga a μ in un senso opportunamente definito. Si parla di legge forte dei g. n. quando _n converge a μ quasi certamente, cioè quando si ha che è uguale a 1 la probabilità che il limite di _n sia μ:P(lim_{n→∞ n}=μ)=1. Si parla di legge debole dei g. n. quando la convergenza di _n a μ è in probabilità, vale a dire che lim_n→∞ P|_n−μ |<ε)=1 per ogni ε>0. Si hanno leggi dei g. n. diverse a seconda del grado di dipendenza e di eterogeneità delle variabili aleatorie che compongono la successione X₁, X₂,... . In statistica, le leggi dei g. n. sono uno strumento fondamentale nello studio delle proprietà asintotiche di uno stimatore (➔). Per es., si invoca una legge dei g. n. per provare che lo stimatore _n della media μ di una popolazione è consistente.