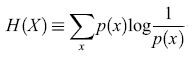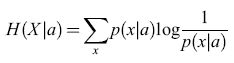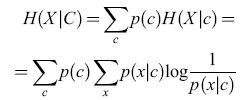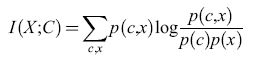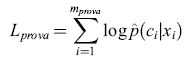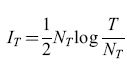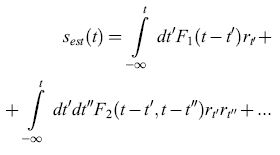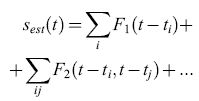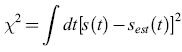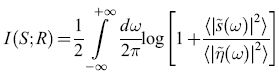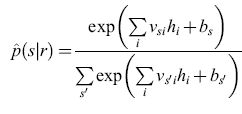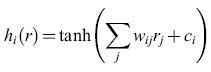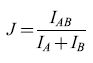I risultati dell'elaborazione neuronale come fonte dell'informazione

I risultati dell'elaborazione neuronale come fonte dell'informazione

Una parte consistente della neurofisiologia si occupa dell'interpretazione dei messaggi che i neuroni codificano attraverso le loro sequenze di impulsi. Per molto tempo si è ritenuto che l'informazione fosse codificata solo attraverso l'identificazione di quali neuroni siano attivi (codifica basata sull'identificazione) e attraverso la velocità delle loro emissioni di impulsi (codifica basata sulla frequenza). Ricerche più recenti hanno esaminato, nel contesto della teoria dell'informazione, la possibilità che i neuroni sfruttino in modo più effìciente la loro capacità di trasmissione dell'informazione, codificando i messaggi attraverso la struttura temporale delle sequenze di impulsi che emettono. In questo saggio passeremo in rassegna gli studi sulla decodifica delle sequenze di impulsi emessi dal neurone H1 di una mosca, e quelli sui neuroni del sistema visivo della scimmia. Nel primo caso buona parte del codice neuronale è ormai compresa abbastanza bene. Anche nel secondo caso si sono compiuti notevoli progressi, ma alcune domande fondamentali rimangono senza risposta. Tra i problemi aperti figura, in particolare, quello della codifica congiunta da parte di gruppi di neuroni.

Introduzione

L'elaborazione neuronale viene svolta collettivamente da insiemi di milioni di neuroni, ognuno dei quali riceve segnali da migliaia di altri neuroni e ad altrettanti ne invia. L'output dell'elaborazione elementare effettuata da ogni singolo neurone è di fatto binario. l segnali inviati da un neurone sono sequenze di impulsi identici. Uno degli obiettivi principali della neurofisiologia consiste nel comprendere il codice neuronale, cioè il modo in cui l'informazione viene rappresentata tramite queste sequenze. Gli studi che passeremo in rassegna in questo saggio rappresentano dei tentativi di studiare tale problema in termini quantitativi, nel contesto della teoria dell' informazione.

Cominceremo col riassumere la natura del problema del codice neuronale e la storia delle ricerche svolte in questo campo, e col richiamare alcuni aspetti fondamentali della teoria dell'informazione. Questo preparerà il terreno per un resoconto più dettagliato di due insiemi di studi recenti, condotti rispettivamente sugli invertebrati e sui mammiferi: i lavori di W. Bialek, R.R. de Ruyter van Steveninck e collaboratori sul neurone Hl nel sistema visivo del moscone, e quelli di B.J. Richmond, J. Hertz e collaboratori sulle cellule complesse nella corteccia visiva primaria delle scimmie rhesus. Questi studiosi hanno affrontato il problema come compito di decodifica: con quale accuratezza si può ricostruire lo stimolo, a partire dalla sequenza di impulsi evocata dallo stimolo stesso? Nell'insieme, queste ricerche illustrano vari modi per misurare l'informazione trasmessa nei treni di impulsi neuronali, e mostrano come analisi di questo tipo possano aiutare a comprendere aspetti fondamentali dell'elaborazione neuronale.

La codifica neuronale

l primi progressi nella comprensione del codice neuronale furono compiuti quando si scoprì che aree cerebrali diverse sono associate a funzioni diverse. L'attività neuronale nella corteccia visiva veicola informazione su ciò che l'animale sta vedendo, l'attività nella corteccia motoria sui movimenti che sta per compiere, e così via. Questa architettura funzionaIe si estende anche a scale più piccole. Nella corteccia visiva primaria dei mammiferi, di solito, i neuroni sono più sensibili a stimoli (strisce o barre) disposti con una certa orientazione in una certa parte del campo visivo; i neuroni che si trovano entro una distanza di pochi decimi di millimetro l'uno dall'altro tendono a rispondere con più forza a stimoli orientati quasi allo stesso modo (Hubel e Wiesel, 1962; 1968). All'interno di tali regioni, neuroni diversi rispondono in modo diverso ad altre caratteristiche dello stimolo, anche se la loro organizzazione spaziale diventa meno sistematica. Questa selettività rispetto a caratteristiche particolari di uno stimolo, che si estende anche ad altre modalità sensoriali, fornisce un esempio della codifica basata sull'identificazione: la conoscenza di quali neuroni nel cervello siano attivi fornisce informazione sull' ambiente in cui si trova l'animale e sul suo stato comportamentale. La codifica basata sull'identificazione è strettamente connessa all'idea secondo la quale i neuroni delle aree sensoriali fungono da rivelatori di caratteristiche: a identificare i neuroni sono le caratteristiche (o gli insiemi di caratteristiche) di uno stimolo, che il sistema individua.

Il cervello utilizza certamente una codifica basata sull'identificazione, ma il codice neuronale è sicuramente molto più complesso. Il lavoro classico di E.D. Adrian (1926) ha dimostrato che i neuroni utilizzano una codifica basata sulla frequenza: un numero di impulsi elevato segnala uno stimolo intenso, mentre un numero basso indica uno stimolo debole. Questo fatto non costituisce una necessità logica: nell'ambito di una codifica basata puramente sull'identificazione, una maggiore contrazione muscolare potrebbe semplicemente corrispondere, in linea di principio, a un maggior numero di neuroni motori attivi. Questa descrizione, però, non corrisponde al comportamento dei neuroni osservato sperimentalmente: viene utilizzato un ulteriore grado di libertà del segnale, la frequenza degli impulsi, in modo tale che l'intensità del movimento possa essere codificata da un solo neurone. Il funzionamento di questo meccanismo di codifica si basa sul fatto che le cellule che ricevono questi segnali li integrano su un certo intervallo di tempo, cosicché il potenziale postsinaptico riflette in modo efficace la frequenza di emissione presinaptica.

Può sembrare che stiamo insistendo troppo su un punto semplice, ma questo è un esempio utile di come il sistema nervoso possa sfruttare un grado di libertà ulteriore nelle sequenze di impulsi, incrementando così la sua potenziale efficienza. Inoltre, questo esempio illustra come la capacità di utilizzare gradi di libertà aggiuntivi del segnale dipenda dalla disponibilità di un meccanismo in grado di 'leggere' questi gradi di libertà. Vale la pena di tenere presenti entrambi questi insegnamenti nel compiere il passo logico ulteriore, che consiste nel chiedersi se il cervello faccia uso di ulteriori gradi di libertà nel suo modo di codificare i messaggi e, in particolare, se qualche elemento relativo alla temporizzazione degli impulsi veicoli l'informazione. La codifica basata sulla frequenza viene utilizzata anche nella corteccia, come fu dimostrato per la prima volta nei lavori di D. Hubel e T. Wiesel sulla corteccia visiva primaria, cui abbiamo già accennato. D'altra parte, le sequenze di impulsi corticali sono qualitativamente diverse da quelle emesse dai neuroni motori, in quanto appaiono molto più irregolari (Abeles, 1991; Softkye Koch, 1993). Se si effettuano varie misurazioni della risposta di un neurone corticale a uno stimolo, si osserva una dipendenza sistematica della frequenza di emissione dai parametri dello stimolo (come l'orientazione), ma le temporizzazioni degli impulsi appaiono casuali. Non sappiamo se la corteccia sia intrinsecamente un sistema stocastico, o se questo rumore apparente esprima in realtà un qualche genere di traffico interno sulla rete di comunicazione del cervello. Ciononostante, è chiaro che le frequenze di emissione misurate codificano in effetti l'intensità delle caratteristiche degli stimoli visivi. Conclusioni simili si applicano ad altre modalità sensoriali e alla corteccia motoria.

La domanda circa la possibilità che le componenti irregolari delle sequenze di impulsi dei neuroni corti cali possano veicolare qualche tipo di informazione è rimasta aperta per almeno quarant'anni, ma è stata in genere ignorata dalla neurofisiologia dominante. Il modello combinato, fondato sulla codifica basata sull'identificazione e su quella basata sulle frequenze, ha fornito l'ipotesi di lavoro standard per due generazioni. Questo paradigma era sia ragionevole che funzionale. In primo luogo, le sequenze di impulsi corticali altamente irregolari non mostravano nessuna caratteristica evidente correlata allo stimolo, al di fuori della loro frequenza media comune. In secondo luogo, questa ipotesi rendeva praticabile l'analisi dei dati. Il conteggio degli impulsi era facile, e un numero modesto di prove ripetute risultava sufficiente a quantificare l'errore sulle frequenze. Se ci fosse stato qualche effetto sistematico legato alla temporizzazione degli impulsi, sarebbe stato necessario un numero enorme di prove, in considerazione dell'irregolarità delle sequenze di impulsi, per estrarre questo effetto dal rumore. Anche la sola gestione dei dati necessaria per un lavoro di questo tipo risultava scoraggiante e, con i calcolatori disponibili una o due generazioni fa, l'unica opzione praticabile era quella di lavorare con la codifica basata sulla frequenza, e sperare che contenesse almeno una parte della verità.

Nella concezione dei neuroni come rivelatori di caratteristiche è implicita la seguente idea: c'è così tanta informazione sensoriale che si ripercuote sul cervello, che uno dei principali compiti dei sistemi sensoriali deve essere quello di trascurare le informazioni meno importanti, trasmettendo ai centri superiori descrizioni semplificate dell'ambiente, codificate in termini delle loro caratteristiche e intensità. Una considerazione di questo tipo può risultare ragionevole e corretta in alcuni contesti, ma può essere solo una parte della verità. In un approccio più generale, sviluppato per la prima volta da H.E. Barlow (1961; 1981), si ipotizza che la funzione del sistema sensoriale sia quella di elaborare rappresentazioni efficienti dell'ambiente. Se la capacità del canale è piccola, ciò richiede di trascurare una gran quantità di informazione, e una descrizione in termini di un piccolo numero di caratteristiche risulta naturale. D'altra parte, il principio richiede anche che si faccia il miglior uso possibile della capacità di canale disponibile: l'informazione non deve essere scartata se non è necessario. Questo concetto ha consentito di ricavare, a partire da principi primi, una comprensione unitaria di buona parte del primo stadio dell'elaborazione visiva, almeno nell' ambito di una codifica basata sulla frequenza linearizzata (Li, 1996; Olshausen e Field, 1996). L'applicazione di questa idea agli aspetti temporali dei segnali neuronali suggerisce la seguente conclusione: se i neuroni possono codificare informazione attraverso la temporizzazione degli impulsi, e se questa informazione può essere letta in modo affidabile dagli altri neuroni, il cervello potrebbe costruire una rappresentazione dell'ambiente più densa di informazione rispetto alla sola codifica basata sulla frequenza.

Teoria dell'informazione: concetti fondamentali

Esiste uno schema matematico ben sviluppato all'interno del quale si può provare a formulare e a studiare il problema della codifica neuronale: la teoria dell' informazione (Shannon, 1949). La grandezza fondamentale nella teoria dell' informazione è l' entropia, un concetto tratto dalla meccanica statistica. Essa rappresenta, come ora vedremo, una misura della variabilità di una variabile casuale X, ed è definita matematicamente nel modo seguente. Supponiamo che X possa assumere dei valori x con probabilità p(x). Se X è continua, supponiamo che vi sia un limite di risoluzione per la sua misura, e ordiniamo i suoi valori in intervalli di dimensione pari alla risoluzione. Possiamo quindi procedere come se X fosse una variabile a valori discreti. Inoltre, supporremo che X sia una grandezza scalare, ma la descrizione è applicabile anche al caso di una grandezza a più componenti. L'entropia è definita come

formula [1]

Questa quantità vale zero se X non varia, cioè se p(x) = l per un certo valore di x e p(x) = O per tutti gli altri valori. Se ci sono N valori possibili per X, H(X) raggiunge il suo massimo valore, logN, quando tutti gli N valori sono equiprobabili (variabilità massima), cosicché tale funzione risulta essere un'adeguata misura della variabilità. Per una variabile con distribuzione normale, con deviazione standard σ, H è, a meno di una costante additiva, semplicemente il logaritmo di σ: H = log(√2πeσ). Consideriamo ora la codifica dei messaggi attraverso i valori di X. Per essere concreti, ipotizziamo che i messaggi diano indicazione sul fatto che un certo sistema si trovi nella condizione a o b, cosicché i valori di x osservati sotto la condizione a sono in genere diversi da quelli osservati sotto la condizione b. Più precisamente, le probabilità p(xla) che, data la condizione a, X valga x sono diverse da quelle che corrispondono al verificarsi della condizione b. Per esempio, le osservazioni subordinate al verificarsi della condizione a potrebbero essere raggruppate intorno a un particolare valore Xa, e i messaggi condizionati a b intorno a un diverso valore Xb. In questo caso, le distribuzioni condizionate p(xla) e p(xlb) saranno tra loro diverse, e ognuna sarà meno uniforme della distribuzione incondizionata p(x). Così l'entropia condizionata

formula [2]

sarà minore dell' entropia incondizionata dell'equazione [1]. La differenza tra queste due quantità viene detta informazione sulla condizione a. La media di questa differenza, e la media corrispondente per le osservazioni condizionate a b (pesate con le rispettive probabilità nell'insieme statistico, se sono diverse) è l'informazione media trasmessa in un messaggio.

È semplice estendere queste considerazioni a situazioni con più condizioni. Denotando l'insieme delle condizioni con C e le condizioni individuali con c, l'entropia condizionata media, o equivocazione, è:

formula [3]

e l'informazione (media) trasmessa è:

I(X;C) ≡ H(X) − H(X∣C). [4]

Qualsiasi misura della trasmissione di informazione si riduce così alla stima di queste entropie. In un sistema binario l'unità di misura convenzionale per l'entropia è il bit; le equazioni scritte sono espresse in bit se si passa ai logaritmi in base 2. Un messaggio di p bit veicola un'informazione sufficiente per classificare 2^P condizioni, tutte a priori equiprobabili.

Ci sono alcuni aspetti da sottolineare a questo punto. In primo luogo, non si può parlare del contenuto di informazione di un singolo messaggio x, poiché la teoria dell'informazione è formulata solo in termini di variabili casuali (X). In secondo luogo, l'informazione deve riguardare qualcosa di definito (come l'insieme delle condizioni C). In terzo luogo, la formulazione della teoria è simmetrica rispetto allo scambio della variabile di segnale X con l'insieme delle condizioni C. Potremmo partire dall'entropia H(C) dell'insieme di condizioni e dal suo valore H ( qx) condizionato a un valore x della variabile di segnale X Di qui, costruendo un'equivocazione H(C∣x) con la media H(C∣x) pesata dalle probabilità p(x), si arriva a un'informazione

I(C;X) ≡ H(C) − H(C∣X). [5]

Scrivendo le probabilità condizionate p(clx) che compaiono in H(C∣X) in termini di probabilità congiunte, p(clx) =p(c,x)/p(x), l'informazione trasmessa, definita dall'equazione [4], si può porre nella forma simmetrica:

formula [6]

Se x o c sono continue, le somme corrispondenti sono sostituite da integrali. L'informazione trasmessa è spesso chiamata informazione mutua di X e C.

Infine, i valori che otteniamo per l'entropia e per l'informazione dipenderanno, in generale, dal modo in cui suddividiamo in intervalli i valori osservati. Se c'è una certa informazione contenuta nella variazione di un segnale misurato con una data risoluzione (per esempio, pari all'1% del suo valore medio), ma raggruppiamo i segnali in intervalli lO volte più grandi, la nostra stima dell'informazione trasmessa sarà minore del valore corretto. Questo punto può sembrare banale, ma ci fornisce uno strumento per valutare la codifica: confrontando i risultati ottenuti per diverse dimensioni degli intervalli, possiamo determinare quanta dell'informazione totale venga codificata ai diversi livelli di risoluzione.

Questa osservazione si può estendere dalla semplice variazione nella suddivisione in intervalli a ogni aspetto della codifica. Per esempio, se parliamo di neuroni, il messaggio completo è costituito dall'insieme dei tempi di emissione neuronali. Altre rappresentazioni del messaggio (per esempio la frequenza di emissione) possono condurre a valori minori per l'informazione trasmessa, ma non a valori maggiori. Supponiamo di trovare che la frequenza di emissione veicola n₁ bit di informazione su uno stimolo (mediando su un certo intervallo di tempo), e che l'informazione totale contenuta nella sequenza di impulsi è di n₂ bit. Allora ne segue che n₂ - n₁ bit sono codificati in qualche aspetto legato alla temporizzazione degli impulsi. In linea di principio, elaborando ulteriormente questo tipo di ragionamento, siamo in grado di stabilire in che modo l'informazione sia codificata nella sequenza di impulsi. La teoria dell'informazione non fa alcuna ipotesi (per esempio, la linearità) sui meccanismi fisici attraverso i quali si codificano i messaggi, e questo è al tempo stesso un vantaggio (poiché, in effetti, di questi meccanismi si sa poco) e uno svantaggio (poiché la teoria non ci dice nulla in proposito).

Considerazioni statistiche

Tutti gli studi nel campo della teoria dell'informazione sono frnalizzati a effettuare inferenze statistiche affidabili a partire da quantità limitate di dati. Il problema fondamentale è che le probabilità condizionali o congiunte, che figurano nelle espressioni dell'informazione, vanno stimate a partire dalle frequenze di particolari coppie stimolo-risposta (ovvero condizione-segnale) osservate sperimentalmente. Se lo stimolo e la risposta hanno molti gradi di libertà e sono specificati con elevata precisione, o si verifica anche una sola delle due condizioni, corrispondentemente vi saranno molti intervalli in cui ripartire i dati, e avremo bisogno di molti eventi in ciascun intervallo, per ottenere una buona stima delle probabilità. l campioni piccoli distorcono sempre l'entropia condizionata, spingendola verso valori bassi, e quindi distorcono l'informazione trasmessa, portando la a valori più alti. Lo stesso effetto distorce anche la stima dell'entropia a priori, ma non in maniera così drammatica come per l'entropia condizionata, poiché nel calcolo i dati sono classificati in funzione dello stimolo o della risposta, non di entrambi.

Per capire da cosa tragga origine questa distorsione, consideriamo una variabile casuale distribuita in modo uniforme in un certo intervallo. Supponiamo di organizzare le misure di questa grandezza in un certo numero N (grande) di intervalli della stessa dimensione. Se avessimo a disposizione un numero infrnito di dati, otterremmo un valore logN per l' entropia, poiché tutti gli intervalli hanno la stessa probabilità, l/N. D'altra parte, per qualsiasi dimensione finita del campione vi saranno certamente delle variazioni casuali nelle popolazioni dei vari intervalli, e questo porta a una sotto stima dell' entropia. Gli effetti legati alla dimensione finita del campione, perciò, non introducono soltanto incertezza nelle nostre stime dell'informazione trasmessa, ma le distorcono anche sistematicamente verso valori più alti. La contromisura ovvia consiste nell 'usare intervalli più grandi, in modo che la dimensione relativa delle fluttuazioni nelle popolazioni di un intervallo sia minore. Il prezzo da pagare è una minore risoluzione: potremmo perdere dell'informazione effettivamente presente nei dati. Analoghe considerazioni si applicano ad altre stime, diverse dalla semplice suddivisione in intervalli. Ne passeremo in rassegna alcune in seguito. È chiaro che c'è bisogno di un criterio sia per scegliere in modo ottimale la dimensione dell'intervallo sia per correggere la stima ottenuta a partire da una data dimensione di questo.

Convalida incrociata e verosimiglianza logaritmica

Il metodo standard per scegliere in modo ottimale la dimensione dell'intervallo prevede la cosiddetta convalida incrociata (cross-validation; Stone, 1974). La descrizione che ne daremo è formulata in termini della scelta ottimale della dimensione dell'intervallo, ma l'argomento che porteremo si generalizza facilmente ad altri casi. L'idea di base consiste nel verificare la qualità delle probabilità stimate utilizzando dati indipendenti. Supponiamo dunque di avere due insiemi di dati: i dati di addestramento, utilizzati per ricavare le stime delle probabilità condizionate o congiunte per i diversi intervalli, e i dati di prova. Consideriamo, per semplicità, un problema di classificazione binaria. Possiamo semplicemente passare in rassegna i dati di prova e contare quante volte, nell'intervallo in questione, la classificazione nota è in disaccordo con la maggioranza dei valori dei dati di addestramento. Il tasso di errore sarà alto sia se gli intervalli sono molto piccoli (poiché la previsione derivata dai dati di addestramento sarà basata su una statistica insufficiente), sia se essi sono molto grandi (poiché si perde la dipendenza sistematica delle probabilità dalla variabile rispetto alla quale è stata effettuata la suddivisione in intervalli). Il tasso di errore avrà un valore minimo per qualche dimensione intermedia dell'intervallo e per calcolare l'informazione dovremmo usare proprio tale dimensione.

Rimane il problema che, come la dimensione finita dell'insieme di addestramento porta a stime inaffidabili delle probabilità, così la dimensione frnita dell'insieme di prova porta a stime inaffidabili del tasso di errore. Questo problema si può affrontare mediando sui diversi modi in cui l'insieme totale dei dati disponibili si può suddividere nei due insiemi di addestramento e di prova.

Il tasso di errore che abbiamo definito non è la sola misura possibile della qualità delle stime di probabilità. Un'altra misura usata spesso è la verosimiglianza logaritmica dei dati di prova. Consideriamo un semplice esempio di classificazione binaria: supponiamo che per alcuni valori di una variabile casuale, x, una classe sia più probabile, mentre per altri valori sia più probabile l'altra. Per semplicità, consideriamo una x discreta; se x è continua, possiamo raggruppare i dati in intervalli e procedere come nel caso discreto. Abbiamo a disposizione la classificazione corretta (c = ±) per un insieme di valori, scelti a caso, di x. Per stimare le 'vere' probabilità condizionate p(clx) utilizzando questi dati possiamo costruire una stima di p(clx), che chiameremo p̂(+lx), uguale alla frazione di dati (per quel valore della x) per cui sappiamo che la classe è +. Ora, per ogni esempio di prova {xi,ci}, consideriamo la probabilità che una classificazione effettuata a caso sulla base delle probabilità stimate p(clxi) sia in accordo con quell'esempio. Questa probabilità non è altro che p(cilxi). Un'idonea misura di qualità è la probabilità di accordo su tutti gli esempi dell'insieme di prova, e, nel caso di esempi indipendenti, questa grandezza non è altro che il prodotto delle probabilità dei singoli esempi. In modo equivalente, possiamo usare il logaritmo di questa quantità,

formula [7]

che prende il nome di verosimiglianza logaritmica dei dati. Se L_prova è grande, le stime sono buone; se è piccola, sono cattive. Se vogliamo continuare a parlare in termini di un errore sull'insieme di prova, possiamo usare Eprova = -Lprova come misura dell'errore. Nei calcoli che seguiranno useremo questa misura.

Vincoli fondamentali sulla trasmissione dell'informazione da parte dei neuroni

Come abbiamo già notato, la capacità dei neuroni di sfruttare i gradi di libertà temporali nelle sequenze di impulsi per costruire rappresentazioni più ricche, e perciò più efficienti, dipende sia dalla possibilità che i tempi di emissione degli impulsi codifichino effettivamente ulteriore informazione, sia dal fatto che la bio fisica dei neuroni permetta, in qualche modo, di 'leggere' tale informazione. Il primo di questi problemi fu affrontato da D.M. McKay e W.S. McCulloch (McKaye McCulloch, 1952) appena pochi anni dopo l'avvento della teoria dell'informazione. Essi formularono il problema nel modo seguente: trascurando tutti i problemi relativi alla decodificabilità dei segnali neuronali, qual è la frequenza massima alla quale i neuroni possono trasmettere informazione? La risposta è semplice: un neurone può, al massimo, emettere impulsi circa una volta al millisecondo, e ognuno di questi eventi di emissione (o non emissione) veicola l bit di informazione, cosicché la frequenza massima è di 1000 bit/s. Questa è però una sovrastima, poiché si ipotizza che un neurone emetta con una probabilità a priori del 50% in qualsiasi intervallo di l ms, e questo è impossibile dal punto di vista energetico. In realtà, 100 impulsi al secondo rappresentano una frequenza di emissione molto alta, poiché le frequenze tipiche dell'attività corticale sono comprese tra 1 e 10 impulsi al secondo. Un limite superiore all'informazione estraibile da una sequenza di impulsi in un dato intervallo di tempo è imposto dalla sua entropia a priori,

H₀ = -plogp- (1-p)log (1-p), [8]

in cui p è la probabilità di emettere nell'intervallo dato. Considerando intervalli di 1 ms, una tipica frequenza media di emissione di 30 impulsi al secondo (p = 0,03) fornisce un tasso di informazione massimo di 210 bit/s. In questa stima si ipotizza che le sequenze di impulsi siano processi di Poisson. Qualsiasi correlazione temporale tra gli impulsi porterà a una diminuzione delle frequenze massime, ma questi effetti sono piccoli: come abbiamo già notato, le sequenze di impulsi appaiono molto irregolari.

Gli ordini di grandezza di questi limiti sono più alti rispetto ai valori ottenibili da un singolo neurone che usi la sola codifica basata sulla frequenza. Per esempio, consideriamo le cellule semplici, sensibili all'orientazione, del tipo di quelle trovate per la prima volta da Rubel e Wiesel nella corteccia visiva. In condizioni normali, l'occhio rimane fermo in una data posizione per circa mezzo secondo; il passaggio dall'una all'altra di queste posizioni avviene con movimenti oculari rapidi, chiamati movimenti saccadici. Tra due movimenti saccadici, un neurone tipico può emettere impulsi per 16 ± 4 volte, fornendo a una persona (ovvero ai neuroni a valle) una quantità media di 2 bit di informazione, ovvero una frequenza di 4 bit/s. Vedremo più avanti che i valori misurati si discostano leggermente da quelli ipotizzati, essendo inferiori alla stima, probabilmente, per un fattore 2 o 3. Comunque, in qualsiasi modo la otteniamo, la frequenza risulta inferiore per un paio di ordini di grandezza rispetto alla frequenza a cui i neuroni sono capaci di trasmettere informazione.

Il codice basato sulla frequenza, in questo esempio, fornisce una cattiva prestazione. Ciò è dovuto principalmente al fatto che l'intervallo sul quale si deve stimare la frequenza di emissione a partire dal conteggio degli impulsi (cioè l'intervallo tra i movimenti saccadici) è troppo lungo (mezzo secondo). Intervalli lunghi permettono stime relativamente buone della frequenza di emissione (e quindi una maggiore quantità di informazione trasmessa in ogni intervallo), ma il tasso di trasmissione dell' informazione si riduce, poiché le stime vengono effettuate meno frequentemente. W.R. Softky ha esaminato questo aspetto in modo sistematico. Consideriamo la seguente gamma di possibilità per codificare un messaggio neuronale in un tempo T. A un estremo abbiamo il puro codice binario, all'altro il codice basato esclusivamente sulle frequenze. Possiamo costruire una famiglia intermedia di codici dividendo il tempo totale T in NT intervalli, e utilizzando una codifica basata sulla frequenza all'interno di ogni intervallo. Per sequenze di impulsi casuali, in un intervallo di durata T/NT, le fluttuazioni nel conteggio degli impulsi saranno dell'ordine di √T/N_T. Dunque, il numero effettivo di livelli di frequenza distinguibili è (T/N_T)/ √T/N_T = √T/N_T, e la massima informazione per intervallo è (1/2)log(T/NT). L'informazione totale che si può trasmettere nell'intero periodo è quindi

formula [9]

il fattore logaritmico favorisce gli intervalli lunghi (NT piccoli), ma questo effetto è debole. La dipendenza lineare da NT è decisiva: la funzione I_T(NT) (formula [9]) ha un massimo per NT = T/e, cui corrisponde un'informazione per intervallo di soli (2log 2) -1 = 0,72 bit. Questa stima è molto vicina a un codice puramente binario: dal punto di vista della teoria dell'informazione, il codice basato sulla frequenza non è mai conveniente.

Decodifica neuronale

La discussione precedente si è basata solo sul fatto che i segnali neuronali consistono in sequenze di impulsi, e su alcuni tempi e frequenze caratteristiche associabili a queste sequenze. La considerazione che altri neuroni devono decodificare o elaborare le sequenze di impulsi pone dei vincoli più severi al codice neuronale. Le differenze temporali tra gli impulsi afferenti non possono veicolare informazione funzionalmente rilevante, a meno che non producano output diversi nei neuroni a valle. Sfortunatamente, la nostra comprensione dell'elaborazione al livello del singolo neurone non è ancora abbastanza buona da permetterci di trarre conclusioni chiare su questi vincoli. D'altra parte, ciò che sappiamo è almeno sufficiente a fornirci qualche indizio sui loro effetti.

Neuroni integratori con perdita

Spesso si adotta per un neurone il modello grossolano di un integratore con perdita delle sue correnti sinaptiche di input. Ogni impulso nel segnale presinaptico produce così un salto (con un tempo di crescita pari a una frazione di millisecondo) nel potenziale interno del neurone. Nel modello più semplice si ignora tutta la struttura dell'albero dendritico; si ipotizza che il potenziale sia uniforme ovunque nella cellula, e che i diversi input sinaptici si sommino in modo lineare, determinando simultaneamente i cambiamenti del potenziale sul soma. Si ipotizza quindi che questi cambiamenti del potenziale subiscano un decadimento a causa delle correnti di perdita attraverso la membrana, in un tempo costante, tipicamente di 10÷20 ms. Quando il potenziale raggiunge un particolare valore critico, il neurone emette un impulso, e l'impulso viene trasmesso ad altri neuroni; successivamente, ripristinando si il valore iniziale del potenziale, il ciclo si ripete.

Se i segnali afferenti sono sequenze di impulsi emesse con sufficiente rapidità, allora ha senso parlare difrequenza degli impulsi in un intervallo temporale pari alla costante di tempo della membrana. In questo caso l' output del neurone è, con buona approssimazione, una funzione della frequenza degli impulsi afferenti. Un neurone di questo tipo non può far uso di alcuna struttura temporale più fine; dunque, anche se tale struttura veicolasse informazione, nel senso della teoria dell'informazione, questa non potrebbe avere alcuna rilevanza funzionale. Come vedremo, questo schema è troppo semplificato e può talvolta risultare molto fuorviante, ma offre una giustificazione alle osservazioni secondo le quali, nel cervello, la codifica basata sulla frequenza è molto usata. In effetti, è raro che i neuroni sensoriali corticali emettano abbastanza velocemente da produrre più di pochi impulsi nel tempo di integrazione di un neurone ricevente (10÷20 ms), cosicché il concetto stesso di frequenza viene messo in discussione. Un modo per aggirare questo problema consiste nell'ipotizzare che esistano insiemi di centinaia di neuroni che funzionano tutti allo stesso modo e che realizzano tutti contatti sinaptici con lo stesso insieme di neuroni (Shadlen e Newsome, 1994; 1995). Allora il concetto di frequenza ha senso, ma non è chiaro se tale schema sia corretto o meno.

Neuroni rivelatori di coincidenze temporali

Un'alternativa all'integratore con perdita, spesso proposta, si basa sull'idea del neurone come rivelatore di coincidenze (Abeles, 1991), secondo la quale un neurone emette se gli giunge un numero sufficiente di impulsi in una frazione temporale molto piccola (pochi millisecondi). Questa sensibilità a piccole variazioni temporali degli impulsi afferenti offre la speranza di poter sfruttare le elevate capacità di trasmissione sopra discusse, che non si possono raggiungere mediante una codifica basata solo sulla frequenza. Come si può comprendere tale modalità di elaborazione in termini della bio fisica fondamentale del neurone? Lo schema del semplice integratore con perdita trascura effetti importanti, che potrebbero avere come effetto il funzionamento del neurone come un rivelatore di coincidenze. In primo luogo, assumendo che il neurone sia caratterizzato da un solo potenziale uniforme, vengono trascurati tutti gli effetti della geometria dei dendriti. I modelli hanno mostrato d'altra parte che, in dendriti molto sottili, le diverse correnti sinaptiche possono interagire in modo non banale, con la possibilità di produrre perfino degli impulsi dendritici, a patto di essere quasi simultanee (Softky, 1994). L'effetto che ne risulta dipende da un incremento locale molto elevato del potenziale. Poiché le cariche locali in eccesso, fluite nella cellula negli eventi di trasmissione sinaptica, si diffondono molto velocemente, questi eventi devono essere quasi simultanei per poter interagire (entro millisecondi di differenza l'uno dall'altro, secondo stime derivate da modelli). Sarà molto difficile determinare se queste interazioni sinaptiche abbiano effettivamente luogo e se giochino un ruolo funzionale, poiché non è stato possibile, finora, inserire degli elettrodi nei dendriti molto sottili in cui ci si attende l'effetto.

In secondo luogo, la descrizione semplice che abbiamo fornito del neurone (che abbiamo implicitamente assunto eccitatorio) ignora l' input dai neuroni inibitori circostanti (Shadlen e Newsome, 1994; Softky, 1995). Le sinapsi inibitorie più comuni agiscono mediante 'shunting', creando cioè rapide scariche nella membrana. In questo modo, quando l'inibizione è attiva, la costante di tempo efficace per la scarica della membrana è minore di quanto sarebbe in assenza di inibizione. Softky ha stimato che potrebbe essere di l ms o anche meno, il che permetterebbe al neurone, entro questa tolleranza temporale, di comportarsi essenzialmente come un rivelatore di coincidenze per gli impulsi eccitatori in ingresso.

Non sembra dunque che vi siano forti argomenti, basati sulla conoscenza del modo in cui i neuroni elaborano i loro input, per escludere l'uso di codici che coinvolgano la temporizzazione degli impulsi, anche a una risoluzione dell'ordine del millisecondo. Quello che sembra rumore, nelle sequenze di impulsi dei neuroni corticali, potrebbe essere, in realtà, un qualche tipo di segnale.

Il background storico

Diversi studiosi hanno effettuato, negli anni Cinquanta e Sessanta, misure della trasmissione di informazione da parte di singoli neuroni ma sempre nell'ambito di modelli specifici (fondati in genere sul codice basato sulla frequenza). I primi a tentare una trattazione non vincolata a un modello sono stati R. Eckhorn e B. Pöpel (Eckhorn e Pöpel, 1974; 1975). Questi autori hanno studiato i neuroni del nucleo genicolato laterale del gatto, usando come stimolo una luce lampeggiante in modo casuale. Il calcolo dell'informazione è stato effettuato ricavando separatamente i due termini a secondo membro nell'equazione [4] (entropia a priori ed equivocazione) e valutando ne la differenza. Il tempo era suddiviso di solito in intervalli di 2 ms, e le risposte erano rappresentate da vettori con componenti binarie; il valore l della componente n-esima rappresentava l'esistenza di un impulso nell'n-esimo intervallo di 2 ms, nel periodo in cui era definita la risposta. Proprio la natura impulsiva dello stimolo consentiva l'utilizzo di una rappresentazione binaria. In linea di principio, sarebbe preferibile usare una finestra temporale (corrispondente alla dimensionalità dei vettori) più grande possibile, in modo da cogliere tutte le possibili strutture temporali nel codice, ma questo renderebbe difficile la stima delle probabilità nell'espressione dell' entropia e dell' equivocazione (a partire dalle popolazioni relative delle classi di dati per combinazioni diverse dei vettori degli stimoli e delle risposte). In pratica, per la quantità di dati disponibile fu necessario lavorare con periodi piuttosto brevi, dell' ordine di 20 ms.

Eckhorn e Pöpel hanno trovato tassi di trasmissione intorno ai 30 bitls per le cellule del nucleo genicolato laterale del gatto. Gli stessi autori hanno anche effettuato un'analisi analoga, ma raggruppando in classi le risposte solo rispetto al conteggio totale degli impulsi, cioè secondo un codice basato sulla frequenza. I tassi di trasmissione di informazione così trovati erano solo circa un terzo di quelli trovati utilizzando il codice binario completo a 2 ms di risoluzione. Ciò mostrava che circa due terzi dell'informazione totale era codificata in qualche caratteristica della temporizzazione degli impulsi. Eckhorn e Pöpel hanno in seguito trovato risultati qualitativamente simili per altri tipi di neuroni (Eckhorn et al., 1976). Tutto ciò suggerisce che la codifica temporale sia una caratteristica generale dell'elaborazione neuronale.

Se, da un lato, la semplicità degli stimoli utilizzati ha reso possibile la raccolta di una quantità di dati sufficiente per calcolare l'informazione, dall'altro le sequenze casuali di lampi luminosi non rappresentano stimoli naturali per i neuroni del sistema visivo. Questo inconveniente si può aggirare in due modi. Uno consiste nel rivolgere l'attenzione ad animali con sistemi nervosi relativamente piccoli, per i quali si conoscono in dettaglio le funzioni di molti neuroni e il modo in cui sono connessi. In tal caso si sa esattamente quali sono gli stimoli significativi, e si può sperare di ottenere una caratterizzazione quantitativa e sistematica delle funzioni di un neurone utilizzando stimoli semplici, come vedremo più avanti.

fig. 1

L'altro metodo consiste nel continuare a lavorare con animali complessi, ma usando stimoli più naturali. Questo approccio è stato adottato da Richmond, L.M. Optican e collaboratori, che hanno studiato neuroni nel nucleo genicolato laterale, nella corteccia visiva primaria (area VI) e nella corteccia inferotemporale (IT) di macachi non anestetizzati (Richmond e Optican, 1987; 1990; McClurkin et al., 1991). Come abbiamo già notato, in condizioni normali di attività visiva l'occhio rimane fermo per circa mezzo secondo, tra due movimenti saccadici; in questo periodo è come se si accendesse uno stimolo che rimane stazionario. Richmond e Optican hanno riprodotto questa situazione nei loro esperimenti, sottoponendo il campo recettivo di un neurone a 'lampi' consistenti in immagini stazionarie della durata di 320 ms ciascuna. Sebbene il tempo morto tra due stimoli fosse molto più lungo di quello occorrente per compiere un movimento saccadico, recenti misure (Jin et al., 1995) hanno mostrato che la durata dell'intervallo tra gli stimoli non influenza in modo significativo le risposte, purché si mantenga maggiore o uguale rispetto all'intervallo naturale corrispondente ai movimenti saccadici. Idealmente, sarebbe opportuno utilizzare stimoli naturali, ma per ragioni tecniche ci si limita a pattern geometricamente semplici, costituiti da un insieme di 128 stimoli basati sulle funzioni di Walsh (fig. 1). Questi pattern contengono una struttura spaziale con modulazione in direzioni diverse e su varie scale, cosicché essi costituiscono una prima approssimazione ragionevole per il genere di stimoli con cui il sistema visivo ha a che fare in condizioni normali.

Per calcolare l'informazione trasmessa dalle risposte neuronali a questo insieme di stimoli, Richmond e Optican hanno adottato un metodo leggermente diverso rispetto a quello usato da Eckhorn e Pöpel. Le ragioni sono di natura statistica. Questi autori erano interessati alla struttura temporale nell'intero periodo di risposta, che durava almeno quanto il tempo di attivazione dello stimolo (320 ms). Se suddividiamo il tempo in intervalli di 2 ms, otteniamo 160 intervalli temporali, e quindi 2¹⁶⁰ possibili vettori di risposta a componenti binarie. Bisogna chiaramente scendere a compromessi sulla risoluzione temporale. La soluzione diretta consisterebbe, per esempio, nello scegliere intervalli temporali di 20 ms: con ciò si otterrebbero una complessità computazionale e una quantità di dati confrontabili con quelli dell' esperimento di Eckhom e Pöpel. La scelta degli intervalli può però introdurre errori, perché, a causa del limitato numero di dati, esiste una sensibile dipendenza dalla scelta degli estremi degli intervalli. Richmond e Optican hanno scelto la seguente strategia ad hoc. Partendo da intervalli temporali di l ms, hanno prima eliminato le singolarità degli impulsi eseguendo una media pesata su un intervallo di tempo tipicamente di 5 ms, e hanno ricampionato a intervalli di 5 ms il segnale regolarizzato ottenuto in questo modo. Così la rappresentazione vettoriale a componenti binarie delle risposte, a 320 dimensioni, viene sostituita da una rappresentazione a 64 dimensioni e a valori continui. Gli autori hanno poi effettuato una scomposizione in componenti principali dei dati posti in questa forma, trascurando tutte le componenti principali tranne le prime cinque (o un numero prossimo), ottenendo con ciò una rappresentazione della risposta a cinque dimensioni. Può essere utile a questo punto ricordare in che cosa consista la scomposizione in componenti principali. L'intero insieme di dati si può vedere come una 'nuvola' di punti nello spazio a 64 dimensioni. La direzione in questo spazio lungo la quale la nuvola ha la massima dispersione (in senso quadratico medio) costituisce il primo asse principale; la direzione perpendicolare a questo, con il successivo valore della dispersione in ordine decrescente, è il secondo asse principale, e così via. Se vogliamo una rappresentazione compressa di un insieme di dati, è chiaramente più efficiente fornire le sue componenti lungo alcune tra le prime direzioni: queste prendono il nome di componenti principali. Nei dati in questione, si trovò che la prima componente principale pesava il segnale sempre con lo stesso segno, ovvero risultava fortemente correlata con la frequenza media di emissione. Anche le altre componenti principali avevano dei fattori temporali di peso variabili abbastanza lentamente nel tempo (esibendo tipicamente una struttura temporale su intervalli di 50÷100 ms). Dunque la struttura temporale più forte, nei segnali provenienti da questi neuroni, era a frequenze abbastanza basse (10÷20 Hz).

Partendo da questa rappresentazione della risposta, Richmond e Optican hanno determinato le probabilità congiunte stimolo-risposta p(s,r), che figurano in modo simmetrico nell'equazione [6] per l'informazione trasmessa, nel modo seguente (s indica le classi di stimoli, da l a 128, ed r è un vettore a 5 dimensioni formato dalle prime 5 componenti principali della risposta). Per ogni s, hanno costruito p(s,r) come somma di gaussiane, centrate ognuna in uno dei punti r, nello spazio delle risposte a 5 dimensioni, in cui si è misurata una risposta a quello stimolo. La larghezza delle gaussiane era dell'ordine della distanza tipica tra le coppie di vettori di risposta, cosicché le diverse gaussiane corrispondenti alla stessa classe di stimoli avevano una notevole sovrapposizione, producendo una funzione regolare nello spazio delle risposte. Questo modello per il fit si chiama modello afinestra di Parzen. Con questo fit per p(s,r), e per p(r) = ∑_s-p(s,r), è possibile effettuare numericamente l'ins tegrale a 5 dimensioni su r che figura nell'equazione [6]. Anche se la compressione della risposta a una rappresentazione vettoriale a 5 dimensioni taglia fuori buona parte della struttura temporale fine delle risposte (in effetti è simile a un filtro passa-basso, con un taglio ad almeno 25 Hz), Richmond e Optican hanno trovato che informazione non trascurabile è codificata nella variazione residua, a bassa frequenza, dei segnali e, inoltre, che una parte non trascurabile di questa informazione non è veicolata dal conteggio degli impulsi. Se da un lato una migliore analisi statistica (che descriveremo più avanti) ha ridotto i valori numerici delle loro stime di questa informazione, il fatto che informazione statisticamente significativa venga codificata in base alle temporizzazioni è stato confermato, come vedremo, da lavori successivi. Al contrario di questo filtro passa-basso, il calcolo di Eckhorn e Pöpel realizzava in effetti un filtro passa-alto, con un taglio ad almeno 25 Hz, cosicché i due metodi hanno rivelato codifiche temporali in regimi di frequenza diversi.

l calcoli che abbiamo descritto finora sono basati sull'equazione [4] (Eckhorn e Pöpel) o sull'equazione [6] (Richmond e Optican). La terza possibilità, ovvero quella fornita dall'equazione [5], può offrire ulteriori elementi per comprendere la natura della codifica. In questo caso le probabilità da stimare sono le p(slr), cioè le probabilità delle classi di stimoli condizionate alla risposta. In questo caso, cioè, si vuole risolvere un problema di decodifica: dato che abbiamo osservato una certa risposta r, cosa possiamo dire dello stimolo che l'ha provocata? Specificamente, quali sono le probabilità dei diversi stimoli s? In questo approccio, in effetti, si assume 'il punto di vista dell'organismo', poiché i neuroni che ricevono questi messaggi devono pur decodificarli in qualche modo.

De Ruyter van Steveninck e Bialek hanno adottato questo approccio, lavorando in primo luogo su sistemi nervosi semplici di invertebrati, per i quali potevano essere sicuri della funzione dei neuroni che stavano registrando. Richmond, Hertz e collaboratori hanno impiegato il paradigma di decodifica in ulteriori studi del sistema visivo delle scimmie. Nel seguito di questo saggio focalizzeremo l'attenzione, principalmente, sui risultati ottenuti da questi due gruppi di ricerca.

Neuroni sensoriali specializzati

De Ruyter van Steveninck e Bialek si sono concentrati su un particolare neurone, chiamato Hl, nel sistema visivo di una mosca (Calliphora erythrocephora). È noto che questa cellula è sensibile al movimento orizzontale (nel sistema solidale alla mosca) del campo visivo. La risposta è asimmetrica: un movimento verso l'interno (la direzione preferita della cellula) provoca un'emissione intensa, mentre un movimento verso l'esterno (la direzione nulla) ha poco effetto. La mosca effettua cambiamenti nella direzione di volo, in risposta ai segnali forniti da Hl, entro un tempo pari a circa 30 ms, e in questo intervallo il neurone emette al massimo qualche impulso. Le sequenze di impulsi che provengono da questo neurone devono perciò essere molto ricche di informazione.

Per quantificare la funzione svolta da Hl, de Ruyter van Steveninck e Bialek (1988) hanno presentato alle mosche dei pattern casuali in movimento casuale. La distribuzione delle velocità di questi pattern era gaussiana. La velocità dello stimolo veniva registrata a intervalli di 2 ms, e gli istanti di emissione degli impulsi erano registrati con una precisione di l ms. l dati sono stati suddivisi in registrazioni di 100 ms e, all'interno di ogni registrazione, le risposte sono state classificate secondo i tempi di emissione di un certo numero di impulsi tra quelli emessi per ultimi. Per ogni classe si è effettuato un fit gaussiano della distribuzione di velocità dello stimolo, condizionata alla risposta, utilizzando le matrici di media e covarianza su successioni di stimoli che avevano suscitato le risposte in quella classe. Come abbiamo già discusso, la differenza di entropia (variabilità) tra la distribuzione a priori dello stimolo e quella condizionata all'osservazione di una determinata risposta è l'informazione acquisita dall'osservazione della risposta. In questo schema, il centro della gaussiana (la media condizionata alla risposta) è una decodifica di massima vero simiglianza della risposta, e l'informazione trasmessa si può esprimere analiticamente in termini dei cambiamenti del valore medio e della varianza tra la distribuzione a priori dello stimolo e quella condizionata alla risposta.

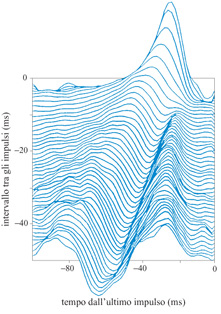
L'esame di pochi casi semplici permette di comprendere il modo in cui Hl codifica gli stimoli. Consideriamo la più semplice classe di risposte: un solo impulso osservato alla fine di una delle registrazioni di 100 ms (questa classe si potrebbe suddividere in sottoclassi secondo lo schema di attività che precede questo impulso finale, ma cominceremo senza alcuna ulteriore suddivisione). Un grafico della velocità media dello stimolo in funzione del tempo, condizionata alla presenza di questo impulso, mostra un picco circa 25 ms prima dell'impulso, con una larghezza di circa 15 ms. Consideriamo ora le risposte in cui non c'era nessun impulso negli ultimi 50 ms. Per queste, la media condizionata della velocità dello stimolo è negativa, cioè il non aver emesso fornisce una dimostrazione del fatto che lo stimolo si stava muovendo nella direzione nulla del neurone. Le risposte in cui l'ultimo impulso si presentava circa 30 ms prima della fine della registrazione mostravano curve della media condizionata della velocità dello stimolo con un picco positivo circa 25 ms prima dell'impulso, e un picco negativo più vicino alla fine dell'intervallo. L'osservazione di un impulso seguito da un periodo di quiescenza dimostra che la velocità dello stimolo è stata positiva, ma probabilmente ha poi cambiato segno.

fig. 2

La decodifica di impulsi relativamente ben separati segue molto bene questo schema generale. La figura (fig. 2) mostra la media condizionata della velocità dello stimolo per coppie di impulsi, in funzione dell'intervallo tra loro. Ogni impulso produce un picco positivo nella curva della velocità dello stimolo circa 25 ms prima della sua comparsa, e gli intervalli sufficientemente lunghi tra gli impulsi producono picchi negativi. D'altra parte, gli impulsi ravvicinati (entro circa 5 ms) producono picchi circa il 50% più alti di quanto si otterrebbe semplicemente sommando i valori delle curve dei singoli impulsi. In queste risposte, quindi, si manifesta chiaramente una codifica non lineare. Inoltre, si osserva che anche il picco negativo nella curva della velocità dello stimolo, condizionata a un periodo senza impulsi che segue una coppia di impulsi ravvicinati, viene amplificato in modo non lineare, prevedendo una velocità negativa particolarmente alta.

Questi risultati permettono di comprendere meglio il problema della precisione della temporizzazione degli impulsi: quanta irregolarità temporale possiamo aggiungere alle sequenze di impulsi, prima di danneggiare seriamente la stima della velocità dello stimolo? La risposta chiaramente non è un singolo numero, ma dipende piuttosto dalla statistica locale della sequenza di impulsi stessa. In altri termini, se gli intervalli tra gli impulsi sono maggiori di 10÷15 ms, un'irregolarità di 5 ms non avrà molto effetto. D'altra parte, se la cellula emette due impulsi a 5 ms l'uno dall'altro, la loro separazione temporale contiene informazione. De Ruyter van Steveninck e Bialek suggeriscono un principio generale, secondo il quale la precisione temporale è proporzionale all'intervallo tra gli impulsi. Merita una particolare attenzione anche il modo in cui l'informazione trasmessa, condizionata allo stimolo, varia con la temporizzazione degli impulsi. Cominciamo di nuovo considerando registrazioni che finiscono con un singolo impulso. L'osservazione di una risposta, in questa classe, porta 0,36 bit di informazione sulla velocità che lo stimolo aveva in precedenza. Se l'impulso è preceduto da un intervallo senza impulsi, di durata to, l'informazione trasmessa che ne risulta è abbastanza bassa (meno di 0,5 bit) per to minore di circa 20 ms. Per valori maggiori di t_o, essa cresce lentamente con t_o. La pendenza con cui cresce (17 bitls) è il tasso al quale l'assenza di emissione veicola informazione. Le risposte che hanno anche un impulso ulteriore a un tempo to prima della fine della registrazione veicolano molta più informazione, se to è piccolo: più di 2 bit se questa separazione è minore di 5 ms, cioè quasi tre volte il valore che ci si aspetterebbe (0,72 bit) se gli impulsi veicolassero informazione in modo indipendente. D'altra parte, se t_o > 20 ms, l'informazione veicolata è la stessa che si avrebbe se il primo impulso non fosse stato emesso: l'informazione aumenta semplicemente al tasso di 17 bit/s, associato all'intervallo di quiescenza di durata t_o.

Si può stimare la trasmissione netta di informazione, fornita dall' equazione [5], mediando i risultati condizionati alla risposta sulla distribuzione delle risposte. Considerando registrazioni dello stimolo di durata 100 ms, e risposte fino a 50 ms, si ottiene un risultato di 87 bit/s.

Questo modo esaustivo per studiare e caratterizzare la trasmissione fornisce una comprensione dettagliata della codifica effettuata da questo neurone, ma si limita a registrazioni di stimolo e risposta abbastanza brevi. In un lavoro successivo, Bialek, de Ruyter van Steveninck e collaboratori (Bialek et al., 1991) hanno adottato un diverso approccio, tentando di stimare la velocità dello stimolo direttamente, sulla base della sequenza di impulsi. Specificamente, la stima della velocità dello stimolo, S_est(t), viene sviluppata in una serie di Taylor rispetto alla risposta r:

formula [10]

Per le sequenze di impulsi, r(t) è semplicemente un insieme di funzioni delta di Dirac in corrispondenza ai tempi di emissione degli impulsi, ti, e quindi

formula [11]

Le funzioni filtro Fn vengono quindi stimate minimizzando l'errore quadratico medio di stima

formula [12]

L'approssimazione lineare, che consiste nel conservare solo il primo termine (quello dipendente da F₁), risulta buona; i termini non lineari che abbiamo discusso per coppie di impulsi ravvicinati non danno un grosso contributo a X².

fig. 3

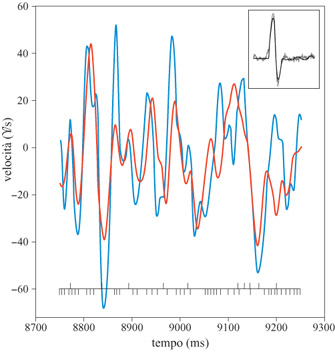
Per effettuare i calcoli, sia lo stimolo che la risposta sono stati sviluppati in componenti di Fourier, effettuando l'analisi separatamente per ogni frequenza. Il metodo è stato applicato a registrazioni della durata di 1 s. Per ognuno di questi intervalli si possono calcolare le componenti di Fourier dell'effettiva velocità dello stimolo, s ̃(ω), e di quella stimata, s ̃_est(ω). Per ogni frequenza ω queste quantità si possono riportare in un grafico, l'una in funzione dell'altra. Le deviazioni di questi dati rispetto a un fit lineare rappresentano un rumore η(ω). Il grafico della distribuzione di η(ω), ottenuto campionando su migliaia di intervalli di 1 s, fornisce, con buon grado di accuratezza, una gaussiana. È istruttivo effettuare l'antitrasformata di Fourier e riportare in un grafico la velocità vera dello stimolo e quella stimata, in funzione del tempo (fig. 3). Le deviazioni sono più marcate per velocità alte, per le quali, come abbiamo già notato, la relazione lineare tra stimolo e risposta non vale più.

Poiché, per come è stato progettato l'esperimento, la distribuzione a priori della velocità dello stimolo era anch' essa gaussiana, tutte le densità di probabilità necessarie per calcolare l'informazione trasmessa sono gaussiane. Per ogni frequenza il calcolo è di tipo standard; il risultato si può semplicemente integrare rispetto alla frequenza, ottenendo:

formula. [13]

Poiché la potenza del segnale, ‹ls ̃(ω)∣²›, e del rumore, ‹lη ̃(ω)∣²›, sono state misurate, nel processo che abbiamo descritto, per ogni frequenza, allo scopo di separare il segnale dal rumore, è semplice calcolare il tasso di trasmissione dell'informazione. Il risultato è 64± l bit/s. Questo valore è alquanto più basso di quello ottenuto mediante l'analisi precedente, forse a causa del fatto che le rare coppie di impulsi ravvicinati, che sono descritte male in questa analisi lineare, quando si presentano portano molta informazione. D'altra parte è confortante il fatto che gli effetti di correlazione tra gli impulsi a tempi lunghi (maggiori di 50 ms), che nell' analisi precedente venivano ignorati, non sono grandi.

Successivamente Bialek e collaboratori hanno effettuato calcoli più completi della trasmissione di informazione da parte di Hl (Strong et al., 1998; v. anche il saggio di W. Bialek, Potenzialità e limitazioni nella misura della trasmissione dell'informazione neuronale), questa volta senza decodifica. In questo calcolo viene valutata, per esempio dall'equazione [4], la differenza tra l'entropia a priori della sequenza di impulsi e l'entropia media, condizionata a una certa registrazione dello stimolo. Sono state utilizzate registrazioni fino a 100 ms e si è posta particolare attenzione per garantire che gli effetti legati alla dimensione frnita del campione non alterassero l'accuratezza della stima. Sia l'entropia a priori che quella condizionata dipendono dalla risoluzione con la quale si misurano i tempi di emissione degli impulsi, per cui i calcoli sono stati effettuati con dimensioni degli intervalli per gli impulsi, Δτ, comprese tra 0,7 e 12 ms. Il tasso risultante di trasmissione dell'informazione varia più o meno logaritmicamente con Δτ, coerentemente con l'ipotesi che la precisione temporale delle risposte scali con l'intervallo tra gli impulsi. In questo modo si trova, alla risoluzione maggiore, un tasso di 90 bit/s.

L'esistenza di rumore impulsivo (shot noise) per i fotoni limita l'informazione totale sulla velocità dello stimolo disponibile sulla griglia dei fotorecettori. Questo limite si può stimare e Hl ne trasmette una frazione notevole. In linea di principio è possibile, sulla base di 30 ms (uno o due impulsi) della sua risposta, stimare l'ampiezza di una variazione di velocità a 20 Hz con una precisione superiore a 0,1°, oltre un ordine di grandezza meno della spaziatura dei fotorecettori. Quindi il neurone si comporta quasi come un canale ottimale, limitato solo da vincoli fisici fondamentali.

Il gruppo di Bialek ha effettuato l'analisi lineare di decodifica anche su vari altri neuroni sensoriali (Rieke et al., 1993). Per i recettori vibrisse della rana toro, il tasso misurato di trasmissione dell'informazione è 155 ± 3 bit/s, e per il neurone del pelo filiforme del grillo risulta di 294 ± 6 bit/s. Questi numeri comprendono piccole correzioni (di poche unità percentuali) che derivano dall'inclusione del termine quadratico nello sviluppo dell' equazione [10]. Dividendo questi tassi per la frequenza di emissione si ottiene il numero di bit per impulso. Il risultato varia tra 2,5 e 3,2 bit per impulso, il che implica che gli intervalli tra gli impulsi devono avere una precisione di 2 o 3 bit. La temporizzazione relativa di una coppia di impulsi separati da 5 ms sembra quindi essere più precisa del millisecondo. Si può ricavare una misura relativa oggettiva dell'efficacia di questi neuroni confrontando l'informazione trasmessa con l'entropia a priori, Ho, delle sequenze di impulsi. Il risultato è che essi trasmettono informazione a un tasso uguale a circa la metà del limite superiore assoluto, fissato dalla loro entropia a priori. Essi, quindi, non aggiungono rumore, come si potrebbe credere; gran parte della variabilità nei loro pattern di emissione viene in effetti utilizzata per veicolare informazione, e la temporizzazione degli impulsi può essere precisa al millisecondo.

Neuroni del sistema visivo dei primati

Richmond e collaboratori, in calcoli svolti nella prima metà degli anni Novanta sulla trasmissione di informazione da parte di neuroni del sistema visivo della scimmia (Hertz et al., 1992; 1995; Kjær et al., 1994; Heller et al., 1995), hanno adottato l'approccio basato sulla decodifica, partendo dall' equazione [5]. Nei loro esperimenti, i diversi pattern di stimolazione vengono presentati con uguali frequenze, in modo che l'entropia a priori H(S) dello stimolo sia data semplicemente dal logaritmo del numero di pattern (7 bit per l'insieme completo di 128 pattern di Walsh). Il problema si riduce quindi a calcolare l'equivocazione H(SIR), il che richiede la conoscenza delle probabilità p(slr) degli stimoli, condizionate alle risposte, delle quali si deve stimare la dipendenza funzionale dalle risposte r.

fig. 4

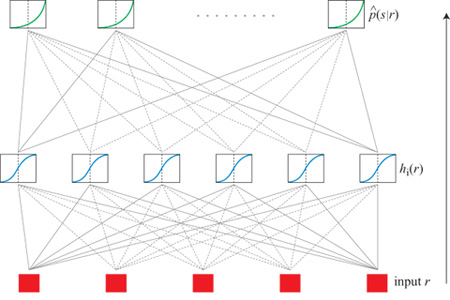
Per effettuare questa stima si è utilizzata una rete neurale artificiale (fig. 4), parametrizzando la forma stimata p̂(slr) come

formula, [14]

dove

formula. [15]

Nell'equazione precedente, rj è la componente j-esima in una qualche rappresentazione della risposta (per esempio quella a componenti principali), e ν_si, wij, b_s e c_i sono i parametri del fit. Nel linguaggio delle reti neurali, rj è il j-esimo input; gli input vengono sommati con i pesi wij e traslati di c_i per fornire l'input netto a un insieme di unità nascoste, i cui output, hi, sono costituiti dalla tangente iperbolica di queste somme pesate e traslate. A loro volta, queste unità nascoste fungono da input a un insieme di unità di output, che effettuano operazioni simili di somma pesata e traslazione sui loro input, calcolano l'esponenziale del risultato e normalizzano il risultato di questa operazione, in modo tale che la somma

delle probabilità stimate per tutti gli stimoli sia 1. A parte quest'ultimo passo, questo modello di rete neurale è quello utilizzato più comunemente in tutte le applicazioni al fit di una qualche funzione. Naturalmente questa rete neurale non ha alcun rapporto con la rete corticale reale nella scimmia. È solo un comodo strumento di analisi statistica. Avendo in mano una forma parametrizzata per p(slr), dobbiamo semplicemente prende re un insieme di risposte r, mediare

su s tali risposte per ricavare H(SIR) e da questa, infine, ottenere l'informazione trasmessa.

I parametri per il fit si trovano attraverso un algoritmo di auto apprendimento, che massimizza la verosimiglianza 10garitmica definita nell'equazione [7] su un insieme di dati campione. Con questo criterio di ottimizzazione, il metodo si riduce a una tecnica standard, la regressione logistica, se non vi siano unità nascoste. La presenza delle unità nascoste consente al modello di rappresentare i possibili effetti di combinazioni non lineari degli input.

Se ci sono abbastanza unità nascoste, il modello definito dalle equazioni [14] e [15] è capace di effettuare il fit di dipendenze funzionali di p(slr) da r arbitrariamente complicate. D'altra parte, un numero elevato di parametri richiede una quantità elevata di dati per determinarli, e il fit è stato controllato mediante convalida incrociata. In questo caso, invece della dimensione della classe, come nel caso che abbiamo discusso prima, i parametri controllati erano il numero di unità nascoste, il numero (e il tipo) di input utilizzati per rappresentare la risposta e il tempo di arresto. Con il termine tempo di arresto intendiamo quanto segue: per valori dati della dimensionalità dell'input e del numero di unità nascoste, la rete potrebbe essere capace di adattarsi a una struttura più ricca di quella effettivamente presente nei dati. Perciò, via via che l'algoritmo viene iterato, e l'errore sull'insieme di addestramento, -L_add, diminuisce, potremmo raggiungere un punto in cui cominciamo a fare il fit del rumore presente nei dati, invece che della vera relazione sistematica tra stimolo e risposta. Ci si guarda da questo effetto controllando l'errore, -L_prova, compiuto su una porzione dei dati separata dall'insieme campione. Ripetendo la procedura molte volte, e con molti insiemi di prova diversi, possiamo determinare il tempo di arresto ottimale. I parametri, a questo punto dell'addestramento, definiscono la migliore stima p̂(slr). Si è anche provato un approccio più convenzionale (il decadimento dei pesi) per evitare questo effetto di 'overfit', e si è trovato che esso fornisce essenzialmente gli stessi risultati ottenuti con questo metodo di arresto precoce. Quest'ultimo richiede però calcoli meno pesanti, e perciò è stato utilizzato nella maggior parte dei casi.

Non c'è nessuna ragione particolare per effettuare un fit utilizzando tangenti iperboliche ed esponenziali, come nelle equazioni [14] e [15]. In effetti si sono provate diverse forme, incluse alcune che includevano gaussiane normalizzate al posto degli esponenziali normalizzati. In assenza di unità nascoste, anche questo è un metodo statistico standard, detto modello a gaussiane miste. Inoltre, il modello a finestra di Parzen utilizzato nel lavoro originale di Richmond e Optican si può realizzare tramite una rete neurale. Abbiamo provato tutte queste alternative, ottimizzandole mediante convalida incrociata e confrontando le versioni ottimali con la rete ottimale della forma dettata dalle equazioni [14] e [15], cioè paragonando i valori di -L_prova. Nessuna di queste alternative ha fornito un fit migliore rispetto alle equazioni [14] e [15], e perciò abbiamo usato questa rete in tutti i calcoli successivi.

Finora non abbiamo detto nulla sulla rappresentazione della risposta. Quella più diretta consiste in una rappresentazione vettoriale a componenti binarie, con l come n-esima componente se c'è un impulso ne II ' n-esimo intervallo temporale. Un'altra utilizza la 'regolarizzazione' (smoothing) della sequenza di impulsi e le componenti principali, come nel lavoro di Richmond e Optican che abbiamo descritto. Una terza possibilità consiste nel fermarsi dopo la fase di regolarizzazione e ricampionamento, e utilizzare i dati in questa forma. Vi sono anche altre possibilità: usare i tempi di emissione degli impulsi, gli intervalli tra gli impulsi, i loro reciproci, o sotto insiemi di questi (come per esempio il primo tempo di emissione). Infine, è utile effettuare i calcoli rappresentando la risposta solo tramite il conteggio degli impulsi, per determinare quanta informazione aggiuntiva viene veicolata (se ciò accade) dalla struttura temporale della risposta.

Con l'eccezione del vettore a componenti binarie e della lista completa dei tempi di emissione, tutte queste rappresentazioni non tengono conto di una certa quantità di informazione. Perciò, se troviamo la stessa informazione trasmessa in due diverse rappresentazioni, per una delle quali è stato rimosso qualche aspetto della risposta (per esempio, attraverso un filtro passa-basso), possiamo concludere che nessuna informazione viene trasmessa dalla parte della risposta che era stata filtrata.

J. Heller e collaboratori (1995) hanno studiato molte di queste rappresentazioni, sia per neuroni in VI che in IT, confrontandole sulla base dell'errore di prova medio. Gli stimoli erano i primi 32 raggruppamenti dei pattern di Walsh che abbiamo descritto (i più grossolani). Sono state esaminate porzioni della risposta di varie lunghezze, comprese tra 16 e 320 ms, e si è trovato che per periodi più brevi di 25 ms, in VI, nessuna rappresentazione era apprezzabilmente migliore rispetto al conteggio degli impulsi per ogni singolo neurone.

Per porzioni più lunghe della risposta si è trovato, coerentemente, che la migliore rappresentazione consisteva in un numero compreso tra l e 5 di componenti principali della risposta regolarizzata, oltre al conteggio degli impulsi. Il numero ottimale di componenti principali variava da neurone a neurone, ma tanto più lungo era l'intervallo, tanto più risultava utile un numero elevato di componenti. Poiché sia la regolarizzazione che la trasformazione nelle componenti principali sono delle forme di filtro passa-basso, questo risultato indica che la parte più ricca di informazione, nella struttura temporale della risposta, è a basse frequenze.

fig. 5

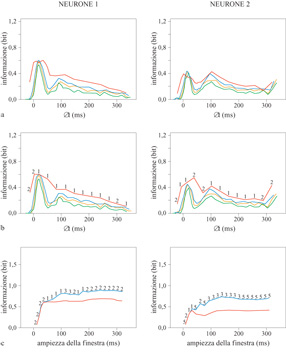
D'altra parte l'ampiezza della finestra temporale sulla quale venivano regolarizzate le risposte, prima di effettuare la trasformazione nelle componenti principali, sembrava comportare una piccola ma sistematica differenza nel valore medio dell'errore di prova e dell'informazione trasmessa. I risultati migliori si sono ottenuti con una larghezza a mezza altezza di 5 ms, il che suggerisce che un tale livello di precisione nella temporizzazione potrebbe veicolare l'informazione. Precisioni di questo stesso ordine sono state riscontrate nel ritardo di emissione del primo impulso dei neuroni dell'area MT (un'area sensibile al movimento) delle scimmie (Bair e Koch, 1996). D'altra parte, nei dati analizzati da Heller e collaboratori, l'informazione aggiuntiva associata a una precisione di 5÷10 ms nella temporizzazione degli impulsi sembra piccola (circa il 5% del totale). Saranno necessari studi ulteriori, e un numero maggiore di dati, per capire in quale misura questi neuroni utilizzano una tale precisione. Nella corteccia IT accadono quasi le stesse cose, a parte il fatto che tutte le scale dei tempi sono incrementate di circa un fattore 2. Si è osservato che l'informazione totale veicolata dai diversi neuroni sul periodo di risposta (320 ms) variava tra 0,1 e l bit, di cui in media il 75% (per VI) o 1'85% (per IT) era contenuto nel conteggio degli impulsi. La popolazione di neuroni era abbastanza eterogenea; per alcuni neuroni l'informazione codificata temporalmente era trascurabile, mentre per altri risultava quasi pari a quella contenuta nel conteggio degli impulsi. In tutti i neuroni analizzati, se si fa scorrere una finestra mobile di 16 ms attraverso le risposte e si segue l'andamento temporale dell'informazione trasmessa, si trova un grosso picco nei primi 50 ms (fig. 5). Infatti il conteggio degli impulsi in questa sola scarica contiene la maggior parte dell'informazione disponibile in tutti i 320 ms della risposta (tipicamente i 3/4). Un risultato simile è stato ottenuto anche da Tovée e collaboratori (1993) in IT, con stimoli diversi, che comprendevano anche facce di scimmie e di esseri umani. Comunque l'informazione codificata temporalmente, sia all'interno di questa finestra che nel resto della risposta, è statisticamente significativa. Se convertiamo l'informazione in questa finestra temporale in un tasso di trasmissione, dividendola per l'ampiezza della finestra, otteniamo delle frequenze massime fino a 30 bit al secondo. Nella maggior parte dei neuroni c'è un secondo picco nell'informazione che si presenta in qualche punto tra i 50 e i 200 ms dopo quello iniziale. Effettuando i calcoli per l'informazione, con la risposta rappresentata una prima volta dal conteggio degli impulsi in una finestra centrata sul primo picco, e una seconda volta dai conteggi in una coppia di finestre centrate sui due picchi, si può determinare se il secondo picco ha veicolato nuova informazione, o se ha semplicemente ripetuto il messaggio del primo. I risultati variano da cellula a cellula, ma in media, in VI, circa la metà dell'informazione nella seconda scarica è nuova. Questa frazione è leggermente più alta in IT.

fig. 6

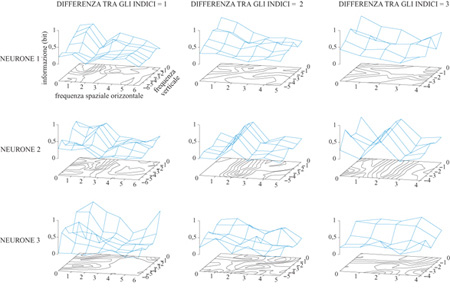
In un'altra serie di calcoli, T.W. Kjær e collaboratori (Kjær et al., 1994) si sono concentrati sul problema del contenuto di questi messaggi neuronali. Questi autori hanno effettuato i calcoli che abbiamo descritto per un sottoinsieme di stimoli all'interno dell'insieme di Walsh (considerando sempre la risposta su tutti i 320 ms). Guardando il modo in cui l'informazione trasmessa variava con le caratteristiche spaziali dei diversi insiemi, essi hanno potuto dare una descrizione sistematica delle caratteristiche spaziali sulle quali questi neuroni trasmettevano informazione. I sotto insiemi venivano scelti nel modo seguente. Nell'insieme degli stimoli di Walsh completo, consideriamo quello composto da quattro quadrati adiacenti, più i corrispondenti invertiti (v. figura 1). Un tale insieme possiede caratteristiche spaziali strutturali in entrambe le direzioni (orizzontale e verticale) su una scala di lunghezza caratteristica. Se si trova che le risposte neuronali veicolano informazione significativa su questo insieme, si può pensare al neurone come a un rivelatore di caratteristiche su quella scala. Spostando l'insieme studiato nello spazio di Walsh, e costruendo le curve di livello dell'informazione trasmessa, si ottiene una rappresentazione del tipo di caratteristiche prese in considerazione dai messaggi neuronali (fig. 6).

Un particolare neurone potrebbe non avere risoluzione sufficiente per rispondere in modo molto diverso a pattern che sono adiacenti nello spazio di Walsh. Tuttavia ciò potrebbe accadere se il sottoinsieme di pattern per i quali si era calcolata una prima volta l'informazione trasmessa avesse caratteristiche spaziali su scale maggiormente differenziate. Perciò Kjær e collaboratori hanno effettuato gli stessi calcoli per insiemi di stimoli per i quali la differenza di indice di Walsh era anche pari a 2 o 3 (al posto del valore l, come nel caso precedente) nella direzione orizzontale, o in quella verticale, o in entrambe.

Le curve di livello trovate erano eterogenee, e mostravano diversi tipi di strutture. In un'interpretazione in termini di rivelatore di caratteristiche, queste cellule in genere rivelano diverse caratteristiche spaziali a diverse scale di approssimazione. I tipi più comuni di strutture osservate erano crinali e altipiani che si estendevano lungo una direzione nello spazio di Walsh. In confronto, dei picchi localizzati comparivano più raramente. La sensibilità dell'informazione trasmessa rispetto agli spostamenti perpendicolari a un crinale indica, in accordo con quanto trovato da Rubel e Wiesel (e, successivamente, da molti altri studiosi), che questi neuroni tendono a essere selettivi rispetto all'orientazione degli oggetti nel campo visivo. D'altra parte, la relativa 'dolcezza' del crinale indica un'insensibilità alla modulazione spaziale in quella direzione. Lavori successivi di T.I. Gawne e collaboratori (Gawne et al., 1996b) hanno esteso questi risultati: sembra che per questi neuroni (cellule complesse, nella classificazione di Rubel e Wiesel) la struttura all'interno delle barre orientate venga codificata più nel ritardo della risposta che nella sua intensità complessiva.

Problemi statistici

In molti dei risultati che abbiamo descritto, appare evidente che è veicolata più informazione nelle rappresentazioni in cui l'informazione era stata filtrata dalle risposte (come quelle che impiegano le componenti principali), che in quelle che contengono, in linea di principio, tutta l'informazione (come il vettore a componenti binarie completo). Ciò non si verificherebbe se le risposte fossero prive di rumore, ma in presenza di rumore la procedura di convalida incrociata scarta in effetti le componenti della risposta per le quali il segnale è dominato dal rumore (in questo caso quelle ad alta frequenza). Non possiamo quindi dire che non ci sia trasmissione di informazione in queste componenti; possiamo solo dire che non abbiamo abbastanza dati per determinare se c'è. D'altra parte, il fatto che non la possiamo vedere nei dati che abbiamo pone dei limiti sulla sua possibile entità.

Kjær e collaboratori (Kjær et al., 1994) hanno svolto uno studio del problema, limitato ai pochi neuroni per i quali avevano il maggior numero di prove (32 per ogni stimolo), effettuando i calcoli su sotto insiemi dei loro dati. Per sottoinsiemi più piccoli risulta difficile estrarre il segnale dal rumore, e l'informazione trasmessa risulta, di conseguenza, minore. L'informazione estratta da una componente principale della risposta raggiunge un valore limite per dimensioni degli insiemi di dati superiori a circa 10 prove ripetute per stimolo, ma con 5 componenti la saturazione non è evidente neppure con 32 prove ripetute per stimolo. Un'analisi più sistematica è stata effettuata recentemente da Golomb e collaboratori (Golomb et al., 1996) su dati artificiali, ma realistici. Le sequenze di impulsi utilizzate sono state generate da un modello (Golomb et al., 1994) basato sui campi recettivi spazio-temporali misurati per il nucleo genicolato laterale (Reid e Shapley, 1992). È stato possibile generare insiemi di dati arbitrariamente grandi e calcolare l'informazione trasmessa per le componenti principali della risposta, fino alla terza componente principale, con un'accuratezza superiore a 0,01 bit, usando una semplice suddivisione in intervalli su 10⁶ prove. Quindi si è potuto effettuare il calcolo basato sull 'uso della rete, come per i dati reali, e confrontare il risultato con quello 'quasi' esatto.

I risultati hanno indicato che il numero di prove per stimolo necessarie a stimare bene l'informazione trasmessa, usando il calcolo basato sulla rete neurale, è approssimativamente uguale alla dimensione dell'insieme degli stimoli (32, in questo caso). Quando il metodo sbaglia, ciò è dovuto invariabilmente a una sotto stima dell'informazione. Questa è una conseguenza della natura conservativa della strategia di convalida incrociata: tale strategia assicura che non si possa scambiare il rumore con una struttura sistematica. Risultati quasi identici sono stati ottenuti (con un tempo di calcolo inferiore di ordini di grandezza) attraverso una procedura di suddivisione in classi più sofisticata (Panzeri e Treves, 1996), usando classi ugualmente popolate, e un'opportuna correzione per la dimensione finita del campione. Questo metodo non usa la decodifica; segue cioè l'equazione [4], calcolando l' entropia incondizionata e quella della risposta condizionata alla stimolo, e sottraendo la seconda dalla prima. Con qualsiasi metodo si è visto che si può calcolare l'informazione codificata temporalmente con un'accuratezza di 0,05÷0,1 bit: circa il 10% dell'informazione trasmessa in totale, sulla base di 64 prove ripetute per stimolo (il doppio del numero degli stimoli).

Codifica a più neuroni

Le misure su neuroni singoli sono solo l'inizio nell'esplorazione di un sistema che è, dopo tutto, una rete di miliardi di unità interagenti. Gawne e collaboratori (Gawne e Richmond, 1993; Gawne et al., 1996a) hanno fatto un primo passo verso la comprensione del modo in cui gruppi di neuroni codifichino informazione, con i loro studi di coppie di neuroni adiacenti nelle aree VI e 1T delle scimmie reso. In questo ambito definiamo adiacenti due cellule che vengono registrate dallo stesso elettrodo; i due tipi di impulsi sono distinti attraverso le diverse forme che presentano su scale temporali inferiori al millisecondo. l pattern di stimolazione utilizzati ne includevano alcuni simili a barre orientate, oltre all'insieme di Walsh.

In termini qualitativi, vi sono tre tipi di codice che potremmo osservare in una coppia di neuroni. Il primo è un codice ridondante, in cui i due neuroni mandano lo stesso messaggio; solo i loro rumori sono diversi. Questo è un codice che è naturale aspettarsi, se si parte con l'ipotesi che i neuroni siano intrinsecamente affetti da rumore; per vincere il rumore si usa una forma di multiplex del segnale. La seconda possibilità, quella di un codice indipendente, si presenta nel caso in cui i due neuroni inviano messaggi essenzialmente diversi. Questo è quanto ci aspetteremmo dal principio di rappresentazione efficiente (Barlow, 1961; 1981) se il rumore intrinseco è basso. Infine, i due neuroni potrebbero veicolare un messaggio che non si può estrarre da nessuno di essi separatamente, cioè un codice congiunto. Questa sarebbe la situazione, per esempio, se i messaggi venissero veicolati dalla sincronizzazione degli impulsi. l diversi casi si possono descrivere in termini di teoria dell' informazione, considerando l'informazione trasmessa da ogni neurone separatamente, e quella trasmessa dai due congiuntamente. In termini della rete di decodifica che abbiamo descritto, questo significa che il calcolo viene effettuato utilizzando una rete in cui alcuni input rappresentano la risposta di un neurone, mentre gli altri input rappresentano la risposta dell'altro. Indicando i due neuroni con le lettere A e B, chiamando rispettivamente lA e IB le quantità di informazione che essi veicolano separatamente e indicando l'informazione contenuta nel loro segnale congiunto con IAB, i tre casi corrispondono a IAB=max(IA,IB) (codice ridondante), IAB = lA + IB (codice indipendente) e, infine, IAB > lA + IB (codice congiunto). Naturalmente, sono anche possibili casi intermedi. Il risultato principale è che il codice è in buona approssimazione un codice indipendente. La media sulla popolazione di cellule del rapporto

formula [16]

vale 0,9, sia in VI che in IT. In altri termini, il 20% dell' informazione congiunta totale è condivisa. Studi in altre parti del sistema visivo, e in altri animali (Ghose et al., 1993; Maldonado e Gray, 1994) sono almeno qualitativamente in accordo con l'ipotesi che questo livello di indipendenza sia caratteristico della corteccia. Questi risultati suggeriscono che i neuroni corti cali non siano fonte di eccessivo rumore e che, di conseguenza, il sistema sfrutti soprattutto l'ampia banda resa disponibile dalla presenza di molti di loro.

Lo studio di animali più semplici, come avviene al livello del singolo neurone, può fornire un'opportunità per una descrizione più completa e sistematica di esempi particolari di codifica a più neuroni. G.A. Miller e i suoi collaboratori (Miller et al., 1991; Theunissen e Miller, 1991) hanno compiuto uno studio sistematico della codifica congiunta dell'informazione sulla direzione del vento da parte di un insieme di 4 neuroni nel sistema dei cerci del grillo. Questi autori hanno scoperto che le posizioni e le ampiezze dei campi recettivi dei neuroni, in funzione dell'angolo di direzione del vento, sono nell'insieme quasi ottimali per massimizzare la trasmissione di questa informazione. Vi sono anche, in altri contesti, risultati indicativi dell 'uso di un codice ridondante o congiunto. Nella corteccia motoria è ben noto che le somme pesate delle frequenze di emissione di neuroni sensibili alla direzione predicono con accuratezza i movimenti, cioè si usa una codifica basata sul numero di impulsi (Georgopoulos et al., 1993). Nel sistema visivo vi sono prove di una simile codifica delle caratteristiche delle facce nella corteccia 1T (Gochin et al., 1994).

Un esempio di codifica congiunta è dato dalla sincronizzazione delle risposte oscillatorie dei neuroni quando i loro campi recettivi giacciono all'interno dello stesso oggetto nel campo visivo (Singer, 1993). Gli oggetti, in questi esperimenti, sono regioni che contengono pattern di intensità in movimento, modulati sinusoidalmente. Se opportunamente regolati in orientazione, frequenza spaziale e velocità di spostamento, questi pattern possono suscitare risposte oscillatorie forti (pur se intermittenti) da cellule corticali visive, e le fasi di queste risposte non sono fissate dalla modulazione dello stimolo. Si trova che le fasi delle oscillazioni di neuroni diversi sono le stesse se i loro campi recettivi cadono all'interno dello stesso oggetto, ma non lo sono se cadono su oggetti diversi. La risposta di una cellula qualsiasi codifica solo il tipo di oggetto presente (la sua orientazione, la sua grandezza e la velocità di spostamento). Non codifica nulla circa la dimensione, la forma e i bordi dell'oggetto. Si potrebbe immaginare che vi siano altre cellule che fanno questo, ma il compito combinatorio è immenso: dovrebbero esserci neuroni per tutte le forme e le posizioni distinguibili, ma non è stato identificato alcun neurone di questo tipo. Sembra invece che la segmentazione della scena visiva in oggetti sia codificata nel modo in cui viene fissata la fase delle oscillazioni.

Non si sa quanto questo meccanismo di codifica sia generale. Negli esperimenti con stimoli costituiti da 'lampi' stazionari, come quelli di Richmond e Optican che abbiamo descritto (che simulano meglio le condizioni visive nel riconoscimento di oggetti naturali), non sono state osservate oscillazioni; probabilmente, in questo caso, questo particolare meccanismo non è disponibile. Anche nei casi in cui si producono delle oscillazioni, non sappiamo se esse siano essenziali per il meccanismo di codifica, o se siano solo un fattore secondario.

Un caso di sincronizzazione in assenza di oscillazioni è stato osservato recentemente nella corteccia uditiva della scimmia (deCharms e Merzenich, 1996). Si è trovato che il grado di sincronizzazione nell'emissione di neuroni diversi segnala la presenza di uno stimolo, anche nei casi in cui le loro frequenze di emissione non veicolano alcuna informazione. L'effetto è debole per una sola coppia di neuroni, ma si può ottenere un'informazione significativa dal grado di sincronizzazione di popolazioni maggiori. Questo sistema impiega dunque una codifica basata sul numero di impulsi, ma la variabile da sommare sui neuroni è il grado di correlazione degli impulsi, invece della frequenza di emissione.

Conclusioni

In apparenza, i due tipi di neuroni studiati in queste ricerche sembrano avere modi di trasmettere informazione piuttosto diversi. I neuroni sensoriali specializzati (principalmente negli invertebrati) sembrano essere vettori di informazione molto efficienti, veicolando circa 3 bit per impulso, e mantenendo tassi di trasmissione stabili alla metà o più del limite superiore fissato dalle entropie delle loro sequenze di impulsi. Se da un lato essi codificano la maggior parte dell'informazione a una risoluzione temporale meno fine di 10 ms, anche la temporizzazione degli impulsi al livello di l ms porta con sé dell'informazione misurabile, almeno nella cellula Hl della mosca. Al contrario, i neuroni del sistema visivo dei primati non sembrano veicolare più di circa l bit per impulso, e i loro tassi di picco misurati (30 bit/s) sono solo una piccola frazione (forse il 15%) del massimo teorico. Sembra che in questo caso anche il rumore sia più forte: la precisione di codifica temporale maggiore di cui vi sia dimostrazione finora è di 5÷10 ms, un ordine di grandezza peggiore della corrispondente precisione in H1. Come dobbiamo interpretare queste evidenti differenze? Perché i neuroni corticali (e del talamo) dei mammiferi dovrebbero essere canali di informazione peggiori, rispetto ai neuroni sensoriali, in quelli che consideriamo, normalmente, animali più primitivi?

Bisogna stare attenti nel confrontare i risultati di diversi tipi di esperimenti. Le misure di de Ruyter van Steveninck e Bialek sono state effettuate tutte con stimoli scelti accuratamente per verificare le funzioni note dei neuroni in questione. Così, per esempio, si è utilizzato il movimento globale orizzontale del campo visivo per il neurone Hl della mosca. I neuroni corticali visivi sono dispositivi di impiego più generale, che veicolano l'informazione su una varietà di attributi dello stimolo: pattern spaziale, contrasto, colore, cambiamento temporale (incluso il movimento), e forse altri ancora. Gli stimoli utilizzati negli esperimenti che abbiamo passato in rassegna variavano rispetto a uno solo di questi attributi (il pattern spaziale), ed è probabile che prenderne in considerazione un numero maggiore possa alzare le stime sul tasso di trasmissione. J.W. McClurkin e collaboratori (McClurkin et al., 1994; McClurkin e Optican, 1996) hanno osservato che l'informazione sul colore veicolata dai neuroni corticali visivi è confrontabile con quella trasmessa sul pattern spaziale.

In tale contesto vale anche la pena di notare che la stima originale di Eckhorn e Pöpel per i neuroni nel nucleo genicolato laterale del gatto era effettuata con uno stimolo che variava solo nel tempo, mentre gli esperimenti di Richmond, Optican e collaboratori usavano stimoli statici per tutta la durata del periodo di risposta analizzato. Inoltre, i diversi metodi di analisi utilizzati dai due gruppi erano progettati per estrarre l'informazione in bande di frequenza essenzialmente disgiunte (al di sopra e al di sotto di 25 Hz).

Se da un lato è rischioso azzardare ipotesi su come questi effetti si possano combinare per fornire una migliore stima del tasso di trasmissione dell'informazione, se aggiungiamo 20 bit/s per il contrasto e il colore, e altri 20 bit/s per la struttura temporale dello stimolo (la quantità trovata da Eckhorn e Pöpel, codificata nella struttura temporale della risposta all'interno di una finestra temporale di 20 ms), arriviamo a un tasso vicino a quello di Hl, alla stessa risoluzione temporale. Anche se c'è ancora un fattore 3 di separazione tra il risultato e l'entropia a priori della sequenza di impulsi, alcune delle differenze più eclatanti tra i due tipi di neuroni si riducono a differenze quantitative.

Considerazioni analoghe potrebbero valere per la precisione della temporizzazione degli impulsi. Come abbiamo visto, l'informazione in eccesso veicolata da Hl, al livello di precisione di l ms, sembra associata a una codifica non lineare in periodi, relativamente rari, di emissione intensa. Nel neurone Hl queste risposte insolite, e il loro contributo al tasso di trasmissione dell'informazione, sono stati analizzati separatamente all'interno del paradigma della decodifica. Un tipo di analisi simile dovrebbe essere possibile anche per le cellule corticali dei mammiferi, ma non è stata ancora effettuata.

Comunque, la quantità media di informazione sui 'lampi' di pattern stazionari, codificata attraverso una temporizzazione degli impulsi così precisa, non può essere grande (non più di circa il 10% del totale), altrimenti i metodi di misura usati dal gruppo di Richmond l'avrebbero già rivelata. Se quindi, da un lato, l'esistenza di questa precisione nella temporizzazione rimane un'interessante questione aperta, la sua importanza quantitativa, ai fini della trasmissione dell'informazione legata allo stimolo da parte di questi neuroni, è probabilmente molto limitata.

Una domanda più interessante riguarda il possibile uso della grande entropia residua nelle risposte dei neuroni della corteccia visiva. Ci si chiede cioè se il rumore che si vede nelle sequenze di impulsi non sia indicatore di qualcosa che non siamo stati ancora capaci di identificare (Bullock, 1970). Una possibilità è che le differenze tra le varie prove ripetute dipendano da piccole differenze nell'inquadratura. Questo vorrebbe dire che gli stimoli non sono realmente gli stessi da prova a prova, e le risposte fluttuano di conseguenza. Questo sembra però improbabile. A livello qualitativo, è noto già da tempo che le risposte degli animali svegli e attivi sono molto simili a quelle degli animali anestetizzati, per cui l'inquadratura non cambia (Wurtz, 1969). Recentemente, Kjær (1996) ha studiato quantitativamente la variabilità in un esperimento in cui si misuravano gli errori di inquadratura insieme alle risposte. Il risultato è che, per errori di inquadratura tipici, l'informazione contenuta nelle risposte sulla posizione dell'inquadratura era circa un ordine di grandezza minore di quella veicolata nelle stesse risposte sul pattern di stimolo. Dunque ben poca dell'informazione mancante si può spiegare in questo modo. Bisogna tenere presente che i neuroni corticali non sono semplicemente dei trasduttori sensoriali. Essi fanno parte del cervello, e un tipico neurone della corteccia visiva riceve un numero di input da altri neuroni corti cali dieci volte maggiore rispetto a quello che riceve dai neuroni del nucleo genicolato laterale, che trasmettono i segnali visivi dalla retina. Se il principio di Barlow dell'uso efficiente della capacità neuronale è valido, lo deve essere per l'intero sistema, ed è difficile per noi capire se la capacità ulteriore sarà usata per costruire una rappresentazione più completa dell'ambiente sensoriale o per soddisfare priorità di elaborazione interne di qualche tipo. Non sappiamo, quindi, in quale misura un neurone corticale visivo veicoli messaggi sugli stimoli esterni, e in quale misura le sue sequenze di impulsi prendano parte a qualche elaborazione interna. Sembra probabile che, prima di poter risolvere questo puzzle, dovremo imparare a capire meglio la codifica a più neuroni.

Naturalmente, a questo stadio non possiamo escludere la possibilità che il rumore che appare nei segnali neuronali corticali sia realmente rumore. Forse l'evoluzione ha trovato un modo efficiente per far funzionare i cervelli come macchine stocastiche, o forse non c'è alternativa: potrebbe essere impossibile costruire cervelli grandi e deterministici che funzionino in modo affidabile.

È opportuno osservare, infine, che il fatto di trovare l'informazione codificata in qualche modo particolare nelle sequenze di impulsi neuronali (per esempio la temporizzazione precisa degli impulsi) non significa necessariamente che questa informazione venga utilizzata dal cervello. Il principio di efficienza dice che è vantaggioso per un animale sviluppare modi per decodificare l'informazione, ma questo sviluppo è soggetto a vincoli fisici, cosicché la struttura temporale osservata potrebbe essere semplicemente un epifenomeno. Un possibile esempio è fornito dalla scoperta, in registrazioni dalla corteccia frontale della scimmia, di intervalli tra impulsi riproducibili, fino a centinaia di millisecondi, con precisione fino a 1÷ 2 ms (Abeles et al., 1993a; 1993b). Il particolare pattern osservato sembra veicolare informazione sullo stato comportamentale dell'animale. Non è bio fisicamente plausibile che ogni singolo neurone che riceve questi segnali debba possedere un meccanismo di decodifica specifico per una struttura temporale di questa precisione, su intervalli di tempo di questa lunghezza. M. Abeles e collaboratori (1991) suggeriscono che questi neuroni si comportino come rivelatori di coincidenze. Secondo la loro interpretazione, la precisione nella coincidenza dei segnali afferenti attribuisce una forte coerenza temporale alla dinamica della rete. Questo si riflette nella riproducibilità di lunghi intervalli tra impulsi, ma questi intervalli non hanno, in sé, alcun significato funzionale.

Bibliografia citata

ABELES, M. (1991) Corticonics: neuronal circuits of the cerebral cortex. Cambridge, Cambridge University Press.

ABELES, M., BERGMAN, H., MARGALIT, E., VAADIA, E. (1993a) Spatiotemporal firing pattems in the frontal cortex of behaving monkeys. J. Neurophysiol., 70, 1629-1638.

ABELES, M., VAADIA, E., BERGMAN, H., PRUT, Y., HAALMAN, I., SLOVIN, H. (1993b) Concepts in Neuroscience, 4, 131-158.

ADRIAN, E.D. (1926) J. Physiol., 61, 47.

BAIR, W., KOCH, C. (1996) Temporal precision of spike trains in extrastriate cortex of the behaving macaque monkey. Neural Comput., 8, 1185-1202.

BARLOW, H.B. (1961) In Sensory communication, contributions (Symposium on principles of sensory communication), a c. di Rosenblith W. A., Cambridge, Mass., MIT Press.

BARLOW, H.B. (1981) The Ferrier Lecture, 1980. Critical limiting factors in the design of the eye and visual cortex. Proc. R. Soc. Lond. B Biol. Sci., 212, 1-34.

BIALEK, W., RIEKE, F., DE RUYTER VAN STEVENINCK, R.R., WARLAND, D. (1991) Reading a neural code. Science, 252, 1854-1857.

BULLOCK, T.H. (1970) The reliability of neurons. J. Gen. Physiol., 55, 565-584.

DECHARMS, R.C., MERZENICH, M.M. (1996) Primary cortical representation of sounds by the coordination of action-potential timing. Nature, 381, 610-613.

ECKHORN, R., GRUSSER, O.-J., KROLLER, J., PELLNITZ, K., PÖPEL, B. (1976) Efficiency of different neuronal codes: information transfer ca1cu1ations for three different neuronal systems. Biol. Cybern., 22, 49-60.

ECKHORN, R., PÖPEL, B. (1974) Rigorous and extended application of information theory to the afferent visual system of the cat. I. Basic concepts. Kybernetik, 16, 191-200.

ECKHORN, R., PÖPEL, B. (1975) Rigorous and extended application of information theory to the afferent visual system of the cat. II. Experimental results. Biol. Cybern., 17 , 71-77.

GAWNE, T.J., KiJER, T.W., HERTZ, J.A., RICHMOND, B.J. (1996a) Adjacent visual cortical complex cells share about 20% oftheir stimulus-related information. Cereb. Cortex, 6, 482-489.

GAWNE, T.J., KIJER, T.W., RICHMOND, B.J. (1996b) Latency: another potential code for feature binding in striate cortex. J. Neurophysiol., 76, 1356-1360.

GAWNE, T.J., RICHMOND, B.J. (1993) How independent are the messages carried by adjacent inferior temporal cortical neurons? J. Neurosci., 13, 2758-2771.

GEORGOPOULOS, A.P., TAIRA, M., LUKASHIN, A. (1993) Cognitive neurophysiology of the motor cortex. Science, 260, 47-52.

GHOSE, G.M., OHZAWA, I., FREEMAN, R.D. (1993) Soc. Neurosci. Abstr., 19, 84.

GOCHIN, P.M., COLOMBO, M., DORFMAN, G.A., GERSTEIN, G.L., GROSS, C.G. (1994) Neural ensemble coding in inferior temporal cortex. J. Neurophysiol., 71, 2325-2337.

GOLOMB, D., HERTZ, J.A., PANZERI, S., RICHMOND, B.J., TREVES, A. (1996) How well can we estimate the information carried in neuronal responses from limited samples? Neural Comput., 9, 649-653.

GOLOMB, D., KLEINFELD, D., REID, R.C., SHAPLEY, R.M., SHRAIMAN, B.L (1994) On temporal codes and the spatiotemporal response of neurons in the lateral geniculate nucleus. J. Neurophysiol., 72, 2990-3003.

HELLER, J., HERTZ, J.A., KIJER, T.W., RICHMOND, B.J. (1995) Information flow and temporal coding in primate pattem vision. J. Comput. Neurosci., 2, 175-193.

HERTZ, J.A., HELLER, J., KIJER, T.W., RICHMOND, B.J. (1995) Information spectroscopy of single neurons, Int. J. Neural Systems (suppl.), 6, 123-132.

HERTZ, J.A., KIJER, T.W., ESKANDAR, E.N., RICHMOND, B.J. (1992) Measuring natural neural processing with artificial neural networks, Int. J. Neural Systems (suppl.), 3, 91-103.

HUBEL, D., WIESEL, T. (1962) J. Physiol., 160, 106-154.

HUBEL, D., WIESEL, T. (1968) Receptive fields and functional architecture of monkey striate cortex. J. Physiol., 195, 215-243.

JIN, G.X., GAWNE, T.J., HERTZ, J.A., RICHMOND, B.J. (1995) Soc. Neurosci. Abstr., 21, 1650.

KJÆR, T.W. (1996) Tesi di Ph.D., Copenhagen University.

KJÆR, T.W., HERTZ, J.A., RICHMOND, B.J. (1994) Decoding cortical neuronal signals: network models, information estimation and spatial tuning. J. Comput. Neurosci., 1, 109-139.

LI, Z. (1996) A theory of the visual motion coding in the primary visual cortex. Neural Comput., 8, 705-730.

MALDONADO, P.E., GRAY, C.M. (1994) Soc. Neurosci. Abstr., 20, 625.

McCLURKIN, J.W., OPTICAN, L.M. (1996) Primate striate and prestriate cortical neurons during discrimination. I. Simultaneous temporal encoding of information about color and pattem. J. Neurophysiol., 75, 481-495.

McCLURKIN, J.W., OPTICAN, L.M., RICHMOND, B.J., GAWNE, T.J. (1991) Lateral geniculate neurons in behaving primates. II. Encoding of visual information in the temporal shape of the response. J. Neurophysiol., 66, 794-808.

McCLURKIN, J.W., ZARBOCK, J.A., OPTICAN, L.M. (1994) In Cerebral Cortex, a c. di Jones E.G., Peters A., voI. 10, New York, Plenum Press, pp. 443-467.

McKAY, D.M., McCULLOCH, W.S. (1952) Bull. Math. Biophys., 14, 127-135.

MILLER, J.P., JACOBS, G.A., THEUNISSEN, F.E. (1991) Representation of sensory information in the cricket cercaI sensory system. I. Response properties of the primary intemeurons. J. Neurophysiol., 66, 1680-1689.

OLSHAUSEN, B.A., FIELD, D.J. (1996) Emergence of simple-cell receptive field properties by leaming a sparse code for natural images. Nature, 381, 607-609.

PANZERI, S., TREVES, A. (1996) Network, 7, 87-101.

REID, R.C., SHAPLEY, R.M. (1992) Spatial structure of cone inputs to receptive fields in primate lateral geniculate nucleus. Nature, 356, 716-718.

RICHMOND, B.J., OPTICAN, L.M. (1987) Temporal encoding of two-dimensional pattems by single units in primate inferi or temporal cortex. III. Information theoretic analysis. J. Neurophysiol., 57,162-178.

RICHMOND, B.J., OPTICAN, L.M. (1990) Temporal encoding of two-dimensional pattems by single units in primate primary visual cortex. II. Information transmission. J. Neurophysiol., 64, 370-380.

RIEKE, F., WARLAND, D., BIALEK, W. (1993) Europhys. Lett., 22, 151-156.

RUYTER VAN STEVENINCK, R.R. DE, BIALEK, W. (1988) Proc. R. Soc. Lond. B, 234, 379-414.

SHADLEN, M.N., NEWSOME, W.T. (1994) Noise, neural codes and cortical organization. Curr. Opin. Neurobiol., 4, 569-579.

SHADLEN, M.N., NEWSOME, W.T. (1995) Is there a signal in the noise? Curr. Opin. Neurobiol., 5, 248-250. SHANNON, C.E. (1949) Proc. IRE, 37, 10-21.

SINGER, W. (1993) Annu. Rev. Physiol., 55, 349-374.

SOFTKY, W.R. (1994) Neuroscience, 58, 13-41. SOFTKY, W.R. (1995) Simple codes versus efficient codes. Curr. Opin. Neurobiol., 5, 239-247.

SOFTKY, W.R., KOCH, C. (1993) The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci., 13, 334-350.

STONE, M. (1974) J. Roy. Stato Soc. B, 36 (2), 111-147.

STRONG, S.P., KOBERLE, R., DE RUYTER V AN STEVENINCK, R.R., BIALEK, W. (1998) Entropy and information in neural spike trains, Phys. Rev. Lett., 80, 197-200.

THEUNISSEN, F.E., MILLER, J.P. (1991) Representation ofsensory information in the cricket cercaI sensory system. II. Information theoretic calculation of system accuracy and optimal tuning-curve widths of four primary intemeurons. J. Neurophysiol., 66,1690-1703.

TOVÉE, M.J., ROLLS, E.T., TREVES, A., BELLIS, R.P. (1993) Information encoding and the responses of single neurons in the primate temporal visual cortex. J. Neurophysiol., 70, 640-654.

WURTZ, R.H. (1969) Visual receptive fields of striate cortex neurons in awake monkeys. J. Neurophysiol., 32, 727-742.

Bibliografia generale

ARBIB, M.A., a c. di, Handbook of brain theory and neural networks. Cambridge, Mass., MIT Press, 1995.

BIALEK, W., DEWEESE, M., RIEKE, F., WARLAND, D. (1993) Bits and brains: information flow in the nervous system. Physica A, 200, 581-593.

BIALEK, W., RIEKE, F. (1992) Reliability and information transmission in spiking neurons. Trends Neurosci., 15, 428-434.

BRILLOUlN, L., Science and information theory, 2a ed., New York, Academic Press, 1962.

COVER, T.M., THOMAS, J.A., Elements oJinJormation theory. New York, Wiley, 1991.

HERTZ, J.A., KROGH, A.S., PALMER, R.G., Introduction to the theory of neural computation. Redwood City, Addison-Wesley, 1991.

KANDEL, E.R., SCHWARTZ, J. H., JESSELL, T.M., a c. di, Principles of neural science, 3aed., New York, Elsevier, 1991.

KOCH, C., DAVIS, J.L., Large scale neuronal theories of the brain. Cambridge, Mass., MIT Press, 1994.

PERKEL, D.H., BULLOCK, T.H. (1968) Neural Coding. Neurosciences Res. Prog. Bull., 6, 221-348.

RIEKE, F., WARLAND, D., DE RUYTER VAN STEVENINCK, R., BIALEK, W., Spikes exploring the neural code. Cambridge, Mass., MIT Press, 1997.