Il Rinascimento. L'astronomia
Il Rinascimento. L'astronomia
L'astronomia
Gli storici dell'arte e delle discipline umanistiche si sentirebbero forse a proprio agio definendo 'Rinascimento' il periodo che va dal 1400 al 1600, e tuttavia su una data d'inizio così tarda potrebbero non mancare riserve. Per parte loro, molti storici della scienza sarebbero invece contrari ad accettare come termine a quo una datazione così alta. Nello sviluppo dell'astronomia, infatti, la 'rinascita', associata con il recupero dei testi greci, si fa risalire all'opera di Georg von Purbach (1423-1461) e del suo allievo Johann Müller di Königsberg, meglio conosciuto come Regiomontano (1436-1476). Il Concilio di Firenze, nel 1438, quando Bessarione (1403 ca.-1472), metropolita di Nicea, passò dalla Chiesa orientale alla Chiesa occidentale, fa da antefatto e sfondo solenne a questo inizio. Sarà presso Bessarione, infatti, che Purbach e soprattutto Regiomontano, qualche decennio dopo, studieranno il greco.
Così, sebbene non sia questa la sede per definire il concetto di 'Rinascimento', una maggiore attenzione alla storia della scienza non può che contribuire alla comprensione dei cambiamenti intellettuali che ebbero luogo nel periodo di cui stiamo parlando. In particolare, lo studio dello sviluppo delle scienze esatte tende a manifestare un notevole grado di continuità all'interno di un periodo storico rispetto al quale molti storici hanno cercato, piuttosto, di sottolineare gli elementi di novità. Infatti, fin dall'Antichità, l'astronomia è stata caratterizzata dai tratti distintivi della scienza poiché faceva ricorso all'osservazione, aveva un impianto matematico e consentiva predizioni verificabili mediante osservazione.
Nei capitoli iniziali del Libro I della Fisica, sicuramente uno dei testi più influenti mai scritti, Aristotele identificava lo studio della Natura con lo studio del moto e del cambiamento. Una conferma esemplare di ciò si riscontra ancora nell'astronomia anteriore al XVIII sec., in cui poca attenzione era riservata alla volta celeste con le sue stelle fisse ‒ chiamate in questo modo perché si supponeva che esse rimanessero fisse le une rispetto alle altre ‒ mentre si prestava molta più attenzione alla spiegazione dei movimenti delle 'stelle erranti', ovvero dei pianeti, le cui posizioni cambiano in relazione a questo modello. Tuttavia, è incerto se Aristotele abbia considerato l'astronomia come parte integrante della filosofia naturale. Dal tempo di Boezio (480 ca.-524/525), comunque, l'astronomia era annoverata tra le arti del quadrivio, accanto alla geometria, all'aritmetica e alla musica. Insieme alle arti del trivio (grammatica, retorica e dialettica), queste discipline formavano le 'sette arti liberali'. La classificazione delle arti liberali fu particolarmente longeva e costituì la base della formazione culturale nelle università medievali, nelle quali l'istruzione iniziava con le arti del trivio per poi proseguire con quelle del quadrivio, di contenuto più complesso. A partire dalla fine del XVI sec. la classificazione perde parte del suo significato culturale più ampio; le sette arti liberali non figureranno più, per esempio, nel gruppo delle personificazioni esposte nella versione francese dell'Iconologia di Cesare Ripa (edita per la prima volta a Padova nel 1611), pubblicata a Parigi nel 1644, e che ebbe diverse edizioni. La sua inclusione di figure per le singole arti liberali è un'indicazione preziosa della loro prolungata importanza negli schemi iconografici del tempo, oltre che nelle elaborate decorazioni su pareti e soffitti dei palazzi. In ogni caso, nel mondo dotto, e soprattutto in quello delle università, sembra che nel 1600 l'astronomia fosse generalmente considerata parte della matematica, proprio come era avvenuto nel 1400; infatti, Tycho Brahe (1546-1601) e Johannes Kepler (1571-1630) lavorarono come astronomi per l'imperatore del Sacro Romano Impero, Rodolfo II, con il titolo di 'matematici imperiali'.
L'astronomia come branca della matematica
Classificare l'astronomia all'interno della matematica significava considerare l'astronomia teorica quale applicazione della geometria, allo stesso modo in cui la teoria musicale era considerata un'applicazione dell'aritmetica. Così era del tutto normale che Regiomontano presentasse il suo trattato De triangulis come qualcosa da studiare preliminarmente alla sua opera sull'astronomia di Tolomeo. Né, del resto, può sorprendere che egli avesse scritto un libro interamente dedicato alla geometria astratta. Di fatto, l'opera risulta di grande interesse storico per la ricostruzione dello sviluppo della matematica tecnica; in particolare, essa include la prima enunciazione conosciuta di ciò che ora è noto come 'teorema dei seni': in un triangolo i lati sono direttamente proporzionali al seno degli angoli opposti. Regiomontano fornisce una dimostrazione di questo importante teorema, ma non afferma che il risultato o la dimostrazione da lui fornita siano nuovi, rendendo così impossibile stabilire fino a che punto questa parte del suo lavoro sia originale. Il teorema dei seni è particolarmente utile in astronomia perché si applica ai triangoli sferici (cioè a quei triangoli aventi, come lati, archi di cerchio massimo), trattati normalmente dalla disciplina.
Comunque, esso può anche essere usato per risolvere problemi di agrimensura, ove i triangoli coinvolti sono rettilinei. Sembra che il libro di Regiomontano sui triangoli continuò a essere il testo fondamentale sull'argomento fino a ben oltre il 1600, quando il suo lavoro di astronomo era ormai di gran lunga superato, e l'opera contribuì significativamente alla sua fama postuma di grande matematico. All'epoca, un astronomo doveva passare molto del suo tempo a occuparsi di 'matematica'. Le osservazioni astronomiche, se non puramente qualitative, di fatto erano tutte misurazioni di angoli; talvolta gli angoli erano misurati in modo diretto, talvolta essi erano ricavati dai lati dei triangoli. In ogni caso, erano necessari molti calcoli per 'ridurre' queste osservazioni, cioè per organizzarle sì da poterle poi utilizzare per costruire modelli del moto del Sole o della Luna.
Il fatto che l'astronomia fosse considerata una branca della matematica implicava che fosse compito dell'astronomo calcolare e fare previsioni, ma non fornire spiegazioni sul modo di procedere della natura in quanto queste erano di competenza del filosofo naturale. Così spettava a quest'ultimo di pronunciarsi sulla natura del moto e su quali moti fossero 'naturali' per i corpi celesti, mentre erano gli astronomi a fornire i modelli matematici dei movimenti osservati in base al moto 'prescritto' dai filosofi.
L'astronomia insegnata nelle università concerneva soprattutto descrizioni qualitative, piuttosto semplici, della struttura dell'Universo e del posto dell'uomo al suo interno. Poiché "i cieli narrano la gloria di Dio", come è scritto nel Salmo 19, 2, lo studio dell'astronomia faceva chiaramente parte dello studio della natura di Dio, e in quanto tale era propedeutico a uno studio più approfondito che sarebbe stato impartito nei corsi di teologia. Ma l'astronomia era considerata utile anche nella vita quotidiana. In particolare, qualche conoscenza d'astronomia era necessaria ai medici, dal momento che ci si aspettava da essi un uso intelligente dell'astrologia nella diagnosi e nel trattamento dei pazienti. Mentre poco si conosce dei dettagli della loro formazione professionale, è accertato che le università con grandi facoltà mediche promuovevano anche l'insegnamento della matematica. Se forse è eccessivo suggerire un legame diretto tra la facoltà medica e la fiorente Scuola di algebra di Bologna all'inizio del XVI sec., è tuttavia certo che quando Galileo Galilei era professore di matematica all'Università di Padova, dal 1592 al 1611, egli insegnava astronomia geocentrica, e molti dei suoi ascoltatori erano studenti di medicina.
I termini moderni 'astronomia' e 'astrologia' derivano dal greco, ove, tuttavia, essi non avevano lo stesso significato dei loro corrispettivi odierni. Nei primi testi, il termine 'astrologia' era tendenzialmente usato per riferirsi sia allo studio dei moti delle stelle (inclusi i pianeti), ossia a ciò che nel XX sec. si chiamerebbe 'astronomia', sia allo studio degli effetti di questi corpi e dei loro moti sulla Terra, ossia a ciò che, in termini odierni, si chiamerebbe 'astrologia'. Il termine 'astronomia' sembra di origine successiva ed era usato, a quanto pare, unicamente per riferirsi a un ambito disciplinare analogo all'odierna astronomia. Questi rilievi filologici non sono secondari, se si pensa all'insistenza rinascimentale sull'uso corretto, e quindi classico, o presunto tale, del termine 'astrologia', o di termini affini. È dunque probabile che, almeno nella mente di qualche autore, questo uso terminologico contribuisse a conferire all'astrologia parte della vetustà e quindi della riconosciuta rispettabilità propria dell'astronomia. A prescindere dai termini usati, è chiaro che gli Antichi tennero di fatto distinte le due discipline. Tolomeo esprime con estrema chiarezza la differenza del loro statuto epistemico, proprio all'inizio del suo breve lavoro in quattro libri sull'astrologia (usualmente conosciuto con il titolo greco Apotelesmatikḕ sýntaxis tetrabíblos o, nella sua traduzione latina, Quadripartitum), dove egli presenta le previsioni astrologiche come di gran lunga meno affidabili di quelle astronomiche. Questa opera fu ben conosciuta durante tutto il Medioevo. Se molto di ciò che Tolomeo afferma nella Tetrabiblos sembra decisamente irrazionale, tuttavia si deve notare come ci fosse un fondo razionale dietro il principio fondamentale dell'astrologia per cui i corpi celesti influenzerebbero la Terra. Questo principio apparteneva infatti alla cosmologia; si credeva che l'Universo fosse costituito da un sistema di sfere, di cui la più grande era approssimativamente o esattamente concentrica, e che l'origine di tutti i moti all'interno del sistema risiedesse all'esterno. Così tutto era trasmesso da un motore esterno verso la Terra che era al centro del sistema. La natura regolare del moto delle sfere superiori causava cambiamenti ciclici nelle sfere inferiori. Tra questi cicli, il più evidente era l'alternarsi delle stagioni nel corso dell'anno. Di conseguenza, il fatto che le diverse stagioni corrispondessero alle diverse posizioni del Sole rispetto alle costellazioni dello Zodiaco, era considerato un fattore importante a sostegno della tesi di un'influenza dei corpi celesti sulla Terra. La possibilità, invece, che fosse l'influenza della Luna sulle acque a causare le maree era considerata piuttosto dubbia. Si pensava che gli altri pianeti esercitassero influenze più deboli, sebbene ci fossero molti indizi che deponevano (con argomenti più o meno razionali) contro tale ipotesi. In un periodo in cui le economie di tutti gli stati erano largamente basate sull'agricoltura, l'astrologia trovò un uso importante nelle previsioni meteorologiche. Affermatosi l'uso della stampa, in molte regioni si incaricarono gli astronomi locali di redigere un calendario contenente annotazioni di ogni interessante evento astronomico, come le eclissi, e di fornire le previsioni del tempo per l'anno successivo. Dal momento che questi calendari erano relativamente economici, stampati in modo grossolano e di scarso interesse una volta concluso l'anno in questione, pochi di essi sopravvissero, ma testimonianze indirette suggeriscono che dovevano essere numerosi a quei tempi.
L'utilità dell'astrologia contribuì di sicuro all'insegnamento dell'astronomia e le previsioni astrologiche consentirono agli astronomi di disporre di un ulteriore supporto finanziario, tuttavia non sono queste le uniche ragioni per cui l'astrologia di questo periodo riveste un particolare interesse per la storia della scienza. L'astrologia, infatti, apportò un contributo altamente significativo e longevo all'astronomia soprattutto con la nozione di 'forza'. Gli astrologi credevano che i corpi potessero influenzarsi reciprocamente senza un contatto effettivo, proprio come, per esempio, la Luna influenzava il mare, e quest'azione a distanza fu chiamata 'forza' (vis in latino). La maggior parte dei filosofi naturali si tenne lontano da questa nozione. Non solo infatti la modalità di azione di una tale forza rimaneva inesplicata, ma sembrava intrinsecamente inesplicabile, ossia occulta nel senso di 'nascosta', che era poi il senso usuale della parola presso i filosofi aristotelici. Il concetto di forza dovette quindi aspettare il XVII sec. per acquisire dignità scientifica ma, di certo, esso fu abbastanza conosciuto per tutto il XVI secolo.
Calendario e osservazioni astronomiche
Se l'astrologia fu uno dei fattori che promosse lo studio dell'astronomia nel periodo dal 1400 al 1600, sicuramente ci fu anche un altro fattore a giocare un ruolo cruciale; il calendario in uso nell'Europa occidentale ‒ introdotto da Giulio Cesare nel 46 a.C. (707 ab Urbe condita, secondo il calcolo romano) ‒ era, in tutta evidenza, inadeguato. Ciò era tanto più rilevante quanto più incideva sulla data da assegnare alla Pasqua (e, naturalmente, su tutte quelle festività religiose le cui date erano ricavate da quella della Pasqua). La Chiesa cristiana delle origini aveva infatti adottato una variante del metodo ebraico per calcolare la data della Pasqua. Ciò era stato fatto convenientemente, dal momento che l'ultima cena di Cristo ebbe luogo nella pri-ma sera della Pasqua ebraica. Il calendario ebraico, tuttavia, non era affidabile nel tentativo di conciliare l'esigenza di assegnare all'anno la giusta durata (in modo da poter stabilire, per esempio, una data fissa per la festa della mietitura) con il desiderio di usare le lunazioni come base per stabilire divisioni più brevi all'interno dell'anno. Infatti, dodici lunazioni abbracciano un arco di tempo inferiore a un anno e tredici un arco di tempo superiore. Di conseguenza, ogni calendario basato sui cicli lunari s'imbatteva nel problema del ciclo solare annuo. La regola per determinare la Pasqua era la seguente: il giorno di Pasqua cadeva la domenica successiva alla prima Luna piena dopo la prima domenica successiva all'equinozio di primavera. La difficoltà nel fissare la data corretta per la Pasqua ereditava una difficoltà già insita nel calendario giuliano: la determinazione della data dell'equinozio di primavera, ossia del momento dell'anno in cui il Sole, nella sua traiettoria apparente, interseca l'equatore celeste da sud a nord. Prima della riforma giuliana, Romani e Greci avevano adoperato diversi calendari, che però dedicavano scarsa attenzione ai fatti astronomici, contenendo piuttosto un numero di festività annuali dettate dai governanti e dal loro desiderio di accrescere il consenso popolare. Gli astronomi che, com'è comprensibile, preferivano usare anni di eguale lunghezza, si basavano sulle date fissate dal calendario egizio, il cui anno di 365 giorni era diviso in dodici mesi di trenta giorni ciascuno, più cinque giorni supplementari (epagomeni) da aggiungere alla fine di determinati anni. Questo calendario non teneva conto in modo accurato del moto apparente del Sole o della Luna. I cambiamenti meteorologici stagionali non erano, infatti, molto evidenti in Egitto; tuttavia lì aveva luogo un evento stagionale d'enorme importanza, la cui data doveva essere ben conosciuta: l'inondazione annuale del Nilo. Gli Egizi erano in grado di prevedere tale data tramite osservazioni astronomiche dirette; infatti, quando Sirio era visibile all'alba, mancavano quindici giorni all'inondazione del Nilo. La data della levata eliaca di Sirio era usata anche per fissare l'anno sidereo, che era indipendente dal calendario civile, giacché la data della levata eliaca cambiava nel corso del tempo. D'altra parte, gli elaborati sistemi degli Egizi, che non tenevano affatto conto della durata effettiva dell'anno solare, non potevano essere usati in quei paesi in cui i cambiamenti stagionali erano marcati più nettamente. Giulio Cesare si avvalse dei consigli di dotti astronomi del suo tempo, prima di introdurre il calendario che porta il suo nome e che mostra, in modo evidente, tracce sostanziali delle sue origini sincretiche greco-romane-egizie.
Sebbene il calendario giuliano fosse basato sulle migliori osservazioni disponibili all'epoca, esso era inevitabilmente abbastanza imperfetto da richiedere modifiche successive. Nel corso del XV sec. la sua inadeguatezza era generalmente riconosciuta. Era trascorso, infatti, un tempo sufficiente perché le date degli eventi astronomici si fossero notevolmente allontanate dalle loro collocazioni originarie nel calendario. Tra queste vi era anche la data dell'equinozio di primavera, la cui oscillazione rendeva incerta l'esatta determinazione della Luna piena, utile per stabilire la data della Pasqua. Come già aveva fatto Giulio Cesare, anche i governanti del XV sec. (ecclesiastici e non) si avvalsero dei consigli di astronomi per riformare il calendario. In particolare, ciò che essi chiedevano era che l'equinozio di primavera fosse stabilito ancora una volta laddove Giulio Cesare aveva originariamente pensato di fissarlo, il 21 marzo. Il problema risiedeva in quello che oggi sarebbe chiamato il 'moto apparente' del Sole, e il particolare periodo, che era necessario conoscere per fissare esattamente la data dell'equinozio, era ciò che oggi è conosciuto come 'anno tropico'. L'aggettivo 'tropico' deriva da un verbo greco (trépō) che significa "volgere" e si riferisce a quei punti, nella traiettoria apparente del Sole lungo l'eclittica, in cui esso raggiunge la sua massima declinazione. Questi punti sono il solstizio d'estate, quando il Sole è al suo punto più alto (90° di declinazione N sul piano dell'equatore celeste) e la durata del dì è la più lunga dell'anno, e il solstizio d'inverno, quando il Sole è al suo punto più basso (90° di declinazione S rispetto all'equatore celeste) e la durata del dì è la più breve dell'anno. Ora, identificare o anche misurare il giorno più lungo e quello più corto dell'anno potrebbe sembrare ragionevolmente facile, ma non è così.
Non è sufficiente, infatti, una rilevazione approssimativa della data del solstizio per costruire un opportuno calendario che abbia la pretesa di rimanere valido nel corso del tempo. Inoltre, il Sole, nel suo moto apparente, si muove più lentamente in prossimità dei punti solstiziali, cosicché è difficile stabilire esattamente quando li raggiunge. È più semplice cercare di stabilirne la posizione in prossimità dei punti equinoziali, ove la velocità di moto del Sole lungo l'eclittica è massima. Tuttavia, non c'è alcuna garanzia che il Sole raggiunga un punto equinoziale proprio nel momento in cui si può misurare la sua posizione. A parte l'imprevedibili-tà dei fattori meteorologici, rimane ancora la possibilità che il momento del passaggio del Sole nel punto equinoziale possa avvenire di notte. Analoghe difficoltà si presentano per la determinazione del passaggio del Sole nei punti solstiziali. Inoltre, è generalmente difficile osservare il Sole; non si può, infatti, misurarne la posizione rispetto alla volta delle stelle fisse poiché, se il Sole è sopra l'orizzonte, la luce delle stelle ne verrà offuscata.
Così, si deve misurare la posizione del Sole in relazione a un sistema di coordinate locali e poi fare qualche calcolo per convertire queste osservazioni nella corrispondente posizione del Sole rispetto alle stelle fisse. Tali calcoli implicano la conoscenza della propria latitudine geografica e una valutazione ben adeguata del moto dei cieli. Dunque, l'osservazione della posizione del Sole implica sempre una componente teorica, a differenza di quanto richiesto dalla mera osservazione di una stella fissa.
Nel complesso, il problema della riforma del calendario si rivelò risolvibile per mezzo di osservazioni, in quanto il calendario giuliano non aveva di fatto bisogno di grandi modifiche. L'operazione fu felicemente condotta a termine nel tardo XVI secolo. Papa Gregorio XIII decretò che fossero omessi dieci giorni dopo il 4 ottobre 1582, sì da riportare, immediatamente, la data dell'equinozio al 21 marzo, e cambiò le date del calendario per tutti i giorni dedicati ai santi, perché nessuno fosse omesso. Inoltre, egli modificò il sistema degli anni bisestili in modo tale che il mese di febbraio avesse 29 giorni ogni quattro anni, come già avveniva nel calendario giuliano, fatta eccezione quando il numero dell'anno corrispondeva a un numero completo di secoli, nel qual caso l'anno sarebbe stato bisestile solo se il numero dei secoli fosse stato, a sua volta, divisibile per quattro. Poiché, alla luce di questa regola, l'anno 1600 fu bisestile ‒ come, del resto, sarebbe stato anche nel calendario giuliano ‒ la modifica risultò impercettibile fino al 1700. Tuttavia non passò certo inosservata l'eliminazione di dieci giorni, che alla maggioranza non colta dovette certo sembrare puramente arbitraria o almeno ad hoc. La riforma fu accettata dal mondo cattolico e da molti astronomi di altre confessioni. In altri ambiti, essa si impose più lentamente, in parte, di sicuro, per la riluttanza ad accettare una riforma promossa dalla Chiesa cattolica. Il sospetto dei protestanti sul contenuto astronomico della riforma gregoriana era, a quanto sembra, giustificato nella misura in cui vi era in gioco anche un elemento politico. Gregorio XIII aveva vinto una gara. Molti governanti del XVI sec. avevano fatto del loro meglio per apporre il loro nome alla riforma; e se si vuole accertare, a livello storico, se un certo autore godeva di buona reputazione come matematico, è sufficiente verificare l'esistenza di documenti che attestino la richiesta, da parte di un mecenate, di un suo parere in merito alla riforma del calendario. Infatti, sembra che il problema del calendario, che era ricondotto al problema di comprensione del moto del Sole e di quello della sfera delle stelle fisse (che, come sopra accennato, era richiesto per far quadrare i risultati delle osservazioni del Sole), abbia fornito un notevole stimolo all'astronomia teorica come pure all'attività pratica. La necessità di una sua riforma è menzionata nel testo usato per l'insegnamento dell'astronomia nel XIV e XV sec., il De sphaera mundi scritto nella metà del XIII sec. da Giovanni di Sacrobosco. Il lavoro di Sacrobosco è molto elementare; esso fornisce una buona descrizione introdutti-va dei fenomeni astronomici e discute brevemente la misurazione del tempo, ma non fornisce un'adeguata base per intraprendere una riforma del calendario. Tuttavia, il riferimento di Sacrobosco mostra come egli considerasse significativo il problema del calendario, e la diffusione del suo libro, senza dubbio, contribuì a far conoscere tale problema alle successive generazioni.
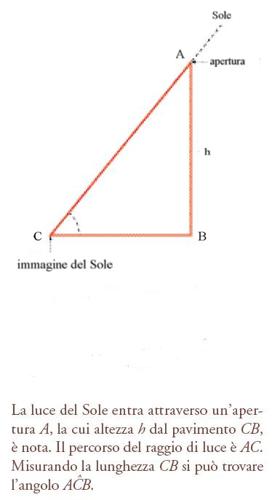
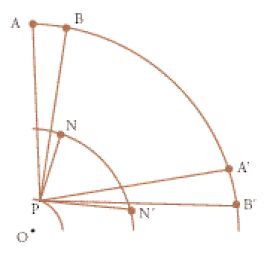
Molte osservazioni astronomiche erano dunque destinate alla riforma del calendario; Paolo dal Pozzo Toscanelli (1397-1482), per esempio, installò uno gnomone nel Duomo di Firenze. Sfruttando un'apertura opportuna fatta sul davanzale di una delle finestre della lanterna del Duomo, la luce del Sole entrava nella navata centrale della chiesa, che quindi funzionava come un'enorme camera oscura, permettendogli di calcolare misure molto accurate dell'altezza del Sole. Il principio di questa esperienza osservativa è illustrato nella fig. 3. Non abbiamo scritti dello stesso Toscanelli sull'argomento (di cui, peraltro, sappiamo molto poco), ma un resoconto del suo lavoro fu presentato in un libro pubblicato nel XVIII sec. da un colto storico gesuita. Leonardo Ximenes fornisce un resoconto dettagliato della storia dello gnomone e una descrizione della pianta della chiesa e dell'anello in metallo pesante (bronzina) collocato sul davanzale di una finestra, situata sul lato meridionale della lanterna, per far entrare la luce solare. L'anello, di cui fornisce uno schema, non si può far risalire a una fase anteriore al restauro eseguito nel 1510. Ximenes attribuisce lo gnomone a Toscanelli sulla base della medesima attribuzione fornita nell'opera di Egnazio Danti (1536-1586) La prospettiva di Euclide (1573). L'affidabilità di questa testimonianza è stata confermata, negli anni Settanta del XX sec., dal ritrovamento di un documento (datato 16 agosto 1475) attestante il pagamento per la fusione di un modello d'armatura per "maestro pagholo medicho", da collocare nella lanterna. Il peso dell'armatura doveva essere di 23 libbre e 4 once, ossia poco meno di otto chilogrammi. L'armatura originale doveva essere dunque molto simile alla copia (ammesso che di una copia si trattasse) descritta da Ximenes e che è ancora oggi al suo posto. Purtroppo, la struttura architettonica della chiesa è tale che lo gnomone di Toscanelli poteva essere usato soltanto per qualche giorno immediatamente prima o dopo il solstizio estivo. Dal momento che era consuetudine per gli astronomi elaborare le loro descrizioni del moto del Sole a partire dalle osservazioni della sua altezza, non soltanto in occasione dei due solstizi, ma anche degli equinozi, è probabile che lo stesso Toscanelli si rendesse conto dei limiti del suo strumento. D'altra parte, esso aveva il vantaggio delle ampie dimensioni, poiché l'apertura sulla lanterna si trovava a un'altezza di circa 90 m rispetto al pavimento della chiesa. Se è difficile rinvenire a quell'epoca considerazioni formali sul concetto di accuratezza o di errore d'osservazione, era tuttavia generalmente riconosciuto che uno strumento di ampie dimensioni avrebbe fornito risultati migliori.
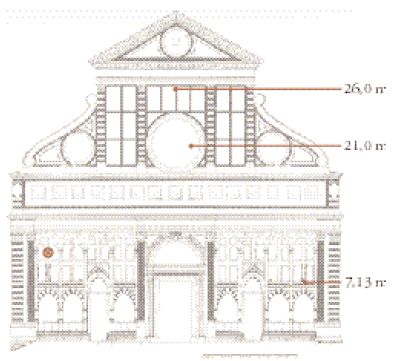
L'interesse di Danti per lo gnomone di Toscanelli non era puramente accademico. Professore all'Università di Bologna, negli anni Settanta del 1500 si trasferì, in qualità di cosmografo, presso il granduca di Toscana, il quale, essendo un Medici, si dichiarava discendente di Giulio Cesare, e aveva così una ragione ulteriore per desiderare di apporre il nome della sua famiglia alla riforma del calendario. Danti costruì due gnomoni nella chiesa di Santa Maria Novella a Firenze, installando anche due piccoli strumenti d'osservazione, un'armilla equatoriale e un quadrante, sulla facciata della chiesa che era rivolta a sud. L'apertura d'entrata per il primo gnomone fu ricavata nel rosone (occhio). In seguito, Danti costruì un'altra apertura, più in alto, nelle tarsie a marmi verdi e bianchi che sovrastano l'occhio. Per far entrare la luce nella navata centrale della chiesa da questa apertura più alta, si rese necessario creare una feritoia nella volta della chiesa, visibile ancora oggi. Nella fig. 5 sono illustrate schematicamente le posizioni degli strumenti astronomici sulla facciata della chiesa e le aperture per i due gnomoni. Lo gnomone più basso poteva essere usato durante tutto l'anno, mentre la feritoia nella volta limitava l'uso dell'altro gnomone alle date prossime agli equinozi.
Quando negli anni Settanta del XX sec. furono eseguiti i lavori di restauro dell'occhio, ci si accorse che una piccola parte della vetrata era molto più nuova di quanto fossero le parti vicine e di conseguenza si ipotizzò che coincidesse con l'apertura dello gnomone inferiore. Il resoconto di Danti includeva uno schema che mostrava la dimensione dell'apertura in questione, sulla cui base si decise che doveva essere stata eseguita una copertura della feritoia originaria. Verso mezzogiorno, in date prossime all'equinozio, l'immagine che il Sole, passandovi, proiettava sul pavimento della chiesa doveva essere un'ellisse di lunghezza 38,5 cm e di larghezza 28,5 cm. Dopo aver lasciato i Medici, nella metà degli anni Settanta del 1500, egli lavorò come matematico presso la corte papale a Roma (dove fu debitamente consultato sulla proposta di riforma del calendario).
L'astronomia accademica
Come si è già detto, l'insegnamento dell'astronomia, all'epoca considerata una branca della matematica, era basato sul De sphaera di Sacrobosco. Quest'opera analizzava il moto della sfera delle stelle fisse, l'ordine delle sfere planetarie e quello degli 'elementi' (fuoco, aria, acqua e terra), il moto del Sole e, più approssimativamente, quello della Luna, allo scopo di spiegare le cause delle eclissi solari e lunari. Il Sole e la Luna erano generalmente classificati come 'pianeti', sebbene talvolta fossero caratterizzati come 'luminari'. In ogni caso, non era fatta alcuna netta distinzione tra la natura del loro moto e quello degli altri pianeti, cosicché l'introduzione all'astronomia fornita dal testo di Sacrobosco, scritta evidentemente a fini didattici per l'insegnamento presso l'Università di Parigi, doveva sembrare più generale ai lettori contemporanei di quanto non appaia oggi. La matematica propriamente detta era confinata da Sacrobosco a un livello minimo d'analisi, mentre era fornito un compendio dei primi due libri dell'Almagesto di Tolomeo. Maggiori dettagli matematici, e in particolare discussioni sul moto degli altri pianeti, erano contenute nella Theorica planetarum, che circolava sotto il nome di Gherardo da Cremona (1114 ca.-1187). In realtà, Gherardo fu solamente il traduttore di quest'opera, scritta in arabo nel IX sec. dall'astronomo musulmano al-Farġānī (l'Alfragano dei latini). Quest'ultimo, che visse a Baghdad, aveva basato il suo trattato sull'Almagesto. L'opera di Tolomeo, che presuppone una notevole conoscenza matematica da parte dei suoi lettori, era infatti ben conosciuta presso gli astronomi islamici, a partire dal IX secolo. Il livello dell'istruzione matematica sembra sia stato considerevolmente più alto nei paesi musulmani che nell'Occidente latino almeno fino alla prima parte del XV secolo. Probabilmente non fu un fattore secondario, nell'interesse dei Musulmani per l'astronomia, il fatto che competenze astronomiche fossero necessarie per stabilire i tempi della preghiera e, ancor più, la direzione della Mecca. L'esistenza di un numero rilevante di testi introduttivi, indica come, anche nel mondo islamico, l'Almagesto fosse considerato un testo troppo difficile per chi non avesse ampie conoscenze astronomiche. Gherardo da Cremona tradusse, oltre alla Theorica planetarum, anche l'Almagesto, in modo da renderlo accessibile agli studiosi di lingua latina. Questa traduzione fu stampata nel 1515, quale editio princeps dell'opera di Tolomeo. Poiché, allora come oggi, gli editori preferivano dare alle stampe opere che avessero un profitto, la stampa della traduzione di Gherardo è sintomatica della diffusione di cui quest'opera già da tempo godeva, mentre il fatto che nuovi commentari sul De sphaera di Sacrobosco continuassero a essere scritti e pubblicati fino al XVII sec. è una chiara conferma del fatto che anche questo libro continuasse a essere usato come manuale introduttivo.
Purbach e Regiomontano
Nello sviluppo della scienza astronomica, il revival associato al recupero dei testi greci si fa generalmente risalire al lavoro di Georg von Purbach (1423-1461) e del suo allievo Regiomontano (Johann Müller di Königsberg, 1436-1476).
Il nome Regiomontano è una versione latinizzata del nome del suo villaggio nativo Königsberg (Regiomontum in Franconia), ed egli stesso usa la forma Johann de Monte Regio. La famiglia Müller sembra essere stata sufficientemente agiata per sostenere l'educazione di Johann. Poco si conosce dei suoi primi studi; nel 1447, all'età di undici anni, entrò all'Università di Lipsia (fondata nel 1409). All'epoca era normale per i ragazzi entrare all'università superati da poco i dieci anni, e Regiomontano era un ragazzo solo un po' più giovane della maggior parte dei suoi compagni di corso.
Purtroppo si conosce ben poco dell'insegnamento impartito a Lipsia a lui e agli altri allievi, ma Regiomontano mostrò presto la sua competenza astronomica calcolando alcune tavole delle posizioni planetarie giorno per giorno (effemeridi) per gli anni 1447-1448. Nel 1450 si recò a studiare all'Università di Vienna, più distante ma molto più famosa. È molto probabile che a motivare questa scelta fosse la fama di Vienna in campo astronomico. Uno degli studiosi più in vista all'epoca, Georg von Purbach, era entrato in quella università nel 1446, ma non abbiamo nessun documento che vi attesti il suo insegnamento prima del 1454; Regiomontano lo menzionerà ripetutamente come suo insegnante. Il rapporto tra i due sembra essere diventato ben presto di collaborazione, piuttosto che un semplice rapporto tra maestro e allievo, ed essi eseguirono insieme osservazioni astronomiche.
Purbach può a buon diritto essere considerato una figura di spicco nel panorama culturale dell'epoca, ma è soprattutto la valutazione a posteriori dello storico che tende a far apparire la sua opera più significativa, nel suo apporto, rispetto a quella del suo famoso allievo. A lui, che aveva una grande esperienza come astronomo, si attribuiva la conoscenza a memoria di tutto l'Almagesto, nella versione latina di Gherardo da Cremona. Presumibilmente, fu la conoscenza completa del testo che lo spinse a scrivere una versione migliorata del compendio di Gherardo, o meglio di al-Farġānī (v. sopra). Egli chiamò questo suo nuovo trattato Theoricae novae planetarum. In questo contesto, il termine 'teorie' fa riferimento ai modelli per i moti dei pianeti. Da un punto di vista moderno, l'opera di Purbach sembra notevolmente differente da quella di Tolomeo per un aspetto estremamente significativo; mentre nell'Almagesto tutti i moti sono descritti da cerchi (che erano naturalmente prescritti dalle nozioni aristoteliche sul movimento dei corpi celesti), in Purbach figurano sistemi di sfere reali. In alcune delle prime edizioni a stampa, le sfere erano colorate in modo brillante, quasi certamente per agevolare la comprensione degli schemi altrimenti piuttosto complicati. Accentuare troppo questa differenza sarebbe tuttavia fuorviante. Infatti l'Almagesto può essere descritto, in un modo più appropriato, come un manuale avanzato di cinematica celeste in quanto l'opera si occupa esclusivamente di costruire modelli dei moti osservati. Sappiamo, infatti, da altri testi di Tolomeo, soprattutto dalle sue Ipotesi dei pianeti, che egli stesso assunse l'esistenza di un certo tipo di sfere, il cui moto era responsabile dei moti osservati dei pianeti. Così, il complesso di sfere di Purbach, che era di uso ormai comune al suo tempo, non è così tipicamente 'medievale' come si potrebbe supporre. Purbach l'aveva infatti ereditato da fonti islamiche, che, da ultimo, possono essere fatte risalire ai Greci. Inoltre, Purbach aveva effettivamente approntato un sistema di combinazione dei cerchi analogo a quello di Tolomeo, con i ben noti cerchi deferenti, ovvero le circonferenze lungo le quali si supponeva si muovesse il centro dell'orbita (epiciclo) di ogni pianeta. Tale sistema, come la combinazione delle sfere, era impiegato per ricostruire l'orbe di ciascun pianeta, ovvero l'insieme completo dei moti che potevano spiegare le posizioni osservate nel cielo. Questo impiego del termine orbis (orbe) non era affatto universale in quel periodo, ma è comunque utile dal momento che permette di distinguere la complicata entità composta dalle parti più semplici di cui essa è formata. Si deve anche notare che le 'sfere', che restituiscono nel loro complesso l'orbe di un pianeta, sono involucri sferici vuoti, di solito con una superficie interna che non è concentrica rispetto all'esterna. Così, 'sfera' è un termine fuorviante. In ogni caso, il contenuto dell'opera di Purbach, completata nel 1454, è esposto in modo molto chiaro e l'autore tiene in debito conto l'applicazione dei suoi risultati alla pratica astrologica, sicché ben presto l'opera finì col sostituire, nell'insegnamento dell'astronomia, la più vecchia Theorica planetarum. Le prime copie sono manoscritte (una è trascritta da Regiomontano di suo pugno), ma l'opera fu presto stampata e nuove edizioni, generalmente con commentari, furono pubblicate, a distanza di dieci anni l'una dall'altra, per tutto il corso del XVI secolo. Qualche edizione fu anche pubblicata nel corso del XVII secolo.
Il 5 maggio 1460 Bessarione, divenuto cardinale, arrivò a Vienna. Vi giungeva in qualità di nunzio apostolico di Pio II, per chiedere il sostegno del Sacro Romano Impero all'organizzazione di una Crociata contro i Turchi che avevano preso Costantinopoli il 29 maggio 1453. La Crociata si spinse, in realtà, solo fino ad Ancona, dove si arrestò a seguito della morte del papa, nel 1464. Pio II (al secolo Enea Silvio Piccolomini) fu un eminente umanista e mecenate di umanisti, ed egli stesso era stato segretario presso la cancelleria imperiale a Vienna, dal 1443 al 1455; nulla di strano, quindi, che egli scegliesse, come suo nunzio in questa circostanza, un umanista di grande erudizione, e per di più esperto conoscitore della lingua greca e della situazione bizantina. Le conseguenze intellettuali della missione si rivelarono, infatti, di gran lunga più interessanti di quelle politiche e militari. Non v'è dubbio che lo stesso Bessarione abbia nutrito un interesse per l'astronomia fin dalla giovinezza (v. cap. II); inoltre, egli aveva anche iniziato a tradurre in latino l'Almagesto da un manoscritto greco in suo possesso (che alla fine donò, insieme a tutta la sua magnifica collezione di manoscritti, alla Repubblica di Venezia, costituendo il nucleo iniziale di quella che sarà la Biblioteca Marciana di Venezia), ma i numerosi impegni gli impedirono di realizzare questo progetto. Tuttavia non lo abbandonò del tutto; piuttosto lo trasmise, in forma modificata, a Purbach, incontrato per l'appunto a Vienna, di cui certamente conosceva la grande fama di matematico, proponendogli di seguirlo a Roma e d'insegnargli il greco, con lo scopo di metterlo nelle condizioni di scrivere un compendio autorevole dell'Almagesto, basato sul testo originale in lingua greca. A sua volta, Purbach chiese e ottenne il permesso di portare Regiomontano con sé. Tutti e tre naturalmente ritenevano, come era consueto presso tutti gli umanisti del XV sec., che il testo greco originale avrebbe consentito una migliore e più chiara comprensione dell'astronomia rispetto a quella che si poteva ottenere dalla traduzione latina di Gherardo da Cremona, derivata a sua volta da una versione araba.
Purbach morì l'8 aprile 1461 e non portò a termine il suo lavoro sull'Almagesto. Da un'annotazione di Regiomontano, si può desumere che egli ne avesse completata circa metà. Condotto a Roma da Bessarione in quello stesso anno, Regiomontano terminò il lavoro sull'Almagesto, chiamato Epytoma in Almagestum Ptolomaei, nel 1462, rivedendo probabilmente anche la stesura della prima parte curata da Purbach. Il manoscritto terminato fu dedicato a Bessarione; l'opera fu stampata nel 1496. Questa edizione fu ampiamente letta dal momento che forniva il compendio più coerente dell'Almagesto disponibile all'epoca.
L'unica traduzione latina integrale dell'Almagesto, fatta dal greco, era stata completata nel 1451 a opera di Giorgio di Trebisonda, ma fu per lo più trascurata e considerata inutile, presentando, a quanto sembra, palesi fraintendimenti del contenuto matematico. Anche dopo la stampa del testo greco dell'Almagesto (nel 1583), l'Epitome di Regiomontano rimase la guida più utile per orientarsi nell'opera. Per ragioni che saranno considerate in seguito, non ci furono traduzioni dal testo greco finché l'Almagesto non divenne, nel XIX sec., un testo d'interesse puramente storico. Nel Rinascimento, gli studiosi che volevano conoscere Tolomeo avevano così due alternative, o leggerlo in greco o studiare l'Epitome di Regiomontano. Quest'ultima non è un semplice riassunto dell'Almagesto, il contenuto del trattato di Tolomeo vi risultava modificato così da divenire più rispondente alle esigenze dei contemporanei di Regiomontano; l'opera era organizzata in modo abbastanza differente dall'originale e includeva tanto i metodi matematici di Tolomeo, quanto aggiunte ricavate da fonti arabe più recenti. Il lavoro di Regiomontano fu quello di un astronomo, non di un filologo; egli aveva letto il testo di Tolomeo al fine di usarne i metodi e i risultati, non per farne un'analisi filologica e comprenderla nei suoi termini originali. Questa modalità di lettura era abbastanza comune tra i matematici rinascimentali, e si deve anche ricordare che molte pubblicazioni, per esempio l'eccellente traduzione di Archimede (1554) fatta da Federico Commandino, avevano, per la maggior parte dei loro lettori, un interesse matematico più che storico.
L'Epitome si rivelò utile ai successori di Regiomontano. Utili in modo meno immediato e decisamente rivolte al futuro furono alcune sue osservazioni astronomiche, o per meglio dire, le conclusioni che egli ne trasse. Il 17 dicembre 1461 Regiomontano osservò un'eclissi lunare a Roma. In quella circostanza, i pianeti Saturno, Marte e Venere erano abbastanza vicini tra loro, ed egli ebbe così modo di osservarne le posizioni. Le misurazioni furono naturalmente eseguite in rapporto alle stelle fisse più vicine. Quando le osservazioni furono convertite in calcoli, divenne chiaro che le tavole astronomiche tradizionali, le famose Tavole alfonsine, fornivano posizioni errate per tutti e tre i pianeti e per le stelle fisse. Altre osservazioni avevano sollevato difficoltà analoghe e Regiomontano non fu l'unico a notare i limiti di queste tavole. Tuttavia, uno sguardo al modello del moto di un pianeta di Purbach, che pur aveva semplificato effettivamente il quadro astronomico omettendo qualche dettaglio più sottile, servirà a ricordare come il sistema completo fosse, in realtà, molto complicato. Era perciò difficile decidere quali parti del complesso modello dovessero essere modificate. Al pari dei suoi contemporanei, sembra che Regiomontano fosse convinto che tutto ciò che si richiedeva era una semplice modifica.
Ma le cose non si rivelarono così semplici. Per la soluzione si dovette, infatti, aspettare oltre il 1600, con l'accurato lavoro di Johannes Kepler sulla traiettoria di Marte. L'applicazione dei metodi usati dagli Antichi e riportati a nuova luce dagli sforzi degli umanisti, fu importante per il successo finale di Kepler; ma cruciale fu soprattutto la sua adesione alla teoria copernicana. Il sistema copernicano fu senza alcun dubbio il contributo astronomico più importante di questo periodo.
Niccolò Copernico
Niccolò Copernico (1473-1543) era nato a Thorn, una città della Polonia, e non sappiamo quale fosse la sua lingua nativa. La famiglia apparteneva al ceto medio ed era abbastanza facoltosa. Copernico trascorse molto tempo della sua vita nell'entourage dello zio materno, Luca Watzelrod, vescovo della Warmja. Egli studiò prima all'Università di Cracovia, dal 1491 al 1495, dove imparò i primi rudimenti di astronomia, e fece quindi due viaggi in Italia. Frequentò corsi di diritto canonico e civile a Bologna (1496-1501), corsi di medicina a Padova (1501-1503), e alla fine si laureò in diritto canonico presso l'Università di Ferrara nel 1503. Soggiornò anche a Roma. Mentre si trovava in Italia, Copernico eseguì qualche osservazione astronomica, all'inizio in collaborazione con il suo insegnante di matematica a Bologna, Domenico Maria Novara, ma non c'è alcuna indicazione di una sua intenzione di dedicarsi alla carriera di mathematicus. Tuttavia, egli deve aver mostrato una notevole competenza, dal momento che tenne lezioni di astronomia a Roma, e gli fu chiesto di esprimere un'opinione sui più recenti progetti di riforma del calendario (richiesta che egli poi declinò). Molto probabilmente, l'idea di presentare un modello dell'Universo in cui il Sole fosse immobile, e la Terra in movimento intorno a esso, risale proprio agli anni trascorsi in Italia. Un breve compendio, generalmente conosciuto come Commentariolus, sembra sia stato scritto nel 1513 su richiesta di un cardinale romano. Questo scritto non fu stampato, ma circolava in forma manoscritta, e lo stesso Tycho Brahe ne possedeva una copia. Dopo essersi addottorato a Ferrara, Copernico ritornò nella sua terra natale. Sembra che egli avesse stabilito pochi contatti con altri studiosi, e che si fosse semplicemente limitato a continuare a sviluppare una versione completa del suo sistema. Calcolò anche alcune effemeridi, che, a quanto pare, furono completate entro il 1535; ma queste tavole non furono stampate e quasi certamente sono andate perdute. Nel rielaborare i dettagli del suo sistema, Copernico fece diverse osservazioni delle posizioni planetarie. Lo strumento adoperato era derivato da una descrizione di Tolomeo ed era usualmente chiamato 'regolo parallattico'; molti anni dopo, sarà Tycho Brahe a realizzare una sua versione di questo strumento, quale è illustrata nel suo libro, Astronomiae instauratae mechanica. Copernico utilizzò diciassette delle sue osservazioni nella descrizione del moto dei pianeti contenuto nel De revolutionibus. Sebbene sopravviva un manoscritto autografo dell'opera che riporta questo titolo, l'opera pubblicata a Norimberga nel 1543 presentava il titolo più esteso di De revolutionibus orbium coelestium. Nell'introduzione Copernico afferma di aver lavorato alla sua realizzazione per più di ventisette anni. Dal momento che il manoscritto andò alle stampe nel 1542, Copernico dovrebbe aver iniziato l'opera prima del 1515. Tuttavia, egli asserisce anche di essere stato riluttante a darlo alle stampe; in tal caso, si dovrebbe supporre che egli non impiegò esattamente ventisette anni per completare l'opera (sebbene si debba tener conto dell'uso retorico di affermazioni simili). Occuparsi d'astronomia non fu comunque l'unica attività svolta da Copernico. Come canonico della cattedrale di Frauenburg, era anche amministratore della diocesi di Warmja; esercitò inoltre la professione di medico, campo nel quale riscosse una certa reputazione per le sue competenze. Una xilografia, che risale probabilmente a non molto tempo dopo la sua morte, lo ritrae con uno stelo di mughetto, tipico emblema dei medici (il mughetto era usato, infatti, nel trattamento di malattie cardiache).
Nonostante il suo isolamento (come Copernico stesso lo chiama), il suo lavoro astronomico sembra sia stato conosciuto nella cerchia dei dotti, probabilmente attraverso scambi epistolari, sebbene non rimanga nessuna lettera al riguardo. Un giovane professore di matematica dell'Università di Wittenberg, Georg Joachim von Lauchen, meglio noto come Rhaeticus o Retico (1514-1576), venne a sapere del lavoro di Copernico e lo andò a trovare a Frauenburg. La città, collocata sull'estuario del fiume Vistola, vicino al porto di Danzica, non era così inaccessibile come i commenti di Copernico potrebbero indurre a pensare: Rhaeticus vi giunse nel 1539. Sembra che abbia molto apprezzato la compagnia di Copernico, del quale scrisse in un tono encomiastico. Il suo entusiasmo incise certamente nel convincere Copernico a pubblicare il De revolutionibus superando la sua iniziale riluttanza. Si ha ragione di credere che Copernico avesse in origine sperato che il suo sistema fosse più semplice di quello tradizionale geocentrico (v. sotto) e ciò non corrispondeva del tutto con il risultato finale. Rhaeticus lo convinse anche a lasciargli scrivere una breve esposizione riassuntiva del nuovo sistema, che pubblicò sotto il titolo di Narratio prima de libris revolutionum (1540). Il fatto che Copernico permettesse quest'operazione editoriale, fa supporre che non avesse ancora completato il lavoro sul De revolutionibus.
Copernico non ha lasciato alcuna traccia di come giunse a considerare un modello di sistema planetario in cui il Sole e le stelle fisse sono immobili e i moti comunemente attribuiti a essi dagli astronomi sono invece attribuiti alla Terra. Probabilmente considerò ciò trascurabile, dal momento che non rivendica mai l'originalità della sua teoria. Anzi, afferma che essa risale ai tempi antichi, e precisamente che fu sostenuta dai pitagorici e in particolare da Aristarco di Samo (310 ca.-250 a.C.; il riferimento ad Aristarco, che si trova solo nel manoscritto, risulta cancellato nella versione a stampa del De revolutionibus). Gli studiosi moderni concordano con Copernico nell'attribuire ad Aristarco un sistema planetario eliocentrico, ma appare anche chiaro che, sebbene i pitagorici credessero che la Terra si muovesse, essi ritenevano che sia essa sia il Sole, insieme agli altri pianeti, si muovessero intorno a un 'fuoco centrale'. Inoltre, non si hanno motivi particolari per annoverare Aristarco tra i pitagorici. Possiamo comunque notare che nel XVI sec. la credenza relativa al moto della Terra era usualmente designata come 'pitagorica'; per questa ragione il termine si applicò comunemente ai sostenitori della teoria copernicana.
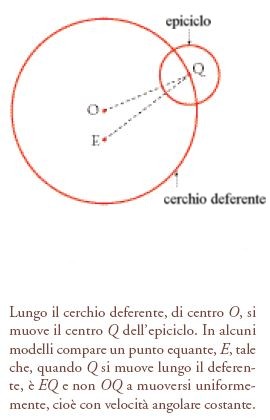
L'obiezione principale di Copernico contro l'astronomia tradizionale nel De revolutionibus concerne la filosofia naturale. Se i cieli devono avere solo moti circolari uniformi, come i filosofi sostengono, allora non è lecito permettere che il centro di un epiciclo si muova lungo un deferente con una velocità che appare uniforme solo se riferita alla velocità angolare di una linea congiungente il centro dell'epiciclo con un punto che non è il centro del cerchio deferente. Questo era, infatti, il genere di moto circolare usato dagli astronomi; il punto rispetto al quale la rotazione era uniforme, era chiamato 'equante' (fig. 8). È chiaro che questo genere di moto, che non è uniforme rispetto al centro geometrico della sfera, non sarebbe possibile se la sfera fosse concepita come un corpo rigido. L'uso degli equanti non è dunque compatibile con il sistema di sfere ruotanti, che restituisce l'orbe planetario illustrato nello schema di Purbach. Gli astronomi facevano uso degli equanti perché in questo modo potevano descrivere più esattamente il moto osservato dei pianeti. In generale, essi non erano chiamati a giustificare questa procedura. Come risulta evidente da vari passi del De revolutionibus, Copernico credeva anch'egli nelle sfere solide. Questa credenza sarebbe parsa accettabile a molti filosofi naturali suoi contemporanei, i quali, nondimeno, avrebbero senza dubbio convenuto con l'obiezione di Copernico sugli equanti. Tuttavia, la soluzione che egli propose fu estremamente radicale, non meno però dell'ascrivere il movimento alla Terra, in modo del tutto incompatibile con le idee tradizionali della fisica. Ma non era del tutto evidente in che modo il sistema modificato avrebbe potuto evitare gli equanti; Copernico si limitava a dire che, nel corso dell'opera, avrebbe mostrato questa caratteristica del sistema. Sebbene l'insoddisfazione per gli equanti non appaia nel Commentariolus, Copernico affermava in quel primo abbozzo della sua teoria che il suo nuovo sistema sarebbe stato più semplice dell'astronomia geocentrica tradizionale. Quest'affermazione non compare più nel De revolutionibus. Il motivo evidente di questa omissione è dovuto al fatto che il sistema copernicano, esposto nella sua interezza in quella sede, non è affatto più semplice. Almeno, non lo è se si applica il criterio di contare il numero dei moti circolari, cioè i deferenti, gli epicicli, e così via. Alcuni storici si sono divertiti a mostrare che Copernico finì addirittura con l'ipotizzare più cerchi di Tolomeo. La spiegazione di questo risultato sarà data più avanti. In ogni caso, sembra molto probabile che, non appena ebbe elaborato i dettagli del suo sistema, Copernico notasse la sua crescente complessità rispetto a quanto egli aveva in origine sperato. Può essere stato proprio questo imprevisto e scomodo aumento di complessità a trattenerlo così a lungo dal dare alle stampe il lavoro. È possibile che dietro l'affermazione secondo cui gli equanti potevano essere omessi, affermazione che troviamo nel testo definitivo dell'opera De revolutionibus, ci fosse quella stessa speranza di una maggiore semplicità espressa nel Commentariolus. Sebbene le opinioni degli storici siano tutt'altro che unanimi riguardo al modo in cui Copernico giunse alla sua teoria, molti probabilmente sarebbero d'accordo nell'attribuire al problema degli equanti una qualche importanza nel processo di scoperta.
D'altra parte, perché egli propose l'alternativa di una Terra in movimento? Si può supporre che dietro questa decisione stiano le sue idee sulla fisica, che ai suoi tempi erano lungi dall'essere ampiamente accettate (e così avverrà anche in seguito), ma ciò non sembra molto probabile. Non esiste alcuna evidenza che Copernico abbia mai fatto uno studio approfondito degli aspetti rilevanti della filosofia naturale, cioè dei concetti di forma e moto. Le sue idee in proposito sembrano invece derivare, più o meno direttamente, dalla filosofia naturale di Niccolò Cusano, il cui interesse per la filosofia naturale fu quello di un teologo. In particolare, egli considerò la matematica come un modo per condurre l'anima a riflettere su verità trascendenti, fino a comprendere la natura stessa di Dio, attraverso procedimenti anagogici.
Questo particolare punto di vista non consente sempre di elaborare una buona matematica; sono numerosi gli esempi di autori che hanno piegato il rigore della dimostrazione matematica alle esigenze di una tesi teologica. Tuttavia, Cusano fu un matematico competente, ebbe idee originali, e il suo De docta ignorantia (1440) contiene aspetti, per esempio la discussione sull'infinito, interessanti da un punto di vista matematico; questo spiega il motivo per cui, sebbene oggi si tenda a considerare Cusano come un 'mistico', Kepler, che era un grande matematico e che al tempo stesso concepì tutta la filosofia naturale come anagogia, tenne in gran conto il lavoro di Cusano. Quest'ultimo abbracciò l'idea per cui ogni corpo può essere considerato in relazione al proprio centro, piuttosto che in relazione al centro dell'Universo (egli credeva, infatti, che l'Universo fosse infinito e dunque non avesse un centro), e l'idea secondo cui un corpo sferico esprime la sua natura mediante la rotazione poiché, così facendo, esso si muove nel volume che già occupa. Ecco quindi che le sfere dei cieli ruotano non perché sono costituite di etere (come sosteneva Aristotele), ma per il semplice fatto di essere sfere. Nella descrizione aristotelica del moto, ciascun elemento aveva un moto naturale e un proprio luogo naturale cui esso naturalmente tendeva.
Il moto naturale dell'elemento Terra era verso il basso e dunque il suo stesso luogo naturale era il più basso, nel centro del sistema, quello appunto occupato dalla Terra nel sistema tolemaico. L'alternativa di Cusano rendeva possibile collocare la Terra in un luogo che non fosse il centro. Copernico adottò questa alternativa nel De revolutionibus, senza tuttavia menzionare mai Cusano. Si può ragionevolmente supporre che egli ne conoscesse l'opera già dal suo soggiorno in Italia. Il De docta ignorantia fu stampato, in una raccolta di scritti di Cusano, nel 1490 e ancora nel 1502, mentre il De quadratura circuli uscì insieme con la prima edizione a stampa del De triangulis di Regiomontano, un abbinamento indicativo della grande considerazione di cui Cusano godeva come matematico. La sua evidente dipendenza dalle idee di Cusano rende piuttosto improbabile che la fisica non tradizionale, proposta da Copernico a supporto del moto della Terra, fosse il punto di partenza effettivo per la progettazione del nuovo sistema astronomico. Gli storici hanno avanzato diverse ipotesi per ricostruire la genesi del sistema copernicano, per individuare ciò da cui egli concretamente prese le mosse; nessuna di esse, tuttavia, appare del tutto soddisfacente. L'ipotesi, abbastanza semplice, che svilupperemo qui di seguito è sorretta da molte evidenze circostanziali e può contribuire a far luce sul modo in cui Copernico giunse a proporre il suo sistema 'pitagorico'.
Nella sua introduzione al De revolutionibus, Copernico menziona la ripresa del modello del sistema planetario proposta da Eudosso di Cnido (408 ca.-355 a.C. ca.) in cui tutte le sfere hanno lo stesso centro, ma una varietà di assi. Copernico si lamentava di vivere in un angolo di mondo, senza poter essere aggiornato sugli sviluppi intellettuali, cosicché può destare meraviglia la sua conoscenza degli Homocentrica sive de stellis di Girolamo Fracastoro (1483 ca.-1553), pubblicati a Padova nel 1530. D'altra parte, egli può aver conosciuto l'autore; Fracastoro studiò, infatti, medicina a Padova nello stesso periodo in cui vi si trovava Copernico.
Uno degli effetti più evidenti della rinascita di interesse per i testi antichi nel XV sec. consistette proprio nell'attenzione che gli studiosi cominciarono a prestare anche alle opere di autori meno noti di Aristotele e di Tolomeo. La ricostruzione operata da Fracastoro della teoria di Eudosso ne è un chiaro esempio. Tanto lui quanto Copernico discussero i due principali sistemi planetari, a loro tempo menzionati e respinti da Aristotele e da Tolomeo, e decisero di ricostruirli. Dei due, Fracastoro si occupò del sistema di Eudosso e Copernico di quello dei pitagorici.
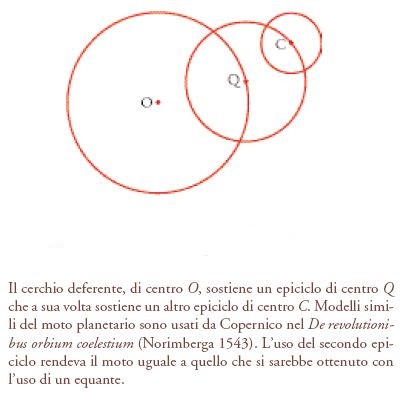
Come Copernico, anche Fracastoro era fermamente convinto che gli unici moti possibili dovessero essere uniformi e circolari. Egli cita semplicemente l'autorità di Aristotele in materia, e i suoi ripetuti riferimenti allo Stagirita sono il segno tangibile della presentazione di argomenti scientifici. Un'opinione dotta sull'opera fu espressa, in modo succinto dall'allievo di Commandino, Bernardino Baldi, nell'ultimo decennio del 1500 quando, nella sua biografia su Fracastoro, affermò che gli Homocentrica erano corretti dal punto di vista della filosofia (cioè, della filosofia naturale) ma non erano in accordo con le osservazioni astronomiche. Ben diversamente agì Copernico. Egli fece un certo numero di osservazioni che l'aiutarono a fissare la dimensione dei cerchi e la posizione dei loro centri. I calcoli richiesti erano di fatto quelli standard nell'astronomia del tempo, poiché i modelli del moto planetario di Copernico erano costruiti esattamente nello stesso modo di quelli di Tolomeo, se si eccettua l'aggiunta di ulteriori epicicli, centrati a loro volta sugli epicicli originari, per riprodurre gli effetti di moto tradizionalmente spiegati mediante il ricorso agli equanti. Questo procedimento fu applicato alla maggior parte dei modelli; soltanto in pochi di essi furono lasciati gli equanti (fig. 9). La vera differenza tra il sistema di Copernico e quello geocentrico tradizionale risiedeva, naturalmente, nella collocazione del Sole immobile al centro dell'Universo, attribuendo il suo moto annuale alla Terra, e considerando immobile la sfera delle stelle fisse (assegnando, anche in questo caso, la sua rotazione diurna alla Terra). C'è tuttavia poco di innovativo nello schema copernicano. La versione a stampa è abbastanza fedele alle proporzioni mostrate nella figura del manoscritto finale autografo di Copernico e l'illustrazione è molto simile a quelle usate per il sistema planetario geocentrico. In entrambi i casi si possono vedere soltanto le superfici degli orbi planetari, è omesso invece il complesso sistema di sfere che restituiscono ogni singolo orbe. Disegnando poi gli orbi come aventi quasi tutti un eguale spessore, Copernico ha di fatto trascurato una delle proprietà più caratteristiche del suo sistema, che permette di calcolare, a partire dalle osservazioni, quale dimensione ciascun orbe debba avere, e conseguentemente di mostrare i pianeti nell'ordine corretto di disposizione rispetto al Sole. Ciò può essere fatto perché nel sistema copernicano ciascuna componente annuale nel moto apparente di un pianeta (vista rispetto al cielo delle stelle fisse) deriva dal moto annuale della Terra, e la sua estensione angolare è determinata proprio dalla sua distanza da essa. In altre parole, gli epicicli dei moti dei pianeti 'superiori' (quelli al di sopra del Sole nel vecchio sistema geocentrico) e i deferenti dei pianeti 'inferiori' (quelli al di sotto del Sole nel sistema geocentrico) sono effetti determinati dal moto della Terra. Copernico menziona, nella sua opera, questa proprietà sistematica della sua nuova teoria planetaria, mettendo a diretto confronto le parti del sistema planetario con quelle del corpo umano.
Questo implica che la proporzione corretta sia significativa, ma egli non affronta l'argomento ulteriormente e, come Tolomeo, si occupa separatamente del moto di ciascun pianeta, senza tentare di mostrare una qualche relazione tra le varie orbite. Inoltre, i moti planetari sono basati così da vicino su quelli descritti nell'Almagesto che non è realmente corretto chiamare il sistema di Copernico eliocentrico. Di fatto, esso afferma solo l'immobilità del Sole. Il centro dei moti, cioè il centro comune rispetto a cui i cerchi deferenti sono variamente bilanciati, non è in realtà il Sole ma il centro dell'orbita della Terra. Così il fantasma del geocentrismo continua ad aleggiare nel sistema planetario di Copernico.
Inoltre, a giudicare dal numero dei cerchi usati per ricostruire il completo insieme degli orbi planetari, il sistema copernicano non era più semplice di quello geocentrico. Se visto con gli occhi di un matematico del XX sec., è facile riconoscere come il sistema copernicano, con tutti gli orbi planetari riferiti al centro dell'orbe terrestre, sia semplicemente una variante del sistema tolemaico, considerato rispetto a un centro differente. I moti sono stati trasferiti dal Sole e dalle stelle fisse alla Terra, ma non sono stati in sé stessi modificati, e neppure lo è stato l'apparato usato per ricostruirli. Ci sono motivi sufficienti per credere che i due sistemi usassero lo stesso numero di cerchi componenti, dal momento che tutta la novità del sistema copernicano si riduce in realtà a una mera trasformazione di coordinate.
Questo modo di ragionare era tuttavia del tutto sconosciuto nella prima metà del XVI secolo. In particolare, esso implica il concetto di moto relativo piuttosto che assoluto, un concetto che si rivelò difficile da afferrare all'epoca. Molti degli argomenti addotti contro il moto della Terra nel XVI e XVII sec. fanno perno proprio sulla difficoltà che si aveva a concepire il moto relativo; ne sono esempi classici l'argomento per cui, se la Terra stesse ruotando, una palla da cannone sparata verso est, cioè nella direzione della rotazione diurna della Terra, dovrebbe percorrere una distanza maggiore di quella percorsa da una palla da cannone sparata verso ovest, e l'altro argomento per cui se la Terra fosse in movimento, un corpo lasciato cadere dall'alto di una torre non cadrebbe esattamente ai suoi piedi.
La ricezione dell'astronomia di Copernico
Copernico morì il 24 maggio 1543; il De revolutionibus orbium coelestium fu pubblicato nello stesso mese, e si racconta che una copia stampata fosse data a Copernico sul letto di morte. In ogni caso, il libro dovette combattere la sua battaglia senza l'aiuto dell'autore e non mancarono complicazioni. L'editore Andreas Osiander (1498-1552), rispettato teologo riformato, aveva scritto una prefazione senza firma, che apparve nell'opera stampata e, in assenza di altri nomi, fu ascritta naturalmente allo stesso Copernico. Osiander stava lavorando a Norimberga, all'epoca in cui Copernico si trovava a Frauenburg, e Rhaeticus, il precedente editore, insegnava all'Università di Lipsia; la comunicazione tra i tre dovette procedere molto lentamente, sicché Osiander si risolse a pubblicare la sua prefazione senza aver consultato né Copernico né Rhaeticus. È evidente che non li consultò poiché la sua prefazione, su molti punti, è in disaccordo con quanto asserito nell'opera scritta da Copernico. Osiander dice che il nuovo sistema ha carattere semplicemente matematico, fornisce un nuovo modo di calcolare le posizioni apparenti dei pianeti e, come tutte le ipotesi astronomiche del genere, non deve essere considerato vero o probabile, ossia non ha la pretesa di possedere la verità ultima sulla struttura dell'Universo. Una simile posizione è oggi chiamata 'finzionalismo'. Essa rappresenta una forma forte della separazione generalmente accettata tra astronomia (come matematica) e filosofia naturale. Nell'accogliere esplicitamente, in questo contesto, il 'finzionalismo', Osiander può aver seguito le sue idee in materia di religione. Copernico, fedele alla Chiesa cattolica, aveva dedicato la sua opera a papa Paolo III (Alessandro Farnese, nato nel 1468, fu papa dal 1534 al 1549), ma Osiander era probabilmente consapevole dell'ostilità di Martin Lutero, che qualche anno prima aveva detto di Copernico: "Questo insensato vuole sovvertire l'intera scienza astronomica. Ma, come dichiarano le Sacre Scritture, fu al Sole e non alla Terra che Giosuè ordinò di fermarsi" (Tischreden, 4638, IV, pp. 412-413). Il passo biblico, cui Lutero allude è Giosuè, 10, 12, dove Giosuè, rivolgendosi al Sole e alla Luna, dice: "O sole fermati a Gabaon e tu, o luna, alla valle di Aialon". I versetti successivi raccontano come il desiderio di Giosuè fosse esaudito: "E il sole si fermò, e la luna ristette […]. Il sole stette fermo in mezzo al cielo e non s'affrettò al tramonto quasi un giorno intero". Questi due versetti tratti dal libro di Giosuè, e altri passi simili tratti da altri libri del Vecchio Testamento, furono ripetutamente usati nel secolo successivo come argomenti contro la verità del sistema copernicano. Dal momento che la verità letterale del testo biblico era materia sulla quale i cattolici, soprattutto dopo il Concilio di Trento, cercavano di sembrare altrettanto intransigenti dei protestanti, negli ultimi anni del XVI sec. e nei primi del XVII sec., tale argomento crebbe in importanza anziché diminuire.
Tra i matematici professionisti, ai quali era primariamente indirizzata, l'opera di Copernico fu accolta con rispetto e con moderato entusiasmo. La sua teoria dei pianeti, ossia i suoi modelli matematici per i moti, fu ben accolta sia in sostituzione dei modelli più vecchi, sia per la capacità di incorporare nuovi parametri, dedotti da osservazioni recenti. Le nuove osservazioni e le nuove teorie avrebbero consentito, questo almeno nelle speranze, di superare alcuni dei problemi sollevati dalle teorie più vecchie.
Il De revolutionibus orbium coelestium e l'Almagesto hanno una struttura simile; Copernico tratta dapprima del sistema del mondo, inclusi argomenti generali tratti dalla fisica, e quindi si occupa dei singoli pianeti, in termini puramente matematici. Adottando questo piano di esposizione, egli tende a sottolineare gli aspetti tecnici del suo lavoro, facilitando così un'interpretazione in linea con il finzionalismo di Osiander. In ogni caso, sembra che molti degli astronomi che lessero il De revolutionibus videro in quest'opera nient'altro che un testo in grado di fornire un nuovo approccio matematico, o comunque interessante solo da questo punto di vista. Essa godette di molto prestigio come opera a carattere matematico, ed Erasmo Reinhold (1511-1553), che insegnò matematica all'Università di Wittenberg, se ne servì come base per calcolare, nel 1551, nuove tavole, le Tavole pruteniche (Tabulae Prutenicae, cioè 'Tavole prussiane'). Fu soprattutto tra i filosofi naturali che la nuova forma di astronomia fu apprezzata per la sua capacità di aprire nuove questioni che andavano ben oltre il campo dell'astronomia e appartenevano piuttosto al regno della filosofia naturale. Lo stesso Copernico dovette avvertire la presenza di tali risvolti, quando afferma, per esempio, che considerando immobile la sfera delle stelle fisse, egli aveva di fatto inficiato il tradizionale argomento contro la sua natura infinita, vale a dire la dimostrazione aristotelica, esposta nella Fisica, per cui un corpo infinito non può muoversi. Egli, tuttavia, consegnava immediatamente la questione ad altri: "Infatti, il movimento è l'argomentazione fondamentale su cui si fa leva per dire che il mondo è limitato. Se il mondo sia finito o infinito, lasciamo pure alla disputa dei filosofi naturali" (De revolutionibus orbium coelestium, I, cap. 8).
Dal momento che Copernico conosceva alcune delle idee fisiche sostenute da Cusano nel De docta ignorantia, egli presumibilmente era anche a conoscenza della discussione cusaniana sulla natura infinita dell'Universo, che costituisce uno degli argomenti principali del trattato. Non si conosce quale fosse esattamente la diffusione delle opere di Cusano, ma il tenore del suo lavoro è conforme alla tendenza summenzionata propria degli umanisti di volgere l'attenzione, dalle opere ben conosciute di Aristotele, a quelle di autori relativamente trascurati. Tra questi si deve annoverare anche Platone, il quale nei secoli precedenti era stato conosciuto quasi esclusivamente per il Timeo, ampiamente studiato attraverso la mediazione di un commentario di Calcidio (IV-V sec. d.C.), il quale, peraltro, dedicava scarsissima attenzione al contenuto matematico dell'opera. Non è difficile accorgersi come dietro l'uso anagogico che Cusano fa della matematica, si trovi qualcosa di molto simile alla credenza platonica per cui le verità della matematica sono tali da poter determinare la struttura del mondo e le proprietà dei corpi. Le opere di Cusano e di Platone potevano essere apprezzate da un filosofo propenso a vedere le ipotesi astronomiche non come una mera base per calcoli, ma piuttosto riferite alla vera struttura dell'Universo.
Questa fu, per esempio, la posizione sostenuta da Giordano Bruno (1548-1600). Sebbene sia difficile stabilire fino a che punto Bruno avesse compreso l'opera di Copernico, egli si presentò comunque come un suo difensore e tale fu generalmente considerato. Oltre all'importanza che riveste il Sole nel nuovo sistema, Bruno sostiene la necessità di un Universo infinito. Di conseguenza egli non colloca il Sole vicino al centro geometrico del sistema planetario; infatti, rendendo l'Universo infinito egli aveva rinunciato alla possibilità di considerare il Sole ciò che Copernico chiamava "una lampada" posta al centro per illuminare il mondo (De revolutionibus orbium coelestium, I, cap. 10).
Abbastanza rapidamente si venne a sapere che la prefazione al De revolutionibus era di Osiander, probabilmente perché si seppe che Rhaeticus e altri amici di Copernico avevano cercato, inutilmente, di persuadere l'editore a ritirarla. All'epoca, tuttavia, fu il finzionalismo a dominare; esso fece di Copernico il dotto matematico il cui lavoro servì da base per le nuove tavole calcolate da Reinhold. Tuttavia, con il passare degli anni anche le Tavole pruteniche cominciarono a mostrare i loro limiti. Il loro successo iniziale era dovuto alla capacità di incorporare osservazioni recenti, ciò implicava che il modello usato per fare predizioni non richiedeva ulteriori ricognizioni di dati oltre quelli già disponibili. Con il tempo si rese però necessaria una maggiore estrapolazione dei dati, mentre l'affidabilità dei risultati si riduceva. Questo era già accaduto a tutte le tavole precedenti; la loro progressiva inadeguatezza nel tempo era un fatto ben conosciuto, sebbene non compreso. Era dunque necessario fare nuove osservazioni e calcolare le nuove tavole. Quel che accadde nella seconda metà del XVI sec. fu tuttavia una sorta di distruzione totale. Per ragioni che solo parzialmente sono chiare, fu eseguito un gran numero di osservazioni, molto più di quante fossero in principio necessarie per fissare i parametri dei modelli dei moti planetari. Si affermò anche un nuovo interesse, o almeno un nuovo grado di interesse, per la precisione (misurare su una scala che consentisse di effettuare misurazioni precise di entità molto piccole), probabilmente derivante da una migliore comprensione di quel che oggi verrebbe chiamato 'errore d'osservazione' (l'incertezza in una misurazione dovuta alle condizioni al contorno). Storicamente, l'idea secondo cui raccogliere una gran quantità di dati costituisce un valido aiuto nella formulazione di una risposta corretta, sembra appartenere a settori non matematici della filosofia naturale come la medicina. La sua diffusione nel XVI sec. può forse essere associata all'enfasi con cui, per esempio, Paracelso raccoglieva dati. In astronomia, grandi raccolte di dati furono effettuate dal langravio Guglielmo IV d'Assia-Cassel (conosciuto come Guglielmo il Saggio, 1532-1592) e da Tycho Brahe.
Il langravio d'Assia-Cassel
Guglielmo IV, langravio d'Assia-Cassel, ricevette un'ampia educazione umanistica in cui la teologia aveva avuto un posto importante, succedette formalmente a suo padre nel 1567, sebbene già prima di quella data avesse preso parte all'attività di governo. Fu un abile governante, e oltre questa sua attività pubblica, nutrì anche uno spiccato interesse per l'astronomia. Le sue ricerche furono finalizzate alla determinazione sempre più accurata delle posizioni delle stelle fisse. Le posizioni di tutti i corpi celesti furono misurate considerando le loro distanze angolari relative alle stelle fisse più vicine adeguatamente visibili. Tuttavia, a parte un'eccezione, queste ricerche non produssero nessuna grande sorpresa né causarono direttamente un cambiamento nella teoria astronomica. Così, nonostante la sua innegabile importanza, e l'ampio riconoscimento presso i contemporanei, il lavoro del langravio è menzionato soltanto brevemente dalla maggior parte degli storici. L'eccezione di cui si diceva, consiste nella serie di osservazioni relative alla 'nuova stella' che apparve nella costellazione di Cassiopea l'11 novembre 1572. Poiché egli aveva passato anni a fare precise misurazioni delle posizioni delle stelle fisse e dei corpi celesti, era particolarmente ben preparato a osservare anche il nuovo fenomeno. Le sue osservazioni rivelarono come questa 'nuova stella' non si muovesse rispetto al cielo delle stelle fisse; essa dava piuttosto la sensazione di appartenere alla loro stessa sfera. Le osservazioni di Tycho Brahe in proposito confermarono il suo parere (v. oltre). Questa conclusione era naturalmente contraria all'usuale credenza aristotelica secondo cui niente si modifica nel mondo celeste. Il supporto che il langravio fornì a queste conclusioni contribuì notevolmente a minare il generale assenso su questo punto. Fortunatamente, la costellazione di Cassiopea è circumpolare alla latitudine dell'osservatorio del langravio a Cassel (poco sopra 52° N), ossia, osservate da Cassel, le stelle di Cassiopea sono sufficientemente vicine al Polo Nord celeste da rimanere visibili tutta la notte. Infatti, all'inizio la 'nuova stella' era così luminosa da essere visibile anche di giorno. La sua alta latitudine celeste aveva anche un altro vantaggio, oltre quello di permettere una serie ininterrotta di osservazioni, infatti maggiore è l'altezza sull'orizzonte celeste, minore è l'interferenza causata dalla rifrazione dovuta all'atmosfera terrestre. Già gli antichi Greci avevano notato che quando i corpi celesti erano osservati in prossimità dell'orizzonte, la loro separazione angolare verticale non era la stessa di quando essi erano osservati a una latitudine celeste maggiore. Dal momento che non si poteva sempre evitare di eseguire osservazioni di corpi celesti a una bassa latitudine, furono sviluppate alcune regole che permettevano aggiustamenti appropriati a una certa altezza osservata sopra l'orizzonte. Quando l'altezza superava un certo numero di gradi, gli aggiustamenti erano considerati nulli. Queste regole per compensare gli effetti della rifrazione erano dedotte dalle stime dell'altezza dell'atmosfera terrestre e dalle varie modalità di combinazione del raggio incidente con quello rifratto (la legge di rifrazione, usualmente chiamata legge di Snellius dal nome del filosofo naturale Willebrordus Snellius ‒ il quale in realtà non la scoprì ‒ rimase infatti sconosciuta fino all'inizio del XVII sec.). Le stime dell'altezza della parte rifrangente dell'atmosfera terrestre erano generalmente basate sulle misurazioni della rifrazione, mentre attraverso ripetute misurazioni dell'altezza delle stelle, si verificava che l'altezza osservata fosse in accordo con quanto previsto dalle tavole. Il calcolo era in tal modo viziato da uno spiccato elemento di circolarità, ogni volta che le stime relative alla rifrazione erano applicate per correggere le posizioni delle stelle riportate nelle tavole. Di conseguenza, il langravio dovette fare ripetute osservazioni delle medesime stelle a differenti altezze. Tutte le posizioni delle stelle erano misurate considerando la loro distanza dalle stelle luminose più vicine, cosicché si rendeva innanzi tutto necessario misurare le posizioni di queste stelle, per stabilire una struttura di punti di riferimento rispetto alla quale le posizioni delle altre stelle potessero poi essere facilmente misurate. Il langravio non eseguì da solo, ovviamente, tutte le osservazioni, ma poté fare affidamento sulla collaborazione di un gruppo di astronomi.
Il più noto tra questi fu Christopher Rothmann, che godette di ampia stima nel mondo intellettuale. La ricchezza di cui il langravio poteva disporre gli consentì anche di poter avere i migliori strumenti astronomici dell'epoca. I nuovi modelli dei dispositivi furono realizzati dagli artigiani in cooperazione sia con il langravio sia con i suoi astronomi, e già i contemporanei restarono ammirati dall'alta qualità del lavoro artigianale testimoniata da tali strumenti. Infatti, le persone a cui il langravio li commissionò erano tra i più importanti e rinomati artigiani del tempo; tra essi, il famoso artefice di strumenti e orologiaio Jobst Bürgi (1572-1632). Pochissimi dei suoi strumenti sono pervenuti fino a noi; probabilmente una volta vecchi o superati, erano fusi e il metallo riutilizzato. È rimasto, tuttavia, qualche globo celeste che Bürgi e altri realizzarono per il langravio, nel quale un ingegnoso complesso di ingranaggi consente di riprodurre i moti della sfera delle stelle e quelli dei pianeti lungo l'eclittica. Qualche globo più grande presenta tacche in corrispondenza delle posizioni delle stelle, in modo tale da consentire di puntare gli angoli con il compasso e, così facendo, di eseguire calcoli approssimati implicanti triangoli sferici, così come è richiesto per ricavare le posizioni dalle mere osservazioni astronomiche. Dopo la morte del langravio, Bürgi si trasferì a Praga, a servizio dell'imperatore del Sacro Romano Impero, Rodolfo II. Lì ebbe modo di conoscere Johannes Kepler, il quale lo stimava non soltanto come esperto progettista e artefice di ingranaggi, ma anche come matematico.
La decisione del langravio di studiare la sfera delle stelle fisse può essere stata in parte suggerita da considerazioni legate alla riforma del calendario, che egli dovette sicuramente prendere in considerazione. Infatti, Andreas Christianus, un dottore in legge, nella sua lunga orazione funebre per Guglielmo IV, ove era principalmente ricordata la sua attività di governante, paragonava l'interesse del langravio per l'astronomia a quello di Gaio Giulio Cesare, citando a testimonianza un verso di Lucano, e aggiungendo che il langravio teneva sempre con sé, quando viaggiava, un globo celeste e un globo terrestre, e quantunque le sue occupazioni fossero gravose, riusciva sempre a trovare il tempo per dedicarsi all'astronomia. In quel periodo, l'unico rivale di Guglielmo IV nelle osservazioni astronomiche era il più giovane Tycho Brahe, un uomo meno nobile e di ben altro temperamento, cui si deve un nuovo, originale sistema astronomico.
Tycho Brahe
Il nome originale di Tycho Brahe era Tyge, latinizzato nella forma Tycho. Egli era nato in una nobile famiglia danese che da diverse generazioni metteva al servizio della monarchia di Danimarca la propria competenza militare e politica. La famiglia naturalmente si aspettava che egli seguisse una carriera simile a quella dei suoi avi e predispose la formazione culturale del ragazzo di conseguenza. Sembra che Tycho sia stato piuttosto riluttante verso questo tipo di educazione; comunque dal 1559 (quando aveva tredici anni) frequentò debitamente le Università di Copenaghen, Lipsia, Wittenberg e Rostock, accompagnato da un tutore personale nominato dalla famiglia. Sembra che a quel tempo Tycho non avesse un'idea molto chiara di cosa volesse realmente fare nella vita. La corrispondenza epistolare testimonia soprattutto la sua caparbia ostilità nei confronti dello studio del diritto e dei reiterati sforzi del suo tutore a tal proposito. Egli mostrava piuttosto un interesse particolare per l'astronomia. Stando al suo stesso racconto, una delle sue prime osservazioni riguardò la congiunzione di Giove e Saturno nell'agosto 1563. La congiunzione di due pianeti, in cui entrambi si muovono lentamente fino ad avere la stessa longitudine eclittica e apparire così molto ravvicinati nel cielo, è rara. Infatti, l'intervallo tra due successive occorrenze di queste 'grandi congiunzioni' è di circa vent'anni, e ogni volta l'esatta posizione della congiunzione tende a spostarsi lungo l'eclittica di circa 1/3, cioè di circa quattro segni zodiacali (o 120º). Le grandi congiunzioni, e la serie dei tre segni zodiacali in esse coinvolti, erano considerate molto importanti in astrologia. Nell'osservare la grande congiunzione del 1563, Tycho notò che la data fornita dalle Tavole alfonsine era errata di un mese, e quella delle Tavole pruteniche di qualche giorno. Tali imprecisioni erano abbastanza grandi da essere smascherate attraverso osservazioni piuttosto semplici, sebbene si debba notare come, dal momento che i pianeti in occasione di una congiunzione si muovono lentamente, l'errore contenuto nelle Tavole pruteniche non era così grande, se misurato in gradi lungo l'eclittica. In modo del tutto tradizionale, Tycho decise che erano necessarie nuove osservazioni per correggere le tavole. Nel 1569, mentre si trovava ad Augusta, installò un quadrante nel giardino di un amico che viveva poco fuori dalla città. Questo fu il più grande di tutti i suoi strumenti d'osservazione, più grande anche di quelli dell'osservatorio che egli, più tardi, doveva costituire in Danimarca. Descrivendolo, Tycho definisce il quadrante "enorme" (ingens), e spiega che il modello incrociato dei supporti dentro il quadrante, il cui raggio era di 14 cubiti (circa 5,43 m), fu progettato in modo da assicurare che il quadrante rimanesse piano, mentre il cubo traforato alla base del supporto principale era interrato per assicurare che lo strumento rimanesse esattamente diritto. L'arco di cerchio graduato fu realizzato separatamente in ottone. Tycho ci racconta come esso fosse "diviso nel modo consueto, perché […] non avevo ancora trovato l'altro metodo di divisione, più conveniente, che poi ho usato negli altri strumenti" (Astronomiae instauratae mechanica). Il metodo "più conveniente" di divisione era quello delle diagonali, lo stesso che, all'incirca in quel periodo, Egnazio Danti usava per dividere la scala del quadrante che aveva collocato sulla facciata di Santa Maria Novella a Firenze. Il metodo delle diagonali (per una scala diritta) sembra sia stato escogitato da Lēwī ben Gēršōn (1280-1344), probabilmente in connessione con un nuovo strumento, da lui inventato, la ballestriglia, il cui arrangiamento è tale da rendere la scala relativamente compatta e da richiederne un'alta sensibilità. Jobst Bürgi usava le diagonali per la divisione delle scale degli strumenti da lui costruiti per il langravio ed escogitò anche un modo per rendere la procedura più precisa quando si trattava di applicarla a una scala curva. Tycho probabilmente apprese tale procedura in occasione di una sua visita al langravio, a Cassel nel 1575. Le diagonali furono, infatti, usate per dividere le scale degli strumenti installati nell'osservatorio di Tycho intorno al 1580; e sebbene egli ritenesse valida la vecchia regola secondo cui gli strumenti di osservazione più grandi sono i migliori, era comunque ‒ proprio in virtù di questa nuova procedura ‒ soddisfatto dei suoi strumenti usati in questi anni, ben più piccoli del ricordato quadrante di Augusta. Tycho ritornò definitivamente in Danimarca nel 1570, dopo aver ereditato una quantità di denaro sufficiente per vivere indipendentemente da ogni vincolo familiare.
Mentre il suo interesse per l'astronomia scemava, la sua principale occupazione intellettuale divenne l'alchimia, che era connessa con l'astronomia attraverso l'astrologia, giacché si credeva che le posizioni dei corpi celesti influissero sul comportamento della materia nelle reazioni alchemiche. Date dunque le connessioni tra alchimia e astrologia, non sorprende che sia stata una stella a cambiare il corso delle ricerche di Tycho. La stella in questione era la 'nuova stella' avvistata nel 1572. L'11 novembre di quell'anno infatti, Tycho era immerso nella prima oscurità della sera, dopo un lungo lavoro di sperimentazione alchemica, quando, con un rapido sguardo al cielo, avvistò una stella mai osservata prima nella costellazione di Cassiopea, quasi sopra la sua testa. La sua reazione iniziale fu di estrema cautela scientifica; egli rifiutò di credere ai suoi occhi e subito chiamò un suo assistente per avere una conferma dell'effettiva presenza della stella. La stella era luminosa al punto da rimanere visibile durante tutto il giorno, sebbene nei mesi successivi essa divenisse progressivamente meno luminosa, fino a non essere più visibile nel corso del 1574. L'osservazione della stella non presentava grandi difficoltà; più difficile semmai era osservarla con sufficiente accuratezza in modo da decidere, al di là di ogni ragionevole dubbio, se appartenesse ai fenomeni celesti oppure se fosse un mero fenomeno locale del mondo sublunare (come si credeva che fossero le comete). La sfida presentata dalla 'nuova stella' fece rinascere in Tycho l'interesse per l'astronomia. Il criterio usato per stabilire se la 'nuova stella' fosse alla stessa distanza delle stelle fisse è illustrato nella fig. 12, dove le distanze sono state rese in modo non fedele alla realtà per necessità di chiarezza. Sia l'arco di centro O e passante per P la superficie della Terra, ove P rappresenta la posizione dell'osservatore; siano i punti A, B, N le posizioni di due stelle fisse e della 'nuova stella' in un certo istante di tempo, e A′, B′, N′ le posizioni delle medesime in un istante successivo. Lo scorrere del tempo è misurato dalla rotazione dell'Universo (o della Terra se si è copernicani) intorno al centro O. Poiché le stelle e la 'nuova stella' non hanno cambiato le loro rispettive posizioni, l'angolo A′OB′ è eguale all'angolo AOB, e quello B′ON′ all'angolo BON. Se l'osservatore fosse in O, gli angoli tra le tre stelle rimarrebbero eguali con il passare del tempo. Ma l'osservatore è in realtà in P e, come si può evincere dalla figura e dimostrare matematicamente, gli angoli visti da P cambiano. Questo fenomeno è noto come parallasse diurna. Poiché le stelle fisse sono più lontane, l'angolo compreso tra queste subisce variazioni meno evidenti di quelle che si verificano nell'angolo compreso tra una di esse e la 'nuova stella'. Per esempio, si può vedere chiaramente nella figura che l'angolo B′PN′ è minore dell'angolo BPN, così, quando era osservata in un istante di tempo successivo, la nuova stella sembrava essersi avvicinata alla stella fissa. Nella fig. 12 le distanze di A, B e N dalla Terra sono state ridotte rispetto a quelle effettive, in modo da rendere gli angoli, e le loro variazioni, ben visibili. In realtà, queste distanze sono grandi e la loro osservazione non è facile da eseguire. In particolare, la parallasse sarà tanto più grande quanto maggiore sarà il tempo che intercorre tra due osservazioni successive, ma si deve tenere conto anche di come la rifrazione disturbi le osservazioni eseguite quando l'oggetto è vicino all'orizzonte, nel qual caso saranno necessarie correzioni. Comunque, nel caso della nuova stella del 1572 ‒ che è ora usualmente conosciuta come 'supernova di Tycho' ‒ la stella fu visibile per un lungo arco di tempo, cosicché le osservazioni poterono essere ripetute molte volte, rendendo i risultati più sicuri e affidabili. In realtà, la distanza delle stelle fisse dalla Terra era troppo grande per poter osservare una qualche variazione nelle loro posizioni relative, a causa della rotazione diurna dell'Universo (o della Terra), così nel caso della nuova stella, si cercò di dimostrare come essa non presentasse alcun fenomeno riscontrabile di parallasse diurna. Ciò lasciava comunque adito ai filosofi naturali di sostenere che la nuova stella non fosse realmente lontana come tutte le altre stelle fisse, mentre gli astronomi avevano dimostrato che essa era certamente più lontana della Luna (la quale presenta, in modo molto evidente, il fenomeno della parallasse diurna); così non fu più sostenibile la dottrina secondo la quale nessun cambiamento poteva occorrere nell'Universo, fatta eccezione per il mondo sublunare.
Tycho pubblicò un breve saggio sulla stella, De nova ... stella (1573), per poi intraprendere un viaggio per l'Europa che lo portò fino a Cassel, dove ebbe l'occasione di incontrare il langravio, e poi in molti altri centri di studio, tra cui Augusta, Norimberga, Wittenberg e perfino Venezia. L'incontro di Tycho con il langravio nel 1575 ebbe, come esito, l'inizio di uno scambio epistolare che continuò fino alla morte del langravio nel 1592, e che fu pubblicato nel 1596. Le lettere erano, naturalmente, il mezzo usuale per scambiarsi notizie scientifiche in quel periodo. Sembra fu nel corso dei suoi viaggi e delle sue conversazioni con altri astronomi che Tycho cominciò a pensare alla costruzione di un osservatorio. Questo avrebbe dovuto essere l'osservatorio meglio attrezzato di tutta Europa (sebbene analoghi ne esistessero nel mondo islamico). I piani erano così ambiziosi che, per quanto Tycho fosse ricco, in nessun modo sarebbe stato in grado di finanziare il progetto autonomamente. Così egli cercò e ottenne il patrocinio del re di Danimarca, Federico II, che nel 1576, gli concesse la piccola isola di Hveen nel Sund, a Copenaghen, come luogo da destinare all'osservatorio. L'osservatorio è descritto con dovizia di particolari nel volume in folio intitolato Astronomiae instauratae mechanica, pubblicato nel 1598 dalla tipografia privata di Tycho in un'edizione limitata per la distribuzione a monarchi, nobili, e altri futuri mecenati. Le tavole, in molte delle copie sopravvissute della prima edizione, sono dipinte a mano. Un'edizione meno pregiata, che utilizza le stesse tavole per le illustrazioni, apparve a Norimberga nel 1602. L'opera è ricca di illustrazioni. Inizia con una descrizione del posto e dell'edificio principale, che ospitò Tycho, la sua famiglia, la servitù e i suoi collaboratori. Lo stile dell'edificio è nordico, ma rivela anche elementi associati alla sensibilità umanistica, come il gusto per le proporzioni (la cui importanza si poteva trovare evidenziata in Vitruvio) e qualche elemento decorativo di derivazione classica. L'illustrazione dell'edificio, con la sua combinazione di sezioni e disegni prospettici, e una pianta separata sembrano derivati dai trattati di architettura di Sebastiano Serlio (1475-1554), ampiamente letti in questo periodo. Dalla stessa fonte probabilmente provengono anche i dettagli della decorazione. Questo testimonia come i valori del Rinascimento avessero raggiunto la Danimarca. Ulteriore conferma di questo influsso, anche se con aggiunte caratteristiche di Tycho, si ritrova nella descrizione che accompagna questa illustrazione, ove si parla della cerimonia iniziale con cui fu posta la prima pietra, inclusi i dettagli relativi al tempo propizio, deciso su basi astrologiche, in cui ciò ebbe luogo e l'oroscopo che fu preparato appositamente per l'osservatorio. Il coinvolgimento fu tale che persone di alto rango sociale considerarono opportuno, per motivi astrologici, partecipare alla cerimonia, nonostante fosse tenuta prima dell'alba. Che Tycho fosse un convinto sostenitore dell'astrologia è, tra l'altro, testimoniato chiaramente da un discorso sulla matematica che egli tenne all'Università di Copenaghen nel 1574 e che fu in seguito pubblicato sotto il titolo Oratio de disciplinis mathematicis (1610). In questa orazione c'è una ferma difesa dell'astrologia, su basi empiriche e teologiche, non soltanto per la sua utilità nelle previsioni meteorologiche, ma anche per l'elaborazione di oroscopi dettagliati. A questo proposito, Tycho osservava che Giovanni Pico della Mirandola, che si era scagliato contro l'astrologia, morì tuttavia giovane, proprio come si poteva predire dal suo oroscopo, che Tycho continuò quindi a interpretare.
Dal punto di vista storico, l'importanza dell'Astronomiae instauratae mechanica risiede nella magnifica documentazione sugli strumenti d'osservazione ivi contenuta. Il testo di Tycho è così dettagliato che uno studio basato su di esso risulterebbe probabilmente più proficuo di uno fondato sull'esame diretto degli strumenti, ammesso che essi fossero pervenuti fino a noi. Inoltre, non sarebbe affatto facile dedurre dagli strumenti stessi le informazioni che Tycho ci fornisce sulla cura con cui essi furono collaudati, vale a dire facendo molte osservazioni e modificando quindi ogni volta gli strumenti di conseguenza. Tycho afferma che la maggior parte degli strumenti descritti nel suo libro sono il risultato di almeno due, tre modifiche successive. Deve essere sicuramente stata la coerenza dei dati d'osservazione che ne derivò, così come la natura stessa degli strumenti, a convincere il mondo scientifico dell'affidabilità delle osservazioni di Tycho. Tra gli strumenti più grandi, presenti nell'osservatorio di Uraniborg, e certamente uno dei più belli, vi era un largo quadrante murale, completato nel 1582, che aveva un raggio di circa 1,94 m. La descrizione fornita da Tycho registra in dettaglio i perfezionamenti che egli aveva introdotto per assicurarne l'accuratezza delle letture. La scala era realizzata in ottone e, poiché il raggio era molto grande, ciascun grado era largo abbastanza da poter suddividere ulteriormente i minuti primi, permettendo letture fino a dieci o anche cinque secondi d'angolo. Tale sensibilità della scala è descritta e illustrata nella figura per mezzo di linee trasversali. La figura mostra anche come erano eseguite le osservazioni, con l'aiuto di due assistenti, uno dei quali leggeva gli orologi (usati per misurare solo brevi intervalli di tempo), mentre l'altro prendeva nota delle letture. Sempre nella figura compare, dentro la forma del quadrante, lo stesso Tycho, raffigurato nell'atto d'indicare l'apertura che consentiva alla luce di entrare all'interno della scala del quadrante, mentre un cane dorme ai suoi piedi e sullo sfondo compare una rappresentazione in sezione dell'interno di Uraniborg; questo scorcio mostra gli strumenti astronomici sul tetto, assistenti impegnati nei calcoli nel piano sottostante, e i laboratori alchemici nei piani inferiori. In una nicchia ricavata nel muro, dietro Tycho, è visibile un globo celeste abbastanza grande; un passo successivo del libro fornisce una dettagliata illustrazione di questo globo e racconta come esso fosse realizzato per eseguire calcoli approssimati, puntando gli angoli con il compasso. Il fatto che il quadrante fosse fissato su di un muro lo rendeva stabile e perciò affidabile, ma la maggior parte degli strumenti di Tycho doveva essere realizzata per essere manovrabile.
Uno dei più grandi era l'anello equatoriale di metallo, illustrato nella fig. 15. Il suo diametro era di circa 2,72 m. Come si può osservare dalla figura, esso aveva una robusta struttura di sostegno e fu montato in una cavità i cui lati, costituiti da gradini, permettevano all'osservatore di accedere alla posizione appropriata per fare osservazioni. Come il grande quadrante manovrabile di Augusta, anche l'anello equatoriale aveva una serie di sostegni per la sua struttura. Nella descrizione dello strumento, Tycho ancora una volta si riferisce alla sensibilità della scala, dove i gradi sono talmente larghi che i singoli minuti primi possono essere suddivisi in quattro parti. Egli prosegue spiegando come uno dei vantaggi della realizzazione di questo particolare strumento consistesse proprio nel suo essere abbastanza grande da rendere possibile una tale suddivisione.
Nel frattempo accadde un altro evento spettacolare nel cielo, l'apparizione, nel novembre 1577, di una cometa molto luminosa. All'epoca si credeva generalmente che le comete fossero fenomeni meteorologici che avevano luogo nella parte superiore dell'atmosfera terrestre, causati dall'ignizione di vapori probabilmente esalati dalla Terra. La cometa del 1577 fu però di una lucentezza non comune. Presumibilmente fu alla luce dell'esperienza della 'nuova stella' che Tycho, e altri, si accinsero a misurare la sua distanza dalla Terra. Il metodo era ancora una volta quello della parallasse, ma in questo caso subentrò, a complicare i calcoli, il moto percettibile della cometa rispetto al cielo delle stelle fisse; ciò doveva essere tenuto in conto nel calcolare quanto del cambiamento misurato nella posizione della cometa fosse imputabile alla parallasse. Tycho si convinse che la parallasse in questo caso era di gran lunga troppo piccola perché la cometa potesse essere nella parte superiore dell'atmosfera terrestre, come supponeva la tradizionale spiegazione aristotelica. La parallasse che egli misurò era leggermente minore di quella del pianeta Venere, così concluse che la cometa doveva trovarsi nell'orbe di questo pianeta. Alla luce di quel che successe poi, si ha la tentazione di immaginare che ciò può averlo indotto a riflettere sull'ordine degli orbi planetari, e quindi sulle differenze tra il sistema geocentrico (in cui, procedendo verso l'interno, l'ordine usualmente accettato era il seguente: cielo delle stelle fisse, Saturno, Giove, Marte, Sole, Venere, Mercurio, Luna, Terra) e il sistema copernicano (in cui l'ordine era invece il seguente: cielo delle stelle fisse, Saturno, Giove, Marte, Terra e Luna, Venere, Mercurio, Sole). In ogni caso, la perplessità circa l'ordine effettivo delle sfere planetarie, potrebbe rappresentare il motivo per cui Tycho decise di non pubblicare immediatamente i risultati delle sue osservazioni, ove egli sosteneva che la cometa avvistata si trovava al di sopra del cielo della Luna, e che perciò, come già si era verificato per la 'nuova stella', erano stati osservati cambiamenti in quella regione superiore, che tradizionalmente si supponeva ne fosse priva.
Nel 1582 Tycho intraprese una serie di osservazioni che sembrano realizzate allo scopo di distinguere i differenti sistemi planetari. In particolare iniziò a studiare la parallasse di Marte. Nel sistema geocentrico (tolemaico), l'orbe di Marte è centrato su di un punto abbastanza vicino alla Terra mentre gli orbi di Venere, di Mercurio e della Luna sono compresi tra esso e la Terra. Così nel sistema tolemaico la distanza di Marte dalla Terra non cambia molto quando il pianeta si muove; non è effettivamente possibile calcolare, mediante osservazioni, quale debba essere la dimensione di ciascun orbe (in termini di una qualche misura comune), e perciò non si può calcolare neppure dove ciascun orbe giace in rapporto agli altri. Comunque, lo stesso Tolomeo seguiva una tradizione ben consolidata nel decidere che l'ordine appropriato era quello in cui, procedendo verso l'interno, si sarebbero trovati periodi di rivoluzione sempre più brevi, così come erano misurati rispetto alle stelle fisse. Alla base di ciò, era stabilita una conoscenza di antica data, desunta dagli studi sulle eclissi, ovvero che il Sole era più distante della Luna, e il suo moto rispetto alle stelle era anche più lento di quello della Luna.
A differenza di quello tolemaico, il sistema copernicano permetteva di calcolare le dimensioni delle sfere planetarie, sulla base della dimensione dell'orbe terrestre (detto talvolta 'il grande orbe' forse per distinguerlo dalla sfera molto più piccola costituita dal corpo effettivo della Terra). Così, nel sistema copernicano l'orbe di Marte è prossimo a quello della Terra, e di conseguenza la distanza tra i due pianeti può variare di molto (fig. 16). La figura è stata semplificata disegnando gli orbi dei due pianeti come semplici cerchi, e le distanze non sono rese in scala. Comunque è chiaro che, se le posizioni della Terra e di Marte nelle loro rispettive sfere planetarie sono T ed M, allora la distanza tra i due pianeti è di molto minore di quella che si avrebbe se essi fossero in T' e M'. Se si considera ciò che si vede dalla Terra in queste situazioni, è chiaro che la distanza minima di Marte dalla Terra corrisponde al pianeta visto da un'angolazione di 180° dal Sole (cioè 'in opposizione' al Sole), e la distanza massima corrisponde al pianeta visto nella stessa direzione del Sole (cioè, 'in congiunzione').
Ovviamente, non è possibile osservare Marte effettivamente in congiunzione con il Sole, poiché il pianeta verrebbe offuscato dalla luce solare. Inoltre, se lo si osserva in prossimità della congiunzione, esso risulterà basso nel cielo, ciò implicherà la necessità di eseguire correzioni a causa dell'elemento d'incertezza introdotto dalla rifrazione. Fortunatamente, nel caso di Marte, il cambiamento di distanza previsto dal sistema copernicano è grande abbastanza da essere individuabile senza dover osservare il pianeta in prossimità della sua distanza massima, cioè in congiunzione con il Sole. Viceversa, il sistema tolemaico prevede che Marte sia sempre più lontano del Sole.
Tra il lavoro sulla cometa del 1577 e la nascita del progetto di Tycho sulla parallasse di Marte, nel 1582, era accaduto qualcosa che dette alla questione un significato differente poiché Tycho aveva ideato un proprio sistema planetario. La Terra vi risulta immobile al centro del sistema, mentre la Luna si muove intorno a essa. Tutti gli altri pianeti ruotano intorno al Sole che, a sua volta, ruota intorno alla Terra, trascinando con sé gli altri pianeti. Come quello copernicano, anche questo sistema aveva precedenti. Un sistema geo-eliocentrico di questo genere fu proposto per esempio da Eraclide Pontico nel IV sec. a.C. Nei termini matematici odierni, il sistema ticonico costituisce un altro cambiamento di coordinate, e l'ovvio confronto è con il sistema copernicano. La rotazione diurna è stata trasferita dalla Terra ai cieli, e il moto annuale della Terra è stato trasferito al Sole, e così anche la componente annuale nel moto di ciascun pianeta. In questo modo la Terra è di nuovo immobile al centro dell'Universo, ciò significa che è possibile continuare a ritenere valide le nozioni tradizionali della fisica terrestre. Dal momento che nel sistema ticonico i pianeti si muovono con il Sole, è possibile calcolare la dimensione dei loro orbi, proprio come nel sistema copernicano.
Inoltre, è chiaro come il sistema potesse apparire attraente agli occhi di chi era abituato all'osservazione astronomica. Tutte le tavole dovevano fornire le posizioni planetarie come erano viste dalla Terra e, allo scopo di fissare le dimensioni dei loro modelli del moto planetario, gli astronomi erano abituati a misurare le distanze massime di ciascun pianeta dal Sole (la loro massima 'elongazione'). Questi tratti caratteristici dell'astronomia si ritrovano ben evidenti nel modello ticonico. Esisteva comunque una seria difficoltà nel considerare tale modello come una rappresentazione dell'effettiva disposizione planetaria in quanto esso era incompatibile con l'assunto delle sfere reali. Come si può vedere nella figura di Tycho, la traiettoria del Sole interseca quella di Marte, oltre a quelle di Mercurio e di Venere. In questo modo, il sistema ticonico, se aboliva il problema copernicano del moto della Terra, aveva però introdotto un nuovo problema relativo al moto dei pianeti. Di fatto, sembra che Tycho e alcuni dei suoi contemporanei non fossero del tutto propensi a credere nella realtà delle sfere planetarie. Dai lavori sulla cometa del 1577, come quelli dell'astronomo del langravio, Christopher Rothmann o del professore di matematica presso l'Università di Tubinga, Michael Mästlin (1550-1631), sembrava che la traiettoria seguita dalla cometa avesse attraversato regioni che avrebbero dovuto essere occupate dalle sfere solide comprese all'interno di ogni orbe. Come si è visto, lo stesso Tycho collocò la cometa nell'orbe di Venere. Tra gli astronomi non esisteva un consenso definitivo sulle traiettorie delle comete e la questione era complicata dal fatto che le comete cambiano in modo evidente nel loro aspetto e nell'intrinseca lucentezza quando si muovono, piuttosto rapidamente; così la nuova evidenza che sembrava deporre contro le sfere reali non era così straordinaria come gli storici talvolta l'hanno dipinta. D'altro canto, i sostenitori del sistema ticonico non potevano rifugiarsi agevolmente nel finzionalismo, senza ridurre il sistema a un mero modello di calcolo. L'obiezione al sistema copernicano era fisica; il possibile moto della Terra era qualcosa che rientrava nel territorio di competenza del filosofo naturale, mentre il sistema ticonico aveva accuratamente evitato di attribuire il moto alla Terra.
Tycho non riconosce debiti intellettuali per il suo sistema, né fornisce spiegazioni di come giunse alla sua ideazione. È però probabile che ci sia una connessione tra l'origine del sistema e la presenza a Hveen, nell'estate del 1580, di un astronomo assistente di Tycho. Il suo nome era Paul Wittich (1555-1587); proveniva da Wittenberg, dove Tycho poteva averlo incontrato nei suoi viaggi del decennio precedente. Wittich era un matematico estremamente competente.
È sopravvissuta una sua copia del De revolutionibus di Copernico che sul retro presenta alcuni fogli, con la sua grafia, contenenti schizzi di possibili sistemi planetari alternativi che sembrano forme intermedie tra il sistema copernicano e quello ticonico. Questi schizzi potrebbero rappresentare alcune idee personali, indipendenti, di Wittich, oppure i risultati delle discussioni con Tycho; in ogni caso sembra possibile che le discussioni con Wittich sul copernicanesimo e sui problemi astronomici connessi possano, quanto meno, aver giocato un qualche ruolo nell'origine del sistema di Tycho. Il sistema fu reso pubblico per la prima volta nel 1588, nel De mundi aetherei recentioribus phaenomenis (che, sebbene pubblicato prima, costituisce il Libro II delle Astronomiae instauratae progymnasmata). Wittich era morto nel 1587. Il sistema di Tycho non fu pubblicato fino all'anno seguente la morte di Wittich, ma voler vedere in questo qualcosa più di una semplice coincidenza può apparire eccessivo, ciò, tuttavia, prova almeno che Wittich non poté venire a conoscenza del sistema ticonico dal libro stampato.
Il sistema di Tycho fu molto popolare nel XVII sec. perché rimuoveva il problema di una Terra in movimento, ed evitava la contraddizione con ciò che è scritto, a proposito del Sole e della Luna, nel libro di Giosuè. Con il senno di poi, il sistema ticonico può sembrare una sorta di compromesso, ma certamente non fu percepito così al suo tempo, e in particolare dal suo autore. Come si può vedere nello schema riprodotto nella fig. 17, il sistema di Tycho prevede che Marte si possa trovare talvolta più vicino alla Terra di quanto lo sia il Sole. Così, fu nella ricerca di evidenze in grado di corroborare la propria teoria, e non quella di Copernico, che Tycho iniziò a misurare la parallasse di Marte. I risultati furono soddisfacenti. L'obiettivo principale era, naturalmente, quello di elaborare un modello completo per il moto di ciascun pianeta. Tycho realizzò ciò per il moto della Luna, che le sue osservazioni rivelarono essere ancora più complicato di quanto gli astronomi avessero pensato. Tale modello del moto lunare fu pubblicato dopo la sua morte nel Libro I delle Astronomiae instauratae progymnasmata, stampato a Praga nel 1602, edito e rivisto da un altro assistente di Tycho, Johannes Kepler. Non furono comunque altrettanto positivi i risultati relativi agli altri pianeti. I modelli ticonici dei moti seguivano Copernico anziché Tolomeo nell'uso di un doppio epiciclo al posto dell'equante, ma erano per il resto tradizionali, e in accordo con la fisica aristotelica, nel basare tutto il sistema sul moto circolare uniforme. Rispetto ai modelli matematici degli orbi planetari era irrilevante dubitare delle sfere solide. In linea di principio, ci si sarebbe aspettati che Tycho eseguisse un numero relativamente piccolo di osservazioni di ciascun pianeta per fissare le dimensioni e le posizioni dei vari cerchi usati nel modello del suo moto poiché così aveva fatto Copernico nella versione completa del suo sistema. Invece Tycho eseguì un numero enorme di osservazioni, rilevate notte dopo notte. La sua decisione in proposito può essere stata influenzata da ciò che egli sapeva sul lavoro del langravio in merito alle stelle fisse, ove osservazioni reiterate dei medesimi oggetti erano state un fattore essenziale del programma. Numerosi furono i visitatori eminenti dell'osservatorio ‒ tra cui, nel 1590, Christopher Rothmann e il re Giacomo VI di Scozia (che era in Danimarca per sposare Anna, la figlia del re). Nonostante la presenza di molti studenti e assistenti, era essenzialmente Tycho a gestire tutta l'organizzazione. Simile a un nobile che dirige una corte, il piccolo mondo di Hveen era un'azienda efficiente, anche se non sempre felice per tutti coloro che in essa vivevano. Tycho acquisì rapidamente la fama di padrone poco amato, e le cause intentate, inclusa quella che verteva sulla rottura di un contratto di matrimonio per una sua figlia, suggeriscono che egli avesse un carattere piuttosto litigioso in ogni sua occupazione. Sicuramente il suo rango nobiliare lo autorizzava a comportarsi in modo autoritario. Egli aveva al suo servizio assistenti che si occupavano di effettuare osservazioni, e matematici che eseguivano i calcoli richiesti. Tra essi, alcuni contribuirono in modo notevole al progresso della ricerca di Tycho. Per esempio, Christen Sørensen (1562-1647), noto con il nome latino di Longomontanus, che lavorò a Hveen dal 1589 al 1597 e successivamente si unì alle ricerche di Tycho per elaborare i dettagli matematici della teoria lunare (che in seguito furono pubblicati sotto il nome di Tycho).
Federico II morì nel 1588. A lui successe il figlio Cristiano IV, ancora bambino, sicché il paese fu di fatto governato da un reggente. Tycho a poco a poco si accorse che il suo favore presso la corte era ormai in declino, e nel 1597 gli fu chiaro che sarebbe stato necessario lasciare Hveen. Dopo il ritiro nella sua residenza di Wandsbeck, sembra che egli si sia convinto che se voleva un altro osservatorio, di una certa grandezza, avrebbe dovuto lasciare la Danimarca. Partì dunque alla ricerca di un altro mecenate. Il libro sul suo osservatorio, l'Astronomiae instauratae mechanica, fu concepito come una sorta di propaganda dei suoi risultati e copie di presentazione furono spedite a diversi nobili eminenti da cui egli sperava di avere un aiuto. L'osservatorio a Hveen fu abbandonato, e all'inizio del XVII sec. Uraniborg fu demolito per riusarne i mattoni. Tycho rimosse gli strumenti, di cui nessuno è pervenuto fino a noi. Nel 1598 visitò Praga, dove incontrò l'imperatore del Sacro Romano Impero Rodolfo II, il quale nutriva un serio interesse per l'astronomia, e uno ancor più serio per l'astrologia e ‒ sembra ‒ per l'alchimia. A differenza della maggior parte dei governanti Rodolfo II, che era cattolico, si faceva vanto di non badare al credo religioso delle persone che metteva al suo servizio, e così nessuna obiezione fu sollevata contro la confessione protestante di Tycho; circa un anno dopo egli era nominato 'matematico imperiale' e gli fu data la possibilità di scegliere la proprietà imperiale dove collocare il suo nuovo osservatorio. Alla fine egli scelse il piccolo castello di Benatki, un vecchio padiglione di caccia, distante meno di un giorno di viaggio da Praga, collocato su di una bassa collina e con un ampio orizzonte. Benatki era certamente più piccolo di Uraniborg, e Tycho non fece in tempo a installare lì la maggior parte dei suoi strumenti. Si è pensato per lungo tempo che Tycho e la sua famiglia avessero vissuto al primo piano e che il secondo fosse adibito alle osservazioni astronomiche. Intorno alla metà dell'ultimo decennio del XX sec., è stato possibile avere conferma di questa ipotesi, quando il secondo piano del castello, ora ospitante un museo, è stato restaurato. In una delle piccole stanze che guardano a sud ci si è accorti che il pavimento era segnato da una linea, tracciata lungo la direzione nord-sud, molto accurata e allineata con il margine sinistro del telaio della finestra. Chiaramente, essa dovette servire a installare qualche strumento che faceva uso del piano meridiano.
Tycho voleva elaborare modelli dettagliati dei moti planetari nel suo nuovo sistema. Pensava non soltanto di essere un osservatore molto abile, ma anche di aver reso un importante contributo alla teoria astronomica. Da parte sua, Rodolfo II desiderava essere immortalato mediante l'apposizione del proprio nome alle tavole astronomiche che sarebbero derivate dalla teoria di Tycho. Con meno colpi di scena di quanti la storia talvolta ha in serbo, entrambi ottennero più o meno ciò che avevano desiderato, ma ciò per merito di Kepler, il quale venne a Praga la prima volta alla fine del 1599 e vi ritornò l'anno seguente in qualità di assistente matematico di Tycho.
Johannes Kepler
Kepler, che era nato nel villaggio di Leonberg, vicino Weil der Stadt (Württemberg), era il figlio maggiore di un soldato mercenario e della figlia di un locandiere. La sua data di nascita, il 27 dicembre, giorno di San Giovanni evangelista, può spiegare il suo nome. Quando Johannes aveva sei anni, suo padre partì per la guerra nei Paesi Bassi, per non fare più ritorno. Kepler fu allevato nella locanda di suo nonno, ove aiutava a servire i clienti. Senza dubbio ciò gli dette una notevole pratica nell'aritmetica. In seguito egli raccontò come il suo primo interesse per l'astronomia emerse all'età di cinque anni, quando la madre lo portò fuori a vedere la cometa, nell'inverno del 1577. C'è tuttavia un'inesattezza in questo racconto poiché nel 1577 le comete non erano generalmente considerate oggetti astronomici (v. sopra). La famiglia, intuendo le grandi capacità di Johannes, fece in modo che avesse un'educazione appropriata. Fu avviato alla carriera ecclesiastica e studiò teologia all'Università di Tubinga, allora, come oggi, centro dell'ortodossia luterana. A Tubinga, suo insegnante di astronomia fu Michael Mästlin (che aveva studiato la cometa del 1577, v. sopra). Fedele alla tradizione, Mästlin insegnava astronomia geocentrica, riservando ai suoi allievi migliori accenni al lavoro di Copernico. Fu lui a riferire a Kepler che la prefazione non firmata del De revolutionibus non era di Copernico, ma di Osiander, e sembra che Kepler abbia preso sempre da lui la convinzione che il sistema copernicano potesse essere vero dal punto di vista fisico.
Nel suo primo libro sull'astronomia, il Mysterium cosmographicum (1596), Kepler spiega molto attentamente quelli che egli considera i vantaggi del sistema copernicano. Gli argomenti a sostegno del nuovo sistema sono filosofici. Per esempio, egli sostiene che Copernico sia in grado di rispondere a domande che gli Antichi non sollevarono oppure sollevarono invano, come quella sul perché Mercurio e Venere non sono mai visti lontani dal Sole, mentre Marte, Giove e Saturno possono essere visti in opposizione al medesimo. Inoltre, Kepler considera, quale argomento a favore della maggiore efficacia del sistema copernicano rispetto a quello geocentrico, il fatto che esso permetta di dedurre dalle osservazioni le effettive dimensioni degli orbi planetari, e quindi il loro ordine di successione. Lo stesso Copernico aveva messo in rilievo questa caratteristica, ma senza soffermarsi, mentre Kepler ne fa il punto di partenza della sua difesa del copernicanesimo. Egli fornisce anche il primo schema che mostra il sistema copernicano con gli orbi correttamente disegnati in scala. Il Mysterium cosmographicum contiene una teoria matematica che spiega perché esistano esattamente sei pianeti (nella teoria geocentrica i pianeti sono sette) e perché gli spazi tra i loro orbi risultino essere proprio quelli calcolati a partire dalle osservazioni attraverso l'uso della teoria copernicana. Così facendo Kepler presentava la prima cosmologia matematica. Scrivendo a Mästlin, egli commentava così la propria teoria: "mentre Copernico ufficia all'altare maggiore, è abbastanza per me che io possa sorvegliare le porte con la mia scoperta". Come è stato già notato, nel sistema geocentrico non c'è modo di calcolare le dimensioni degli orbi, così, in accordo con il modello fisico accettato delle sfere solide, i vari orbi planetari erano considerati in reciproco contatto, ritenendo che quello più esterno fosse mosso dal di fuori e potesse così trasmettere il moto a quelli interni. Nel sistema copernicano, dove si può calcolare la loro dimensione, ci sono ampi spazi, di dimensioni differenti, tra orbi planetari contigui. Nonostante il sistema copernicano abbia all'incirca lo stesso numero di cerchi di quello geocentrico, gli epicicli copernicani sono molto piccoli, cosicché, sebbene un orbe sia definito in modo da includere gli epicicli (a differenza di quanto accade nel modello di Kepler, v. oltre), otterremo ancora una volta un insieme di orbi che non hanno contatto tra loro. La presenza di spazi interposti costrinse Copernico ad adottare una nuova fisica per spiegare come gli orbi planetari potessero ruotare congiuntamente. Tali spazi vuoti erano nuovi per l'astronomia, e questo è presumibilmente il motivo per cui Kepler scelse di provare a spiegare le loro dimensioni piuttosto che esaminare le distanze di ognuno di essi dal Sole. Egli dovette affrontare questo problema in un secondo momento, quando provò a calcolare l'orbita di Marte.
Kepler non credeva né nella realtà delle sfere (che, nel cap. 16 del Mysterium cosmographicum, definisce "assurde" e "mostruose"), né nella realtà dei cerchi usati per ricostruire le traiettorie dei pianeti. Egli definisce l'orbe di un pianeta come la cavità compresa tra due superfici sferiche concentriche, che determina i limiti della traiettoria del pianeta. In un primo momento, seguendo Copernico, riferisce i moti planetari al centro del grande orbe (quello definito dal moto annuale della Terra), ma nel seguito del lavoro (nel cap. 15) passa a considerare come centro il Sole. Per la prima volta si è in presenza di un sistema planetario veramente eliocentrico. A partire da questo momento, Kepler relazionò tutti gli orbi planetari, e quindi tutte le orbite, al Sole. Fu cruciale per il successo della sua teoria il fatto che nei suoi calcoli sul moto di Marte tutte le posizioni fossero misurate in relazione al Sole. Tuttavia, la teoria cosmologica in sé sembra meno promettente. La tavola che la riassume è mostrata nella fig. 20. Procedendo dall'esterno del sistema, se si inscrive un cubo nella superficie interna dell'orbe di Saturno, allora la sfera che toccherà quel cubo nei punti centrali delle sue facce (la sfera inscritta nel cubo) sarà la superficie esterna dell'orbe di Giove, e così via, con il tetraedro collocato tra Giove e Marte, il dodecaedro tra Marte e la Terra, l'icosaedro tra la Terra e Venere, e l'ottaedro tra Venere e Mercurio. I solidi geometrici usati nella teoria di Kepler sono i cinque poliedri regolari noti fin dall'Antichità. Le loro proprietà distintive sono le seguenti: le facce di ciascun solido sono poligoni equiangoli ed equilateri di un unico genere (triangoli equilateri per il tetraedro, quadrati per il cubo, e così via) e gli angoloidi sono regolari uguali. In uno scolio della proposizione finale degli Elementi di Euclide (XIII, prop. 18) è dimostrato che esistono esattamente cinque solidi del genere. Così, nei limiti di un confronto costante con i dati d'osservazione, Kepler aveva fornito una spiegazione soddisfacente del numero dei pianeti. Nonostante ciò possa sembrare inverosimile, la teoria dei poliedri ‒ come Kepler mostra in dettaglio ‒ è in buon accordo con le dimensioni effettive degli orbi dedotte dalle osservazioni. Tale accordo con i dati dell'osservazione è molto alto e copre quasi tutti i casi (eccetto quello di Mercurio, il pianeta che fu sempre il più difficile da osservare accuratamente a causa della sua vicinanza con il Sole). Ma Kepler, che era un devoto luterano (sebbene non del tutto ortodosso), credeva di guardare a un Universo creato da Dio in cui non poteva esserci imperfezione; un tale atteggiamento non poteva tollerare nemmeno una minima soglia di errore. Inoltre, egli non era stato in grado di elaborare una relazione matematica soddisfacente che spiegasse i differenti periodi dei pianeti a partire dalla dimensione dei loro orbi. Così decise che doveva pervenire a osservazioni più accurate per provare in modo più stringente la sua teoria. Spedì una copia del libro a Tycho Brahe e fece in modo che una copia arrivasse anche a un professore di matematica dell'Università di Padova; fu così che il Mysterium cosmographicum pervenne a Galileo Galilei. Questi scrisse a Kepler una lettera di ringraziamento, in cui diceva che il libro gli sembrava molto interessante, che non vedeva l'ora di leggerlo, e che era anch'egli (sebbene per altre ragioni) convinto della correttezza del sistema copernicano. Leggendo tra le righe, si può constatare come Galileo si guardasse bene dal discutere i dettagli della teoria con il suo autore. Kepler, da parte sua, gli riscrisse in tono entusiastico salutandolo come seguace di Copernico ed esortandolo a fare osservazioni astronomiche che potessero confermare la teoria. Galileo stavolta non replicò alla lettera.
Meno cortese di Galileo fu Tycho Brahe. Dalla summenzionata tavola dei pianeti, egli aveva tratto l'ovvia conclusione, che comunicò esplicitamente a Kepler, di non credere nelle sfere reali (lettera di Tycho a Kepler, 1° aprile 1598). Ai margini della lettera, Kepler annotò: "lo stesso vale per me e per il mio libro". Tycho intanto, in contatto con Mästlin (che aveva elaborato materiale da aggiungere al libro di Kepler), aveva continuato a esplorare in dettaglio la teoria planetaria di Copernico e a dare alle stampe i risultati. Aveva infatti spedito a Mästlin una copia del De mundi aetherei recentioribus phaenomenis ‒ la quale, con una dedica autografa datata 14 maggio 1588, è ora alla British Library di Londra ‒ e, essendo alla ricerca di qualche ulteriore assistente in campo matematico, gli chiese se Kepler fosse realmente un matematico così bravo come sembrava. Mästlin rispose affermativamente, e Kepler ottenne così un impiego a Praga. Giunto lì, usò le osservazioni di Tycho per fornire la più stringente dimostrazione della correttezza della teoria copernicana disponibile all'epoca, mentre le sue prime due leggi del moto planetario (pubblicate nel 1609) apportarono un contributo cruciale alla validità delle Tavole rudolfine (1627), la cui prolungata affidabilità, constatata nei decenni successivi, contribuì a persuadere gli astronomi della validità dell'ipotesi di Copernico. Tuttavia, qualcosa in più deve essere detto sui rapporti tra Kepler e Tycho, dal momento che l'uso che il primo fece delle osservazioni del secondo dipese in modo determinante dalla valutazione della loro affidabilità. Per spiegare dunque l'atteggiamento di Kepler si deve tornare di nuovo alle osservazioni di Tycho.
Precisione ed errore
Kepler era un astronomo molto attento. Così, quando egli affermava che gli errori nelle osservazioni di Marte eseguite da Tycho non superavano i cinque minuti primi, traendo da ciò conseguenze molto importanti (il rigetto, infatti, di un errore più grande, di otto minuti, lo portò ad assegnare un'orbita ellittica al pianeta), si deve concludere che avesse buone ragioni per credere in questa stima numerica. I suoi risultati per le orbite dei pianeti sono corretti fino alla quinta cifra decimale, così è chiaro che le osservazioni di Tycho dovevano essere molto accurate.
Dal momento che l'esatta entità degli errori d'osservazione di Tycho fu di grande portata storica ‒ essendo essi sufficientemente piccoli da permettere a Kepler di trovare le orbite ellittiche ‒ gli storici dell'astronomia hanno effettivamente verificato le posizioni planetarie osservate sulla base di ciò che ora si conosce delle posizioni dei pianeti in certi periodi di tempo rilevanti, attraverso l'uso di programmi che tengono debitamente in conto i cambiamenti secolari nelle orbite planetarie, e così via. Da tali studi emerge che le osservazioni di Tycho erano davvero così accurate come egli vantava. Tuttavia ciò non consente ancora di rispondere al motivo per cui Kepler ebbe fiducia in lui. Nella Astronomiae instauratae mechanica Tycho menziona diverse volte la sensibilità della scala di qualche suo strumento (v. sopra), e rileva che essa poteva essere suddivisa ulteriormente fino alle frazioni di minuto. La coerenza che egli si vantava di ottenere tra osservazioni eseguite con strumenti differenti, o con lo stesso strumento arrangiato in modo diverso (per es., volgendo l'anello equatoriale di 180°), ci introduce al concetto di 'errore d'osservazione'. Da quanto Tycho racconta dei suoi strumenti, è chiaro che, nelle verifiche di coerenza, l'errore di cinque minuti primi menzionato da Kepler a proposito dell'osservazione di Marte, sarebbe stato rilevabile. Inoltre, dopo tali verifiche, qualcuno degli strumenti era ricostruito due o anche tre volte. Non è detto che cosa concretamente s'intendesse per coerenza, ma si deve sicuramente presumere che fossero eseguite molte osservazioni con diversi arrangiamenti, le quali, una volta messe a confronto, erano considerate coerenti se convergevano tutte intorno a uno stesso valore. In un caso ideale, si sarebbe ottenuto ogni volta semplicemente lo stesso valore osservato, ma sembra molto improbabile che Tycho si aspettasse un esito così felice, almeno non dopo aver fatto ricostruire più di una volta lo strumento. Sembra anche probabile che egli accettasse qualche consiglio da parte del langravio e dei suoi assistenti, i quali erano esperti nel fare ripetute osservazioni. In ogni caso, l'eseguire procedure di verifica necessarie per stabilire la coerenza deve aver messo in risalto il fatto che misurare precisamente, rispetto a una buona scala, non implica necessariamente ottenere un risultato assolutamente affidabile. Il concetto di errore è necessario per fare una stima numerica dell'affidabilità dei risultati e Tycho sembra essere pervenuto a ciò. È improbabile tuttavia che egli sia giunto autonomamente al concetto di errore, e non piuttosto per intervento di Kepler.
Dal suo libro sull'osservatorio emerge che egli fece copie di diversi strumenti antichi, il motivo originario può essere legato a un interesse antiquario ma, almeno in un caso, sembra esserci stata anche una conseguenza astronomica. Uno degli strumenti ricostruiti è, infatti, il regolo parallattico descritto da Tolomeo. Tycho può aver effettivamente usato questo strumento. Senza dubbio esso era estremamente antiquato, ed egli dovette divenire presto consapevole di quanto esso fosse poco accurato rispetto ai suoi strumenti più moderni. Comunque continuò a usarlo abbastanza a lungo, fino a ricostruirne i margini di errore. Kepler afferma con sicurezza che l'accuratezza delle osservazioni di cui poteva disporre Tolomeo era di soli dieci minuti di arco. Questo rilievo si trova nello stesso passo in cui egli discute l'accuratezza delle osservazioni di Marte eseguite da Tycho. In quella stessa sede, egli suggeriva anche che la modesta entità di questo errore fu la ragione per cui Tolomeo si ritenne soddisfatto dei propri modelli del moto planetario. Kepler, che aveva una grande ammirazione per Tolomeo, considerava ovvio che quest'ultimo applicasse il suo stesso criterio, quello secondo cui i modelli devono dare risultati in accordo con le osservazioni entro i margini d'errore noti. Poiché Tolomeo in realtà non affrontò l'argomento, sembra estremamente probabile che l'analisi che Kepler fa dei suoi errori fosse desunta dall'opera di Tycho. Naturalmente, Tycho a sua volta potrebbe aver costruito i regoli parallattici per effettuare le sue verifiche su Copernico piuttosto che su Tolomeo, sapendo soprattutto che le Tavole pruteniche non erano accurate, ma il commento di Kepler ci fornisce comunque una testimonianza di considerevole peso per poter sostenere che Tycho usò effettivamente regoli parallattici, e che rifletté sull'errore d'osservazione implicito nel loro uso.
Filosofia naturale e matematica
Fin qui, sono stati considerati soprattutto i cambiamenti verificatisi nell'astronomia del 1400-1600 i quali, da un punto di vista tecnico, hanno contribuito all'accettazione finale di un sistema planetario eliocentrico. Ci furono comunque altri fattori che sembrano aver contribuito al processo di cambiamento. Qualcuno è già stato affrontato, ma essi meritano un esame più ampio.
Anzitutto, si deve tener presente che le idee e le opinioni discusse nei paragrafi precedenti interessarono solo un'esigua minoranza di cittadini in tutta Europa. Nel 1400 quasi tutti avrebbero accettato l'idea che la struttura dell'Universo era, più o meno, quella descritta da Dante, all'inizio del XIII sec., seguendo il sistema di Tommaso d'Aquino (1225/1226-1274). Tale idea era ancora accettata nel 1600; solo alcuni specialisti molto competenti nelle scienze matematiche si discostavano da questa credenza generale, e pochi altri cominciavano a cambiare idea. Gli storici hanno più volte sottolineato la complessità del sistema planetario geocentrico, con gli orbi planetari concentrici, e racchiuso all'esterno dal cielo delle stelle fisse. Questa complessità è spesso messa a confronto con la semplicità del sistema copernicano, così come Kepler l'aveva rivisitato, eliminando le combinazioni dei cerchi e sostituendo le traiettorie dei pianeti con ellissi. Tale semplicità è generalmente considerata non solo elegante da un punto di vista estetico, ma anche attraente sul piano scientifico. Tuttavia, ciò significa ignorare i criteri estetici e scientifici del periodo precedente. Laddove un uomo del XX sec. vede soltanto una complessità che sarebbe meglio evitare, un uomo rinascimentale poteva scorgere una ricchezza e una complicazione appropriate alla dignità di Dio, creatore dell'Universo. E dove l'uomo del XX sec. vede un groviglio di cerchi (o di sfere), il filosofo naturale del Rinascimento vedeva trionfalmente realizzata la possibilità di analizzare i moti complicati in perfette componenti semplici. Ciò del resto risulta evidente nel De revolutionibus, dove Copernico sostituisce al modello che utilizza gli equanti i doppi epicicli; circa quarant'anni più tardi, Tycho seguì il suo esempio. Questa preferenza per le componenti semplici piuttosto che per una semplicità generale si trova anche nelle dimostrazioni matematiche del tempo. Sembra sia stato considerato migliore il metodo di fornire una dimostrazione che si basasse solo su risultati elementari, come le proprietà dei triangoli simili, piuttosto che provvedere una dimostrazione più breve basata però su teoremi più avanzati. Riguardo al sistema planetario, il giudizio estetico è ben riassunto dai versi con cui Dante termina il Paradiso: "ma già volgeva il mio desio e 'l velle,/ sì come rota ch'igualmente è mossa,/ l'amor che move il sole e l'altre stelle".
Tuttavia, è chiaro che, almeno da parte dei dotti, a partire dal XV sec. si cominciò ad avvertire un certo disagio per l'incapacità della scienza astronomica di fornire un calendario affidabile e, più in generale, per l'evidente imprecisione delle maggiori tavole astronomiche. Dal momento che l'osservazione astronomica non era alla portata di tutti, gli astrologi facevano generalmente uso delle tavole per trovare le posizioni dei pianeti, così la loro imprecisione si ripercuoteva nella vita di tutti i giorni, per esempio nella medicina. Sembra comunque che nessun astronomo del XV sec., così come nessuno dei più importanti filosofi e scienziati dell'epoca, abbia pensato che il sistema astronomico sul quale erano basate le tavole contenesse un grave difetto di base.
L'interesse di Regiomontano per l'opera di Tolomeo è tipico dell'Umanesimo rinascimentale; esso rappresentò il tentativo di ritornare al sistema dei Greci che, ottimo in origine, si riteneva fosse stato corrotto dalle aggiunte successive. Non vi era in atto alcun 'sommovimento' nel mondo degli astronomi che spingesse verso una riforma, e non fu certo un impulso del genere a stimolare Copernico.
L'interesse per un sistema astronomico radicalmente differente non sembra sia stato occasionato neppure da un qualche specifico problema astronomico dell'epoca. Piuttosto sembra un prodotto dell'istruzione umanistica, di una generazione successiva a quella di Regiomontano, allorché gli studiosi presero a rivolgersi verso autori meno conosciuti del mondo antico. Tra questi, Platone. L'incarico dato da Cosimo de' Medici a Marsilio Ficino di tradurre varie opere in latino, fra cui quelle di Platone, ebbe come primo risultato la traduzione delle opere ritenute più antiche e attribuite a un autore di area egizia noto come Ermete Trismegisto. Soltanto agli inizi del XVII sec. fu dimostrato che queste opere erano state scritte probabilmente nel II o III sec. d.C., ma nel XV sec. la loro antichità era ricavata sulla base di quanto era affermato nelle loro pagine.
È possibile che Copernico abbia conosciuto le opere di Ficino in Italia, pur essendo assai distante sia dalla filosofia naturale dell'umanista fiorentino, sia dall'astrologia, completamente assente dai suoi scritti.
L'assoluto disinteresse di Copernico per l'astrologia era certamente inconsueto per uno studente di medicina. Lo stesso Rhaeticus inserisce elementi di astrologia nella sua Narratio prima; ma non c'è nulla di simile nel De revolutionibus. Si può congetturare che Copernico, il quale, come si è visto, aveva avvertito come il suo sistema rendesse plausibile l'ipotesi dell'Universo infinito, abbia forse anche notato che non era assolutamente necessario ammettere una sfera per le stelle fisse; in questo modo forse le costellazioni dello Zodiaco, tanto importanti per gli astrologi, non avrebbero rappresentato, agli occhi di Copernico, reali raggruppamenti di stelle nello spazio. Formulare tale congettura significa però prestare a Copernico argomenti posteriori; fu infatti paradossalmente Kepler ‒ interessato all'astrologia ‒ a rigettare le costellazioni. Da questo punto di vista si può dire che Copernico sia stato meno copernicano di Kepler. In ogni caso, sembra che conoscesse abbastanza l'opera di Ficino, da aver appreso qualcosa circa le opinioni di Ermete Trismegisto. Ne riporta, per esempio, la definizione del Sole come di un Dio visibile. Essendo il Dio Sole (Ra) la principale divinità egizia, questa non era una dichiarazione controversa per i lettori originari di Ermete; per Copernico, invece, era un riferimento agli Antichi, che serviva a corroborare il proprio argomento relativo alla nobiltà del Sole, e quindi alla sua collocazione al centro dell'Universo, come un re nella sua corte. Nello stesso passo, Copernico cita anche l'Elettra di Sofocle ove il Sole è chiamato "onniveggente" (espressione che si potrebbe far risalire a Omero). Citare le fonti classiche è, naturalmente, un tipico modo umanistico di sostenere un argomento. Copernico tuttavia si discosta dalla tradizione che considerava la posizione della Terra la più bassa, perché molto distante dai cieli più alti abitati da Dio e dagli angeli. Anzi, una delle obiezioni che spesso era sollevata contro il suo sistema era che esso aveva nobilitato la Terra facendone un corpo celeste, mentre nel contempo aveva diminuito la dignità quasi regale del Sole. Kepler fornì, a questo proposito, un argomento di risposta modificando l'analogia cusaniana della sfera e della Trinità ‒ avendo la sfera tre parti indivisibili ma distinguibili: il centro, la superficie e il volume ‒ e usandola per descrivere le tre componenti ferme del sistema copernicano. Egli fece del Sole (in qualità di Padre) il centro della sfera, della sfera delle stelle fisse la superficie (il Figlio) e dello spazio intermedio il volume (lo Spirito Santo). Con gli anni, tuttavia, Kepler rinunciò all'idea che ci fosse una sfera delle stelle fisse, dunque egli stesso dovette distaccarsi da quest'analogia.
Copernico, d'altra parte, non sembra consapevole di un possibile conflitto tra il suo sistema astronomico e quanto asserito nel libro di Giosuè, almeno se non consideriamo la dedica del De revolutionibus a Paolo III come una misura precauzionale. Nel complesso, sembra più probabile che egli, come del resto molti suoi contemporanei, non prevedesse il disagio che scaturiva dall'interpretazione letterale della Scrittura, disagio che avrebbe segnato cattolici e protestanti nella seconda metà del XVI sec. e per buona parte del XVII secolo. Nel considerare la possibilità di una Terra in movimento, c'era già stato un precedente nel XIV secolo. Nell'opera Le livre du ciel et du monde, un importante commentario al De caelo di Aristotele, completato nel 1377, Nicola Oresme (1320 ca.-1382), che insegnò all'Università di Parigi e in seguito fu vescovo di Lisieux, non solo aveva suggerito la possibilità che il mondo fosse infinito, ma sosteneva anche che non era possibile decidere con l'osservazione, se fosse l'Universo oppure la Terra a compiere la rotazione diurna. Egli si appellava alla fede nelle Scritture per appianare tale questione, ma evidentemente era pronto a considerarla indecidibile nei termini della filosofia naturale.
Non è chiaro se si debba considerare ciò come un'audace speculazione, o piuttosto come un mero esercizio dialettico, sia pure molto elegante. In ogni caso, le dottrine espresse nella Sacra Scrittura sembrano aver poco a che fare con l'accettabilità della questione come materia di disputa. Presumibilmente, fu in parte a causa della Riforma che il trattato di Copernico ebbe una diversa ricezione ‒ a partire da quella del suo editore. Si deve però anche tener presente l'effetto della stampa in quanto ci si aspettava che il De revolutionibus orbium coelestium raggiungesse molti più lettori del libro di Oresme, e certamente fu così. È chiaro, del resto, che ci furono molti astronomi che non lo lessero, o almeno non lo ritennero meritevole di esser discusso. Comunque, anche dopo un periodo di relativa non popolarità ‒ se si eccettua l'uso indiretto nelle Tavole pruteniche ‒ il fatto che l'opera fosse stata stampata assicurò che rimanessero disponibili copie per i lettori della successiva generazione.
Come si è visto, la prefazione di Osiander al De revolutionibus orbium coelestium solleva la questione dell'interpretazione da accordare ai modelli del moto planetario elaborati dai matematici (ossia dagli astronomi). Nell'includere alcune riflessioni di filosofia naturale nella parte della sua opera che descrive nell'insieme il sistema, Copernico stava seguendo l'esempio di Tolomeo.
Nell'Almagesto, tuttavia, lo studio della fisica del sistema è più succinto di quello che compare nel De revolutionibus orbium coelestium; forse perché egli era naturalmente consapevole di star difendendo qualcosa di totalmente nuovo per i suoi lettori, sebbene non per l'astronomia. Gli argomenti che contrapponevano ciò che oggi, in materia di ipotesi astronomiche, è chiamato 'realismo' a ciò che, sempre in termini moderni, è noto come 'finzionalismo', emersero solo nel successivo dibattito sul copernicanesimo, ma queste stesse parole non hanno alcun equivalente nella cultura rinascimentale. È tuttavia ragionevole domandarsi se Copernico abbia espresso un'opinione esplicita sulla questione, e sembra che la risposta debba essere negativa. Il testo del De revolutionibus suggerisce, comunque, con una certa forza, una posizione (per usare termini moderni) 'realista' di Copernico. Egli si aspettava che il modello matematico fosse in accordo con quello fisico; anzi che l'analisi fisica dettasse e guidasse la formulazione matematica, come è evidente dal suo argomento sugli equanti. Ciò è interamente in accordo con i principî generalmente aristotelici che sono alla base della sua opera; nonostante il necessario discostarsi dai dettagli della fisica aristotelica per introdurre il moto della Terra, il nuovo sistema astronomico, che è realmente una nuova cosmologia, non rappresenta una rottura radicale rispetto ai principî aristotelici. La sua versione della fisica di Cusano considera ciascun corpo celeste come il centro di sé stesso, di modo che gli oggetti del mondo lunare faranno riferimento alla Luna, quelli di Giove a Giove, e così via. Una molteplicità di centri assumono il ruolo che Aristotele aveva assegnato alla Terra, mentre il sistema è costruito ancora per conservare l'aristotelica rotazione delle sfere celesti. In ogni caso, i lettori sembrano aver prestato poca attenzione alla fisica di Copernico e neppure gli anticopernicani della generazione successiva si preoccuparono di confutarla; essi costruirono semplicemente i loro argomenti contro il moto della Terra, ignorando la fisica che sottostava a tale concezione.
Storicamente, il più importante astronomo lettore di Copernico fu Kepler. Al tempo in cui Mästlin lo introdusse al De revolutionibus orbium coelestium, il libro aveva più di quarant'anni e le tavole su di esso basate, le Tavole pruteniche di Reinhold (1551), si erano rivelate di poco più accurate di quelle precedenti basate sull'astronomia tolemaica. Gli argomenti di Kepler a favore del sistema copernicano erano così differenti da quelli di Copernico che è necessario guardare indietro alla natura e alla storia dei suoi interessi filosofici. Nel Mysterium cosmographicum Kepler deduce il numero e gli spazi tra i pianeti, cioè le proprietà fisiche dell'Universo, dalle proprietà dei cinque solidi regolari descritti nell'ultimo libro degli Elementi di Euclide (v. sopra). La credenza secondo cui le verità del mondo osservabile possono essere derivate dalle più alte verità geometriche risale a Platone, ed è del tutto ragionevole classificare le opinioni filosofiche di Kepler come platoniche, sebbene egli abbia anche letto autori neoplatonici come Proclo (410-485 d.C.) ‒ gli studiosi rinascimentali non separavano, infatti, gli autori del periodo 'classico' da quelli della Tarda Antichità. La sua ispirazione platonica non deve nulla alla mediazione di Ficino; egli studiò greco ed ebraico a Tubinga, e sembra quasi certo che abbia letto tutte le opere in greco originale. Quando si accorse che il testo greco degli Harmonica di Tolomeo non era disponibile su carta stampata, chiese a un amico di aiutarlo a trovare un manoscritto in greco. Lo studio del greco era ampiamente diffuso all'epoca, probabilmente favorito dal fatto che esso era utile per lo studio teologico dei testi patristici, al punto che per esempio si rese inutile integrare l'Epytoma di Regiomontano con una traduzione completa dell'Almagesto. Se Kepler era dotato di un talento straordinario, la natura della sua educazione universitaria era tuttavia più o meno in linea con quella della fine del XVI secolo.
La posizione filosofica che traspare dalle sue opere cosmologiche (Mysterium cosmographicum e Harmonices mundi libri V, 1619) è analoga a quella del Timeo di Platone, nel quale le proprietà della materia sono spiegate in termini delle proprietà matematiche dei cinque solidi regolari (conosciuti anche come 'solidi platonici' proprio per l'uso che di essi fa Platone in questo dialogo). Di fatto, dei due trattati cosmologici di Kepler è l'ultimo a mostrare le affinità più strette con il Timeo, sebbene entrambi autorizzino ad annoverare Kepler tra i platonici. Le sue deduzioni a priori della natura dell'Universo sono altrettanto fondamentali di quelle di Platone e notevolmente più dettagliate. In particolare, laddove Platone pronuncia giudizi qualitativi sulle proprietà degli elementi (cioè, i quattro elementi del mondo naturale: terra, aria, fuoco e acqua), Kepler formula asserti quantitativi sugli spazi e sulle dimensioni degli orbi. Sebbene sia più evidente negli scritti cosmologici, il platonismo pervade tutto il suo programma di ricerca; e di un vero e proprio programma si tratta, dal momento che egli si era proposto di mostrare la verità, vale a dire la verità fisica del sistema copernicano. Il continuo successo delle Tavole rudolfine, che corroboravano l'eliocentrismo, lo portò molto vicino alla realizzazione di questo obiettivo.
Kepler credeva nella verità fisica del sistema copernicano; vale a dire, in materia di ipotesi astronomiche, era un 'realista'. Il realismo può essere certo connesso al suo platonismo, poiché, secondo tale prospettiva, le verità matematiche determinano effettivamente quelle fisiche. Kepler, infatti, ammette esplicitamente, nel Mysterium cosmographicum, di essere in cerca non semplicemente di una spiegazione matematica per il sistema planetario, ma della sua unica vera spiegazione matematica. Qualche anno dopo, Tycho gli ordinò di replicare, da parte sua, al matematico imperiale suo predecessore, Nicolaus Reymers, che aveva tentato di avanzare diritti sul sistema ticonico; Kepler cominciò così a scrivere un libro che, tra le altre cose, prende in esame la natura delle ipotesi astronomiche. Questo libro, tuttavia, non fu mai portato a termine ‒ probabilmente egli intraprese il compito soltanto perché gli fu chiesto ‒ ma esso fornisce allo storico un quadro dettagliato del realismo e del finzionalismo nel 1600. Purtroppo, poiché il libro non fu mai pubblicato, non si conosce che cosa ne pensassero i contemporanei e sembra non abbia avuto alcuna influenza. L'opera è incompleta, con un forte accento polemico contro Reymers, e presumibilmente non circolò in forma manoscritta. Comunque l'abbozzo rivela chiaramente quello che Kepler pensava su ciò che attualmente si chiama 'storia' e 'filosofia' della scienza. Da questo punto di vista, egli sembra anticipare la nozione di progresso del XVII sec., piuttosto che guardare indietro alla convinzione umanistica del primato della tradizione classica. Secondo Kepler, rispettare Tolomeo significava usare i metodi che egli considerava tipici di questo autore, piuttosto che prendere per buono tutto ciò che si poteva leggere nei suoi testi.
Bibliografia
Field 1988: Field, Judith V., Kepler's geometrical cosmology, London, Athlone Press, 1988.
‒ 1993: Renaissance and revolution. Humanists, scholars, craftsmen and natural philosophers in early modern Europe, edited and introd. by Judith V. Field and Frank A.J.L. James, Cambridge-New York, Cambridge University Press, 1993.
Hall 1983: Hall, A. Rupert, The revolution in science 1500-1750, 3. ed. rev., London-New York, Longman, 1983 (1. ed.: The scientific revolution 1500-1800. The formation of the modern scientific attitude, London-New York, Longman, Green, 1954; 2. ed.: 1962; trad. it.: La rivoluzione scientifica, 1500-1800. La formazione dell'atteggiamento scientifico, Milano, Feltrinelli, 1976).
Hamann 1980: Regiomontanus Studien, hrsg. von Günther Hamann, Wien, Verlag der Österreichischen Akademie der Wissenschaften, 1980.
Leopold 1986: Leopold, John H., Astronomen, Sterne, Geräte. Landgraf Wilhelm IV. und seine sich selbst bewegenden Globen, Luzern, Fremersdorf, 1986.
Manno 1987: Cultura, scienze e tecniche nella Venezia del Cinquencento, a cura di Antonio Manno, Venezia, Istituto Veneto di Scienze, Lettere ed Arti, 1987.
Schmeidler 1970: Schmeidler, Felix, Nikolaus Kopernikus, Stuttgart, Wissenschaftliche Verlagsgesellschaft, 1970.
Tester 1987: Tester, S. Jim, A history of western astrology, Woodbridge, Boydell Press, 1987.
Thoren 1990: Thoren, Victor E., The Lord of Uraniborg. A biography of Tycho Brahe, with contributions by John R. Christianson, Cambridge-New York, Cambridge University Press, 1990.
Thorndike 1949: Thorndike, Lynn, The Sphere of Sacrobosco and its commentators, Chicago, University of Chicago Press, 1949.
Van Helden 1985: Van Helden, Albert, Measuring the universe. Cosmic dimensions from Aristarchus to Halley, Chicago, University of Chicago Press, 1985.
Walker 1958: Walker, Daniel P., Spiritual and demonic magic from Ficino to Campanella, London, Warburg Institute, 1958.
Whitfield 1995: Whitfield, Peter, The mapping of the heavens, London, British Library, 1995.
Zinner 1938: Zinner, Ernst, Leben und Wirken des Johannes Müller von Königsberg, genannt Regiomontanus, München, C.H. Beck'sche Verlagsbuchhandlung, 1938.