implicazione
implicazione
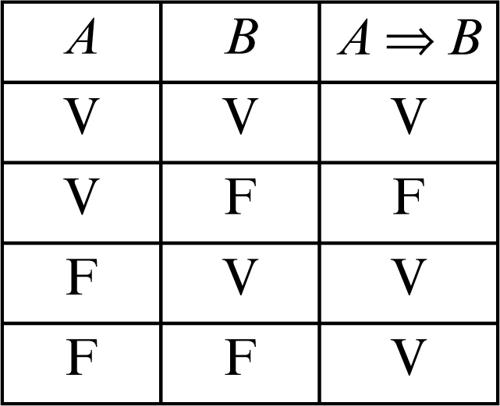
implicazione connettivo logico che corrisponde, nella lingua italiana, all’espressione «se... allora» e si indica con il simbolo ⇒. Dati due enunciati A e B, l’enunciato A ⇒ B (si legge «A implica B») è una implicazione in cui A e B sono rispettivamente detti antecedente e conseguente. Per esempio, la frase «se dormo mi riposo» può essere espressa simbolicamente dalla scrittura A ⇒ B, dove A indica l’enunciato «dormo» e B l’enunciato «mi riposo». Una implicazione è falsa se e solo se l’antecedente è vero e il conseguente è falso, se cioè il vero implica il falso. In tutti gli altri casi l’implicazione è vera. Ne consegue che se l’antecedente è falso l’enunciato complessivo è sempre vero, in linea con la asserzione latina «ex falso quodlibet» (che significa «dal falso può discendere qualsiasi cosa»). I valori di verità dell’implicazione sono quindi rappresentati nella seguente tavola di verità:
Dalla tavola di verità segue immediatamente che l’enunciato A ⇒ B è logicamente equivalente all’enunciato ¬A ∨ B (→ equivalenza logica). Si consideri la proposizione: «Se n è un multiplo di 3 allora n è un numero dispari». In aritmetica la proposizione è falsa, come si deduce considerando n = 6; in questo caso l’antecedente, «6 è multiplo di 3», è vero, mentre il conseguente, «6 è dispari», è falso.
Se l’antecedente è falso allora l’implicazione è sempre vera indipendente dal valore del conseguente. Si consideri per esempio, con tutti i limiti che esempi di espressioni formali tratti dal linguaggio comune comportano, la frase: «se farai il bravo ti darò un premio», pronunciata da un padre al proprio figlio; si hanno le seguenti possibilità:
• il figlio fa il bravo (antecedente vero) e il padre gli dà il premio (conseguente vero): si può dire che la promessa è stata mantenuta, cioè che l’implicazione è vera;
• il figlio fa il bravo (antecedente vero) ma il padre non gli dà il premio (conseguente falso): la promessa non è stata mantenuta e l’implicazione è falsa;
• il figlio non fa il bravo (antecedente falso); il padre non è più legato dalla promessa che ha fatto, quindi sia che decida di dargli lo stesso il premio (conseguente vero) sia che decida di non darglielo (conseguente falso) la promessa è stata ugualmente mantenuta e l’implicazione è vera.
L’implicazione inversa di una data implicazione quale per esempio A ⇒ B si ottiene scambiando l’antecedente A con il conseguente B e corrisponde all’enunciato «B implica A» espresso simbolicamente dalla formula B ⇒ A. È importante notare che il valore di verità dell’implicazione A ⇒ B è indipendente dal valore di verità dell’implicazione inversa B ⇒ A, cioè l’implicazione A ⇒ B può essere vera anche nel caso in cui la sua implicazione inversa B ⇒ A sia falsa e viceversa. Per esempio, la frase A ⇒ B: «se manca l’elettricità, allora l’elettrodomestico si blocca» è una implicazione vera, tuttavia la sua implicazione inversa, B ⇒ A: «se l’elettrodomestico si blocca, allora manca l’elettricità» è falsa ed è logicamente equivalente alla proposizione A ∨ ¬B.
L’implicazione A ⇒ B è invece logicamente equivalente all’implicazione ¬B ⇒ ¬A (si legge «non B implica non A»), detta contronominale dell’implicazione data. Riprendendo l’esempio precedente, la frase «se l’elettrodomestico non si blocca, allora non manca l’elettricità» risulta equivalente alla frase «se manca l’elettricità, allora l’elettrodomestico si blocca»: se è vera la prima, è vera anche la seconda e viceversa.
Nel linguaggio degli enunciati il connettivo dell’implicazione è legato alla derivazione logica dal teorema di deduzione, che stabilisce che se dalla formula A e dagli assiomi di S è dimostrabile la formula P, allora A ⇒ B è un teorema di S. Più sinteticamente: se A ⊢s P allora ⊢s A ⇒ P.
Attraverso il teorema di deduzione, la catena di derivazione che porta dall’ipotesi A alla conclusione P si riflette nel connettivo di implicazione, divenendo così interna al linguaggio formale. Per questo, l’equivalenza logica fra i due enunciati
è spesso utilizzata nelle deduzioni formali e, in particolare, nelle dimostrazioni per assurdo. Per esempio, per dimostrare l’implicazione «Se n2 è un numero pari allora n è pari» si parte dalla negazione del conseguente: «n non è pari» cioè «n è dispari»; se ne deduce la negazione dell’antecedente («n è dispari») attraverso i seguenti passaggi:
• se n è dispari, allora può essere scritto nella forma n = 2k + 1, dove k è un numero naturale;
• allora il quadrato di n è (considerandolo come quadrato di un binomio) n2 = (2k + 1)2 = 4k 2 + 4k + 1 = 2(2k 2 + 2k) + 1;
• allora n2 è un numero dispari.
È così dimostrata l’implicazione data. Va notato che in questo schema dimostrativo si è fatto ricorso al principio del → terzo escluso.
Per la congiunzione di una implicazione e della sua inversa si veda → doppia implicazione.