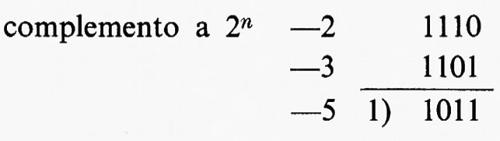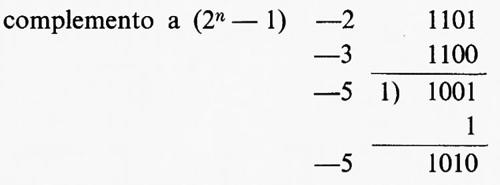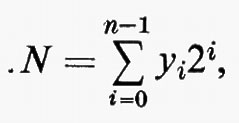Informatica

Informatica

di Luigi Dadda, Peter J. Denning

INFORMATICA

Informatica ed elettronica dei calcolatori

di Luigi Dadda

sommario: 1. Introduzione. 2. Evoluzione storica degli elaboratori: a) Fno a circa il 1940. b) Dal 1940 al 1950. c) Dal 1950. 3. Concetti introduttivi all'informatica. 4. L'elaboratore come automa per la memorizzazione e la sostituzione di simboli: a) Gli elaboratori elettronici e i programmi.  b) Gli algoritmi e le macchine di Turing. 5. Elaboratori e linguaggi. 6. Classificazione dell'informazione: a) Informazione numerica o algebrica. b) Informazione fisica. c) Informazione strutturata o modulare. d) Testi in linguaggio naturale. e) Testi in linguaggi artificiali. 7. La codificazione dell'informazione: a) L'elaborazione dell'informazione codificata. b) Rappresentazione dei numeri in forma ‛normalizzata' (floating-point). 8. I principî della teoria delle reti logiche o binarie o di commutazione. 9. L'evoluzione della tecnologia dei circuiti elettronici binari. 10. L'evoluzione della tecnologia delle memorie. 11. L'evoluzione dell'architettura delle memorie. 12. L'evoluzione dell'architettura degli elaboratori. a) L'architettura dei sottosistemi. b) L'architettura dei sistemi di elaborazione: il collegamento dei sottosistemi. c) I microprocessori. 13. Le reti di calcolatori. □ Bibliografia.

1. Introduzione

I calcolatori elettronici sono nati come branca distinta dell'elettronica intorno all'anno 1950, dando origine sia a una nuova disciplina, l'informatica, sia a un nuovo importante settore industriale e influendo anche su molte altre discipline (scientifiche e umanistiche) nonché su molti aspetti della vita associativa. Tali influssi sono tuttora in continuo aumento e una valutazione della loro linea di sviluppo verrà tratteggiata in questo articolo.

I calcolatori elettronici sono noti essenzialmente come macchine da calcolo che sollevano l'uomo dall'arido compito di eseguire le lunghe sequenze di operazioni aritmetiche richieste dai calcoli scientifici e tecnici. Ci si è resi però presto conto che tali macchine costituivano uno strumento più generale di quello che inizialmente era stato concepito, in quanto erano capaci di compiere le più svariate elaborazioni su ‛stringhe' di simboli, non necessariamente limitati alle cifre numeriche. Ciò allargava enormemente la portata della macchina calcolatrice (giustamente denominata ‛elaboratore di informazione' nella nostra lingua), estendendone il campo di applicazione dall'informazione puramente numerica a quella codificata in stringhe di simboli, per esempio alfabetici. Mentre però l'informazione numerica era già da tempo fondata sull'importante costruzione matematica sviluppata precedentemente al calcolatore elettronico, l'elaborazione di una stringa di simboli qualsiasi pose nuovi problemi di carattere sintattico e semantico, che coinvolgevano le teorie dei linguaggi artificiali e naturali. È per tale motivo che l'informatica si è incontrata con le scienze umanistiche, come già accennato. Tale incontro si è sviluppato, peraltro, anche per altre vie, quali quelle percorse dagli studi sull'‛intelligenza artificiale' e sul riconoscimento automatico delle forme o configurazioni, studi diretti a sondare le possibilità degli elaboratori nello svolgimento di compiti che vanno al di là della pura e semplice elaborazione dell'informazione codificata; si tratta, infatti, di indagini rivolte a simulare e indagare il meccanismo delle più importanti funzioni del cervello umano.

Le applicazioni degli elaboratori ai problemi di carattere scientifico e tecnico si sono sviluppate a tal punto che essi sono ormai considerati strumenti insostituibili. Le applicazioni in settori amministrativi e organizzativi, iniziate con lo svolgimento di compiti elementari, sono state sviluppate al punto da rendere significativo il paragone tra ‛sistema informativo' di un'azienda e sistema nervoso di un organismo. Il superamento di alcune limitazioni tecnologiche ancora oggi presenti permetterà la realizzazione di sistemi informativi capaci di gestire i grandi servizi pubblici (sanità, territorio, trasporti, anagrafi di vario tipo). L'influenza di tali sistemi sulla vita associata sarà tale da porre anche problemi di grave momento, come quello della protezione legislativa delle libertà individuali che sarebbero minacciate da una diffusione non controllata e da un accesso indiscriminato alle ‛banche di dati' contenenti le informazioni sui vari aspetti della vita degli individui.

In questo articolo verranno esaminati, nell'ordine, l'evoluzione storica degli elaboratori, i vari aspetti che essi presentano al momento attuale e le prospettive di sviluppo.

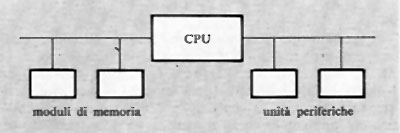
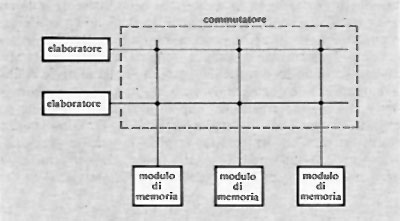
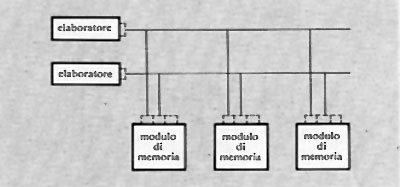
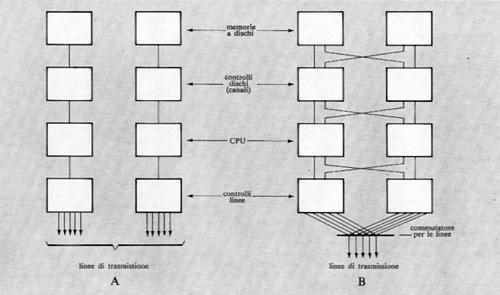
2. Evoluzione storica degli elaboratori

a) Fino a circa il 1940

I dispositivi che possono considerarsi predecessori degli odierni elaboratori sono quelli che sono stati usati o proposti nel corso dei secoli come ausili alle operazioni del contare e aritmetiche.

L'arte del contare e del computare è stata sviluppata indipendentemente in culture indipendenti. L'applicazione di tale arte alle osservazioni degli astri le ha conferito un carattere divino e i numeri hanno acquisito per tale motivo un carattere mistico. Ma la stessa arte è stata coltivata anche per motivi pratici, specialmente nel commercio, come testimoniano tavolette sumeriche di cinquemila anni fa e il fatto che molti dei libri che Gutenberg stampò furono testi di aritmetica commerciale. Lo strumento tipico dell'antica arte del computare fu l'abaco (ancora oggi largamente usato nei paesi asiatici e dell'Europa orientale).

L'arte del computare fu sempre considerata molto difficile e tediosa e il suo sviluppo cominciò a verificarsi solo con l'adozione dell'attuale sistema di numerazione decimale, fondato sul concetto di ‛base' e utilizzante i simboli originati in India, diffuso per opera di Muḥammad ibn Mūsā al-Khuwārizmī (quest'ultimo è il nome di un villaggio dell'attuale Uzbekistan sovietico; da esso deriva la parola ‛algoritmo'). La diffusione del sistema decimale fece gradualmente scomparire l'uso dell'abaco in Europa, per la maggiore potenza e praticità delle regole di calcolo con numeri decimali (ancora nel XVI secolo, l'università di Altdorf attraeva gli studenti con la promessa che avrebbero imparato perfino la divisione). L'introduzione dei logaritmi da parte di J. Napier e H. Briggs rivoluzionò l'arte del computare, in particolare per i calcoli ‛tecnici' come quelli necessari per la navigazione su grandi distanze. La pubblicazione delle tavole dei logaritmi e delle funzioni circolari caratterizza tale epoca, ed è importante sottolineare il ruolo assunto da tali tavole come strumento per tutti i calcoli tecnici e scientifici (si può dire che soltanto oggi, con l'avvento degli elaboratori elettronici, la loro importanza è definitivamente declinata). I logaritmi sono peraltro la base dei ‛regoli calcolatori' (ove i numeri sono rappresentati appunto da segmenti la cui lunghezza è proporzionale al loro logaritmo e che perciò si prestano bene per le operazioni di divisione e di moltiplicazione).

La notazione decimale è la base dei primi veri e propri meccanismi di calcolo, il più significativo dei quali fu quello costruito nel 1642 da Pascal (all'età di 19 anni) per offrire un ausilio al padre intendente di finanza a Rouen. Successivamente Leibniz costruì (1673) una sua macchina che fu esposta alla Royal Society di Londra (è interessante citare quanto Leibniz scrisse nel 1671: ‟non è conveniente che uomini eccellenti perdano, come schiavi, ore di lavoro per calcoli che potrebbero essere affidati a chiunque altro se si utilizzassero delle macchine").

Nel 1878 lo svedese Odhner inventò un nuovo dispositivo per l'addizione e i suoi brevetti furono utilizzati in Germania per la costruzione delle note macchine da tavolo Brunsviga.

Tutte le macchine da tavolo, pur costituendo un importante strumento, richiedono l'intervento dell'operatore per ogni operazione aritmetica. Molti dei calcoli, in particolare quelli di tipo tecnico-scientifico, richiedono una lunga successione di tali operazioni e perciò si presenta ancora, sia pure a un livello superiore, l'inconveniente della laboriosita che aveva indotto alla costruzione dei primi meccanismi. Era pertanto ragionevole pensare di compiere un ulteriore passo nell'automazione dei calcoli, rendendo possibile l'esecuzione automatica successiva delle operazioni necessarie per compiere un calcolo complesso.

Tale pensiero venne per la prima volta coltivato dal matematico inglese Ch. Babbage (1792-1871), che propose una macchina (the difference engine) capace di calcolare tavole numeriche, basata sul ‛calcolo delle differenze'. Dopo la presentazione di un piccolo modello funzionante, realizzato con l'appoggio della Royal Society e del governo inglese, il Babbage iniziò la costruzione di un modello più grande (con numeri di 20 cifre e capace di calcolare fino alle seste differenze) concepito per calcoli effettivi, la cui costruzione però venne sospesa. Successivamente un esemplare venne completato e utilizzato nel 1863 per il calcolo delle tavole di vita usate poi per molti anni dalle compagnie assicuratrici. Nel frattempo il Babbage aveva concepito l'analytical engine, cioè una macchina capace di qualsiasi tipo di calcolo e basata sugli stessi concetti che sono alla base dei moderni elaboratori elettronici. Essa infatti comprendeva una ‛memoria' per dati e programmi, un'unità di calcolo e una per il controllo della sequenza delle operazioni. L'elemento fondamentale era il programma di calcolo, costituito dall'indicazione delle successive operazioni. Erano previste, in particolare, operazioni che permettevano alla macchina la scelta tra due successive diverse sequenze di istruzioni.

L'analytical engine non venne mai completato. È interessante notare che il Babbage pensò di risolvere il problema di controllare la successione delle numerose operazioni necessarie per un calcolo completo adottando un dispositivo inventato da Jacquard per il controllo dei telai di tessitura e basato sull'uso di schede perforate per ottenere la ripetizione di disegni e trame nei tessuti.

Vent'anni dopo la morte di Babbage, il responsabile dell'American Bureau of the Census, Hollerith, di fronte al problema di elaborare i dati di un censimento, ricorse al metodo di registrare tali dati tramite perforazioni su schede di carta e inventò una serie di macchine per ordinare le schede e per analizzare i dati su esse registrati. Le idee di Hollerith furono sviluppate dalla International Business Machines Corporation (IBM) in America e dalla British Tabulating Machine Company in Inghilterra, mentre le Società Powers-Samas e Remington Rand svilupparono le idee di Powers, assistente di Hollerith. In Francia, successivamente, la Compagnie de Machine Bull si basava per gli stessi scopi sui brevetti del norvegese Bulì. Le suddette società hanno contribuito, fino all'avvento degli elaboratori elettronici, a diffondere l'impiego delle macchine a schede perforate soprattutto per la soluzione dei problemi amministrativi; si può ritenere che la rapida affermazione degli elaboratori nelle applicazioni amministrative e organizzative sia in gran parte dovuta alla preparazione raggiunta nell'epoca precedente con l'uso delle macchine a schede perforate che, seppure grandemente inferiori agli elaboratori elettronici, hanno contribuito a sviluppare una mentalità che ha reso relativamente facile l'accettazione del nuovo più potente strumento. Inoltre le macchine a schede perforate costituiscono uno dei più noti strumenti per l'ingresso dei dati negli stessi elaboratori. Sebbene le macchine a schede fossero particolarmente concepite per le elaborazioni amministrative, si ebbero anche significative applicazioni a calcoli scientifici e ciò valse probabilmente di stimolo a concepire macchine più adatte allo scopo.

b) Dal 1940 al 1950

L'idea di una macchina calcolatrice universale secondo la concezione di Babbage rivisse negli Stati Uniti e successivamente in Inghilterra (oltre che in Germania) a cominciare dal 1938, anno nel quale il prof. Aiken dell'Università di Harvard, con la collaborazione della IBM, iniziò il progetto del calcolatore Mark I (completato nel 1944). Esso era costituito da organi elettromeccanici (relè e selettori rotanti) ed eseguiva, su numeri decimali di 23 cifre, operazioni la cui successione era controllata da un nastro di carta perforata al ritmo di 200 operazioni al minuto. La programmazione fu tuttavia limitata, rispetto a quella concepita da Babbage, dal fatto che vi erano soltanto due alternative possibili: continuare con l'operazione successiva o fermarsi. Mark I venne intensamente usato per il calcolo di ogni genere di tabelle numeriche.

Nel 1946 presso la Moore School of Electrical Engineering dell'Università di Pennsylvania, J. W. Mauchly e J. P. Eckert completarono la prima macchina interamente elettronica, chiamata E.N.I.A., C. (Electronic Numerical Integrator and Calculator). Essa comprendeva 18.000 tubi elettronici e 1.500 relè e la sua struttura poteva considerarsi come un analogo elettrico del Mark I, rispetto al quale risultava molte centinaia di volte più veloce.

Nel 1945 il prof. J. von Neumann, della stessa Moore School, pubblicava un rapporto sul progetto logico dei calcolatori elettronici, in cui i concetti precedentemente noti venivano completati ed estesi alla luce delle possibilità offerte dalla tecnologia elettronica (in particolare veniva proposto l'uso del sistema binario già preconizzato da Leibniz e si illustrava la necessità di disporre di memorie elettroniche di grandi capacità), in modo da ottenere macchine molto più potenti di quelle fin allora concepite e con un minor numero di componenti elettronici. È importante osservare che la struttura delle macchine attuali può considerarsi come derivata per evoluzione da quella suggerita da von Neumann.

Nel 1948 la IBM completava una macchina denominata Selective Electronic Calculator, composta da 23.000 relè e 13.000 tubi elettronici. Tale macchina è stata forse la prima a permettere la biforcazione condizionata di un programma, secondo le concezioni di Babbage. Essa fu intensamente utilizzata, in particolare dalla Atomic Energy Commission.

Nel 1950 presso il National Bureau of Standard entrava in funzione la macchina SEAC (Standard Eastern Automatic Computer), caratterizzata da memorie a linee di ritardo in mercurio e da organi di entrata e uscita a filo magnetico.

Un'intensa attività di ricerca si svolgeva contemporaneamente in Gran Bretagna all'Università di Manchester, a quella di Cambridge, al National Physical Laboratory, ad Harwell, al Telecommunication Research Establishment, all'Empirial College, al Royal Aircraft Establishment.

In particolare a Manchester veniva sviluppata una macchina con una memoria basata sull'uso di tubi a raggi catodici, sulla cui superficie veniva controllato il deposito di una matrice di cariche elettriche assunte a rappresentare cifre binarie. La nuova memoria caratterizzava fino a circa il 1955 molte altre macchine, costruite anche in serie, e fu in seguito soppiantata dalla memoria a nuclei magnetici.

A Cambridge, nel 1949, veniva completata l'EDSAC (Electronic Delay Storage Automatic Calculator), ispirata dal citato rapporto di von Neumann, con la quale si fecero importanti esperienze di programmazione, con l'uso sistematico di sottoprogrammi. La macchina usava memorie a linee di ritardo in mercurio.

Anche in Germania e Svizzera, a opera di Zuse, si svolgeva un'interessante attività nel campo delle calcolatrici automatiche.

c) Dal 1950

A cominciare da tale data, si assiste da una parte al moltiplicarsi di iniziative nei laboratori di ricerca, dall'altra al sorgere di iniziative industriali che si sono oggi sviluppate al punto tale da fare dell'industria degli elaboratori una delle massime dal punto di vista del valore della produzione. Tali iniziative industriali traevano stimolo dall'applicazione delle nuove macchine nel campo delle elaborazioni amministrative, dapprima come semplici complementi ed estensioni delle preesistenti macchine a schede perforate, in seguito come macchine espressamente concepite per tali elaborazioni, che rivoluzionavano le stesse tecniche amministrative e organizzative.

Lo sviluppo degli elaboratori è caratterizzato dall'av- vento di nuove tecnologie e nuovi concetti, convenzionalmente inquadrati in successive ‛generazioni' di macchine.

La ‛prima generazione' (fino a circa il 1955) era caratterizzata dall'uso dei tubi elettronici e di memorie a tubi catodici, elementi che limitavano grandemente l'affidabilità delle macchine. Le tecniche di programmazione erano ancora nella prima fase di sviluppo, con i primi tentativi verso i linguaggi di programmazione.

La ‛seconda generazione' era caratterizzata dall'avvento del transistore, che permetteva di ridurre notevolmente il tasso dei guasti. Come conseguenza, la potenza di calcolo delle macchine subiva un forte incremento, anche grazie all'introduzione delle memorie a nuclei magnetici. Contemporaneamente, la programmazione compiva, soprattutto nel campo dei linguaggi, importanti progressi che permettevano di ridurre considerevolmente le difficoltà della programmazione. L'elaboratore veniva concepito non più come una singola, indivisibile macchina, ma come un sistema formato di moduli variamente componibili per meglio adattarli alle esigenze di ogni applicazione.

La ‛terza generazione' può caratterizzarsi con l'avvento dei circuiti integrati, coi quali le caratteristiche delle macchine sono state ulteriormente migliorate, con riduzione dei costi. Dal punto di vista della programmazione, le tecniche di ‛multiprogrammazione', di time sharing, di ‛elaborazione in tempo reale' estendono ulteriormente gli impieghi, permettendo sia l'uso simultaneo di una stessa macchina da parte di più utenti, sia la possibilità di usare l'elaboratore in modo più strettamente collegato con l'organizzazione che lo adotta. La trasmissione a distanza dei dati permette inoltre di estendere le capacità di elaborazione su aree geografiche molto estese, consentendo anche il collegamento tra elaboratori.

Nel seguito si cercherà di illustrare, i concetti e le tecnologie di base degli elaboratori, descrivendone l'evoluzione e formulando i problemi che si presentano oggi nell'ulteriore sviluppo di quest'applicazione tecnologica.

3. Concetti introduttivi all'informatica

I concetti che oggi sono riconosciuti come fondamentali per gli elaboratori si sono sviluppati e precisati gradualmente, a cominciare da quelli primitivi di Babbage e di von Neumann. Tali concetti primitivi si riferivano all'elaboratore concepito essenzialmente come macchina da calcolo, ma lo sviluppo delle applicazioni ha messo presto in evidenza come la nuova macchina fosse, più in generale, un elaboratore automatico dell'informazione espressa sotto forma di stringhe di simboli. I risvolti concettuali più importanti di tale modo di vedere l'elaboratore verranno sviluppati nel seguito. Ci si vuole qui invece soffermare a introdurre alcune considerazioni preliminari e generali sull'elaboratore.

Analizziamo il flusso delle informazioni in due casi tipici, il primo relativo a due interlocutori umani che comunicano indirettamente tramite un elaboratore (può essere il caso di due interlocutori ‛diretti' che parlano lingue diverse e in cui l'elaboratore compie la traduzione, oppure di due interlocutori ‛indiretti' che comunicano con lo stesso elaboratore programmato per gestire un'azienda, per es. una banca), il secondo relativo invece a un osservatore che si serve dell'elaboratore per indagare il mondo esterno (per es., un ricercatore fisico che si serve dell'elaboratore per lo studio di fenomeni). I due casi si prestano alle seguenti osservazioni.

1. Il mondo reale viene sempre osservato attraverso un modello (anche quando non lo si definisce esplicitamente) che può evolvere in funzione delle stesse osservazioni. Analogamente due interlocutori assumono sempre reciprocamente un modello, oppure si tratta del modello dell'azienda in cui operano.

2. L'informazione viene sempre rappresentata con ‛dati'. Nel caso dell'osservazione del mondo esterno si tratta per esempio di misure, nel caso di due interlocutori può trattarsi di stringhe di simboli, cioè di linguaggi. Anche quando i due interlocutori sono per esempio due operatori di terminali di elaboratori aziendali, essi usano speciali linguaggi. È importante notare che i dati vengono qui considerati dipendenti dal modello stesso: per esempio, uno strumento di misura non viene mai messo in un impianto a caso, ma come il modello suggerisce.

È ancora importante notare che qui si suppone che i due interlocutori comunichino solo attraverso l'elaboratore, cioè esclusivamente tramite linguaggi. Le comunicazioni tra interlocutori umani avvengono, fortunatamente, anche in forma diretta e, anche se si supponesse il linguaggio naturale trattabile dalle macchine (ciò che non è, come verrà meglio detto in seguito), sarebbe difficile pensare di trattare automaticamente gli innumerevoli altri modi di comunicazione umana, come i gesti, le occhiate, ecc.

3. I dati vengono successivamente consegnati ai ‛pro-grammi' per mezzo dei quali vengono elaborati e occorre tener presente che tali programmi consistono nella descrizione dell'elaborazione voluta, descrizione eseguita tramite uno dei ‛linguaggi' di programmazione che la macchina data è capace d'interpretare. Inoltre la gestione dei programmi, dei traduttori di linguaggio e in generale di tutte le risorse della macchina è compiuta tramite un ‛programma base' o ‛sistema operativo', non accessibile all'utente. Per quanto ora detto, l'informazione fornita coi dati viene elaborata in vari stadi dal complesso di tutti i programmi della macchina costituenti il cosiddetto software.

4. Sotto il controllo del programma base le informazioni, rappresentate finalmente nella forma interna alla macchina, cioè con atomi di informazione detti bits, vengono elaborate dai circuiti della macchina, cioè da ciò che è chiamato l'hardware della macchina stessa.

I risultati dell'elaborazione ottenuti nell'hardware sotto forma di bits devono poi ripercorrere a ritroso tutta la catena precedentemente illustrata, per essere infine presentati all'osservatore.

L'illustrazione fatta fornisce, pur nella sua sommarietà, un'indicazione delle numerose trasformazioni che l'informazione subisce quando viene elaborata con macchine. Il più importante problema che emerge dall'illustrazione suddetta è quello delle condizioni che devono verificarsi affinché l'elaborazione automatica delle informazioni sia di qualche utilità, e sembra di poter affermare che la condizione più importante è la ‛conservazione del significato' dell'informazione attraverso tutta la catena delle trasformazioni.

La conservazione del significato dell'informazione assume aspetti diversi nei diversi stadi dell'elaborazione. Al livello più basso, dell'hardware, essa richiede innanzitutto che la sequenza di bits esprimente in un dato codice un dato simbolo venga riconosciuta sempre allo stesso modo nelle varie parti della macchina. Ma ai livelli superiori ciò non è sufficiente, perché lo stesso simbolo in relazioni diverse rispetto ad altri può assumere significati diversi. Si incontrano pertanto i problemi tipici della teoria dei linguaggi, sui quali si tornerà successivamente.

Può essere interessante confrontare la condizione di conservazione del significato con la condizione di conservazione della quantità di informazione di un segnale studiata nella teoria dell'informazione (v. elettronica). Mentre quest'ultima condizione dipende dall'effetto del rumore nei canali di trasmissione del segnale, la conservazione del significato è di carattere linguistico e prescinde dalla precedente condizione, che si presume, anzi, sempre verificata.

4. L'elaboratore come automa per la memorizzazione e la sostituzione di simboli

Come già detto, l'elaboratore moderno, concepito inizialmente come macchina per l'esecuzione di calcoli numerici, si è rivelato ben presto di natura molto più generale: esso è cioè una macchina per la memorizzazione e la sostituzione di simboli.

È importante notare come molte delle operazioni del cervello umano non siano di natura creativa, ma si riducano a un'automatica sostituzione di simboli. Quando, per esempio, eseguiamo una moltiplicazione, ricorriamo sistematicamente alla tavola pitagorica memorizzata durante l'infanzia e operiamo una pura e semplice sostituzione di simboli. Così pure, quando eseguiamo elaborazioni algebriche o differenziazioni o integrazioni di funzioni, operiamo prevalentemente con sostituzioni di simboli, o stringhe di simboli, memorizzati o reperibili in tabelle e manuali. Un altro esempio simile ai precedenti è costituito dall'elaborazione di equazioni di equilibrio chimico.

Gli esempi precedenti sono tratti da campi nei quali la formalizzazione dei rispettivi ‛linguaggi' (cioè delle regole per costituire stringhe significative di simboli per comunicare le informazioni relative al campo considerato) era stata perfezionata anteriormente all'avvento degli elaboratori. Tutte le volte che è stato affrontato il problema di applicare l'elaboratore in settori nei quali tale formalizzazione non era stata ancora perfezionata, ci si è imbattuti in gravi difficoltà, che non possono essere superate se non con una precisa formalizzazione che permetta di sfruttare l'unica vera importante proprietà dell'elaboratore e cioè quella di essere una macchina per la sostituzione e per la memorizzazione di simboli. Tale formalizzazione è stata relativamente facile nel settore delle elaborazioni amministrative e gestionali, ma trova gravissime difficoltà, per esempio, nella soluzione di un problema che è tipicamente un problema di pura sostituzione di simboli e che gli esseri umani sanno compiere con relativa facilità, e cioè la traduzione di testi espressi con linguaggi naturali.

Due sono i più importanti aspetti dell'elaboratore che verranno qui di seguito illustrati, quello del ruolo dell'elaboratore come trasformatore di stringhe di simboli e quello del significato della stessa stringa di simboli.

Infatti l'elaboratore non può essere visto dall'esterno se non come una macchina che accetta stringhe di simboli e che fornisce come risultato stringhe di simboli. Poiché una stringa di simboli può essere considerata come un testo in un certo linguaggio, lo studio dei linguaggi risulta d'importanza rilevante per la comprensione degli elaboratori.

Dal punto di vista interno ci interessa invece il meccanismo di sostituzione di simboli che avviene per effetto di un programma (anch'esso composto di stringhe di simboli), propriamente un ‛algoritmo': è pertanto quest'ultimo l'altro concetto rilevante per la comprensione degli elaboratori. Essi verranno illustrati più avanti.

a) Gli elaboratori elettronici e i programmi

fig. 2

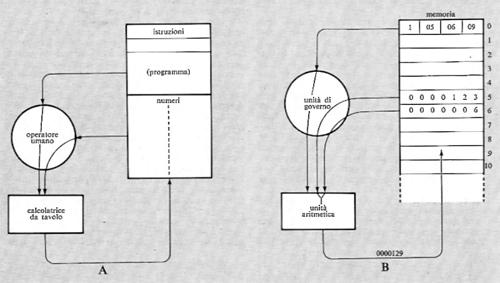
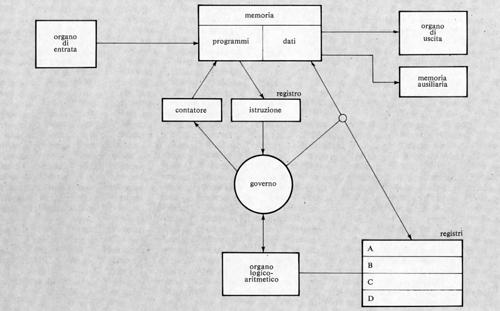
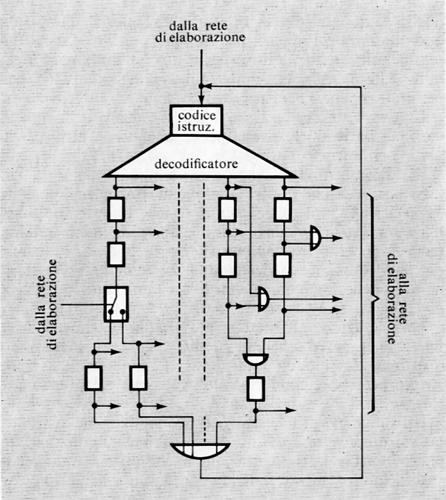
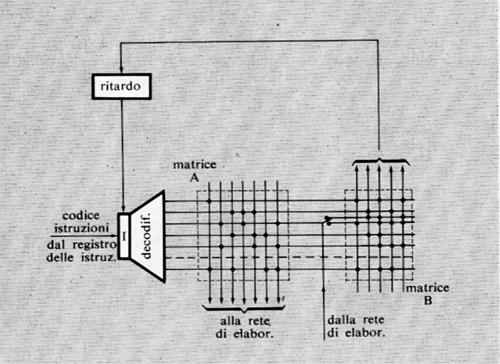
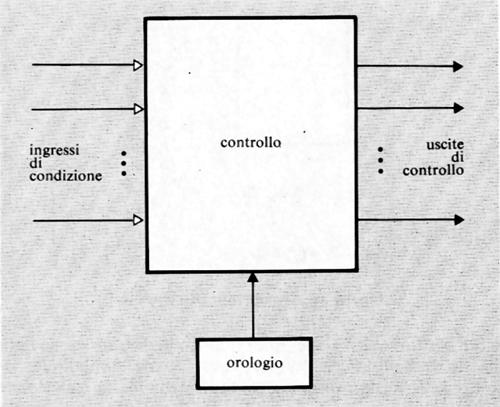
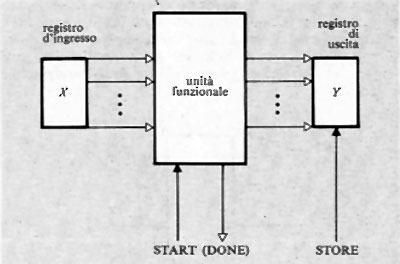
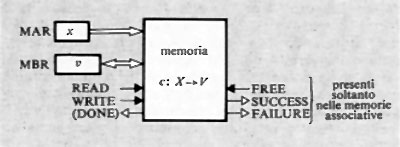
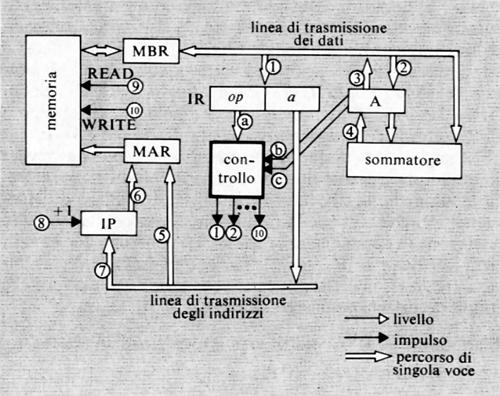
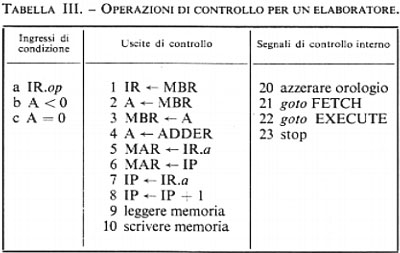
Come è stato ricordato nella precedente esposizione storica, la concezione che Babbage aveva di un calcolatore universale derivava dalla constatazione che calcolazioni comunque complicate potevano essere compiute da persone anche ignare del problema, una volta che la sequenza delle operazioni fosse stata accuratamente e preventivamente descritta. Tale sequenza di operazioni forma l'algoritmo per una certa classe di problemi. La similitudine tra la calcolazione tramite operatori umani e quella tramite una macchina è mostrata nella fig. 2. Nella fig. 2A l'operatore umano deve solo interpretare fedelmente le istruzioni costituenti il programma e saper eseguire (magari con l'ausilio di una calcolatrice da tavolo) le operazioni richieste; non deve assolutamente prendere alcuna iniziativa autonoma. Nella fig. 2B l'operatore umano è sostituito da una parte della macchina (l'unità ‛di governo' o ‛di controllo'), capace d'interpretare le istruzioni del programma. Queste sono registrate in un organo detto di governo o di controllo, corrispondente al foglio di carta della fig. 2A e contenente anche i dati numerici su cui operare. Le istruzioni del programma sono rappresentate in forma codificata con 7 cifre decimali di cui: la prima rappresenta il tipo di operazione (l'elenco delle operazioni eseguibili dalla macchina è rappresentato nella tab. I); le due successive coppie di cifre rappresentano ‛l'indirizzo' dei due ‛operandi', nell'esempio i due addendi; l'ultima coppia rappresenta l'indirizzo di memoria ove s'intende che venga riposto il risultato (nelle usuali memorie, quando si registra una nuova informazione in una certa cella, il contenuto precedente viene perduto e sostituito dal nuovo. Per contro, quando l'organo di controllo preleva l'informazione, per esempio un operando, da una cella, l'informazione stessa rimane registrata nella stessa cella).

Oltre alle istruzioni di tipo ‛aritmetico', un elaboratore è capace di eseguire molti altri tipi di istruzioni. Di particolare rilevanza sono quelle dette di ‛salto' o ‛biforcazione'. È importante osservare che di regola (cioè con qualsiasi altro tipo di istruzione) l'unità di governo provvede a eseguire le istruzioni nell'ordine in cui esse sono registrate nelle celle della memoria. Un'istruzione di salto permette invece di interrompere l'esecuzione per indirizzi sequenziali, obbligando l'elaboratore a compiere un salto a un qualsiasi altro indirizzo (v. l'istruzione di salto della tab. I), iniziandovi una nuova successione di istruzioni. Tale salto è, peraltro, condizionato dal risultato di un confronto (come per l'istruzione di salto della tab. I) oppure dal segno di un numero o da qualsiasi altra condizione (anche esterna all'elaboratore stesso), come avviene in pratica nelle macchine che sono munite di numerose istruzioni di salto.

L'istruzione di salto è di fondamentale importanza per la strutturazione di programmi complessi. Essa è infatti indispensabile per realizzare due dei più importanti concetti nella programmazione, e cioè i ‛cicli' e i ‛sottoprogrammi', utili sia per facilitare la scrittura dei programmi, sia per ridurre il numero di istruzioni componenti un programma.

fig. 3

Un ciclo viene ottenuto in un programma mediante un'istruzione di salto che rinvia a un'istruzione precedente quella del salto stesso, in modo tale da poter ripetere la parte di programma compresa tra essa e quella di salto (v. fig. 3, ove l'istruzione di salto 28 rimanda all'istruzione 21 tutte le volte che il contenuto della cella 50 risulti maggiore di quello della cella 51).

L'esecuzione di un ciclo può essere utile in due casi principali. Il primo è quello in cui il ciclo rappresenti un programma di calcolo di tipo ‛iterativo', come si richiede nell'applicazione di procedimenti di calcolo detti ‛per approssimazioni successive'. Tali procedimenti sono basati su schemi di calcolo che permettono di ottenere un certo risultato soltanto in forma approssimata e insieme permettono anche di determinare di quanto la soluzione ottenuta si discosti da quella cercata (cioè l'errore della soluzione). L'istruzione di salto permette allora di ripetere il calcolo fintanto che non sia stata raggiunta l'approssimazione desiderata. Il secondo caso in cui un ciclo si rivela utile è quello in cui si desidera ripetere un prefissato numero di volte un certo programma, applicato a dati diversi. Ciò può essere ottenuto se, ogni volta che il ciclo viene ripetuto, vengono anche modificati gli indirizzi nelle istruzioni che si riferiscono a tali dati.

È infatti importante notare che i numeri esprimenti gli indirizzi in un'istruzione possono essere trattati come qualsiasi altro numero, in particolare possono essere modificati con opportune istruzioni, nelle quali gli operandi sono delle istruzioni essi stessi. La possibilità di modificazione delle istruzioni tramite altre istruzioni si rivela come uno dei più potenti strumenti per la programmazione.

fig. 4

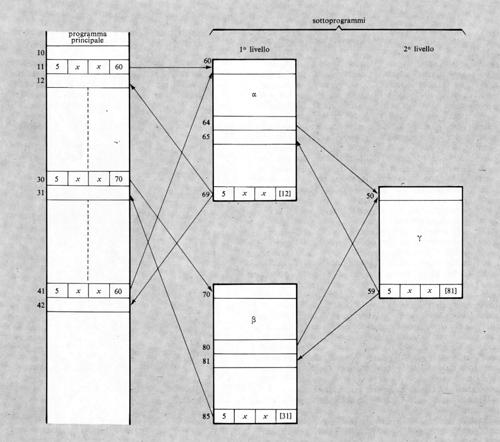
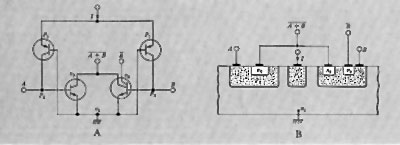
L'altro importante uso dell'istruzione di salto si ha nei cosiddetti ‛sottoprogrammi' o subroutines (v. fig. 4). Si supponga che in un programma vi siano delle elaborazioni (per es. il calcolo di una particolare funzione) che vengono richieste più volte nel corso del programma stesso e in posizioni diverse. Anziché ripetere le relative istruzioni nel programma ogni volta che tale elaborazione viene richiesta, esse vengono scritte una volta sola. Ogniqualvolta nel programma considerato (programma principale) si richiede l'esecuzione di tale gruppo di istruzioni o sottoprogramma, si predispone un'istruzione di salto alla prima istruzione del sottoprogramma (si consideri, nell'esempio, l'istruzione 11 che salta all'istruzione 60, la prima del sottoprogramma α). Una volta eseguito il sottoprogramma, l'ultima istruzione di questo dovrà rinviare di regola all'istruzione successiva a quella che ha provocato il salto.

Poiché un certo sottoprogramma (per es. α nella fig. 4) può essere richiesto in più punti del programma principale, l'ultima istruzione di salto del sottoprogramma (detta anche istruzione di ritorno) dovrà rinviare a un indirizzo di volta in volta diverso (ciò è stato espresso nella fig. 4 segnando tra parentesi quadra tale indirizzo). Con vari metodi, che qui per brevità non si illustreranno, tale indirizzo di ritorno può essere automaticamente determinato sia da opportune istruzioni sia con dispositivi circuitali all'uopo predisposti. Si noti anche che un sottoprogramma può richiedere a sua volta un altro sottoprogramma, come mostra la fig. 4 ove i sottoprogrammi α e β richiedono il γ. I vari sottoprogrammi possono classificarsi in vari ‛livelli' (v. la fig. 4 che mostra sottoprogrammi di 1° e di 2° livello). Il numero di livelli può essere qualsiasi.

Un concetto collegato a quello di sottoprogramma è quello di ‛recursività'. Si ha un calcolo recursivo quando il relativo programma richiama se stesso come sottoprogramma, e ciò avviene per un numero indefinito di livelli.

Quelli precedentemente illustrati sono i concetti più elementari della programmazione degli elaboratori elettronici, che risultano, per quanto detto, macchine capaci di eseguire qualsiasi calcolo che sia stato espresso con una successione di istruzioni, cioè un algoritmo espresso tramite un programma. Il concetto di algoritmo è pertanto fondamentale per la comprensione della natura degli elaboratori.

b) Gli algoritmi e le macchine di Turing

In base a quanto illustrato al precedente punto sui programmi per elaboratori, si può dare dell'algoritmo la seguente definizione: ‟un insieme di istruzioni che definiscono una sequenza di operazioni mediante le quali si risolvono tutti i problemi di una determinata classe".

Qualunque elaborazione che possa essere eseguita da una macchina può definirsi e descriversi come un algoritmo. Diversamente, si può anche dire che tutti gli algoritmi che, allo stato attuale delle nostre conoscenze, possono essere definiti, possono in linea di principio essere eseguiti da una macchina.

Quest'ultima affermazione richiede tuttavia qualche precisazione. Come è noto, le memorie degli elaboratori hanno necessariamente una capacità che, anche se in taluni casi è molto grande (fino a 10¹² bits), è comunque sempre finita. Può allora darsi che un algoritmo, benché perfettamente noto e definito, risulti concretamente non realizzabile per la limitazione della memoria. Si dice allora che l'algoritmo è ‛realizzabile potenzialmente' se il risultato viene raggiunto in un numero finito di passi, per quanto grande sia. Lo stesso algoritmo sarebbe cioè realizzabile in una macchina con capacità di memoria illimitata.

Nel 1937 il matematico inglese A. M. Turing dava una definizione del concetto di algoritmo basata su una macchina ideale, che può essere considerata come la semplificazione al massimo grado di un elaboratore elettronico dotato di memoria illimitata. La cosiddetta ‛macchina di Turing' è uno strumento tramite il quale la nozione di algoritmo può essere rigorosamente definita e indagata. È interessante notare come ricercatori diversi abbiano fornito della nozione di algoritmo definizioni diverse, per essere partiti da altri punti di vista; tuttavia le varie definizioni risultarono tra loro equivalenti, nel senso che esse definivano lo stesso concetto. Ciò dimostra il carattere di grande generalità della nozione di algoritmo e di macchina di Turing.

fig. 5

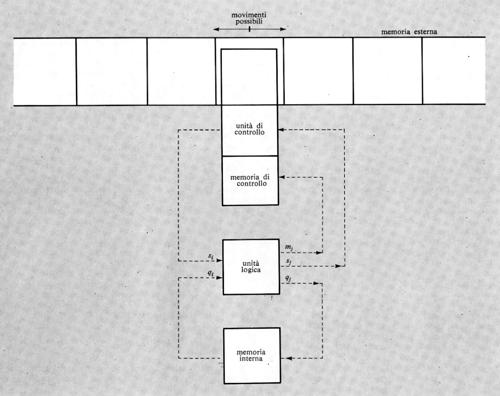
Una macchina di Turing è costituita nel modo seguente (v. fig. 5).

1. Un'unità di memoria, detta ‛memoria esterna', costituita da un nastro illimitato nei due sensi, suddiviso in celle, ciascuna delle quali può contenere uno dei k + 1 simboli s₀, s₁, ... s_k costituenti l'alfabeto ‛esterno'. Per motivi di generalità è conveniente supporre che tra i simboli ve ne sia uno, s₀, che sta a indicare ‛cella vuota' e che si suppone registrato in tutte le celle che non contengono altri simboli.

Ogni cella può contenere al massimo un simbolo e l'informazione iniziale nella memoria esterna è costituita da una stringa finita di simboli, non comprendente s₀, registrati in celle consecutive del nastro.

2. Un'unità di memoria ‛interna', capace di immagazzinare uno dei simboli q₀, q₁, ..., q_m costituenti l'alfabeto interno'. Tali simboli rappresentano gli stati possibili della macchina (simboli di stato) e uno di essi, q₀, sta a indicare lo stato di arresto della macchina.

3. Un'unità di ‛controllo', in grado di leggere il carattere nella cella in esame, di registrare un nuovo simbolo nella stessa cella e di comandare lo spostamento del nastro di una cella in uno dei due versi.

L'unità di controllo è munita allo scopo di una memoria ‛di controllo' nella quale viene immagazzinato uno dei simboli S, D, F detti ‛simboli di movimento', indicanti rispettivamente gli ordini di esame della cella adiacente a sinistra, oppure a destra, oppure della stessa cella.

4. Un'unità ‛logica' avente due ingressi e tre uscite. I due ingressi sono costituiti dal simbolo dell'alfabeto esterno, s_i contenuto nella cella in esame e letto dall'unità di controllo, e dal simbolo q_i contenuto nella memoria interna. Per ogni coppia di valori di ingresso l'unità logica produce una terna di valori in uscita consistenti: 1) nel simbolo s_j che deve essere registrato nella cella in esame; 2) nel simbolo q_j che deve essere registrato nella memoria interna; 3) nel simbolo di movimento m_j per la memoria di controllo.

Il legame stabilito dall'unità logica tra la terna (s_j, q_j, m_j) e la coppia (s_i, q_i) è rappresentabile con una tavola composta da k + 1 righe ed m colonne contenenti agli incroci le terne (s_j, q_j, m_j). Tale tavola è chiamata ‛matrice funzionale' e rappresenta completamente il funzionamento della macchina di Turing.

Tale funzionamento avviene infatti come segue. Innanzitutto la macchina si trovi in una ‛configurazione iniziale'. L'unità di controllo, in base ai valori (s_i, q_i), produce la terna (s_j, q_j, m_j) che porta la macchina in una nuova configurazione, dalla quale essa evolve con lo stesso meccanismo nella successiva e così via.

Se dopo un numero finito di passi la macchina si ferma (avendo trovato il simbolo q₀), si dice che la macchina è applicabile' all'informazione contenuta inizialmente sul nastro, che è stata trasformata nell'informazione che si trova sul nastro all'atto dell'arresto.

Se invece la macchina non trova mai l'ordine di arresto q₀ e quindi non si ferma mai, si dice che la macchina non è applicabile all'informazione contenuta inizialmente sul nastro.

Diremo anche che una macchina può risolvere una data classe di problemi se essa risulta applicabile all'informazione rappresentante (con una data codificazione) un qualunque problema della classe e se trasforma tale informazione in quella rappresentante la soluzione (nello stesso codice).

Malgrado l'estrema (o voluta) semplicità della macchina di Turing, essa risulta capace (con adatto assegnamento della matrice funzionale) di risolvere problemi di grande complessità, ma la sua importanza non sta ovviamente in tale capacità (per la quale sono molto più convenienti gli elaboratori reali), ma nell'essere uno strumento concettuale che permette di definire rigorosamente gli algoritmi e di ottenere risultati di grande generalità.

Le ricerche finora condotte fanno pensare che qualsiasi algoritmo possa essere realizzato mediante una macchina di Turing. Tale ipotesi viene detta ‛ipotesi fondamentale della teoria degli algoritmi' e l'accettarla significa che si considera la teoria degli algoritmi coincidente con la teoria della macchina di Turing. Pertanto il problema relativo all'esistenza di un algoritmo per risolvere una certa classe di problemi può ridursi alla ricerca o alla dimostrazione dell'esistenza di una macchina di Turing.

Si è già detto come siano state date altre definizioni equivalenti della nozione di algoritmo.

Il concetto di macchina di Turing può essere esteso a quello di macchina di Turing universale, capace di simulare il funzionamento di una macchina di Turing dotata di una matrice funzionale qualsiasi. Ciò viene ottenuto registrando in forma codificata la matrice funzionale data sul nastro della macchina universale definita da una matrice funzionale in grado d'interpretare qualsiasi matrice funzionale registrata nella sua memoria. La sua importanza è dovuta al fatto che essa è paragonabile a un elaboratore capace di interpretare un qualsiasi programma. Ne discende anche che un programma qualsiasi può essere pensato come una macchina per risolvere una data classe di problemi.

Tra i risultati concettualmente importanti della teoria della macchina di Turing si citerà qui quello relativo all'esistenza di problemi non risolubili per via algoritmica, per il quale si rimanda alla letteratura.

5. Elaboratori e linguaggi

Si è già fatto notare come la nozione di linguaggio, insieme a quella di algoritmo, sia di carattere fondamentale per la comprensione degli elaboratori.

Come risulta dall'esposizione storica, i linguaggi per elaboratori (o linguaggi artificiali) furono inizialmente introdotti per ragioni di ordine pratico, e furono le stesse ragioni che indussero a porre il problema della definizione dei linguaggi e della costruzione dei relativi traduttori su basi teoriche sicure, proprio allo scopo di evitare gli inconvenienti, pratici oltre che concettuali, delle primitive impostazioni.

L'importanza del linguaggio, in generale, deriva dal fatto che con esso noi comunichiamo ai nostri simili l'informazione e, in definitiva, il nostro pensiero. Per tale motivo, a cominciare dal secolo scorso, i linguaggi divennero oggetto di indagini filosofiche. Pertanto, così come la teoria degli algoritmi collega il tema degli elaboratori alla logica e alla matematica moderna, la teoria dei linguaggi stabilisce un collegamento con le scienze filosofiche e umane.

Nella teoria dei linguaggi non vi è limite inferiore alla complessità di un linguaggio: un insieme molto semplice di segni e regole di combinazione può pertanto legittimamente chiamarsi linguaggio.

La teoria dei linguaggi o semiotica (teoria dei segni), si compone di tre principali capitoli, che rappresentano diversi livelli d'indagine: 1) la sintassi; 2) la semantica; 3) la pragmatica.

1. La sintassi riguarda le regole per la costruzione di stringhe di simboli rispondenti a regole assegnate, senza riguardo al loro significato e alle motivazioni del linguaggio. Le regole di combinazione dei simboli (in parole, frasi e testi) nel caso ideale sono perfettamente note e prive di eccezioni: pertanto la verifica di correttezza formale sintattica di un testo può essere effettuata tramite un algoritmo, cioè automaticamente.

2. La semantica attiene al significato dei simboli e delle loro costruzioni. La verifica di correttezza semantica costituisce un problema di grande difficoltà. Si tratta infatti di verificare se le relazioni espresse dalle espressioni del linguaggio considerato siano conformi alle relazioni che si volevano descrivere tra gli oggetti cui il linguaggio è applicato. Un insieme di regole valide per la determinazione del significato di un testo può essere stabilito solo per linguaggi artificiali; su tale punto si ritornerà.

3. La pragmatica considera gli scopi per cui il linguaggio è concepito. Nel campo dei linguaggi naturali l'indagine inizia col considerare come un linguaggio viene usato e successivamente ne studia la sintassi. Nel caso dei linguaggi artificiali per elaboratori si è spesso portati a iniziare dalla definizione formale della sintassi, ma in realtà è proprio dalla pragmatica che si deve cominciare affinché siano preventivamente definiti gli scopi per cui un linguaggio viene costruito.

Come esempio di quanto detto, nel linguaggio dell'algebra, un'espressione corretta sintatticamente è la seguente: a − (bc + d), mentre un'espressione non corretta sarebbe per esempio: a) bc + (d. Due espressioni sintatticamente corrette sono pure le seguenti: A = a² e A = a⁵; una sola, la prima, è semanticamente corretta se l'espressione vuole esprimere l'area di un quadrato.

Una peculiare difficoltà che emerge nello studio dei linguaggi è data dal fatto che nel discorrere di un linguaggio si adopera un linguaggio: quest'ultimo viene chiamato ‛metalinguaggio' e le sue espressioni devono essere chiaramente distinte da quelle del linguaggio per cui viene usato. Per rendere chiara tale distinzione potrebbe essere conveniente usare un altro alfabeto oppure, più praticamente, ricorrere a qualche segno speciale (sottolineature, virgolette) per individuare le espressioni del linguaggio di cui si parla.

Per parlare del metalinguaggio si richiederebbe un metametalinguaggio, o un metalinguaggio di secondo livello, e così via.

Per porre un limite al livello dei metalinguaggi occorrerebbe un metalinguaggio che potesse definire se stesso senza ambiguità. La questione è tuttora aperta ed è inevitabile oggi adottare il linguaggio naturale come metalinguaggio finale.

È opportuno ora commentare brevemente il concetto di informazione e la sua classificazione.

6. Classificazione dell'informazione

Al livello sintattico la rappresentazione dei simboli di un alfabeto in un elaboratore è risolta tramite la codificazione, di cui si dirà successivamente, e tale problema non presenta difficoltà concettuali notevoli.

Il problema della semantica dell'informazione codificata è invece notevolmente più complesso e a tale riguardo è opportuno distinguere tra i seguenti tipi d'informazione.

a) Informazione numerica o algebrica

Una stringa di cifre estratte dall'alfabeto corrispondente a una data base (2, 8, 10, 12, 16, ecc.) costituisce una parola numerica la cui interpretazione è legata alla posizione di ciascuna cifra rispetto alla virgola. Così pure si può costruire una stringa di caratteri alfabetici e di simboli di operazioni in modo non ambiguo, nel linguaggio dell'algebra o della logica, come: (a + b) : c; (x > y) ⋀ (z = 1) ecc.

Espressioni numeriche, algebriche e logiche sono ben note come mezzo per la descrizione di algoritmi e il procedimento di formalizzazione della semantica in relazione a tale descrizione è basato su convenzioni oramai universalmente accettate e pertanto non ambigue. Si può addirittura affermare che, nel caso dell'informazione qui considerata, il problema semantico è ridotto alle regole elementari dell'aritmetica e della logica e che tutta la semantica della matematica può ridursi alla stessa sintassi.

b) Informazione fisica

È noto come ogni grandezza fisica si possa rappresentare come il prodotto di un valore numerico e di una dimensione o corrispondente unità. L'indicazione di tali dimensioni risolve completamente il problema semantico dell'informazione fisica, nel senso che, una volta scelto un sistema di unità di misura (per es. quello internazionale), l'elaborazione dell'informazione fisica si riduce a elaborazioni di grandezze numeriche o algebriche.

Quanto sopra spiega come l'applicazione degli elabora- tori ai problemi matematici e fisici sia avvenuta senza sostanziali difficoltà interpretative.

c) Informazione strutturata o modulare

Indichiamo così quell'informazione la cui interpretazione è determinata dalla posizione dell'informazione stessa rispetto ad altre informazioni a essa associate.

Come esempio, in un'istruzione di macchina come quella della tab. I, la prima cifra denota l'operazione, la seconda coppia di cifre l'indirizzo di un operando, ecc. È importante notare che l'informazione utilizzata nelle applicazioni amministrative può considerarsi di tipo strutturato: infatti i vari libri o registri sono costruiti come moduli, ove ogni campo stabilisce anche il significato dell'informazione che vi verrà registrata. Il problema semantico delle informazioni amministrative può dunque considerarsi preventivamente risolto dalle convenzioni adottate nei moduli in uso per le varie applicazioni.

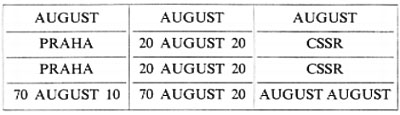
La conoscenza delle definizioni semantiche dei vari campi di un modulo è indispensabile, per quanto detto, per l'assegnamento del significato dell'informazione registrata e senza tale conoscenza possono sorgere problemi praticamente insolubili, come mostra il seguente esempio (v. Zemanek, 1973):

L'informazione contenuta nel quadro sarebbe difficilmente comprensibile se non si sapesse che essa è relativa a un modulo di polizia di frontiera, modulo che specifica la semantica dei vari campi come segue:

(e se non si sapesse che in lingua ceca august significa clown).

Un altro esempio è dato dai moduli di censimento ove sono spesso contenuti, a chiarimento del significato dei vari campi (per es. domicilio, professione ecc.), dettagliate delucidazioni intese a risolvere completamente (nella speranza dell'estensore) il problema semantico.

Il problema semantico dell'informazione strutturata può considerarsi risolto in quei casi in cui una lunga consuetudine ha condotto alle necessarie convenzioni interpretative, ma in campi ove tali convenzioni non si siano stabilizzate il problema rimane irrisolto. Si consideri l'esempio di informazioni di tipo statistico per l'importazione e l'esportazione e il vantaggio di utilizzare una stessa informazione per vari tipi d'indagine statistica, non tutti però prevedibili al momento della formulazione dei moduli. Si verifica facilmente il caso d'impossibilità di attribuire significati corretti per l'indagine statistica voluta. Si consideri il caso del vitello. È a tutti noto che un vitello è una mucca giovane. Sembrerebbe dunque che, una volta convenuta una certa età, il problema delle statistiche sui vitelli sia risolto. Ma in realtà così non è. Infatti con vitello noi indichiamo anche un tipo di carne, che però non è semplicemente la carne di un vitello, ma di un vitello che sia stato nutrito con latte e non con erba. Risulta così insufficiente il parametro età e il problema si complicherebbe ulteriormente se si volesse discutere sulle parti dell'animale che sono propriamente da considerarsi vitello, nel senso di carne di vitello.

Si vede dunque come l'elaborazione dell'informazione non puramente numerica o fisica incontri gravi difficoltà, non appena si voglia affrontare il problema dell'uso dell'informazione al di fuori di campi ben definiti e per i quali la semantica è stata accuratamente predisposta.

La pratica costituzione di banche di dati (quelle di tipo statistico sono un esempio notevole), nelle quali una certa informazione può venire associata ad altre in modo arbitrario e imprevedibile, è condizionata a un'attenta valutazione e accurata soluzione del problema semantico dell'informazione strutturata.

d) Testi in linguaggio naturale

Le informazioni espresse in linguaggio naturale presentano il massimo delle difficoltà. Lo dimostra il sostanziale fallimento dei diversi tentativi fatti per realizzare la traduzione automatica delle lingue. Fiumi di inchiostro sono stati versati sull'argomento, per la sua importanza concettuale e pratica, ma si deve oggi riconoscere che una traduzione soddisfacente non può essere ottenuta dalle macchine per l'enorme e imprevedibile massa di relazioni che nel linguaggio naturale si stabilisce non solo tra le parole, ma anche con l'ambiente in cui il discorso è fatto.

Si racconta che V. Hugo, dopo aver affidato a un editore un suo romanzo, ansioso di conoscerne l'accoglienza da parte dei lettori, scrisse all'editore una lettera composta di un solo simbolo: un punto interrogativo. La risposta consisté in una lettera contenente anch'essa un solo simbolo: un punto esclamativo, e fornì allo scrittore tutta l'informazione che attendeva. È chiaro che nessuna macchina potrebbe tradurre tali lettere, la cui semantica è determinata da una situazione esterna che supera di gran lunga la simbologia e che semmai dimostra le straordinarie capacità di associazione della mente umana. Tutte le esperienze raccolte nello studio del linguaggio naturale mostrano che la sua semantica è ben al di là di un insieme di regole meccanizzabili: essa, come mezzo principe per l'espressione di una cultura, non è trasferibile a una macchina.

e) Testi in linguaggi artificiali

Sono quelli costruiti coi linguaggi di programmazione. La loro definizione sintattica rappresenta il problema più facile. Il metodo più usuale (proposto dal matematico americano J. Backus e utilizzato sistematicamente per la prima volta nella definizione del linguaggio ALGOL) consiste nel fornire un insieme di regole per la costruzione di frasi ‛ben strutturate'. Un sistema completo di tali regole è chiamato ‛grammatica generativa' (Backus normal form). Vedasi per esempio:

La suddetta ‛grammatica' definisce (:: =) in modo del tutto generale una <espressione aritmetica> come: un <fattore>, oppure (∣) una <espressione aritmetica> seguita dal segno + seguito da un <fattore>, oppure una <espressione aritmetica> seguita dal segno − seguito da un − <fattore>. La definizione 〈fattore> successiva esprime un − <fattore>, e così via fino ai caratteri terminali, alfabetici (L) e numerici (N).

La definizione formale della semantica presenta invece gravi difficoltà. Un metodo di notevole interesse, applicato alla verifica semantica del linguaggio PL/I, consiste nella definizione e nell'uso di una macchina astratta, che elabora testi nel linguaggio considerato e che, partendo da uno stato iniziale, evolve attraverso una serie di stati fino a raggiungere lo stato finale. L'osservazione della sequenza di stati causata da un dato testo permette all'osservatore umano di constatare il significato del testo e di compiere tutte le verifiche necessarie per l'analisi semantica.

Lo sviluppo dell'elaboratore come macchina universale dipende, per quanto detto, in larga misura dai progressi della teoria dei linguaggi, in particolare per quel che riguarda la loro definizione formale. Potremo probabilmente risolvere soddisfacentemente i problemi dell'informazione strutturata, in modo da rendere possibile un sicuro uso di banche di dati generalizzate, ma sarà forse impossibile definire formalmente la sintassi e la semantica del linguaggio naturale: molti argomenti inducono a pensare che non vi possa essere algoritmo di verifica semantica.

L'elaboratore, per contro, è un sistema non naturale, ma costruito, cui si applicano bene linguaggi artificiali. Il vero problema sarà quello della comunicazione tra mondo naturale, uomo e sistemi artificiali, la cui efficacia come strumenti di elaborazione è strettamente legata al rigore delle definizioni formali. L'elaboratore non potrà rimpiazzare l'uomo, che è meno sistematico ma è molto di più di un automa e può controllare e decidere sul significato di ciò che vuole o fa. In definitiva, il problema dello sviluppo dell'informatica sarà principalmente quello di determinare la più adatta combinazione di strutture di elaborazione artificiali con la capacità umana.

7. La codificazione dell'informazione

Come detto, un elaboratore elettronico può considerarsi come una macchina per la manipolazione (sostituzione) di simboli, tramite i quali si intende rappresentare l'informazione.

Per ragioni di carattere tecnologico, d'altronde, è conveniente che i circuiti destinati a elaborare l'informazione siano semplificati al massimo grado e la massima semplificazione si ottiene costituendoli in modo che essi elaborino due soli simboli, rappresentati da due valori di una qualsiasi grandezza (tensione o corrente elettrica, flusso magnetico ecc.). Tali simboli (detti bits) possono rappresentarsi con H (per high) e L (low), oppure con 0 e 1. Dato che i simboli degli alfabeti usati per la rappresentazione esterna sono più di due, si deve preliminarmente risolvere il problema della rappresentazione dei simboli dell'alfabeto esterno con i due soli dell'alfabeto interno, il che si ottiene con un'operazione di ‛codificazione', che fa corrispondere una disposizione di bits a ciascun simbolo esterno. Poiché con n bits si possono avere 2ⁿ disposizioni, altrettanti saranno i simboli esterni codificabili con n bits. In altre parole, se N è il numero di simboli esterni, n dovrà essere maggiore del log₂ N.

Poiché, inoltre, la corrispondenza tra disposizioni e simboli è arbitraria, si potranno definire numerose diverse codificazioni con lo stesso numero di bits.

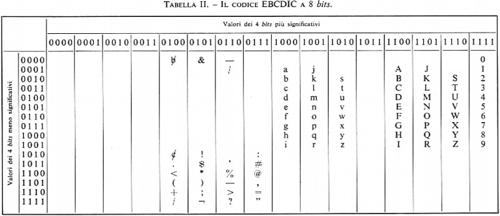
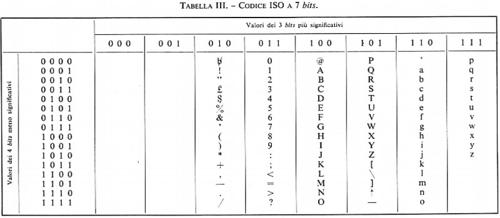
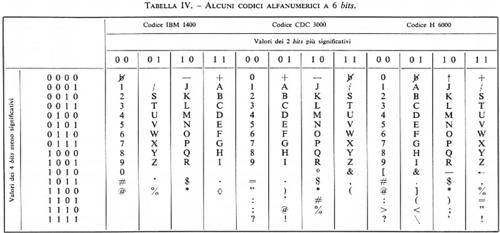
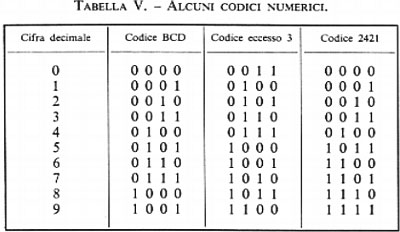
Le tabelle II, III e IV mostrano codici a 8, 7 e 6 bits rispettivamente, per caratteri alfabetici, numerici e speciali.

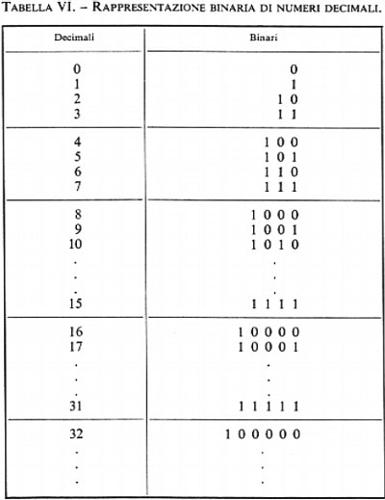
Nel caso che l'informazione da codificare sia puramente numerica, si possono seguire due strade distinte. Con la prima si codificano i 10 caratteri numerici (e i segni +,−) e per tale scopo occorre un minimo di 4 bits: la tab. V mostra alcuni codici numerici. La seconda strada consiste nell'adottare la numerazione binaria per la rappresentazione del numero dato (espresso in forma decimale): in tal caso non vi è più corrispondenza tra ciascuna cifra decimale e gruppi di bits, ma è il numero nel suo complesso che viene codificato dal gruppo di bits costituenti il numero binario equivalente a quello dato. La tab. VI rappresenta la corrispondenza tra i primi numeri della serie naturale espressi in decimale e in binario.

È importante notare che nella codificazione di simboli alfanumerici si usa spesso un numero di bits maggiore di quello strettamente necessario, come mostrano le tabb. II e III: in questo caso molte delle 2ⁿ disposizioni possibili con n bits non corrispondono a nessun simbolo. Tale ridondanza è spesso voluta allo scopo di conferire al codice proprietà di rivelazione o di autocorrezione di errori nella trasmissione: la teoria dell'informazione fornisce gli strumenti concettuali per tale problema, e a essa si rimanda il lettore.

a) L'elaborazione dell'informazione codificata

Per quanto detto, tutta l'informazione di un elaboratore è rappresentata in forma codificata binaria. Per la comprensione dei circuiti destinati a questa elaborazione è pertanto importante illustrare i tipi di elaborazione che su tale informazione si possono eseguire.

Informazione numerica. - Le elaborazioni che su tale in- formazione possono eseguirsi sono tutte quelle necessarie per l'esecuzione di calcoli. Le più semplici elaborazioni risultano essere quelle aritmetiche e tra queste le più elementari sono l'addizione e la sottrazione. La moltiplicazione e la divisione sono le operazioni di complessità immediatamente superiore ed è noto come esse possano ottenersi con un'opportuna successione di addizioni e sottrazioni, rispettivamente. Si osservi anzi come l'usuale metodo per l'esecuzione della divisione richieda anche un'operazione di confronto tra due numeri, per determinarne l'uguaglianza o la disuguaglianza (e, in tal caso, quale dei due sia il maggiore).

È ben noto dal calcolo numerico come qualsiasi calcolo, in particolare la determinazione di qualsiasi funzione, possa ottenersi con una successione di operazioni aritmetiche e di confronto (cioè un ‛programma'). Il calcolo di ‛funzioni' può per esempio essere ottenuto sia tramite consultazione di tabelle (per cui è fondamentale l'operazione del confronto), sia tramite espressioni razionali che approssimano la funzione voluta con errori noti e che possono calcolarsi con operazioni aritmetiche.

Per tali motivi, le operazioni elementari di addizione e di sottrazione nonché quella di confronto sono alla base di qualsiasi calcolo e sono pertanto presenti in qualsiasi cal- colatore. Un'ulteriore semplificazione è possibile osservando che è molto importante che le operazioni di somma e differenza eseguite da un calcolatore risultino di tipo algebrico: in tal caso la differenza può ridursi alla somma dopo aver cambiato il segno al sottraendo. Inoltre, con opportuna scelta del modo di rappresentazione dei numeri negativi, le operazioni di addizione e sottrazione possono ridursi alla sola operazione di addizione. Ciò può essere ottenuto rappresentando i numeri col metodo dei ‛complementi'. Si considerino numeri di n bits e si convenga di rappresentare il negativo negA di un intero positivo A, supposto inferiore a 2^n-1, col suo complemento a 2ⁿ oppure a 2ⁿ−1. Si ha allora:

negA → 2ⁿ − A (complemento a 2ⁿ)

negA → (2ⁿ−1) − A (complemento a 2ⁿ−1).

La tab. VII mostra tali rappresentazioni per n = 4. Si noti che il primo bit può sempre considerarsi come rappresentante il segno del numero.

Si può mostrare che, con tali rappresentazioni, la somma algebrica si riduce sempre a una sola operazione di somma binaria dei due addendi, interpretando il bit di segno come una cifra binaria, con le seguenti regole: 1) nel caso del complemento a 2ⁿ si trascura il riporto eventualmente generato nella somma dei bits di segno; 2) nel caso del complemento a (2ⁿ − 1) tale riporto viene addizionato ‛in coda', come mostrano i seguenti esempi:

Le operazioni di divisione e di moltiplicazione possono essere ottenute coi metodi noti, con ripetute addizioni e sottrazioni rispettivamente. In tal modo, la durata di queste operazioni risulta notevolmente maggiore di quella delle addizioni. Si può ridurre tale durata con metodi vari, alcuni dei quali tendono a ridurre il numero delle addizioni necessarie, altri ottengono invece il risultato con una sola operazione che può essere realizzata circuitalmente in modo da ottenere l'esecuzione del prodotto in un tempo di poco superiore a quello della somma.

b) Rappresentazione dei numeri in forma ‛normalizzata' (floating-point)

Nell'esecuzione manuale di calcoli numerici si ha l'abitudine di tenere conto della posizione delle virgole adottando come fattori potenze di dieci, che equivalgono al numero di spostamenti della virgola stessa necessari a ottenere un numero che non sia né troppo più piccolo né troppo più grande dell'unità. Se non si facesse ciò, s'incorrerebbe in inconvenienti pratici quando, per esempio, si richiedesse un eccessivo numero di zeri dopo la virgola prima delle prime cifre significative.

Se non si adottasse la stessa soluzione nelle rappresentazioni numeriche degli elaboratori, considerando cioè le virgole in posizione predeterminata e fissa, si incorrerebbe in inconvenienti anche peggiori poiché, dato che il numero di bits assegnati a ogni numero non può essere troppo grande, si finirebbe col perdere in precisione dovendo trascurare qualcuna o addirittura tutte le cifre significative.

A tali inconvenienti si può rimediare con una rappresentazione simile a quella prima illustrata, come mostrano i seguenti esempi:

+3.277,53 = +0,327753 × 10⁴ che si scrive:

+327753 + 4

−0,000085234 = −0,85234 × 10⁴ che si scrive:

−85234 − 4.

Tale rappresentazione è oggi comunemente utilizzata anche in alcuni calcolatori elettronici ‛tascabili' per uso scientifico.

Informazione alfabetica. - Nel caso di informazione alfabetica codificata, non hanno ovviamente significato le operazioni aritmetiche, mentre assume grande importanza quella di confronto. Si ricordi infatti come in questo caso l'elaboratore debba essere pensato essenzialmente come una macchina per il riconoscimento, la sostituzione e la memorizzazione di simboli. Per l'esecuzione di tali funzioni generali si rivela essenziale l'operazione del riconoscimento di uguaglianza di due simboli.

Risulta inoltre di grande utilità pratica la possibilità del confronto tra due simboli per determinare, oltre che l'uguaglianza, le relative posizioni nell'alfabeto considerato ove essi sono convenzionalmente ordinati (si pensi all'operazione del mettere in ordine alfabetico dei nomi di persona, come frequentemente può essere richiesto nelle applicazioni amministrative). Tale operazione di ordinamento può essere eseguita o con il confronto di ogni simbolo dato con la tabella ordinata dell'alfabeto (con l'uso ripetuto della determinazione dell'uguaglianza) oppure con il confronto dei due simboli come se fossero numeri binari (ciò richiede che il codice sia come quello delle tabb. II, III e IV), in modo che il loro ordinamento come numeri binari coincida con l'ordinamento alfabetico corrente.

8. I principî della teoria delle reti logiche o binarie o di commutazione

È stato illustrato come convenga che le informazioni in un elaboratore elettronico siano in forma binaria e si è anche discusso su alcuni principî relativi alla loro elaborazione. Allo scopo di disporre di uno strumento concettuale che sia di ausilio nella progettazione delle reti elettriche che ottengono le elaborazioni volute, è opportuno prescindere per il momento dall'effettiva realizzazione elettrica (che verrà studiata in seguito) definendo in modo astratto degli enti capaci di elaborare informazioni binarie, cioè le reti logiche o binarie.

fig. 6

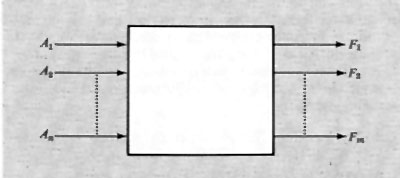
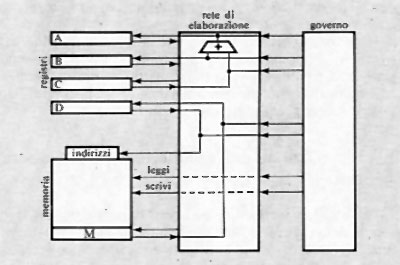
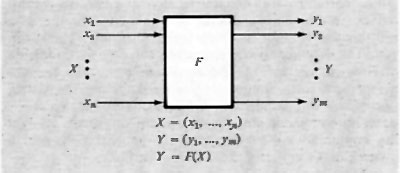
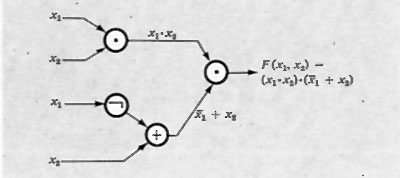
Una prima considerazione generale sulle reti binarie (dette anche ‛di commutazione') può essere fatta con riferimento alla dipendenza che una certa rete stabilisce tra variabili binarie d'ingresso e variabili d'uscita (prodotte cioè dalla rete; v. fig. 6). Tale dipendenza può esprimersi come funzione, scrivendo:

F₁=F₁(A₁, A₂, ...A_n).

Esiste una fondamentale distinzione tra due tipi di rete, in relazione a tale dipendenza. La rete può infatti essere tale che la F₁ dipenda dal valore assunto in un certo istante dalle variabili d'ingresso e sia indipendente dai valori che esse possono aver assunto precedentemente, oppure può anche dipendere da questi ultimi valori.

Nel primo caso si dice che la rete è di tipo ‛combinatorio', nel secondo che è di tipo ‛sequenziale'. Si può dire, con altre parole, che le reti sequenziali, contrariamente alle reti combinatorie, conservano memoria dell'evoluzione delle variabili d'ingresso.

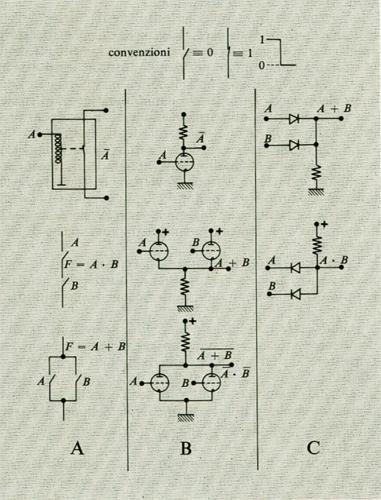
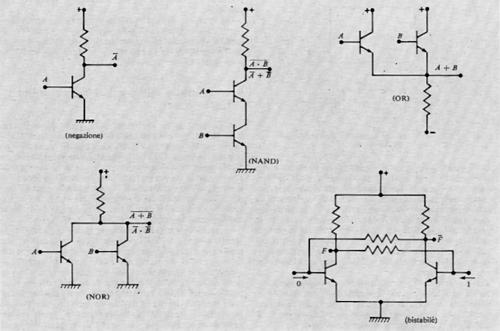
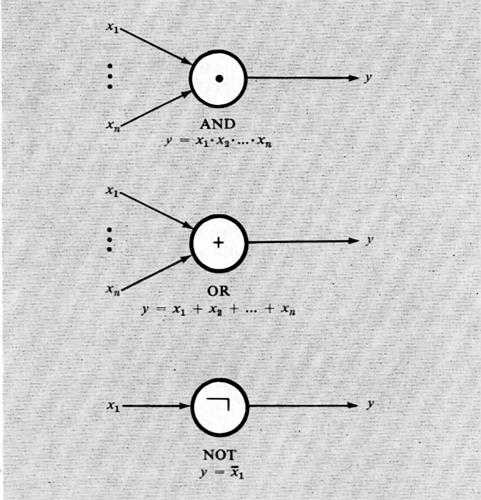
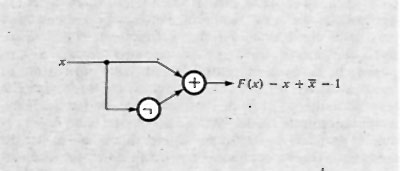
Considerando ora le reti combinatorie, si è portati a indagare sulle proprietà delle funzioni che le descrivono. La più semplice funzione è quella di una sola variabile, A, che fa corrispondere 0 a 1 e viceversa, ed è nota come ‛negazione' o funzione NOT. Essa si scrive:

F = Ā

Tra le funzioni di due o più variabili alcune assumono significati particolari, anche perché sono realizzabili facilmente in forma circuitale.

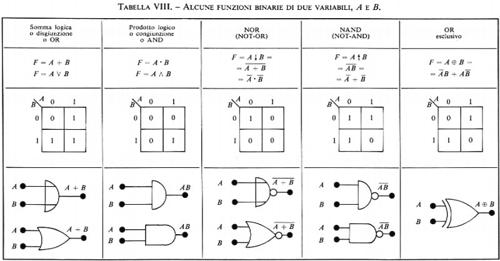
Le più importanti funzioni di più variabili sono rappresentate nella tab. VIII, insieme ai simboli grafici e alle loro espressioni.

La manipolazione di tali espressioni si effettua in base alla cosiddetta ‛algebra di Boole', della quale sono fornite nella tab. IX le identità fondamentali.

Il problema fondamentale nella teoria delle funzioni ‛combinatorie' può definirsi come segue: assunta una o più funzioni da considerare come funzioni elementari e assegnata una funzione arbitraria (per es. per mezzo di una tabella), esprimere tale funzione con l'uso esclusivo delle funzioni elementari.

Si può mostrare che ‛insiemi minimi' di funzioni elementari sono costituiti da: negazione e disgiunzione; negazione e congiunzione; NOR; NAND. Naturalmente gli insiemi di funzioni elementari possono comprendere altre funzioni; per esempio, la negazione e la congiunzione possono essere usati in luogo della disgiunzione.

Il problema illustrato è fondamentale per il progetto delle ‛reti combinatorie' che realizzano un'assegnata funzione, e la scelta delle funzioni elementari è allora suggerita dalla loro realizzabilità con circuiti elettronici. Più avanti si illustreranno le più importanti realizzazioni delle funzioni elementari con vari tipi di circuito.

Si può mostrare che un'assegnata funzione può essere espressa in varie forme con l'impiego di date funzioni elementari. Assume allora grande importanza il problema di scegliere quella forma che, realizzata con un determinato tipo di circuito, presenti il costo totale minimo.

fig. 7

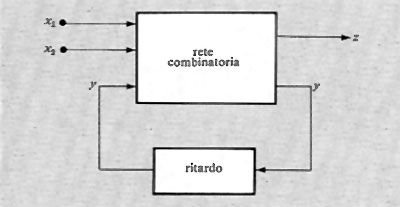
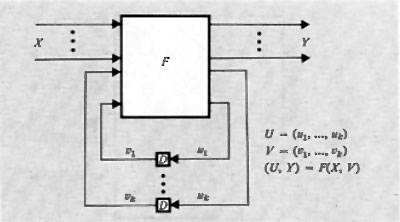
Le ‛reti sequenziali' possono essere schematizzate in relazione a varie modalità di funzionamento. Lo schema concettualmente più interessante è quello corrispondente a una rete funzionante nel ‛modo fondamentale' (v. fig. 7). Questo schema mette in evidenza come una rete sequenziale possa essere schematizzata con una rete combinatoria nella quale un certo numero di ingressi è collegato con altrettante uscite. Tali collegamenti rendono conto delle capacità di memoria proprie delle reti sequenziali. I ritardi segnati in figura rappresentano anche i ritardi eventualmente presenti nelle stesse reti combinatorie, di modo che la rete sequenziale risulta funzionare, nello schema, in modo ideale, cioè senza ritardi propri.

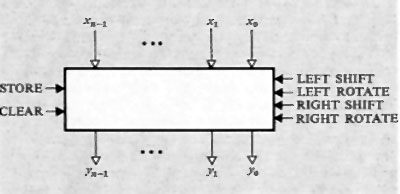
Per la teoria delle reti sequenziali si rimanda alla letteratura. Qui basterà dire che il numero degli stati interni possibili in una rete sequenziale (numero che misura la sua capacità di memorizzazione) è determinato dal numero delle variabili y, dette variabili secondarie o interne.

fig. 8

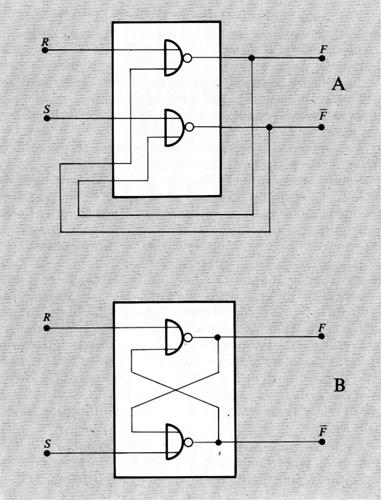
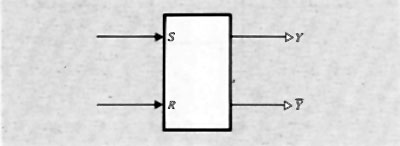
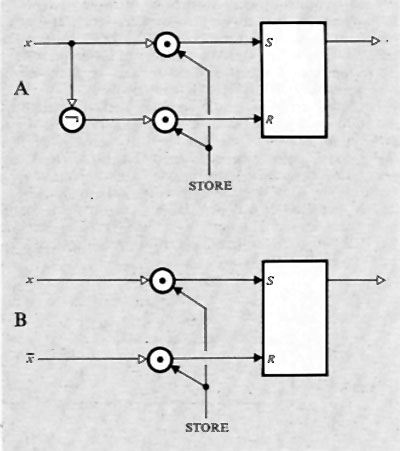
Nella fig. 8 è rappresentato lo schema della più elementare rete sequenziale usata negli elaboratori e cioè il ‛bistabile' o flip-flop capace di memorizzare un bit, il cui valore può essere modificato agendo con segnali opportuni alle entrate.

Gli strumenti della teoria della comunicazione permettono lo studio dal punto di vista logico (ma non elettrico) di tutte le reti usate negli elaboratori, in particolare permettono il progetto di reti che compiano operazioni assegnate in vista delle elaborazioni volute.

9. L'evoluzione della tecnologia dei circuiti elettronici binari

Si è già detto come l'adozione della codificazione binaria negli elaboratori elettronici sia dovuta alla necessità di utilizzare circuiti elettronici di massima semplicità, allo scopo di poter costruire sistemi di grandissima complessità ma con funzionamento sufficientemente sicuro. Ciò viene ottenuto con circuiti in cui per esempio un transistore funziona semplicemente come interruttore, interrompendo o permettendo la circolazione della corrente in un circuito e facendo corrispondere ai due stati di funzionamento lo 0 e l'1 della codificazione binaria.

Le operazioni logiche elementari, con le quali si costruiscono i sistemi di calcolo, possono essere ottenute con varie tecnologie. Il primo dispositivo usato, di tipo elettrico, è stato, com'è noto, il relè, nel quale la chiusura e l'apertura di contatti viene ottenuta con un elettromagnete: la sua modesta velocità (i ritardi introdotti da un relè possono essere al minimo di circa 1 ms) ne ha giustificato la sostituzione con i tubi elettronici a vuoto (che possono ottenere risultati equivalenti in tempi di pochi microsecondi) per la costruzione di elaboratori più veloci e più sicuri (per l'assenza di parti in movimento). I tubi a vuoto in unione con diodi (a vuoto inizialmente, a semiconduttore dopo il 1953) sono stati gli elementi di base per la prima generazione di elaboratori.

flg. 9

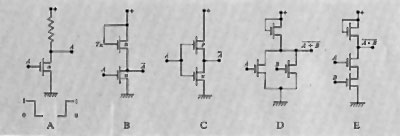
La flg. 9 mostra gli schemi di alcuni circuiti logici elementari del tipo finora considerato.

L'avvento dei transistori ha fatto presto intravedere in essi un elemento ideale per la costruzione degli elaboratori. Infatti il transistore si presta a essere usato in circuiti simili ai circuiti a tubi, è molto più piccolo, consuma meno energia e ha una vita utile e un'affidabilità molto maggiori del tubo elettronico. I transistori hanno caratterizzato, insieme alle memorie a nuclei magnetici e ai linguaggi di programmazione, la seconda generazione di elaboratori.

fig. 10

La fig. 10 mostra gli schemi di alcuni circuiti logici elementari. Sono stati molto usati circuiti logici misti, per esempio a diodi e transistori. L'evoluzione della tecnologia dei semiconduttori ha condotto (1963 circa) ai circuiti integrati che caratterizzano la terza generazione di elaboratori insieme alla tecnica di multiprogrammazione e di time sharing.

Le tecniche dei semiconduttori e dei circuiti integrati sono illustrate nell'articolo elettronica al quale si rimanda il lettore. Qui si illustrano le caratteristiche dei circuiti logici ottenuti con tali tecniche.

È noto come le tecniche dei circuiti integrati permettano di ottenere non più soltanto un singolo componente (un transistore, un diodo) ma un intero circuito logico su una piastrina di semiconduttore (silicio). I circuiti integrati hanno pertanto esaltato le caratteristiche di piccole dimensioni, di basso consumo e di grande affidabilità dei precedenti circuiti, permettendo la costruzione di sistemi sempre più complessi.

La tendenza a integrare su un solo dispositivo circuiti sempre più grandi (fino a migliaia di componenti elementari come i transistori) è tuttora in atto, e a essa si dà il nome di Large Scale Integration (LSI) o ‛integrazione in grande'. Prima di discutere le tendenze di tale evoluzione e le prevedibili conseguenze, si illustreranno brevemente i tipi principali di circuiti logici integrati.

Nei primi dispositivi integrati si è cercato di riprodurre i tipi di circuiti logici già noti, dando origine alle famiglie di circuiti come la Resistor Transistor Logic (RTL) e la Diode Transistor Logic (DTL).

La prima è basata sui circuiti del tipo di quelli illustrati nella fig. 10, mentre la seconda utilizza circuiti e diodi per l'operazione di prodotto o somma logici e il transistore per l'operazione di negazione.

La famiglia RTL è stata abbandonata per prima e la stessa sorte è più tardi toccata alla famiglia DTL.

Sono state infatti nel frattempo individuate strutture circuitali che meglio si adattano alle tecniche di integrazione, permettendo di ottenere circuiti che occupano minori aree sulle piastrine di silicio e offrono perciò i vantaggi di un minor costo e di più elevate velocità di funzionamento.

11A

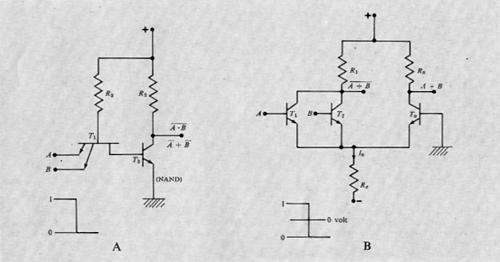
Appartiene a tale categoria di circuiti la famiglia nota come Transistor Transistor Logic (TTL), il cui schema fondamentale è rappresentatò nella fig. . La caratteristica principale è data dal transistore T₁ dotato di più emettitori, che è molto facile da costruire con la tecnica ‛planare' (v. elettronica). Allorquando uno dei due morsetti d'ingresso (A, B) è a potenziale basso (0), il transistore T₁ è portato in saturazione e di conseguenza il transistore T₂ viene bloccato, ottenendo cosi al collettore di T₂ un potenziale alto (1). Ciò può essere descritto con una funzione logica A NAND B, cioè A̅  •  B̅, come segnato in figura.

Una seconda famiglia di nuovi circuiti integrati, caratterizzata da una velocità di funzionamento superiore a quella delle precedenti, è nota come Emitter Coupled Logic (ECL) e anche Current Mode Logic (CML); il suo schema fondamentale è rappresentato nella fig. 11B. In tale circuito la base del transistore T₀ è sempre a potenziale nullo e nel resistore R_e si suppone circolante una corrente costante. Tale corrente circolerà tutta in T₀ se T₁ e T₂ saranno bloccati (A = B = 0), mentre ‛verrà deviata in R₁ se saranno in conduzione (A = 1 o B = 1). Ciò produce ai collettori di T₁, T₂ e T₀ le funzioni A̅  + B  e A + B rispettivamente.

I circuiti ECL risultano di funzionamento molto veloce (ritardi dell'ordine del nanosecondo), ma sono più costosi dei circuiti TTL: essi sono pertanto usati in quelle parti degli elaboratori dove si richieda una velocità molto alta, come nelle unità aritmetiche.

fig. 12

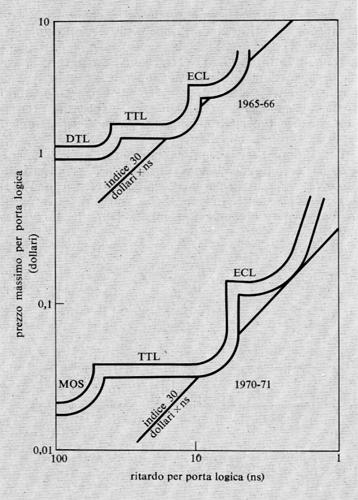
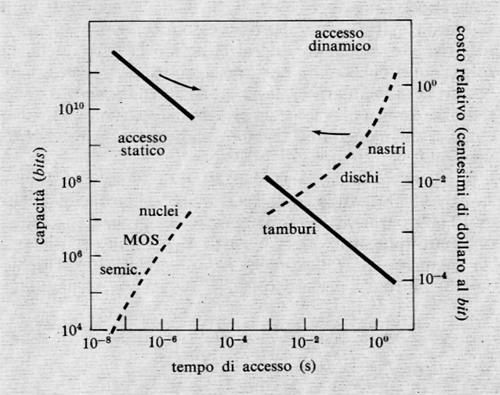
La fig. 12 mostra un diagramma che mette in relazione il costo per circuito elementare (‛porta logica') con il ritardo dello stesso, per le diverse famiglie e in due epoche diverse. Si noti come in una certa epoca il prezzo specifico per una certa famiglia cresca rapidamente, al di sotto di un certo ritardo, e come dunque convenga adottare un'altra famiglia (se questa è disponibile, s'intende). Si veda anche come i ritardi critici per una certa famiglia diminuiscano col tempo, grazie ai perfezionamenti tecnologici.

Al momento, la famiglia ECL è quella che fornisce i ritardi minimi.

Un'importante famiglia di circuiti logici è la MOS (Metal Oxide Semiconductors) che, malgrado presenti ritardi maggiori di altre, è di grande interesse per il suo costo che è invece il minimo di quelli oggi ottenibili. Infatti i transistori di tipo MOS occupano nei circuiti integrati aree di gran lunga minori dei transistori bipolari, permettendo così la costituzione di circuiti sempre più complessi su una stessa piastrina di silicio e inoltre richiedono un procedimento costruttivo più semplice. Per tali motivi, i circuiti integrati MOS rendono possibile la costruzione di dispositivi ‛a grande integrazione' (LSI), in particolare memorie e anche intere unità di calcolo (CPU) su un'unica piastrina.

fig. 13

I principali circuiti logici di tipo MOS sono illustrati nella fig. 13, nella quale si osserva in B l'impiego di un transistore T_R in sostituzione del resistore del circuito A; risulta infatti che ciò è conveniente, dato quanto si è già detto e dato che i resistori sono gli elementi che occupano aree di piastrina molto grandi rispetto ai transistori MOS. Nel circuito C si ha un negatore del tipo ‛complementare' (CMOS), in quanto si utilizzano due transistori MOS, di cui uno a ‛canale n' e l'altro a ‛canale p' (v. elettronica). Con esso si consegue il grande vantaggio di un ridottissimo consumo di energia, in quanto uno dei due transistori è sempre bloccato (salvo nelle transizioni della variabile di entrata). I circuiti D ed E mostrano infine come si possano realizzare le funzioni logiche NOR e NAND. Altre più complesse funzioni logiche sono facilmente realizzabili con i circuiti di tipo MOS.

fig. 14

È stata recentemente scoperta un'ulteriore famiglia di circuiti logici, la IIL (Integrated Injection Logic), il cui circuito base è rappresentato nella fig. 14 insieme alla sua realizzazione in forma integrata. Quest'ultima risulta molto semplice e compatta, permettendo così di raggiungere alte densità di integrazione. Il suo sviluppo è ancora in corso, soprattutto per quanto riguarda il miglioramento della velocità. Lo studio e l'applicazione dei circuiti logici di tipo MOS si stanno sempre più diffondendo, con l'intento di migliorarne la velocità di funzionamento ed estenderne l'impiego ai casi in cui non si richieda una velocità estremamente alta. Parallelamente anche le dimensioni dei circuiti bipolari (in particolare IIL) tendono ad aumentare (LSI): sono già oggi disponibili circuiti con migliaia di componenti elementari. Una particolare attenzione merita la tecnologia C-MOS realizzata su supporti di zaffiro, che è potenzialmente capace di raggiungere la velocità di funzionamento dei circuiti TTL, ma a minor costo e soprattutto con consumi di energia ridottissimi.

È presumibile che per parecchi anni la tecnologia dominante per i circuiti logici rimarrà quella dei semiconduttori, che offre ancora larghi margini di miglioramento.

Le innovazioni tecnologiche sono più rilevanti, come si vedrà, nel caso delle memorie, per le quali, peraltro, i semiconduttori stanno offrendo soluzioni molto interessanti.

Tra le tecnologie che nel futuro potrebbero emergere, si cita quella basata sul ‛criotrone a tunnel' di Josephson, caratterizzata da grande velocità di funzionamento e dalla possibilità di prestarsi sia per i circuiti logici, sia per le memorie.

Numerose altre tecnologie sono state studiate e anche impiegate nel passato, come i circuiti basati su elementi magnetici saturabili (‛logiche magnetiche') e quelli basati su fenomeni di superconduttività (criotroni). Esse sono state tutte soppiantate dalla tecnologia dei semiconduttori e rivestono oggi un interesse puramente concettuale e storico.

10. L'evoluzione della tecnologia delle memorie

La necessità di una memoria concepita come organo distinto dai circuiti di elaborazione è stata riconosciuta già al tempo dei primissimi calcolatori elettronici. Infatti, i programmi di calcolo e i dati richiedevano l'uso di speciali tecniche capaci di memorizzare e recuperare a comando notevoli quantità di informazioni; si riconobbe perciò subito come la tecnologia usata nei circuiti di elaborazione (basata sull'uso dei tubi elettronici) non si prestasse per ragioni di costo alla costituzione di memorie.

Le memorie usate nei primi elaboratori furono, come e già stato detto, quelle basate su fenomeni di propagazione (linee di ritardo, a mercurio o metalliche o elettriche), su fenomeni elettrostatici (memorie con tubi a raggi catodici, di Williams) e su fenomeni magnetici (tamburi, dischi, nastri o nuclei magnetici). Di tali tecnologie solo l'ultima è rimasta negli odierni sistemi (e, anzi, continua a svilupparsi). Le prime sono state invece rapidamente sostituite dalle memorie basate sull'uso di nuclei magnetici a ciclo di isteresi rettangolare che, apparsi intorno al 1955, stanno per essere sostituiti a loro volta dalle nuove memorie a semiconduttori.

fig. 15

Lo schema di una memoria a ‛dischi' magnetici è rappresentato nella fig. 15. In A è rappresentato un disco, rotante a velocità costante intorno al suo asse e ricoperto sulle due facce da un sottile strato di materiale ferromagnetico (ossido magnetico). È pure rappresentata una testina T di registrazione/lettura che si affaccia su una delle superfici del disco ed è portata da un braccio che può essere spostato radialmente. Quando la testina è tenuta immobile, essa interessa una sottile corona circolare dello strato magnetico (pista magnetica). Spostando la testina radialmente si vengono a determinare nuove piste di registrazione. La testina è composta da un circuito magnetico con traferro (v. fig. 15B). Se negli avvolgimenti della testina T si fa circolare corrente, avviene che il flusso magnetico nelle vicinanze del traferro investe lo strato magnetico del disco in modo che per effetto del movimento vengono determinate sulla pista delle magnetizzazioni residue il cui verso dipende dal verso della corrente. L'informazione da registrare è rappresentata dai versi che la corrente percorre in intervalli successivi per rappresentare una successione di bits. La lettura dell'informazione avviene tramite le f.e.m. che vengono indotte negli avvolgimenti della testina, per effetto delle variazioni. di flusso ottenute quando la testina ripassa sulla pista precedentemente registrata. Si noti che l'operazione di lettura lascia immutata l'informazione registrata sulla pista.

Nella fig. 15C è rappresentata una pila di dischi, con un insieme di testine che possono essere spostate radialmente in modo simultaneo. Poiché lo spostamento delle testine richiede un notevole tempo, nelle memorie a disco più veloci si provvede a porre su ogni braccio non una sola testina ma gruppi di più testine interessanti altrettante piste adiacenti, oppure una testina fissa per ogni pista (naturalmente il costo totale aumenta considerevolmente).

La fig. 15D mostra la struttura di una memoria a tamburo, i cui principî di funzionamento sono identici a quelli di una memoria a dischi.

Le caratteristiche più salienti di una memoria sono: il tempo di accesso all'informazione e la sua capacità in bits.

Nel caso delle memorie a disco, il tempo di accesso è definito come il ritardo tra l'istante in cui viene comandata la lettura (o registrazione) in una certa posizione e l'istante di inizio della lettura stessa. Tale ritardo è composto dall'eventuale tempo di spostamento del braccio per raggiungere la pista voluta e dal tempo di rotazione (tempo di latenza) del disco perché la posizione voluta su quella pista venga raggiunta. I due ritardi sono ovviamente variabili e dipendono dalle posizioni iniziali e finali del braccio, il primo, e dalla posizione della testina rispetto alla posizione voluta sulla pista, il secondo. Il ritardo di spostamento varia da decine a centinaia di millisecondi, il ritardo di rotazione è mediamente pari al semiperiodo di rotazione (dell'ordine di decine di millisecondi). La diminuzione di tali ritardi non può essere ottenuta se non con un aumento delle velocità meccaniche, che non possono tuttavia essere spinte molto oltre i limiti già raggiunti. Nelle memorie rotanti più veloci si è talvolta fatto ricorso a più testine per pista, allo scopo di minimizzare il tempo di latenza tramite la scelta della testina più vicina al punto della pista desiderato.

La capacità di una memoria a dischi è proporzionale alla superficie totale disponibile e alla densità di registrazione.

La densità superficiale è pari al prodotto della densità (lineare) tangenziale lungo la pista e della densità radiale (numero di piste per unità di raggio). Valori tipici di densità raggiunte con le più recenti memorie sono di circa 1.800 bits/cm e 80 piste/cm, e sono da attendersi ancora sensibili aumenti di tali valori.

L'aumento della densità è stato reso possibile da perfezionamenti apportati alle testine, che oggi sono normalmente del tipo ‛galleggiante', essendo il loro distanziamento dalla superficie del disco ottenuto per effetto di un velo d'aria tra le due parti.

Le memorie a ‛nastro magnetico' sono basate su una tecnologia del tutto simile a quella descritta per le memorie a disco. Il supporto delle informazioni è qui costituito da un nastro magnetico fatto scorrere sotto un insieme di testine di registrazione/lettura determinanti altrettante piste parallele ai bordi del nastro. Il movimento del nastro può avvenire nei due sensi per mezzo di un apposito meccanismo, che comprende anche due bobine sulle quali sono avvolte le due estremità del nastro.

Il tempo di accesso nella memoria a nastro dipende dalla distanza tra la testina e l'informazione voluta, dipende perciò anche dalla lunghezza del nastro e dalla velocità di ricerca e può raggiungere valori di qualche minuto. Le informazioni sono raggruppate a blocchi, tra loro distanziati da un tratto di nastro non registrato, per permettere l'accelerazione del nastro all'inizio del movimento per la lettura del blocco e la sua decelerazione. La capacità di un nastro è dell'ordine dei 10÷20 milioni di bytes (un byte equivale a otto bits).

fig. 16

Le memorie a ‛nuclei magnetici' sono state dal 1955 ampiamente usate come memorie di lavoro. Il principio di funzionamento di tali memorie può essere illustrato mediante la fig. 16. Esse sono composte da numerosi nuclei toroidali di materiale ferromagnetico (ferrite), il cui ciclo di isteresi, di forma praticamente rettangolare, è rappresentato in B. Ogni nucleo può essere saturato magneticamente con una corrente, I_S, e al cessare di questa esso potrà trovarsi in uno dei due punti segnati con 0 e 1 a seconda del verso della corrente. Tali punti rappresentano flussi magnetici residui il cui verso è assunto come corrispondente ai due valori binari. La lettura dell'informazione viene ottenuta tramite f.e.m. indotta in apposito avvolgimento concatenato al nucleo stesso, operando come se si volesse scrivere per esempio lo 0. Nel caso che tale sia lo stato precedente, il punto rappresentativo sul diagramma si sposterà da 0 a 0′ con una modesta variazione del flusso, e pertanto con una piccola f.e.m. Se invece lo stato precedente fosse 1, la variazione di flusso sarebbe considerevole, con una notevole f.e.m. indotta. Come si vede, la lettura dell'informazione si ottiene distruggendo l'informazione stessa (‛lettura distruttiva').

Il problema principale nella costruzione delle memorie a nuclei è quello di organizzare un numero molto grande di nuclei (anche molti milioni per ogni memoria) minimizzando il costo dei circuiti elettronici destinati a produrre le necessarie correnti e ad amplificare i segnali in lettura. Ciò viene ottenuto disponendo i nuclei, come mostra la fig. 16A, in ‛matrici' composte da n conduttori orizzontali e m conduttori verticali, concatenati nei punti di incrocio con n × m nuclei. n e m possono superare il valore 100, di modo che in una matrice possono essere compresi anche più di 10.000 nuclei.

La lettura di un determinato nucleo avviene alimentando i conduttori della rispettiva linea e colonna con le correnti rappresentate nella fig. 16C, composte ciascuna da impulsi di valore I_s/2, di modo che, mentre nel nucleo prescelto le due correnti sommano i loro effetti equivalendo cosi a una corrente I_s sufficiente ad azzerare il nucleo, nei restanti nuclei della riga e della colonna considerate la corrente I_s/2 è insufficiente a modificare gli stati di magnetizzazione.

In un avvolgimento che concatena tutti i nuclei (v. fig. 16A) viene indotta una f.e.m. rappresentata dalla fig. 16Cb nel caso che il nucleo fosse nello stato 0 e dalla fig. l6Cc per lo stato 1.

Le memorie a nuclei sono generalmente predisposte in modo da riscrivere l'informazione letta e distrutta nel processo di lettura. Ciò viene ottenuto facendo seguire nella stessa riga e colonna due impulsi negativi sempre di valore I_s/2, i quali perciò, agendo da soli, registrerebbero sempre 1. Allo scopo di poter registrare anche lo zero, viene predisposto sulla matrice un ulteriore avvolgimento (non mostrato nella fig. 16A) che concatena tutti i nuclei e si chiama avvolgimento di ‛inibizione'. Allorquando si voglia lasciare il nucleo nello stato 0, è sufficiente alimentare l'avvolgimento di inibizione con la corrente rappresentata dalla fig. 16C, di modo che la corrente totale del nucleo corrisponda a (−I_s/2−I_s/2 + I_s/2 = −I_s/2) insufficiente a portare il nucleo nello stato 1.

Tale impulso di inibizione non viene invece inviato quando si vuole che nel nucleo sia registrato lo stato 1.

Si noti che l'operazione di registrazione di nuove informazioni si fa con lo stesso procedimento, determinando la generazione degli impulsi di inibizione non in funzione dell'informazione prima contenuta, ma di quella fornita dall'esterno.

fig. 17

Gli stessi circuiti per la generazione della corrente di riga e colonna possono essere anche utilizzati da più matrici, disposte come nella fig. 17, in modo da leggere simultaneamente il contenuto di tutti i nuclei che nelle varie matrici si trovano nella stessa posizione. Si ottiene così lo schema di una memoria a nuclei del tipo ‛parallelo', in cui i bits di una o più parole possono essere letti o registrati simultaneamente. Si noti che, in tal caso, ogni matrice deve disporre di un proprio circuito di lettura e di un circuito per la generazione degli impulsi di inibizione.

Quello descritto è lo schema di base delle memorie a nuclei usate per quasi un ventennio. La durata del ciclo di funzionamento è stata via via ridotta dai circa 10 μs delle prime memorie ai circa 300 ns delle memorie più recenti. Ciò è stato possibile sia con accorgimenti circuitali, sia col miglioramento delle caratteristiche delle ferriti costituenti i nuclei, sia con la riduzione delle dimensioni dei nuclei stessi (fino a pochi decimi di millimetro).

Il costo delle memorie a nuclei non può essere ridotto quanto si desidererebbe, soprattutto perché i procedimenti costruttivi, solo in parte automatizzabili, richiedono notevole mano d'opera.

Una tecnologia che sembrava a suo tempo poter diventare competitiva con quella dei nuclei magnetici è quella delle memorie a pellicola magnetica, basate sull'impiego delle proprietà magnetiche di sottili pellicole di materiale ferromagnetico depositate su substrati piani o filiformi.

Tuttavia le tecnologie costruttive si sono rivelate difficoltose e, soprattutto, l'avvento delle ‛memorie a semiconduttori' ha aperto una strada molto più promettente.

Le memorie a nuclei stanno infatti per essere sostituite dalle ‛memorie a semiconduttori', che ormai hanno non solo raggiunto costi competitivi, ma presentano anche altri vantaggi rispetto alle prime. Uno dei più importanti tra questi è dato dal fatto che, essendo la tecnologia usata comune ai circuiti logici e alle memorie, vengono eliminati i problemi di ‛interfaccia' che si dovevano invece affrontare con le memorie a nuclei, il che permette di ottenere, fra l'altro, dimensioni e consumi di energia notevolmente minori. La riduzione dei costi è resa possibile dall'uso della tecnologia dei circuiti integrati LSI che risulta in gran parte automatizzabile, in quanto con un solo procedimento si realizza la costruzione simultanea di migliaia di celle elementari di memoria su una piastrina di silicio.

La costruzione della cella di memoria, in grado di memorizzare un bit, può ottenersi con una delle note tecnologie: la distinzione principale è tra le tecnologie ‛bipolari', colle quali si costituiscono circuiti logici del tipo DTL, TTL o ECL, e la tecnologia MOS.

Lo schema tipico di una cella di memoria può essere quello del circuito bistabile, ottenibile (come illustrato nel cap. 8) col collegamento di due circuiti NOR o NAND. Si possono cosi ottenere bistabili con ciascuna delle tecniche citate, con le relative caratteristiche già illustrate per i circuiti logici.

Le unità di memoria comprendono, oltre all'insieme delle celle elementari (organizzate con uno schema ‛a matrici' simile a quello delle memorie a nuclei), anche i circuiti detti di selezione, che permettono la scelta della cella in base al suo indirizzo. La lettura e la registrazione avvengono in genere in parallelo per tutte le celle di una riga.

Risulta da quanto detto a proposito delle varie tecnologie che le memorie bipolari sono molto più veloci di quelle MOS (pochi nanosecondi di tempo di accesso per i tipi ECL, decine per i tipi TTL, centinaia per i tipi MOS). Per contro, le dimensioni delle celle sulle piastrine di silicio sono minime per i tipi MOS e massime per i tipi ECL.

Ne consegue che le memorie bipolari (TTL, ECL) sono quelle più veloci, ma a capacità minore (per es. 1.024 bits), mentre quelle MOS sono più lente ma hanno capacità maggiori (per es. 4.096 bits) a parità di dimensioni del cristallo.

fig. 18

Le memorie del tipo MOS possono costituirsi con celle elementari secondo uno degli schemi della fig. 18. In A si ha uno schema di bistabile, con sei transistori; in B si ha una cella a quattro transistori, in cui si approfitta delle capacità parassite C per la memorizzazione dell'informazione. Tale memorizzazione è tuttavia solo temporanea, in quanto le capacità tendono a scaricarsi. Un dispositivo provvede pertanto a leggere e riscrivere automaticamente e periodicamente in tutte le celle della memoria l'informazione in modo da ‛rinfrescarla'. La fig. 18C rappresenta un'ulteriore semplificazione con l'uso di una sola capacità e di soli tre transistori e la fig. 18D mostra uno schema comprendente un unico transistore per cella.

Tutti i precedenti perfezionamenti permettono oggi la costruzione di circuiti integrati con capacità di 16.384 bits e tempi di accesso inferiori a 100 ns.

È da aspettarsi nei prossimi anni un aumento di tale capacità (fino a parecchie centinaia di migliaia di bits per piastrina di silicio) e una riduzione dei tempi di accesso. Anche i costi di fabbricazione stanno diminuendo e tutto ciò porta a concludere che entro breve termine le memorie principali degli elaboratori utilizzeranno sistematicamente la nuova tecnologia che, essendo, come già detto, ampiamente utilizzata anche nei circuiti logici, caratterizzerà la prossima generazione di elaboratori.

Si ricava dall'esposizione precedente che le varie memorie oggi disponibili sono caratterizzate da tempi di accesso e capacità tra loro molto differenti. Ciò pone problemi nel loro impiego, che verranno discussi nei punti seguenti, e continua a stimolare le ricerche intese a individuare nuovi tipi di memoria, in particolare quelle a grande capacità (‛di massa').

Tra le tecnologie più suscettibili di prestare un contributo alla soluzione dei problemi delle memorie, si illustreranno brevemente quelle basate su: l'indirizzamento ottico, l'uso dei semiconduttori e le ‛bolle' magnetiche.

Le memorie a ‛indirizzamento ottico' (beam addressable files) si basano sull'uso di un fascio di luce (laser) o di elettroni, deviato con dispositivi elettroottici e incidente su un materiale magnetico o fotosensibile speciale sul quale la registrazione può avvenire, per esempio, tramite fenomeni magnetotermici e la lettura con fenomeni magnetoottici. Le tecnologie relative richiedono ancora notevoli sviluppi prima di poter competere con le attuali memorie, ma gli sforzi sono giustificati dalle migliori caratteristiche del tempo di accesso, per l'eliminazione di organi in moto e per le grandi densità di registrazione che potrebbero essere realizzate.

fig. 19

La tecnologia dei semiconduttori può offrire soluzioni basate su dispositivi del tipo ‛registri a scorrimento', costituiti da una catena di celle elementari nelle quali l'informazione passa da una cella a quella successiva tramite un comando. L'informazione ricavata dall'ultima cella può essere introdotta nella prima realizzando così una catena chiusa in cui si ha ricircolazione dell'informazione stessa, la quale appare in un punto qualsiasi della catena come l'informazione letta dalla pista di un disco magnetico. Per la costituzione dei registri a scorrimento si possono adottare due tecniche principali: la prima utilizza celle costituite da transistori MOS, di tipo simile a quelle già illustrate; la seconda utilizza un particolare dispositivo detto charge coupled (o transfer) device (dispositivo a trasferimento di carica), il cui principio di funzionamento è illustrato nella fig. 19. Si tratta di un cristallo di silicio, ricoperto da una striscia di isolante (ossido di silicio) su cui sono depositati elettrodi metallici, tra loro connessi come mostra la figura e alimentati da un sistema trifase di impulsi di tensione tutti riferiti a una tensione costante di polarizzazione V_b. La carica elettrica, introdotta tramite una giunzione pn in corrispondenza del primo condensatore A, viene trasferita al condensatore B quando a esso sia applicata una tensione 2V_b, e cosi via.

fig. 20

Le ‛bolle magnetiche' costituiscono un fenomeno che si verifica su una pellicola di materiale magnetico anisotropo il cui asse di magnetizzazione stabile sia normale alla superficie della pellicola (nella memoria pellicolare prima citata, tale asse risulta invece parallelo alla superficie). In assenza di campo magnetico esterno i domini magnetici nella piastrina sono in parte orientati in un verso e in parte nel verso opposto e l'applicazione di un campo magnetico esterno tende a far diminuire gli uni in favore degli altri finché, al crescere del campo, i primi si riducono a piccoli cilindretti (‛bolle'), che spariscono se il campo viene ulteriormente intensificato. Le bolle ivi create possono essere spostate sulla pellicola per azione di campi magnetici esterni. La presenza o l'assenza di una bolla può essere assunta a rappresentare un bit d'informazione. Rimane il problema di controllare lo spostamento delle bolle nonché di generarle. Ciò può essere ottenuto disponendo sulla pellicola sottili strati, opportunamente configurati, di materiali ad alta permeabilità (permilloy; v. fig. 20).

Le memorie a bolle realizzano come si vede un ‛registro a scorrimento', come i dispositivi a semiconduttori. Rispetto a questi ultimi, godono del vantaggio della non volatilità della registrazione, che rimane anche in caso di interruzione dell'alimentazione elettrica. Anche per le memorie a bolle rimangono da risolvere problemi tecnici, dopo di che potranno forse sostituire i dischi a piccola capacità, offrendo velocità maggiori sia pure a maggiori costi.

Per altre tecnologie potenzialmente capaci di contribuire alla soluzione dei problemi delle memorie si rimanda il lettore alla bibliografia.

11. L'evoluzione dell'architettura delle memorie

Come si è ripetutamente constatato, la capacità di elaborazione di un sistema è limitata sia dalla velocità, sia dalle dimensioni della sua memoria. Il costo delle memorie di più elevata velocità oggi disponibili (quelle a semiconduttori) impedisce che la memoria possa avere dimensioni sufficienti a contenere programmi completi, soprattutto nei sistemi a multiprogrammazione e a time sharing, che servono simultaneamente più utenti.

Il problema è stato risolto sin dai primordi degli elaboratori associando alla ‛memoria di lavoro', veloce ma di dimensione limitata, una memoria ‛ausiliaria' di più grande capacità, ma con un costo per bit minore. Le informazioni vengono trasferite nella memoria principale quando e nella misura in cui servono e il trasferimento avviene solitamente in ‛blocchì' o ‛pagine' corrispondenti a numerose celle della memoria di lavoro.

Lo sfruttamento razionale dei diversi tipi di memorie oggi disponibili ha condotto a elaborare una vera e propria architettura delle memorie, che s'inquadra nell'architettura generale dei sistemi di elaborazione.

fig. 21

La situazione attuale complessiva dei vari tipi di memorie è rappresentata nella fig. 21. Da essa appare come le memorie più veloci siano quelle a semiconduttore (ECL) con tempi di accesso di pochi nanosecondi: esse sono tuttavia troppo costose per costituire la memoria di lavoro, che comprende di solito 10⁵ ÷ 10⁵ bits e che può realizzarsi con la tecnologia a nuclei o MOS, con tempi di accesso di centinaia di nanosecondi. Il divario aumenta se si passa alle memorie a tamburi o dischi, che possono offrire capacità anche molto elevate (10⁸ ÷ 10¹⁰ bits), ma con tempi di accesso che vanno da decine a centinaia di millisecondi. Ancora più lenti sono i nastri magnetici, che tendono peraltro a essere usati prevalentemente come memoria ‛di archivio', non direttamente accessibile da parte dell'elaboratore.

Attualmente si tende a realizzare metodi in cui la gestione delle varie memorie di un sistema viene automaticamente effettuata dallo stesso sistema sia con soluzioni circuitali (hardware), sia con soluzioni software (cioè con adatte particolarità del programma base o sistema operativo). Si cerca con tali soluzioni di ottenere il trasferimento automatico delle informazioni dalle memorie più lente a quelle più rapide e viceversa in funzione della richiesta, in modo che l'informazione richiesta da un utente risieda nella memoria più veloce solo durante l'uso. Se tale obiettivo potesse essere perfettamente raggiunto, la memoria sarebbe per l'utente virtualmente tutta alla più alta velocità. Inoltre, poiché la capacità totale della memoria può essere molto grande, si potrebbe anche dire che l'utente ha a disposizione una memoria virtuale tutta ad alta velocità e con una capacità grandissima. In realtà la velocità media di un'elaborazione risentirà dei processi di trasferimento e risulterà inferiore a quella delle memorie più veloci, tuttavia il vantaggio sarebbe ancora considerevole.

La realizzazione del concetto di memoria virtuale tende perciò a ridurre il divario delle caratteristiche tra le varie memorie e viene oggi ottenuta in misura varia in tutti i nuovi sistemi; se ne illustreranno qui i principî fondamentali.

Si consideri innanzitutto il collegamento tra la memoria di massa (a dischi) e quella di lavoro (nuclei, semiconduttori). Si è già detto che il trasferimento tra le due memorie conviene avvenga per ‛blocchi' di dati allo scopo di minimizzare l'effetto del tempo d'accesso (decine o centinaia di ms) rispetto al tempo di trasferimento effettivo delle informazioni, che cresce col crescere delle dimensioni del blocco. Per facilitare la gestione dei trasferimenti e anche l'utilizzazione delle memorie principali, conviene che i blocchi, che si chiameranno ‛pagine', siano tutti delle stesse dimensioni, per esempio di 1.000 parole.

fig. 22

Si consideri l'esempio (v. fig. 22) di una memoria di massa di 100.000 parole, associata a una memoria di lavoro di 10.000 parole e si supponga che un programma possa utilizzare tutti gli indirizzi virtuali disponibili nella memoria di massa, da 00.000 a 99.999. Quando la CPU richiede un indirizzo, per esempio 29.328, questo viene suddiviso in due parti: 29 e 328. L'ultima è subito posta nel registro di indirizzamento della memoria di lavoro. La prima parte (29) indica il numero della pagina virtuale nella memoria di massa: l'elenco delle pagine residenti in memoria di lavoro è registrato in un ‛dizionario', che le mette in corrispondenza col posto loro assegnato nella memoria di lavoro. Nell'esempio considerato, la pagina richiesta, 29, figura in tale dizionario, dal quale si ricava l'‛indirizzo di pagina' reale, 3, che viene associato a 328 per formulare l'indirizzo reale nella memoria di lavoro.

Se invece la pagina 29 non risultasse in memoria, il programma base provvederebbe a richiamarla dalla memoria di massa, assegnandole una delle pagine disponibili nella memoria di lavoro e registrandola nel dizionario. Nel caso che la memoria fosse già tutta occupata, il programma base dovrebbe provvedere a espellere una delle pagine presenti (per es. in base al grado di utilizzazione fino ad allora verificato) sostituendola con quella voluta e aggiornando conseguentemente il dizionario.

Le operazioni richieste per la trasformazione degli indirizzi virtuali in reali sono, come si vede, piuttosto complesse. Per ridurre l'effetto negativo sulla velocità di elaborazione, si può automatizzare l'operazione di consultazione del dizionario (la più onerosa in termini di tempo) mediante l'uso di una ‛memona associativa', caratterizzata dalla capacità d'individuare una parola non mediante il suo indirizzo (come nelle memorie usuali) ma tramite il suo contenuto. Nel caso considerato, se il dizionario è posto in una memoria associativa, è sufficiente fornirle il numero della pagina cercata (29, nell'esempio) e, se questa esiste nel dizionario, si ottiene subito l'indirizzo reale (3) evitando le operazioni di ricerca sequenziale. Memorie associative di capacità sufficiente a realizzare il suddetto dizionario sono oggi disponibili sotto forma di circuiti integrati.

Il vantaggio derivante dall'uso delle suddette tecniche può valutarsi come segue. Se T_M è il tempo necessario per individuare e leggere una parola nella memoria di lavoro, e T_D il corrispondente tempo per la memoria a disco, il tempo medio di accesso T_A diviene:

T_A T_M + (1 − h)T_D,

dove h rappresenta il ‛rapporto di presenza', cioè la frazione degli indirizzi richiesti che mediamente si trova già nella memoria di lavoro. Per T_D ≫ T_M, si ha T_A ≃ (1−h) T_D e, per h = 0,9, T_A ≃ 0,1 T_D.

Lo stesso concetto sopra illustrato può essere applicato anche per attenuare il divario tra memorie di lavoro a nuclei o MOS e memorie bipolari. Si predispone allora una piccola memoria ausiliaria, detta cache, tra la memoria di lavoro e la CPU. Ogniqualvolta questa richiede un indirizzo alla memoria di lavoro, se esso non è ancora presente nella cache, viene letta dalla memoria una pagina (più piccola di quella precedentemente considerata). Se invece l'indirizzo richiesto è già presente, la relativa cella viene letta dalla cache, molto più veloce. Per ragioni di velocità il meccanismo di traduzione degli indirizzi di ricerca nella cache viene eseguito con appositi circuiti. Anche qui il vantaggio deriva dal fatto che gli indirizzi che vengono richiesti in un breve intervallo di funzionamento sono con grande probabilità già presenti nella cache.

Possono considerarsi come parte dell'architettura della memoria anche la sua struttura modulare e i modi di collegamento dei vari moduli di memorie con gli altri moduli della macchina, come illustrati nel prossimo capitolo.

Possono ancora considerarsi parti dell'architettura della memoria i vari schemi di ‛indirizzamento'.

L'indirizzamento ‛diretto' è quello in cui l'indirizzo scritto nelle varie istruzioni è da intendersi come indirizzo reale delle memorie di lavoro. L'indirizzamento ‛virtuale' è quello or ora illustrato. Altri modi di indirizzamento sono i seguenti. Indirizzamento ‛indiretto': l'indirizzo reale è contenuto nella cella il cui indirizzo è quello indicato nell'istruzione. L'indirizzamento indiretto può essere a più livelli, quando il contenuto della cella indirizzata viene interpretato come indirizzo a sua volta indiretto, che rimanda perciò a un'altra cella. Indirizzamento ‛con indice': l'indirizzo reale viene ottenuto sommando all'indirizzo dato nell'istruzione il contenuto di uno o più registri, detti ‛registri indice'.

Il più importante uso dei suddetti modi di indirizzamento è quello che permette di costruire programmi nelle cui istruzioni gli indirizzi vengono modificati solo indirettamente o con gli indici, di modo che il programma nella memoria non sia mai direttamente modificato.

Un altro importante vantaggio è dato dalla possibilità di assegnare a una pagina di programma una posizione qualsiasi nella memoria di lavoro, senza dover preventivamente modificare i suoi indirizzi di salto (che dipendono dalla posizione assegnata alle pagine in memoria).

12. L'evoluzione dell'architettura degli elaboratori

Un elaboratore elettronico può considerarsi composto, come già detto, da varie parti cui sono demandate particolari funzioni: memorie, unità aritmetico-logiche, organi di controllo o di governo, organi di entrata e di uscita. Lo studio della struttura delle varie parti, del loro proporzionamento e dei modi in cui possono essere tra loro interconnesse costituisce il tema dell'‛architettura' dei sistemi di elaborazione.

È importante osservare subito che, anche se l'aspetto più rilevante ditale studio riguarda i sottosistemi hardware della macchina, esso ha però connessioni molto strette con il ‛programma (o software) base' (o ‛sistema operativo') che è destinato a governare e a gestire tutte le risorse, hardware e software, della macchina. Si è anzi da tempo riconosciuto come il progetto di un sistema di elaborazione debba considerare simultaneamente tutti i sottosistemi hardware e software, essendo tra l'altro uno dei problemi quello di decidere quali funzioni realizzare con hardware e quali con software (tenuto conto che molte delle funzioni interne di un elaboratore possono spesso realizzarsi nei due modi). Si vedrà pure come la distinzione tra hardware e software si sia attenuata, con l'introduzione di una concezione intermedia che consiste nell'immagazzinare programmi in unità di memoria speciali dette ‛memorie morte' o ‛a sola lettura' (ROM: Read Only Memory, o ROS: Read Only Store), nelle quali l'informazione viene determinata all'atto della costruzione e non può successivamente venire alterata. I programmi registrati in memorie morte si dicono costituire il firmware. Il firmware risulta di rilevante importanza nell'architettura dei sistemi di elaborazione.

Lo studio dell'architettura dei sistemi di calcolo può essere suddiviso in due livelli: il primo riguardante la connessione degli elementi funzionali già studiati fino a costituire sottosistemi (unità centrali di calcolo o CPU, memorie di lavoro, memorie di massa, unità periferiche ecc.); il secondo concernente invece il collegamento dei vari sotto- sistemi in un sistema di elaborazione completo.

a) L'architettura dei sottosistemi

fig. 23

Lo schema della fig. 2B è servito di base per l'illustrazione dei principi fondamentali di funzionamento degli elaboratori, la cui struttura effettiva ci proponiamo qui di sviluppare. Un primo passo è rappresentato dallo schema della fig. 23 che permette di illustrare più particolareggiatamente il funzionamento di un elaboratore, cioè il processo di esecuzione delle istruzioni.

Si supponga allora che la memoria sia stata preventivamente caricata coi dati e col programma che s'intende eseguire e che tutti i registri siano azzerati. Per iniziare il programma è necessario poter introdurre nel ‛contatore' l'indirizzo della prima istruzione del programma e si suppone che ciò possa farsi con mezzi esterni, per esempio una tastiera. In base a tale indirizzo, comunicato alla memoria, la memoria stessa legge la prima istruzione, che viene trasferita nel ‛registro delle istruzioni'. In base al contenuto di tale registro, l'organo di governo emette segnali di comando che innanzitutto ottengono il trasferimento degli operandi dalla memoria (cui viene fornito il relativo indirizzo) ai registri (A, B, C, D), successivamente fanno eseguire all'organo logico-aritmetico l'operazione voluta e infine, eventualmente, comandano il trasferimento del contenuto di uno dei registri a una cella di memoria (il cui indirizzo si trovi nell'istruzione considerata). Con ciò l'esecuzione della prima istruzione è completa. Simultaneamente a tale esecuzione, il numero sul contatore è stato incrementato di un'unità. Ripetendo pertanto la stessa sequenza di operazioni, si otterrà l'esecuzione della seconda istruzione e così via.

Un'istruzione di salto viene semplicemente ottenuta sostituendo al contenuto del contatore l'indirizzo cui il programma è rinviato (se, naturalmente, è stata verificata la condizione per cui il salto debba avvenire).

fig. 24

Dalla suddetta descrizione risulta che il funzionamento di un elaboratore può essere descritto come una successione di trasferimenti d'informazioni tra memoria e registri e tra registri; tali trasferimenti devono essere comandati con opportuni segnali emessi dall'organo di governo, in relazione al tipo d'istruzione da eseguire. Risulta allora che l'architettura interna di una macchina e il suo funziona- mento sono determinati essenzialmente dall'organo di governo, come mostra la fig. 24 nella quale è mostrato l'insieme dei registri e della memoria, l'insieme dei ‛circuiti di elaborazione' e il governo, destinati a fornire le corrette sequenze dei segnali di trasferimento. Come esempio è mostrato il circuito che ottiene la somma dei contenuti dei registri B e C e ne trasmette il risultato in C. La memoria comprende un registro di indirizzamento che determina in quale cella introdurre il dato preventivamente posto nel registro M, oppure in quale cella leggere il dato da registrare in M.

L'organo di governo può essere concepito in vari modi. I due modi più significativi sono quello a ‛rete di ritardi' e quello a ‛microprogramma'.

fig. 25

Un organo di governo del tipo a ‛rete di ritardi' è composto, come mostra la fig. 25, da una sequenza di elementi di ritardo collegata con un decodificatore che emette un impulso non appena nel registro che lo alimenta è posto il codice di un'istruzione. L'impulso si propaga lungo una delle sequenze e, comparendo all'uscita di ciascun elemento di ritardo, produce un trasferimento nella rete di elaborazione, in modo da provocare l'esecuzione dell'istruzione prescritta. Al termine di questa, viene sempre prodotto il caricamento (dal registro delle istruzioni) del codice della successiva istruzione, e così via.

Si notano, nella rete dei ritardi, alcune particolarità: la prima consiste nel confluire di due sequenze in una sola, quando le parti finali delle sequenze di più istruzioni coincidono; la seconda consiste nella biforcazione della sequenza per effetto di un segnale proveniente dalle reti di elaborazione (per es. nel caso di istruzioni di salto condizionato). Inoltre due o più segnali di uscita della rete di ritardi possono riunirsi, in quanto si richiede lo stesso trasferimento in istruzioni diverse, o in più istanti nell'esecuzione di una data istruzione.

Un'importante variante dell'unità suddetta si ha quando il ritardo tra due successivi trasferimenti lungo una sequenza, anziché essere predeterminato e fisso, è determinato da speciali circuiti nella rete di elaborazione, che permettono il comando del successivo trasferimento non appena quello precedente è completato (funzionamento ‛asincrono'). Poiché l'intervallo tra i due può dipendere dal particolare contenuto dei registri (per es., nel trasferimento attraverso un addizionatore, il caricamento del risultato che appare alla sua uscita può farsi solo quando il riporto si sia completamente propagato), nello schema della fig. 25 occorre proporzionare il relativo ritardo in modo che sia non inferiore al valore massimo di tale intervallo.

fig. 26

Il secondo tipo di organo di governo, a ‛microprogramma', è di gran lunga il più versatile e, sebbene proposto da M. V. Wilkes già nel 1951, solo nell'ultimo decennio ha trovato sempre più vasta applicazione. Lo schema di Wilkes, rappresentato nella fig. 26, è composto da un decodificatore, alimentato da un registro dove viene trasferito, all'inizio di ciascuna istruzione, il codice dell'istruzione stessa. Una delle uscite del decodificatore viene cosi attivata. Essa alimenta due matrici, A e B, ciascuna costituita dai conduttori orizzontali in uscita, dal decodificatore e da un insieme di altri conduttori (verticali) incrocianti i precedenti: i punti segnati su certi incroci stanno a indicare che un segnale proveniente da una delle uscite del decodificatore alimenta il conduttore verticale. Le uscite dalla matrice A alimentano la rete di elaborazione, mentre le uscite dalla matrice B vengono trasferite, dopo un ritardo, nello stesso registro I che alimenta il decodificatore. Di conseguenza verrà attivata un'altra uscita, un nuovo insieme di segnali verrà inviato dalla matrice A alla rete di elaborazione e un nuovo contenuto di I sarà generato dalla matrice B.

Si può dire che i segnali che ogni volta vengono emessi da A costituiscono una ‛microistruzione' che perviene alla rete di elaborazione (ciascuna microistruzione si compone di tanti ‛microordini' che provocano un dato trasferimento) e che tali microistruzioni sono registrate nella memoria costituita dalla stessa matrice A. L'indirizzamento di tali microistruzioni avviene attraverso il decodificatore alimentato dal registro I in cui vengono inviati dalla matrice B (o dal registro delle istruzioni, inizialmente) gli indirizzi delle successive microistruzioni. L'esecuzione di una data istruzione può, con altre parole, essere descritta come una successione di microistruzioni, che può chiamarsi anche il ‛microprogramma' della stessa istruzione.

L'importanza dello schema di Wilkes risiede nell'elevato grado di sistematicità con cui è possibile progettare un elaboratore che esegua un assegnato gruppo di istruzioni. Sono possibili molte varianti del sistema illustrato, ma esse non verranno qui trattate.

Un particolare commento meritano gli aspetti realizzativi delle matrici A e B, che possono concepirsi come memorie morte o a sola lettura (ROM). L'applicazione sistematica della microprogrammazione nei sistemi di elaborazione si è sviluppata quando sono state sviluppate convenienti soluzioni tecnologiche per le ROM.

È interessante notare che le ROM possono applicarsi non solo alle unità di governo microprogrammate, ma anche per contenere parti dei programmi (in particolare quelli di base) di un elaboratore, quando esse non siano soggette a modifiche. Per contro, si possono pensare unità microprogrammate nelle quali si adottino vere e proprie memorie (e cioè memorie con capacità di scrittura oltre che di lettura). Ciò permette di modificare a piacimento il microprogramma, potendo così trasformare su una data macchina le istruzioni eseguibili, allo scopo di adattarle ai vari problemi. La stessa sostituzione del microprogramma può essere ottenuta automaticamente, per effetto di uno speciale programma ausiliario o anche di una sola speciale istruzione.

I vari microprogrammi possono essere conservati nella memoria delle macchine, come qualsiasi altro dato.

b) L'architettura dei sistemi di elaborazione: il collegamento dei sottosistemi

Si può ora considerare il problema della struttura di un sistema di elaborazione, considerato come insieme di vari sottosistemi, ciascuno dei quali è internamente strutturato mediante una delle tecniche illustrate precedentemente. L'interesse del problema è dato non solo dalla ricerca di strutture che rendono massima la capacità di elaborazione con assegnati tipi di sottosistemi, ma anche dall'utilità di disporre di sistemi ‛modulari', che possono essere composti in vario modo (per es. con più moduli di memoria, oppure con più unità di calcolo, ecc.) per adattare le caratteristiche del sistema all'applicazione voluta.

Si considererà per primo il problema dei sistemi modulari, di grande importanza pratica in quanto permettono la costituzione di ‛famiglie di moduli' tra loro compatibili, coi quali si possono costruire sistemi di varia complessità, soprattutto nel caso di sistemi di piccola e media capacità elaborativa.

I moduli che vengono tra loro collegati (cioè moduli di memoria, unità periferiche come memorie a dischi, stampatrici, lettori di schede, unità di controllo di linee di trasmissione) sono da concepirsi come altrettanti elaboratori speciali di per se stessi, talvolta dotati di proprie unità di memoria e di controllo, e capaci perciò di svolgere automaticamente le operazioni loro assegnate, e talvolta invece agenti sotto il controllo di un'unica unità di governo.

fig. 27

Un esempio di quest'ultimo tipo è rappresentato nella fig. 27 che mette anche in evidenza come la funzione principale del collegamento tra diverse unità sia quella dello scambio di informazioni.

Lo schema illustrato contiene una barra (bus) per l'entrata e l'altra per l'uscita dei dati dei vari moduli che permettono il trasferimento di informazioni tra due unità qualsiasi. Esso può essere più sinteticamente rappresentato con la fig. 27B, dove il bus deve essere concepito come comprendente le funzioni di trasmissione bidirezionale dei dati tra le varie unità, sotto un unico governo. Su esso vengono immessi dati, indirizzi, segnali di controllo.

fig. 28

Lo stesso sistema può essere generalizzato come mostra la fig. 28, nella quale gli elaboratori vanno intesi sia come unità centrali di calcolo (CPU), sia come elaboratori speciali, quali moduli di memoria a disco, controlli per linee di trasmissione, ecc. La barra di trasmissione è usata per una trasmissione alla volta e viene assegnata dal ‛controllore (che comprende anche i vari circuiti di interfaccia) a seconda delle richieste dai vari moduli. Essa viene cioè usata con la tecnica detta ‛a partizione di tempo'.

Un'importante particolarità presente in molti sistemi è quella detta dell'‛accesso diretto alla memoria' (DMA) da parte di unità periferiche, per esempio unità di disco. Tale particolarità permette il trasferimento (all'unità periferica) di blocchi di dati senza il diretto intervento della CPU, che pertanto rimane libera per altri compiti.

fig. 29

Una variante degli schemi illustrati è quella della fig. 29, con due barre distinte, una per la memoria, l'altra per le unità periferiche.

figg. 30

31

Il collegamento tra elaboratori e moduli di memoria può farsi anche secondo altri sistemi, illustrati nelle figg. 30 e 31. Nella fig. 30 il collegamento avviene tramite uno schema a crossbar nel quale è possibile a ogni incrocio stabilire un collegamento tra una barra orizzontale e una verticale.

Quando il numero dei moduli da connettere cresce, il numero delle interconnessioni e la complessità costruttiva diventano presto eccessive.

Una soluzione alternativa, più semplice, è quella della fig. 31: nel nuovo schema i circuiti di commutazione sono distribuiti tra i moduli di memoria, ciascuno dei quali è costruito per essere connesso a un certo numero di elaboratori.

Un vantaggio di tale schema (a commutazione distribuita) sul precedente è dato dalla possibilità di poter variare più facilmente la configurazione anche in impianti già costruiti. Inoltre, mentre attende dati da un modulo, un elaboratore può incominciare a fare nuove richieste ad altri moduli. Lo svantaggio è dato dal numero dei cavi che fanno capo a ciascun modulo di memoria.

fig. 32

La fig. 32 mostra due sistemi, ciascuno composto da una catena di sottosistemi tipici (memorie a dischi, unità di controllo, CPU e unità di controllo delle linee di trasmissione). Il secondo sistema, però, è dotato anche di circuiti che permettono il collegamento, a scelta, con i sottosistemi adiacenti della stessa catena o con quelli dell'altra catena. In caso di guasto di uno dei sottosistemi, il sistema può essere riconfigurato (anche automaticamente) in modo che continui a funzionare, anche se con capacità ridotte.

L'architettura dei sistemi si avvale di altre tecniche quando si tratta di ottenere le massime capacità di elaborazione raggiungibili con i sottosistemi oggi disponibili e se ne vedranno ora alcuni esempi significativi, nei quali si tende a sfruttare al massimo la capacità di far funzionare in parallelo più sottosistemi.

Il primo esempio è fornito dal sistema ILLIAC IV, composto da 64 elaboratori funzionanti in parallelo e disposti ‛a matrice' (8 × 8). I 64 eleboratori, controllati da un elaboratore centrale, possono svolgere le stesse operazioni in parallelo su dati diversi. L'applicazione tipica è l'elaborazione di matrici, per esempio, per calcoli di programmazione lineare o per la soluzione di sistemi di equazioni alle derivate parziali. Il sistema è capace di eseguire 240 milioni di istruzioni di addizione per secondo.

Il secondo esempio è costituito dall'elaboratore CDC STAR (String Array), comprendente nove elaboratori per i diversi compiti: gestione del sistema operativo generale, gestione della memoria e degli apparati di entrata-uscita più un grande elaboratore centrale costruito per elaborare direttamente stringhe di dati (vettori), con unità di elaborazione detta a pipe line, capace di ricevere ed elaborare 100 milioni di parole da 32 bits al secondo. La memoria è capace di erogare 12,8 gigabits/s. È interessante notare che la concezione dello STAR è stata direttamente influenzata dal linguaggio di programmazione APL (A Programming Language).

Si è fin qui considerato quell'aspetto dell'architettura dei sistemi che è fisicamente più evidente perché concerne le modalità di connessione dei vari sottosistemi. Negli elaboratori è peraltro di grandissima importanza anche un altro aspetto della loro architettura, che considera invece il software, cioè l'insieme dei programmi indispensabili perché una macchina diventi un sistema funzionante per una data applicazione.

Tre sono le parti in cui può suddividersi il software di una macchina: il sistema ‛applicativo' (dipendente dalla particolare applicazione considerata), i ‛linguaggi' (cioè i traduttori per la traduzione del linguaggio usato in quello delle macchine), coi quali si costruiscono i programmi del tipo precedente, e il ‛programma base' o ‛sistema operativo', che gestisce l'uso delle varie risorse della macchina ed è di supporto a tutti gli altri programmi.

La struttura del sistema operativo può considerarsi strettamente legata all'architettura del sistema.

Nei sistemi della prima generazione il sistema operativo era praticamente inesistente. Con la seconda generazione di elaboratori comincia a delinearsi un embrione di sistema operativo, sotto forma di un programma capace di far eseguire automaticamente una successione di elaborazioni (lettura dei dati e del programma, ricerca e uso del relativo traduttore, stampa dei risultati); ha così origine la cosiddetta elaborazione a ‛lotti' o batch.

Con la terza generazione il sistema operativo assume importanza grandissima, perché è solo grazie a esso che possono risolversi i metodi di multielaborazione, time sharing, in sistemi di grande complessità per la presenza di vari tipi di memoria, di più elaboratori e di terminali collegati a distanza. Il meccanismo di gestione della memoria illustrato nel precedente capitolo è appunto la base di tali sistemi e viene realizzato con un adatto sistema operativo. La costruzione razionale dei sistemi operativi è oggetto attualmente d'intense ricerche e si rimanda alla letteratura specializzata per l'approfondimento del tema.

c) I microprocessori

Lo sviluppo della tecnologia dei semiconduttori ha portato alla realizzazione in forma integrata, su una sola piastrina di silicio, di un completo elaboratore, comprendente sia i circuiti logici di calcolo e di controllo sia la memoria: il ‛microprocessore'. Tale risultato è la naturale conseguenza dello sviluppo che ha già portato alle memorie a semiconduttore, con la messa a punto di procedimenti atti a ottenere piastrine di silicio di dimensioni sempre maggiori nonché circuiti elementari richiedenti aree sempre minori.

Sono oggi disponibili già alcune decine di diversi tipi di microprocessori; essi si distinguono tra loro per l'organizzazione interna, per la lunghezza della parola (4, 8, 12 o 16 bits) e per la velocità di esecuzione delle singole istruzioni (dell'ordine del microsecondo per i più veloci).

L'avvento dei microprocessori rappresenta il fatto più significativo nella tecnologia informatica di questo decennio, ed è destinato a influenzare profondamente l'architettura stessa dei sistemi di elaborazione. Essi infatti, col mettere a disposizione notevoli capacità elaborative a basso costo, inducono a costituire sistemi di calcolo nei quali l'elaborazione può essere eseguita in numerosi punti (per es. negli stessi terminali) anziché essere concentrata in pochi punti come nei sistemi attuali (‛informatica distribuita').

Un risultato dello sviluppo dei microprocessori sono i calcolatori elettronici ‛tascabili', di uso oramai molto diffuso.

13. Le reti di calcolatori

Come è stato già detto, i sistemi a time sharing costituiscono il primo esempio di un sistema di calcolo capace di servire a distanza e simultaneamente numerosi utenti tramite terminali collegati al sistema con linee telefoniche.

Il passo successivo in tale direzione è costituito dal collegamento ‛in rete' di numerosi elaboratori, anche molto distanti fra loro, in modo tale che un utente, da un qualsiasi terminale, possa accedere a scelta a uno qualsiasi degli elaboratori collegati.

Si raggiunge così una situazione simile a quella dei servizi, come quello telefonico o quello per la distribuzione dell'energia elettrica, e si può giustamente dire che la rete di calcolatori permetterà la costituzione di un nuovo servizio pubblico per la distribuzione di informazioni e di possibilità di calcolo.

Le motivazioni che spingono a realizzare un tale servizio sono numerose e si citeranno qui le principali: la possibilità di accedere a banche di dati di varia natura (il cui costo di costruzione e manutenzione impedisce che vengano riprodotte in molti centri), la convenienza di specializzare i vari elaboratori per famiglie di applicazioni (ciascuno di essi potrà costruire e mantenere una ‛programmoteca' specifica), la convenienza di ripartire il carico tra più elaboratori migliorandone l'utilizzazione, ecc.

Numerose sono le reti sperimentali in funzione o in fase di progetto. Esse possono distinguersi in reti omogenee (costituite da calcolatori tutti della stessa origine o comunque della stessa famiglia, cioè tra loro compatibili) e reti disomogenee (costituite da calcolatori diversi). Le seconde risultano in pratica le più importanti, anche perché dovrebbero permettere il collegamento tra calcolatori di diverso costruttore e di diverse epoche. La più importante rete disomogenea oggi in funzione è la rete ARPA, collegante qualche decina di calcolatori sparsi sul territorio USA. In Europa, la CEE ha promosso la costruzione di una rete analoga (EIN, European Informatic Network).

fig. 33

Lo schema di una rete di calcolatori è rappresentato nella fig. 33.

I calcolatori H (hosts) sono tra loro collegati da un sottosistema di comunicazione composto da ‛centri nodali' collegati da linee di trasmissione. I terminali di utente possono essere del tipo ‛diretto' (T_d), collegati direttamente a un centro nodale, o del tipo ‛indiretto', collegati a un host. È importante notare che i terminali diretti non dipendono da nessun host particolare, ma sono terminali della rete nel suo complesso. I terminali indiretti, invece, possono accedere ai vari hosts solo tramite l'host cui sono collegati.

Il sottosistema di comunicazione può essere basato su due diversi principi di funzionamento e cioè la ‛commutazione di linea' e la ‛commutazione di messaggio'.

La commutazione di linea è quella normalmente utilizzata nelle attuali reti telefoniche e permette il collegamento tra due qualsiasi utenti tramite la preventiva costituzione di una linea di trasmissione diretta tra i rispettivi centri nodali, ottenuta con dispositivi di commutazione automaticamente azionati dall'utente chiamante. La linea tra i due utenti viene mantenuta per tutta la durata della comunicazione.

Nelle reti a commutazione di messaggio non viene mai stabilito un collegamento diretto e permanente tra due utenti: infatti la trasmissione di un messaggio da un utente all'altro avviene con l'invio al centro nodale connesso coll'utente trasmittente di un ‛messaggio' (costituito da un treno di impulsi) nel quale è compreso, oltre al testo da far pervenire a destinazione, anche l'‛indinzzo' della destinazione stessa. Il centro nodale (costituito da un calcolatore appositamente programmato), una volta ricevuto il messaggio, esamina l'indirizzo di destinazione e invia il messaggio a uno degli altri centri nodali, che ripete l'operazione fino a che il messaggio giunge al centro di destinazione. Il funzionamento di una rete a commutazione di messaggio deve tener conto di strategie di istradamento che tendono a evitare congestioni di traffico, anche nel caso che uno o più collegamenti risultino fuori servizio.

Un ulteriore problema deriva dal fatto che, mentre i messaggi che due utenti si scambiano possono risultare di lunghezza qualsiasi, i messaggi sulle linee di trasmissione tra i centri nodali non possono avere una lunghezza superiore a un certo limite, a causa degli errori di trasmissione la cui probabilità cresce con la lunghezza del messaggio.

I centri nodali devono pertanto provvedere a suddividere in partenza il messaggio dell'utente in ‛pacchetti' e a trasmetterli come messaggi indipendenti; il centro nodale ricevente deve riunirli nel corretto ordine prima di consegnarli al terminale ricevente. Le reti a commutazione di messaggio offrono qualità di flessibilità che le rendono particolarmente adatte al collegamento di calcolatori, tuttavia non tutti i problemi che tali reti presentano sono ancota stati sufficientemente chiariti e le sperimentazioni in corso hanno anche tale scopo.

Una tendenza di sviluppo che si considera a scadenza più lunga è quella delle reti di trasmissione in cui tutte le informazioni, comprese quelle vocali, avvengono sotto forma codificata, con la tecnica PCM (Pulse Code Modulation). Tale tecnica è oggi utilizzata per il collegamento tra centrali telefoniche e si può prevedere che, con l'avvento delle centrali telefoniche di tipo elettronico, tutte le informazioni saranno manipolate, sia per la trasmissione sia per la commutazione, sotto forma d'impulsi (reti integrate).

Le reti di calcolatori richiedono anche la definizione di adatte procedure o ‛protocolli' che regolino lo scambio di messaggi tra processi di calcolo presenti in diversi calcolatori. La definizione formale dei protocolli costituisce un tema di ricerca che solo recentemente si è cominciato a considerare e che richiederà uno sviluppo adeguato per fornire sicuri fondamenti teorici alla costruzione e al funzionamento delle reti di calcolatori.

Bibliografia

Backus, I. W., The syntax and semantics of the proposed international algebraic language, in Proceedings of the International Conference on Information Processing, Paris 1959, pp. 125-132.

Bowden, B. V., Faster than thought, London 1953.

Chomsky, A. N., Aspects of the theory of syntax, Cambridge, Mass., 1965 (tr. it.: Aspetti della teoria della sintassi, in Saggi linguistici, vol. II, Torino 1970, pp. 41-258).

Harker, M. J., Chang, H., Magnetic disks for bulk storage. Past and future, in Spring joint computer conference, 1972, pp. 945-955.

Lucas, P., Walk, K., On the formal description of PL/I, in Annual review in automatic programming (a cura di L. Bolliet), vol. VI, New York 1969, pp. 105-182.

Matick, R. E., Review of current proposed technologies for mass storage systems, in ‟Proceedings of the Institute of Electrical and Electronics Engineers", 1972, LX, pp. 266-289.

Matison, J., The tunnelling cryotron. A superconductive ferroelectric element memory device, in ‟Proceedings of the Institute of Electrical and Electronics Engineers", LV, pp. 172-180.

Rudenberg, H. G., Approaching the minicomputer on a silicon chip. Progress and expectations for LSI circuits, in Spring joint computer conference, 1972, p. 775.

Toschi, R., Neri, A., Tecniche di microprogrammazione, in ‟Alta frequenza", 1973, XLII, 9, pp. 451-460.

Trakhtenbrot, B. A., Algorithms and automatic computing machines, Boston 1963.

Turing, A. M., On computable numbers, with an application to the Entscheidungsproblem, in ‟Proceedings of the London Mathematical Society" (II Series), 1936-1937, XLII, pp. 230-265.

Wilkes, M. V., The best way to design an automatic calculation machine, in Manchester University Computer Inaugural Conference Proceedings, Manchester 1951, p. 16.

Zemanek, H., Some philosophical aspect of information processing, in The skyline of information processing, Amsterdam 1973, p. 93.

Organizzazione e gestione dei calcolatori

di Peter J. Denning

sommario: 1. Introduzione. 2. Organizzazione dell'hardware. a) Hardware di base. b) La memoria; c) Lelaboratore; d) Ingresso e uscita (I/O). 3. Organizzazione del sistema operativo di un elaboratore. a) Che cosa è un sistema operativo. b) Eementi di struttura dei sistemi; c) Progettazione di un sistema operativo. □ Bibliografia.

1. Introduzione

È invalso l'uso di suddividere l'era dell'elaborazione elettronica in ‛generazioni'. Gli elaboratori elettronici della prima generazione furono sviluppati fra il 1940 e il 1950. La seconda generazione si ebbe fra il 1950 e il 1964. La generazione degli odierni elaboratori è la terza e si riserva la denominazione di ‛terza avanzata' per indicare la generazione cui appartengono gli elaboratori sviluppati dopo il 1968. Le caratteristiche principali che contraddistinguono le diverse generazioni sono riportate nella tab. I. Il termine ‛generazione' fu introdotto nell'uso corrente all'inizio della terza generazione, nel 1964. Sebbene originariamente il termine venisse utilizzato per indicare le differenze tecnologiche delle apparecchiature elettroniche (hardware), in seguito si è finito con l'applicarlo all'intero sistema composto dall'hardware e dai programmi operativi (software) piuttosto che al solo hardware. D'altra parte gli utenti stessi, quando pensano alla ‛macchina', hanno in mente l'intero sistema hardware-software piuttosto che il solo hardware, dal momento che raramente (se non mai) si esegue un calcolo senza l'assistenza di speciali programmi forniti dal sistema, che vanno sotto il nome di ‛sistema operativo'.

La trattazione che segue è stata articolata in due parti principali. La prima tratta dell'organizzazione dell'hardware, o architettura, di un sistema di elaborazione: i componenti principali, il meccanismo centrale e un metodo per eseguire un programma memorizzato nella macchina. La seconda tratta dell'organizzazione del sistema operativo di un elaboratore: le caratteristiche principali, il controllo dell'esecuzione dei programmi, l'amministrazione delle risorse (particolarmente della memoria), la possibilità di eseguire più programmi simultaneamente (multiprogrammazione) e un esempio di esecuzione di un semplice programma.

2. Organizzazione dell'hardware

L'hardware di un sistema di calcolo si può suddividere in tre parti: elaboratori, memorie e apparati di ingresso/uscita, I/O, dall'inglese input/output. Un elaboratore è un dispositivo che esegue le varie fasi di un programma, secondo le specifiche fornite da una serie di istruzioni. Una memoria è un dispositivo che immagazzina le rappresentazioni codificate dei programmi e i dati su cui i programmi devono operare. Le apparecchiature di I/O consistono di varie interfacce che permettono il colloquio fra l'utente e il sistema.

La maggior parte dei sistemi di calcolo, specialmente quelli dotati di molte memorie e di molti dispositivi di I/O, si avvalgono di due tipi di elaboratori. Il primo tipo, comunemente denominato ‛unità di elaborazione centrale' (CPU, dall'inglese Central Processing Unit), viene utilizzato per eseguire programmi che effettuano operazioni aritmetiche e booleane sui dati. L'altro tipo, denominato ‛elaboratore periferico', o ‛controllore di I/O', o ‛canale', viene utilizzato per eseguire programmi la cui funzione consiste nel controllo del trasferimento dell'informazione fra i dispositivi di memoria e quelli di I/O. Alcuni grossi sistemi contengono diversi elaboratori di entrambi i tipi. Il motivo per cui si includono diversi elaboratori con diverse funzioni nello stesso sistema è quello di permettere la simultaneità delle operazioni che agiscono sulla memoria e sugli apparati di I/O, aumentando così la velocità e la capacità del sistema. Molti sistemi di piccole dimensioni (ad esempio i ‛mini-elaboratori') combinano le funzioni di elaborazione centrale e periferica in una singola unità di elaborazione, riducendo così il costo, ma anche la capacità.

La maggior parte dei sistemi di elaborazione contengono molti dispositivi di memoria, sistemati in una ‛gerarchia di memorie', o ‛memoria a più livelli'. I livelli della gerarchia di memorie sono generalmente raggruppati in due classi: la ‛memoria centrale' e la ‛memoria ausiliaria'. La caratteristica fondamentale della memoria centrale è ‛l'elevatissima velocità, accompagnata da un alto costo per unità memorizzata; viene utilizzata per tenere i programmi e i dati che devono essere a disposizione immediata dell'elaboratore. La memoria ausiliaria ha la caratteristica di essere più lenta e molto meno costosa per unità memorizzata; viene utilizzata come magazzino di riserva, per memorizzare programmi e dati per i quali non v'è necessità che siano disponibili immediatamente per l'elaborazione, e come magazzino per dati molto numerosi da tenere memorizzati per lungo tempo 0 indefinitamente.

Il motivo per cui si utilizzano memorie su due o più livelli è quello di trovare un compromesso fra velocità e capacità, condizionatamente ai vincoli imposti dal costo. Mediante attenta progettazione si possono ottenere velocità di memoria quasi uguali a quella della memoria centrale a un costo medio per unità memorizzata che è quasi uguale a quello della memoria ausiliaria. Per esempio, si consideri un sistema con 100 unità di memorizzazione, 99 delle quali siano di memoria ausiliaria e 1 di memoria centrale. Si supponga che la memoria centrale sia 10 volte più costosa di quella ausiliaria e 1.000 volte più veloce e si supponga che la probabilità di trovare l'informazione desiderata nella memoria centrale sia del 99% (questi numeri sono di un ordine di grandezza corretto per sistemi di medie e grosse dimensioni). Questa configurazione opera a una velocità media 100 volte maggiore di quella della memoria ausiliaria e costa soltanto il 90% in più di 100 unità di memoria ausiliaria, mentre, se tutte e 100 le unità fossero di memoria centrale, si avrebbe una capacità di memorizzazione minore quasi di un fattore 10, a parità di costo. La configurazione di memoria a più livelli è, pertanto, un principio della progettazione di sistemi e tale rimarrà fintanto che i costi per unità memorizzata saranno minori per memorie più lente che per memorie più veloci.

La maggior parte dei sistemi di elaborazione contiene numerosi tipi di apparecchiature di I/O, in relazione alle necessità degli utenti. Queste unità consistono di lettori e perforatrici di schede, lettori e perforatrici di nastri di carta, unità di registrazione e lettura di nastri magnetici, stampatrici, visualizzatori grafici, telescriventi per fornire istruzioni e ricevere messaggi e interfacce di telecomunicazione per altri calcolatori.

Nei paragrafi successivi si descriverà in maggior dettaglio ciascuna delle tre categorie in cui è suddiviso l'hardware. È opportuno iniziare la trattazione con una rassegna dei principi dell'hardware del calcolatore. Conviene pure anteporre la descrizione dei dispositivi di memorizzazione a quella degli elaboratori e delle apparecchiature di I/O.

a) Hardware di base

1. Uno sguardo in generale. - In tutte le macchine calcolatrici è possibile identificare quattro funzioni fondamentali. La funzione di ‛memorizzazione' riguarda i dati in ingresso e in uscita e tutti gli altri dati di un programma; è pure utilizzata generalmente per sostenere una rappresentazione codificata delle istruzioni che costituiscono il programma. La funzione di ‛elaborazione' realizza i tipi di istruzioni fondamentali che la macchina è in grado di eseguire; opera sui dati effettuando ordinatamente su di essi le operazioni di ciascuna istruzione. La funzione di ‛controllo' assicura la corretta sequenza di tutte le operazioni; in particolare assicura che le istruzioni del programma vengano eseguite nell'ordine corretto e che i dati vengano trasferiti dalle memorie alle unità di hardware che realizzano le istruzioni. La funzione di ‛ingresso/uscita' trasferisce i dati dal calcolatore al mondo esterno e viceversa, effettuando la conversione delle rappresentazioni esterne comprensibili dagli utenti nelle rappresentazioni interne utilizzate dalla macchina e viceversa. Raramente le quattro funzioni sono dislocate in parti del sistema fisicamente separate; la maggior parte degli elaboratori, delle memorie e degli apparati di I/O contiene quelle parti del!a funzione di controllo che agiscono specificamente su di essi e molti elaboratori e apparati di I/O contengono dei registri speciali per memorizzare informazioni utili localmente.

Il ‛sistema binario', in cui tutte le quantità sono rappresentate da sequenze di bits (cioè di cifre o e 1), è universalmente accettato come base delle rappresentazioni interne delle macchine. La ragione fondamentale di ciò risiede nell'affidabilità dei dispositivi di calcolo. In una macchina binaria i circuiti di base trattano soltanto due valori di segnale (generalmente denominati 0 e 1) che corrispondono alle due condizioni di non passaggio di corrente' e ‛passaggio di corrente'. Il problema tecnico di costruire dispositivi che rispondano a queste due sole condizioni è assai più semplice di quello di costruire dispositivi che distinguano e rispondano correttamente a tre o più condizioni di flusso di corrente. Oggigiorno non esiste una tecnologia per costruire circuiti integrati i cui componenti trattino più di due condizioni di flusso di corrente, mentre si possono comunemente trovare circuiti di grande affidabilità comprendenti 1.000 o più componenti contenuti in un'area di 0,1 cm² con 2 condizioni di flusso.

È ormai invalso universalmente l'uso di codificare sia il programma, sia i suoi dati, prima di inserirli nella memoria di un calcolatore. Pertanto la funzione di controllo deve comprendere un meccanismo adatto per decodificare le istruzioni così rappresentate. Questa caratteristica consente a un calcolatore di avere applicazione universale, cioè di poter eseguire qualunque programma assegnato. Tali macchine sono state definite ‛macchine a programma memorizzato', in contrapposizione alle ‛macchine a programma cablato' utilizzate all'epoca dei primi calcolatori, quando l'operatore doveva programmare la macchina mediante cavi e connettori. Gli odierni calcolatori elettronici tascabili sono un esempio di ‛macchina a programma fisso' per applicazioni speciali. Queste macchine non sono in grado di memorizzare un qualunque programma, ma forniscono funzioni determinate in risposta alle battute dell'utente sulla tastiera.

fig. 1

2. Circuiti-porta. - Come si è accennato prima, i circuiti elettronici utilizzati per gli apparati di calcolo sono progettati per rivelare e rispondere alle condizioni di corrente o e 1. I componenti elementari di questi circuiti si chiamano ‛porte' e commutano le condizioni di flusso di corrente alla loro uscita su 1 o 0 a seconda delle condizioni di corrente presenti al loro ingresso. I tre tipi più comuni di porta si chiamano AND, OR e NOT (v. fig. 1). La porta AND genera una corrente in uscita se e soltanto se tutti i suoi ingressi sono in stato di conduzione. La porta OR genera una corrente in uscita se e soltanto se almeno uno dei suoi ingressi è in stato di conduzione. La porta NOT genera una corrente in uscita se e soltanto se non vi è corrente al suo ingresso (questo circuito viene spesso chiamato porta ‛invertitrice' o ‛complementare'). Le notazioni che descrivono la funzione di ciascuna porta nella fig. 1 sono un esempio di espressioni dell'algebra booleana; questa denominazione è entrata nell'uso corrente da quando Cl. Shannon, nel 1938, si accorse che la teoria dei circuiti di commutazione è isomorfa alla logica delle proposizioni studiata dal logico G. Boole nel 1854. A causa di ciò, le reti di porte vengono frequentemente chiamate ‛circuiti logici' e la parte fondamentale dell'hardware di un calcolatore viene spesso chiamata ‛hardware logico',

fig. 2

Si consideri ora una rete non ciclica di porte AND, OR e NOT, come esemplificato nella fig. 2. Poiché la rete non ha diramazioni di ritorno, una certa configurazione di uscita Y = (y₁, y₂, ... y_m) verrà generata dalla rete dopo un breve tempo (chiamato ‛tempo di commutazione') da quando si è presentata in ingresso una configurazione X = (x₁, x₂, ..., x_n). Una configurazione di ingresso o di uscita è definita dall'insieme dei valori 0 e 1 presenti a ciascun ingresso o uscita. Nella fig. 2 vi sono 2ⁿ possibili configurazioni in ingresso e 2^m possibili configurazioni in uscita. La rete della fig. 2 evidentemente realizza una funzione (denominata funzione ‛di commutazione' o ‛booleana') Y = − F(X) che mette in corrispondenza la configurazione di ingresso con quella di uscita. Un risultato fondamentale della teoria delle commutazioni è che esiste sempre un circuito composto di sole porte AND, OR e NOT che permette di realizzare una qualunque funzione di commutazione (v. Kohavi, 1970).

fig. 3

Inoltre è possibile associare un'unica espressione algebrica a un dato circuito non ciclico di porte. Poiché vi sono molte espressioni (cioè circuiti) che realizzano la stessa funzione di commutazione, sono state sviluppate diverse teorie per escogitare il modo di impiegare il minor numero possibile di porte (ibid.). La fig. 3 mostra un esempio in cui l'espressione in uscita viene ottenuta specificando di volta in volta le uscite di ciascuna porta, procedendo dagli ingressi verso le uscite del circuito (la barra sopra un simbolo ne indica il complementare, cioè 0 se x = 1 e 1 se x = 0).

fig. 4

La fig. 4 esemplifica un altro problema cui la teoria delle commutazioni fornisce una soluzione. Nella figura è rappresentata una funzione F(x) = x + x sempre uguale a 1. Si può allora verificare che, se entrambe le porte hanno tempo di commutazione T; una variazione di x dal valore 1 al valore 0 produce un'uscita parassita 0 di durata T, dovuta al fatto che il segnale viene ritardato nel passaggio attraverso la porta NOT. Questa circostanza viene chiamata ‛azzardo'. Se in un circuito avviene un azzardo, possono sempre conseguirne ritardi di propagazione non coordinati in diverse parti di un circuito in seguito a variazioni in ingresso che non dovrebbero produrre alcuna variazione del segnale in uscita. La teoria insegna come realizzare funzioni di commutazione prive di azzardi, senza bisogno di inserire ritardi di compensazione nei circuiti (ibid.).

I circuiti che realizzano le funzioni di commutazione sono spesso chiamati ‛circuiti combinatori', poiché l'uscita è ottenuta combinando i dati presenti in ingresso secondo i percorsi e le porte presenti nel circuito. Questo termine pone in contrapposizione questi semplici circuiti con i ‛circuiti sequenziali' di cui si dirà al prossimo punto. In questi ultimi l'uscita non è più una semplice combinazione dei dati presenti in ingresso, ma è una funzione dell'intera sequenza di dati che si sono succeduti in ingresso.

3. Circuiti sequenziali. - I circuiti di commutazione descritti finora sono caratterizzati da una relazione funzionale fra ingresso e uscita: prescindendo dai ritardi di commutazione del circuito, il risultato in uscita dipende soltanto dai dati presenti in ingresso. Si descriveranno ora dei circuiti i cui dati di uscita dipendono sia dai dati presenti in ingresso, sia da quelli che sono stati forniti in ingresso in precedenza. Poiché tali circuiti possono essere descritti come se generassero sequenze di uscite che dipendono da sequenze di ingressi, questi circuiti vengono denominati circuiti sequenziali.

fig. 5

La differenza fondamentale fra i semplici circuiti combinatori del paragrafo precedente e i circuiti sequenziali è che i primi non contengono rami di ritorno, mentre i secondi li contengono. A causa di questi rami di ritorno, i segnali di uscita possono essere immessi nuovamente nel circuito, influenzando così i futuri segnali di uscita e dando possibilità di memorizzare i segnali di ingresso passati. La fig. 5 illustra queste considerazioni. In essa un circuito generico viene supposto come composto da una parte priva di ramo di ritorno che realizza una funzione di commutazione mediante semplici circuiti combinatori e da alcune linee lungo le quali alcuni segnali di uscita vengono reinseriti in ingresso con certi ritardi. Poiché il circuito ora opera in modo dipendente dal tempo, si deve associare a ciascun valore del segnale il parametro tempo (t). È opportuno assumere (senza tuttavia perdere di generalità) come unità di tempo il ritardo introdotto dalle linee di ritorno e considerare trascurabile il tempo di commutazione della rete combinatoria F; in tal caso sarà sufficiente definire il comportamento del circuito soltanto agli istanti di tempo t = 0, 1, 2 ... I valori di V = (v₁, v₂, . . . , v_k) all'istante t definiscono lo ‛stato' del circuito al tempo t. Dati V(0) e la sequenza di segnali in ingresso X(t), per t > 0, si possono determinare uscite e stati a ogni istante di tempo successivo valutando iterativamente le equazioni: [U(t), Y(t)] = F[X(t), V(t)] e V(t + 1) = U(t). Poiché vi sono 2^k possibili stati di questo circuito, la funzione di transizione dello stato (che fornisce il nuovo stato V partendo dall'ultimo stato di V e dagli ultimi segnali in ingresso X) può essere rappresentata come una tabella con 2^k righe (per i possibili stati) e 2ⁿ colonne (per i possibili ingressi, essendo n la dimensione di X(t)). Circuiti come quello illustrato si dicono anche ‛macchine a stati finiti', per ovvi motivi.

La teoria delle macchine sequenziali tratta problemi del tipo: a) ricerca della funzione di transizione di stato per un dato circuito; b) ricerca di un circuito che realizzi una funzione di transizione di stato arbitrariamente assegnata; c) ricerca di un altro circuito equivalente a uno dato (che, cioè, si comporti in maniera identica rispetto all'uscita) ma che richieda il minor numero possibile di stati; d) ricerca ed eliminazione di eventuali azzardi in transizioni di stato; e) ricerca di gruppi di sequenze d'ingresso che conducano a un particolare stato. Questi sono soltanto alcuni dei molti problemi affrontati dalla teoria. Infatti la teoria delle macchine a stati finiti costituisce la base della teoria dell'automatismo finito, che caratterizza la potenza di calcolo di tali circuiti (v. Kohavi, 1970; v. Hellerman, 1967; v. Minsky, 1967).

4. Il principio della progettazione modulare. - Un principio fondamentale di ogni progettazione è la scomposizione del problema in pochi componenti, facilmente comprensibili; per ciascun componente si progetta un sottosistema e quindi si combinano tutti i sottosistemi per formare il sistema che risolve il problema originale. Questo principio viene utilizzato largamente nella progettazione dell'hardware di un calcolatore. Nelle situazioni pratiche di progettazione, obiettivi come la modularità, la possibilità di effettuare facilmente modifiche, di diagnosticare gli errori, di effettuare la manutenzione e di localizzare sottosistemi critici che necessitino di ottimizzazione, sono ritenuti di gran lunga più importanti dell'obiettivo di realizzare dispositivi con il minimo numero di porte. Pertanto i risultati della teoria della commutazione riguardanti la minimizzazione dei circuiti non si applicano universalmente. Invece le industrie producono una grande varietà di componenti funzionali che possono essere utilizzati dai progettisti per realizzare sottosistemi maggiori a partire da sottosistemi più piccoli.

fig. 6

Un esempio di componente utilizzato frequentemente è il flip-flop. Esso consiste di un circuito sequenziale a due stati (v. fig. 6) capace di memorizzare un singolo bit. L'uscita Y è il valore selezionato dal flip-flop (cioè il suo stato). Nella configurazione di riposo gli ingressi S ed R hanno entrambi il valore 0. Quando l'ingresso S (‛attivazione') riceve un ‛impulso' (cioè un segnale di breve durata che sale da 0 a 1 e quindi torna a 0) il flip-flop entra nello stato Y = 1 (il che si indica come ‛attivazione del flip-flop'). Quando un impulso viene ricevuto all'ingresso R (‛azzeramento') il flip-flop entra nello stato Y = 0 (il che si indica come ‛azzeramento del flip-flop'). Nessun cambiamento di stato avviene finché S ed R hanno il valore 0. I flìp-flops più semplici non sono in grado di dare risposta sensata se entrambi i segnali in S ed R valgono 1, quando cioè i circuiti che li controllano tendono ad attivare e azzerare simultaneamente. Vi sono dei flip-flops più complessi nei quali la combinazione S = 1 ed R = 1 causa l'inversione dello stato. Alcuni flip-flops hanno un ingresso T (‛scatto') che causa l'inversione dello stato. Tutti i flip-flops producono anche l'uscita complementare Y̅; la richiesta di segnali complementari è altrettanto grande quanto la richiesta dei segnali stessi e i circuiti flip-flop producono con altrettanta facilità sia Y che Y̅  (v. Hellerman, 1967; v. Kohavi, 1970).

7A

Come si vede, i flip-flops producono segnali di uscita il cui valore è costante (tali segnali vengono chiamati ‛segnali di livello'); ma essi sono pilotati da ‛segnali pulsati', cioè da segnali di valore eguale a 1 di breve durata. La fig. 7A illustra come un segnale di livello (indicato con una freccia bianca) può essere memorizzato in un flip-flop quando viene applicato un segnale pulsato (indicato con una freccia nera) all'ingresso denominato STORE. Nel caso siano disponibili sia l'ingresso x che l'ingresso x̅, si può utilizzare il più semplice circuito della fig. 7B.

fig. 8

Si è accennato in precedenza che i calcolatori trattano sequenze di bits. Il valore di una particolare sequenza di n bits può essere memorizzato in un gruppo di n flip-flops, che viene chiamato ‛registro'. La fig. 8 mostra un tipo generale di registro, insieme con ingressi pulsati che permettono di effettuare varie operazioni sul ‛contenuto' del registro (cioè sui valori memorizzati nei suoi flip-flops). I tipi di operazione sono illustrati nella tab. II. I valori degli ingressi x e delle uscite y all'istante t sono denotati rispettivamente x_n-1x_n-2 ... x₁x₀ e y_n-1y_n-1y₀. Il segnale centrale viene applicato all'istante t e il registro impiega un'unità di tempo per completare l'operazione iniziata dal segnale di controllo. Si osservi che, se y_n-1y_n-2 ... y₁y₀ viene interpretato come un numero intero secondo il sistema binario, cioè

lo slittamento a sinistra corrisponde a calcolare 2ⁿ mod 2ⁿ (resto della divisione di 2ⁿ per 2ⁿ) e lo slittamento a destra la parte intera di N/2; queste due operazioni fondamentali vengono utilizzate nella costruzione di dispositivi per la moltiplicazione e la divisione. Le operazioni stesse sono realizzate mediante reti di porte AND e OR connesse fra i flip-flops del registro. Non tutti i registri eseguono tutte le operazioni menzionate nella fig. 8, ma tutti eseguono almeno l'operazione STORE (v. Hellerman, 1967).

fig. 9

Un altro esempio di utile componente è il ‛contatore', mostrato nella fig. 9. Esso consiste di un certo numero n di flip-flops insieme con i relativi circuiti. Il contenuto del flip-flop è considerato come un numero binario intero N, nel senso descritto prima. L'operazione CLEAR pone N = 0, l'operazione ‛+ 1' dispone il contenuto del contatore al valore N + 1 mod 2ⁿ e l'operazione ‛-1' dispone il contenuto del contatore al valore N − 1 mod 2ⁿ. L'operazione STORE può essere utilizzata per disporre il contatore a un certo valore iniziale x_n-1x_n-2 ... x₁x₀.

fig. 10

fig. 11

Come già notato, i segnali di una macchina calcolatrice sono di due tipi. I segnali pulsati vengono generati dalla ‛unità di controllo' del calcolatore; essi vengono utilizzati per dare il via alle operazioni che vengono realizzate dalle ‛unità funzionali'. I segnali di livello vengono generati dai flip-flops o da reti combinatorie i cui ingressi sono dei flip-flops; essi generalmente rappresentano i bits delle sequenze binarie relative ai dati su cui vengono applicate le operazioni. La fig. 10 illustra il concetto di unità di controllo. Essa possiede ingressi di livello, che la informano sulle condizioni delle altre parti della macchina, e un ingresso temporizzatore che comprende un treno di impulsi regolarmente spaziati, la cui separazione viene assunta come unità base dei tempi. L'unità di controllo fornisce uscite pulsate che ritornano verso le altre parti della macchina. La fig. 11 illustra il concetto di unità funzionale. Appena ricevuto un segnale START dall'unità di controllo, l'unità funzionale inizia la sua operazione, utilizzando i valori di ingresso memorizzati nel suo o nei suoi registri. Dopo un tempo conveniente T, l'unità di controllo emette un segnale STORE che comanda la memorizzazione dell'uscita dell'unità funzionale su un registro di uscita. Nel caso in cui il tempo operativo T dipenda dai dati di ingresso, l'unità funzionale può contenere un'uscita condizionale (denominata DONE nella fig. 11) mediante cui notifica all'unità di controllo che l'operazione è stata completata. Lo scambio fra le unità di controllo e di funzione di un semplice elaboratore saranno illustrate più in dettagiio nel segnito, quando si presenterà lo schema di un elaboratore. Dettagli sulle tecniche di codificazione di numeri, simboli e istruzioni in forma di sequenze binarie, nonché sulla costruzione di unità funzionali (specialmente aritmetiche) che agiscono direttamente sui codici binari, possono essere trovati nel testo di Hellerman citato in bibliografia (v., 1967).

b) La memoria

1. Tecniche di indirizzamento. - Il termine ‛memoria' indica tutti gli elementi di un calcolatore che vengono utilizzati per immagazzinare informazione. Nella sua essenza la funzione della memoria è quella di memorizzare un'associazione fra un nome e un valore, cioè di realizzare la funzione c : X → V  fra un insieme di nomi X e un insieme di valori V. Nella maggior parte degli hardwares ciascun nome x dell'insieme X è associato con un'unica posizione della macchina; in tal caso ciascuno di tali x viene spesso chiamato un ‛indirizzo' e l'insieme X è chiamato lo ‛spazio degli indirizzi' di memoria. Il valore memorizzato, cioè associato con l'indirizzo x, è denotato con v = c(x) e c(x) è chiamato ‛il contenuto di x'.

Come per tutte le quantità in un calcolatore, gli indirizzi e i valori sono codificati come sequenze binarie (chiamate anche ‛parole' binarie). Se n è il numero di bits della parola relativa al valore e k il numero di bits della parola relativa all'indirizzo, il numero massimo di locazioni distinte sarà 2^k e il contenuto di ciascuna di esse sarà uno dei 2ⁿ possibili valori distinti. I valori di k variano fra 8 bits nei minicalcolatori e 24 bits nei calcolatori molto grandi; i valori più tipici sono compresi fra 12 e 18. I valori di n variano fra 12 e 60 e i più comuni sono 32 e 36. Nel caso comune in cui ciascun indirizzo x dell'insieme {o, 1,..., 2^k−1} denota una posizione, è conveniente immaginare le posizioni di memoria come un vettore Mem [0, 1, ..., 2^k−1], dove Mem[x] denota la posizione il cui indirizzo è x.

fig. 12

La fig. 12 illustra lo schema funzionale di una memoria. L'indirizzo x è specificato in un registro degli indirizzi di memoria denominato MAR (da Memory Address Register). Vi è poi un registro tampone MBR (da Memory Buffer Register) che, durante un'operazione READ, riceve il valore c(x) da Mem[x], mentre durante un'operazione STORE specifica un nuovo valore c(x) da inviare a Mem[x]. Utilizzando la notazione R₁ ← R₂ per significare l'operazione di trasferimento di registro (cioè ‛porre c(R₁) uguale a c(R₂)'), le operazioni di lettura e scrittura si possono specificare esattamente come:

READ: MBR ← Mem[MAR]

WRITE: Mem[MAR] ← MBR.

Naturalmente queste operazioni richiedono un certo tempo, chiamato ‛tempo d'accesso', che dipende dalla tecnologia utilizzata per realizzare la memoria. Le memorie che hanno tempo di accesso variabile possono segnalare l'avvenuta esecuzione dell'operazione mediante un'uscita condizionale quale la DONE della fig. 12. Normalmente, più breve è il tempo di accesso, più alto è il costo per bit memorizzato.

La memoria finora descritta è organizzata secondo il principio di associare in maniera biunivoca gli indirizzi X e le locazioni di memoria. Un principio alternativo porta alla definizione delle ‛memorie associative'. In queste ciascuna locazione contiene n + k bits, k dei quali vengono utilizzati per l'indirizzo x dell'insieme X e i rimanenti n per un valore v dell'insieme V. In altre parole, il contenuto di una locazione ha la forma (x, v). Durante un'operazione READ in cui c(MAR) = x, vengono esaminate tutte le locazioni per trovarne una della forma (x, v). Se ne viene trovata una, il valore v viene copiato in MBR; altrimenti se ne segnala la mancanza. Durante un'operazione WRITE in cui c(MAR) = x, vengono esaminate tutte le locazioni per trovarne una della forma (x, v). Se ne viene trovata una, il valore v viene sostituito da c(MBR); altrimenti (x, v) viene collocato in una locazione libera. L'operazione FREE, che rende libera una locazione, viene effettuata nel seguente modo: se è x = c(MAR) e una certa locazione è occupata da (x, v), quella locazione viene posta al valore (0, 0). Evidentemente non vi è alcuna corrispondenza precostituita fra indirizzi e locazioni. Si ha il vantaggio che solamente gli elementi utili di X (cioè quelli cui è stato assegnato un valore) richiedono memorizzazione. Lo svantaggio consiste nella necessità di ricercare la locazione definita da c(MAR). Se tale ricerca viene effettuata linearmente, i tempi di esecuzione sono lunghi; se la ricerca viene effettuata in parallelo su tutte le locazioni i tempi sono brevissimi, ma l'hardware diviene estremamente complesso. In generale le memorie convenzionali sono considerate più efficienti delle memorie associative, sebbene delle piccole memorie associative si siano dimostrate utili per certe applicazioni, come la realizzazione di memorie virtuali (v. Denning, 1970).

2. Dispositivi di memorizzazione. - Un dispositivo di memorizzazione e a ‛indirizzo posizionale' quando, in generale, utilizza un movimento meccanico per stabilire la corrispondenza fra la locazione specificata dal registro degli indirizzi MAR e il registro tampone MBR. Ciò si può ottenere sia muovendo una testina di lettura/scrittura sulla locazione indirizzata (come con i dischi a braccio mobile), sia muovendo il mezzo di memorizzazione in modo da portare la locazione indirizzata in corrispondenza delle testine di lettura/scrittura (come con i tamburi magnetici rotanti, o con i nastri magnetici), sia combinando i due movimenti. In queste memorie il tempo di accesso a una voce è variabile e dipende dalla sua posizione nel mezzo di memorizzazione in rapporto alla posizione delle testine di lettura/scrittura nel momento in cui l'operazione di accesso (lettura o scrittura) s'inizia. Un dispositivo di memorizzazione si dice ad ‛accesso casuale' se il tempo di accesso è lo stesso per tutte le locazioni. Dischi, tamburi e nastri sono esempi di dispositivi ad accesso posizionale; registri a flip-flop e memorie a nuclei magnetici sono esempi di dispositivi ad accesso casuale.

La maggior parte delle memorie ad accesso casuale utilizzano qualche forma di commutazione elettronica per indirizzare una locazione: ne risultano tempi d'accesso molto brevi e fissi. Valori tipici per il tempo d'accesso di una memoria con registri a flip-flop sono inferiori a 100 microsecondi; per una memoria a nuclei magnetici il tempo d'accesso è dell'ordine di un microsecondo (il tempo d'accesso viene anche chiamato ‛tempo di ciclo di memoria'). La maggior parte delle memorie ad accesso posizionale hanno tempi d'accesso maggiori e variabili, da una media di 100 millisecondi per i tamburi piu veloci fino a oltre 300 millisecondi per dischi a braccio mobile.

I principî in base a cui lavorano i principali dispositivi di memorizzazione sono brevemente illustrati qui di seguito, mentre per i dettagli si rimanda alla bibliografia (v. Burroughs Corp., 1969²; v. Hellerman, 1967).

Considereremo dapprima i registri a flip-flop e le memorie a nuclei magnetici. Nei primi una locazione è costituita semplicemente da un registro a n bits, nelle seconde da un insieme di n nuclei. Un circuito combinatorio chiamato ‛decodificatore' seleziona una delle 2^k locazioni (assumendo indirizzi di k bits). Il decodificatore possiede k ingressi (che ricevono dati dal MAR) e 2^k uscite; esso genera un 1 sull'i-esima uscita se e soltanto se la configurazione in ingresso consiste della codificazione binaria del numero intero i (cioè i = c(MAR)). Nel caso di una memoria a registro a flip-flop, si possono direttamente utilizzare circuiti a porta per stabilire la connessione fra il registro selettore e l'MBR.

Una memoria a nuclei magnetici contenente 2^k voci di n bits comprende un meccanismo selettore come quello ora descritto e n•2^k nuclei magnetici. Un ‛nucleo magnetico' è costituito da un minuscolo anello di ferrite del diametro di pochi millimetri. Ciascun nucleo può avere due stati di flusso magnetico residuo, corrispondenti a 0 e 1 a seconda che il verso del campo nel nucleo sia orario o antiorario. Durante un'operazione di lettura i nuclei di una prescelta locazione vengono portati nel loro stato 0 facendo passare una corrente attraverso un filo avvolto attorno a essi; quelli che si trovavano in precedenza nello stato 1 cambieranno il loro flusso magnetico e questo cambiamento si può misurare e utilizzare per porre uguali a 1 i corrispondenti bits dell'MBR. Poiché questa operazione azzera il contenuto dell'intera locazione prescelta, si deve successivamente rigenerare tale contenuto ricopiando c(MBR) nella locazione. Durante un'operazione di scrittura la locazione prescelta viene dapprima azzerata come appena descritto, ma lasciando immutato l'MBR, quindi si applica il ciclo di rigenerazione. Evidentemente una memoria a nuclei deve contenere i suoi circuiti interni di controllo e di temporizzazione per effettuare nel dovuto ordine le operazioni di lettura e di rigenerazione. Il tempo totale richiesto da un ciclo di lettura e rigenerazione si chiama ‛tempo di ciclo di memoria e generalmente varia da 0,7 a 2,0 microsecondi.

Per i sistemi di memoria a tamburo e a disco è consuetudine considerare come unità di locazione di memoria e di trasferimento di dati il ‛blocco' (gruppo di voci con indirizzi contigui) anziché la singola voce. Se i blocchi hanno tutti la stessa lunghezza, essi vengono chiamati ‛pagine'. Si usano i blocchi anziché le singole voci perché ciascun tempo di accesso comprende un ritardo per il posizionamento meccanico seguito dal tempo necessario al trasferimento. Se a ogni accesso si dovesse trasferire una sola voce, il tempo totale di impiego del dispositivo sarebbe dominato dal tempo di posizionamento e il dispositivo sarebbe assai poco efficiente. A differenza dei semplici indirizzi a una sola componente utilizzati per individuare le locazioni in una memoria a nuclei o a registro, la richiesta per indirizzare un blocco in una memoria a tamburo o a disco deve avere la forma (b, l), dove b indica l'indirizzo iniziale del blocco ed l la sua lunghezza (cioè il numero di voci da trasferire).

Un tamburo magnetico consiste di un tamburo cilindrico che ruota attorno al proprio asse a una velocità costante con periodo T (generalmente 30 millisecondi). La faccia esterna del cilindro è ricoperta di materiale magnetico. Vi è un insieme di testine di lettura/scrittura disposte lungo il tamburo, parallelamente all'asse di rotazione, cosicché ogni punto del tamburo passa sotto una testina una volta per ogni rivoluzione. Le testine sono divise in gruppi; ciascun gruppo contiene n testine, dove n è il numero di bits di una voce. La striscia di superficie di tamburo che ruota sotto le testine di un gruppo è detta ‛traccia'. Ciascuna traccia contiene un certo numero W di voci e ciascuna voce è disponibile per l'indirizzamento soltanto una volta per rivoluzione. Le singole voci si trovano nei punti di coordinate (t, ϑ) della superficie del tamburo, dove t è un ‛indice di traccia' e ϑ è un ‛indice di angolo'. Pertanto, la richiesta di un blocco sul tamburo ha la forma (t, ϑ, l), dove (t, ϑ) definisce la posizione di partenza di un blocco ed l (che al massimo vale W) la sua lunghezza. Quando il tamburo inizia a servire una richiesta, il canale di comunicazione (che sostituisce l'MBR, poiché ora si devono trasmettere gruppi di voci) si connette alla traccia prescelta t e le testine si pongono nello stato di lettura o scrittura a seconda dell'operazione che è stata specificata; quindi il meccanismo attende per un tempo (variabile fra 0 e T) chiamato ‛tempo di latenza', finché la posizione desiderata ϑ si presenta sotto le testine, e finalmente inizia il trasferimento, che si completa quando sono state trasferite l  voci (cioè dopo il tempo Tl / W). In associazione con il tamburo (anzi, generalmente inserito nel programma di controllo che gestisce il tamburo) vi è un meccanismo che mette in lista d'attesa le eventuali richieste addizionali che giungono mentre il tamburo è impegnato a servire una data richiesta. Pertanto il tempo d'attesa cui una particolare richiesta viene assoggettata consiste di tre componenti separate: un ritardo per l'attesa del proprio turno, il tempo di latenza e il tempo necessario a trasferire il blocco. Se il tempo medio di latenza è T / 2 e la lunghezza media di un blocco è l, e se le richieste vengono prese in considerazione secondo il loro ordine d'arrivo, il tamburo non può servire richieste con un ritmo maggiore di una richiesta ogni T / 2 + Tl̅ / W secondi (v. Coffman e Denning, 1973).

Nel caso delle pagine, in cui tutti i blocchi sul tamburo hanno la stessa prefissata lunghezza l, le posizioni angolari permesse ϑ sono ridotte a un piccolo numero di ‛indici di settore', in corrispondenza con gli inizi di prefissate aree di memorizzazione per le pagine. In questo caso è conveniente ed efficace organizzare il meccanismo di lista d'attesa in modo da servire le richieste nell'ordine che produce il minimo tempo di latenza per ciascuna richiesta; ciò ha l'effetto di migliorare in modo significativo le prestazioni del tamburo, poiché il tempo di latenza complessivo su un lungo intervallo di tempo sarà notevolmente minore di quello che si avrebbe se le richieste venissero servite secondo il loro ordine d'arrivo. Per un tamburo con N settori, questo sistema di minimizzazione del tempo di latenza riuscirà a gestire un flusso di dati circa N / 2 volte maggiore di quello che si avrebbe con il sistema convenzionale secondo l'ordine d'arrivo descritto in precedenza (v. Coffman e Denning, 1973; v. Denning, 1970).

Nelle memorie a disco una serie di piatti circolari sono montati parallelamente l'uno all'altro su uno stesso asse che ruota con velocità costante e periodo T. Ciascun piatto è rivestito su una o su entrambe le facce con materiale magnetico. Per ciascuna superficie magnetica di ciascun piatto vi è un braccio fornito all'estremo di testine di lettura/scrittura, che si protende da una struttura di bracci. L'intera struttura si muove di conserva lungo una linea avvicinandosi o allontanandosi dall'asse di rotazione, in modo tale che i bracci possono essere posizionati in una qualsiasi di una certa serie di posizioni; la corona circolare di ciascun piatto accessibile quando i bracci si trovano in una data posizione si chiama ‛traccia'. L'insieme di tutte le tracce situate alla stessa distanza dall'asse sui vari piatti costituisce un ‛cilindro'. Una richiesta di accesso al disco ha la forma (c, s, ϑ), in cui c è l'indice del cilindro, s è l'indice del piatto (si noti che (c, s) definisce una traccia), ϑ è la posizione angolare (si noti che (c, s, ϑ) definisce l'indirizzo da cui inizia un blocco) ed l  è la lunghezza del blocco. Il ritardo con cui viene soddisfatta una richiesta è composto dai seguenti tempi: il tempo da trascorrere in lista d'attesa; il ‛tempo di ricerca' necessario per muovere i bracci fino al cilindro desiderato; eventualmente un nuovo tempo in lista d'attesa se vi sono altre richieste di accesso allo stesso cilindro; il tempo di latenza; il tempo di trasferimento. In generale il tempo di ricerca varia fra 100 e 300 millisecondi ed è dominante rispetto al tempo di latenza.

Alcuni dischi sono progettati con una serie completa di testine per ciascun cilindro; questi dischi a testine fisse eliminano il tempo di ricerca e si comportano come tamburi (i cilindri concentrici sono equivalenti a un tamburo).

Le unità a nastro magnetico operano essenzialmente in base agli stessi principi che vengono utilizzati comunemente per le registrazioni audio e video.

Tutte le unità descritte finora includono generalmente in ciascuna locazione alcuni bits in più dello stretto necessario; questi bits vengono utilizzati per rivelare se vi sono stati errori di lettura o di scrittura. Di solito, quando un errore viene rivelato, esso può essere corretto automaticamente (v. Burroughs Corp., 1969²; v. Hellerman, 1967).

Per il loro breve tempo d'accesso e per la proprietà di accesso casuale, le tecnologie dei registri a flip-flop e dei nuclei magnetici vengono frequentemente impiegate per la memoria centrale dei calcolatori. Le caratteristiche richieste ai dispositivi di memoria centrale (in particolare il tipo di tecnologia e la natura del meccanismo di selezione di indirizzo) rendono costose queste memorie. Al contrario, tamburi, dischi e nastri hanno il vantaggio di essere poco costosi e lo svantaggio di avere tempi d'accesso lunghi e variabili; essi sono pertanto utilizzati comunemente come dispositivi di memoria ausiliaria.

c) L'elaboratore

1. I programmi. - L'elaboratore è un dispositivo destinato a eseguire le fasi di un programma. Un programma è composto da uno ‛spazio dei nomi' X e da una ‛serie di istruzioni', una delle quali si identifica come istruzione di partenza. Lo spazio dei nomi consiste dell'insieme di tutti i nomi che possono essere utilizzati dal programma per identificare valori. Per gli scopi di questo capitolo è sufficiente considerare lo spazio dei nomi identico allo spazio degli indirizzi della memoria centrale, di cui si è già detto; parlando, comunque, di memoria virtuale, si vedrà che lo spazio dei nomi di un programma non coincide con lo spazio degli indirizzi del calcolatore. Ogni elemento x dello spazio X dei nomi del programma ha come valore o un'istruzione codificata o un dato codificato. Ogni istruzione comprende: a) un ‛nome di operazione', o comando; b) gli ‛indirizzi degli operandi' (in X), che vengono utilizzati per ottenere dati di ingresso e per memorizzare i risultati determinati dai comandi di istruzione; c) l'indirizzo (nuovamente in X) dell'istruzione successiva.

Si definisca una variabile IP (‛indicatore di istruzione' o instruction pointer) il cui valore è contenuto nello spazio X dei nomi del programma. Se avviene che c(IP) = x, allora c(x) è la rappresentazione codificata della successiva istruzione da eseguire. Una rappresentazione astratta di un'operazione di elaboratore è la seguente.

Il passo ‛ottenere l'istruzione IP' consiste nel cercare c(x) dove x = c(IP), e il passo ‛decodificarla' è necessario per comprendere quale comando essa contenga e gli operandi su cui quel comando deve applicarsi. Il passo ‛IP ←  istruzione successiva' inserisce nell'indicatore di istruzione la successiva istruzione da eseguire e il passo finale ‛eseguire l'operazione sui dati in X' indica l'esecuzione del comando contenuto nell'istruzione. Nel caso in cui risulti decodificata l'istruzione STOP, il passo ‛eseguire' porrà termine al programma fermando l'elaboratore.

2. Tipi di istruzione. - Per specificare con maggior dettaglio il modo di operare dell'elaboratore, è necessario definire i tipi di istruzione che possono presentarsi. Un tipo classico di istruzione è l'operazione binaria, un'operazione che è così denominata perché prende due operandi e li combina formando un singolo risultato. Per questo tipo di istruzione si vede subito che ciascuna istruzione deve specificare quattro indirizzi: due per gli operandi in ingresso, uno per l'operando risultato e uno per l'istruzione successiva. Fortunatamente, se si fanno due ipotesi semplici e non troppo restrittive, si possono semplificare le istruzioni in modo che sia necessario specificare al massimo soltanto un indirizzo: a) in generale si assume che l'istruzione successiva segua quella presente in sequenza (cioè, il suo indirizzo può essere calcolato come il valore dell'espressione IP + 1); b) uno speciale registro, chiamato ‛accumulatore' A, fornisce sempre uno degli operandi di ingresso e riceve sempre il risultato di un'operazione. La prima ipotesi elimina la necessità di specificare nell'istruzione l'indirizzo dell'istruzione successiva. La seconda ipotesi elimina altri due indirizzi, poiché A costituisce implicitamente una delle locazioni per gli operandi e anche la locazione per il risultato.

Sia (op, a) la notazione che indica un'istruzione del formato ora specificato, dove op è il codice di un'operazione e a un indirizzo nello spazio X dei nomi del programma. Vi sono quattro classi fondamentali di istruzioni, secondo il valore di op. Là prima è quella delle operazioni binarie'. L'effetto di un'operazione binaria F è quello di assegnare A ← F(A, X[a]), dove X[a] è l'elemento dello spazio dei nomi denotato dall'indirizzo a. Alcuni esempi di operazioni binarie sono le ‛operazioni aritmetiche', come l'addizione, la sottrazione, la moltiplicazione e la divisione, e le ‛operazioni logiche', come OR e AND, applicate bit dopo bit. La seconda classe è quella delle ‛operazioni unarie', che operano su un solo operando. L'effetto di un'operazione unaria F è A ← F(A). Alcuni esempi sono operazioni aritmetiche, come il cambiamento di segno, il valore assoluto e la radice quadrata, e operazioni logiche, come il complemento bit per bit. La terza classe è quella delle ‛operazioni per trasferire informazione' fra A e lo spazio dei nomi del programma. Sono le operazioni LOAD, il cui effetto è ‛A ← X[a]', e STORE, il cui effetto è ‛X[a] ← A'. La quarta classe è quella delle ‛operazioni di trasferimento del controllo'. Esempi di queste sono il comando di trasferimento incondizionato GOTO, il cui effetto è ‛IP ← a' e il comando di trasferimento condizionale GOTO IF C, il cui effetto è ‛se C allora IP ← a', per una certa condizione C. Si noti che le istruzioni GOTO servono per saltare il calcolo ‛IP ← IP + 1', che è il metodo normale per determinare l'indirizzo dell'istruzione successiva.

Tenendo conto di queste considerazioni, si può descrivere in modo più elegante il modo di operare di un elaboratore. Si assuma che l'elaboratore contenga un ‛registro di istruzione' IR, che sostiene la rappresentazione codificata della istruzione in corso di elaborazione. IR contenga due campi, denotati IR.op e IR.a; se l'istruzione in esame è (op,a), allora IR.op = op e IR.a = a. L'operazione dell'elaboratore in questo caso si definisce come segue.

Questa definizione è corretta ma può trarre in inganno: in effetti non riflette il fatto che nell'hardware si esegue in parallelo (cioè simultaneamente) il maggior numero possibile di operazioni.

I metodi per realizzare le unità funzionali aritmetiche e logiche (che nella precedente discussione abbiamo chiamato operazioni F  binarie e unarie) sono discussi in profondità da Hellerman (v., 1967), Knuth (v., 1969) e Rosin (v., 1969). I metodi per realizzare i relativi meccanismi di controllo sono discussi nel prossimo paragrafo.

fig. 13

3. Microprogrammazione. - Per illustrare i principî di progettazione utilizzati per il meccanismo di controllo di un elaboratore facciamo ricorso a un esempio molto semplice. La fig. 13 mostra gli elementi dell'hardware. La memoria centrale figura nel diagramma con il registro degli indirizzi di memoria MAR, il registro della memoria tampone MBR e gli ingressi di controllo READ e WRITE definiti nel cap. 2, § b. L'unità stessa di controllo contiene tre registri: l'indicatore di istruzione IP, il registro delle istruzioni IR e l'accumulatore A. L'IP è un contatore, come quello della fig. 9. Un'unità funzionale, l'ADDER (sommatore), calcola la somma dei numeri binari contenuti in A e in MBR. La linea di trasmissione degli indirizzi e la linea di trasmissione dei dati sono semplicemente dei percorsi lungo cui possono transitare i codici binari degli indirizzi e dei dati. Infine l'unità di controllo pone in ordine e coordina tutte le operazioni, come è stato accennato nel cap. 2, §  a. L'unità di controllo ha tre ingressi condizionali, che informano sul codice d'operazione (IR.op) e se il numero contenuto in A è uguale o minore di zero. L'unità di controllo fornisce dieci segnali, denominati 1, 2,..., 10, che controllano le operazioni fluenti attraverso l'elaboratore, come è specificato nella tab. III. Vi sono quattro segnali di controllo, denominati 20, 21, 22 e 23, utilizzati internamente dall'unità di controllo per ordinare se stessa, come si spiegherà fra breve.

Nell'elenco che segue sono definite le operazioni specifiche dell'elaboratore.

Si può notare che ciò che viene descritto è semplicemente un perfezionamento della definizione data precedentemente dell'Elaboratore 2. Si osservi che le varie operazioni dell'elaboratore possono esprimersi in termini di sequenze di segnali di controllo, come è mostrato nella parte destra della sequenza elencata. Per esempio la sequenza di controlli che realizzano FETCH è data da FETCH = (6, 9, 1, 8, 22) e la sequenza per ADD è data da ADD = (5, 9, 4, 21). Queste sequenze di controlli sono chiamate ‛microprogrammi'.

fig. 14

Ovviamente l'operazione di elaboratore non è specificata completamente finché non si fornisce la temporizzazione dei segnali di controllo in ciascuna sequenza. A questo scopo supponiamo che ciascuna operazione di registro richieda 0,1 microsecondi e che la memoria richieda 0,8 microsecondi per completare un'operazione di lettura o di scrittura (questi numeri sono del corretto ordine di grandezza). La fig. 14 mostra l'organizzazione dell'hardware dell'unità di controllo atta ad imporre gli appropriati requisiti di ordine e temporizzazione. L'anello di temporizzazione' trasmette impulsi sulle linee verticali c₁, c₂, ..., c₁₀ del diagramma, uno alla volta in sequenza. Il meccanismo dell'anello di temporizzazione è equivalente a un registro di scorrimento che produce le uscite c₁, c₂, ..., c₁₀; un impulso sull'ingresso RESET azzera il registro e memorizza un 1 sul flip-flop più a sinistra; gli impulsi di temporizzazione successivi (uno ogni 0,1 microsecondi) provocano uno scorrimento a destra. Per ciascuna sequenza di controlli identificata nell'elenco precedente vi è una linea orizzontale nel diagramma; l'inizio di una sequenza di controlli comanda il corrispondente flip-flop e la fine di quella sequenza lo azzera. Il tondino pieno posto nei punti di incrocio della matrice della fig. 14 indica la presenza di una porta AND con un ingresso sulla linea verticale, uno sull'orizzontale e con le uscite che controllano i segnali di controllo specificate dai numeri dati. La microistruzione ‛goto FETCH' è realizzata generando il segnale 21, che attiva il flip-flop più in alto. La sequenza di controllo del FETCH (6, 9, 1, 8, 22) viene quindi generata in sincronismo con gli impulsi temporizzatori sulle linee verticali. Si osservi che un ritardo di 0,8 microsecondi viene inserito dopo il segnale 9 per permettere alla memoria di completare l'operazione di lettura. La microistruzione ‛goto EXECUTE' è realizzata come generazione del segnale 22, che viene addizionato alle uscite di un decodificatore per attivare il flip-flop che deve eseguire l'istruzione. Si osservi che con ciascuno dei due segnali ‛goto' l'anello temporizzatore deve essere azzerato per eseguire la sequenza di controllo successiva dall'inizio; per questo fine si include il segnale 20. Infine l'istruzione STOP azzera semplicemente l'anello temporizzatore e disinserisce l'orologio; per rimettere in funzione la macchina è necessario l'intervento dell'operatore del calcolatore (che deve premere il bottone START).

Sono possibili molteplici estensioni dello schema di base. Si possono aggiungere nuove istruzioni; ciascuna richiederà una o più linee orizzontali nella matrice di controllo, a seconda del numero delle diverse sequenze di controlli necessarie per realizzarla. L'elaboratore può avere più di un registro di tipo A; in tal caso saranno necessarie più istruzioni di caricamento e memorizzazione e più complessi codici di istruzione per specificare quale registro o quali registri partecipino all'esecuzione di una data istruzione. Si possono realizzare migliori schemi di indirizzamento utilizzando i ‛registri di indice' o l' ‛indirizzamento indiretto'. Un registro di indice consiste semplicemente di un registro il cui contenuto va sempre a sommarsi al numero posto in MAR durante la fase esecutiva del ciclo di istruzioni. La sua funzione principale è quella dell'indirizzamento di blocchi: il programmatore può memorizzare l'indirizzo di base di un blocco di dati nel registro di indice e da quel punto in poi gli indirizzi degli operandi nelle istruzioni saranno trattati come se si riferissero alla base del blocco. Si può far in modo che gli stessi segmenti di istruzioni si applichino a blocchi differenti, cambiando semplicemente il contenuto del registro di indice. L'indirizzamento indiretto è una tecnica secondo cui si possono costruire in memoria delle catene di posizioni in cui ciascuna contiene l'indirizzo di quella successiva. A ogni accesso l'hardware di elaborazione segue automaticamente ciascuna catena fino al termine. L'indirizzamento indiretto viene applicato principalmente per trasferire parametri da una subroutine all'altra. I microprogrammi non sono necessariamente realizzati completamente in hardware, come nella fig. 14. Al contrario, essi possono essere codificati come numeri binari e memorizzati in memorie costituite da registri di flip-flop ad alta velocità (generalmente ‛memorie per sola lettura' o ROM da Read Only Memory); per cercare, decodificare e tradurre oggetti di controllo in segnali di controllo si utilizza una semplicissima versione dell'Elaboratore 1. Ne risulta una maggiore flessibilità della concezione dell'elaboratore, poiché si possono effettuare cambiamenti di vecchie istruzioni e inserimento di nuove istruzioni semplicemente ricaricando la ROM. Per ragioni che sarebbe troppo difficile spiegare in breve termine, le tecniche per realizzare controlli elaborativi microprogrammati in versione interamente hardware sono divenute comunemente note come ‛microprogrammazione orizzontale', le tecniche basate sulla memorizzazione nelle ROM di sequenze di controlli codificati sono state denominate ‛microprogrammazione verticale' (v. Rosin, 1969).

d) Ingresso e uscita (I/O)

1. Produttori, consumatori, tamponi. - Non è possibile, nei presenti limiti di spazio, passare in rivista la miriade di dispositivi di ingresso e uscita. Comunque si possono riassumere i principi di base utilizzati per la comunicazione fra l'elaboratore e i dispositivi di I/O. La forma più semplice di comunicazione fra un elaboratore e un dispositivo è illustrata nella fig. 15. Vi è un registro tampone che ha la funzione di contenere una singola voce di dati. L'elaboratore dà un'istruzione STARTIO (x,d) che, appena eseguita, produce un impulso che ordina al dispositivo d di iniziare la lettura o la scrittura, a seconda che x indichi lettura o scrittura. Allora il dispositivo d copia (oppure carica) il contenuto del registro tampone sul (oppure dal) mezzo che esso controlla, se l'istruzione ricevuta è quella di scrittura (oppure lettura). Allorquando l'operazione è completata, il dispositivo attiva un flip-flop indicatore, che può essere ispezionato e azzerato dall'elaboratore.

È importantissimo osservare che l'elaboratore e il dispositivo operano simultaneamente (cioè in parallelo) senza sincronizzazione, se non quella fornita dall'istruzione STARTIO e dal flip-fiop indicatore, e che il registro tampone costituisce un'area di dati in comune fra elaboratore e dispositivo. Perché la comunicazione venga operata correttamente è assolutamente necessario osservare certe semplici procedure: a) l'elaboratore non deve mai cercare di memorizzare o caricare il contenuto del registro tampone mentre il dispositivo è impegnato; b) l'elaboratore non deve trasmettere una nuova istruzione STARTIO fintanto che non può constatare che il flip-flop indicatore è stato attivato e prima di averlo azzerato; c) il dispositivo non può caricare o memorizzare il contenuto del registro tampone a suo arbitrio: esso deve infatti essere ‛asservito' all'elaboratore. Se si violano queste procedure, possono occorrere errori come i seguenti: l'elaboratore scrive un nuovo dato nel registro tampone prima che il dispositivo lo abbia rimosso; il dispositivo rimuove lo stesso dato due volte, prima che l'elaboratore ne abbia generato un altro; l'elaboratore non riesce a inviare un nuovo segnale STARTIO prima di entrare in un circolo vizioso attendendo indefinitamente che venga attivato il flip-flop indicatore.

fig. 15

A causa della sua eccessiva semplicità, il meccanismo illustrato nella fig. 15 è raramente utilizzato direttamente fra un elaboratore e un dispositivo. Poiché generalmente la velocità dell'elaboratore è molto maggiore di quella del dispositivo, è preferibile realizzare un'area tampone abbastanza vasta da contenere un intero blocco di informazioni; l'elaboratore può ‛inserire o rimuovere informazione da quest'area rapidamente, lasciando che il dispositivo operi sul contenuto del tampone a suo piacimento. Comunque ragioni economiche costringono generalmente a porre l'area tampone nella memoria centrale, il che comporta qualche problema per la gestione delle memorie, complica i problemi di sincronizzazione e richiede che il dispositivo sia capace di indirizzare la memoria centrale. Inoltre si può sprecare tempo prezioso dell'elaboratore nel caso in cui questo entri in un circolo vizioso attendendo che il dispositivo attivi l'indicatore (cosa particolarmente grave quando l'elaboratore ha altro lavoro da svolgere). Si può pure sprecare capacità di elaborazione quando l'elaboratore viene impegnato per eseguire banali programmi di gestione del registro tampone e controllo del dispositivo, senza utilizzare i costosi apparati aritmetici in esso contenuti. Per ovviare a questi problemi sono state apportate due innovazioni: i ‛controllori di dispositivi', che sono costituiti da piccoli, semplicissimi elaboratori capaci di eseguire programmi di controllo di dispositivi, e i ‛comandi d'interruzione', che sono dei segnali che reclamano la disponibilità prioritaria dell'elaboratore allorquando il controllore di dispositivo ha completato il lavoro assegnatogli dall'elaboratore centrale. Il controllore di dispositivo solleva l'elaboratore dal lavoro banale di supporto alle operazioni di I/O, lasciandogli più tempo per applicare i suoi costosi apparati aritmetici all'esecuzione di programmi per cui questi sono indispensabili. Il meccanismo d'interruzione elimina la possibilità che l'elaboratore attenda inutilmente che il dispositivo attivi l'indicatore, poiché esso requisisce l'elaboratore e lo costringe a eseguire qualunque programma debba essere eseguito quando viene attivato l'indicatore.

È difficile e delicato trovare appropriate soluzioni per i problemi di sincronizzazione che sorgono quando due programmi eseguiti in concomitanza comunicano per mezzo di un'area tampone. È stata trovata una soluzione elegante a questo problema, risolvendo il cosiddetto ‛problema del produttore/consumatore', in cui un programma di produzione colloca prodotti in un tampone dal quale vengono successivamente prelevati da un programma di consumo (v. Brinch-Hansen, 1973; v. Coffman e Denning, 1973).

2. Controllori. - Nella fig. 16 è illustrato lo schema di utilizzazione di un controllore di dispositivo. Il controllore C comunica con una serie di dispositivi, ciascuno collegato come nella fig. 15. L'elaboratore genera un programma di controllo dei dispositivi e comanda al controllore di dispositivo di eseguirlo mediante un'istruzione STARTIO (x), in cui x rappresenta la posizione iniziale del registro indicatore di istruzione del controllore. Mentre il controllore di dispositivo esegue il programma di controllo, i richiami agli operandi contenuti nelle sue istruzioni lo fanno accedere all'area tampone in cui scrivere o da cui leggere i dati. Completata la transazione, il controllore di dispositivo invia un segnale di ‛lavoro eseguito' all'elaboratore, distogliendolo dal programma che questo sta eseguendo e facendogli iniziare l'esecuzione del programma di interruzione per lavoro eseguito. Quest'ultimo programma genererà un altro programma di controllo di dispositivo, specificando la nuova transazione che il controllore dovrà eseguire; esso farà partire nuovamente il controllore e riporterà quindi l'elaboratore sul programma che era stato interrotto.

Si osservi che l'indicatore di istruzione dell'elaboratore (P.ip) e l'indicatore di istruzione del controllore (C.ip), in generale, percorreranno i loro rispettivi programmi simultaneamente e indipendentemente e che sia l'elaboratore sia il controllore si richiameranno per le loro operazioni alle rispettive aree dei dati (l'area dei dati del controllore è il tampone). Comunque, poiché i dispositivi operano lentamente rispetto all'elaboratore, il controllore avrà bisogno di accedere alla memoria molto più raramente dell'elaboratore. Poiché il meccanismo di memoria centrale è costruito in modo da permettere l'accesso a una posizione per volta, l'elaboratore e il controllore non possono di fatto accedere alla memoria centrale simultaneamente. Generalmente l'hardware è costruito in modo da dare priorità di accesso al controllore. Ciò comporta che l'elaboratore sarà costretto ad attendere il suo turno per accedere alla memoria centrale ogni qual volta il ciclo di memoria è impegnato a servire il controllore, così che la velocità efficace della memoria centrale risulterà ridotta, dal punto di vista dell'elaboratore. Questo fenomeno è denominato ‛interferenza di memoria' (familiarmente ‛furto di ciclo'). Fortunatamente, poiché la maggior parte dei dispositivi opera tanto lentamente che l'interdizione di accesso per l'elaboratore è puramente occasionale, l'interferenza di memoria non rappresenta normalmente un problema significativo (v. Burroughs Corp., 1969²; v. Hellerman, 1967).

3. Comandi di interruzione. - Un ‛comando di interruzione' è un segnale inteso a requisire l'elaboratore distogliendolo da qualsivoglia programma esso stia eseguendo e assegnandolo immediatamente all'esecuzione di un ‛programma di gestione del comando di interruzione'. Al termine di tale programma, l'elaboratore riprende l'esecuzione del programma originario dal punto in cui esso è stato interrotto. I comandi di interruzione sono utili per mettere in grado l'elaboratore di reagire immediatamente a svariate condizioni che richiedano risposta immediata.

Un semplice meccanismo di interruzione può essere costituito come segue. Dapprima si identifica un certo numero di condizioni. Si assume che, entro un breve tempo dal rilevamento di ciascuna di queste condizioni, debba essere portato in esecuzione un corrispondente programma di gestione del comando di interruzione. Un esempio di tali condizioni è la conclusione di un lavoro da parte di un dispositivo; vi sarebbe infatti una grave perdita di efficienza se la successiva operazione di trasferimento in lista d'attesa non venisse impostata appena il dispositivo diviene disponibile. Altro esempio di tali condizioni sono gli errori (come gli errori di macchina, gli errori di aritmetica, gli errori di indirizzamento, gli errori di violazione di parti protette del sistema); infatti non si può esser sicuri che le operazioni successive del programma o del calcolatore siano corrette fintanto che non sia stato eliminato l'errore. Altri esempi di tali condizioni sono i tentativi, da parte dei programmi di utenza, di richiamare i programmi del sistema operativo (le cosiddette ‛chiamate del supervisore'); infatti è necessario provare la validità di tali chiamate, per assicurare una corretta azione da parte del supervisore. L'hardware effettua la sorveglianza di tutte le condizioni.

Dopo il meccanismo di identificazione delle condizioni, vi è nell'elaboratore un flip-flop associato ad ogni condizione, il quale è denominato ‛cella di condizione' (una generalizzazione degli indicatori discussi in precedenza). Ogni qual volta l'hardware rileva il verificarsi di una condizione, la corrispondente cella di condizione viene attivata. Generalmente le condizioni sono numerate 1, 2,..., n, con i numeri più bassi associati a condizioni più importanti (cioè di maggior priorità). Vi è un circuito combinatorio che sorveglia in continuazione le celle di condizione e produce, in codice binario, l'indice della cella di maggior priorità fra quelle attivate (cioè aventi valore 1). Questo indice è denominato ‛codice di condizione' e verrà collocato su comando in uno speciale registro che chiameremo CODE. Infine vi è un altro flip-flop denominato MASK, o ‛cella di mascheramento'; l'elaboratore accetterà comandi di interruzione se e soltanto se MASK = 1. Lo scopo di questa cella è di disattivare il meccanismo di interruzione quando necessario.

Oltre le condizioni e le celle di condizione, vi è la modifica del controllo dell'elaboratore in modo tale che, al termine di ciascun ciclo intero di istruzioni, venga esaminato il segnale S = MASK•(C₁ + C₂ + ... + C_n). Tale segnale vale 1 se e soltanto se avviene simultaneamente che sia MASK = 1 e che almeno una delle celle di condizione sia attivata (C_i = 1). Se risulta S = 1, ha inizio la seguente sequenza di controlli:

MAR ← 0; MBR ← IP; scrivere in memoria;

MASK ← 0;

CODE ← codice di condizione;

IP ← 1;

goto FETCH.

Questa sequenza di controlli colloca il valore assunto dall'indicatore di istruzione nella locazione di memoria 0 e inizia l'esecuzione di un programma denominato ‛disbrigo' che inizia dalla locazione 1. Il disbrigo esamina il registro CODE e richiama il corrispondente programma di gestione. Un programma di gestione della condizione i può descriversi generalmente come segue:

azzerare C_i;

preservare i registri dell'elaboratore nella memoria locale; agire sulla condizione;

recuperare i registri dell'elaboratore precedentemente preservati;

RESUME.

La speciale istruzione RESUME attiva MASK al valore 1, carica l'indicatore di istruzione IP precedentemente collocato nella locazione 0 e inizia la sequenza FETCH.

Si osservi che, durante l'esecuzione del disbrigo e della gestione, rimane sempre MASK = 0; pertanto l'elaboratore ignorerà ulteriori comandi di interruzione fintanto che non avrà gestito quello presente. Un motivo per questa restrizione è che un secondo comando di interruzione causerebbe la sovrapposizione di un nuovo valore di IP su quello memorizzato nella locazione 0, rendendo impossibile il ritorno di controllo al programma interrotto. Un'altra ragione è che un programma di gestione, mentre opera su dati coerenti con il sistema, può tenerli in uno stato di momentanea incoerenza fintanto che non termina; se un altro programma di gestione si trovasse a operare in concomitanza, il primo potrebbe compiere operazioni errate, trovandosi ad agire su dati incoerenti con il sistema. Ovviamente il progettista di programmi di gestione avrà il preciso compito di rendere tali programmi quanto più veloci possibile, in modo da rendere minimo il periodo di tempo in cui il meccanismo di interruzione è disattivato.

Un'importante generalizzazione del meccanismo di interruzione permette che una condizione di maggiore priorità possa interrompere il programma di gestione di una condizione di minore priorità. Ciò si ottiene associando a ciascuna condizione una separata cella di mascheramento. Il progettista di programmi di gestione deve scrivere tali programmi in modo che, se interrotti da programmi di gestione di maggior priorità, essi non vengano indotti in errore (v. Burroughs Corp., 1969²; v. Hellerman, 1967; v. Organick, 1973).

È evidente che il meccanismo di interruzione è qualcosa al limite fra l'hardware e il software di un sistema; i programmi di gestione sono infatti parte del software di sistema operativo. È quindi il momento giusto per concludere questa nostra breve rassegna sull'hardware di un calcolatore e rivolgere l'attenzione verso i sistemi operativi e il software.

3. Organizzazione del sistema operativo di un elaboratore

a) Che cosa è un sistema operativo

1. Definizioni. - Si suole definire come elaborazione l'esecuzione di un programma. Un sistema di calcolo si può definire in termini delle varie funzioni di supervisione e controllo messe a disposizione degli utenti per effettuare delle elaborazioni. Tali funzioni consistono nel: a) generare e rimuovere i programmi; b) controllare che le elaborazioni procedano, assicurando, in particolare, che ciascun programma che sia stato accettato proceda con la dovuta rapidità e che nessun programma possa ritardare indefinitamente l'esecuzione degli altri; c) gestire le condizioni eccezionali (segnalate dai comandi di interruzione) che possano occorrere durante un'elaborazione (ad esempio, errori di aritmetica o di macchina, inconvenienti di indirizzamento, istruzioni non lecite, violazione di regole di sicurezza); d) amministrare le risorse dell'hardware fra le elaborazioni in corso; e) permettere l'accesso alle risorse del software, quali i files, gli editori, i compilatori, gli assemblatori, le librerie di subroutines e i sistemi di programmazione; f) fornire all'informazione protezione, controllo di accesso e sicurezza; g) assicurare l'intercomunicazione fra le elaborazioni. Queste funzioni devono essere assicurate dal sistema, poiché non è possibile che i programmi stessi da elaborare le includano trattandole adeguatamente. Il software del sistema di calcolo che mette l'hardware in grado di realizzare queste funzioni è denominato ‛sistema operativo'.

Raramente (o quasi mai) gli utenti eseguono un calcolo senza essere assistiti dal sistema operativo. Molti sistemi consentono agli utenti di ridefinire o aggiungere un piccolo nucleo di programmi di sistema operativo, cosicché, in linea di principio, ciascun utente può avere a disposizione una macchina diversa. L'insieme dell'hardware più il software di sistema operativo, che definiscono l'ambiente entro cui un dato utente può eseguire i suoi programmi, viene spesso denominato ‛la macchina virtuale' relativamente a quel determinato utente.

2. Tipi di sistemi. - È enorme il numero e la varietà dei sistemi di calcolo disponibili oggigiorno. Vi sono sistemi per programmi di generale applicazione, sistemi per il controllo in tempo reale, sistemi in partizione di tempo, sistemi per servizi di informazione ed elaborazione a distanza e sistemi di reti di calcolatori. Tutti i sistemi forniscono l'uno o l'altro dei servizi ‛elaborazione su programma' e ‛interattivo' (e talvolta entrambi). Nel servizio di elaborazione su programma l'utente fornisce all'inizio il programma e i dati relativi al suo lavoro, insieme con le informazioni di controllo illustranti che cosa deve fare il sistema del suo lavoro. Tutto ciò è generalmente fornito sotto forma di schede, sia a una certa stazione di ingresso del centro di calcolo, sia a una stazione di ingresso remota connessa col centro di calcolo mediante una linea di comunicazione. Le schede che descrivono che cosa deve fare il sistema con le schede riguardanti il lavoro vengono chiamate ‛schede di controllo'; esse contengono informazioni riguardanti il tempo di elaborazione, lo spazio di memoria e altre risorse necessarie per il lavoro, i nomi dei files da utilizzare come ingresso al lavoro o uscita da esso, i nomi delle procedure di libreria da includere come parte del lavoro, il nome del traduttore di linguaggio da utilizzare per compilare il lavoro e l'indicazione se il lavoro deve essere caricato ed eseguito dopo la compilazione. Il sistema legge le schede, memorizza il loro contenuto in un file e pone il file in lista d'attesa per l'elaborazione (come si vedrà più oltre in dettaglio). Dopo un tempo sufficientemente lungo, l'elaborazione del lavoro viene completata e le schede originali più i prodotti dell'elaborazione vengono restituiti all'utente.

Al contrario, un sistema che fornisce un servizio interattivo generalmente non richiede che l'utente specifichi il proprio lavoro sotto forma di un pacco di schede. La funzione delle schede di controllo è sostituita da una serie di ‛comandi' interpretati da un ‛sistema di comando', che riceve le informazioni di controllo direttamente dall'utente che le imposta su un quadro comandi. Ciascun comando impostato dall'utente produce l'esecuzione di un lavoro, il cui risultato è generalmente trasmesso all'utente e visualizzato sul quadro comandi. In alcuni sistemi l'utente può interagire con il lavoro, modificandolo secondo quanto gli appaia conveniente. I sistemi interattivi possono essere classificati in quattro categorie principali: 1) sistemi di transazione dedicati, come i sistemi di prenotazione di biglietti di compagnie aeree o altri; in questi sistemi l'utente può avviare l'esecuzione di lavori che effettuano transazioni su una base di dati; il numero di transazioni possibili è fisso e piccolo; 2) sistemi interattivi dedicati, come il JOSS (Johnniac Open Shop System), il QUIKTRAN, il BASIC; in questi sistemi gli utenti possono programmare lavori mediante un unico, semplice linguaggio; 3) sistemi interattivi di applicazione generale, utilizzati in molti uffici con servizi in partizione di tempo; in questi sistemi gli utenti possono scrivere ed eseguire lavori in ciascuno dei numerosi linguaggi permessi dal sistema; 4) sistemi estensibili, come il CTSS (Compatible Time Sharing System) e il MULTICS (Multiplexed Information and Computing Service), studiati al Massachusetts Institute of Technology (MIT); in questi sistemi gli utenti, generalmente per il tramite di un sistema di files che permette la memorizzazione a lungo termine e la partizione dei files, possono estendere il sistema di base sviluppando linguaggi e sottosistemi propri e rendendoli disponibili ad altri utenti.

Quasi tutti i sistemi richiedono che ciascun utente abbia preso accordi preventivi con la direzione del centro di calcolo prima di poter accedere al sistema. Ciascun utente prende accordi con il centro di calcolo per ottenere un numero di riconoscimento e accetta di pagare l'affitto dei servizi; spesso gli accordi comportano limitazioni della quantità di risorse che l'utente può utilizzare, così che saranno necessari nuovi accordi quando questi avrà esaurito la sua dotazione. Eccezioni a questa procedura comprendono spessissimo i sistemi di transazione dedicati e i sistemi interattivi dedicati, in cui un utente, nel momento in cui ottiene l'accesso a un terminale dedicato, ottiene l'accesso all'intero sistema. Eccezioni a parte, la prima scheda di controllo di un lavoro affidato a un sistema di elaborazione su programma, o il primo comando impostato su un sistema interattivo serviranno a far riconoscere l'utente dal sistema; l'accesso gli sarà permesso soltanto se egli può farsi identificare dal sistema mediante il suo codice di riconoscimento.

A causa dell'alto volume di comunicazioni fra utente e lavoro, nei sistemi interattivi vi è un maggior dispendio per commutare le risorse (specialmente l'elaboratore e la memoria centrale) fra i vari lavori e pertanto l'esecuzione dei lavori è meno efficiente che nel sistema di elaborazione su programma. In compenso un sistema interattivo costituisce un ambiente molto efficiente per lo sviluppo di un programma: cioè per redigerlo, perfezionarlo e provarlo. Pertanto i sistemi di elaborazione su programma vengono per lo più utilizzati nei centri di calcolo in cui lo sviluppo di programmi rappresenta una parte secondaria del complesso delle attività, mentre si dà più importanza a un flusso produttivo ed efficiente.

I sistemi interattivi vengono per lo più utilizzati nei centri in cui l'attività primaria è costituita dallo sviluppo di programmi e, naturalmente, nei centri in cui l'interattività è richiesta dalla natura del problema da risolvere (ad esempio sistemi per la prenotazione di biglietti, sistemi di controllo in tempo reale).

3. Proprietà comuni ai sistemi. - I modi di concepire i sistemi da parte dei progettisti e dei programmatori sono quasi altrettanto numerosi quanto gli stessi sistemi. Alcuni sistemi sono concepiti come vasti e potenti mezzi per elaborazioni su programma e offrono una grande varietà di linguaggi, di sistemi di programmazione e di servizi (è tale, ad esempio, la maggior parte delle macchine di tipo IBM 360 e 370 e di tipo CDC 6000). Alcuni sono stati concepiti per essere altamente efficienti per applicazioni specifiche (ad esempio il sistema ALGOL delle macchine Burroughs B5700/B6700 e il COBOL delle Burroughs B1700). Alcuni sono concepiti come estensioni di alcuni linguaggi o macchine (ad esempio il sistema MULTICS del MIT, il CAL 6400 di Berkeley e il sistema di macchina virtuale CP-67 dell'IBM). Altri sono concepiti come sistemi di gestione di informazione (ad esempio il sistema di prenotazione SABRE delle compagnie aeree). Altri ancora sono concepiti come strumenti informativi o come macchine passibili di estensione (ad esempio il MULTICS del MIT, il sistema BBN TENEX per il PDP-10, il sistema RC 4000 dell'A/S Regnecentralen e il sistema TSS/360 dell'IBM).

Malgrado la diversità dei tipi delle relative concezioni, la maggior parte dei sistemi operativi ha molto in comune, poiché comuni sono i tre principali obiettivi di progettazione: un ambiente efficiente per sviluppare, raffinare e far eseguire i programmi; una grande varietà di mezzi per risolvere i problemi; la possibilità di eseguire elaborazioni con basso costo amministrando opportunamente le risorse e l'informazione. Le caratteristiche comuni dei sistemi operativi sono illustrate qui di seguito. Non è comunque detto che esse siano tutte presenti in ciascun particolare sistema.

a) Simultaneità. È la proprietà per cui due o più attività vengono condotte in concomitanza; cioè l'unità di elaborazione centrale può eseguire le istruzioni di un lavoro mentre un elaboratore periferico sta eseguendo un'operazione di ingresso/uscita. Ciò che viene indicato come ‛elaborazioni parallele' o ‛lavori paralleli' è una forma di simultaneità, sebbene tale simultaneità sia più di carattere logico che fisico; ciò significa che, in qualunque momento, si può osservare più di un programma in corso di esecuzione.

b) Asincronismo. Questa proprietà è in relazione al fatto che non si può predire esattamente l'ordine in cui gli eventi si susseguiranno. L'asincronismo è una conseguenza della simultaneità e della condivisione delle risorse. A causa dell'influenza della mole totale di lavoro, della mancanza di precisione delle informazioni preliminari fornite dai programmatori circa le risorse richieste dai propri programmi e delle differenze di velocità fra le varie unità hardware del sistema, l'ordine in cui le risorse sono assegnate, rese libere o impegnate dai lavori risulta imprevedibile; i meccanismi per gestire la simultaneità e la condivisione devono essere concepiti per ammettere questa circostanza. Se si desidera imporre un ordine logico a certi eventi, i meccanismi di sincronizzazione devono essere inclusi nella concezione del sistema e il loro uso deve apparire indicato esplicitamente nella programmazione del lavoro; questi meccanismi fanno sì che un lavoro si arresti a un certo punto fino a quando non venga ricevuto un segnale o un messaggio da un altro lavoro.

c) Amministrazione automatica delle risorse. In molti sistemi è incluso un meccanismo centralizzato per l'amministrazione delle risorse, avente il compito di sovrintendere a che le risorse vengano utilizzate in modo da soddisfare gli obbiettivi di un servizio efficiente, specialmente perché vi è la possibilità che lavori completamente indipendenti finiscano con l'interferire l'uno con l'altro nel contendersi le stesse risorse. Il sistema di controllo dell'amministrazione delle risorse deriva dal desiderio di liberare per quanto possibile il programmatore dal peso di amministrarsi le risorse, in modo che possa concentrare pienamente le sue energie sulle proprietà logiche dei suoi algoritmi. Inoltre la natura imprevedibile delle richieste che possono occorrere in sistemi che portano avanti attività concomitanti pone il programmatore in una posizione molto svantaggiosa quando debba prendere autonomamente decisioni efficienti circa l'amministrazione delle risorse.

d) Partizione. Questo termine viene usato in due sensi. In primo luogo ci si può riferire alla partizione dei tipi di risorse, indipendentemente dal fatto che si possano spartire unità individuali di tali tipi. Come esempio di tipi di risorse si possono citare tipi di hardware come elaboratori e memorie e tipi di software come files e messaggi; i corrispondenti esempi di unità sono, rispettivamente, un singolo elaboratore, una pagina di memoria, un file o un messaggio. Un'unità del tipo di una risorsa fisica è normalmente soggetta a essere controllata esclusivamente dal lavoro cui è stata assegnata (poiché il lavoro può manipolare lo ‛stato' interno dell'unità di risorsa); pertanto, per realizzare la partizione, è necessario utilizzare qualche forma di multiplazione (v. oltre). In secondo luogo ci si può riferire alla partizione di informazione. La partizione di informazione è motivata in parte dal desiderio di poter utilizzare, per i propri programmi, eventuali sottoprogrammi o moduli realizzati da altri, in parte dal fatto che vi sono dei problemi quando si utilizza la base centrale di dati e in parte dal desiderio di evitare la proliferazione di copie di procedure che sono di uso comune per più lavori.

e) Memorizzazione a lungo termine. I sistemi della seconda generazione permettevano la memorizzazione a lungo termine soltanto in casi molto limitati (ad esempio nei casi delle librerie di subroutines, accessibili soltanto attraverso compilatori o caricatori); ciò semplificava considerevolmente il problema di gestire e proteggere tale informazione. Al contrario, molti sistemi della terza generazione cercano di fornire meccanismi che permettono all'utente di memorizzare files per periodi di tempo indefiniti. Ciò fa sorgere tre problemi di non banale soluzione: 1) un sistema di files deve essere progettato in modo da gestire l'informazione affidatagli, utilizzando nomi di files simbolici assegnati dagli utenti; 2) vi devono essere garanzie che l'informazione non vada perduta né in caso di avaria del sistema né a causa di errori da parte dell'utente stesso; 3) è necessario un meccanismo di protezione che permetta l'accesso ai files soltanto dietro autorizzazione.

f) Multiplazione. Secondo questa tecnica il tempo viene suddiviso in intervalli separati, durante i quali un'unità di risorsa viene al massimo assegnata a un solo lavoro. L'intervallo di tempo durante cui un lavoro può usufruire del controllo esclusivo di un'unità di risorsa può essere definito in modo naturale, a seconda dell'alternanza fra i periodi in cui il lavoro ha o no bisogno di un'unità di quel tipo; oppure può essere definito artificialmente, mediante suddivisione del tempo e assegnazioni prioritarie. Quest'ultimo metodo viene utilizzato principalmente nei sistemi in partizione di tempo e in altri sistemi in cui sia necessario osservare soglie insuperabili per i tempi di risposta.

Il prefisso ‛multi' viene frequentemente aggiunto a un termine per indicare qualche forma di partizione o multiplazione. ‛Multilavorazione' indica la capacità di un sistema di dare assistenza simultaneamente a due o più programmi in azione, o lavori. ‛Multiprogrammazione' indica la capacità di un sistema di avere in memoria centrale simultaneamente programmi o segmenti di programma di due o più lavori. La multiprogrammazione comprende la multilavorazione, ma non viceversa: ad esempio un sistema può eseguire molti lavori attivi, ma fa ciò caricando ed elaborando in memoria centrale soltanto un lavoro per volta. Lo scopo della multiprogrammazione è quello di consentire ai dispositivi del sistema di operare in concomitanza; poiché in memoria centrale vi sono sempre presenti più programmi, ogni qual volta un programma si arresta per utilizzare un dispositivo di ingresso/uscita, l'elaboratore centrale può essere commutato su un altro programma. ‛Multiaccessibilità' indica la capacità del sistema di rendersi accessibile attraverso due o più stazioni terminali. Questa proprietà non ha alcuna relazione con la multilavorazione e la multiprogrammazione. ‛Multielaborazione' indica la capacità di un sistema di adibire due o più elaboratori all'esecuzione di lavori. In pratica la multielaborazione comprende la multiprogrammazione e quindi pure la multilavorazione. ‛Partizione di tempo' è una tecnica utilizzata in certi sistemi dotati di multiaccessibilità e multilavorazione per permettere a utenti differenti di usufruire simultaneamente dei servizi del sistema. Ciò si ottiene mediante rapida multiplazione dell'elaboratore e della memoria centrale fra i lavori in corso.

b) Elementi di struttura dei sistemi

1. Macchine virtuali. - La struttura dei sistemi operativi si può definire molto elegantemente mediante uno o più livelli di programmi di sistema concepiti a scatola cinese, in cui ciascun livello definisce un sistema più potente di quello in esso contenuto. Pertanto i livelli definiscono sistemi progressivamente più potenti, denominati ‛macchine virtuali' il più potente dei quali è quello che definisce l'ambiente in cui gli utenti impiegano i loro programmi.

Si consideri una macchina M con istruzioni I. Un programma p per la macchina M è composto da una sequenza di istruzioni estratte da I. Le possibilità di M possono essere ampliate aggiungendo un prefissato gruppo di programmi S alla macchina M; l'esecuzione di un programma del gruppo S produce una funzione non disponibile da parte di M (si può più correttamente pensare che I e S siano gruppi di nomi di operazioni). È ora possibile definire una macchina M′ provvista di un gruppo di istruzioni I′, con I′ = I′ + S, contenente le operazioni già possibili per M più le nuove operazioni di S. Questa macchina M′ è denominata ‛macchina virtuale', perché alcune delle sue operazioni sono simulate da programmi di S. M viene chiamata la ‛macchina di base'.

Sia p′ un programma eseguibile sulla macchina M′ (cioè, una sequenza di istruzioni comprese nel gruppo I′ I + S). Dal momento che quelle istruzioni di p′ che fanno parte del gruppo S vengono realizzate su M quando chiamate dalla procedura, l'esecuzione (ipotetica) di p′ su M′ produce gli stessi risultati che si otterrebbero eseguendo p′ sulla macchina estesa (M, S). Questa equivalenza si indica scrivendo M′ = (M, S).

Oltre a estendere le possibilità di una data macchina M, c'è un altro importante motivo per definire una macchina virtuale M′ utilizzante M come base: il ‛principio di astrazione'. Questo principio stabilisce che M′ deve essere ‛concettualmente gestibile': gli utenti di M′ non devono preoccuparsi, anzi devono poter ignorare come siano distribuite le istruzioni tra I ed S, quando usano M′. Questo principio implica che l'esecuzione di una data operazione (avvenga essa in I oppure in S) deve essere indivisibile nei riguardi del programma p′ di M′ che l'ha richiesta; cioè essa deve apparire a come un unico passo. Questo principio comporta pure che, perché M′ operi correttamente, può essere necessario che alcune operazioni di M siano accessibili soltanto mediante programmi (autorizzati) di S; ciò induce a osservare che, in generale, esisterà un sottogruppo P di istruzioni di I, chiamate ‛istruzioni privilegiate' di M rispetto ad S, che risulteranno inaccessibili agli utenti di M′; un programma p′ potrà quindi utilizzare soltanto le istruzioni del gruppo I′ = I − P + S. Benché questa nuova definizione di I′ sia una conseguenza immediata della necessità che M operi correttamente, vi è anche la motivazione indiretta della necessità di rendere concettualmente gestibile M′ limitandone la complessità (dal punto di vista delle dimensioni del suo gruppo di istruzioni).

Una corretta ed efficiente realizzazione di una macchina virtuale richiede notevole assistenza da parte dell'hardware. Vi sono quattro aspetti principali da tener presenti. Primo, il sistema deve garantire che nessun programma del gruppo S possa essere iniziato se non dal suo punto di ingresso. Una soluzione ideale (che diviene sempre più attraente man mano che i costi dell'hardware diminuiscono) sarebbe quella di concepire il meccanismo di esecuzione delle istruzioni della macchina base in modo da riconoscere i nomi delle operazioni di S oltre a quelli delle operazioni di I, così da poter generare le appropriate chiamate su questi programmi. Una soluzione più comune, ma meno efficiente, utilizza l'istruzione ‛chiamata di supervisore' SVC(p), la quale fa sì che il meccanismo di esecuzione delle istruzioni invochi un programma ‛gestione di SVC', il quale a sua volta trasferisce il controllo al programma di sistema p specificato come argomento dell'istruzione SVC (tutti i programmi di S, incluso quello di gestione di SCV, devono essere memorizzati in parti di memoria protette, in punti di ingresso noti soltanto al sistema). Secondo, il sistema deve garantire la riservatezza delle strutture di dati gestite dai programmi del sistema S. Se il sistema è in grado di risolvere il problema della protezione delle chiamate di cui si è detto prima e di memorizzare i dati riservati in un'area di memoria protetta, e se i programmi di S sono sotto completo controllo dell'assegnazione di memoria, questo secondo problema non presenta generalmente alcuna difficoltà. Terzo, il sistema deve garantire che le istruzioni privilegiate P siano accessibili soltanto ai programmi di S ma non a qualunque programma p′ scritto sulla base delle istruzioni del gruppo I′ = I − P + S. A questo scopo molti sistemi hanno nell'elaboratore un ‛registro indicatore di livello', L, che viene posto uguale a 1 quando sta correndo un programma di tipo p′ e uguale a 0 quando corre un programma p di S (i livelli 0 e 1 corrispondono, rispettivamente, ai modi di operazione ‛supervisore' e ‛utente' presenti in molte macchine). Il contenuto di questa cella L varia solamente quando si chiamano i programmi di sistema di S o si esce da essi. Il meccanismo di esecuzione di istruzioni permetterà l'esecuzione di un'operazione del gruppo P se, e soltanto se, al momento in cui viene fornita l'istruzione, si trova a essere L = 0. Quarto, il sistema deve realizzare un insieme di programmi di gestione di condizioni, parti del gruppo S, che vengono chiamati ogni qual volta un errore o una condizione di interruzione vengano rilevati nell'hardware (v. sopra, cap. 2, È d, 3 sui comandi di interruzione). Il lettore interessato ai dettagli delle soluzioni dei quattro problemi ora menzionati potrà trovare una notevole quantità di informazioni nei due testi di E. Organick citati in bibliografia.

2. Macchine virtuali a molti livelli. - Si ritiene che non sia desiderabile tentare di specificare un sistema operativo in un'unica fase come un insieme di programmi S basati sulla macchina M; se non altro perché un alto numero di funzioni in S nuocerebbe alla gestibilità concettuale e renderebbe la comprensione o la documentazione o il perfezionamento o le modificazioni del sistema compiti di proporzioni monumentali. Come alternativa, si può definire il sistema in fasi graduali, come una sequenza di macchine virtuali M₀, M₁, ... , M_n, dove M₀ indica l'hardware del sistema e M_n definisce l'ambiente in cui gli utenti eseguono i loro lavori. I programmi del sistema sono ripartiti secondo una sequenza S₀, S₁, ..., S_n-1 tale che la (k + 1)-esima macchina virtuale è costituita da M_k+1 = (M_k, S_k), con ≤ k 〈 n, con gruppo di istruzioni dato da I_k+1 = I_k− P_k + S_k, con 0 ≤ k 〈 n. La realizzazione di chiamate protette e la riservatezza dei dati di sistema è trattata in questo sistema come nel sistema a due livelli descritto nel precedente paragrafo. La creazione di istruzioni privilegiate è trattata utilizzando il registro indicatore di livello L per mostrare a quale livello viene eseguito il programma: quando è in corso un programma del gruppo S_k risulterà L = k. Inoltre il sistema è costruito in modo che il richiamo di una certa operazione p venga accettato soltanto se in quel momento risulta k₁ ≤ L ≤ k₂, dove k₁ è il livello a cui è definito p (cioè p fa parte del gruppo S_k1) e k₂ è il livello a cui p diviene privilegiato (cioè p fa parte del gruppo Pk₂).

Il meccanismo fondamentale di interruzione in un sistema a due livelli generalmente distingue fra un registro indicatore di livello L e una cella MASK che permette l'accettazione di un comando di interruzione (v. sopra, cap. 2, È d, 3 sui comandi di interruzione). Questa distinzione non è necessaria per un sistema a molti livelli ben progettato, poiché è possibile assegnare il programma di gestione di ciascuna condizione a un certo livello S_k, mentre si può utilizzare il registro indicatore di livello L per interdire comandi di interruzione per lo stesso livello o per livelli superiori. Il sistema a molti livelli pertanto costituisce un meccanismo di interruzione prioritario, entro cui condizioni più importanti possono interrompere la gestione di condizioni meno importanti.

La filosofia della macchina virtuale a molti livelli presenta potenti vantaggi, a patto che le funzioni del sistema operativo possano essere appropriatamente separate in una gerarchia consistente con la gerarchia delle funzioni quale deriva da questa struttura a scatole cinesi (nel cap. 3, È c si vedrà come ciò può essere realizzato). In primo luogo l'incremento di complessità nel passare dal livello k al livello immediatamente successivo (definendo la complessità in termini di dimensioni del gruppo I_k+1 = I_k − P_k + S_k) può essere contenuto in limiti modesti, in modo da rendere facile la comprensione delle operazioni e dell'uso di M_k+1 in termini di M_k. In secondo luogo si può stabilire sistematicamente la correttezza della macchina virtuale M_k+1: una volta che si sia provato che M_k lavora correttamente, basta mostrare che i programmi di S_k sono corretti. In terzo luogo il sistema operativo può essere portato all'operatività passo dopo passo: una volta che M_k è divenuta operativa, vengono aggiunti e provati i programmi di S_k; a questo punto M_k+1 è automaticamente operativa. In quarto luogo, se si verifica un errore che rende inconsistenti i dati riservati di qualche programma di S_k (facendo nascere il sospetto che M_k+1 non sia corretta), è generalmente possibile, se l'errore viene rivelato abbastanza presto, ipotizzare che M_k funzioni ancora correttamente e utilizzare i suoi mezzi per localizzare e correggere l'errore. Ciò va confrontato con la situazione delle precedenti macchine a due livelli M′ = (M, S) in cui, se si rivela un errore nei dati riservati di 5, si hanno a disposizione soltanto i mezzi primitivi di M per localizzare e correggere l'errore.

3. Elaborazioni nelle macchine virtuali a molti livelli. - La discussione precedente si basava sul presupposto che le funzioni di sistema fossero dei programmi richiamabili mediante un meccanismo basato sulle consuete nozioni di procedura di chiamata e ritorno. Un concetto che sta trovando crescente favore fra i progettisti di sistemi operativi è che ogni funzione di sistema e ogni programma di utenza può realizzarsi come un'elaborazione. Un'elaborazione può essere concepita come un programma in esecuzione definito da una sequenza di ‛parole di stato' dell'elaboratore, intendendo per parola di stato l'insieme dei valori memorizzati nei vari registri dell'elaboratore (includendo i registri aritmetici, di indice e di base e in modo specifico l'indicatore di istruzione IP e l'indicatore di livello L). Una struttura di dati detta ‛lista d'elaborazione', PL, contiene le parole di stato di tutte le elaborazioni esistenti; in particolare, PL (p) contiene la parola di stato dell'elaborazione. L'elaborazione p può essere arrestata segnalando all'elaboratore di arrestarsi, conservando quindi la parola di stato in PL(p). L'elaborazione p può essere ripresa dal punto in cui era stata precedentemente interrotta prelevando la sua parola di stato da PL (p) e caricandola nell'elaboratore e quindi attivando l'elaboratore (per ulteriori informazioni sulle elaborazioni e il loro uso il lettore è rinviato a Brinch-Hansen, 1973; Denning, 1970; Tsichritzis e Bernstein, 1974; Wilkes, 1974³).

In ciascun istante un'elaborazione può trovarsi in uno dei due stati principali di esistenza: ‛abilitata' o ‛disabilitata'. Essa è abilitata ogni qual volta può procedere validamente sull'elaboratore. È disabilitata ogni qual volta il proseguimento della sua esecuzione è bloccato in attesa della ricezione di un dato segnale, quale un segnale di ritorno da un'elaborazione richiamata, o un segnale di condizione. In ciascun istante soltanto una fra le elaborazioni abilitate corre; quella, cioè, che possiede il controllo dell'elaboratore. Gli indici di tutte le elaborazioni abilitate vengono registrati in una struttura di dati denominata ‛lista pronta'.

Nella lista pronta a ogni elaborazione viene assegnata una priorità che rispecchia i livelli di definizione nella gerarchia della macchina virtuale. Si supponga che p sia de-. finito come membro del gruppo S_k1 e q come membro di S_k2. Se p precede q nella lista pronta, deve risultare k₁ ≤ k₂. La ‛regola ordinatrice' prevalente stabilisce che l'elaborazione in corso sarà sempre quella di maggiore priorità fra quelle abilitate (cioè quella in testa alla lista pronta). Questa regola ordinatrice è coerente con le proprietà della gerarchia a molti livelli e, di fatto, è diretta conseguenza di questa. Poiché la regola ordinatrice comporta che, ogni volta che un'elaborazione viene abilitata o disabilitata, diviene necessario prendere una decisione sul nuovo ordine e poiché almeno alcune fra le abilitazioni e le disabilitazioni vengono effettuate dal meccanismo di esecuzione delle istruzioni, tale meccanismo deve avere possibilità di accesso sia all'elaborazione che alla lista pronta.

c) Progettazione di un sistema operativo

Questo paragrafo illustra a grandi linee la progettazione di un possibile sistema operativo come struttura di macchina virtuale a molti livelli costruita secondo il meccanismo di base illustrato nel paragrafo precedente. Il sistema che sarà descritto è ipotetico, volutamente semplificato a causa dell'omissione di numerose funzioni presenti invece in molti sistemi. Nondimeno esso contiene molte delle idee importanti presenti nei sistemi operativi e sarà utile per familiarizzare il lettore con questi.

Il discorso s'inizia considerando tre macchine virtuali costruite intorno all'hardware di base M₀; queste macchine costituiscono la parte centrale, o ‛nucleo', del sistema composto da: M₀, l'hardware di base; M₁, il gestore della elaborazione; M₂, il gestore della memoria virtuale; M₃, il sistema di files. La discussione quindi procede definendo un gruppo di programmi scritti per M₃ che, insieme con questa, definiscono un ambiente M₄ dove gli utenti fanno correre i lavori.

1. Gestione dell'elaborazione. - La parte essenziale del gestore dell'elaborazione è già stata descritta in connessione con la filosofia che opera nelle macchine virtuali. Le elaborazioni di livello S₀ sono la gestione di condizione ‛temporizzatore d'intervallo' e le operazioni ‛rimozione', ‛abilitazione', ‛disabilitazione', ‛invio di messaggio', ‛ricezione di messaggio', ‛creazione', ‛cancellazione'. L'operazione ‛rimozione' cancella l'elaborazione che si trova in testa alla lista pronta al momento in cui essa viene chiamata e la memorizza in una posizione designata dal programma che l'ha chiamata; essa verrà utilizzata in certe circostanze da un'elaborazione a più alto livello per disabilitare l'elaborazione che ha chiamato o che è stata interrotta. L'operazione ‛abilitazione inserisce l'indice di un'elaborazione specificata nella lista pronta all'appropriato livello di priorità. L'operazione ‛disabilitazione' rimuove l'elaborazione in corso dalla lista pronta e sposta l'elaborazione verso la successiva elaborazione pronta.

Le operazioni ‛invio' e ‛ricezione di messaggio' vengono utilizzate per scambiare segnali fra le varie elaborazioni; esse manipolano il contenuto di speciali oggetti di dati chiamati ‛code di messaggi', che sono riservati a S₀. Se l'elaborazione p esegue l'operazione ‛invio di messaggio' (m,Q), la coppia (p,m) viene attaccata alla fine di una lista di messaggi Q (mentre la prima coppia della lista viene espulsa); m rappresenta il messaggio che p desidera posizionare in quel luogo. Se l'elaborazione q esegue l'operazione (p,m) ‛ricezione di messaggio' (Q), allora il primo ingresso (p,m) viene rimosso dalla coda Q e restituito. Per assicurare la necessaria sincronizzazione, un eventuale tentativo da parte di q di ricevere un messaggio da una coda vuota si risolverà in una disabilitazione di q; quando poi p invia un messaggio nella coda vuota, q viene riabilitata. La realizzazione delle code di messaggi deve, pertanto, mantenere memoria delle elaborazioni eventualmente bloccate in attesa dell'arrivo di un messaggio. Mediante trasmissione di (p,m) come messaggio totale, piuttosto che del reale messaggio m specificato da p, il sistema garantisce all'organo ricevente un'indelebile identificazione di quello che l'ha chiamato; ciò non soltanto fornisce all'organo ricevente l'opportunità di autenticazione del messaggio, ma anche la possibilità di sapere a quale elaborazione va diretta la risposta finale (v. Brinch-Hansen, 1973).

L'operazione ‛creazione' è utilizzata per assegnare a una nuova elaborazione la parola di stato iniziale specificata dal programma che l'ha chiamata o per creare una nuova coda di messaggio; l'indice dell'elaborazione o della coda create viene restituito al programma chiamante. L'operazione ‛cancellazione' viene utilizzata per disattivare una specifica elaborazione o coda, rendendone libero l'indice per nuovi usi successivi.

Il gestore di condizione ‛temporizzatore d'intervallo' viene utilizzato soprattutto per evitare che qualche elaborazione monopolizzi l'elaboratore. Allorquando l'elaborazione inizia una parte di esecuzione sull'elaboratore, l'orologio che temporizza gli intervalli riparte automaticamente da zero. Se l'elaborazione supera il tempo assegnatole, il gestore di condizione la blocca e la colloca nella posizione più bassa della lista pronta, compatibilmente con la sua priorità.

I programmi di sistema ora menzionati definiscono una macchina virtuale M₁ = (M₀, S₀) in cui l'unico elaboratore non è più individuabile esplicitamente, in quanto vengono simulati molti elaboratori virtuali intercomunicanti (uno per ciascuna elaborazione). In altre parole, M₁ prescinde dal singolo elaboratore dell'hardware sostituendolo con molti processi di elaborazione concorrenti.

fig. 17

2. Memoria virtuale. - L'obiettivo di un sistema di memoria virtuale è quello di simulare una memoria centrale agli occhi dell'utente, mediante le risorse disponibili in termini di memoria centrale e memoria ausiliaria. Ciò si ottiene interponendo un dispositivo denominato ‛compilatore di mappe d'indirizzi' fra l'elaboratore e il sistema di memoria (v. fig. 17). L'insieme degli indirizzi che l'elaboratore può generare per conto di un dato programma è chiamato ‛spazio degli indirizzi' di quel programma e talvolta ‛spazio virtuale degli indirizzi‛ o ‛memoria virtuale', per ricordare che questo spazio è in effetti simulato. L'insieme di indirizzi riconoscibili dall'hardware di indirizzamento della memoria centrale è chiamato ‛spazio di memoria' del sistema. Come si vede dalla fig. 17, l'elaboratore non colloca più gli indirizzi direttamente nel registro degli indirizzi di memoria (denominato MAR nel cap. 2, §  c), ma li colloca in un registro di indirizzi virtuali (VAR). Il compilatore di mappe, allorquando l'elaboratore ha collocato un indirizzo in VAR, esegue una delle due principali azioni seguenti, o entrambe: 1) se l'oggetto indirizzato non si trova nella memoria centrale, il compilatore di mappe fornisce il comando di dirigersi verso la memoria ausiliaria (generalmente un tamburo) per far sì che l'oggetto desiderato venga trasferito nella memoria centrale (se questa è completamente piena, qualcos'altro dovrà esserne rimosso); 2) fatto ciò, il compilatore di mappe genera l'indirizzo della memoria centrale corrispondente all'indirizzo virtuale, lo colloca in MAR e consente che si proceda.

Evidentemente la prima delle due azioni, se necessaria, richiederà molto più tempo della seconda; pertanto l'efficienza del meccanismo dipende dalla sua capacità di mantenere gli oggetti più utili caricati nella memoria centrale, in modo da minimizzare il numero delle azioni di primo tipo necessarie.

L'azione del compilatore di mappe può essere generalizzata con una funzione f_p : A_p → M, che traduce lo spazio degli indirizzi A_p dell'elaborazione p nello spazio di memoria M. Questa mappa è dipendente dal tempo e può essere alterata in qualunque istante, poiché per principio gli obiettivi della memoria virtuale comprendono la possibilità di riposizionare un programma (o parte di esso) in qualunque istante, di ricaricare un programma in una regione della memoria centrale diversa da quella occupata in precedenza e di variare la quantità di spazio assegnata a un programma.

fig. 18A

Vi sono numerosi metodi per realizzare mappe di indirizzi; per una trattazione completa il lettore è rinviato alla bibliografia (v. Brinch-Hansen, 1973; v. Denning, 1970; v. Wilkes, 1974³). La tecnica più semplice è forse quella dell' ‛impaginazione'. Gli spazi degli indirizzi e della memoria si possono concepire come vettori, cioè A_p = {0,1, ..., 2^a − 1},con a > 0, e M = {0, l, ..., 2^m −1},con m > 0. Si noti che a e m rappresentano, rispettivamente, il numero di bits di un indirizzo virtuale e di un indirizzo di memoria centrale. Entrambi questi spazi sono ripartiti in blocchi di eguali dimensioni, chiamati ‛pagine', che vengono utilizzati come unità di memorizzazione e trasferimento. Le pagine di memoria centrale vengono chiamate ‛telai d'impaginazione' per ricordare che esse fungono da luoghi di memorizzazione per le pagine dello spazio degli indirizzi. La dimensione delle pagine è costituita da 2^r indirizzi, con r > 0. (La dimensione utilizzata in un dato sistema dipenderà dalla velocità della memoria ausiliaria. Se, ad esempio, tale memoria ha un grande tempo di latenza, si dovranno usare pagine di grandi dimensioni, per esempio di 1.000 voci, in modo che il tempo di latenza medio per trasferimento di una pagina non sia eccessivamente lungo). Se chiamiamo x_k-1x_k-2 ... x₁x₀ i bits di un indirizzo, allora gli indirizzi di base delle pagine avranno valori interi multipli di 2^r e avranno la forma x_k-1x_k-2 ... x_r+1 x_r00 ... 0; ciò comporta che gli r bits di minor ordine di un indirizzo si possono pensare come uno spostamento d entro una pagina, e i (k−r) bits di ordine maggiore si possono pensare come l'indice di una pagina i. Poiché le pagine vengono memorizzate come unità, il compilatore di mappe è tenuto a traslare soltanto i bits indice di pagina, come si desume dalla fig. 18A. La fig. 18B mostra l'intera traslazione, in cui il compilatore di mappe ricerca f_p(i) nella ‛tavola d'impaginazione', PT_p, dell'elaborazione p (i indica l'indice d'impaginazione' di una pagina, p il riferimento). L'ingresso delle tavole d'impaginazione contiene due campi: il bit di presenza P = 1 se e soltanto se la pagina è presente nella memoria centrale; il campo di indici I, contenente l'indice del telaio d'impaginazione in cui si trova quella pagina se è P = 1, oppure un indicatore che localizza la pagina sul tamburo se è P = 0. Per questo tipo di sistema il tempo necessario a traslare un indirizzo può essere mediamente contenuto al di sotto del 20% del tempo di riferimento della memoria centrale (v. Denning, 1970).

La fig. 19 illustra le azioni necessarie per trattare un errore d'impaginazione nell'elaborazione p. Vi sono due gestori di condizione, uno per la condizione di ‛errore d'impaginazione' e l'altro per la condizione di ‛lavoro eseguito' da parte del tamburo. La condizione di errore d'impaginazione avviene quando l'elaborazione p tenta di far riferimento a una pagina i mancante. Il gestore dell'errore d'impaginazione seleziona un certo telaio x (contenente la pagina j di una certa elaborazione q), lo riassegna all'elaborazione p, fa iniziare al tamburo una transazione che preserva il contenuto del telaio x sul tamburo e quindi carica la pagina i dell'elaborazione p sul telaio x; infine si disattiva. Più tardi, quando il tamburo completa la sua transazione, il gestore di ‛lavoro eseguito' del tamburo riabilita l'elaborazione p che era stata interrotta e quindi si disattiva. La ‛strategia della sostituzione', cioè il principio in base a cui viene scelto il telaio x, è un fattore critico per l'efficienza delle memorie virtuali a pagina; una delle strategie più riuscite consiste nello scegliere quella pagina cui non è stato fatto riferimento per un tempo più lungo che per qualsiasi altra (ibid.).

L'esposizione ora fatta è stata, naturalmente, molto semplificata. Una realizzazione più realistica deve risolvere problemi come ‛errori d'impaginazione in elaborazioni simultanee, identificazione di telai d'impaginazione in cui non vi sia scritto alcunché (in modo che non vi sia bisogno di copiarli sul tamburo), ricerca di criteri per identificare le pagine meno utili (da selezionare per la sostituzione) e accelerazione della fase di traslazione allorquando le tavole d'impaginazione sono memorizzate nella memoria centrale.

Si è già notato che ciascuna elaborazione ha la sua propria tavola d'impaginazione. Ciò comporta la necessità di un registro di elaboratore che indichi la tavola d'impaginazione dell'elaborazione in corso, in modo che il compilatore di mappe possa sempre accedere alla corretta tavola d'impaginazione. Questo registro fa parte della parola di stato di un'elaborazione, che viene stabilita automaticamente all'inizio dell'elaborazione.

Il meccanismo ora descritto è dotato di potenti mezzi di protezione della memoria. Poiché tutti gli accessi vengono collaudati dal compilatore di mappe, è impossibile che l'elaborazione richiami informazioni al di fuori della portata della sua tavola d'impaginazione, cioè informazioni che non siano pertinenti a essa; inoltre, poiché le tavole d'impaginazione sono esse stesse non interferenti l'una con l'altra, nessuna elaborazione (ad eccezione dei gestori di errore d'impaginazione e di lavoro eseguito dal tamburo) può alterare l'informazione in esse contenuta. Molti sistemi includono dei bits di codice d'accesso negli ingressi delle tavole d'impaginazione: se il tipo di accesso che si tenta (lettura, scrittura o ricerca di istruzioni) non è permesso dal codice d'accesso della pagina, il compilatore di mappe genererà una condizione di errore.

Il sistema deve contenere una chiamata ‛creazione di spazio di indirizzi', che fa sì che un insieme specificato di pagine della memoria centrale venga copiato sul tamburo e venga creata una tavola d'impaginazione che ricordi la mancanza di queste pagine. Un'altra chiamata, ‛cancellazione di spazio di indirizzi', viene utilizzata per liberare lo spazio occupato dalla tavola d'impaginazione (nella memoria centrale) e dalle sue pagine (sul tamburo).

A questo punto dovrebbe essere ormai chiaro che i gestori di errore d'impaginazione e di lavoro eseguito dal tamburo e le operazioni di creazione e di cancellazione degli spazi d'indirizzi, insieme con le loro strutture di dati riservati (cioè le tavole d'impaginazione e altre tavole localizzanti pagine del tamburo), definiscono il software S₁ del livello 1 e quindi la macchina virtuale M₂ = (M₁, S₁), in cui la distinzione fra la memoria centrale e il tamburo non è più esplicita. In altre parole, M₂ prescinde dalla memoria centrale del sistema sostituendola con spazi distinti per ciascuna elaborazione.

3. Sistema di files. - Molti programmatori hanno bisogno di creare e cancellare oggetti di dati, per cambiare la dimensione di un oggetto, per frazionare e proteggere oggetti e per memorizzare oggetti per lunghi periodi di tempo. Lo spazio lineare degli indirizzi virtuali realizzato dalla macchina M₂ del precedente punto 2 non fornisce tali mezzi. A questo fine molti sistemi comprendono un ‛sistema di archivi' o files che è un mezzo di memorizzazione a livello di sistema, distinto da ogni spazio di indirizzi dell'elaborazione. Un sistema di files soddisfa tali necessità permettendo ai suoi utenti di creare e cancellare files, di cambiare le dimensioni di un file, di condividerne e salvaguardarne la riservatezza e di memorizzare files per periodi indefiniti.

Molti sistemi forniscono alla maggior parte degli utenti soltanto dei files che vengono usati per il solo tempo necessario, cioè cessano di esistere al termine dell'elaborazione. Anche in questo caso limitativo, un sistema di files è utile perché permette durante un'elaborazione di manipolare oggetti variabili senza dover gestire la memoria nel suo spazio di indirizzi.

È facile aggiungere a un sistema di macchina virtuale a molti livelli un sistema di base di files. Le sue strutture di dati di base comprendono un insieme di guide di files, un insieme di tamponi e una tavola dei files attivi. Tutti i files sono tenuti su memoria a disco. Le elaborazioni che costituiscono il software (S₂) del sistema di files sono il gestore di condizione ‛lavoro eseguito' da parte del disco e le operazioni ‛creazione di files', e cancellazione di files', ‛apertura', ‛chiusura', ‛copiatura'. Questi componenti verranno ora illustrati.

Ogni utente possiede, associato al suo titolo di riconoscimento, una ‛guida di files', contenente gli indicatori (indirizzi di dischi) di tutti i files a lui riservati (se egli non possiede files permanenti, la sua guida, nei momenti in cui non utilizza il sistema, risulterà vuota). Il sistema possiede anche una ‛guida di files' principale, che contiene gli indicatori di tutte le guide di files degli utenti; le guide di files individuali vengono memorizzate sul disco e vengono copiate dal sistema di files nella memoria centrale soltanto allorquando l'utente ha un'elaborazione nel sistema (la guida di files principale può contenere anche altre informazioni, come informazioni generali relative al nominativo di ciascun utente e la sua parola d'ordine per accedere al sistema). Per mantenere traccia delle guide di files delle elaborazioni esistenti, le strutture di dati dei sistemi di files contengono una matrice FD, tale che FD[p] è l'indicatore della guida di files dell'elaborazione p. Ogni qual volta un'elaborazione di utenza richiede un servizio da parte di un'elaborazione di manipolazione di files, è facile per quest'ultima localizzare la guida di files (e quindi i files) della prima.

fig. 20

Un file sarà qui considerato come una semplice matrice lineare o vettore di voci memorizzate su disco. Il suo indirizzo di base e la sua lunghezza sono memorizzati nella guida di files dell'utente proprietario del file stesso (v. fig. 20). A ogni istante un file si può trovare in uno stato attivo o inattivo; non è possibile accedere a files inattivi. Se l'elaborazione p esegue la chiamata del sistema di files ‛apertura (n)', il sistema di files creerà un ingresso per (p,n) nella tavola dei files attivi e assegnerà al file una memoria libera di b voci. Il sistema indicherà che il file è attivo per conto dell'elaborazione p immettendo p nel campo delle elaborazioni utenti della guida data da FD[p]. Inoltre apporrà un indicatore di file all'inizio del file sul disco e un indicatore di tampone alla fine di questo (l'uso di questi indicatori verrà discusso tra poco). Quando l'elaborazione p ha terminato di utilizzare il file, lo disattiva con la chiamata di sistema di files e chiusura (n)', che cancella l'ingresso (p,n) dalla tavola dei files attivi, annulla l'assegnazione della memoria e pone uguale a zero il campo delle elaborazioni utenti dell'ingresso del file n nella guida data da FD[p].

Per creare un file l'elaborazione p emette la chiamata ‛creazione di file (n,l)', che procurerà l'assegnazione di una parte di disco di lunghezza l e indirizzo di base d e farà sì che nella guida data da FD[p] venga formato l'ingresso (0, n, l, d), rispettivamente, per l'elaborazione utente, il nome, la lunghezza e l'indirizzo del disco. Se l'elaborazione p emette la chiamata ‛cancellazione di file (n)', il detto ingresso sarà cancellato e l'area del disco liberata (se il campo di elaborazione utente dell'ingresso del file n è diverso da zero al momento in cui viene dato il comando di cancellazione, anche l'ingresso (p,n) della tavola dei files attivi deve essere cancellato, liberando l'area tampone).

Se l'elaborazione p desidera leggere un file, esegue la chiamata ‛copiatura (read, n, w, a, eof)', che ha l'effetto di copiare le w parole successive dal file n, partendo dal punto dato dall'indicatore di file, scrivendo i dati nello spazio degli indirizzi di p a partire dall'indirizzo a. Il sistema di files non esegue copiature dirette dal disco; esso copia invece le w voci richieste dal tampone, a partire dalla posizione dell'indicatore di tampone, lasciando a questo indicatore di tampone il compito di designare la prima delle posizioni non lette. Qualora l'indicatore raggiunga la fine della memoria prima che la transazione sia completata, il sistema di files genererà una richiesta affinché il disco legga le successive b voci (denominate generalmente records) dal file immettendole nella memoria; queste voci vengono prelevate a partire dalla posizione data dall'indicatore di file. Il gestore d'interruzione per ‛lavoro eseguito' da parte del disco causerà in seguito l'avanzamento di b voci dell'indicatore di file, azzererà l'indicatore di tampone alla base di questo e continuerà l'operazione di lettura dal punto in cui questa è stata interrotta. Il sistema di files controlla se un'operazione di lettura cerca di leggere al di là della fine del file; se ciò avviene, esso copia la rimanente porzione e invia l'indicazione di ‛fine file' ponendo eof = 1. Se l'elaborazione p desidera scrivere dentro un suo file n, essa emette la chiamata di sistema di files ‛copiatura (write, n, w, a, eof)', che si sviluppa in modo analogo all'operazione di lettura. Infine, se l'elaborazione desidera riportare l'indicatore di file all'inizio del file, essa emette la chiamata di sistema ‛riavvolgimento (n)', che provoca il rinvio dell'indicatore di file all'indirizzo di base di questo e dell'indicatore di tampone alla fine di questo.

Molti sistemi forniscono un mezzo speciale mediante cui qualunque operazione di file può essere utilizzata in riferimento a una guida di cui sia specificato l'indicatore. Ciò si può effettuare mediante una chiamata di sistema di files ‛chiamata di file' (indicatore di guida, operazione, parametri), in cui per ‛operazione' si intende una qualunque delle operazioni di un dato file e i ‛parametri' sono gli argomenti di detta operazione. L'operazione ‛chiamata di file' deve essere privilegiata rispetto alle elaborazioni dell'utente, per evitare che queste ottengano accesso non autorizzato alle guide. Comunque questa operazione deve essere disponibile per le elaborazioni di controllo di lavoro autorizzate di cui si discuterà nel prossimo punto 4, poiché queste avranno bisogno di accedere a certi files per conto di elaborazioni di utenza comunque scelte.

Un'estensione ordinaria di questo sistema consente la condivisione dei files da parte di molti utenti. Un metodo per realizzare ciò si avvale di due tipi di ingressi alle guide: quello diretto di cui si è parlato finora e un ‛legame' indiretto che, invece, indica un ingresso di un'altra guida. Una chiamata di sistema di files permette al proprietario di un file di specificare se vi sono altri utenti che possono accedere al file e quali; questa informazione viene memorizzata in una ‛lista di controllo di accesso' nella guida di files del proprietario del file. Un'altra chiamata consente all'utente di creare un ingresso di legame nella sua guida, ammesso che egli sia incluso nella lista di controllo d'accesso dei proprietari di files. Generalmente questi sistemi comprendono codici d'accesso per tutti gli ingressi di guide, per indicare i permessi di lettura e di scrittura (v. Organick, 1972).

Un'altra comune estensione supera il concetto di file sequenziale, cioè l'ipotesi che il file sia una matrice lineare di voci. In questa generalizzazione, un file è costituito da un insieme di records, ciascuno dotato di un numero di indice; il file è organizzato in modo speciale sì da permettere che la ricerca dei records avvenga utilizzando i numeri di indice e anche che un particolare record possa essere localizzato sulla base della presentazione del suo numero di indice senza bisogno di effettuare la ricerca sull'intero file (v. Severance, 1974).

Un'ulteriore estensione elimina la distinzione fra lo spazio degli indirizzi di un'elaborazione e il suo spazio dei files (cioè l'insieme dei suoi files) e, come conseguenza, elimina la necessità che il programmatore includa le operazioni di copiatura fra i due spazi. La generalizzazione, chiamata ‛spazio dei segmenti di indirizzi', combina la memoria virtuale e il sistema di files in un unico livello della macchina virtuale a molti livelli (v. Denning, 1970).

Il meccanismo ora descritto definisce una macchina virtuale M₃ = (M₂, S₂) in cui il disco per memorizzare i files non è più esplicito. In altre parole M₃ prescinde dal dispositivo di memorizzazione dei files sostituendolo con un sistema in cui ciascuna elaborazione viene fornita di uno ‛spazio di files', nel quale i files possono essere manipolati mediante operazioni di sistema di files.

4. Controllo di lavoro. - Il sistema di base a molti livelli possiede ora la capacità di sostenere l'esecuzione di semplici lavori presentati dall'utente. Per illustrare questi principî si consideri il seguente semplice esempio di programma.

Le schede presentate sono di due tipi: le schede ‛controllo', che cominciano con un contrassegno speciale (nell'esempio, la doppia barra) e le schede ‛programma' o ‛dati'. Le prime specificano come il lavoro deve essere trattato dal sistema, le seconde specificano il lavoro stesso. Il lavoro riportato nell'esempio possiede quattro ‛fasi' di lavoro principali, indicate sulle schede controllo. Queste fasi di lavoro verranno realizzate mediante le elaborazioni mostrate nella tab. IV, che costituiscono il software S₃ di una macchina virtuale M₄ (M₄, S₃). Associata a ciascuna di queste elaborazioni (a eccezione del ‛lettore') vi è una speciale coda di messaggio, come mostrato nella tabella. La forma generale di ciascuna elaborazione X della tabella è la seguente:

Ciascun messaggio costituirà un indicatore verso qualche guida di files dell'elaborazione. L'iniziatore ha quasi la stessa forma, ma in esso il comando ‛spedire il messaggio' è sostituito da un'operazione di disabilitazione (v. sotto). Il lettore è di fatto un gestore di condizione che viene attivato non appena viene posto un pacco di schede nel lettore di schede del sistema (v. sotto). Ecco una breve descrizione di ciascuna elaborazione.

‛Lettore'. Legge un pacco di schede dal lettore di schede. Riconosce l'informazione atta a identificare l'utente. Crea una guida di files, indicata con m, con quattro files: ‛comandi', immagini delle schede di controllo delle fasi del lavoro; ‛programma', immagini delle schede del programma; ‛ingresso', immagini delle schede di dati; ‛uscita', inizialmente vuota. Il file ‛comandi' contiene un indicatore del comando successivo, che all'inizio indica il primo comando del file. Quando questo comando viene eseguito, m viene inviato all'interprete dei comandi.

‛Compilatore L'. Riceve il messaggio successivo m. Accede al file ‛programma' e lo compila, producendo un nuovo file di m chiamato ‛programma compilato'. Ciò fatto, invia m all'interprete dei programmi.

‛Caricatore'. Riceve il messaggio successivo m. Accede al file ‛programma compilato' in m e lo carica, insieme con ogni programma di libreria richiesto, entro un nuovo file di m chiamato ‛spazio degli indirizzi'. Ciò fatto, invia m all'interprete dei comandi.

‛Iniziatore'. Riceve il messaggio successivo m. Crea una elaborazione p avente spazio degli indirizzi con valori iniziali dati dallo ‛spazio degli indirizzi' del file di m. La parola di stato iniziale di questa elaborazione ha l'indicatore di istruzione che fornisce il punto d'ingresso del programma, un indicatore della tavola di pagine per lo spazio degli indirizzi e il livello di esecuzione posto più in alto di qualunque programma di sistema. Informa il sistema di files dell'esistenza di p, abilita p e apre i suoi files di ingresso e di uscita.

‛Elaborazione p'. L'esecuzione dell'elaborazione p ora procede a livello di esecuzione L > 4. Si fa l'ipotesi che il compilatore traduca tutte le istruzioni di READ e WRITE del programma nelle corrette chiamate di sistema di files ‛copiatura' (lettura, ingresso, ...) e ‛copiatura' (scrittura, uscita, ...) rispettivamente. Si fa anche l'ipotesi che il compilatore traduca il comando di END del programma nella coppia di chiamate ‛spedire il messaggio' (Ø,T) e ‛disabilitare', in cui 0 rappresenta un messaggio di annullamento (il terminatore capirà l'identità dell'elaborazione da terminare poiché l'elaborazione di invio messaggio annette al messaggio l'indice del programma chiamante).

‛Terminatore'. Riceve il successivo messaggio (p,Ø. Ottiene (dal sistema di files) la guida m utilizzata dall'elaborazione p. Cancella il processo p e chiude i suoi files di ingresso e di uscita. Invia m all'interprete dei comandi.

‛Stampatore'. Riceve il successivo messaggio m. Accede al file di ‛uscita' nella guida m e lo trasmette alla stampante di linea. Ciò fatto, invia m all'interprete dei comandi.

‛Interprete dei comandi'. Riceve il messaggio successivo m. Accede al file ‛comandi' nella guida m. Ottiene il comando successivo e fa avanzare l'indicatore di ‛comando successivo‛ nel file. Se non vi è alcun comando successivo cancella m e tutti i suoi files. Altrimenti invia m in X, dove X rappresenta l'elaborazione che realizza la fase di lavoro citata nel comando.

Rappresentando rispettivamente con S(X) e G(X) gli eventi di invio e di ricezione di un messaggio dalla coda X, la sequenza di eventi che si verificano durante l'esecuzione di un tipico lavoro è la seguente.

In questo esempio, l'interprete dei comandi cancella la guida di files e tutti i files in essa allorquando il lavoro è completato (nelle configurazioni più generali, soltanto i files temporanei sarebbero cancellati). In un sistema in partizione di tempo, le operazioni di base sono le stesse, salvo che generalmente vi e un'unica elaborazione interprete dei comandi associata a ciascun terminale attivo, per elaborare comandi (e altri ingressi e uscite) provenienti da quel terminale.

Le elaborazioni ora presentate possono interpretarsi come il software S₃ di una macchina virtuale M₄ = (M₃, S₃) in cui venga realizzato il controllo di lavoro. In questa macchina un programma di utenza è svolto a livello L ≥ 4. Alcuni sistemi possono definire la maggior parte delle operazioni di sistema (salvo importanti operazioni per inviare messaggi tra elaborazioni e per manipolare i files) come privilegiate al di sopra del livello 4 e inizieranno un'elaborazione al livello L = 4 0 a un livello L > 4 a seconda che essa richieda l'accesso a tutte le operazioni del sistema o no.

5. Conclusione. - Concludendo, val la pena di sottolineare che ciò che è stato detto non è altro che una visione d'insieme di un problema concettuale di grande complessità. A causa dei limiti di spazio si è trattato soltanto superficialmente di problemi molto importanti, come l'amministrazione delle risorse, la protezione e la sicurezza delle informazioni, il controllo e la correzione degli errori e la valutazione dell'efficienza dei sistemi. Trattazioni di questi problemi si possono trovare nei testi di Brinch-Hansen (v., 1973), Denning (v., 1971), Tsichritzis e Beinstein (v., 1974), Wilkes (v., 1974³). Comunque la presente discussione ha fornito gli elementi fondamentali della struttura dei sistemi: come si può impostare la soluzione di problemi quali il controllo di elaborazioni concomitanti, la memoria virtuale, la memorizzazione a lungo termine dei files e il controllo delle operazioni associate all'esecuzione di un lavoro. (V. anche calcolatori).

Bibliografia

Brinch-Hansen, P., Operating systems principles, Englewood Cliffs, N. J., 1973.

Burroughs Corp., Digital computer principles, New York 1969².

Coffman, E. G., Denning, P. J., Operating systems theory, Englewood Cliffs, N. J., 1973.

Denning, P. J., Virtual memory, in ‟Computing surveys", 1970, II, 3, pp. 153-189.

Denning, P. J., Third generation computer systems, in ‟Computing surveys", 1971, III, 4, pp. 175-216.

Hellerman, H., Digital computer system principles, New York 1967.

Knuth, D. E., The art of computer programming, vol. II, Reading, Mass., 1969, cap. 4.

Kohavi, Z., Switching and finite automata theory, New York 1970.

Minsky, M. L., Computation: finite and infinite machines, Englewood Cliffs, N. J., 1967.

Organick, E., The MULTICS system. An examination of its structure, Cambridge, Mass., 1972.

Organick, E., Computer system organization. The B5700/B6700 series, New York 1973.

Rosin, R. F., Contemporary concepts of microprogramming and emulation, in ‟Computing surveys", 1969, I, 4, pp. 197-212.

Severance, D., Identifier search mechanisms. A survey and generalized model, in ‟Computing surveys", 1974, VI, 3, pp. 195-207.

Tsichritzis, D., Bernstein, P., Operating systems, New York 1974.

Wilkes, M. V., Time sharing computer systems, New York-Amsterdam 1974³.