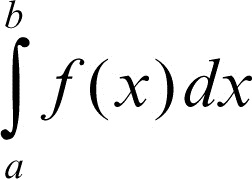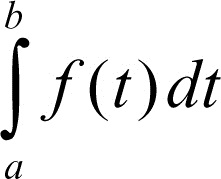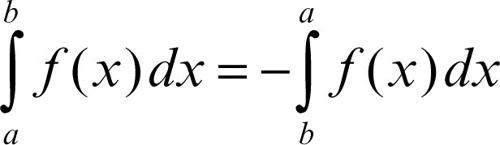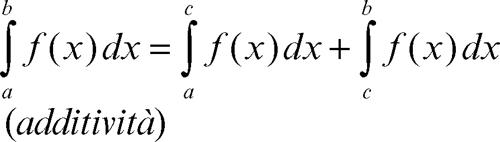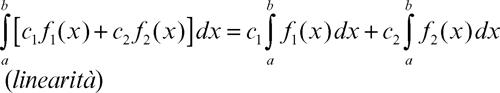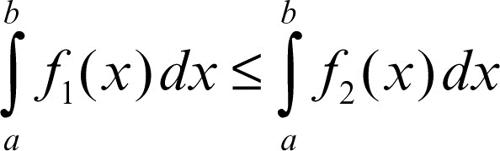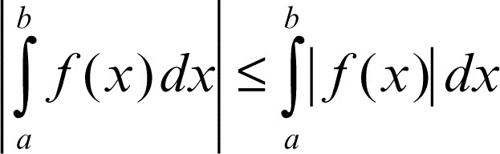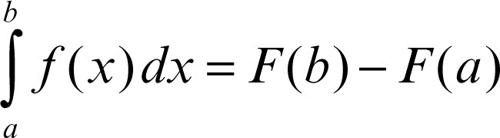integrale definito

integrale definito

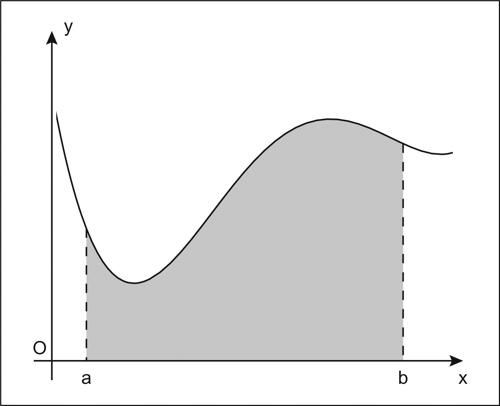
integrale definito nozione che nasce storicamente dal problema del calcolo delle aree. Si supponga in prima istanza che ƒ(x) sia una funzione continua e non negativa in un intervallo limitato [a, b]: la superficie T compresa tra l’asse x e il grafico di ƒ(x), in un certo intervallo [a, b], espressa formalmente da

si chiama trapezoide (o superficie sottesa al grafico della funzione). L’area di tale superficie può essere valutata con un procedimento di approssimazione già impiegato da Fermat e altri, prima della invenzione del calcolo integrale vero e proprio. Si suddivida l’intervallo mediante una sequenza finita di punti x₀ = a < x₁ < x₂ < ... < x_n = b e si ponga

Scelti ad arbitrio dei punti ξ_i ∈ [x_i−1, x_i], con 1 ≤ i ≤ n, si costruiscano le somme integrali

Esse rappresentano l’area di una figura formata dall’unione di n rettangoli, che approssima T. Si dimostra, sotto opportune ipotesi di regolarità per la funzione ƒ, che, indipendentemente dalla scelta dei punti x_i e ξ_i, per δ → 0 il valore di S(δ) ammette un limite finito J, che viene detto integrale definito secondo Cauchy di ƒ(x) relativo all’intervallo [a, b], e si designa col simbolo

(si legga «integrale da a a b di effe di x in di x»). Gli estremi a e b si chiamano rispettivamente primo e secondo estremo di integrazione, la funzione ƒ(x) è detta funzione integranda, x variabile di integrazione, di cui dx è il differenziale. Si precisa che il valore di J dipende solo dall’intervallo di integrazione [a, b] e dalla funzione ƒ, ma non dal nome che si adotta per la variabile di integrazione, che è una variabile muta, per cui

rappresenta esattamente lo stesso numero J. Il procedimento ora indicato fornisce l’area del trapezoide T nell’ipotesi che ƒ(x) sia non negativa, ma ha significato indipendentemente dal segno di ƒ, e, nel caso in cui ƒ cambi di segno nell’intervallo considerato, rappresenta la differenza delle aree che si trovano nel semipiano y > 0 e di quelle che invece stanno in y ≤ 0. Anzi, esso è valido anche nel caso di funzione complessa di variabile reale. È anche possibile operare con a > b, utilizzando una sequenza {x_i} decrescente e in tal caso si ottiene

Le principali proprietà dell’integrale definito, che si mantengono anche nelle successive generalizzazioni, sono le seguenti:

• Se ƒ₁(x) ≤ ƒ₂(x) in [a, b] (con a ≤ b), risulta

da cui in particolare

Il teorema fondamentale del → calcolo integrale lega la nozione di integrale definito a quella di → integrale indefinito, riducendone il calcolo analitico in molti casi a quello di una primitiva della funzione integranda: risulta infatti

dove F(x) è una generica primitiva di ƒ(x) sufficientemente regolare, per esempio continua in [a, b] (→ Newton-Leibniz, formula di). Le ipotesi della continuità di ƒ e di limitatezza dell’intervallo [a, b] possono poi essere mitigate. Sempre restando nell’ottica dell’integrale definito secondo Cauchy si ottiene così la nozione di → integrale improprio (o generalizzato) quando la continuità manchi solo in un numero finito di punti. Più ampia è la generalizzazione che porta all’integrale secondo Cauchy-Riemann (→ Riemann, integrale di).

Una caratterizzazione delle funzioni integrabili secondo Riemann è fornita dal criterio di Lebesgue-Vitali: condizione necessaria e sufficiente perché una funzione limitata nell’intervallo [a, b] sia integrabile è che l’insieme dei punti di discontinuità abbia misura nulla. Pur ampliando assai la classe delle funzioni integrabili, in quanto risultano integrabili tutte le funzioni a variazione limitata, questa nozione non riesce a catturare la generalità necessaria per le applicazioni dell’analisi funzionale, essendo l’integrale ancora un funzionale additivo, ma non numerabilmente additivo. Il passo decisivo venne compiuto, intorno al 1900, mediante la teoria dell’integrazione dovuta a Lebesgue (→ Lebesgue, integrale di).

L’interpretazione geometrica dell’integrale definito si ottiene considerando il grafico cartesiano di ƒ, supposta a valori positivi. Ogni somma inferiore (superiore) fornisce l’area del plurirettangolo unione di rettangoli aventi per base Δx_k e per altezza e′_k(e″_k)mentre l’integrale fornisce l’area del rettangoloide associato alla funzione. Se il grafico di questa attraversa l’asse x, l’integrale fornisce una somma algebrica di aree, considerando negative le aree delle porzioni del rettangoloide al di sotto dell’asse x.