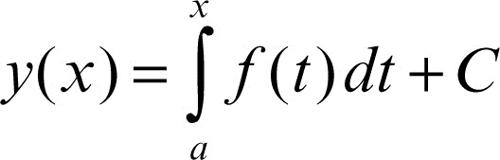integrale
integrale
integrale termine, introdotto da Jakob Bernoulli nel 1695, usato per indicare una delle nozioni fondamentali dell’analisi matematica, collegata sia al problema della determinazione dell’area sottesa al grafico di una funzione di una incognita e delle sue estensioni lineari, spaziali e pluridimensionali, sia al problema inverso della derivazione, cioè della ricerca di una funzione di cui sia nota la derivata (→ calcolo integrale, teorema fondamentale del). Se quest’ultima è questione che venne posta in matematica solo nel Seicento, in relazione soprattutto alla fisica, il problema geometrico delle quadrature fu affrontato con successo già dai geometri greci: essi riuscirono a calcolare aree racchiuse da linee curve e da poligoni con il metodo di esaustione, che consisteva nell’«approssimare» l’area (o il volume) cercata mediante la scomposizione della superficie (o del solido) in un numero infinitamente grande di elementi, ciascuno dei quali infinitamente piccolo. Al metodo del calcolo delle aree concepito come la somma di una infinità di rettangoli di dimensioni infinitesime si richiamarono in seguito i geometri del Seicento (B. Cavalieri, E. Torricelli, P. de Fermat, G.P. de Roberval) con il metodo degli indivisibili. Proprio nel Seicento divenne un problema fondamentale per i matematici quello di ricercare una funzione «primitiva» di una derivata y ′ = ƒ(x), cioè una F(x) tale che F′ (x) = ƒ(x); problema tipico era la determinazione del cammino percorso da un corpo mobile, nota l’espressione della velocità in funzione del tempo. Con Leibniz e Newton divenne definitivamente chiara l’intima connessione, già anticipata da Torricelli e Barrow, che intercorreva tra i due problemi. La scoperta della natura reciproca delle operazioni di derivazione e integrazione portò per lungo tempo a considerare la seconda semplicemente come l’inversa della prima. Solo nell’Ottocento la teoria dell’integrazione cominciò a configurarsi come autonomo campo di ricerca, sia per l’accresciuto dominio delle funzioni studiate dai matematici (funzioni discontinue, definite «a tratti» o mediante limiti), spesso non integrabili con le procedure classiche, sia per la parallela opera di sistemazione critica dei fondamenti del calcolo infinitesimale inaugurata da A.-L. Cauchy e proseguita (per quanto riguarda l’integrale) soprattutto da G.P. Dirichlet, B. Riemann, G. Peano, G. Jordan, T.J. Stieltjes. Infine, una più generale definizione di integrale, direttamente connessa al problema teorico della misura, fu proposta all’inizio del secolo da H. Lebesgue. I due tipi di problemi che hanno portato alle prime formulazioni del calcolo integrale, in realtà molto legati tra loro, giustificano l’utilizzo dello stesso nome: nel primo caso si parla di integrale deƒinito, nel secondo di integrale indeƒinito, anche se si tratta di due enti matematici concettualmente diversi (il primo è un numero, che dà la misura di un’area in un’unità arbitraria, il secondo definisce una classe di infinite funzioni che differiscono per una costante).
Il termine «integrale» riferito a una equazione differenziale equivale a soluzione, per analogia col caso dell’equazione y ′ = ƒ(x), con ƒ integrabile, le cui soluzioni, al variare della costante arbitraria C, sono tutte e sole della forma
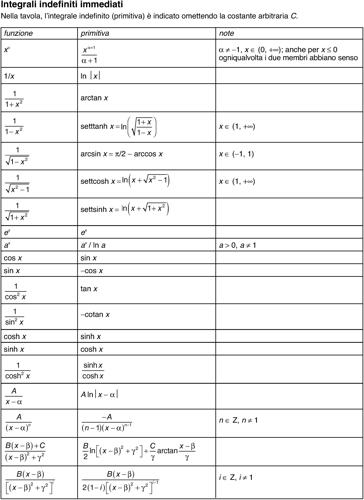
In generale, un integrale di una equazione differenziale è determinato da un problema di → Cauchy; tuttavia non esiste una formula che risolva analiticamente questo problema, ma si è in grado di determinare l’espressione della soluzione solo in casi particolari, raccolti nella tavola degli integrali immediati (si veda la tavola). Per l’inquadramento della nozione di integrale, si vedano i lemmi: → calcolo integrale; → calcolo integrale, teorema fondamentale del; → equazione differenziale. Per le definizioni particolari e le tecniche di calcolo, si vedano i lemmi: → integrale definito; → integrale indefinito; → integrazione.
