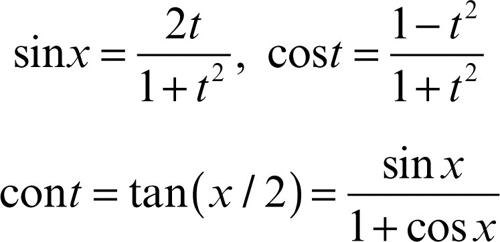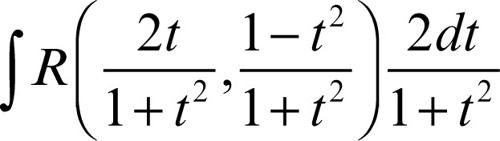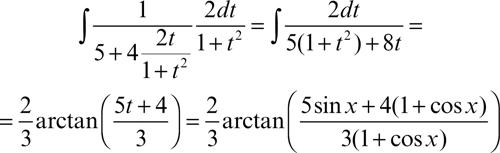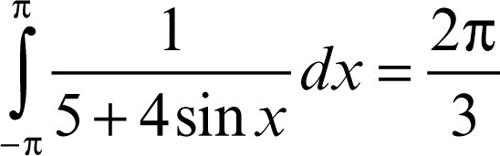integrazione per sostituzione
integrazione per sostituzione
integrazione per sostituzione metodo di integrazione impiegato per ridurre il calcolo di un integrale a espressioni più semplici (in genere, funzioni razionali) mediante opportuni cambiamenti di variabile. Esso corrisponde alla formula di derivazione delle funzioni composte. Indicando con F(x) una primitiva di ƒ(x), da D [F(g(x))] = ƒ(g(x))g′ (x) si deduce ∫f(g(x))g′ (x)dx = F(g(x)) + C. Se si pone t = g(x), risulta dt = g′ (x)dx, e i passaggi formali risultano
Si tratta dunque di individuare nella funzione integranda un “nucleo” g(x), del quale appaia o possa essere fatta apparire, la derivata g′ (x), che consente la sostituzione. Se g′ (x) non compare, si può procedere ugualmente attraverso la funzione inversa x = γ(t) della g(x), per la quale risulta dx = γ′(t)dt. Se φ(x) è la funzione integranda, si ha allora ∫φ(x)dx = ∫φ(γ(t))γ′(t)dt; calcolato questo integrale, si torna alla variabile originaria ponendovi t = g(x). Condizione perché ciò sia lecito è naturalmente la invertibilità di queste funzioni, oltre alla loro regolarità. Molti casi sono standard (→ integrazione). Negli esempi seguenti R rappresenta sempre una funzione razionale dei suoi argomenti; in essi si omette la costante di integrazione:
• ∫R(ex)dx. Si pone t = g(x) = ex, da cui
per cui l’integrale diviene ∫(R(t) / t)dt, razionale. Per esempio:
• ∫R(sinx)cosxdx. Con g(x) = sinx è g′ (x) = cosx, per cui l’integrale diviene ∫R(t)dt. Analogamente per ∫R(cosx)sinxdx;
• ∫R(sinx, cosx)dx. Se questo caso non rientra nei precedenti, si deve ricorrere alle formule parametriche
da cui x = 2arctant. Si ha dx = 2dt /(1 + t 2), e quindi l’integrale è razionale e uguale a
Per esempio,
si trasforma in
Si faccia attenzione al fatto che la corrispondenza è valida solo nell’intervallo (‒π, π), al di fuori del quale la primitiva ora trovata (che è periodica) va incrementata di
Si può mostrare che una primitiva su tutto R è
che differisce per una costante dalla precedente.
• ∫R(xm /n, xp /q , …, xr /s)dx. Posto N = mcm(n, q, …, s), si pone t = xN, e l’integrale si razionalizza:
La sostituzione dipende dalla parità di m: se m è dispari, si pone (a2 − x 2)1/2 = t, mentre se m è pari questa trasformazione non è efficace e si deve porre x = asint.
• Analogamente, per gli integrali
se m è dispari, si pone (x 2 ± a2)1/2 = t, mentre se m è pari si devono usare le funzioni iperboliche, ponendo rispettivamente x = asinht o x = acosht, in modo da sfruttare la identità notevole ch2t + sh2t = 1.
• Per l’integrale
si veda invece il lemma → integrale abeliano.