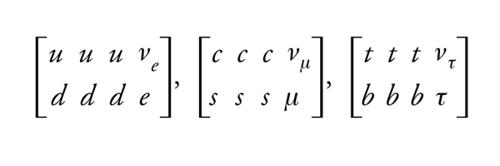Interazioni fondamentali

Interazioni fondamentali

La fisica fondamentale si propone di ricondurre tutti i fenomeni naturali a un insieme di teorie e di leggi che, almeno in linea di principio, spieghino e permettano di predire quantitativamente le osservazioni empiriche. A livello microscopico, tutta la fenomenologia della materia e della radiazione, ossia della fisica molecolare, atomica, nucleare e subnucleare, si può riportare a tre classi di interazioni fondamentali: le forti, le elettromagnetiche e le deboli. Gli elettroni sono legati ai nuclei degli atomi da forze elettromagnetiche e le loro proprietà rendono conto della fenomenologia degli atomi e delle molecole. La luce è una particolare manifestazione di campi elettrici e magnetici (onde elettromagnetiche). Le interazioni forti tengono insieme i protoni e i neutroni dei nuclei, essendo a piccole distanze così intensamente attrattive da prevalere sulla repulsione elettromagnetica tra le cariche di ugual segno dei protoni. Protoni e neutroni sono composti di tre quark tenuti insieme dalle interazioni forti, alle quali sono soggetti i quark medesimi e i gluoni. Alle interazioni deboli sono dovute la radioattività β dei nuclei e le reazioni nucleari che producono l'energia irradiata dal Sole e dalle stelle in generale. Allo stesso modo, si devono alle interazioni deboli i decadimenti del neutrone, dei pioni carichi e delle particelle adroniche più leggere dotate di stranezza (strangeness), charm e beauty (numeri quantici di 'sapore'), il decadimento del quark top ‒ osservato per la prima volta al Tevatron del FNAL (Fermi National Accelerator Laboratory) nel 1995 ‒ e quello dei leptoni carichi pesanti (il muone μ e il tauone τ). Inoltre tutte le interazioni dei neutrini sono dovute alle interazioni deboli.

I tre tipi di interazione sono descritti nel quadro dei principî della meccanica quantistica e della relatività, più precisamente da una teoria locale e relativistica di campi quantizzati, che si basa su un principio di simmetria interna, locale o di gauge, vale a dire una simmetria che ruota, secondo angoli diversi da punto a punto dello spazio-tempo, i gradi di libertà interni (ossia non spaziotemporali). L'insieme delle interazioni forti, elettromagnetiche e deboli, descritto da una teoria di gauge di questo tipo, costituisce il cosiddetto Modello Standard (MS). In realtà, un solo sottogruppo della simmetria del MS è direttamente osservabile nello spettro degli stati fisici, poiché una parte della simmetria è nascosta (meccanismo di Higgs per la rottura spontanea della simmetria di gauge).

Oltre a queste tre interazioni, sulla Terra, per ogni corpo materiale e nei fenomeni geologici, astrofisici e cosmologici ha un ruolo dominante una quarta interazione, la forza gravitazionale, che è invece trascurabile in fisica atomica e nucleare. La teoria della relatività generale costituisce una teoria classica (nel senso di essere non quantizzata) della gravitazione, che va oltre l'approssimazione statica della legge di Newton e descrive anche fenomeni dinamici quali, per esempio, le onde gravitazionali. La formulazione di una teoria quantistica della gravitazione è uno dei problemi centrali della fisica teorica contemporanea, anche se, dato che gli effetti quantistici della gravitazione divengono importanti solamente per concentrazioni di energia che non sono accessibili agli esperimenti, la ricerca di una teoria corretta può avvenire soltanto per via puramente speculativa.

Il Modello Standard

fig. 2

Il Modello Standard (MS) è una teoria coerente, finita e, almeno in linea di principio, calcolabile delle interazioni forti, deboli ed elettromagnetiche. Se al MS si aggiunge la teoria classica della gravitazione, secondo la teoria della relatività generale, si ottiene un quadro teorico di base al quale si può ricondurre la stragrande maggioranza dei fenomeni osservati in natura, dalla fisica microscopica alla cosmologia. Il MS si fonda su una generalizzazione dell'elettrodinamica quantistica (QED, Quantum electrodynamics), ossia rappresenta una teoria di campo che, costruita in base ai principî della meccanica quantistica e della relatività e fondata su una simmetria locale (ovvero valida separatamente in ogni punto dello spazio-tempo), estende l'invarianza di gauge dell'elettrodinamica a un insieme di densità di correnti e di cariche conservate più grande. Nel MS vi sono otto cariche associate alle interazioni forti, dette cariche di 'colore', e quattro cariche elettrodeboli, una delle quali è proprio la carica elettrica. I commutatori di queste cariche non sono tutti nulli, ma si dividono in tre gruppi. Le otto cariche forti non commutano tra loro (in termini tecnici, formano l'algebra di SU(3), il gruppo delle matrici 3×3 unitarie e a determinante uguale a uno), ma commutano con le quattro cariche elettrodeboli. Queste ultime, a loro volta, si dividono in tre che non commutano tra loro e danno luogo a un'algebra di SU(2) (spin isotopico debole), più una che commuta con tutte le altre (algebra di U(1): ipercarica debole). In totale, quindi, la simmetria locale di gauge del MS corrisponde all'algebra SU(3)⊗SU(2)⊗U(1). In QED l'interazione tra due particelle dotate di carica elettrica, per esempio due elettroni, è mediata dallo scambio di un fotone γ (o raramente più di uno) emesso dal primo elettrone e riassorbito dal secondo (fig. 2). Nel MS a ogni carica corrisponde, analogamente, un mediatore (di spin 1, in unità di ℏℏ) della corrispondente forza. Per le interazioni forti vi sono quindi otto gluoni, mentre le forze elettrodeboli sono mediate dai bosoni intermedi delle interazioni deboli, W⁺, W⁻ e Z⁰, e dal fotone γ.

I campi di materia del MS, tutti di spin 1/2 (fermioni), sono i quark e i leptoni. I quark sono i costituenti del protone, del neutrone e di tutte le particelle adroniche (ossia soggette alle interazioni forti): sono colorati, cioè dotati delle cariche forti di colore (ogni specie di quark si presenta in tre repliche di colori diversi) e inoltre posseggono cariche elettrodeboli (in particolare, cariche elettriche 2/3 per i quark di tipo up e −1/3 per i quark di tipo down). I leptoni non hanno colore ‒ e quindi non sono soggetti alle interazioni forti ‒, ma sono dotati di cariche elettrodeboli. I campi di materia sono raggruppati in tre famiglie, o generazioni, con uguali numeri quantici ma con masse differenti. In ogni famiglia abbiamo un doppietto di quark, uno di tipo up e uno di tipo down, e un doppietto di leptoni comprendente un neutrino e un leptone carico, con cariche elettriche, rispettivamente, 0 e −1. I quark di tipo up sono u (up), c (charm) e t (top), quelli di tipo down sono d (down), s (strange) e b (bottom); i leptoni sono ν_e, ν_μ, ν_τ ed e⁻, μ⁻, τ⁻. Al momento non si ha una spiegazione di questa tripla ripetizione delle famiglie di fermioni:

[1] formula

Il fotone e il gluone hanno massa zero (vale a dire che si muovono alla velocità della luce in ogni sistema di riferimento inerziale) e questa è una conseguenza del fatto che le corrispondenti simmetrie sono esattamente conservate. I bosoni deboli W⁺, W ⁻ e Z⁰ hanno invece masse molto grandi sulla scala delle particelle fondamentali (m_W∼80,4 GeV, m_Z∼91,2 GeV, ossia hanno il peso di nuclei di media grandezza come il rubidio e il molibdeno), il che significa che le corrispondenti simmetrie sono malamente rotte. Nel MS la rottura di simmetria è di un tipo particolare, detto rottura spontanea. Come esempio di rottura spontanea di simmetria portiamo quello di un mezzo magnetico a simmetria sferica: in assenza di campo magnetico esterno, la magnetizzazione può avere direzione arbitraria, senza che l'energia totale dipenda da tale direzione. Un dato magnete, tuttavia, ha la magnetizzazione orientata lungo una certa direzione e questa scelta (fissata, per es., dalla direzione del campo magnetico, presente nella fase di raffreddamento del materiale fuso e spento successivamente) determina la rottura spontanea della simmetria sferica.

Tale fenomeno è caratterizzato dal fatto che le cariche e le correnti rimangono conservate, ma lo stato fondamentale della teoria (quello di minima energia) risulta non unico e si ha un continuo di stati di minima energia che, nel suo insieme, rispetta la simmetria. La rottura della simmetria è dovuta al fatto che il sistema si trova in un punto particolare del continuo, in conseguenza di una 'scelta' avvenuta durante i primi istanti della vita dell'Universo. In una teoria di gauge come il MS, la rottura spontanea si realizza con il meccanismo di Higgs: esiste un certo numero di bosoni di Higgs scalari (ossia di spin 0) con un potenziale che determina la non unicità dello stato fondamentale. Una o più di tali particelle scalari devono necessariamente essere presenti nello spettro degli stati, con masse non lontane da quelle dell'intervallo finora esplorato, ma nessuna è stata ancora osservata con certezza e un grande sforzo sperimentale è in atto per rilevare le particelle di Higgs e completare così la verifica del MS.

fig. 3 a sinistra

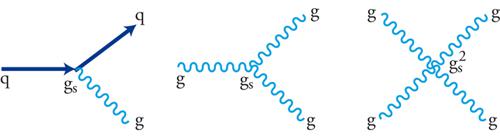
Consideriamo ora più in dettaglio le interazioni di base del MS. In QED i vertici di interazione descrivono le ampiezze di emissione o di assorbimento di un fotone da parte di un quark o di un leptone carico (fig. 2). La simmetria di gauge implica che il fotone sia accoppiato a tutte le particelle cariche con un'ampiezza proporzionale alla carica elettrica. Il fotone, essendo neutro, non è accoppiato a se stesso, vale a dire che non esiste un vertice in cui un fotone sia emesso da un fotone: in assenza di particelle cariche di materia, il campo elettromagnetico si propaga liberamente. Nella cromodinamica quantistica (QCD, Quantum chromodynamics), che è basata sull'invarianza di gauge della simmetria SU(3) di colore, i vertici che descrivono l'emissione o l'assorbimento di un gluone da parte di un quark sono analoghi ai vertici di QED (fig. 3 a sinistra). Sia il fotone sia il gluone hanno la proprietà che la loro emissione o il loro assorbimento da parte di un quark non ne cambia il tipo: per esempio un quark charm emette un fotone o un gluone rimanendo sempre un quark charm; la sola cosa che può cambiare è il colore del quark, in quanto il gluone è colorato. Poiché la simmetria di gauge relativa al colore implica che i gluoni si accoppino a tutte le particelle colorate e i gluoni sono essi stessi colorati, in QCD esistono vertici addizionali che descrivono l'emissione di un gluone da parte di un altro (fig. 3 al centro) e che non hanno analogo in QED. Anche in assenza di quark, quindi, il campo di interazione forte non si propaga liberamente. La costante di accoppiamento g_s del vertice ove il gluone è emesso da un quark è la stessa di quella del vertice dove il gluone è emesso da un gluone. Esiste anche un vertice a quattro gluoni, con costante di accoppiamento g_s² (fig. 3 a destra).

Le proprietà della QCD più rilevanti dal punto di vista fisico sono il confinamento e la libertà asintotica. Confinamento significa che non possono esistere cariche di colore libere: possono esservi solamente stati privi di colore. In particolare, quark e gluoni, essendo colorati, sono confinati, mentre gli adroni che osserviamo consistono in stati legati di quark con colore totale nullo. Ciò avviene in conseguenza del fatto che il potenziale V(r) delle forze di colore tra un quark e un antiquark separati da una distanza r si comporta, per r piccolo, come un potenziale coulombiano (ossia come 1/r), mentre a grandi distanze cresce linearmente con r, V∼σr. Il termine lineare rende impossibile la separazione della coppia qq_. Grandi progressi sono stati compiuti negli ultimi anni grazie alla simulazione della QCD su reticoli spaziotemporali, approfittando dell'elevata potenza e velocità dei moderni calcolatori elettronici. È stato così possibile ricostruire la forma del potenziale V(r) a grande distanza, confermare l'esistenza del termine lineare e valutare il parametro σ; è stato anche possibile calcolarne la dipendenza dalla temperatura e mostrare che σ vale zero a temperature corrispondenti a circa 170 MeV: come un magnete perde la propria magnetizzazione al di sopra della temperatura di Curie, così la fase confinata scompare alla temperatura di deconfinamento, dando luogo a una fase di quark e gluoni liberi (plasma di quark e gluoni). Esperimenti effettuati al CERN negli anni Novanta del secolo scorso e attualmente in corso presso l'acceleratore RHIC (Relativistic heavy ion collider) a Brookhaven, nei quali si fanno collidere ioni pesanti (per es., Au-Au oppure Pb-Pb) dando luogo alla produzione di materia nucleare ad alta temperatura, forniscono indicazioni in favore della formazione, in un piccolo volume spaziotemporale, del plasma di quark e gluoni. Questi studi saranno continuati presso il LHC (Large hadron collider), il nuovo acceleratore del CERN.

La libertà asintotica è una proprietà di tutte le teorie di gauge non abeliane (vale a dire con cariche che formano un'algebra chiusa di commutatori non tutti nulli) in quattro dimensioni spaziotemporali; essa consiste nel fatto che, per effetto delle correzioni quantistiche, la costante efficace di accoppiamento della teoria di gauge varia in funzione della quantità di moto trasferita tra le particelle interagenti, e tende a zero logaritmicamente per grandi valori di quest'ultima grandezza. Nei processi in cui il valore assoluto del quadrato del quadrimpulso trasferito è grande (processi 'duri' o altamente anelastici), le interazioni forti perdono dunque di intensità e i loro effetti divengono calcolabili mediante la teoria delle perturbazioni. Le interazioni deboli introducono alcune caratteristiche nuove. La parità P (simmetria per inversione delle coordinate spaziali x, y, z→−x, −y, −z) e la coniugazione di carica C (simmetria particella-antiparticella), sebbene siano conservate nei vertici della QED e QCD, non lo sono nelle interazioni deboli. Questa violazione delle simmetrie P e C è stabilita nel MS dalle differenti proprietà di trasformazione rispetto al gruppo SU(2)⊗U(1), valide per quark e leptoni con elicità positiva e, rispettivamente, negativa (l'elicità è la componente dello spin lungo l'impulso). Assumendo che sia valida la simmetria indotta dal gruppo SU(2)⊗U(1), i fermioni hanno massa nulla, in quanto termini di massa porterebbero a un mescolamento tra stati di differente elicità, il che non è possibile proprio perché stati di elicità diversa hanno differenti proprietà di trasformazione.

In effetti, nel MS tutti i fermioni, e con essi i bosoni intermedi W⁺, W⁻ e Z⁰ delle interazioni deboli, acquistano massa soltanto quando la simmetria è rotta dal meccanismo di Higgs. La conservazione di P e C per le interazioni del fotone è ottenuta in quanto γ e Z⁰, gli stati di massa definita dopo la rottura di simmetria, sono opportune sovrapposizioni ortogonali di W₃ e B, con un angolo di mescolamento θ_W , dove W₃ è la componente neutra del tripletto W⁺, W⁻ e W₃, e B è il bosone di gauge di U(1). Poiché la conservazione della carica elettrica è preservata nel meccanismo di rottura di simmetria, il fotone rimane a massa nulla e, inoltre, i suoi vertici di interazione con i fermioni conservano P e C. L'angolo di mescolamento θ_W , infatti, è fissato in modo tale che il fotone risulti accoppiato a una pura corrente vettoriale in proporzione alla carica elettrica di ciascun fermione: g_wsenθ_W=g_w′cosθ_W=e, dove g_w e g_w′ sono le costanti di gauge di SU(2) e di U(1), rispettivamente, e −e è la carica dell'elettrone. Ne consegue che le correnti elettromagnetiche e di colore sono puramente vettoriali, mentre le correnti deboli sono sovrapposizioni di correnti vettoriali e assiali con opposte P e C (e uguale CP). In particolare, per le correnti deboli cariche, mediate da W⁺ e W⁻, la combinazione è semplicemente V−A, ossia corrente vettoriale meno corrente assiale, con una costante d'accoppiamento g_w che è collegata alla costante G_F della teoria di Fermi delle interazioni deboli dalla relazione G_F /√2=g_w²/(8m_W²). La combinazione di correnti vettoriali e assiali è in generale più complicata per la corrente debole neutra mediata dalla Z⁰. Per un dato quark o leptone f l'accoppiamento assiale è dato da g_f^A=±g_w/(4cosθ_W) (il segno ± è relativo a stati con spin isotopico −1/2 e +1/2, rispettivamente), mentre il rapporto g_V/g_A degli accoppiamenti vettoriali e assiali è dato per ogni fermione da g_f^V/g_f^A=−1+4∣Q_f∣sen²θ_W, dove Q_f è la carica elettrica in unità pari a e (Q_f=2/3, −1/3, 0, −1 per quark up e down, neutrini e leptoni carichi, rispettivamente).

fig. 4

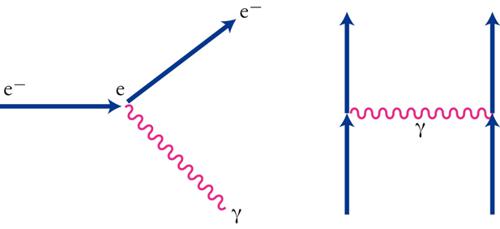
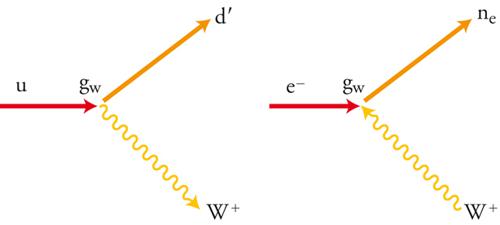
Una proprietà importante delle interazioni deboli è che le correnti cariche mediate dallo scambio di W^± sono le uniche interazioni che cambiano il sapore: per esempio, un quark di tipo up emette un W⁺ e diventa un quark di tipo down, oppure un elettrone e⁻ assorbe un W⁺ e diventa un neutrino ν_e (fig. 4). Il fenomeno molto interessante del mescolamento (mixing) dei quark è dovuto al fatto che, nella transizione u→W⁺d′ originata da un quark u di massa definita, il quark d′, che appare nello stato finale, è in generale una sovrapposizione di stati d, s e b, di tipo down e di massa definita. Tra gli stati d′, s′ e b′, connessi a u, c e t (di massa definita) dall'emissione di un W, e gli stati d, s e b anch'essi di massa definita si ha una trasformazione unitaria V_CKM, introdotta da Nicola Cabibbo e da Makoto Kobayashi e Toshihide Maskawa, specificata da tre angoli di mescolamento e da una fase. Tale fase determina una violazione della simmetria CP, e in effetti è la sola sorgente di violazione di CP nel MS. Grandi progressi sono stati fatti negli ultimi anni nello studio sperimentale degli angoli di mescolamento e della violazione di CP.

Per quanto riguarda i leptoni, se i neutrini avessero masse rigorosamente nulle non si avrebbe il fenomeno del mescolamento, ma i recenti esperimenti sulle oscillazioni di neutrini hanno mostrato che in effetti questi hanno piccole masse e quindi anche per i neutrini si ha una matrice di mescolamento V_P-NMS; nei prossimi anni, un grande impegno sperimentale sarà dedicato a perfezionare e completare la nostra conoscenza degli angoli di mescolamento e delle fasi dei leptoni. Al contrario di quanto succede nelle interazioni da corrente carica, la corrente debole neutra, accoppiata alla particella Z⁰, non cambia il sapore. Questo fatto è una conseguenza dell'unitarietà delle matrici di mescolamento V_CKM e V_P-NMS (si ricordi che il quark charm fu previsto da Sheldon L. Glashow, John Iliopoulos e Luciano Maiani nel 1970, proprio per garantire la conservazione del sapore, osservata sperimentalmente negli accoppiamenti della Z⁰).

Come abbiamo già ricordato, la simmetria di gauge SU(2)⊗U(1) è rotta spontaneamente con il meccanismo di Higgs e solamente la simmetria connessa alla carica elettrica rimane intatta. Come conseguenza della rottura di simmetria, i quark e i leptoni acquistano massa insieme ai bosoni intermedi W⁺ e Z⁰, che hanno i numeri quantici dei generatori delle simmetrie rotte. Mentre per i bosoni intermedi deboli una qualunque rappresentazione per i campi di Higgs, che non sia un singoletto del gruppo, conduce a masse non nulle, soltanto i doppietti di Higgs possono dare origine alle masse dei fermioni. La scelta più 'economica', quindi, è quella di limitarsi a introdurre uno o più doppietti di Higgs; i quali, d'altra parte, conducono a un rapporto preciso tra le masse di W⁺ e Z⁰: m_W²=ϱm_Ζ²cos²θ_W, con ϱ=1 a meno di correzioni radiative piccole e calcolabili. Gli esperimenti, condotti specialmente al LEP (Large electron positron collider) del CERN, hanno confermato che, con grande precisione, il parametro ϱ è vicino a 1 e questo conferma che i bosoni di Higgs sono doppietti, ossia hanno spin isotopico debole uguale a 1/2.

Verifiche di precisione

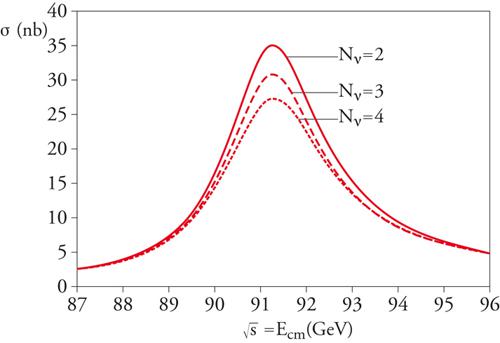
Il CERN ha svolto un ruolo essenziale per lo sviluppo e la verifica di precisione del MS. Gli effetti indiretti della particella Z⁰, vale a dire l'esistenza di processi deboli prodotti da corrente neutra, furono osservati per la prima volta al CERN nel 1973, nell'ambito della collaborazione Gargamelle (dal nome della camera a bolle realizzata per l'esperimento). La produzione diretta delle particelle W^± e Z⁰ nelle collisioni p‒p_ fu osservata nel 1982, sempre al CERN, per mezzo delle collaborazioni UA1 e UA2 (Carlo Rubbia e Simon Van der Meer ebbero il premio Nobel per la fisica per la concezione dell'acceleratore e dell'esperimento). Nel 1989 entrò in funzione presso il CERN il LEP, un grande collisore e⁺e⁻ con una circonferenza di circa 27 km, in cui elettroni e positroni circolavano in sensi opposti, con un'energia di circa 50 GeV per fascio nel corso di una prima fase (detta LEP1), durata dal 1989 al 1995, e di circa 100 GeV in una seconda fase (LEP2), terminata nel 2000, quando il LEP è stato smontato per far posto nella stessa galleria al LHC. La prima fase, LEP1, è stata dedicata allo studio della particella Z⁰: i fasci sono stati calibrati per avere ciascuno un'energia E tale che 2E∼m_Zc²∼91,2 GeV e sono state misurate con grande precisione la massa m_Z e la vita media τ_Z; sono stati poi studiati i decadimenti della particella Z⁰ in tutti i possibili canali fermione-antifermione. Un primo tipo di misurazioni volte a evidenziare le proprietà della Z⁰ consiste nel variare l'energia dei fasci intorno al picco di risonanza. Se si innalza l'energia della coppia e⁺e⁻ fino a un valore sufficiente per produrre la Z⁰, l'annichilazione e⁺e⁻→ Z⁰ diviene possibile e la sezione d'urto cresce bruscamente; dopo un tempo dell'ordine della vita media, la Z⁰ si disintegra in uno stato finale formato da una coppia fermione-antifermione (il fermione può essere un quark di un determinato sapore, un leptone carico oppure un neutrino).

fig. 5

In queste condizioni si osserva un picco di risonanza (fig. 5) con una larghezza intrinseca ΔE∼Γ_Z individuata, per il tramite del principio di indeterminazione, dalla vita media della Z⁰: Γ_Z=ℏ/τ_Z. La curva di risonanza è distorta dalle correzioni radiative; in particolare, per grandi energie ha una lunga coda dovuta al fatto che, prima di produrre la particella Z⁰, la coppia e⁺e⁻ può perdere energia mediante radiazione di fotoni. Dalla posizione del massimo si può risalire a m_Z, mentre dalla forma della curva di risonanza si ottiene Γ_Z. I valori misurati sono: m_Z=(91,1875±0,0021) GeV/c², Γ_Z=(2,4952±0,0023) GeV. La precisione rimarchevole raggiunta nella misurazione di massa richiede una calibrazione accuratissima dell'energia dei fasci, ottenuta mediante un metodo che si basa sulla risonanza magnetica. La conoscenza preliminare di m_Z è essenziale per la predizione teorica delle altre proprietà fisiche della Z⁰ e rappresenta quindi un dato di partenza per le verifiche di precisione della teoria. La larghezza Γ_Z è una di queste predizioni controllabili e dal suo valore sperimentale si ottiene la vita media τ_Z=(2,6379±0,0024)10⁻²⁵ s.

Una volta misurata la forma della curva di risonanza, l'energia dei fasci è fissata in corrispondenza del massimo e si procede a misurare le sezioni d'urto al picco, oltre che un certo numero di osservabili per i vari canali e⁺e⁻→F, ove lo stato finale F può essere, per esempio, F=e⁺e⁻, μ⁺μ⁻ o τ⁺τ⁻ (canali leptonici) oppure F=qq_ (canali adronici), ove q è un quark di un dato tipo o sapore con massa m_q〈m_Z/2, vale a dire di uno dei sapori di quark a eccezione del top. Se aggiungiamo i canali 'invisibili' di tipo F=νν_, ove ν è un neutrino che sfugge all'osservazione nei rivelatori, otteniamo i canali che, con i loro complementi radiativi (cioè gli stessi fermioni, più un certo numero di fotoni o di gluoni), formano praticamente la totalità dei decadimenti della Z⁰. In corrispondenza del picco domina lo scambio della Z⁰, e la sezione d'urto σ_F nel canale F al picco è determinata dal rapporto di decadimento della Z⁰ nel canale F, ossia da Γ_F/Γ_Z. Un importante risultato che si ottiene dalle misurazioni di σ_F è il valore, per differenza, della larghezza parziale invisibile Γ_inv. La larghezza totale Γ_Z, infatti, è ricavata dalla curva di risonanza, mentre le larghezze dei decadimenti nei canali visibili sono misurate dalle sezioni d'urto al picco. Nel MS la larghezza invisibile è dovuta ai canali F=νν_, con neutrini e antineutrini nello stato finale. I neutrini conosciuti sono quelli associati ai leptoni carichi noti. Si hanno quindi ν_e, ν_μ, ν_τ in corrispondenza ai leptoni e⁻, μ⁻ e τ⁻.

Dato che i rapporti Γ_νl/Γ_l tra le larghezze dei neutrini e dei corrispondenti leptoni si possono calcolare ricorrendo a ipotesi abbastanza generali e che le probabilità relative Γ_l /Γ_Z dei canali leptonici si misurano direttamente, si può prevedere il contributo alla larghezza invisibile fornito da ciascuna specie di neutrino. È possibile, quindi, a partire dal valore sperimentale della Γ_inv, risalire al numero dei tipi di neutrino che contribuiscono ai decadimenti della Z⁰. Il risultato (fig. 5) è N_ν=2,9841±0,0083, in buon accordo con il numero N_ν=3 di neutrini effettivamente noti. Si tratta di un riscontro importante: lo spettro dei quark e dei leptoni conosciuto è costituito da tre famiglie con cariche identiche e masse differenti, ciascuna costituita da un doppietto di leptoni e un doppietto di quark, ma, poiché in ogni famiglia c'è un neutrino di massa nulla o molto piccola, se si fosse trovato N_ν≥4 si sarebbe dovuto concludere che esistono altre famiglie di fermioni fondamentali, non ancora scoperte per il semplice fatto di essere costituite da quark e da leptoni carichi di massa troppo elevata. A seguito di questa misurazione, sappiamo quindi che la misteriosa replicazione delle famiglie di quark e di leptoni è terminata.

La misura di Γ_F permette di ricavare la somma (g_f^V)²+(g_f^A)² dei quadrati delle costanti di accoppiamento della Z⁰ al canale F=ff_, di tipo vettoriale e di tipo assiale. In corrispondenza del picco si misura anche un certo numero di asimmetrie, importanti per separare le parti vettoriali e assiali degli accoppiamenti della Z⁰ e, in particolare, per ricavare il rapporto g_f^V/g_f^A. Un'altra macchina del tipo e⁺e⁻, operante alla stessa energia del LEP e, come quest'ultimo, dedicata allo studio della particella Z⁰, era la SLC (SLAC linear collider), situata presso lo Stanford Linear Accelerator Center, in California. L'intensità della SLC era molto inferiore rispetto a quella del LEP, cosicché il numero di particelle Z⁰ che era stato possibile osservare complessivamente era dell'ordine di 100.000 con la prima e circa 16 milioni con il secondo. Un'importante caratteristica dell'acceleratore lineare SLC, tuttavia, consisteva nell'avere il fascio di elettroni polarizzato longitudinalmente, vale a dire che gli elettroni del fascio avevano lo spin diretto come la loro velocità (tutti secondo il verso di quest'ultima, oppure nel verso opposto), mentre nel LEP la polarizzazione longitudinale era in media nulla. La polarizzazione degli elettroni permette di misurare l'asimmetria destra-sinistra, ossia la differenza delle sezioni d'urto totali per elettroni con lo spin diretto nel verso della loro velocità oppure in quello contrario, divisa per la somma di tali sezioni d'urto.

fig. 6

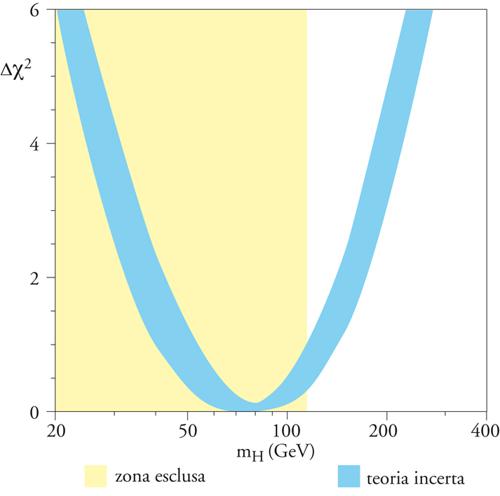
Tutte queste misurazioni hanno permesso di determinare con grande precisione le proprietà fisiche della particella Z⁰. Il LEP ha permesso di misurarne con un alto livello di esattezza i parametri fondamentali: per esempio la massa e la vita media, con una precisione di circa due parti su centomila e dell'uno per mille, rispettivamente. Ha poi consentito di misurare gli accoppiamenti della Z⁰ ai quark e ai leptoni, realizzando con ciò una serie di verifiche molto precise delle previsioni del MS, con un'accuratezza di qualche parte per mille. Il LEP, quindi, ha fornito al MS una solida base sperimentale. La precisione ottenuta negli esperimenti al LEP è così alta che si è potuto verificare l'effetto delle correzioni quantistiche sulle previsioni della teoria. Tali correzioni sono sensibili anche alle masse di quelle particelle che, pur essendo troppo pesanti per essere prodotte nelle reazioni studiate, rientrano nel calcolo teorico dei processi in qualità di stadi intermedi. Per il tramite del LEP, si è così riusciti a predire la massa del quark top prima della sua effettiva scoperta al Tevatron, il collisionatore p‒p_ del FNAL in Illinois (esperimenti CDF e D0). In effetti, assumendo che il MS sia corretto, dai dati relativi ai processi elettrodeboli si giunge oggi a una predizione della massa del top (e del W) in perfetto accordo con il risultato della loro misurazione diretta. Allo stesso modo, dalle correzioni radiative ottenute mediante il LEP, è stato possibile fissare un limite superiore per la massa del bosone di Higgs, di circa 200 GeV (fig. 6), risultato di grande importanza sia teorica, come vincolo imposto a ogni teoria diversa della rottura della simmetria elettrodebole, sia pratica, per le prospettive di rilevare l'esistenza di tale particella.

fig.7

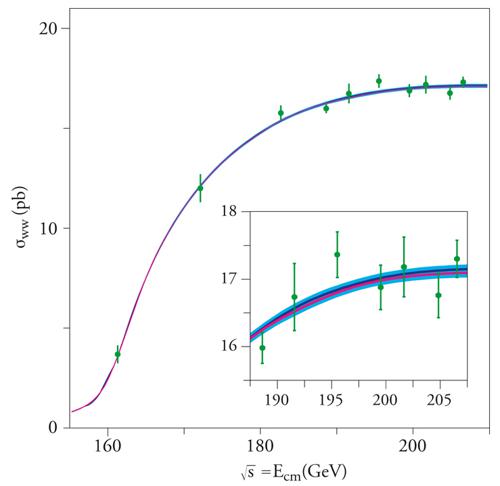
I risultati principali ottenuti mediante il LEP, nella fase di alta energia LEP2, sono stati lo studio del processo e⁺e⁻→W⁺W⁻ e la misurazione della massa del W con una precisione dello 0,5 per mille. La misura di m_W ‒ il valore combinato è m_W=(80,426±0,034) GeV/c² ‒ permette un'ulteriore verifica di precisione del MS, perché tale massa può essere calcolata, a partire da m_Z, dalle masse dei quark e dei leptoni e dalle costanti di accoppiamento, in funzione della massa del bosone di Higgs. Dallo studio della sezione d'urto di produzione di coppie di W⁺W⁻ (fig.7) si ottiene inoltre una verifica degli accoppiamenti fra tre bosoni di gauge, ossia dei vertici W⁺W⁻γ e W⁺W⁻Z⁰, in accordo con il MS. Durante la fase LEP2, infine, il programma principale è stato la ricerca della particella di Higgs e di eventuali nuove particelle. Prima che il LEP entrasse in funzione nel 1989, riguardo alla massa del bosone di Higgs si sapeva solamente che doveva essere più grande di circa 1 GeV/c², mentre oggi consideriamo che essa debba essere maggiore di 114 GeV/c². Grazie alla sperimentazione compiuta al LEP è stato quindi possibile, combinando il limite superiore ottenuto dalle prove di precisione con il limite inferiore fornito dalla ricerca diretta, restringere i valori della massa del bosone di Higgs del MS nel piccolo intervallo 114〈m_H≲200 GeV/c².

Dal complesso delle prove di precisione effettuate al LEP è risultato che le varie interazioni della Z⁰ sono esattamente quelle prescritte dalla simmetria di gauge. Le interazioni, quindi, sono perfettamente simmetriche, mentre le masse non riflettono affatto tale simmetria. Si tratta del comportamento tipico delle simmetrie spontaneamente rotte e del meccanismo di Higgs, e da ciò segue che gli esperimenti al LEP hanno dato una fortissima indicazione sperimentale che il meccanismo di Higgs è effettivamente operante, che la particella di Higgs ha i numeri quantici previsti (in particolare spin isotopico debole uguale a 1/2) e che essa non è troppo pesante. Nelle ultime settimane di funzionamento, il LEP, spinto all'energia massima possibile di oltre 206 GeV, ha prodotto un certo numero di eventi che potrebbero indicare la presenza di una particella di Higgs con massa di circa 115 GeV, un risultato che ha generato grande eccitazione in tutta la comunità dei fisici delle particelle, sebbene il LEP non potesse raggiungere un'energia sufficiente per lo studio di questo segnale. Se in futuro tale risultato sarà confermato, si avrà un ulteriore motivo di soddisfazione per i traguardi che il LEP ha permesso di raggiungere.

fig. 8

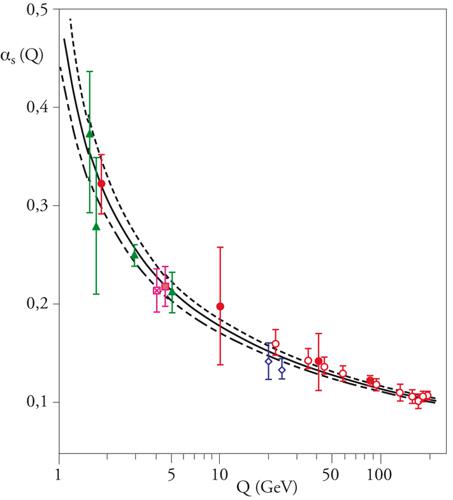
Grandi progressi sono stati fatti durante gli ultimi anni nella verifica della QCD e le misure ottenute per il tramite del LEP hanno avuto una grande importanza anche in tale ambito. Un esperimento particolarmente significativo è costituito dalla misurazione, in processi diversi, della costante di accoppiamento efficace a una certa scala di quantità di moto trasferita α_s(Q²) (si sceglie comunemente Q²∼m_Z²), verificando se, entro gli errori, si ottengano valori tra loro compatibili. Il LEP ha permesso di misurare sia α_s(m_Z²), mediante i decadimenti della particella Z⁰, sia la dipendenza di α_s(Q²) da Q²; quest'ultima mediante il confronto delle misure relative alla Z⁰ con quelle di α_s(Q²) ad alti Q², realizzate durante la fase LEP2, e con le misure dei decadimenti adronici del leptone τ ‒ che a loro volta forniscono direttamente α_s(m_τ²), con m_τ∼1,777 GeV/c². I risultati mostrano chiaramente l'andamento decrescente logaritmico previsto dalla libertà asintotica (fig. 8). Il valore combinato attuale della costante di accoppiamento è, con una valutazione prudente dell'errore, α_s(m_Z²)≈0,118±0,003.

Oltre il Modello Standard

Il MS è stato sottoposto a verifiche molto precise in un insieme assai diversificato di esperimenti. Gli ultimi quindici anni di fisica degli acceleratori e⁺e⁻, p‒p_, e‒p, presso le 'fabbriche' di sapori pesanti (per es., le b-factories BELLE in Giappone e BaBar in California) e con esperimenti a bersaglio fisso, hanno mostrato un accordo con il MS che va ben oltre le aspettative. È vero che la particella di Higgs non è stata trovata e che quindi una parte importante della verifica del MS è ancora mancante, ma d'altro canto non è inverosimile che la massa del bosone di Higgs del MS si trovi nell'intervallo 114〈m_H≲200 GeV/c² indicato dalle attuali conoscenze. Ciò che sorprende è, piuttosto, che non vi siano tracce di deviazioni dal MS entro un livello di precisione di una parte per mille nelle prove di precisione condotte presso il LEP e gli altri acceleratori. Esistono infatti ragioni concettuali molto solide per aspettarsi che a una scala di energie di alcuni TeV si manifestino deviazioni dovute a qualche forma di nuova fisica, e vi sono inoltre argomentazioni fenomenologiche a sostegno di una fisica che vada oltre il MS.

Una prima osservazione è che il MS non può essere considerato una teoria completa ed esatta delle interazioni fondamentali, e ciò emerge da molte considerazioni, ma innanzi tutto dal fatto che il MS non contiene la gravità quantistica, essenziale per energie dell'ordine di M_Plc²≈10¹⁸÷10¹⁹ GeV. D'altra parte, se si fa l'ipotesi che fino a tali energie il MS sia una buona approssimazione e, per un'energia M_GUc²≈10¹⁵÷10¹⁶ GeV non troppo lontana dalla soglia della gravità quantistica, si estrapolano i valori efficaci delle costanti di gauge di SU(3), ossia α_s(Q²), di SU(2) e di U(1), allora le tre costanti tendono a un medesimo valore. Ciò è molto interessante, in quanto rende possibile formulare teorie di Grande Unificazione (GU), nelle quali le tre interazioni di gauge del MS si riducono a una sola, fondata su un gruppo di simmetria di gauge più grande, per esempio SU(5) oppure SO(10). Oltre a ciò, il fatto che, nell'unificazione degli accoppiamenti del MS, M_GU si trovi in prossimità di M_Pl fa sì che la fisica attuale delle particelle non possa ignorare le enormi energie tipiche della gravità quantistica, ed è quindi plausibile un'ulteriore unificazione, come nelle moderne teorie di stringa. Il MS, in questa prospettiva, è al più una teoria approssimata, valida a basse energie, mentre per energie dell'ordine di M_GUc² o M_Plc² si ricorre a una descrizione più fondamentale. In realtà è facile convincersi che il MS non ha una 'stabilità' sufficiente per conservare la propria validità fino a energie così elevate (il cosiddetto problema della gerarchia) e che la vera teoria efficace di bassa energia, capace di spiegare i successi del MS e compatibile con l'idea della GU, implica la comparsa di nuovi effetti a energie dell'ordine di qualche TeV.

Il problema della gerarchia è il seguente. Nell'ambito delle correzioni quantistiche, in ogni teoria di campo realistica sono presenti divergenze ultraviolette, originate, negli integrali che rappresentano i diagrammi di Feynman al di là dell'ordine più basso della teoria delle perturbazioni, dal contributo della regione delle alte quantità di moto; ciò fa sì che i risultati dipendano fortemente dalle regioni di alte energie, dove il MS potrebbe fallire. Poiché il MS è una teoria rinormalizzabile, le divergenze ultraviolette, se regolarizzate mediante l'introduzione di un 'taglio' (cut-off) Λ, possono essere eliminate ridefinendo (ossia rinormalizzando) le costanti di accoppiamento, le masse e la normalizzazione delle funzioni d'onda, che in ogni caso sono parametri liberi della lagrangiana di partenza: il taglio Λ può essere considerato come una parametrizzazione della nostra ignoranza riguardo la fisica alle altissime energie. Una teoria rinormalizzabile riesce comunque a essere predittiva, perché gli effetti di Λ possono essere inglobati nella ridefinizione dei parametri della lagrangiana, che sono poi fatti corrispondere ai valori sperimentali. Tuttavia, se Λ fosse assai grande, come sarebbe se assumessimo che il MS fosse valido fino a Λ∼M_GU oppure Λ∼M_Pl,, bisognerebbe domandarsi se la dipendenza dei parametri rinormalizzati da Λ è ragionevole. Nel MS le masse dei W^±, della Z⁰ e del bosone di Higgs dipendono linearmente da Λ, per via della presenza di campi scalari fondamentali nel settore di Higgs della teoria, e quindi risulta del tutto incomprensibile come il taglio possa essere più grande di tali masse per un fattore 10¹³÷10¹⁷. Per i fermioni il problema non si pone, in quanto la dipendenza da Λ è solamente logaritmica.

Per risolvere il problema della gerarchia, che ha avuto e ha un ruolo centrale nella fisica delle particelle degli ultimi anni, sono state avanzate varie proposte, delle quali l'idea della supersimmetria approssimata è la più compiutamente formulata e predittiva. La supersimmetria è una simmetria che collega fermioni e bosoni ed è un ingrediente importante delle teorie della gravità, ivi compresa la teoria delle stringhe. A ogni particella del MS corrispondono partners supersimmetrici con gli stessi numeri quantici ma con lo spin che differisce di 1/2: ai bosoni di gauge, che hanno spin 1, corrispondono i cosiddetti gaugini, che sono fermioni di spin 1/2; ai quark e ai leptoni corrispondono alcuni scalari (spin 0) detti s-quark o s-leptoni; ai bosoni di Higgs corrispondono gli higgsini di spin 1/2. Può sembrare a prima vista strano che finora nessun s-partner sia stato osservato, ma in realtà, mentre la massa di tutte le particelle osservate è proibita dalle simmetrie di gauge (e questo può spiegare la loro speciale leggerezza), per i loro corrispondenti supersimmetrici la massa è permessa non appena è rotta la supersimmetria. In queste teorie, assumendo che valga la simmetria, la dipendenza lineare dal taglio è sostituita da una dipendenza logaritmica. In presenza di una rottura della supersimmetria, necessaria dal punto di vista fenomenologico, le masse dei W^±, della Z⁰ e del bosone di Higgs diventano dell'ordine della separazione in massa tra i multipletti supersimmetrici (moltiplicata per una costante di gauge). Per risolvere il problema della gerarchia occorre quindi che gli s-partners siano vicini agli attuali limiti sperimentali, con masse dell'ordine di 100÷1000 GeV.

Altre possibili soluzioni sono state ampiamente trattate negli ultimi anni. Una possibilità è di bandire gli scalari dalla lagrangiana fondamentale, visto che il problema nasce dal settore di Higgs: se il bosone di Higgs fosse un aggregato di fermioni, si conserverebbe il meccanismo di Higgs, ma il problema della gerarchia non si porrebbe. Queste teorie, dette di tipo technicolor, presuppongono però l'esistenza di nuove interazioni forti, molto più intense di quelle normali (di un fattore circa 10³), per poter riprodurre la scala caratteristica delle masse elettrodeboli. In presenza di forze così intense è molto difficile evitare correzioni ben visibili nelle verifiche di precisione del MS, e quindi l'esito degli esperimenti al LEP ha di molto diminuito la credibilità dei modelli technicolor. Modelli in cui un regime non perturbativo sia vicino alle energie finora esplorate e risulti in qualche modo compatibile con la piccola massa del bosone di Higgs ‒ e con il successo delle prove di precisione ‒ sono tuttora proposti e studiati.

Negli ultimi anni sono emerse nuove possibili soluzioni. Una classe molto ardita di teorie trae origine dalla constatazione che la massa di Planck ha un valore così elevato a causa del fatto che la gravità è molto meno intensa delle altre interazioni. Una simile valutazione, tuttavia, potrebbe essere modificata se esistessero ulteriori dimensioni spazio-temporali, chiuse su se stesse (compattificate) con un raggio di curvatura molto più grande di quello atteso dalle normali teorie di stringa (R≈10⁻³³ cm): la gravità ci apparirebbe debole perché molte delle linee di forza 'sfuggirebbero' nelle altre dimensioni. Se, sfruttando queste dimensioni spaziotemporali nascoste, la scala delle stringhe fosse non dell'ordine di M_Pl ma dell'ordine di 1 TeV, non vi sarebbe più alcun problema di gerarchia. Si tratta di un'idea molto interessante, intanto perché non si può escludere l'esistenza di deviazioni dalla legge di Newton a distanze submillimetriche (e modelli del tipo appena descritto incoraggiano i difficili esperimenti volti allo studio della gravità a tali distanze); inoltre, questa idea ha fornito lo spunto a studi riguardanti gli effetti che ulteriori dimensioni spazio-temporali potrebbero avere sugli esperimenti di fisica delle particelle realizzabili nei prossimi anni, in particolare al LHC.

Il modello supersimmetrico è, tra tutti quelli proposti, il più completo e predittivo. In effetti, il Modello Standard supersimmetrico minimale (MSSM) è un modello ben definito, rinormalizzabile, calcolabile e compatibile con i dati delle verifiche di precisione del MS. Il MSSM, al contrario delle altre soluzioni proposte, si accorda ottimamente con l'idea della GU. Infatti a differenza delle altre teorie, per le quali, poco oltre le energie di 1 TeV, si incontra un regime non perturbativo che è praticamente impossibile da trattare, nel MSSM si possono condurre calcoli perturbativi fino alle energie tipiche della GU. Un calcolo dell'evoluzione delle costanti di gauge tra la scala debole e M_GU mostra, inoltre, come nel MSSM si abbia una unificazione delle tre costanti di gauge in un solo punto e come questa, dati i valori misurati di tali costanti alla scala debole, sia molto migliore che non nel MS: si tratta di un indizio fenomenologico diretto in favore del modello supersimmetrico. La supersimmetria, inoltre, permette di risolvere altri problemi della GU.

Nelle teorie unificate, quark e leptoni si trovano nella stessa rappresentazione del gruppo unificato. Per esempio, l'antiquark d_in tre colori, un neutrino e un elettrone formano una rappresentazione a cinque componenti del gruppo SU(5). Ciò innanzi tutto spiega la quantizzazione della carica, in quanto la somma delle cariche in ogni rappresentazione deve essere zero (la carica del d_è 1/3 perché vi sono tre colori). Ma che quark e leptoni rientrino nella stessa rappresentazione comporta anche che i bosoni di gauge pesanti di SU(5), con massa ∼M_GU, medino alcune transizioni tra quark e leptoni che violano il numero leptonico L e il numero barionico B. Tali transizioni inducono un'ampiezza di probabilità per il decadimento del protone, che in effetti è una predizione caratteristica delle teorie di GU. Un importante vantaggio della supersimmetria è che il decadimento del protone è molto rallentato rispetto al caso delle teorie di GU non supersimmetriche e i canali preferiti di decadimento sono diversi. I limiti attuali sulla vita media del protone, ottenuti recentemente dalla collaborazione sperimentale SuperKamiokande in Giappone e dell'ordine di τ_p≈10³²÷10³³ s, escludono le teorie più semplici di GU senza supersimmetria, ma sono compatibili con il modello GU supersimmetrico.

Altre indicazioni fenomenologiche per una fisica che vada oltre il MS provengono dalla cosmologia (la materia oscura, la bariogenesi, la costante cosmologica) e dagli esperimenti, in particolare quelli riguardanti le oscillazioni di neutrino. A partire dagli anni Novanta del secolo scorso si è verificato uno sviluppo notevole delle misurazioni quantitative in cosmologia. Sembra ormai chiaro che la grande maggioranza della materia nell'Universo non è visibile, non è barionica ed è per lo più 'fredda', ossia possiede energie non relativistiche al momento del disaccoppiamento dall'equilibrio termico. Il MS non prevede l'esistenza di una particella sufficientemente stabile, la cui massa sia compresa in un intervallo appropriato e che possa essere associata alla materia oscura. Un ovvio candidato sarebbe il neutrino, se non fosse che questo costituisce eventualmente materia oscura 'calda', perché è ultrarelativistico al disaccoppiamento; i neutrini, pertanto, non possono avere massa al di sopra di qualche eV/c² e possono contribuire al più per una frazione modesta della materia oscura. È interessante che i modelli supersimmetrici forniscano invece un ottimo candidato per la materia oscura: il più leggero dei neutralini. Si tratta di uno s-partner di spin 1/2 dei bosoni di gauge neutri (con possibili componenti di higgsino) che nel MSSM è stabile e ha una massa dell'ordine di 100 GeV/c².

Le esperienze di oscillazioni di neutrino hanno fornito negli ultimi anni prove convincenti per quanto riguarda i neutrini solari e i neutrini atmosferici. Dopo l'esperimento pionieristico di Ray Davis nella miniera di Homestake, nel South Dakota, che alla fine degli anni Sessanta suggerì che vi è un difetto numerico dei neutrini solari che raggiungono la Terra, molti esperimenti condotti negli Stati Uniti (da ultimo l'esperimento SNO), in Italia nel Laboratorio Nazionale del Gran Sasso (MACRO, GALLEX, GNO e OPERA), in Russia (SAGE) e in Giappone (Kamiokande, SuperKamiokande, K2K e KamLAND) hanno studiato i neutrini solari e i neutrini atmosferici, evidenziando che i neutrini ν_e emessi dal Sole si trasformano in parte in altri tipi di neutrini (prevalentemente ν_μ e ν_τ), laddove i neutrini atmosferici ν_μ si trasformano prevalentemente in ν_τ. Queste oscillazioni avvengono perché lo stato iniziale, per esempio il ν_μ nel caso dei neutrini atmosferici, è una sovrapposizionedi stati che hanno masse diverse e che perciò acquistano una differente fase con la distanza percorsa. A una distanza L, quindi, lo stato ν_μ non è più ortogonale allo stato dei neutrini ν_τ e si ha una probabilità di oscillazione P_μτ=sen²2θ₂₃sen²(Δm_atm²L/4E) (in unità ℏ=c=1), dove θ₂₃ è l'angolo di mescolamento (che determina la sovrapposizione iniziale), Δm_atm²=m₃²−m₂² è la differenza tra le masse al quadrato degli autostati di massa dei neutrini ed E è l'energia dei neutrini.

Questi esperimenti mostrano quindi che le masse dei neutrini non sono uguali tra loro e, in particolare, almeno due di esse non sono nulle: le osservazioni indicano che Δm_atm²≈3∙10⁻³ eV² e θ₂₃≈45⁰. Per i neutrini solari si ha Δm_atm²≈10⁻⁴ eV² e θ₁₂ grande, sebbene non massimale. Il terzo angolo di mescolamento nella matrice V_P-NMS, θ₁₃, è invece piccolo. Le misure sulle oscillazioni di neutrino determinano soltanto Δm² e non la scala assoluta delle masse dei neutrini, riguardo alle quali esistono tuttavia alcuni limiti diretti. Dalle recenti misurazioni sul decadimento β del trizio si deduce un limite m_νe≤2,8 eV per la massa del neutrino ν_e, che determina la massima energia dell'elettrone. Dai già menzionati limiti cosmologici sulla quantità di materia oscura calda, si ottiene un limite per la somma delle masse dei neutrini (quasi) stabili ∑m_ν≤2 eV. Combinando tra loro questi limiti superiori e i risultati delle oscillazioni, che implicano differenze di massa molto piccole, si ottiene che le masse dei neutrini che partecipano alle oscillazioni debbono essere non nulle, ma inferiori a circa 1 eV. La massa dei neutrini è, quindi, enormemente inferiore rispetto alla massa dei quark e dei leptoni carichi. La spiegazione è con tutta probabilità legata al fatto che i neutrini sono gli unici fermioni fondamentali con carica elettrica nulla. Se il numero leptonico L non è esattamente conservato (come non lo è nelle teorie di GU), non esiste alcun numero quantico conservato che distingua neutrini da antineutrini (particelle di Majorana); si può allora dimostrare che la massa dei neutrini è inversamente proporzionale alla scala di energia M associata alle interazioni che violano la conservazione di L: m_ν=m_D²/M, dove m_D è la massa di Dirac dei neutrini, analoga a quella dei quark e dei leptoni (meccanismo dell'altalena o see-saw mechanism). I dati delle oscillazioni di neutrino sono compatibili con valori di M molto grandi, non lontani da M_GU, ed è così che le oscillazioni di neutrino si rivelano una sorgente di informazioni sulla fisica alle energie delle teorie di GU.

Il più grande progetto sperimentale dei prossimi anni nel campo della fisica delle interazioni fondamentali è il LHC del CERN (collisioni p−p a 14 TeV). Questo acceleratore affronterà il problema centrale della fisica delle particelle, ossia la ricerca della particella di Higgs per completare la verifica del MS, nonché la ricerca delle particelle supersimmetriche o comunque della fisica oltre il MS, che si pensa debba con tutta probabilità esistere nella regione di energia esplorata dal LHC. Un progetto complementare in discussione è la costruzione di un acceleratore lineare e⁺e⁻, detto ILC (International linear collider), con energia totale di 500÷1000 GeV: dovrebbe essere un progetto mondiale, da realizzare negli Stati Uniti, o in Germania presso il Laboratorio DESY di Amburgo (progetto TESLA), oppure in Asia. Si noti che nelle collisioni e⁺e⁻ tutta l'energia è disponibile per lo studio dei processi fondamentali, ossia quelli che avvengono tra quark, gluoni o leptoni (partoni). In un collider adronico, invece, molta dell'energia è spesa in frammenti degli adroni e soltanto una frazione, dell'ordine del 10%, si ritrova nell'urto dei partoni. L'energia utile del ILC è inferiore a quella del LHC, ma non tanto quanto sembrerebbe a prima vista, e l'ILC permette una fisica di precisione, a differenzaa del LHC che è una macchina da esplorazione e scoperta. Altre direzioni promettenti di ricerca sperimentale sono la fisica del sapore, con macchine dedicate, le 'fabbriche' di mesoni con beauty o charm oppure di mesoni K (per es., DAΦNE presso i Laboratori Nazionali di Frascati), lo studio del momento magnetico anomalo (un esperimento di questo tipo è stato recentemente completato a Brookhaven) e quello dei decadimenti rari (per es., le transizioni con cambiamento di sapore μ→eγ). Grande progresso, inoltre, avrà la fisica nei laboratori sotterranei: si svilupperanno lo studio dei neutrini, del decadimento del protone e tutti quegli esperimenti che richiedono una drastica riduzione del fondo cosmico (per questo è utile collocarsi sotto centinaia di metri di roccia). Non vi è dubbio che nei prossimi anni molti problemi basilari della fisica delle interazioni fondamentali saranno chiariti da questo imponente programma sperimentale.

Bibliografia

Altarelli 1992: Altarelli, Guido, Adroni, in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1992, I, pp. 52-62.

Altarelli 1993: Altarelli, Guido, Interazioni deboli, in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1993, III, pp. 238-249.

Altarelli 1995: Altarelli, Guido, Z, particella, in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1995, VI, pp. 605-609.

Barbieri 1993: Barbieri, Riccardo, Grande unificazione (teorie di), in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1993, III, pp. 59-65.

Cabibbo 1963: Cabibbo, Nicola, Unitary symmetry and leptonic decays, "Physical review letters", 10, 1963, pp. 531-533.

Cheng 1984: Cheng, Tu-Pei - Li, Ling-Fong, Gauge theory of elementary particle physics, Oxford, Clarendon, 1984.

Close 2002: Close, Frank - Marten, Michael - Sutton, Christine, The particle odyssey. A journey to the heart of matter, Oxford, Oxford University Press, 2002.

Davis 1968: Davis, Raymond jr - Harmer, Don S. - Hoffman, Kenneth C., Search for neutrinos from the sun, "Physical review letters", 20, 1968, pp. 1205-1209.

Fraser 1998: The particle century, edited by Gordon Fraser, Bristol, Institute of Physics, 1998.

Gatto 1994: Gatto, Raoul, Quark, in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1994, IV, pp. 633-637.

Glashow 1970: Glashow, Sheldon L. - Iliopoulos, John - Maiani, Luciano, Weak interactions with lepton-hadron symmetry, "Physical review D", 2, 1970, pp. 1285-1292.

Kobayashi 1973: Kobayashi, Makoto - Maskawa, Toshihide, CP-violation in the renormalizable theory of weak interaction, "Progress of theoretical physics", 49, 1973, pp. 652-657.

Leader, Predazzi 1996: Leader, Elliot - Predazzi, Enrico, An introduction to gauge theories and modern particle physics, Cambridge-NewYork, Cambridge University Press, 1996, 2 v.

Maki 1962: Maki, Ziro - Nakagawa, Masami - Sakata, Shorki, Remarks on the unified model of elementary particles, "Progress of theoretical physics", 28, 1962, pp. 870-880.

Martin, Shaw 1992: Martin, Brian R. - Shaw, Graham, Particle physics, Chichester-New York, Wiley, 1992 (2 ed.: 1997).

Perkins 2000: Perkins, Donald H., Introduction to high energy physics, 4. ed., Cambridge, Cambridge University Press, 2000 (1. ed.: Reading [Mass.], London, Addison-Wesley, 1972).

Pokorski 2000: Pokorski, Stefan, Gauge field theories, 2. ed,, Cambridge, Cambridge University Press, 2000 (1. ed.: 1987).

Pontecorvo 1957: Pontecorvo, Bruno, Mesonium and anti-mesonium, "Zhurnal eksperimental'noi i teoreticheskoi fiziki", 33, 1957, pp. 549-551.

Rebbi 1993: Rebbi, Claudio, Cromodinamica quantistica, in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1993, II, pp. 66-73.

Remiddi 1993: Remiddi, Ettore, Elettrodinamica quantistica, in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1993, II, pp. 296-314.