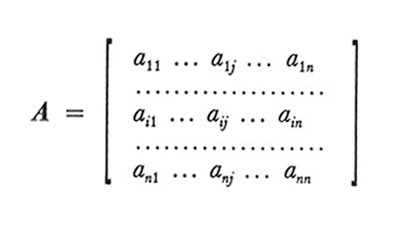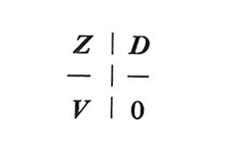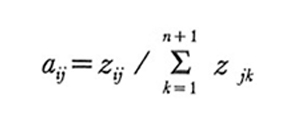Interdipendenze strutturali, analisi delle

Interdipendenze strutturali, analisi delle

1. Introduzione

L'analisi delle interdipendenze strutturali, o analisi input-output, è indissolubilmente legata al nome di Wassily Leontief - cittadino americano, nato però a S. Pietroburgo nel 1906 - che nel 1973 ha ricevuto il premio Nobel per l'economia proprio "per aver sviluppato il metodo input-output e per averlo applicato alla soluzione di importanti problemi economici".

Nell'introdurre The structure of American economy 1919-1929, la prima presentazione organica di quella che verrà poi chiamata l'analisi input-output, Leontief definisce il suo lavoro "un tentativo di applicare la teoria dell'equilibrio economico generale - o meglio, dell'interdipendenza generale - a uno studio empirico delle interrelazioni fra le differenti parti di un'economia [nazionale], che si rivelano attraverso covariazioni di prezzi, produzioni, investimenti e redditi" (v. Leontief, 1941, p. 3).

L'idea di analizzare in dettaglio le relazioni intercorrenti tra le diverse parti di un sistema economico può essere fatta risalire a François Quesnay (v., 1973) e al suo Tableau économique (1758), che è riecheggiato anche nel modello di riproduzione a più settori utilizzato da Karl Marx nella sua analisi dell'interdipendenza delle attività economiche.

Leon Walras (v., 1874) costruisce il prototipo dei modelli matematici di equilibrio economico generale nel quale la produzione è rappresentata da un 'indefinito' numero di settori (mercati); Gustav Cassel (v., 1932) estende e migliora il modello di Walras e suggerisce l'idea di derivare le funzioni di domanda e di offerta del modello di equilibrio generale dall'osservazione empirica piuttosto che deduttivamente dal principio di massimizzazione dell'utilità.

Il modello delle interdipendenze strutturali di Leontief rende operativa l'idea di Cassel semplificando lo schema walrasiano fino a identificare relazioni funzionali che possono essere statisticamente stimate. A questo risultato Leontief arriva: 1) escludendo - almeno dal modello di base - le equazioni di offerta dei fattori primari (quelli non prodotti all'interno dell'economia studiata nell'unità di tempo di osservazione) e quelle di domanda dei beni e servizi finali (quelli non utilizzati come input di altri processi produttivi nell'economia studiata e nell'unità di tempo di osservazione); 2) riducendo, per aggregazione, il numero infinito di mercati di Walras a un numero finito di settori (o industrie, o branche produttive); 3) accettando la semplificazione walrasiana dei 'coefficienti fissi' (v. § 6b) e quindi funzioni di produzione 'lineari' (o 'alla Leontief', come verranno chiamate).

2. Il compromesso tra 'fatti' e 'teoria'

Nella migliore tradizione dell'economia classica il proposito indiscutibilmente ambizioso dell'analisi delle interdipendenze strutturali è quello di studiare la realtà economica in tutta la sua complessità, accettando "un compromesso fra le generalizzazioni senza vincoli del ragionamento puramente teorico e le limitazioni pratiche della raccolta dei dati empirici" (v. Leontief, 1941, p. 4) che consenta di evitare gli opposti pericoli di teorizzazioni eleganti, ma irrilevanti o comunque prive di validazione empirica, da un lato, e, dall'altro, di applicazioni empiriche non ordinate da alcuna ipotesi teorica. Il pericolo che si vuol evitare è l'allargarsi dello scarto tra 'fatti' e 'teoria', che rischia di "mettere a repentaglio l'integrità dell'economia come scienza empirica" (v. Leontief, 1989, p. 3).

Il 'compromesso' si fonda su una teoria che tende a interpretare la realtà economica in termini della sua struttura (tecnologie, stili di vita e quindi di consumo, risorse primarie) e su uno strumento contabile - la tavola input-output, o tavola delle interdipendenze settoriali, o tavola economica intersettoriale - che consente una descrizione coerente dei fatti. La tavola organizza i dati nella logica del modello e il modello diventa credibile perché trova nella tavola conferma della sua operatività.

3. Interdipendenze produttive e duplicazioni contabili

L'interdipendenza strutturale, oggetto sia della descrizione contabile sia della rappresentazione analitica, è innanzitutto quella che si manifesta all'interno della parte 'attività produttiva' del sistema (costituito da parti legate da rapporti di interazione) al quale può essere ricondotta l'economia di una regione, di un paese o anche del mondo intero.

La possibilità di studiare ed eventualmente controllare il comportamento di un sistema economico dipende - nella logica input-output - dalla capacità di rappresentarne, nel modo più disaggregato possibile, le parti e le loro interconnessioni.

figura

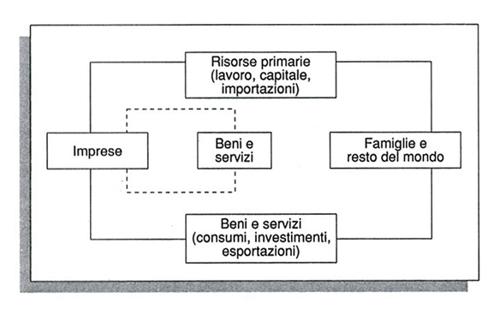
Rispetto alla rappresentazione aggregata del comportamento del sistema, espressa da un circuito economico (v. figura) nel quale 'imprese' producono 'beni e servizi' destinati a 'famiglie e resto del mondo', utilizzatori finali che, a loro volta, forniscono alle imprese le risorse primarie (i beni e i servizi non prodotti dall'economia in questione nell'unità di tempo considerata), l'analisi input-output mette in evidenza solo un sottocircuito in più (la linea tratteggiata nella figura), quello degli scambi di beni e servizi tra le imprese o tra loro raggruppamenti significativi: i settori.

Nell'approccio input-output la descrizione delle interdipendenze intermedie tra settori produttivi (flussi di beni e servizi tra imprese, dettati dalle tecnologie di produzione, che dal punto di vista della contabilità nazionale danno luogo solo a 'duplicazioni' da eliminare ai fini della misura del prodotto interno lordo) integra utilmente la descrizione delle interdipendenze finali tra settori produttivi e impieghi finali, da un lato, e delle interdipendenze primarie tra settori produttivi e risorse primarie, dall'altro.

Il motivo di questa particolare attenzione prestata alle interdipendenze intermedie sta nell'ipotesi implicita che le performances dell'intero sistema economico dipendano in misura prevalente da quanto succede all'interno del mondo della produzione: i rapporti tra le unità produttive influenzano fortemente sia le interdipendenze primarie sia le interdipendenze finali. Poiché i rapporti tra le unità di produzione sono largamente determinati dalle tecnologie produttive, è nella tecnologia e nella evoluzione di quest'ultima che l'analisi delle interdipendenze strutturali ricerca il primus movens della dinamica dei sistemi economici.

Leontief rende empiricamente applicabile il modello di interdipendenza settoriale dal momento in cui si rende conto della possibilità di sfruttare il contenuto informativo delle duplicazioni contabili per calcolare i coefficienti fissi alla Walras.

L'intuizione nasce dall'analisi del grande sforzo di costruzione della contabilità economica dell'URSS nei primi anni venti. È in un articolo pubblicato nel 1925 sul bilancio dell'economia dell'URSS che Leontief (v., 1925) mette in luce le relazioni esistenti tra valore della produzione lorda, valore delle duplicazioni e valore del prodotto netto e, soprattutto, quelle tra disaggregazione settoriale della rappresentazione dei processi produttivi e duplicazioni, che ne misurano l'interdipendenza.

4. Le fortune dell'analisi delle interdipendenze strutturali

Nel 1936 la pubblicazione di Quantitative input and output relations in the economic system of the United States (v. Leontief, 1936) segna la data ufficiale di nascita dell'analisi delle interdipendenze strutturali. L'analisi input-output non avrebbe però fatto molta strada dopo quella data se i continui miglioramenti delle macchine da calcolo, prima, e dei calcolatori elettronici, poi, non avessero permesso di affrontare sistemi di dimensioni comunque elevate.

Le prime tavole rappresentative dell'economia americana del 1919 e del 1929 erano state costruite da Leontief disaggregando la produzione in 42 settori, ma le limitate capacità di calcolo del tempo avevano costretto l'autore ad aggregare il sistema in soli 10 settori per poter impiegare il modello; oggi la soluzione di modelli rappresentativi di economie disaggregate in centinaia, o anche migliaia, di settori produttivi non impegna un calcolatore che per pochi istanti.

Ad altri eventi, quasi altrettanto 'fortunati', va attribuita la graduale riduzione dell'altro ostacolo, costituito dalla limitata disponibilità delle informazioni statistiche di base. I costi, in tempo e denaro, della preparazione delle tavole input-output erano, e restano, molto elevati; la crescente disponibilità degli uffici centrali di statistica a costruirle malgrado ciò è legata alla valutazione della loro utilità anche a prescindere dalla costruzione dei modelli di analisi economica da esse ottenibili.

Soprattutto le tavole più disaggregate, come quelle per il Giappone, la Norvegia, gli Stati Uniti e il Canada, si sono rivelate fonti dirette di informazioni sulla struttura della produzione industriale e dei mercati molto apprezzate dagli analisti di settore e dagli studiosi di marketing.

La fortuna delle tavole input-output al di fuori dell'analisi economica intersettoriale è però legata soprattutto al loro impiego come quadri di coerenza della contabilità nazionale.

Ogni tavola input-output è la rappresentazione, compatta e disaggregata allo stesso tempo, di tre dei conti nazionali fondamentali (il conto della produzione, il conto dell'equilibrio dei beni e servizi, il conto della distribuzione del valore aggiunto). Ogni sistema di contabilità nazionale può esistere anche senza la tavola input-output, ma la sua eventuale presenza assicura il rispetto del vincolo di coerenza fra rilevazioni differenti e, quindi, una maggior affidabilità di tutta la base informativa fornita dalla contabilità nazionale. È per questi motivi che dal 1968 le tavole input-output, pur modificate nel formato secondo i suggerimenti di Richard Stone (v. cap. 5), sono divenute parte integrante del sistema di contabilità nazionale raccomandato dalle Nazioni Unite (v. UN Statistical Office, 1968).

5. Tavola dei flussi e matrice dei coefficienti

Il cuore dell'analisi delle interdipendenze strutturali è costituito dalla matrice dei coefficienti tecnici (o matrice della tecnica o matrice strutturale) e dalla corrispondente tavola dei flussi (o delle transazioni input-output o delle interdipendenze strutturali).

La matrice dei coefficienti tecnici

è una matrice nella quale ogni riga e la corrispondente colonna sono intestate a una delle n merci prodotte nel sistema economico considerato e il cui elemento generico aij indica la quantità della merce i impiegata per la produzione di una unità della merce j (se la riga e la colonna 1 sono intestate alla merce grano e la riga e la colonna 2 sono intestate alla merce fertilizzanti, l'elemento a₂₁ della A indica la quantità di fertilizzante necessario per produrre una unità di grano).

Letta una colonna alla volta, la matrice A descrive la tecnologia di produzione di ogni singola merce e, in quanto tale, può essere costruita ex ante (indipendentemente dalla contabilizzazione del concreto operare dei singoli processi produttivi) sulla base del giudizio di esperti e di informazioni raccolte direttamente da fonti ingegneristiche. Questa procedura di costruzione della matrice A ha avuto qualche applicazione (v. Fisher e Chilton, 1971), anche se la procedura normalmente seguita è quella statistica o ex post che deriva la matrice A dalla corrispondente tavola delle transazioni Z.

La tavola (delle transazioni o dei flussi) input-output è una tabella a doppia entrata nella quale ogni riga e la corrispondente colonna sono intestate a un settore (a un'industria o a una branca produttiva: l'industria automobilistica, l'industria calzaturiera, l'allevamento del bestiame, i servizi assicurativi, ecc.). L'elemento j-esimo della riga i-esima della tavola indica la quantità zij (che può anche essere nulla) di beni o servizi prodotti dal settore i e ceduti al settore produttivo j (j=1, 2, 3, ..., n) o al settore di domanda finale (j=n+1), che comprende assieme consumi delle famiglie, consumi pubblici, investimenti, esportazioni al netto delle importazioni, ecc. L'elemento i-esimo della colonna j-esima della stessa tavola rappresenta la quantità zij (che può essere anche nulla) di beni o servizi prodotti dal settore i e acquistati dal settore j per essere combinati con gli inputs acquistati dal settore degli inputs primari (i=n+1) per produrre il bene j.

Schematicamente il quadro contabile input-output può essere pensato e distinto in quattro quadranti

Il primo quadrante, Z, è quello delle transazioni intersettoriali; il secondo, D, è quello degli outputs finali; il terzo, V, è quello degli inputs primari; il quarto quadrante è nullo. Idealmente gli elementi della tavola rappresentano tutti delle quantità fisiche espresse, riga per riga, da opportune unità di misura, come 'quintali di grano', 'metri di stoffa', 'numero di automobili'. In pratica la maggior parte delle tavole delle interdipendenze strutturali sono espresse in valori, ottenuti applicando un dato sistema di prezzi (quelli correnti o quelli di un qualche anno base) alle misure di quantità. Questo non impedisce di pensare ai valori delle transazioni come comunque rappresentativi di quantità: ridefinendo, riga per riga, l'unità di misura fisica come la quantità del bene considerato acquistabile al prezzo di una unità di conto (per esempio una lira), ogni valore zij risulta dal prodotto di una quantità per un prezzo sempre uguale a 1.

Se merci e industrie sono classificate nello stesso modo e se si può assumere che ogni industria produca una sola merce con una tecnologia unica e stabile, ogni coefficiente della A si ottiene per semplice divisione:

Questo significa accettare, tra l'altro, implicitamente l'ipotesi di specificazione deterministica del modello, che consente di stimare ogni coefficiente aij sulla base di una sola osservazione. Di fatto ogni coefficiente tecnico aij è stimato sulla base di più osservazioni: per ogni coefficiente esiste dunque una distribuzione di probabilità che deve far considerare detti coefficienti come variabili casuali. La stima stocastica dei coefficienti tecnici di produzione (v. Gerking, 1976; v. Martellato, 1978), costosa in tempo e denaro, consentirebbe, ove applicata, di valutare la bontà delle stime e, quindi, di ottenere anche un apprezzamento statistico della rispondenza del modello alla realtà osservata empiricamente.

Ma, anche senza abbandonare l'approccio deterministico, nella realtà molte industrie producono più merci, eventualmente distinguibili tra prodotti primari (quelli che caratterizzano l'industria in questione) e varie categorie di prodotti secondari. Per ovviare a questa mancata corrispondenza biunivoca tra industria e merce prodotta, o la si impone artificialmente (come sostanzialmente fa il SEC, Sistema Europeo di Contabilità, introducendo il concetto di 'branca') o, come ha suggerito Richard Stone - e l'Ufficio statistico delle Nazioni Unite ha convenuto di raccomandare nel suo sistema di contabilità nazionale (v. UN Statistical Office, 1968) -, si contabilizzano gli inputs e gli outputs in due tavole separate e non necessariamente quadrate: una tavola, U, degli assorbimenti (use matrix), che descrive, per colonna, tutte le merci usate come inputs da ogni singola industria, e una tavola, V, dei prodotti (make matrix), che indica, per riga, tutte le merci prodotte, gli outputs, da ogni singola industria.

La procedura per ricavare la matrice A dalle tavole U e V risulta meno banale e comunque non univoca, dipendendo dalle ipotesi sulla natura dei prodotti secondari e sulla loro influenza sulle tecnologie di produzione, che si possono ipotizzare maggiormente condizionate, alternativamente, dal tipo di industria o dal tipo di merce.

Il significato e la qualità dei coefficienti della matrice A ricavati dalla corrispondente tavola Z dipendono anche dal livello di disaggregazione settoriale (il passaggio da un livello all'altro di aggregazione può introdurre degli errori sistematici nella soluzione del modello), dalle configurazioni di prezzo usate (oltre al costo dei fattori il prezzo ex fabrica contabilizza le imposte indirette nette e il prezzo di mercato anche i margini remunerativi del trasporto e della distribuzione commerciale), dall'anno di riferimento dei prezzi (con problemi non banali di deflazione ove l'anno di riferimento debba essere diverso da quello di rilevazione), dal modo in cui sono contabilizzati i flussi di beni e servizi importati, ecc.

6. Il modello base

Nella sua formulazione più semplice il modello input-output si fonda su tre insiemi di relazioni: due che ne rappresentano i vincoli contabili, e che quindi assumono la natura di identità, e il terzo che ne descrive l'ipotesi comportamentale base con un insieme di vere e proprie equazioni.

Le equazioni di bilancio materiale e le equazioni di prezzo

Se i settori produttivi dell'economia considerata sono n (ognuno dei quali produce una sola merce) e il settore (n+1) rappresenta le famiglie, che si immaginano responsabili di tutti gli impieghi finali (consumi, investimenti, esportazioni, ecc.) e detentrici di tutte le risorse primarie, il primo insieme di identità, detto insieme delle equazioni di bilancio materiale, sarà

(X₁ - x₁₁) - x₁₂ - x₁₃ - ... - x_1n - x_{1, n+1}  = 0

- x₂₁ + (X₂ - x₂₂) - x_{2 3}- ... - x_2n - x_{2, n+1} = 0

- x_n1 - x_n2 - x_n3 - ... + (X_n - x_nn) - x_{n, n+1} = 0

nel quale Xi rappresenta (in quantità fisiche) la produzione lorda del settore i-esimo, xij rappresenta la quantità della produzione del settore i-esimo impiegata come input dal settore j-esimo e xii rappresenta la quantità della produzione lorda del settore i-esimo reimpiegata nello stesso settore.

L'insieme di queste identità esprime l'equilibrio ex post tra la domanda e l'offerta di ogni merce, descrivendo il fatto che la produzione lorda di ogni industria Xi è identicamente uguale alla somma delle quantità della merce i consumata da tutte le industrie (impieghi intermedi o duplicazioni) o dalle famiglie (impieghi finali).

Il secondo insieme di identità, detto insieme delle equazioni di prezzo (o equazioni di bilancio finanziario), esprime un secondo vincolo contabile: quello dell'equilibrio tra costi e ricavi. Esso ci dice che ex post il valore della produzione di ogni settore è identicamente uguale al valore di tutti i beni e servizi (compresi quelli primari) impiegati nella sua produzione.

Se pi (con i = 1, 2, ..., n) rappresenta il prezzo della merce i prodotta dal settore produttivo i-esimo e pn+₁ è il prezzo degli inputs primari (non prodotti) forniti dalle famiglie, questo secondo insieme di identità può essere scritto

(X₁ - x₁₁) p₁ - x₂₁ p₂ - ... - x_n1 p_n - x_{n + 1, 1} p_{n + 1}  = 0

- x₁₂ p₁ + (X₂ - x₂₂) p₂ - ... - x_n2 p_n - x_{n+1, 2} p_n+1 = 0

- x_1n p₁ - x_2n p₂ - ... + (X_n - x_nn) p_n - x_{n+1, n} p_n+1   = 0

ed esprime una interdipendenza tra i prezzi non diversa da quella esistente tra le quantità.

Le funzioni di produzione a coefficienti fissi

Perché gli insiemi delle equazioni di bilancio materiale e delle equazioni di prezzo si trasformino da puri vincoli contabili in modelli input-output, rispettivamente delle quantità e dei prezzi, bisogna ricorrere a un terzo insieme di equazioni: quello che descrive le funzioni di produzione settoriali, cioè le relazioni tecniche intercorrenti tra l'output fisico di un settore e tutti gli inputs assorbiti da quel settore nel suo processo produttivo.

Nella scelta della forma funzionale Leontief si rifà a Walras e opta per l'ipotesi che l'ammontare di ciascun elemento di costo sia strettamente proporzionale alla quantità dell'output. L'organizzazione tecnica di ciascuna industria risulta espressa da un insieme di equazioni lineari omogenee del tipo

x_1j = a_1j X_j; x_2j = a_2j X_j; ... x_ij = a_ij X_j; ... x_nj = a_nj X_j.

Le funzioni di produzione che ne derivano assumono la forma

X_j = min { x_1j / a_1j, x_2j / a_2j, ..., x_ij / a_ij, ..., x_nj / a_nj }

nella quale ogni aij=xij / Xj è un coefficiente di produzione dato e costante per il quale xij=aij Xj.

L'ipotesi di costanza dei coefficienti tecnici è ciò che maggiormente distingue l'analisi delle interdipendenze strutturali dalla teoria neoclassica della produzione.L'ipotesi di costanza dei coefficienti tecnici di produzione non comporta necessariamente la loro stabilità nel tempo: l'analisi input-output consente di tener conto del progresso tecnico e di ogni altra causa di mutamento tecnologico, che si rifletterà nella modificazione di un qualche insieme di coefficienti della matrice A.

I coefficienti fissi alla Leontief implicano, invece, rendimenti costanti di scala (assenza di economie di scala) e, soprattutto, assenza di sostituibilità tra i fattori di produzione nell'ambito di un dato processo produttivo (con conseguente ininfluenza dei prezzi relativi dei fattori sulla scelta delle combinazioni di inputs produttivi): due conseguenze che hanno condotto alcuni autori a considerare l'analisi input-output solo come un caso particolare e minore della teoria neoclassica. Leontief ha sempre difeso la scelta dei coefficienti fissi solo come un'utile approssimazione: se è indiscutibile che i coefficienti di produzione non sono fissi, ciò che conta è sapere se la loro variabilità influenza significativamente o no la validità empirica dei calcoli basati sull'approssimazione accettata da Leontief, una domanda alla quale non si può dare una risposta a priori, senza ricorrere a verifiche empiriche.

Il modello delle quantità

Se, per l'ipotesi di funzione di produzione a coefficienti fissi si ha xij=aij Xj, l'insieme delle identità di bilancio materiale può essere riscritto (ponendo xi, n+₁=di) come un sistema di equazioni lineari

(1 - a₁₁) X₁ - a₁₂ X₂ - a₁₃ X₃ - ... - a_1n X_n  = d₁

- a₂₁ X₁ + (1 - a₂₂) X₂ - a₂₃ X₃ - ... - a_2n X_n  = d₂

- a_n1 X₁ - a_n2 X₂ - a_n3 X₃ - ... + (1 - a_nn) X_n  = d_n,

che in forma compatta diventa

(I - A) X = D,

dove A è la matrice dei coefficienti tecnici, I è una matrice identità, X il vettore della produzione totale e D il vettore della domanda finale.

Se il vettore D della domanda finale è assegnato esogenamente, il sistema diventa un sistema lineare di n equazioni in n incognite, la cui soluzione, se il determinante di (I - A) è diverso da zero, è

X = (I - A)^-1 D.

È questo l'esercizio più comune eseguito con il modello input-output, che consente di calcolare lo sforzo produttivo (la produzione totale misurata dal vettore X) necessario per soddisfare ogni dato livello (e struttura) della domanda finale (consumi, investimenti, esportazioni nette, ecc.) rappresentata dal vettore D. Una volta noto il vettore delle produzioni lorde X è poi possibile correlare con il livello e l'articolazione settoriale della domanda finale il fabbisogno totale di risorse primarie (lavoro, capitale, importazioni, ecc.) o altri effetti esterni, quali il consumo di risorse naturali o l'inquinamento prodotto dai processi produttivi.

Alternativamente, se è il vettore X delle produzioni lorde a essere assegnato esogenamente, il sistema di equazioni determina univocamente il vettore di domanda finale D o, ancora, potrà determinare un numero n di elementi incogniti sia di X sia di D, una volta che sia stato fissato esogenamente un numero n di produzioni lorde e/o di domande finali settoriali.

Il modello dei prezzi

Operando in modo analogo sull'insieme delle equazioni di prezzo (sostituendo ogni xij con il corrispondente aij Xj e ponendo xn+₁, i pn+₁=Yi, valore aggiunto del settore i) si può scrivere

(1 - a₁₁) X₁p₁ - a₂₁X₁p₂ - a₃₁X₁p₃ - ... - a_n1X₁p_n = Y₁

- a₁₂X₂p₁ + (1 - a₂₂)X₂p₂ - a₃₂X₂p₃ - ... - a_n2X₂p_n  = Y₂

- a_1nX_np₁ - a_2nX_np₂ - a_3nX_np₃ - ... + (1 - a_nnX_n)p_n = Y_n.

Se si divide la prima equazione per X₁, la seconda per X₂, ..., l'n-esima per Xn e si pone Yi / Xi = vi (coefficiente di valore aggiunto per unità di produzione), si ottiene

(1 - a₁₁) p₁ - a₂₁ p₂ - a₃₁ p₃ - .... - a_n1 p_n  = v₁

- a₁₂ p₁ + (1 - a₂₂) p₂ - a₃₂ p₃ - ... -a_n2 p_n  = v₂

- a_1n p₁ - a_2n p₂ - a_3n p₃ - ... + (1 - a_nn) p_n  = v_n,

che in notazione compatta diventa

(I - A') p = v,

dove p è il vettore dei prezzi e v il vettore dei coefficienti di valore aggiunto e la matrice dei coefficienti tecnici A appare trasposta.

Se il determinante della matrice (I - A) è diverso da zero, il sistema dei prezzi ha soluzione

p = [(I - A)']^-1 v,

che si caratterizza per la sua indipendenza dalla soluzione del modello delle quantità. I prezzi così calcolati si caratterizzano come 'prezzi di produzione' che dipendono solo dalla tecnologia produttiva e dalle remunerazioni dei fattori primari, senza essere influenzati da eccessi di domanda o di offerta temporaneamente presenti sui mercati.

Nel caso del modello dei prezzi l'esercizio classico consiste nel determinare il vettore dei prezzi settoriali p, coerente con un livello assegnato di remunerazioni unitarie settoriali, rappresentato dal vettore v (o con una sua ripartizione tra profitti e salari, in versioni del modello che rendano il tasso di profitto dipendente dal vettore dei prezzi).

Anche con il modello dei prezzi sarà sempre possibile calcolare il vettore dei valori aggiunti unitari settoriali implicato da ogni vettore di prezzi assegnati esogenamente o, ancora, calcolare un insieme di n prezzi e/o valori aggiunti unitari determinato da un insieme di n elementi sia di p sia di v preassegnati.

L'inversa di Leontief e le condizioni di Hawkins-Simon

La significatività economica delle soluzioni sia del modello delle quantità sia del modello dei prezzi dipende dalle caratteristiche della matrice (I - A)-¹, detta anche 'inversa di Leontief' o matrice dei fabbisogni diretti e indiretti di produzione.

Se anche un solo elemento della matrice (I - A)^-¹ (il cui elemento generico αij misura la quantità totale di merce i che deve essere prodotta affinché il settore j sia in grado di destinare una unità di output alla domanda finale) risultasse negativo, non risulterebbe più assicurata la non negatività del vettore X per qualsiasi vettore D (non negativo) della domanda finale, ma livelli negativi di produzione non hanno senso economico, come non lo hanno i prezzi negativi che si otterrebbero dalla soluzione di p = [(I- A)´]^-¹ v. Le condizioni di non negatività di (I - A)^-¹, che garantiscono la vitalità economica del sistema, sono state formulate in vario modo; le più note vanno sotto il nome di 'condizioni di Hawkins-Simon' (v. Hawkins e Simon, 1949): per esse, condizione necessaria e sufficiente perché il sistema X = (I - A)^-¹ D ammetta almeno una soluzione X≥0 per qualsiasi D≥0 è che siano tutti positivi i minori principali della matrice (I - A).

L'interpretazione economica di queste condizioni è che la vitalità del sistema è garantita solo se ogni suo subsistema, di qualunque dimensione, è capace di produrre un surplus, cioè di produrre più di quanto assorba come inputs produttivi.

Interdipendenze strutturali e ottimizzazione

Il modello input-output delle quantità individua il solo vettore di produzione lorda coerente con un dato vettore di domanda finale; allo stesso modo, per il modello dei prezzi, esiste un solo vettore dei prezzi coerente con un dato vettore di remunerazioni unitarie degli inputs primari. Nella formulazione standard dei modelli delle interdipendenze strutturali non ci sono possibilità di scelta e, quindi, non sono rappresentati processi di ottimizzazione.

Il modello input-output può essere riformulato come modello di ottimizzazione (v. Dorfman e altri, 1958) se lo si considera come un caso particolare - quello che ammette corrispondenza biunivoca tra 'attività' e prodotto - di activity analysis (v. Koopmans, 1951): una formulazione generale che considera sia la possibilità che un'attività produca più prodotti sia quella che un prodotto sia ottenuto da più 'attività'.

Se si ammette esplicitamente che si possa scegliere tra tecnologie alternative di produzione di una stessa merce, o che si possa scegliere tra 'attività' che producono e 'attività' che importano un bene, o se si introducono vincoli aggiuntivi relativi all'impiego di risorse primarie (produzioni ad alta intensità di lavoro contro produzioni ad alta intensità di capitale, produzioni che utilizzano o non utilizzano beni importati, ecc.), il modello input-output si presenta come un modello di ottimizzazione di solito risolto con le tecniche della programmazione lineare.

7. Dal sistema produttivo al sistema economico

Quasi tutte le applicazioni empiriche dell'analisi delle interdipendenze strutturali si sono limitate all'impiego del 'modello base'.

Con questa versione del modello (statico perché considera la rete delle interdipendenze che si producono tra le parti del sistema in un solo punto nel tempo, e aperto perché assume che la domanda finale sia da determinare esogenamente) si sono condotte soprattutto analisi strutturali - dalle triangolarizzazioni della matrice A all'analisi dei collegamenti (linkages) ascendenti e discendenti tra settori, al calcolo dei moltiplicatori settoriali di produzione, reddito, occupazione, ecc. - o analisi di simulazione (o di impatto, o di previsione condizionale): misura degli effetti di variazioni del livello o della composizione della domanda finale, degli effetti di mutamenti della tecnologia produttiva di uno o più settori, degli effetti della determinazione esogena della produzione totale di uno o più settori produttivi, ecc. Ma in un modello input-output aperto i livelli del consumo, degli investimenti e degli scambi con l'estero appaiono del tutto indipendenti dai livelli settoriali di produzione, così come - in termini duali - i livelli dei salari, dei profitti e dei prezzi delle importazioni appaiono del tutto indipendenti dai prezzi settoriali delle produzioni.

Per far corrispondere l'analisi delle interdipendenze strutturali al progetto originario di modello di equilibrio economico generale applicato - un modello capace di controllare l'interdipendenza piena tra il momento della produzione e i momenti della distribuzione e della redistribuzione del reddito, del consumo, dell'investimento e dei rapporti con l'estero - Leontief e altri hanno proposto versioni del modello chiuse rispetto a componenti della domanda finale o rispetto alla remunerazione di categorie di inputs primari.

La chiusura rispetto al consumo

La chiusura rispetto al consumo si ottiene rendendo esplicite le relazioni che intercorrono tra ammontare della produzione, reddito percepito da coloro che partecipano al processo produttivo e beni acquistati per il consumo finale. Essa richiede la definizione di due insiemi di coefficienti: una matrice V di coefficienti di valore aggiunto, il cui generico elemento vkj = Vkj / Xj (k = 1, 2, ..., r; j = 1, 2, ..., n) indica il reddito pagato dal settore j al gruppo di percettori k per unità di produzione di j, e una matrice C di coefficienti di (propensioni al) consumo, il cui elemento generico cik = Cik/Yk (i = 1, 2, ..., n; k = 1, 2, ..., r) misura i consumi di prodotti del settore i acquistati dal gruppo di percettori k per unità di reddito (Yk è il totale dei redditi percepiti dal gruppo dei percettori k).

La soluzione del 'modello delle quantità' diventa in questo caso

X = (I - A - CV)^-1 d,

nella quale d rappresenta il vettore delle domande finali diverse dal consumo, e dalla quale si può ricavare la relazione diretta tra reddito e domanda autonoma Y = V (I - A - CV)-¹ d, che, dipendendo dalle tecnologie produttive A, dalle propensioni al consumo C e dai coefficienti di distribuzione del reddito V, può essere letta come un moltiplicatore di Leontief-Keynes-Kalecki (v. Miyazawa, 1976).

Nel modello chiuso rispetto al consumo ogni gruppo di percettori di reddito k viene trattato come un settore produttivo che utilizza i consumi della colonna Ck, come inputs di un processo produttivo che fornisce a tutti i settori produttivi i servizi remunerati secondo la riga Vk: i coefficienti fissi delle matrici C e V non sono più conseguenza dell'ipotesi di tecnologia alla Leontief, ma solo approssimazioni lineari delle relazioni reali.

Se si ipotizza che sia d = 0, che cioè non esistano componenti di domanda finale diverse dal consumo, il modello chiuso diventa rappresentativo del funzionamento di un'economia stazionaria, della quale consente di determinare la struttura (la composizione relativa) delle produzioni lorde e i prezzi relativi dei prodotti, ma non necessariamente il loro livello assoluto.

La considerazione esplicita dei fenomeni di distribuzione (ed eventualmente di redistribuzione privata e pubblica) del reddito e delle relazioni tra reddito e consumo può esser vista come un'estensione del modello delle interdipendenze strutturali al suo 'quarto quadrante', ora non più nullo (v. sopra, cap. 5), o come l'assorbimento dell'analisi input-output, sul lato contabile, nelle matrici di contabilità sociale (Social Accounting Matrix o SAM) (v. Stone, 1961) o, sul lato modellistico, nelle forme più semplici dei modelli di equilibrio economico generale calcolato (Computable General Equilibrium models o CGE models), che condividono con l'input-output l'origine walrasiana.

La chiusura rispetto all'investimento

Per chiudere il modello rispetto agli investimenti occorre, in base a un'opportuna teoria, mettere in relazione il livello e la composizione settoriale del vettore di domanda di nuovi beni capitali classificati per settore di produzione, I, con i livelli di produzione settoriale X.

L'insufficienza del modello input-output statico e aperto a rappresentare adeguatamente questa relazione nasce dallo sfasamento temporale tra il momento della produzione e quello dell'accumulazione.

L'esistenza di un 'periodo di gestazione' nella produzione degli investimenti e la durata della 'vita media' dei beni capitali, entrambi normalmente più lunghi dell'anno solare - assunto come periodo di produzione nella quasi totalità delle applicazioni input-output - rendono la relazione intercorrente tra I e X circolare e dinamica.

Questo problema è stato affrontato fin dall'inizio (v. Leontief, 1953) lavorando attorno all'estensione in un contesto multisettoriale del principio dell'acceleratore, già utilizzato dai modelli dinamici aggregati di tipo Harrod-Domar, che porta alla formulazione di un modello del tipo

(I - A*) Xt - B (X_t+1 - X_t) = D_t con A* = (A+_rA),

dove rA è una matrice il cui elemento generico, raij, misura la quantità di produzione del settore i necessaria per rimpiazzare il capitale consumato dal settore j nella produzione di una unità di j; B è la matrice dei coefficienti di capitale medi e marginali, il cui generico elemento bij misura la quantità di produzione del settore i richiesta dal settore j per costituire il capitale necessario a un aumento unitario della sua (capacità di) produzione, e Dt è il vettore di domanda finale al netto della domanda di investimenti.

Questo modello possiede una soluzione generale,

X_t = [B^-1 (I - A* + B)]^t X₀ + X_t^*,

che può descrivere la crescita multisettoriale del sistema studiato nel solo caso particolare che esso si trovi (e resti) sul sentiero di crescita equiproporzionale o bilanciata.

Se si ipotizza che l'economia studiata reinvesta tutta la produzione eccedente i fabbisogni correnti (che si immaginano comprensivi dei consumi delle famiglie e delle altre componenti della domanda finale), il tasso massimo di crescita bilanciata, se esiste, dipende dall'autovalore massimo di [B-¹ (I - A*+B)]. Da questo autovalore massimo dipende anche il tasso di interesse reale sullo stock di capitale investito in ogni settore, determinato dal modello dinamico 'duale' dei prezzi.

Modelli dinamici di questo tipo presentano problemi di calcolo, che nascono dalla singolarità della matrice B, e problemi teorici legati all'implausibilità di una dinamica del sistema che segua il sentiero di crescita bilanciata (il solo che può consentire di evitare il presentarsi nel tempo di outputs negativi, anche se non garantisce né il rispetto delle 'condizioni terminali', quando il modello è 'risolto in avanti' come modello di simulazione dinamica, né il rispetto delle 'condizioni iniziali', quando il modello è 'risolto all'indietro' con l'inversa dinamica - v. Leontief, 1970 - come modello di programmazione a ritroso teso a individuare i sentieri di crescita settoriale che possono condurre a condizioni finali desiderate) nonché alla connessa irragionevolezza dell'ipotesi di pieno utilizzo della capacità produttiva. Tra gli altri, lo stesso Leontief (v. Leontief e Duchin, 1986) ha recentemente impiegato un modello dinamico che ovvia a gran parte di questi inconvenienti.

La chiusura rispetto al commercio estero

Per tener conto dei rapporti che legano un sistema economico a unità produttive o di consumo appartenenti ad altre economie occorre, infine, partire da una modificazione dell'equazione di bilancio dell'economia studiata, che diventa del tipo

X + M = AX + D + E,

dove appaiono i due nuovi insiemi di variabili, il vettore delle importazioni settoriali M e il vettore delle esportazioni settoriali E.

Il problema della chiusura del modello si pone in modo sostanzialmente diverso per le importazioni e per le esportazioni.

Le importazioni sono, per definizione, variabili che dipendono dal livello della domanda intermedia e/o finale dell'economia considerata e, quindi, dal livello della sua produzione.

Le esportazioni, invece, possono essere rese dipendenti dai livelli di produzione (e quindi rese endogene nella logica input-output) solo partendo dalla constatazione che 'le esportazioni di una economia altro non sono che le importazioni delle altre economie'. Esse dipendono dunque dai livelli di produzione delle economie verso le quali sono dirette; ma queste economie, a loro volta, dipenderanno, per le proprie esportazioni, anche dai livelli di attività del sistema economico analizzato: un modello input-output può essere chiuso rispetto alle esportazioni solo passando a una sua versione multiregionale.

È la chiusura rispetto alle esportazioni che dilata enormemente lo spazio dell'analisi delle interdipendenze produttive, consentendo di passare dalla considerazione della sola interdipendenza intersettoriale a quella dell'interdipendenza intersettoriale e interregionale. Con una versione multiregionale del modello si può misurare il grado di integrazione di diversi subsistemi regionali di una economia, sia in termini di 'effetti di tracimazione' sia in termini di 'effetti di retroazione', ma ci si può anche proporre di studiare gli impatti differenziati sulle diverse economie regionali di politiche di spesa decise a livello centrale, o di studiare gli effetti di rilocalizzazione interregionale delle attività produttive. Il modello multiregionale, infine, consentendo la misura dei flussi interregionali di beni, può essere usato per stimare la domanda interregionale di trasporto o per valutare gli effetti di variazioni dei costi di trasporto sui livelli di produzione e di commercio interregionale delle diverse regioni.

In una economia multiregionale la produzione continua a eguagliare - settore per settore - la domanda (intermedia e finale) a livello dell'intero sistema di regioni, ma questa eguaglianza non è più necessariamente verificata a livello della regione singola: a questo livello territoriale l'equilibrio di bilancio viene assicurato da flussi interregionali di beni e servizi che vengono, simmetricamente, visti come importazioni (interregionali) dalle regioni che li richiedono e come esportazioni (interregionali) dalle regioni che li producono. Ciò significa che la soluzione di un modello input-output multiregionale - l'ottenimento di un vettore di produzione totale specificato sia per settore sia per regione - può essere ricavata solo raccordando la teoria leontieviana della produzione con una qualche teoria del commercio interregionale.

Le forme di questo raccordo si distinguono per il grado di dettaglio con il quale sono descritti i flussi di commercio interregionale e per la determinazione, simultanea o separata, di questi ultimi rispetto a quelli di produzione regionale.

Se rappresentiamo con xrsij il flusso del bene i prodotto nella regione r e utilizzato nella produzione di j nella regione s, l'ipotesi di coefficienti fissi di produzione continuerà a dettare l'entità del bene i necessario per la produzione del bene j nella regione s, asij, ma occorrerà affidare a un trade coefficient, ti, la rappresentazione della quota fornita dalla regione r dell'input i richiesto per la produzione di j nella regione s: xrsij = tiasijxsj.

Le diverse classi di modelli multiregionali si distinguono a seconda della maggiore o minore specificazione settoriale e/o regionale dei trade coefficients, che corrisponde ad altrettante ipotesi sulla stabilità dell'intero pattern di commercio interregionale-intersettoriale, come nel modello 'interregionale puro' di Isard (v., 1951), o sulla stabilità del solo pattern interregionale, come nei modelli alla Chenery-Moses (v. Moses, 1955), o alla sola stabilità dei coefficienti di importazione ed esportazione totale, come nei modelli pool alla Leontief (v. Leontief e altri, 1977).

Sono questi tre gli approcci classici alla chiusura dei modelli input-output rispetto al commercio interregionale, anche se nessuno di essi affronta il problema della codeterminazione dei flussi di commercio interregionale, il quale è affrontato, invece, dal modello input-output 'gravitazionale' di Leontief e Strout (v., 1963), che ha aperto la strada a tutta una famiglia di modelli input-output di interazione spaziale. L'ipotesi comportamentale rappresentata da un modello gravitazionale è che il flusso interregionale del bene i, xrsi, sia direttamente proporzionale alla produzione di i nella regione di origine r, Xri, e alla domanda di i nella regione di destinazione s, Dsi, e inversamente proporzionale a una qualche misura della distanza tra r e s, drs, secondo l'espressione

x_i^rs = k_i X_i^r D_i^s d^{rs (-α(i))},

nella quale ki è un parametro di scala e α(i) è un parametro di sensitività alla distanza, specifico per ogni bene i, da stimare empiricamente.

8. Oltre il sistema economico

Se tra due processi si stabilisce un rapporto di interdipendenza diretta tutte le volte che l'output dell'uno diventa input dell'altro, mentre altri rapporti di interdipendenza indiretta possono essere mediati da un terzo o da un quarto processo, e così via, è evidente che non è solo nell'ambito dell'economia che sono riconoscibili reti di relazioni tra parti che si influenzano tra loro. L'analisi dell'interdipendenza strutturale è andata conseguentemente estendendosi in modo che alcuni dei sistemi input-output più recentemente progettati considerano non solo i processi economici strettamente definiti, ma l'intero ambiente naturale e sociale nel quale si svolgono le attività umane delle società semplici come di quelle industriali avanzate. Lo studio della generazione e dell'abbattimento dell'inquinamento, l'analisi dell'impiego di diverse risorse naturali non rinnovabili, lo studio dei sistemi demografici, l'analisi della produzione di servizi medici e di servizi scolastici, lo studio della struttura della conoscenza scientifica, sono alcuni dei campi nei quali l'analisi delle interdipendenze strutturali si è resa utile, sfruttando la sua possibilità di essere ponte tra i valori monetari della contabilità nazionale e il più ampio mondo delle relazioni tecnologiche, economiche, demografiche e naturali descrivibili in termini puramente fisici. (V. anche Consumi; Contabilità nazionale; Equilibrio economico; Investimenti; Prezzi).

Bibliografia

Cassel, G., Theory of social economy, London 1932.

Costa, P., Marangoni, G., Economia delle interdipendenze produttive, Venezia 1994.

Dorfman, R., Samuelson, P., Solow, R., Linear programming and economic analysis, New York 1958.

Fisher, W., Chilton, C., Developing ex ante input-output flow and capital coefficients, in Input-output techniques (a cura di A. Brody e A. Carter), Amsterdam 1971.

Gerking, S., Estimating stocastic input-output models, Leiden 1976.

Hawkins, D., Simon, H., Some conditions of macroeconomic stability, in "Econometrica", 1949, XVII, pp. 245-248.

Isard, W., Interregional and regional input-output analysis: a model of space economy, in "Review of economics and statistics", 1951, XXXIII, pp. 318-328.

Koopmans, T.C. (a cura di), Activity analysis of production and allocation, New York 1951.

Leontief, W., Die Bilanz der Russischen Volkswirtschaft. Eine methodologische Untersuchung, in "Weltwirtschaftliches Archiv", 1925, XXII, pp. 338-344.

Leontief, W., Quantitative input and output relations in the economic system of the United States, in "Review of economics and statistics", 1936, XVIII, pp. 105-125.

Leontief, W., The structure of American economy 1919-1929, Cambridge, Mass., 1941.

Leontief, W., Dynamic analysis, in Studies in the structure of the American economy di W. Leontief e altri, New York 1953.

Leontief, W., The dynamic inverse, in Contributions to input-output analysis (a cura di A. Carter e A. Brody), Amsterdam 1970.

Leontief, W., Input-output economics, New York 1986².

Leontief, W., Foreword to the Journal of the International Input-Output Association, in "Economic system research", 1989, I, pp. 3-4.

Leontief, W., Carter, A., Petri, P., The future of the world economy, New York 1977.

Leontief, W., Duchin, F., The future impact of automation on workers, New York 1986.

Leontief, W., Strout, A., Multiregional input-output analysis, in Structural interdependence and economic development (a cura di T. Barna), London 1963.

Martellato, D., Metodi per la stima stocastica dei modelli inputoutput, in Interdipendenze industriali e programmazione regionale (a cura di P. Costa), Milano 1978, pp. 259-283.

Miller, R., Blair, P., Input-output analysis: foundations and extensions, Englewood Cliffs 1985.

Miyazawa, K., Input-output analysis and the structure of income distribution, in Lecture notes in economics and mathematical systems, 116, Berlin 1976.

Moses, L., The stability of interregional trading patterns and inputoutput analysis, in "American economic review", 1955, XLV, pp. 803-832.

Pasinetti, L., Lezioni di teoria della produzione, Bologna 1975.

Petri, P. (a cura di), Leontief, Bologna 1982.

Quesnay, F., Il Tableau économique e altri scritti di economia (a cura di M. Ridolfi), Milano 1973.

Rose, A., Miernyk, W., Input-output analysis: the first fifty years, in "Economic systems research", 1989, I, pp. 229-271.

Stone, R., Input-output and national accounts, Paris 1961.

UN Statistical Office, A system of national accounts. Studies in method, series F, N° 2, rev. 3, New York 1968.

Walras, L., Éléments d'économie politique pure, Lausanne 1874.