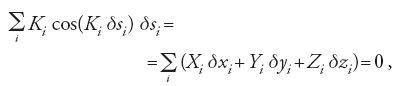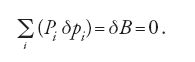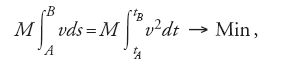L'Età dei Lumi: matematica. Meccanica variazionale
L'Eta dei Lumi: matematica. Meccanica variazionale
Meccanica variazionale
Le locuzioni 'meccanica classica' e 'meccanica newtoniana' sono, tradizionalmente, usate come sinonimi. Si cela, dietro quest'uso, una concezione che ha dominato la storiografia da Ernst Mach a Thomas S. Kuhn: con i suoi Principia, Newton avrebbe rifondato in modo del tutto nuovo la meccanica, ossia avrebbe definito un nuovo 'paradigma'; il XVIII e il XIX sec. non avrebbero fatto altro che fornire alla meccanica, su questa base, un inquadramento matematico e una sistematizzazione. La storiografia degli ultimi decenni, entrata soltanto in minima parte nella coscienza storico-scientifica, mostra tuttavia che tale concezione non può essere sostenuta ulteriormente: la meccanica classica, con la sua ricchezza di concetti, principî e metodi, non può in alcun modo sensato essere ridotta storicamente all'impostazione 'newtoniana'. Essa risale piuttosto a programmi diversi, tra cui, accanto ai genuini contributi di Newton e dei suoi predecessori, va rilevata in particolare, come ramo indipendente, la cosiddetta 'meccanica analitica'. Quest'ultima rappresenta, nei suoi elementi principali, uno sviluppo continentale del tardo XVII e in particolare del XVIII secolo.
Già Leonhard Euler (1707-1783) aveva elaborato, nella sua Mechanica sive motus scientia analytice exposita (1736), una meccanica 'analitica' attraverso i metodi dell'analisi infinitesimale. Effettivamente il termine s'imporrà soltanto in seguito alla pubblicazione della Méchanique analitique (1788) di Joseph-Louis Lagrange (1736-1813). La differenza tra queste due opere analitiche del XVIII sec. si riscontra soprattutto a livello dei principî preposti all'impianto teorico della meccanica. Euler fa sostanzialmente riferimento, nella sua prima opera, agli axiomata sive leges motus dei Principia di Newton e individua nell'analisi lo strumento per la deduzione e l'applicazione di tali principî. Lagrange, invece, si serve già di un 'principio variazionale' (precisamente, il principio delle velocità virtuali), cioè di un principio formulato con l'aiuto del calcolo delle variazioni, al quale egli vorrebbe ridurre tutta la meccanica. La meccanica analitica è, dopo Lagrange (e prevalentemente anche nell'accezione odierna), 'meccanica variazionale' in questo senso, ossia utilizza l'idea di variazione non soltanto come strumento di deduzione e di applicazione, ma anche come mezzo per la formulazione di principî.
Il problema fondamentale della meccanica del XVIII sec. consiste nella determinazione del moto di punti materiali. In base alla concezione atomistica della materia, allora dominante, secondo la quale ogni corpo fisico è costituito da un numero finito di punti materiali, il moto di tutti i corpi doveva poter essere ridotto a sistemi di punti materiali; ma a tal fine era necessario, in primo luogo, comprendere il moto di un punto materiale. Il principio variazionale non si servì quindi, inizialmente, del metodo 'diretto', praticato con successo soprattutto da Newton, consistente nel ricondurre ogni variazione di moto (accelerazione) all'influsso di forze, bensì del metodo 'indiretto' del confronto: l'idea base del principio era di determinare, e quindi individuare univocamente, il moto effettivo del punto materiale tramite altri moti, soltanto pensati ma in linea di principio possibili, le cui particolari proprietà si potessero esprimere per mezzo di grandezze scalari. Se il confronto del moto effettivo con tutti i possibili moti si svolge in un intervallo di tempo finito (e corrispondentemente in un cammino finito) tra due punti del moto, si parla di 'principio variazionale integrale', se invece si svolge in un solo istante di tempo (cammino infinitesimo), si parla di 'principio variazionale differenziale'. Incontriamo i principali rappresentanti di questi due tipi di approccio al problema già nel XVIII sec., con il principio di minima azione e quello delle velocità virtuali.
Prima di rivolgersi alla storia di questi principî, è opportuna un'osservazione introduttiva. Il metodo base della meccanica variazionale, quello del confronto, appare indubbiamente, già a prima vista, artificioso e scomodo. Che cosa può averne motivato l'introduzione? Qui entrano in discussione prima facie punti di vista molto diversi: i principî variazionali integrali sono 'olistici', cioè essi caratterizzano il moto di un corpo fra due punti A e B nel suo complesso. Un punto materiale, che inizia il suo moto in A, sembra quindi sapere quale cammino, tra tutti quelli che terminano in B, sia quello giusto o quello più vantaggioso (dal momento che è il principio che lo caratterizza come tale). Stupisce quindi poco che, nello sviluppo di tali principî, abbiano avuto un ruolo motivi antropomorfico-naturalistici e teleologici. Tuttavia, anche il metodo diretto newtoniano con alcuni problemi relativi a particolari applicazioni meccaniche ‒ per esempio, problemi in cui erano sconosciute le forze che modificano il moto o in cui le forze proposte (come la forza gravitazionale di Newton) apparivano inaccettabili su base filosofica ‒ portò alla ricerca di principî che ponessero all'inizio della teoria grandezze scalari descrittive (azione, energia, lavoro) e non forze vettoriali causali. Un altro problema, più tecnico e non basilare, è quello dell'introduzione diretta delle forze: il moto di un punto materiale è spesso limitato dai cosiddetti 'vincoli' ‒ come la condizione che la massa debba muoversi su una superficie. Questa restrizione si può trattare con i metodi newtoniani se si rappresenta l'appartenenza alla superficie con forze scelte opportunamente (cosiddette 'forze di reazione'), cosa che però porta spesso a calcoli troppo lunghi e complicati. Con i principî variazionali invece si riescono a inserire bene queste condizioni geometriche, nel senso che fin dall'inizio il procedimento di confronto è limitato ai moti che si svolgono su una superficie. Altri vantaggi del principio variazionale si rilevano quando si vuole concepire un corpo rigido come sistema di punti; infatti, le equazioni del moto si possono stabilire senza la conoscenza delle forze interne che consentono la (approssimativa) rigidità del sistema. Di analoga utilità è l'applicazione dei principî variazionali allo studio (qui non ulteriormente illustrato) di corpi elastici e anche di fluidi, quando le forze interne delle particelle che interagiscono sono sconosciute.
Alla base dell'impianto teorico, nell'analisi del moto per mezzo del principio variazionale, vanno ovviamente posti concetti diversi da quello della forza vettoriale newtoniana. Questi sono, nel principio di minima azione, l''azione' stessa e, nel principio delle velocità virtuali, lo 'spostamento virtuale' o il 'lavoro virtuale'. Gli spostamenti virtuali sono slittamenti infinitamente piccoli del sistema, compatibili con i vincoli; ma al contrario di uno spostamento effettivo (anche di tipo infinitesimale), vanno contemplati come effettuati in un tempo nullo. Anche il lavoro necessario per essi è considerato 'virtuale'. Cominciamo l'osservazione storica con il corrispondente principio. Nella forma che abbiamo ereditato da d'Alembert esso richiede di ricondurre la dinamica alla statica, che si assume già sviluppata. Alla statica, cioè all'analisi di problemi di equilibrio, si riconduce anche la comparsa del principio dei lavori virtuali.
Il principio delle velocità virtuali e il principio di d'Alembert
Il principio delle velocità (o dei lavori) virtuali è il più generale principio della statica. Troviamo le premesse alla sua formulazione e alla sua applicazione già nei problemi di meccanica di Aristotele, in Euclide, Archimede ed Erone di Alessandria, soprattutto in collegamento con le ricerche sulla leva. Qui l'unico spostamento virtuale possibile è una rotazione infinitesimale intorno all'asse, e la condizione di equilibrio richiede che per ogni spostamento virtuale sussista l'uguaglianza dei due momenti di rotazione corrispondenti (secondo la terminologia moderna). Giordano Nemorario e la sua scuola (XIII sec.) utilizzano il principio nella forma secondo cui qualcosa che può sollevare un peso G a una certa altezza h, può anche sollevare un peso n volte maggiore all'altezza h/n. Giordano non solo deduce da questa proprietà il principio della leva, ma lo utilizza anche per le ricerche sull'equilibrio nel piano inclinato. Guidobaldo Dal Monte (1545-1607), il patrocinatore di Galilei, estende l'applicazione del principio alla carrucola ‒ tra l'altro prima di Simon Stevin (1548-1620), cui nella letteratura più antica è attribuito questo merito (Benvenuto 1991). Galilei si riallaccia a Dal Monte e, in una delle sue prime opere, Le mecaniche, scritta intorno al 1600, dimostra il principio nel caso della leva, e in tale occasione introduce, per il prodotto del peso di una massa con il suo spostamento infinitesimale iniziale, il termine "momento". Descartes sostiene in seguito ‒ in uno scritto inviato a Constantijn Huygens il 5 ottobre 1637 (pubblicato postumo nel 1668 con il titolo Traité de la méchanique e nel 1672 in traduzione latina con il titolo Explicatio machinarum vel instrumentorum) ‒ l'ipotesi che si possano ricondurre al principio di Giordano varie macchine semplici.
La preistoria del nostro principio acquista una nuova qualità verso la fine del XVII sec., quando l'interesse si sposta dalla formulazione di principî per macchine semplici (come leva, piano inclinato e carrucola), a principî fondazionali per tutta la statica. Pierre Varignon (1654-1722) intraprende presto il tentativo di fondare la statica sul principio del parallelogramma di forze e ne discute nella sua corrispondenza con Johann I Bernoulli (1667-1748); questi, in una lettera del 26 gennaio 1717, formula il principio delle velocità virtuali in una forma decisamente generale. Con la definizione vitesses virtuelles per gli slittamenti infinitesimali della massa, Bernoulli dà anche il nome al principio, e chiama 'energia' il prodotto tra spostamento e forza applicata (cioè il lavoro virtuale). Varignon riprende, inoltre, la formulazione del principio data da Bernoulli nella sua opera postuma Nouvelle mécanique ou statique. Pur non rinunciando alla sua prediletta regola del parallelogramma, egli in quest'opera tratta anche numerosi esempi seguendo l'impostazione fornita dal Bernoulli; riconosce l'utilità del principio di Bernoulli soprattutto per il fatto che è sufficiente conoscere tutte le possibilità di spostamento senza tuttavia dover conoscere il meccanismo concreto che le dovrebbe realizzare. Proprio questa caratteristica risulta poi vantaggiosa nelle applicazioni.
Con notazione moderna, in coordinate cartesiane, il principio delle velocità virtuali di Bernoulli e Varignon esprime l'equilibrio di un punto P, sul quale agiscono più forze Ki, nel seguente modo:
dove Xi, Yi, Zi sono le componenti cartesiane delle forze Ki; δxi, δyi, δzi le componenti cartesiane dello spostamento virtuale δsi secondo la direzione omologa e (Ki δsi) rappresenta l'angolo tra la direzione della forza e lo spostamento virtuale. Gli spostamenti virtuali compaiono, nella notazione storica, solamente come proiezioni lungo le direzioni delle forze a mano a mano considerate. Nella precedente scrittura moderna il lavoro virtuale è rappresentato come il prodotto scalare ∑ Ki δsi dei vettori Ki e δsi, in modo tale che gli stessi spostamenti virtuali δsi diventano visibili. Dato che i vincoli sono espressi per mezzo di equazioni o equazioni differenziali, è sempre possibile, accanto a uno spostamento virtuale δsi lo spostamento opposto −δsi (per es., quando la massa è vincolata su una superficie sferica). Il vincolo può essere anche tale che la massa possa trovarsi soltanto all'esterno (o all'interno) della superficie sferica. In questo caso si deve escludere un cambiamento di segno negli spostamenti virtuali, cioè sono ammessi solamente spostamenti 'unilaterali'. L'equazione precedente diviene allora una disequazione:
La formulazione dell'equilibrio tramite una disequazione si ritrova relativamente tardi e precisamente nel Mémoire sur la statique (1798) di Jean-Baptiste-Joseph Fourier (1768-1830). Louis Poinsot (1777-1859), Carl Friedrich Gauss (1777-1855) e altri matematici si riallacciano, agli inizi del XIX sec., a questa formulazione, che può essere effettuata in termini di coordinate generalizzate e forze.
Torniamo però alla preistoria del nostro principio. Una seconda linea di sviluppo, che accenna già al successivo ampliamento dinamico del principio di d'Alembert, risale come minimo a Galilei e alle sue ricerche sul pendolo matematico. Qui si tratta di un filo considerato privo di massa, al cui estremo libero è attaccato un punto materiale, che oscilla sotto l'influsso della forza gravitazionale. Secondo quanto riferisce il suo allievo Vincenzo Viviani, Galilei già nel 1583 aveva determinato l'isocronismo di un tale pendolo, cioè il fatto che il tempo di oscillazione T non dipende dalla deviazione iniziale del punto materiale rispetto alla verticale, e neppure dalla stessa massa, ma soltanto dalla lunghezza l del pendolo: si dimostra che T è proporzionale alla radice quadrata di l. È presumibile che Galilei abbia potuto determinare sperimentalmente tali collegamenti. Christiaan Huygens (1629-1695), che voleva passare dal caso ideale matematico al pendolo fisico reale (con filo di sospensione dotato di massa), verificò teoricamente l'isocronismo con l'aiuto del principio di conservazione della forza viva (vis viva), un precursore del principio di conservazione dell'energia, e sostituì il pendolo reale con un pendolo matematico oscillante sincronicamente, di lunghezza equivalente ('ridotta').
Jakob I Bernoulli (1654-1705), fratello maggiore di Johann, analizza poi, nel 1686, il risultato di Huygens con l'aiuto di un nuovo ragionamento: egli immagina due punti materiali m1 e m2 su un'asta OB priva di massa e libera di ruotare, distanti rispettivamente l1 e l2 (l1⟨l2) dal centro di rotazione. Questo modello geometrico rappresenta il pendolo fisico. Se i punti materiali non fossero impediti nel loro movimento dall'asta OB, essi cadrebbero con uguale velocità per via della forza di gravità. Più precisamente, il punto materiale m1 più vicino al centro di rotazione avrà una 'perdita' di accelerazione, mentre l'altro punto materiale m2 avrà un 'guadagno'. Complessivamente però, secondo Bernoulli, la perdita e il guadagno si equilibrano tramite l'asta, ed egli riferisce la compensazione al centro di oscillazione M. Bernoulli osserva quindi effettivamente l'estremo M di un pendolo matematico, il quale rispetto al pendolo fisico ha una lunghezza determinata ‒ appunto quella 'ridotta' ‒ e oscilla in sincronia con quello. Egli calcola la lunghezza ridotta sulla base della natura della leva (ex natura vectis).
Jakob I Bernoulli aveva esposto tali riflessioni in un primo lavoro, inizialmente per tempi finiti, così che il suo riferimento alle accelerazioni in gioco è privo di errori; sotto l'influenza di Guillaume François-Antoine de L'Hôpital (1661-1704) corresse la ricerca. Nel 1703 pubblicò infine la versione generale e definitiva del principio da lui utilizzato nella forma di una Démonstration générale, in cui riferisce tutte le osservazioni relative al moto del pendolo a un intervallo di tempo infinitesimale dt e analizza anche pendoli non rettilinei: alla perdita (o guadagno) di velocità di m1 (rispettivamente m2) corrisponde una perdita (o guadagno) di impulso nel tempo dt. Per l'interpretazione delle forze newtoniane, anche la forza gravitazionale applicata in m1 e m2 viene diminuita (o aumentata) di una forza legata all'accelerazione. L'uguaglianza tra perdita e guadagno postulata da Bernoulli rende allora possibile il calcolo della lunghezza ridotta del pendolo.
Il nipote di Jakob I Bernoulli, Daniel (1700-1782), nei "Commentarii" di Pietroburgo (1732-1733), conduce un ragionamento analogo per sistemi di masse puntiformi collegate fra loro in modo elastico. Egli immagina che a un determinato istante di tempo i singoli corpi del sistema si liberino dai loro vincoli, così che i punti assumano, entro un intervallo di tempo infinitesimale dt, una nuova configurazione che non avrebbero potuto assumere in presenza di vincoli. Daniel cerca poi di risalire a quelle cause meccaniche che avrebbero potuto portare il sistema nello stesso stato che avrebbe raggiunto con i vincoli, in modo da determinare le effettive accelerazioni o decelerazioni di un qualunque corpo del sistema. Inoltre verifica che l'ostacolo al moto è causato da forze di reazione, che non contribuiscono all'accelerazione del sistema. Si serve come esempio della generalizzazione di un caso già trattato dallo zio Jakob, ossia di un sistema di masse puntiformi collegate fra loro da fili elastici e sottoposte alla forza gravitazionale; da un punto di vista fisico questo sistema si realizza, per esempio, con una catena sospesa. Nel suo contributo Demonstrationes theorematum de oscillationibus corporum (1734-1735) sostiene che questi metodi sono applicabili a tutti i sistemi materiali elastici e promette ulteriori applicazioni, che però non seguirono.
Accanto ad altri lavori di Johann I Bernoulli e di Brook Taylor (1685-1731) relativi al problema del centro di oscillazione, vi sono le ricerche di Jacob Hermann (1678-1733) nella sua Phoronomia (1716) e i lavori di Leonhard Euler nei "Commentarii" di Pietroburgo del 1734-1736, significativi per la strutturazione del principio, e in cui Hermann ed Euler si avvicinano alla formulazione del principio di d'Alembert.
Il principio di d'Alembert
I lavori di Jakob I e Daniel Bernoulli, Euler e Hermann forniscono importanti spunti a d'Alembert per la formulazione del principio che porta il suo nome. Usiamo l'esempio di Daniel Bernoulli per evidenziare un importante aspetto tecnico di questo principio: Bernoulli non aveva connotato le forze perdute da un sistema meccanico in senso statico, cioè non aveva richiesto che le forze perdute dovessero farsi equilibrio. Un tale concetto di forza, che può essere motivato nell'ambito del metodo statico di misurazione delle forze, ma che non vede più la forza come causa di un moto, rende possibile il passaggio a una concezione più ampia dell''equilibrio tra forze', che si ottiene quando la resistenza inerziale del corpo (la cosiddetta 'forza di d'Alembert' mb, con m massa e b accelerazione) viene inclusa nel computo dell'equilibrio. A ulteriore chiarimento va quindi osservato che il concetto dinamico di forza (forza come causa del moto, Newton) e quello statico forniscono due diverse connotazioni delle forze. Entrambe le concezioni sono di per sé giustificate, ma non è legittimo applicarle contemporaneamente o confonderle. Se, con Newton, s'interpreta una forza come causa del moto, non ha senso parlare, come fa d'Alembert, della forza d'inerzia di un corpo, e viceversa questa forza di d'Alembert non è causa del movimento di un corpo.
Dopo questa osservazione, passiamo alla riduzione di d'Alembert della dinamica alla statica per mezzo del suo principio. Egli lo annuncia nel 1742 in una lettera all'Académie Royale des Sciences, ma lo sviluppa dettagliatamente soltanto nel Traité de dynamique, apparso nel 1743 e ripresentato nel 1758 in una nuova edizione ampliata e modificata. Anche d'Alembert parte qui dal problema generale di un sistema di punti materiali dato attraverso determinati vincoli, che si muove in un certo modo, e in cui le singole parti del sistema non possono seguire il movimento incondizionatamente. Si cerca quindi (in senso vettoriale) quel movimento che corrisponde effettivamente a ogni elemento del sistema. A tal fine s'inizia dall'assunzione che le parti A, B, C… del sistema subiscano in un intervallo di tempo infinitesimale un movimento a, b, c… che si considera composto da un movimento libero (cioè non soggetto a vincoli) a′ di A, b′ di B, c′ di C… e dai movimenti risultanti dai vincoli α, β, γ… Chiamiamo 'forze di reazione' queste forze interne, che ora dipendono dalle connessioni (geometriche) del sistema e vengono introdotte per la loro realizzazione fisica, e chiamiamo 'forze attive' quelle forze che agiscono dal di fuori sul sistema e sono determinate fisicamente. Il pensiero di d'Alembert si spinge poi al punto d'indicare le forze di reazione dK0 necessarie alla 'correzione' del movimento (cioè lo scostamento dal movimento libero) come nuove forze attive dK, cioè a concepirle come causa dei movimenti α, β, γ…, che agiscono sui singoli elementi materiali dm.
Secondo Newton allora, per ogni corpo A, B, C… vale
[3] dK+dK0=bdm
ovvero
[4] dK−bdm=−dK0,
dove b è l'accelerazione.
L'ultima equazione s'interpreta nel senso che le forze attive dK, pur producendo accelerazione, non vengono 'consumate' completamente, e il resto, la forza −dK0, è perduta ai fini dell'accelerazione. Ma dato che il movimento è determinato soltanto dalla dK, il resto deve in totale essere nullo, ossia ∑dK0=0. Le forze perdute si mantengono quindi in equilibrio. L'originalità di questa impostazione non consiste ovviamente nel precedente, banale passaggio (come si legge in alcuni libri di testo), ma proprio nel fatto che si aggiungono alle forze attive dK le accelerazioni negative delle masse −bdm come 'forze apparenti', così che il sistema possa essere considerato statico.
Sulla base delle riflessioni appena esposte, d'Alembert considerò il suo principio come 'dimostrato' con certezza matematica. Tuttavia è importante capire che non si tratta qui di una dimostrazione nel senso della matematica moderna, ma piuttosto di un'illustrazione del contenuto fisico di una proprietà che, nella costruzione della meccanica propria di d'Alembert, doveva essere premessa come 'punto di partenza' indimostrato (appunto come 'principio' nel significato originario della parola).
Il principio delle velocità virtuali nella forma di Lagrange
Fu Joseph-Louis Lagrange a portare il principio nella forma che negli odierni libri di testo è in genere ascritta a d'Alembert. Egli non solo risale al Traité de dynamique di d'Alembert, ma anche allo sviluppo più antico del principio delle velocità virtuali. Lagrange stesso definisce quindi la propria formulazione, già nelle applicazioni alla statica, come una 'combinazione' di quest'ultimo principio con quello di d'Alembert. Pur se nei suoi primi contributi alla meccanica Lagrange aveva posto il principio di minima azione all'inizio, nella dinamica si serve di questa combinazione soltanto nelle Recherches sur la libration de la lune (1764), e ne sviluppa tutte le potenzialità solamente nella grande Méchanique analitique (1788, nella edizione del 1811 come Mécanique analytique). Qui, a proposito del principio di d'Alembert, Lagrange osserva che esso non fornirebbe direttamente le equazioni necessarie alla soluzione dei problemi della dinamica, ma indicherebbe comunque come poter derivare queste equazioni dalle condizioni di equilibrio. Osserva inoltre che i risultati ottenuti in base a tale principio sarebbero quasi sempre più difficili da derivare di quelli ottenuti da principî semplici e diretti. Per questo suggerisce di non partire dalle forze perdute dK0 come aveva fatto d'Alembert, ma di richiedere l'equilibrio delle forze dK−bdm. Su queste condizioni applica poi il principio delle velocità virtuali nella sua forma più antica, e constata che, nel caso di equilibrio, il lavoro virtuale scompare per qualsiasi spostamento virtuale δr. Così si ottiene:
[5] ∑ (dK−bdm) δr=0,
dove la somma è estesa a tutti gli elementi di massa dm. Se usiamo tale forma per un sistema con n elementi materiali discreti mi, sui quali agiscono le forze Ki=(Xi, Yi, Zi), otteniamo in corrispondenza la forma canonica di quello che oggi si chiama principio di d'Alembert. Lagrange ritiene di poter ricondurre alla sua combinazione del principio di d'Alembert e del principio delle velocità virtuali "l'intera teoria della dinamica", e di poter così ridurre la determinazione del moto di punti materiali a una "questione di puro calcolo". Da essa ricava anche le famose 'equazioni lagrangiane del moto'.
Il principio delle velocità virtuali assume importanza nella Méchanique analitique di Lagrange ‒ e in seguito in molte altre opere sulla meccanica ‒ per il fatto di consentire un'organizzazione deduttiva di ampie parti della meccanica della fine del XVIII sec.: Lagrange ne deduce anche il teorema della conservazione del moto baricentrico, la proprietà della conservazione delle superfici (ovvero del momento della quantità di moto), nonché (nel caso in cui il sistema meccanico sia sottoposto a vincoli indipendenti dal tempo e sia 'governato' solamente da forze centrali) la legge della conservazione della forza viva e il principio variazionale (ancora da approfondire) di minima azione. Dal punto di vista di un'organizzazione della meccanica puramente formale e deduttiva si può ben comprendere che egli abbia introdotto la sua generalizzazione del principio delle velocità virtuali nella parte statica della sua opera come "une espèce d'axiome de Méchanique" (Méchanique analitique, p. 12). Più tardi sostenne però che esso non possedeva l'evidenza tradizionalmente necessaria a un assioma. Egli cercò quindi di dimostrarlo per diverse vie; ma queste dimostrazioni, analogamente alle osservazioni di d'Alembert sul proprio principio, devono essere considerate oggi piuttosto come illustrazioni che non come derivazioni logiche da basi sicure.
Il principio di minima azione
L'aspetto teleologico
Il principio di minima azione appartiene in senso stretto alla fisica matematica, ma la sua notevole portata e la sua particolare forma lo hanno spinto al di fuori di questo settore procurandogli attenzione filosofica e teologica, e hanno dato luogo, fino al XX sec., ad ampie dissertazioni di carattere metafisico. In tutta la discussione è penetrante il problema teleologico. Affrontiamo questo punto prima di rivolgerci alla formulazione del principio stesso.
La visione teleologica della Natura, cioè l'interpretazione dei suoi processi e dei suoi oggetti basata sull'idea di finalità, ha una lunga tradizione: dal momento che, di regola, le nostre proprie attività e creazioni umane sono guidate da mete e scopi consapevoli, non solo presupponiamo una finalità generale quando vogliamo motivare il comportamento di altre persone, ma siamo facilmente tentati di estendere questa visione alla comprensione di processi degli esseri viventi non umani così come della Natura inanimata. Una tale interpretazione presuppone che mete e scopi della Natura vengano prefissati da un essere saggio. Nella tradizione cristiana è naturalmente Dio l'autorità che determina gli scopi. A partire dal Rinascimento, però, queste visioni teologiche della scienza naturale cominciarono a essere messe in discussione. In seguito, le nuove scienze e la filosofia ‒ in particolare, Francis Bacon, Descartes e Spinoza ‒ criticarono una scienza naturale che accettasse come spiegazione scientifica l'asserzione di cause finalistiche. La scienza doveva piuttosto prescindere dalla ricerca di un tale 'senso' dei fenomeni naturali e stabilire esclusivamente il rapporto tra cause materiali e loro effetti. Questo pensiero base del meccanicismo restituisce la teleologia alla metafisica speculativa e alla teologia, lasciando alla filosofia naturale la descrizione (meccanico-causale) delle cose. I tentativi di trarre conclusioni sulle ragioni ultime della Natura e sul loro Creatore a partire dagli scopi riscontrati nella Natura, divennero quindi marginali nella filosofia naturale, cosa che si manifestò nella nascita di una cosiddetta 'teologia fisica'. Il termine fu rapidamente ripreso anche nel Continente. L'idea a esso collegata di dimostrare e celebrare Dio, non solo in base alla sua manifestazione, ma anche alla sua creazione trovò però un'eco piuttosto forte in Gran Bretagna. Robert Boyle fu uno dei principali rappresentanti di questa linea, e anche Newton fu vicino alle sue posizioni. Il giovane Pierre-Louis Moreau de Maupertuis (1698-1759), futuro presidente della Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino, fondata da Federico II, conobbe la teologia fisica durante il suo soggiorno a Londra nel 1728. In questo periodo divenne anche seguace della teoria della gravitazione newtoniana, che diffuse al suo ritorno in Francia.
Sotto il tetto comune della teologia fisica si incontravano in modo molto ingenuo diverse pie visioni della Natura, tanto da sfiorare, dal punto di vista odierno, il ridicolo; ciononostante l'idea della parsimonia (lex parsimoniae) ottenne un certo rilievo come aspetto quantificabile (e quindi matematizzabile) di questo pensiero; quantomeno lo sviluppo del calcolo infinitesimale apriva qui nuove possibilità matematiche. Dopo che il pensiero fisico-teologico ebbe superato il suo periodo di fioritura, Christian Wolff (1679-1754) introdusse nella sua Philosophia rationalis sive logica (1728) il termine 'teleologia' per l'interpretazione finalistica della Natura. Con Wolff, influenzato considerevolmente da Leibniz, la prospettiva cominciò a capovolgersi: non è a causa dell'operato di un saggio Creatore che troviamo ordine nella Natura, ma è il fatto di trovare un ordine nella Natura che indica l'esistenza di un Creatore intelligente. Con Leibniz, Wolff sostenne l'idea che la matematica fosse uno degli strumenti più importanti per tale forma di conoscenza della Natura e di Dio.
Maupertuis e la loi du repos della statica
Stimolato da una richiesta della marchesa di Châtelet, la compagna per la vita di Voltaire, Maupertuis inizia il cammino verso il principio di minima azione nell'anno 1740, con il lavoro Loi du repos des corps, nel quale descrive il mantenimento in equilibrio di un sistema materiale di punti Ai (i=1,…, n), sui quali agiscono forze centrali Pi, per mezzo della "somme des forces du repos" cioè, nella terminologia odierna, del potenziale B, così come per mezzo del principio delle velocità virtuali nella forma di Johann I Bernoulli. Nel simbolismo moderno la sua condizione di equilibrio assume la forma seguente:
Qui le δpi sono le proiezioni degli spostamenti virtuali δsi lungo la direzione della forza corrispondente Pi, e quindi la variazione δB del lavoro B scompare, il che rappresenta soltanto una condizione necessaria per il fatto che B sia stazionario (in Maupertuis: massimale o minimale). Maupertuis sembra però considerare questa condizione come sufficiente, perché egli postula l'esistenza di equilibrio quando il potenziale è stazionario; nel caso considerato risulta essere un minimo. Euler corregge più tardi la situazione (in lavori del 1748 e 1751) e generalizza il principio statico di Maupertuis a forze centrali qualunque.
Il principio di Fermat e il principe de la moindre action di Maupertuis
Dopo il 1740 Maupertuis si preoccupa di sviluppare anche per la dinamica un principio equivalente alla Loi du repos. Un importante passo in questa direzione, anche se non privo di problemi, è costituito, nel 1744, dal lavoro Accord des différentes lois de la nature, nel quale egli si riferisce inizialmente all'ottica.
Pierre de Fermat aveva formulato il suo principio del minor tempo di percorrenza, nell'ottica, già nel 1662 come generalizzazione del principio del cammino più breve della luce, che risale a Erone. Utilizzò per la giustificazione anche argomenti teleologici, che conducessero a una finalità della Natura riconoscibile 'matematicamente', cosa che portò a una lunga disquisizione con Descartes e i suoi seguaci. Elemento di perplessità nelle discussioni sull'ottica era soprattutto il fatto che ipotesi diverse sulla velocità della luce in mezzi densi di Fermat e Descartes (e più tardi anche di Newton) portassero allo stesso risultato (la legge di riflessione). Questo problema fu il punto di partenza per la ricerca di Maupertuis di un nuovo principio ottico estremale, nel corso della quale egli riconosce il significato del concetto di azione: Fermat aveva potuto derivare dal suo principio le leggi di riflessione e rifrazione, assumendo che la luce si muovesse più lentamente in un mezzo denso. Maupertuis era invece dell'opinione, sulla scia di Newton, che le cose stessero esattamente in maniera opposta, e che quindi il tempo, nel principio di minimo di Fermat, dovesse essere rimpiazzato da un'altra grandezza. Egli trova quest'altra grandezza nell'azione mvs, cioè nel prodotto fra la massa m della particella di luce, la sua velocità v e il cammino da essa percorso s, inizialmente senza introdurre la massa. Soltanto più tardi Maupertuis chiarisce di aver preso a prestito la sua definizione di 'azione' da Leibniz, che l'aveva già introdotta intorno al 1690, come quantitas actionis formalis. In ogni caso Maupertuis formula, con l'aiuto di questo concetto, un principio di minimo secondo il quale una particella di luce tra due punti prefissati 'sceglie' quel cammino sul quale la somma totale dell'azione è minima. Si osservi che qui si tratta effettivamente di una richiesta di minimo e non, come nel 1740, di una generale richiesta di stazionarietà. Anche se oggi non possiamo accettare il suo principio ottico del 1744, perché è errata l'ipotesi di Newton sulla velocità su cui si basa, tuttavia esso acquistò consensi e divenne importante per lo sviluppo di un principio generale meccanico di azione. Possono esserci proficui sviluppi storici anche a partire da un errore.
Maupertuis presenta il principio meccanico generale due anni dopo, con il lavoro Les lois du mouvement et du repos, quasi come dono d'ingresso del nuovo presidente alla 'sua' Accademia. Ritornando al concetto di azione del 1744, egli afferma qui che 'tutti' i processi della Natura ‒ sia animata sia inanimata ‒ sono spiegabili in base al principio di minima azione (principe de la moindre action). In particolare tutte le leggi note della cinematica e della statica devono essere, secondo Maupertuis, dedotte da questo principio: "Quando nella Natura si verifica un cambiamento, la Quantità d'Azione necessaria a produrlo è la più piccola possibile" (Les lois du mouvement, p. 290). Dal momento che Maupertuis non si limita a sistemi conservativi (nei quali, in termini moderni, si conserva l'energia meccanica), ma al contrario ritiene di poter dimostrare per tali sistemi la conservazione della forza viva, si tratta della 'forma estesa' del principio di minima azione. Questo poté essere formulato in modo matematicamente 'corretto' soltanto verso la fine del XIX secolo.
Il lavoro di Maupertuis del 1746 non è invece affatto eccellente da un punto di vista matematico: la breve parte matematica si esaurisce nell'applicazione del principio ad alcuni esempi fisici (leva, rifrazione e riflessione della luce, urto elastico e anelastico), che in parte oscurano, anziché illuminare, il contenuto del principio e illustrano più un formalismo che non un principio. Maupertuis non riesce neppure ad andare oltre a una formulazione finita del suo principio: non si serve né del calcolo delle variazioni né dell'usuale analisi infinitesimale. Il suo contributo più importante va quindi visto nell'aver riconosciuto l'azione come una grandezza determinante di un principio di stazionarietà dinamico.
Più importante della presentazione matematica fu allora, per la ricezione del principio, la rivendicazione filosofica che Maupertuis vi collega. Egli lo interpreta sotto l'aspetto teleologico e vede in esso la manifestazione della saggezza e del rispetto del principio di economia da parte di Dio. Maupertuis cerca di fornire una giustificazione della sua concezione, che doveva poi trovare antagonisti nell'ambito scientifico della metà del XVIII sec., suggerendo due approcci diversi allo studio della Natura: da una parte c'è l'osservazione e la misura (empirismo), dall'altra la ricerca di quegli scopi della Natura che appaiono conformi al suo Creatore come Être suprême (teleologia). I due approcci si devono completare e i loro risultati devono confermarsi reciprocamente, ma a partire dal 1746 si nota in Maupertuis una chiara asimmetria: egli usa l'empirismo sempre più per criticare concezioni rivali, mentre sostiene teleologicamente le proprie. Così critica Leibniz e Newton perché avrebbero fondato la loro meccanica sull'esistenza di forze causali problematiche, riscontrabili empiricamente, mentre il suo proprio principio si serve dell'azione come di una grandezza puramente descrittiva. Nello stesso momento però in cui Maupertuis interpreta l'azione come espressione di un influsso diretto divino sugli accadimenti naturali, togliendo ai corpi (e alle forze) ogni possibilità di agire gli uni sugli altri direttamente e attivamente, finisce con il ricadere in una soluzione occasionalista del problema del moto, già difesa da Nicolas Malebranche (1638-1715). In particolare il più tardo Essai de cosmologie (1750) di Maupertuis, che può ampiamente essere letto come una difesa filosofica del principio di minima azione, conferma la sua 'testa di Giano' nella fondazione della meccanica, in cui una faccia è rivolta a un empirismo moderno, quasi a volte positivista, mentre l'altra è rivolta alla metafisica tradizionale.
La scoperta indipendente di Euler del principio di minima azione
All'inizio del suo scritto del 1746, Maupertuis fa riferimento a un lavoro di Euler, che egli interpreta come una notevole conferma matematica del proprio principe de la moindre action. Si tratta di fatto dell'Additamentum II, del primo testo in assoluto sul calcolo delle variazioni, che Euler pubblicò nel 1744 con il titolo Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes. Sive solutio problematis isoperimetrici latissimo sensu accepti. Il calcolo delle variazioni era una disciplina relativamente nuova e difficile, i cui metodi apparivano molto promettenti per la trattazione matematica di problemi fisici. Le due appendici del testo di Euler trattano queste applicazioni alla fisica, ed entrambe affondano le loro radici nello scambio epistolare di Euler con Daniel Bernoulli verso la fine degli anni Trenta, in cui Bernoulli spinge il suo amico verso ricerche sull'argomento.
Nell'Additamentum II, scritto già nel 1743, Euler formula, prima di Maupertuis e in forma matematica corretta, un principio di minima azione. Ma egli non correda il proprio principio con la pretesa di universalità di Maupertuis, anzi lo limita ‒ in modo matematicamente ben adeguato alla sua formulazione ‒ a sistemi conservativi, dal momento che deve far uso del principio della conservazione della forza viva per la determinazione del moto. Quindi (diversamente da Maupertuis) Euler formula una 'forma ristretta' del principio di minima azione. In notazione moderna questa si esprime:
dove M rappresenta la massa del corpo, s il cammino da esso percorso tra due punti fissi A e B, v la sua velocità al tempo t. Nel procedimento variazionale di Euler, che determina il percorso effettivo attraverso un minimo del (precedente) valore integrale dell'azione, sono ammesse tutte le curve di confronto tra A e B con la stessa costante energia meccanica. Euler crede di poter distinguere il minimo da altri estremali (in particolare massimi), perché esso esprimerebbe una certa passività del corpo dovuta all'inerzia. Tuttavia questa argomentazione è puramente di natura filosofica e non pertinente da un punto di vista matematico. Al contrario, le applicazioni del principio a diversi problemi di moto sotto l'influsso della forza gravitazionale (moto dei pianeti, traiettorie balistiche, ecc.) sono corrette e illustrano già la grande produttività della formulazione variazionale euleriana.
È da notare che Euler sottolineerà più avanti, ripetutamente, di aver ottenuto il suo principio a posteriori e non, come Maupertuis, a priori. Con ciò egli chiarisce di aver trovato i risultati ottenuti tramite il principio di minima azione prima per altra via, e precisamente con metodi diretti newtoniani, confermando quindi deduttivamente il proprio principio. Nella sua filosofia naturale fortemente improntata a Descartes, Euler non aveva trovato alcuna sensata motivazione alla validità del principio; in particolare non vedeva che l'azione deve essere accettata come premessa al suo principio variazionale senza poter essere giustificata a priori. Solo più tardi, a partire dal 1750, egli fornirà un'interpretazione del principio basata sulla teoria della materia, che è conciliabile con la concezione cartesiana: il principio di minima azione regolava, nell'urto di due corpi, la nascita delle forze in modo che si evitasse, 'con il minimo sforzo possibile', la penetrazione di essi. Dunque questo diventa per lui un principio che esprime la passività dei corpi: le forze non esistono di per sé, ma vengono generate dalla materia in movimento con il minimo sforzo. Per una tale interpretazione, però, il principio va applicato a processi d'urto, come aveva fatto inizialmente Maupertuis nel 1746. L'applicabilità del principio a processi (apparenti secondo Euler) di azione a distanza, come moti sotto l'influsso della gravitazione, è invece, nella filosofia naturale euleriana, secondaria, e tali sono quindi i suoi esempi relativi all'applicazione del principio. Tutto ciò dovrebbe aver contribuito al fatto che Euler non sollevò pretese di priorità relativamente al principio di minima azione, ma anzi sostenne con vigore la paternità di Maupertuis. Potrebbero anche esserci stati motivi di carattere accademico-politico a farlo rinunciare alla priorità, perché egli dirigeva, sotto la presidenza di Maupertuis, la classe di matematica dell'Accademia di Berlino. In aggiunta, la giustificazione teleologica del principio di azione data da Maupertuis potrebbe aver influenzato Euler, profondamente religioso, anche se questi non porta argomentazioni di quel genere in favore del principio. I suoi lavori sul principio di minima azione dal 1748 al 1752 sono caratterizzati piuttosto dal tentativo di dare alla Loi du repos di Maupertuis e al principio di Euler-Maupertuis di minima azione della dinamica una forma matematica unitaria, comprendente la statica e la dinamica, per la quale Maupertuis non aveva neppure fornito i presupposti. Inoltre, Euler estende il principio a più punti materiali ‒ un merito attribuito in genere nella letteratura ai suoi successori ‒ e fornisce alcune premesse per la sua applicazione alla dinamica dei continui. Con l'introduzione del concetto di effort egli effettua, nel 1751, un importante lavoro preparatorio per la formazione di un concetto generale di potenziale e quindi anche per l'ulteriore estensione del principio variazionale in fisica. La superiorità matematica di Euler rispetto a Maupertuis fa sì che non sia sorprendente che matematici di epoche successive, che svilupparono ulteriormente il principio di minima azione, si riferiscano soprattutto al suo Additamentum II della Methodus inveniendi e ai suoi diversi lavori nelle "Histoires" di Berlino. Tra questi, nel XVIII sec. è da menzionare in particolare Lagrange.
Il contributo giovanile di Lagrange
Joseph-Louis Lagrange, nato a Torino, si rivolge a Euler già all'inizio della sua carriera accademica, cominciando con questi una corrispondenza sul nuovo calcolo delle variazioni da lui trovato. In quel periodo egli vede il principio di minima azione come "la chiave universale [la clé universelle] di tutti i problemi, sia della statica che della dinamica" (Lagrange a Euler, 19 maggio 1756, in Oeuvres, XIII, p. 392). In due ampi lavori per la "Miscellanea Taurinensia" degli anni 1760-1761, egli sviluppa poi il suo nuovo calcolo (il cosiddetto 'δ-calcolo') e la sua applicazione alla meccanica. In questa Application Lagrange si rifà all'Additamentum II di Euler e ne generalizza la formulazione del principio di minima azione a problemi con vincoli, a problemi con n punti materiali, e anche alla meccanica dei continui solidi e fluidi. Egli sottolinea la potenzialità deduttiva del principio soprattutto per il fatto di farne derivare, per sistemi sottoposti a forze centrali, la legge di conservazione del moto baricentrico, e la legge di conservazione delle superfici (oggi legge di conservazione del momento della quantità di moto), nonché l'equazione newtoniana del moto in coordinate cartesiane. In particolare è da rilevare che Lagrange supera in questo modo la 'forma ristretta' euleriana del principio di minima azione, e studia un'applicazione del principio a sistemi nei quali non si richiede la conservazione della forza viva. Egli prende qui in considerazione anche una 'forma estesa' del principio di minima azione ‒ una forma che Maupertuis ventilava, ma non riusciva a formulare. Nelle applicazioni Lagrange si limita però sempre a sistemi conservativi, in cui la conservazione della forza viva è garantita, e si serve quindi della forma ristretta di Euler. Il rapporto non chiarito tra la conservazione della vis viva e il principio di minima azione potrebbe essere il motivo per cui egli non perseguì quest'ultimo principio nei suoi lavori successivi, preferendogli quello delle velocità virtuali.
Accoglienza del principio di minima azione nel XVIII secolo
Quando, nel 1754, Lagrange si rivolge al principio di minima azione, quest'ultimo è appena caduto nel vortice di uno scandalo accademico, che in parte turbò e in parte divertì il mondo scientifico europeo: la cosiddetta 'controversia Maupertuis-Koenig'. Già nel 1748 a Lipsia, negli ambienti che facevano capo al poeta e filosofo tedesco Johann Christoph Gottsched (1700-1766), le riflessioni di Maupertuis sul principio di minima azione erano state collegate a Leibniz. Nel 1752 Patrice d'Arcy (1725-1779) sottopose il principio di Maupertuis a una critica contenutistica, ma soprattutto Maupertuis ed Euler, a partire dal 1751, iniziarono un attacco a Samuel Koenig (1712-1757), seguace di Leibniz. Koenig credeva di poter dimostrare, sulla base di una lettera, che il principio di minima azione non fosse di Maupertuis, ma fosse già stato trovato da Leibniz. Il punto controverso non è stato ancora sciolto, anche se attualmente ci sono più argomenti contro l'affermazione di Koenig che a favore. Le pretese di Koenig sulla priorità di Leibniz, l'inabile difesa di Maupertuis e la forma della controversia, più polemico-letteraria che oggettiva, segnarono l'inizio del declino del principio di minima azione, tanto più che Voltaire, con il suo scritto satirico anonimo Diatribe du docteur Akakia (1753), contribuì a rendere ridicolo Maupertuis (e anche Euler). Gli scritti polemici redatti in questa occasione furono pubblicati anonimamente in una raccolta dal titolo Maupertuisiana (1753).
Se Kant in un suo scritto giovanile si esprimeva positivamente sulla teologia di Maupertuis, questa divenne, nella fisica matematica ‒ pur nella marcia trionfale del meccanicismo ‒, un vero ostacolo alla ricezione del principio di minima azione. In successive formulazioni della meccanica il principio è quindi o ignorato, oppure considerato, come fece per esempio Lagrange, un "semplice e generale risultato della meccanica", libero da qualunque corredo metafisico (Méchanique analitique, p. 189).
La trattazione precedente dovrebbe aver chiarito che la meccanica variazionale, con i due principî più importanti, quello delle velocità virtuali e quello di minima azione, rappresenta sostanzialmente una conquista del XVIII secolo. I più avanzati testi di meccanica del XIX sec. proseguono questa tradizione. Dal punto di vista dello sviluppo formale c'è, inizialmente, in primo piano il principio delle velocità virtuali. A questo hanno fornito importanti contributi soprattutto Jean-Baptiste-Joseph Fourier, Louis Poinsot, Augustine Cournot e Michail Vasil´evič Ostrogradskij. Nuovi e produttivi principî variazionali furono proposti da Gauss e William Rowan Hamilton. Carl Gustav Jacob Jacobi si rivolse, influenzato da Euler, Lagrange e Hamilton, sia a questi principî sia a quelli delle velocità virtuali e di minima azione dando un contributo al loro sviluppo formale. Dal punto di vista filosofico va rilevata soprattutto la sua critica all'interpretazione 'assiomatica tradizionale' dei principî variazionali, che dominò il XVIII sec.: la certezza matematica, sottolinea Jacobi, non può essere attribuita ai principî puramente empirici della meccanica né attraverso (presunte) pure dimostrazioni matematiche (d'Alembert e Lagrange, tra gli altri), né attraverso argomentazioni metafisiche (Maupertuis ed Euler, tra gli altri).
Il principio di minima azione vive dunque una rinascita, soprattutto grazie al principio generale di conservazione dell'energia, con il quale è sistematicamente in stretto rapporto, ma grazie anche allo sviluppo del calcolo delle variazioni a partire dalla metà del XIX sec., che culmina verso la fine del secolo nel tentativo di Hermann von Helmholtz di farlo diventare un principio universale della fisica. Nel XX sec. Max Planck, in Das Prinzip der kleinsten Wirkung (Il principio di minima azione, 1915), vede in esso la migliore realizzazione dello scopo delle scienze naturali "di riassumere in un unico semplice principio tutte le manifestazioni della Natura osservate e quelle ancora da osservare" (Das Prinzip, ed. 1949, p. 95). Questa valutazione sarà rafforzata dall'ulteriore sviluppo della teoria della relatività e della meccanica quantistica fino al metodo degli integrali curvilinei di Richard Feynman. Tuttavia oggi non si tratta tanto dell'idea teleologica di un'economia della Natura, quanto dell'idea di ricerca pratica di un'economia della scienza, che assicura all'approccio variazionale in fisica matematica una continua attenzione e diffusione.