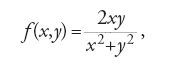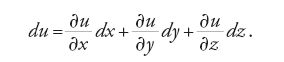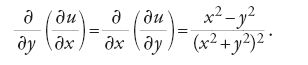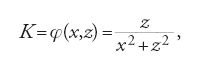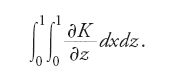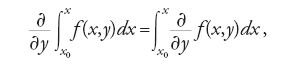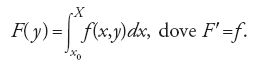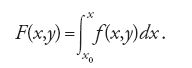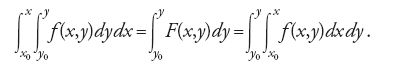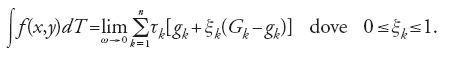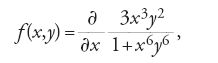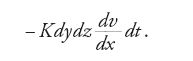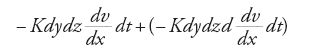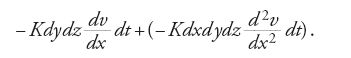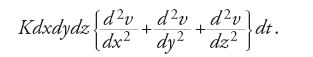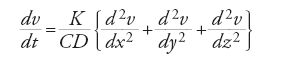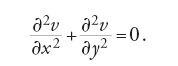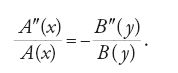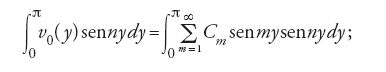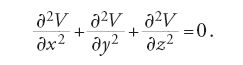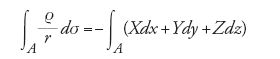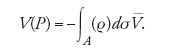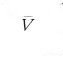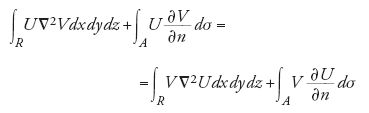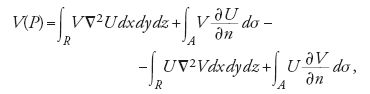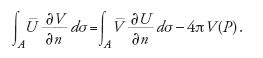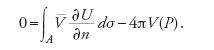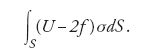L'Ottocento: matematica. Equazioni differenziali alle derivate parziali
L'Ottocento: matematica. Equazioni differenziali alle derivate parziali
Equazioni differenziali alle derivate parziali
Nel corso del XIX sec. la teoria delle funzioni di più variabili reali non era una disciplina concettualmente unitaria e l'assenza di una sua trattazione indipendente nei libri di testo del periodo ne è una evidente conferma. La grande importanza attribuita, per buona parte del secolo, alla teoria delle funzioni di una variabile complessa ha portato certamente a usare le funzioni di due variabili reali, ma soltanto in quel contesto specifico, impedendo che ci si interessasse più in generale a una teoria delle funzioni reali di più variabili. Dal momento che l'accento sul dominio e l'immagine di una funzione è stato posto solo successivamente all'opera di Karl Theodor Wilhelm Weierstrass, e in particolar modo dopo l'emergere della teoria degli insiemi, l'idea di considerare come oggetti di indagine insiemi di funzioni definite in sottoinsiemi dello spazio reale a n dimensioni ℝn e a valori in sottoinsiemi di ℝn, da studiare sistematicamente caso per caso, era lontana dallo sfiorare la mente della maggior parte dei matematici di allora.
Nonostante ciò, le funzioni di più variabili reali sono state usate correntemente per tutto il secolo, soprattutto nella fisica matematica, dove i problemi tridimensionali erano all'ordine del giorno, specialmente nelle equazioni alle derivate parziali e nella teoria del potenziale. Lo studio di quelle funzioni ha contribuito così allo sviluppo dell'analisi reale dell'Ottocento e ha consentito inoltre di introdurre un gran numero di metodi che avrebbero avuto un ruolo fondamentale per la maturazione della teoria nel secolo successivo, contribuendo al completo sviluppo del concetto di funzione. Le sottili questioni che riguardano i limiti e la continuità delle funzioni di più variabili, nonché la distinzione tra integrali multipli e integrali iterati, sono infatti la conseguenza delle riflessioni condotte nel XIX sec., nelle quali viene quanto meno abbozzata l'idea del differenziale come applicazione lineare. Frutto di quell'epoca sono anche certi risultati basilari che oggi vengono normalmente considerati di natura vettoriale, così come l'approccio vettoriale stesso. Infine, sempre nel corso dell'Ottocento, appaiono molti altri risultati particolari, tra i quali, per esempio, la determinazione dei valori estremali e la dimostrazione completa dell'uguaglianza delle derivate miste. Nelle pagine seguenti si troverà un breve riassunto di alcuni sviluppi della teoria di base. Il resto della trattazione sarà dedicato alle applicazioni delle funzioni di più variabili reali, soprattutto nell'ambito delle equazioni alle derivate parziali e in quello della teoria del potenziale.
Funzioni di più variabili reali
Nel corso del XVIII sec. si era soliti assumere, spesso in modo acritico, molte delle principali proprietà delle funzioni di più variabili reali. Le considerazioni generali che seguono si propongono soltanto di dare al lettore un'idea dello status quo ante, ma occorre tener presente che per quasi ogni affermazione generale su ciò che all'epoca si intendeva o si fraintendeva, ci sono quasi sempre eccezioni, intuizioni incomplete o anticipazioni controverse. Comunque, se si leggono introduzioni come quelle scritte per esempio da Leonhard Euler e Joseph-Louis Lagrange ai loro libri ‒ che esercitarono grande influenza sui lettori del XIX sec. ‒ se ne ricava l'immagine seguente: le variabili indipendenti venivano concepite come coordinate cartesiane, alle quali Euler aggiunse per primo le coordinate sferiche e cilindriche.
Anche le variabili dipendenti venivano a volte concepite come coordinate, ma non così spesso come sarebbe avvenuto in seguito, e ciò perché le interpretazioni geometriche erano spesso complicate, soprattutto per quanto riguarda le equazioni differenziali. Iterare gli integrali per calcolare aree, volumi o forze esercitate tra corpi estesi era una pratica diffusa, quantunque non si facesse distinzione tra integrazione multipla (nella quale gli elementi differenziali sono multidimensionali) e integrazione iterata; questo accadeva perché, per esempio, si considerava ingenuamente che un elemento di volume avesse come sue 'dimensioni' dei differenziali unidimensionali. In quelle situazioni multidimensionali si procedeva a cambiamenti di variabili nello stesso modo adottato nei casi unidimesionali, e lo 'jacobiano' ‒ certo non indicato con questo termine ‒ era ben noto per i sistemi di variabili più usati. Persino negli integrali impropri si invertiva l'ordine di integrazione senza una giustificazione rigorosa.
Sembra che sia stato Euler il primo a utilizzare, a partire dagli anni Quaranta del XVIII sec., l'idea di derivata parziale. Il successivo sviluppo delle equazioni alle derivate parziali segnò l'avvento delle serie di più variabili trattate, secondo una consuetudine settecentesca, come espressioni puramente formali. In questo contesto la nozione di differenziale di una funzione di più variabili reali aveva un concreto significato algoritmico, sebbene fosse a volte di difficile interpretazione. Non sembra che sia esistito in quel periodo alcun abbozzo dell'idea di concepire il differenziale di una funzione di più variabili come applicazione lineare, sebbene sia stata indiscutibilmente presente l'idea della derivazione parziale (di qualsiasi ordine) come operatore. Euler si rese conto dell'identità delle derivate parziali miste e la enunciò nelle Institutiones calculi differentialis del 1755, ma la dimostrazione è stata rivista diverse volte nel corso del XIX secolo. Egli formulò anche con chiarezza la regola per la differenziazione di funzioni composte. Sempre Euler mise a punto tecniche per individuare massimi e minimi, ma definì 'odioso' il caso di una funzione di tre variabili e non riuscì a trovare un procedimento generale. Il metodo dei moltiplicatori di Lagrange per la soluzione di problemi di estremo vincolato era strettamente legato ai suoi sforzi compiuti nell'affrontare le equazioni alle derivate parziali, ed era noto in molti ambienti. Alcuni aspetti della teoria delle equazioni alle derivate parziali e della teoria del potenziale del XVIII sec. saranno esposti più avanti.
Continuità
Non stupirà il fatto che il primo ad assumersi un significativo impegno nel riconsiderare i fondamenti della teoria delle funzioni di più variabili sia stato Augustin-Louis Cauchy nel famoso corso tenuto nel 1821 all'École Polytechnique. Egli propose il seguente ragionamento per mostrare come la continuità rispetto a ciascuna variabile sia sufficiente a garantire la continuità di una funzione di più variabili.
Sia f(x,y,z,…) una funzione di più variabili x,y,z,… e supponiamo che nelle vicinanze di particolari valori X,Y,Z,… assegnati a quelle variabili, f sia continua separatamente come funzione di x, come funzione di y, come funzione di z, […]. È facile dimostrare che, se si indicano con α,β,γ,… grandezze infinitamente piccole, e se si attribuiscono a x,y,z,… i valori X,Y,Z,… o valori molto vicini, la differenza f(x+α,y+β,z+γ,…)−f(x,y,z,…) è anch'essa infinitamente piccola. (Cauchy 1821a, pp. 45-46)
Egli proseguiva affermando che, se α,β, ecc. decrescono indefinitamente, lo stesso accade ai valori
[1] f(x+α,y,z,…)-f(x,y,z)
e così via; cosicché anche la differenza
[2] f(x+α,y,+β,z+γ,…)-f(x,y,z,…)
tende ad annullarsi.
Questo ragionamento, piuttosto lacunoso, non ha comunque compromesso il lavoro di Cauchy; infatti il suo intento principale era di usare tale risultato nel caso in cui tutte le variabili fossero funzioni (continue) di un'unica variabile t. L'uso di espressioni come 'grandezza infinitamente piccola' sarebbe rimasto problematico fino agli anni Settanta del XIX sec., così come era un problema l'incapacità di cogliere sistematicamente il fatto che le grandezze infinitamente piccole debbano, in qualche senso, tendere a zero simultaneamente.
Certamente Weierstrass si accorse che qualcosa non andava nella definizione di Cauchy e, negli anni Sessanta del XIX sec., egli usava ormai una definizione moderna, che Hermann Amandus Schwarz ricorda di aver adottato "nei suoi primi studi di matematica".
f(x,y) è una funzione continua dei suoi argomenti reali, variabili con continuità in un intorno di una coppia di valori x0, y0 se, in corrispondenza di una quantità positiva ε comunque piccola, è sempre possibile delimitare nell'intorno di tale coppia un dominio esteso nelle due direzioni tale che, per ogni coppia di valori x0+h, y0+k appartenenti sia al dominio originale delle variabili ove è definita la funzione sia al dominio delimitato, la differenza f(x0+h, y0+k)−f(x0,y0) è, in valore assoluto, minore di ε. (Schwarz 1872)
Schwarz nota, inoltre, che se ciò accade in ogni punto (x0,y0) del dominio, allora la funzione è continua nel dominio stesso.
Nonostante questa formulazione fosse molto chiara, Weierstrass non la pubblicò, e così di quella definizione furono inizialmente a conoscenza soltanto i suoi studenti. Altri, in contatto con l'ambiente di Weierstrass, in breve tempo compresero le lacune della definizione data da Cauchy; lacune evidenziate da Eduard Heine nel 1870. Nello stesso anno Karl Johannes Thomae fornì l'esempio della funzione
(presumibilmente posta uguale a 0 nell'origine), che non è certo continua in (0,0) sebbene lo sia separatamente rispetto a ciascuna variabile in quello stesso punto. Questo sembra essere il primo di molti altri esempi simili. Thomae, pur non essendo uno studente di Weierstrass ‒ proveniva infatti dal gruppo di Riemann che operava a Gottinga ‒, era in contatto, per altri motivi, con ex studenti di Weierstrass: pertanto, può darsi che l'esempio tragga origine da Weierstrass stesso o da un suo allievo.
Differenziali e derivate parziali
Nei primi decenni del XIX sec. i differenziali erano un argomento centrale della teoria del calcolo differenziale di più variabili. Cauchy, per esempio, basava la definizione di differenziale su quella di derivata parziale da lui stesso elaborata, ottenendo la nota espressione del differenziale primo di una funzione in termini delle sue derivate parziali, che per una funzione u di tre variabili x, y e z si scrive:
Egli utilizzava questa espressione allo scopo di individuare una condizione necessaria per l'esistenza di valori estremali della funzione. Supponiamo che u=f(x,y,z) abbia un punto di massimo (relativo), vicino al quale possiamo definire F(α)=f(x+αh,y+αk,z+αl)⟨f(x,y,z)=F(0): secondo la teoria del calcolo in una sola variabile, in un punto di massimo si ha dF/dα=0, ossia du=0 (supponendo, come egli afferma, che u sia continua). Ciò, a sua volta, implica che tutte le derivate parziali siano uguali a 0 in un punto di massimo.
In modo simile Cauchy definiva i differenziali di ordine superiore, che utilizzava per stabilire un criterio per l'esistenza di estremi relativi nel caso di funzioni di più variabili analogo a quello unidimensionale della 'derivata seconda', affermando, nel corso del suo lavoro, che le derivate parziali miste sono identicamente uguali. Per esempio, se u=arctan(x/y), allora
L'identità tra le derivate parziali miste segue dalla possibilità di scambiare l'ordine dei limiti con i quali si calcolano le derivate seconde; un procedimento che ben presto destò sospetti e stimolò alcuni tentativi, peraltro non riusciti, di giustificarne la validità (Blanchet 1841). Tra coloro che ripresero l'argomento negli anni successivi al contributo di Weierstrass vi furono Ernst Leonhard Lindelöf, Angelo Genocchi e in particolare Schwarz (1872), che ne diede una dimostrazione 'moderna'.
Il criterio della derivata seconda proposto da Cauchy è il seguente: supponiamo di aver individuato un punto dove la funzione u sia continua nel senso di Cauchy, e dove du=0; allora "il corrispondente valore di F(α) è un massimo o un minimo per α=0 se per tutti i possibili valori di dx, dy, ecc. la prima delle grandezze F′(0),F″(0),… che non si annulla in quel punto corrisponde a un indice [numero di differenziazioni] pari e mantiene sempre un segno costante" (1823b, pp. 93-94).
Questo criterio fu enunciato in modo più chiaro da Ludwig Otto Hesse (1811-1874), uno studente di Jacobi, in un articolo del 1844, Über die Elimination der Variabeln aus drei algebraischen Gleichungen vom zweiten Grade mit zwei Variabeln (Sull'eliminazione delle variabili da tre equazioni algebriche di secondo grado in due variabili) dove si introduce il noto determinante hessiano della matrice delle derivate parziali seconde. Il principale obiettivo di Hesse era di applicare l'analisi matematica a problemi geometrici; egli usava questo determinante per approfondire lo studio di invarianti di forme quadratiche e cubiche. Il lavoro di Hesse era la naturale prosecuzione di precedenti studi di Carl Gustav Jacob Jacobi sulla eliminazione di variabili da sistemi di equazioni omogenee, studi che, come ebbe a riconoscere lo stesso Jacobi, si fondavano a loro volta su quelli di Cauchy.
Calcolo integrale
a) Scambio dell'ordine di integrazione. Già nella sua prima memoria del 1814 sugli integrali definiti, Cauchy aveva notato che gli integrali doppi sono a volte indeterminati, in quanto possono assumere valori diversi a seconda dell'ordine con il quale si procede all'integrazione. Il principale obiettivo della sua monografia consisteva in realtà nel porre le basi di quel "passaggio dal reale all'immaginario" che Euler e Pierre-Simon de Laplace avevano utilizzato in modo così efficace nel calcolo di integrali definiti. Cauchy osservava che nel passare dalla retta reale al piano complesso una funzione di una variabile reale si trasforma in una di due variabili, e quindi, quando si integra, si ha a che fare con un integrale doppio (Cauchy 1814 [1882, p. 332]). Egli precisava quindi che le singolarità potrebbero già comparire dopo la prima integrazione e come esempio considerava la seguente funzione
e l'integrale
L'integrale [7], calcolato nell'ordine appena scritto, vale −π/4; invertendo l'ordine di integrazione vale π/4. Egli citava numerosi altri esempi, sempre nell'ottica di calcolare particolari integrali definiti di funzioni di una sola variabile.
Cauchy riteneva anche che la 'continuità' ‒ intesa come continuità rispetto a ciascuna variabile separatamente ‒ fosse sufficiente a garantire la liceità dello scambio dell'ordine di integrazione. Nella dimostrazione di questo risultato, che appare in un corso tenuto nel 1829, Cauchy si serviva della identificazione tra i concetti di differenziabilità e continuità e, in effetti, in quella dimostrazione egli deriva sotto il segno di integrale.
Dopo aver stabilito che
egli ipotizza che f(x,y) sia continua rispetto a ciascuna variabile e, fissato un punto X, definisce
Per valori di x interni al dominio di integrazione egli ottiene l'espressione
E così, derivando sotto il segno di integrale, si ha
In realtà, come nota lo stesso Cauchy, si sta "integrando sotto il segno di integrale" in base al teorema fondamentale del calcolo. Ancora una volta l'uso principale di questo teorema all'interno del corso del 1829 riguarda il calcolo di integrali di funzioni di una sola variabile, o anche la risoluzione di equazioni differenziali di ordine superiore.
Lo scambio dell'ordine di integrazione si praticava anche su integrali impropri; lo aveva fatto, per esempio, Peter Gustav Lejeune Dirichlet nel suo articolo del 1839 sull'attrazione di ellissoidi, in cui aveva introdotto il metodo del 'fattore discontinuo' per trasformare integrali propri in integrali impropri. Quest'autorevole lavoro fu frequentemente utilizzato da studiosi di teoria del potenziale, anche se uno di essi sembra aver quanto meno avvertito la necessità di giustificare lo scambio dell'ordine di integrazione. Pensiamo a Franz Mertens, che in uno scritto pubblicato sul "Journal" di Crelle nel 1864, utilizzando le tecniche di Dirichlet, affermava che è possibile praticare lo scambio dell'ordine di integrazione quando la funzione da integrare è non negativa.
Nel XVIII sec. erano ben noti metodi ad hoc per operare un cambiamento di variabile in integrali multipli, come ben noti erano gli 'jacobiani' delle trasformazioni da coordinate cartesiane a coordinate sferiche o di altro tipo. Il nome di Jacobi è legato al determinante con il quale si calcola il fattore da introdurre in un cambiamento di coordinate, in quanto egli fu il primo a enunciarne l'uso come metodo generale, esprimendo il risultato tramite determinanti. Egli impiegò questa tecnica persino nel caso in cui le nuove coordinate erano funzioni implicite delle vecchie, ricorrendo essenzialmente alla regola di Cramer sulla versione lineare (differenziale) del sistema di funzioni che esprime la trasformazione.
b) Integrali doppi. La definizione di integrale definito, data da Riemann, e l'uso che se ne fece per distinguere tra funzioni integrabili e funzioni continue, condusse a una concezione moderna dell'integrale, che permette anche di distinguere gli integrali multipli da integrali iterati. La definizione di Riemann venne pubblicata nel 1867 e Jean-Gaston Darboux cominciò a utilizzarla nel 1873: divenne così 'universalmente' nota. Le idee un po' vaghe a proposito della continuità, esemplificate dalle osservazioni di Heine e di Thomae precedentemente citate, sollevarono il problema di come applicare tale definizione a funzioni di più variabili. È difficile a tal proposito attribuire una priorità: in ogni caso le due figure principali furono Paul Du Bois-Reymond e Thomae. Quest'ultimo, nel suo testo del 1875, Einleitung in die Theorie der bestimmten Integrale (Introduzione alla teoria degli integrali definiti), fornisce la seguente definizione: sia T una regione del piano, che suddividiamo in parti τ1,τ2,τ3,… che possiamo supporre semplicemente connesse, e tali che "tutte le loro dimensioni lineari", così come le rispettive aree, siano più piccole di un numero reale positivo ω. La funzione f(x,y) sia limitata inferiormente e superiormente in ciascun τk rispettivamente da gk e Gk; definiamo
Con questa definizione Thomae ottiene l'analogo bidimensionale della condizione di integrabilità di Riemann. Una definizione simile fu data, sempre nel 1875, da Henry J.S. Smith.
Thomae si accorse che per le funzioni discontinue, si incontrano problemi nel ridurre integrali doppi a integrali iterati. Anche Otto Stolz, in quello stesso periodo, notò delle difficoltà, che evidenziò con il seguente esempio
per il quale, se l'integrale rispetto a x ha come limiti di integrazione 0 e infinito, vale 0 o π a seconda dell'ordine di integrazione. Tale questione venne ripresa per gli integrali impropri da Du Bois-Reymond nel 1883, il quale, però, riuscì a stabilire condizioni soltanto per casi particolari. La teoria degli integrali doppi basata sulla teoria della misura e i relativi teoremi che riguardano lo scambio dell'ordine di integrazione, sono sviluppi dei primi anni del XX sec., che esulano pertanto dalla presente trattazione.
Equazioni alle derivate parziali del primo e del secondo ordine
Nel XVIII sec. si era assistito all'introduzione delle equazioni alle derivate parziali nello studio di alcuni fenomeni fisici. L'analisi della corda vibrante (che condusse all'equazione d'onda monodimensionale) a opera di Euler, Daniel Bernoulli e d'Alembert, lo studio di quest'ultimo sulle 'cause dei venti' (fluidodinamica) e altre ricerche pionieristiche, consentirono la formulazione di varie equazioni, le cui soluzioni venivano ottenute soprattutto con manipolazioni formali di serie di potenze. Una classe di problemi fondamentali, riguardanti attrazioni e repulsioni di corpi soggetti a forze di tipo newtoniano nell'ambito della meccanica celeste e dell'elettrostatica, venne riformulata da Laplace in termini di equazioni alle derivate parziali soddisfatte da una funzione V (introdotta da Lagrange) che ha come sue derivate parziali l'opposto delle componenti della forza. L'importanza attribuita a simili problemi e alle funzioni che li risolvono, conosciute in seguito come potenziali della forza, fu all'origine della teoria del potenziale, una disciplina che non è totalmente inscrivibile in quella delle equazioni alle derivate parziali.
Tali importanti equazioni alle derivate parziali della fisica sono, per la maggior parte, del secondo ordine e lineari, a differenza dei sistemi di equazioni differenziali ordinarie usati nella dinamica di semplici masse puntiformi (formulazione anch'essa tipica del XVIII sec.). La vasta esperienza accumulata da Lagrange nello studio delle equazioni differenziali ordinarie della meccanica gli consentì di escogitare un metodo per ridurre equazioni alle derivate parziali del primo ordine, in due variabili indipendenti, a sistemi di equazioni differenziali ordinarie. Questo metodo, scoperto nel 1774, si trova esposto nel suo trattato del 1806, e il tentativo di estenderlo a più di due variabili avrebbe condotto alla prima sistematizzazione di un ramo della teoria delle equazioni alle derivate parziali: quello delle equazioni del primo ordine.
Equazioni del primo ordine
Come già osservato, le equazioni alle derivate parziali del primo ordine in due variabili indipendenti erano già state studiate da Lagrange il cui metodo (poi completato dal suo studente Paul Charpit) richiede n(n−1)/2 condizioni per determinare n−1 funzioni incognite. Se n=2 tutto funziona bene, ma nel caso generale il metodo incontra delle difficoltà. Sia Charpit sia Gaspard Monge tentarono di risolvere problemi con un numero maggiore di variabili, ma i primi risultati significativi, per un numero di variabili superiore a due, li ottenne nel 1815 Johann Friedrich Pfaff, uno dei maestri di Gauss.
Nel metodo di Pfaff si riscrive l'equazione alle derivate parziali come un'equazione differenziale totale in 2n variabili e poi si esegue una riduzione di ordine. In seguito anche Cauchy formulò in modo indipendente lo stesso metodo e comprese, assieme a Jacobi, che impostando opportunamente il procedimento di Pfaff era possibile far funzionare il metodo di Lagrange e Charpit.
Jacobi aveva studiato le equazioni del primo ordine in stretta relazione con le sue ricerche di meccanica teorica e, in particolare, con le estensioni della dinamica hamiltoniana. Tra i tanti risultati ottenuti, ricordiamo qui il suo criterio per l'esattezza di una forma differenziale espresso mediante le parentesi di Poisson. Supponendo di avere n−1 soluzioni fi di un'equazione del primo ordine f(x1,x2,…,xn,p1,…,pn)=0 (dove pi sono, al solito, le derivate parziali), e immaginando di esplicitare le pi in funzione delle variabili indipendenti, allora la forma differenziale Σpidxi è esatta se e soltanto se tutte le parentesi di Poisson delle coppie di soluzioni si annullano. Porre uguale a zero le parentesi di Poisson determina un sistema di equazioni alle derivate parziali lineari nelle incognite, che Jacobi riuscì a ridurre a un sistema di equazioni differenziali ordinarie utilizzando ciò che oggi si chiama identità di Jacobi per le parentesi di Poisson. Il matematico tedesco completò questo lavoro negli anni Trenta del XIX sec.; tuttavia questi e altri risultati analoghi vennero pubblicati solo in parte prima che, nel 1862, Clebsch desse alle stampe il trattato di Jacobi.
Fourier e l'equazione del calore
All'inizio del XIX sec. vi erano fondamentalmente due modi per trattare matematicamente i problemi fisici. Uno di questi, certamente il più diffuso, riduceva la realtà fisica soggiacente a un modello ideale da descrivere poi matematicamente. L'altro approccio era di tipo fenomenologico: non si occupava dei processi ultimi ma cercava di descrivere soltanto il comportamento delle grandezze osservabili. Si possono risolvere problemi con entrambi gli approcci ricorrendo alla meccanica teorica e al calcolo integrale e differenziale.
Attorno al 1800 il modello dominante assumeva che processi fisici fossero governati da forze agenti a distanza in modo istantaneo. Questa concezione, attribuibile a Laplace e Poisson, ha dato origine alla teoria del potenziale. Jean-Baptiste-Joseph Fourier, adottando un'impostazione diversa da quella della scuola di Laplace, non si preoccupava molto della natura fisica soggiacente al processo della conduzione del calore. In un lavoro scritto nel 1807, pubblicato solamente negli anni Venti, Fourier definisce le equazioni differenziali che descrivono la propagazione del calore. Assumendo che il calore si trasmette a una molecola di una sostanza attraverso il flusso positivo o negativo proveniente dalle sue immediate vicinanze e facendo opportune ipotesi sul flusso che attraversa i bordi della sostanza sottoposta a riscaldamento, Fourier ottiene un'equazione differenziale alle derivate parziali che descrive il flusso termico. Per comprendere il suo modello, vediamo una parte del ragionamento che gli permise di stabilire la legge di propagazione del calore in un solido cubico (Fourier 1822).
Si consideri un piccolo elemento del solido, cioè un cubo infinitesimo i cui vertici opposti siano individuati dalle coordinate (x,y,z) e (x+dx, y+dy, z+dz). Fourier ipotizza che la trasmissione del calore avvenga per trasferimento continuo tra porzioni contigue del corpo e verso l'esterno. Così la quantità di calore che si trasferisce in un istante dt è determinata dalla differenza tra il calore che entra nel cubo infinitesimo e il calore che ne esce. Sia v(x,y,z,t) la temperatura del punto (x,y,z) del corpo all'istante t, che all'inizio si suppone essere una costante positiva in tutto il corpo. Si immagini ora che il corpo sia immerso in una corrente uniforme di aria mantenuta alla temperatura costante di 0 gradi; in tal modo la temperatura sui bordi del corpo rimane costante. Se K è una costante caratteristica del corpo che ne rappresenta il coefficiente di conduttività, allora la quantità di calore che fluisce nella molecola durante il tempo dt attraverso il rettangolo dydz (perpendicolare a dx) è
Il segno meno è dovuto a una scelta convenzionale: la derivata si considera negativa ogniqualvolta il solido si raffredda. Fourier determina la quantità di calore che esce dal rettangolo opposto "scambiando x con x+dx nella espressione precedente, ossia […] aggiungendo a quella espressione il suo differenziale rispetto a x" (ibidem, par. 104). Secondo la tecnica infinitesimale di Fourier, ciò corrisponde alla quantità
(ove il differenziale d è parziale rispetto a x), ossia
Se si fa la differenza tra le due espressioni [14] e [16] si ottiene la variazione infinitesima nella direzione x. Espressioni analoghe regolano il flusso del calore nelle altre due direzioni y e z; pertanto il flusso totale nel tempo dt è dato da
Per ottenere la variazione di temperatura nell'unità di tempo, basta dividere la [17] per la quantità di calore che serve a innalzare la temperatura di un grado; Fourier la indica con CDdxdydz, dove C è il calore specifico del corpo e D la sua densità e ottiene l'equazione del calore:
(Fourier non usa il simbolismo delle derivate parziali).
Per illustrare gli strumenti matematici necessari a risolvere questo problema e l'importanza che le ipotesi fisiche hanno per la matematica, si consideri il caso di una lamina rettangolare, un'ipotesi che consente di ridurre a due le variabili spaziali nel caso stazionario, ossia quando la temperatura rimane costante nel tempo.
Si supponga che la lamina abbia una larghezza di π unità, e che una delle sue estremità sia mantenuta a temperatura costante. Il caso stazionario corrisponde all'equazione di Laplace in due variabili
Fourier fu il primo a risolvere un'equazione alle derivate parziali con il metodo della separazione delle variabili, cioè assumendo che la soluzione v si possa scrivere come un prodotto: v=A(x)B(y); in tal caso l'equazione differenziale [19] diventa:
Fourier osserva che, essendo la precedente un'identità, entrambi i suoi termini devono essere uguali a una costante e ciò fornisce due equazioni differenziali ordinarie lineari del secondo ordine
[21] A"(x)=m2A(x), B"(y)=-m2B(y).
Le condizioni al contorno impongono che m sia un numero intero. Risolvendo tali equazioni con metodi già noti, Fourier perviene alla seguente relazione:
L'ipotesi che una estremità della lamina, per esempio, il punto x=0, abbia una temperatura costante, consente a Fourier di calcolare i coefficienti Cm. Infatti, ponendo nella [22] v0(y)=v(0,y) e integrando dopo aver moltiplicato ambo i membri per senny, egli ottiene:
scambiando poi l'ordine tra integrazione e somma, e sfruttando nel membro a destra la proprietà di ortogonalità delle funzioni trigonometriche, egli ricava la formula dei coefficienti di Fourier.
Un esempio interessante dell'influenza esercitata da Fourier lo fornisce il modo in cui Georg Simon Ohm stabilì, nel 1826, la legge che porta il suo nome. Forse non era una coincidenza che Ohm fosse il maestro di Dirichlet, il quale in seguito studiò con lo stesso Fourier. I risultati di Ohm si basano su una semplice intuizione: la propagazione di elettricità attraverso un materiale conduttore non deve essere diversa dalla diffusione di calore attraverso una sbarra, e pertanto è possibile utilizzare una tecnica simile a quella adottata da Fourier per ottenere le equazioni differenziali della conduzione del calore. Ohm considerò il problema unidimensionale trovandone la soluzione che oggi è conosciuta come legge di Ohm. Il suo risultato, se confrontato con quello di Fourier, appare assai poco sofisticato dal punto di vista matematico. L'abilità di Ohm consistette essenzialmente nell'individuazione delle grandezze fisiche del problema elettrico in modo che l'argomentazione di Fourier fosse ancora applicabile.
Teoria del potenziale e teoremi integrali
Laplace
La teoria del potenziale affonda le sue radici nelle tecniche di studio del comportamento dei corpi che interagiscono secondo leggi conservative. Si trattava soprattutto di tecniche per la soluzione di problemi di attrazione gravitazionale e elettrostatica (in un certo senso, di teoria elettromagnetica generale) e di propagazione del calore in condizioni stazionarie, in pratica di tutti quei processi descrivibili mediante le equazioni di Laplace e di Poisson. I risultati fondamentali del calcolo integrale e vettoriale (i teoremi di Gauss, Green e Stokes), e la loro applicazione alla soluzione di problemi al contorno con l'utilizzo del metodo della funzione di Green, furono tutti strumenti di grande importanza per coloro che, per primi, cercarono di fornire soluzioni a particolari problemi fisici. L'attenzione per gli aspetti puramente matematici di quei problemi come, per esempio, i teoremi di esistenza in alcuni problemi al contorno, emerse solo più tardi nel corso del secolo, in relazione alle critiche mosse da Weierstrass ai fondamenti dell'analisi. Una parte significativa dell'impegno profuso per raffinare le tecniche che descrivono i fenomeni fisici mediante equazioni alle derivate parziali fu dedicata al tentativo di estendere i risultati ottenuti proprio nella teoria del potenziale a situazioni descritte da altri tipi di equazioni.
Il primo riconoscimento dell'esistenza di una funzione che sia il potenziale della forza gravitazionale di Newton si trova nella memoria di Lagrange Sur l'équation séculaire de la Lune del 1774, nella quale viene utilizzata una funzione di questo tipo per il calcolo delle componenti della forza in differenti sistemi di coordinate. Nel 1777 Lagrange dedicò un breve scritto ad alcune proprietà delle funzioni potenziali, includendovi un'applicazione relativa al problema del moto di un sistema di corpi, risolto attraverso l'analisi del moto del suo centro di massa.
È stato però Laplace a fare ampio uso della funzione potenziale negli studi sull'attrazione degli sferoidi e nel Traité de mécanique céleste (1799-1825). È essenzialmente per merito di questo lavoro che si diffuse la pratica di utilizzare la funzione potenziale nella soluzione di equazioni alle derivate parziali. Nell'articolo Théorie des attractions des sphéroïdes et de la figure des planètes (1785), Laplace introduce la funzione potenziale (senza accennare, nemmeno di sfuggita, a Lagrange) e dimostra che essa soddisfa quella che oggi chiamiamo 'equazione di Laplace in coordinate sferiche'. In una memoria successiva sugli anelli di Saturno, egli introduce questa equazione in coordinate cartesiane:
Laplace era interessato ad applicare queste funzioni a problemi di attrazione e, a tale scopo, considera sviluppi in serie di potenze della funzione potenziale V, nella forma V5U1/r11U2/r21… dove ciascuna Ui è armonica, cioè soddisfa l'equazione di Laplace [24].
Dal momento in cui Charles-Augustin Coulomb verificò che la forza elettrostatica è di tipo newtoniano e inversamente proporzionale al quadrato della distanza, l'equazione di Laplace assunse un'importanza centrale nell'elettrostatica. In numerose situazioni, tuttavia, è importante anche studiare gli effetti all'interno del corpo che genera il campo di forze, dove non vale l'equazione di Laplace. Nel 1813 Poisson sostenne che, se la densità è una funzione continua, allora il potenziale V è ancora ben definito. In tali circostanze il potenziale soddisfa la cosiddetta 'equazione di Poisson', che ammette come caso particolare l'equazione di Laplace: =2W524pr dove r è la densità. Solitamente gli storici attribuiscono perlopiù l'argomentazione a Laplace, ma in effetti egli la 'passò' a Poisson, che era un suo protetto.
I risultati di Laplace e Poisson hanno semplificato notevolmente la soluzione di alcuni problemi al contorno nella teoria dell'attrazione, soprattutto nel caso di sferoidi non troppo diversi da sfere, in cui le prime funzioni armoniche sferiche rappresentano buone soluzioni approssimate. Per la prima volta i due matematici dedicarono particolare attenzione ai problemi al contorno, specialmente in elettrostatica.
Tuttavia la possibilità di applicare queste tecniche direttamente era fortemente limitata dagli aspetti geometrici dei problemi; infatti, in molti casi, è impossibile integrare in modo diretto la funzione potenziale. I teoremi integrali di Green e Gauss, assieme al metodo della funzione di Green, consentivano di estendere la tecnica di Laplace e Poisson, fornendo un procedimento risolutivo efficace in numerosissime situazioni geometriche e offrendo anche un metodo per formulare dimostrazioni di esistenza di soluzioni. I teoremi di Green, Gauss e Stokes sono stati ricavati inizialmente senza far uso di metodi vettoriali (o legati ai quaternioni); per questo motivo, nel trattare tali teoremi, saranno considerati sempre nel contesto delle coordinate ortogonali dello spazio cartesiano.
L'Essay di Green
George Green (1793-1841), figlio di un mugnaio di Nottingham, in Inghilterra, non aveva intrapreso gli studi universitari ma aveva seguito le orme del padre lavorando come panettiere e mugnaio per ventisette anni. Incoraggiato, a quanto pare, dai suoi primi maestri, Green continuò a studiare per proprio conto interessandosi sempre di più ai lavori dei matematici francesi. Approfondì in particolare il Traité de mécanique céleste di Laplace, lesse i resoconti delle ricerche di Henri Cavendish sull'elettricità e tentò di applicare i metodi matematici di Laplace a problemi di elettricità e magnetismo. Il risultato è l'Essay on the application of mathematical analysis (1828), un lavoro pionieristico di grande originalità e di perenne valore, elaborato in perfetta solitudine e pubblicato a proprie spese. Nel 1833, poco dopo aver compiuto 40 anni, Green andò a studiare a Cambridge. Tra il 1837 e il 1839 pubblicò sei articoli su vari aspetti della fisica matematica nelle "Transactions" della Cambridge Philosophical Society, fra i quali i più notevoli sono quelli che studiano alcuni fenomeni ottici per mezzo di teorie meccaniche. Questi lavori esercitarono una certa influenza e alla fine riuscirono ad attirare l'attenzione di William Thomson sull'Essay che, grazie al suo interessamento, fu ripubblicata nel "Journal" di Crelle tra il 1850 e il 1854. Soltanto da quel momento le tecniche di Green sono entrate nell'uso corrente.
Green contrappone il proprio approccio a quello adottato fino ad allora; secondo il vecchio metodo
supponiamo che si debba determinare in che modo si distribuisce la carica sulla superficie chiusa A, considerata priva di spessore, di un conduttore sottoposto all'azione di generiche forze elettriche; […] secondo l'impostazione classica, l'equazione che determina ϱ [la densità], quando è ridotta alla sua forma più semplice, diventa
il primo integrale, relativo a dσ, è esteso all'intera superficie A, mentre il secondo rappresenta la funzione il cui differenziale totale è Xdx+Ydy+Zdz… [qui dσ è un elemento di superficie, e X, Y e Z sono le componenti note di una forza che agisce sulla superficie]. (Green 1828, p. 10)
Quando una siffatta equazione è risolvibile, osserva Green, ciò accade perché c'è qualcosa che "rende […] la soluzione relativamente semplice" ed egli contrappone a tale evenienza il suo nuovo metodo:
Sia B=∫Xdx+Ydy+Zdz… [eV(P)]=∫ϱdσ/r quando P è un qualsiasi punto sulla superficie, [eV′(P)]=∫ϱdσ/r′ quando p è esterno ad essa: [V e V′] […] hanno la proprietà di soddisfare [l'equazione di Laplace]. Se ora potessimo ottenere i valori di V e V′ da queste equazioni, dovremmo avere immediatamente, differenziando, il valore richiesto di ϱ, e ciò verrà dimostrato qui appresso. (ibidem)
Green osserva poi che, integrando un'equazione differenziale del secondo ordine, si ottengono due funzioni arbitrarie che, per essere determinate, necessitano di due ulteriori condizioni. La prima è data dalla condizione al contorno che egli indica con la [25] e che tiene conto del comportamento delle cariche elettriche sulla superficie A; la seconda condizione è data dal fatto che le derivate parziali di V rimangono finite nei punti interni al corpo. Quando sono soddisfatte entrambe le condizioni, afferma Green, si deve avere
dove (ϱ) è "una quantità dipendente dalle rispettive posizioni di P e dσ" e
è il valore di V sulla superficie A.
Il metodo introdotto da Green, detto 'della funzione di Green', ha avuto un enorme impatto sui lavori successivi sia di tipo teorico che applicativo. Per risolvere problemi di elettrostatica, Green applica il suo metodo utilizzando al tempo stesso alcune identità che coinvolgono integrali multipli. La chiave del metodo sta nel trovare la cosiddetta funzione di Green, indicata con (ϱ) nella formula precedente, che consente di determinare il potenziale V all'interno della regione, conoscendone il comportamento sulla frontiera A.
La possibilità di individuare una tale funzione è strettamente legata alle identità integrali stabilite da Green nel suo Essay. Mentre ogni singola identità vale per qualsiasi funzione dal comportamento regolare, definita in una regione limitata che abbia frontiera uniforme (le ipotesi nel lavoro di Green erano vaghe e restarono tali ancora per molti anni), il metodo della funzione di Green dipende in modo sostanziale da funzioni che siano dei potenziali. Green usa l'integrazione per parti e un metodo di proiezione per trasformare integrali iterati in integrali di superficie. Egli mostra in tal modo che se le funzioni U e V non hanno alcuna singolarità all'interno della regione R limitata dalla superficie A, allora
(dove n è il versore normale alla superficie A diretto verso il suo interno).
Nel caso in cui una delle due funzioni possieda una singolarità all'interno della regione, è possibile modificare la relazione [27] ‒ nota come seconda identità di Green ‒ in modo opportuno. Supponiamo, per esempio, che U abbia una singolarità nel punto P interno alla regione e che attorno al punto P la funzione U sia "ragionevolmente uguale a 1/r, dove r è la distanza tra il punto […] e l'elemento dxdydz" dove si valutano quegli integrali (Green 1828, p. 26). In queste ipotesi, rielaborando un procedimento già adottato da Poisson, Green scrive la relazione
e usando questa identità, introduce il metodo della funzione di Green per risolvere un caso particolare del 'problema al contorno di Dirichlet'.
Quando è dato il valore della funzione potenziale [ Formula ]
su una qualsiasi superficie chiusa A, esiste una sola funzione V che può soddisfare contemporaneamente sia l'equazione [∇2V=0] sia la condizione che V non abbia punti singolari su quella superficie. E ciò in quanto […] supponendo [∇2U=0],
In questa equazione si suppone che U abbia un solo valore singolare, quello nel punto P, e che, infinitamente vicino a esso sia quasi uguale alla funzione 1/r […]. Se ora consideriamo una funzione di U, che, oltre a soddisfare le condizioni dette più sopra, sia uguale a zero sulla superficie, abbiamo
e l'equazione [29] diventa
Ciò mostra che […] il valore di [V nel punto P] è noto quando è nota la funzione
sulla superficie. (ibidem, p. 31)
Pertanto, se esiste una siffatta funzione U, si ha una soluzione del problema al contorno. Green motiva tale esistenza matematica con l'esistenza fisica; un ragionamento che risulta convincente, se le superfici che delimitano la regione sono regolari, è il seguente: "Per convincersi che esiste in effetti una funzione che possieda le caratteristiche imposte alla funzione U, immaginiamo che la superficie sia un conduttore perfetto messo a contatto con la terra e che una unità di elettricità positiva sia concentrata nel punto P; allora la funzione potenziale totale prodotta da P e dalla elettricità indotta sulla superficie corrisponde proprio alla funzione U da noi cercata" (ibidem, p. 32).
Le identità di Green e i metodi utilizzati nell'Essay del 1828 per risolvere problemi al contorno sarebbero diventati essenziali per la ricerca in questo campo, anche se la scarsa notorietà della loro pubblicazione ne ostacolò l'influenza fino alla fine degli anni Quaranta del XIX secolo.
L'Allgemeine Lehrsätze di Gauss e il teorema della divergenza
Carl Friedrich Gauss (1777-1855) si interessò costantemente a temi legati alla fisica matematica. In particolare diversi filoni del suo lavoro sono collegati all'argomento che stiamo discutendo. L'attività di astronomo lo portò a indagare ‒ in un trattato del 1813 sulle attrazioni di ellissoidi omogenei ‒ i metodi della teoria del potenziale. Questo scritto era collegato alle sue ricerche di geodesia intraprese in occasione dei rilevamenti cartografici dello Stato di Hannover. Quelle ricerche avevano diversi legami con la matematica, tra i quali lo studio delle applicazioni conformi mediante l'uso di funzioni di una variabile complessa e la geometria differenziale delle superfici. Gli antecedenti immediati del lavoro che intendiamo affrontare in questa sede sono gli studi sul magnetismo e l'elettricità che Gauss condusse assieme a Wilhelm Weber e i tentativi compiuti in tale contesto per concepire una teoria del magnetismo terrestre, collegati anch'essi al problema delle linee geodetiche. Quest'opera culminò con la pubblicazione nel 1839 dell'Allgemeine Theorie des Erdmagnetismus (Teoria generale del magnetismo terrestre).
Nella memoria del 1813 sull'attrazione degli elissoidi, Gauss aveva già studiato alcuni casi particolari dei teoremi integrali che Green avrebbe trattato in seguito. Tuttavia fu soltanto nel 1839 che Gauss presentò la lunga memoria sulle forze inversamente proporzionali al quadrato della distanza che, assieme al lavoro di Green, avrebbe costituito la base delle ricerche successive sull'argomento fino agli anni Sessanta del XIX secolo. Nell'Allgemeine Theorie des Erdmagnetismus Gauss era già intervenuto su un aspetto critico della teoria: dal momento che è evidentemente impossibile osservare un monopolo magnetico, risultava problematico giustificare o riformulare quella teoria (dovuta, tra gli altri, a Poisson) che considera le forze magnetiche come il risultato di una separazione, permanente oppore indotta, di 'fluidi magnetici' interni al corpo. Nella memoria del 1838, Gauss aveva risolto questo problema supponendo un ideale strato superficiale in grado di produrre effetti equivalenti a una qualsiasi distribuzione di cariche elettriche che fosse interna al magnete.
Green aveva formulato l'ipotesi di densità superficiali di carica equivalenti; nel suo caso, però, lo scopo era quello di risolvere problemi che sorgono in modo analogo quando si esamini la relazione tra integrali di superficie e integrali di volume. Nel caso del magnetismo terrestre la distribuzione superficiale equivalente ha una grande importanza teorica; infatti soltanto la superficie terrestre è accessibile alle sperimentazioni magnetiche.
Ed è proprio il teorema che afferma l'esistenza di una distribuzione superficiale equivalente che Gauss considera centrale nel suo Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs - und Abstossungskräfte (Teoremi generali relativi alle forze attrattive e repulsive agenti in rapporto inverso al quadrato della distanza). "Per quanto riguarda i fondamenti del teorema in questione, richiedono anch'essi strumenti matematici abbastanza compositi; il teorema stesso sembra un caso particolare di uno più generale, che da parte sua costituisce l'ultimo elemento di una catena di teoremi generali chiaramente correlati. Lo sviluppo completo di queste ricerche è oggetto della presente trattazione" (Gauss 1840 [1867, p. 306]).
Questi teoremi, sostiene Gauss, non sono da concepirsi solamente come una successione di proposizioni che porta al teorema finale, in quanto ciascuno di essi è interessante di per sé nello studio di forze inversamente proporzionali al quadrato della distanza. Tra i vari risultati, egli decide di evidenziare i seguenti punti:
1) Data una qualsiasi superficie chiusa che risulti essere equipotenziale per un sistema di masse esterne a essa, è nulla la risultante delle forze applicate a tutti i punti della superficie e del volume che essa racchiude. Ciò dimostra l'inutilità di una delle ipotesi di Poisson riguardo l'esistenza di una distribuzione di equilibrio delle cariche elettriche su una superficie chiusa.
2) Su una superficie chiusa esiste un'unica distribuzione di cariche tale che la forza risultante nei punti interni sia nulla. Risultato questo che ne contraddiceva uno recente di Chasles, ossia che di tali distribuzioni ne esisterebbero infinite.
Il secondo risultato segue dalla risoluzione del cosiddetto problema di Gauss, e cioè: data una funzione definita su una superficie S, determinare una distribuzione di carica a strato singolo la cui funzione potenziale abbia il valore assegnato su S. Per risolvere questo problema Gauss adotta un procedimento piuttosto lungo, che nel punto cruciale manca di rigore. Supponiamo che S sia la frontiera della regione e consideriamo una massa M distribuita su S con densità di carica σ positiva. Con U indichiamo la funzione potenziale di quella distribuzione e con f una funzione continua su S. Gauss afferma l'esistenza di una distribuzione di carica che, oltre a soddisfare le ipotesi precedenti, minimizza l'integrale di superficie
Per la distribuzione che realizza quel minimo, U−f deve essere costante su S. Se f=0, anche U è costante su S e pertanto è possibile aggiungere a U un opportuno multiplo del potenziale, che corrisponde al caso f=0, in modo tale da soddisfare le condizioni al contorno. A questo punto è facile dedurre l'unicità della distribuzione.
Il problema insito in questo ragionamento, e in molte altre dimostrazioni di esistenza di soluzioni di problemi al contorno date nei decenni successivi, è che non necessariamente l'integrale assume un valore minimo se non si pongono ulteriori limitazioni sulla regione e sulla densità.
Come afferma lo stesso Gauss, i teoremi sui quali si basa la dimostrazione hanno un interesse intrinseco. Tra questi possiamo citare il risultato oggi conosciuto sotto il nome di teorema della media aritmetica di Gauss: "Se
è il potenziale di una massa distribuita come sempre nell'elemento ds di una superficie sferica di raggio R, allora, se si integra sull'intera superficie sferica si ha ∫ Vds=4π(RM0+RRV0) dove M0 indica l'intera massa che si trova all'interno della sfera nel centro della sfera, e [V0] il potenziale nel centro della sfera della massa che si trova all'esterno di essa" (Gauss 1840 [1867, p. 222]).
La dimostrazione del teorema di Gauss, indicato più frequentemente col nome di teorema della divergenza, si trova nella sezione 24 dello stesso lavoro. La sua dimostrazione è molto simile a quella presente in un odierno libro di testo e, in effetti, il livello di rigore è stupefacente. Anche le identità di Green assunte implicitamente nel procedimento deduttivo cominciarono a essere usate una volta noti i risultati e le tecniche di Gauss. In effetti la memoria di Gauss fu presto tradotta sia in inglese sia in francese.
È bene osservare, comunque, che anche altri matematici avevano in precedenza enunciato casi particolari dei teoremi di Gauss e di Green. Già nel 1760 Lagrange aveva ridotto un integrale triplo a un integrale doppio e simili risultati erano comparsi inaspettatamente di tanto in tanto anche altrove, come per esempio nell'opera di Poisson. Inoltre Michail Vasil´evič Ostrogradskij nel 1826 aveva dimostrato il teorema di Gauss con maggiore generalità e l'aveva addirittura presentato all'Académie di Parigi. Il suo lavoro fu pubblicato nel 1831 a San Pietroburgo ma, a quanto sembra, passò inosservato, eccezion fatta per l'originale versione francese. Poisson, che era stato uno dei relatori della memoria di Ostrogradskij presentata all'Académie, usò il risultato in un articolo del 1828, senza però attribuirlo ad alcuno.
Il teorema di Stokes
Il teorema di Stokes, come quelli di Gauss e Green, mette in relazione l'integrale di una funzione su un dato insieme con l'integrale di un'altra opportuna funzione su un insieme di dimensione inferiore. Può essere quindi considerato come una generalizzazione a funzioni di più variabili reali del teorema fondamentale del calcolo integrale per funzioni di una variabile. Oggi lo si enuncia di solito utilizzando il linguaggio delle forme differenziali, che consente di comprendere tutti gli altri risultati (i teoremi di Gauss e di Green). Nella formulazione vettoriale, meno astratta, il teorema di Stokes afferma che se S è una superficie regolare a tratti, avente come bordo una curva chiusa e semplice C anch'essa regolare a tratti, e F è un campo di vettori che possiede derivate parziali continue su tutta una regione che contiene S, allora
[30] ∫CF∙dr=∬SrotF∙dS.
Anche questo risultato, come i precedenti, aveva avuto dei precursori, tra i quali un caso particolare ottenuto da André-Marie Ampère (1826). Sembra che nella sua versione classica sia stato formulato nel 1850, o poco prima, da William Thomson, che lo comunicò a George G. Stokes. Questi, a sua volta, lo presentò come problema d'esame al premio Smith del 1854, un concorso indetto ogni anno presso l'Università di Cambridge in occasione degli esami finali per il conseguimento del diploma di laurea di primo grado. Non è noto se quel problema sia stato risolto da qualche candidato, ma fra questi era preseente James C. Maxwell, il quale venne a sapere che Stokes aveva avuto il teorema da Thomson. Maxwell potrebbe essere stato il primo a pubblicare una dimostrazione del teorema in inglese. In assoluto la prima pubblicazione della dimostrazione della [32] è dovuta a Hermann Hankel, contenuta in un trattato del 1861 sul moto dei fluidi; per questo motivo scienziati tedeschi (come Carl Gottfried Neumann) intorno al 1870 hanno spesso citato il teorema di Stokes attribuendolo a Hankel. Analogamente i francesi, seguendo Duhem, lo chiamano 'teorema di Ampère'.
Questi teoremi trovarono un'espressione appropriata nel contesto dei quaternioni di William R. Hamilton, scoperti negli anni Quaranta del XIX sec. e poi entusiasticamente studiati da molti altri, tra i quali è importante ricordare Peter Guthrie Tait. Fu quest'ultimo a formulare i teoremi integrali che scaturiscono utilizzando i quaternioni e che furono enunciati, verso la fine del XIX sec., da Josiah W. Gibbs e Oliver Heaviside come proposizioni riguardanti campi di vettori. Tale approccio 'vettoriale' al calcolo è stato ampiamente adottato da fisici e ingegneri, in particolar modo nel mondo anglosassone.
Gauss, con la sua accurata analisi delle ipotesi che sono alla base della teoria del potenziale, aveva indicato il percorso da seguire per chiarire i concetti generali dei problemi al contorno. Nel caso della teoria del potenziale le sue ipotesi sono principalmente di due tipi: condizioni sulla densità, riguardanti la continuità, la differenziabilità e altre proprietà analitiche; e condizioni sulle frontiere delle regioni, condizioni che, pur essendo spesso descritte analiticamente, hanno tuttavia un carattere decisamente geometrico. Questi aspetti dei problemi al contorno continuarono a essere oggetto di ulteriori ricerche. Nel frattempo, erano state effettuate alcune importanti scoperte che si sarebbero rivelate decisive per il nuovo indirizzo di ricerca in questi settori.
Riemann e il metodo della funzione di Green
Alcune importanti innovazioni si devono a Riemann. Ispirato, attraverso Dirichlet, dal metodo della funzione di Green, ma anche esperto nell'analisi complessa di Cauchy, il matematico tedesco adottò entrambe le tecniche per risolvere un problema posto da Gauss: mostrare che ogni regione semplicemente connessa può essere trasformata in un disco di raggio unitario per mezzo di un'applicazione conforme (che conserva cioè gli angoli tra le curve). Riemann ricondusse il problema all'esistenza di una funzione di Green per la regione di partenza, esistenza che egli afferma sussistere per il principio di Dirichlet. In effetti l'idea stessa di definire funzioni basandosi sulla conoscenza delle loro singolarità ‒ motivazione fondamentale delle successive ricerche di Riemann ‒ deve certamente parte del suo sviluppo, se non addirittura la sua origine, alla nozione di funzione di Green. L'idea chiave è, a nostro giudizio, di natura fisica: come le masse puntiformi corrispondono a singolarità dei loro potenziali, e possono quindi determinare ciò che avviene nello spazio circostante per l'azione a distanza delle forze che esercitano, così è lecito pensare in generale che una qualsiasi funzione dipenda dalle sue singolarità. Il problema tecnico consiste nel fatto che non tutte le funzioni hanno una relazione con le proprie singolarità altrettanto utile quanto quella posseduta dalle funzioni potenziali.
Teoria generale delle equazioni alle derivate parziali e dei potenziali
Le lezioni di Dirichlet: teoria dell'esistenza, classificazione dei problemi
Il lavoro di Gauss aveva evidenziato l'importanza della teoria del potenziale in generale, sia nelle questioni di matematica pura, come l'esistenza di soluzioni di problemi al contorno, sia nelle applicazioni. La traduzione tedesca dello scritto di Green arricchì il repertorio dei lavori in cui si cercava di affrontare problemi legati ai potenziali. La prima parte dell'Essay, di maggior rilievo, apparve sul giornale di Crelle nel 1850. Non deve sorprendere il fatto che, agli inizi degli anni Quaranta del XIX sec., ci sia stata una proliferazione di ricerche che adottò metodi di teoria del potenziale; contemporaneamente iniziarono a comparire, soprattutto in Germania, cicli di lezioni su tale teoria. A questo proposito possiamo citare Joseph Liouville al Collège de France (1839-1940); Franz Ernest Neumann a Königsberg a partire dal 1838; Dirichlet a Berlino e Gottinga a partire almeno dalla metà degli anni Quaranta; infine Rudolf Clausius (1822-1888) a Zurigo e Bonn, all'inizio degli anni Cinquanta. Gli appunti degli ultimi tre corsi furono pubblicati gradualmente, a cominciare dal manuale di Clausius (prima edizione del 1859). Le lezioni di Dirichlet del 1856-1857 furono stampate soltanto nel 1876, mentre l'edizione delle lezioni tenute da Neumann durante l'anno accademico 1852-1853 fu curata da suo figlio e venne edita nel 1887.
Naturalmente il contenuto di base offerto da quelle lezioni variava notevolmente da corso a corso. In questa sede facciamo riferimento alle lezioni di Dirichlet soprattutto per l'influenza che esercitarono tanto lui quanto i suoi studenti, fra i quali Kirchhoff e Riemann. Dirichlet tratta la nozione di potenziale nello spazio, l'esistenza e la continuità delle sue derivate e il fatto che esso soddisfa l'equazione di Laplace-Poisson. Egli introduce i potenziali di superficie e la discontinuità della derivata normale alla superficie. Discute i teoremi di Green e il metodo della funzione di Green, così come le loro applicazioni a problemi di esistenza sotto forma di principio di Dirichlet. Forse è proprio a partire da queste lezioni che è stata adottata l'espressione 'problema di Dirichlet' per riferirsi a un problema al contorno relativo a una equazione alle derivate parziali e alla conoscenza del valore delle soluzioni sulla superficie (o sulla curva) che delimita la regione del problema.
A questo punto è opportuno menzionare il cosiddetto principio di Dirichlet (in realtà già utilizzato da Thomson). Dirichlet cercava di dimostrare l'esistenza di soluzioni di problemi al contorno, che studiava mediante l'uso di un procedimento variazionale non dissimile da quello impiegato da Gauss. Egli mostrava che l'esistenza di una soluzione del problema in esame equivaleva all'esistenza di una funzione che rende minimo un certo integrale, minimo che Dirichlet asseriva esistere in quanto l'integrale risulta limitato inferiormente. L'erroneità di questa affermazione, oggi palese, non era per nulla evidente a quei tempi, tanto che quella conclusione fu accettata da moltissimi studiosi, tra i quali val la pena di citare lo stesso Riemann, prima di venire duramente criticata negli anni Sessanta del XIX sec. da Weierstrass e dai suoi allievi.
Le lezioni di Dirichlet contenevano anche un discreto numero di applicazioni che illustravano la potenza dei metodi che aveva sviluppato. Anzi, quasi metà dell'opera è dedicata a tali questioni, tanto da poterla definire l'antecedente diretta degli odierni manuali di matematica applicata che ben conosciamo. Tra i problemi che egli discuteva citiamo l'attrazione di ellissoidi, la densità di carica indotta su un involucro sferico da una carica che si trovi internamente o esternamente a esso e il magnetismo terrestre. A queste applicazioni altri autori ne aggiunsero di nuove: Franz Neumann, per esempio, trattò il flusso stazionario di calore. In tal modo le tecniche fornite da Dirichlet nelle sue lezioni, integrate dai lavori già noti sull'argomento, costituirono la spina dorsale della ricerca svolta da diversi studiosi, quali Gustav Robert Kirchhoff, nei suoi articoli del 1857 sulle equazioni del moto dell'elettricità in conduttori estesi, Riemann, nella sua discussione sugli anelli di Nobili del 1855 e nella sua teoria delle funzioni di variabili complesse, dove le funzioni di Green sono uno strumento fondamentale e Clausius, in numerosi articoli sui condensatori dei primi anni Cinquanta del XIX secolo.
Successivi sviluppi: Hölder, Neumann, e Schwarz
Attorno alla metà degli anni Settanta del XIX sec., si era ormai creata una notevole separazione tra le ricerche matematiche degli studiosi interessati a problemi fisici e le ricerche puramente matematiche. I matematici applicati continuavano a elaborare un insieme di tecniche per formulare e risolvere particolari equazioni differenziali e per studiare le funzioni speciali che ne sono la soluzione. D'altra parte, la letteratura sui problemi al contorno iniziava a essere dominata da questioni di natura più strettamente matematica. Si possono citare tre esempi: il contributo di Carl Gottfried Neumann, riassunto nella sua memoria del 1877 sui potenziali logaritmico e newtoniano; gli studi di Hermann Amandus Schwarz, che discutono soprattutto il problema di Dirichlet; il lavoro di Otto Hölder nella sua dissertazione del 1882. Hölder, uno studente di Weierstrass, tentò di porre su basi solide la teoria del potenziale sviluppandola in termini più rigorosi. Fece uso di nozioni topologiche di base, quali gli insiemi chiusi e gli insiemi aperti, adottando definizioni rigorose di continuità e differenziabilità che erano state da poco sviluppate da Georg Cantor, Eduard Heine, Jacob Lüroth e altri, con l'intento di procedere a una nuova indagine sul comportamento della funzione potenziale, da affiancare a quella elaborata precedentemente da Dirichlet.
Quell'intenzione, tuttavia, si arrestò di fronte a un problema divenuto ormai classico, vale a dire l'esistenza di soluzioni del problema di Dirichlet. Anche Hölder si scontrò infatti con l'ostacolo posto dalle obiezioni di tipo fondazionale al principio di Dirichlet.
Di tali problemi si occupò Neumann, il quale mostrò che, se la regione considerata nel problema è convessa, allora il problema di Dirichlet possiede in effetti una soluzione. In realtà gran parte della monografia di Neumann è dedicata a un'analisi dettagliata delle condizioni che deve soddisfare una regione dello spazio oppure del piano affinché in essa valgano i principali teoremi della teoria del potenziale. Tali condizioni di regolarità dei domini limitati, delle superfici che li delimitano e delle funzioni definite sulla frontiera sono piuttosto complesse e una loro analisi dettagliata ci allontanerebbe troppo dall'obiettivo che ci siamo proposti.
Schwarz, sin da quando era studente di Weierstrass, aveva manifestato interesse per i problemi relativi alle applicazioni conformi. Quasi contemporaneamente a Neumann, egli enunciò un metodo per dimostrare l'esistenza di soluzioni del problema di Dirichlet per regioni delimitate da curve analitiche. In particolare, egli indicò che usando un 'procedimento alternato' è possibile estendere soluzioni da regioni nelle quali la soluzione è nota (per es., il cerchio) a regioni che da queste possano essere ricoperte. Questo lavoro, assieme a quello di Neumann, estese la classe di regioni nelle quali è possibile fornire costruttivamente soluzioni al problema di Dirichlet. Un ulteriore contributo ai metodi per la soluzione di problemi al contorno fu fornito dalle cosiddette applicazioni di Schwarz-Christoffel, le quali trasformano il semipiano superiore in poligoni; tali trasformazioni furono scoperte, verso la fine degli anni Sessanta del XIX sec. da Elwin Bruno Christoffel e, in modo indipendente, da Schwarz.
Tentativi di classificazione delle equazioni alle derivate parziali si trovano nell'opera di Sophus Lie e Paul Du Bois-Reymond. Lie tentò di applicare nello studio delle equazioni alle derivate parziali un punto di vista geometrico complessivo mediante l'uso delle trasformazioni di contatto, cioè delle trasformazioni infinitesimali che conservano la tangenza. A partire dal 1870 ca., utilizzando l'apparato della allora nascente teoria dei gruppi continui, egli studiò le condizioni rispetto alle quali due soluzioni di una stessa equazione alle derivate parziali si possono trasformare l'una nell'altra. Questo approccio prometteva di semplificare notevolmente la relazione, altrimenti molto confusa, tra aspetti analitici e aspetti geometrici delle soluzioni di equazioni differenziali di ordine superiore in più variabili, in quanto consentiva di usare la teoria degli invarianti e la teoria dei gruppi per suddividere le soluzioni in classi caratterizzate da proprietà geometriche essenzialmente diverse. In effetti i risultati di Lie suscitarono molto ottimismo sul futuro della teoria. Tuttavia questa fiducia ebbe vita breve, poiché i calcoli necessari per fare chiarezza erano in generale troppo complessi. Per molti decenni l'aspetto geometrico del lavoro di Lie fu considerato il suo più importante lascito. Soltanto di recente, grazie al più sofisticato apparato analitico degli spazi di Sobolev, l'approccio di Lie ha iniziato ad avere l'efficacia che il suo artefice aveva auspicato. Du Bois-Reymond, a sua volta, introdusse, in un articolo postumo del 1889, l'odierna e ben nota classificazione in equazioni differenziali di tipo ellittico, iperbolico e parabolico. Tuttavia di tale classificazione non si fece un grande uso fino al lavoro di Jacques Hadamard dei primi anni del XX secolo.
Bibliografia
Archibald 1925: Archibald, Raymond C., The writings of Peirce, "American miscellany monthly", 32, 1925, pp. 20-30.
Bottazzini 1995: Bottazzini, Umberto - Tazzioli, Rossana, Naturphilosophie and its role in Riemann's mathematics, "Revue d'histoire des mathématiques", 1, 1995, pp. 3-38.
Cannell 1993: Cannell, Doris M., George Green, mathematician and physicist 1793-1841. The background to his life and work, London, Athlone, 1993.
Cooke 1984: Cooke, Roger, The mathematics of Sonya Kovalevskaya, New York, Springer, 1984.
Crowe 1967: Crowe, Michael J., A history of vector analysis. The evolution of the idea of a vectorial system, Notre Dame, University of Notre Dame Press, 1967 (ed. corretta, con nuova pref.: New York, Dover, 1985).
Demidov 1982: Demidov, Sergei S., The study of partial differential equations of first order in the 18th and 19th centuries, "Archive for history of exact sciences", 26, 1982, pp. 325-350.
‒ 1992: Demidov, Sergei S., La théorie des équations différentielles à la limite des XVIIIe-XIXe siècles, in: Amphora. Festschrift für Hans Wussing zu seinem 65. Geburtstag. Festschrift for Hans Wussing on the occasion of his 65th birthday, edited by Sergei S. Demidov [et al.], Basel, Birkhäuser, 1992, pp. 157-169.
Dieudonné 1983: Dieudonné, Jean, History of functional analysis, Amsterdam-New York-London, North Holland, 1983 (1. ed.: 1981).
Engelsman 1980: Engelsman, Steven B., Lagrange's early contributions to the theory of first-order partial differential equations, "Historia mathematica", 7, 1980, pp. 7-23.
‒ 1984: Engelsman, Steven B., Families of curves and the origins of partial differentiation, Amsterdam, North-Holland, 1984.
Gray 1985: Gray, Jeremy J., Linear differential equations and group theory from Riemann to Poincaré, Boston-Basel, Birkhäuser, 1985 (2. ed.: 2000).
‒ 1996: Gray, Jeremy J., Poincaré and electromagnetic theory, in: Henri Poincaré. Science et philosophie, édité par Jean-Louis Greffe, Gerhard Heinzmann et Kuno Lorenz, Paris, Blanchard; Berlin, Akademie Verlag, 1996, pp. 193-208.
Hawkins 1989: Hawkins, Thomas W., Time geometry, differential equations and the birth of Lie's theory of groups, in: The history of modern mathematics, edited by David E. Rowe and John McCleary, Boston, Academic Press, 1989-1994, 3 v.; v. II: Institutions and applications, 1989, pp. 275-327.
Katz 1979: Katz, Victor J., The history of stokes' theorem, "Mathematics magazine", 52, 1979, pp. 146-156.
Koblitz 1983: Koblitz, Anne Hibner, A convergence of lives. Sofia Kovalevskaya, scientist, writer, revolutionary, Boston, Birkhäuser, 1983.
Lützen 1987: Lützen, Jesper, The solution of partial differential equations by separation of variables. A historical survey, in: Studies in the history of mathematics, edited by Esther Phillips, Washington (D.C.), Mathematical Association of America, 1987, pp. 242-277.
‒ 1990: Lützen, Jesper, Joseph Liouville 1809-1882. Master of pure and applied mathematics, New York-Berlin, Springer, 1990.
Monna 1975: Monna, Antonie F., Dirichlet's principle. A mathematical comedy of errors and its influence on the development of analysis, Utrecht, Oosthoek, Scheltema & Holkema, 1975.
Smith 1989: Smith, Crosbie - Wise, Norton M., Energy and empire. A biographical study of Lord Kelvin, Cambridge, Cambridge University Press, 1989.
Stokes 1905: Stokes, George G., Mathematical and physical papers, Cambridge, Cambridge University Press, 1880-1905, 5 v.; v. V, 1905.