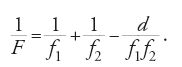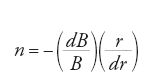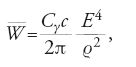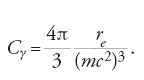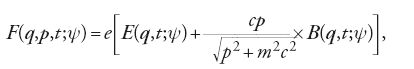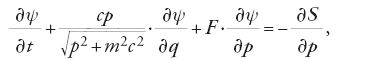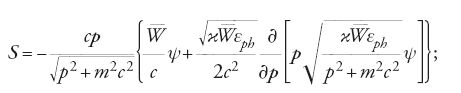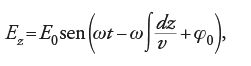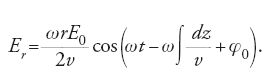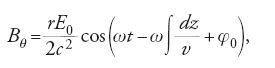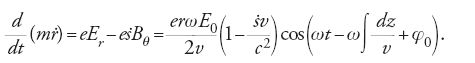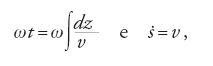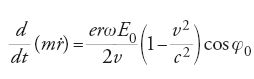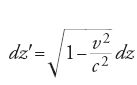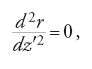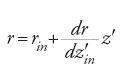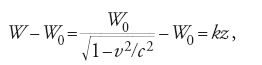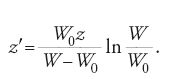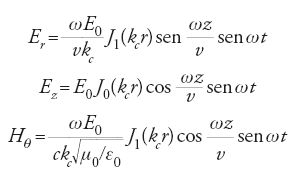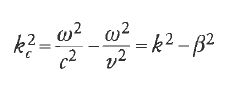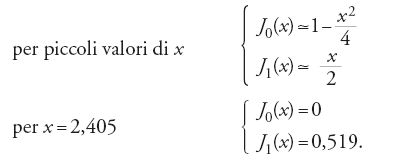La grande scienza. Gli acceleratori di particelle
La grande scienza. Gli acceleratori di particelle
Gli acceleratori di particelle
Gli acceleratori di particelle sono strumenti che permettono di studiare le proprietà dei nuclei e quelle delle particelle elementari e, quindi, le proprietà della materia.
Fasci di protoni, ioni ed elettroni di alta intensità, urtando contro i nuclei atomici producono la rottura del nucleo, generando così nuclei di altro tipo o isotopi instabili. L'interazione dei fasci di particelle con i nuclei del bersaglio genera sovente nuove particelle e dalle misure delle proprietà di queste ultime si può risalire alle strutture dei nuclei. Le misure delle distribuzioni angolari e di altre proprietà cinematiche e dinamiche permettono di studiare gli stati eccitati del nucleo.
Gli isotopi radioattivi prodotti negli acceleratori sono stati usati come traccianti per studiare le proprietà chimiche di diverse sostanze; sono stati, inoltre, utilizzati in biologia, in medicina e in altre discipline scientifiche. Gli acceleratori sono molto usati anche per scopi industriali (Schopper 1998).
Con la costruzione degli acceleratori di alta energia sono iniziati gli studi delle proprietà delle particelle elementari: i protoni, i neutroni, gli elettroni, i neutrini, e le loro antiparticelle. Aumentando l'energia degli acceleratori si sono potute mettere in evidenza altre entità che erano più nascoste: i quark, costituenti sia dei protoni sia dei neutroni e di altre particelle con proprietà più 'esoteriche', di vita media brevissima e masse diverse, alcune delle quali anche più grandi della massa del protone.
La produzione di antiparticelle ha costituito un trionfo della teoria di Dirac e ha messo in evidenza l'esistenza di profonde simmetrie in fisica. Recentemente la costruzione di anelli di collisione ha consentito di raggiungere energie così elevate (100GeV÷1000GeV) da permettere la produzione di bosoni pesanti, carichi e neutri, quali i W± e Z0. Questi risultati hanno ulteriormente messo in evidenza simmetrie profonde già per altro previste dalla teoria. Tali simmetrie hanno unificato la teoria delle interazioni deboli, responsabili dei decadimenti radioattivi, e quella elettromagnetica, responsabile delle proprietà elettriche e magnetiche in Natura, permettendo di formulare il Modello standard della teoria elettrodebole, recentemente verificato con grande precisione al Large electron-positron collider (LEP) del CERN (Myers e Picasso 1990) e allo Stanford linear collider (SLC).
Il ruolo dell'energia e dell'intensità negli acceleratori
In questo contesto, rispetto alla varietà di acceleratori, realizzati con caratteristiche differenti anche in relazione allo sviluppo tecnologico, riteniamo opportuno illustrare i principî fisici su cui si basa uno degli acceleratori più recenti: un anello di collisione elettrone-positrone. Questo ci permetterà di sviluppare considerazioni generali che sono alla base del funzionamento di molti acceleratori circolari.
Prima di descrivere a grandi linee un anello di collisione, chiamato anche 'storage ring' o 'collider', è opportuno fare ancora qualche considerazione. Esistono due classi ben distinte di acceleratori: quelli lineari e quelli ciclici. Noi descriveremo in maggior dettaglio gli acceleratori ciclici, rimandando alla bibliografia specializzata il lettore che voglia approfondire l'argomento di quelli lineari (Lapostolle 1987, 1998).
Gli acceleratori ciclici hanno lo scopo di produrre e studiare le proprietà di fasci secondari di protoni, di pioni e di altre particelle che, guidate attraverso canali magnetici, urtano un bersaglio fisso generando particelle secondarie di varia natura. Negli acceleratori nei quali circolano fasci di protoni, di elettroni e di ioni, in ragione del principio di funzionamento si possono raggiungere energie differenti, comunque sempre sostanzialmente limitate dal fatto che parte dell'energia totale Ep, relativa ai fasci primari incidenti sul bersaglio fisso, viene dissipata. L'energia utile per produrre una reazione nucleare è sempre inferiore all'energia cinetica della particella incidente. Se, per esempio, la massa M0 del nucleo bersaglio è a riposo nel sistema del laboratorio e la particella incidente di massa m0 ha una energia cinetica ε=Ep−m0c2, l'energia utile, cioè l'energia nel centro di massa del sistema, è W=[(m0+M0)2c4+2M0εc2]1/2, dove c è la velocità della luce. La situazione è diversa nel caso degli anelli di collisione, dove due particelle di uguale massa e quantità di moto opposta si urtano per esempio frontalmente: in questo caso tutta l'energia è utile, cioè va tutta a produrre la reazione in esame.
Prima dell'avvento dei collider l'energia degli acceleratori, a partire dagli anni Trenta, aumentava più o meno con una legge esponenziale. L'aumento di energia, dovuto principalmente alla scoperta di nuovi principî di funzionamento e di moderne invenzioni tecnologiche, corrispose alla progressiva realizzazione di macchine acceleratrici quali i ciclotroni, i betatroni, i sincrotroni, i sincrociclotroni, i sincrotroni a gradiente alternato, gli acceleratori lineari e gli anelli di collisione (Livingston e Blewett 1962; Livingston 1966; Briant e Johnsen 1993).
I primi acceleratori lineari utilizzarono solamente campi elettrici. Le enormi difficoltà di operare con alte tensioni, dovute tra l'altro alla necessità di evitare scariche ad arco e a corona, portarono a escogitare macchine che non richiedessero campi elettrici molto intensi. Rolf Wideröe nel 1928 propose di sottoporre le particelle del fascio all'azione di differenze di potenziali minori ma applicate più volte, come si usa oggi negli acceleratori circolari.
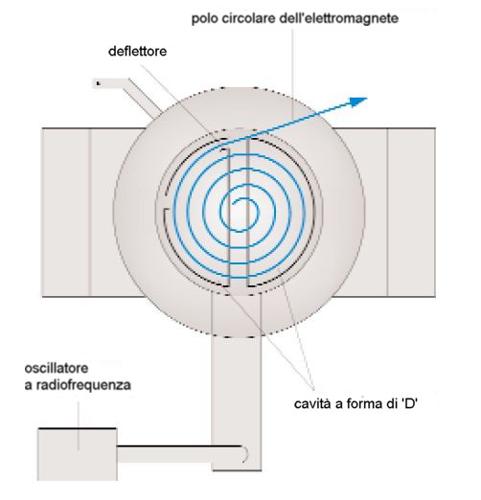
L'idea del ciclotrone (fig. 2) venne contemporaneamente a vari fisici, tra i quali Leo Szilard, ma lo sviluppo e la costruzione del primo ciclotrone fu opera di Ernest O. Lawrence e dei suoi collaboratori a Berkeley. Il ciclotrone di Lawrence e Milton S. Livingston, del 1931, fu il primo acceleratore in cui si utilizzò un campo magnetico che costringe le particelle a percorrere un'orbita a spirale, attraversando più volte un campo elettrico accelerante. Questo strumento nel quale si raggiunsero alte energie con un apparato abbastanza compatto, aprì una nuova era nella ricerca dei costituenti elementari della materia. I limiti di funzionamento intrinseci al ciclotrone non consentivano però di accelerare le particelle fino a raggiungere energie relativistiche. Tali difficoltà furono superate con gli ingegnosi schemi di Vladimir Veksler (1945) e Edwin M. McMillan (1945), che sfruttano la 'stabilità di fase'. La combinazione della stabilità di fase e del principio dell'acceleratore a gradiente alternato, che consente di concentrare i fasci in piccole dimensioni, permette di raggiungere energie elevate e di ottenere nello stesso tempo fasci molto intensi. Il principio del gradiente alternato fu proposto nel 1950 da Nicholas C. Christofilos (1956) e indipendentemente da Ernest D. Courant, Livingston e Hartland S. Snyder (Courant et al. 1952).
Attualmente l'ostacolo principale per raggiungere energie sempre più elevate è il costo degli acceleratori. In questo contesto, i collider hanno consentito di ottenere energie elevate nel centro di massa facendo urtare direttamente due fasci di particelle l'uno contro l'altro, diminuendo così i costi di produzione per unità di energia. Affinché gli acceleratori siano strumenti utili per la ricerca, non solo occorre ottenere le energie desiderate, ma è anche necessario riuscire ad avere fasci intensi di particelle. Oltre a inventare schemi di accelerazione sempre più efficienti, occorre anche assicurare che i fasci di particelle siano stabili durante il processo di accelerazione e di collisione. Inoltre è importante il ciclo utile, definito come il rapporto fra il tempo durante il quale i fasci restano in collisione all'energia voluta e il tempo totale impiegato nel compiere un ciclo di funzionamento (iniezione dei fasci, accelerazione, collisione ed estrazione); è opportuno ottenere un ciclo utile elevato.
Un esempio pratico: l'anello di collisione elettrone-positrone
Consideriamo un anello di collisione elettrone-positrone come esempio 'tipico' di un acceleratore (l'anello di collisione che stiamo descrivendo è 'tipico' nel senso che è un acceleratore a gradiente alternato e usa la stabilità di fase per accelerare i fasci; non è tipico se si considera che la ciambella, il recipiente ad alto vuoto in cui si muovono le particelle, è percorsa da due fasci in senso opposto e che essi sono accumulati per tempi lunghi). Due fasci di alta energia, dell'ordine di 100GeV, circolano in senso opposto nella macchina acceleratrice e si incrociano in più punti, essendo costituiti da pacchetti di particelle (bunch). Un anello di collisione è formato in generale da una serie di dipoli magnetici che vincolano particelle di impulso prefissato lungo un'orbita di equilibrio; da un insieme di quadrupoli magnetici che inducono le particelle, tendenti ad allontanarsi dalla traiettoria di equilibrio, a percorrere orbite oscillanti attorno alla stessa; da un insieme di sestupoli e ottupoli magnetici che compensano gli effetti non lineari dovuti alle molteplici perturbazioni introdotte dalle imperfezioni del sistema magnetico; infine dai solenoidi situati in vicinanza degli apparati sperimentali, laddove i fasci di particelle si incontrano. Per ottenere fasci di dimensioni trasverse estremamente ridotte rispetto alle dimensioni del fascio nel resto della macchina, occorre far uso di sistemi di quadrupoli a elevato gradiente situati a una decina di metri dal punto di incrocio.
I fasci sono costituiti da particelle di quantità di moto diverse, a ognuna delle quali corrisponde un'orbita di equilibrio. Un parametro importante nel progettare un anello di collisione, sia di elettroni-positroni sia di protoni-antiprotoni e di protoni-protoni, è la luminosità. Infatti, la frequenza degli eventi che si vogliono studiare è data dal prodotto di due quantità: la luminosità media L e la sezione d'urto σ del processo fisico che si osserva. La luminosità media dipende dalla luminosità massima accumulata nell'anello, dalla legge con cui la luminosità varia nel tempo e dal tempo che occorre per ripristinarne il valore massimo. La luminosità di un collider è proporzionale al numero di particelle in ciascun fascio, cresce al diminuire della sezione trasversale e, moltiplicata per la sezione d'urto, consente di calcolare il numero di eventi che si possono produrre.
Le cavità di radiofrequenza disposte nelle sezioni dritte dell'anello accelerano le particelle fino a raggiungere l'energia cinetica voluta. Nella ciambella, dove circolano i fasci di particelle, occorre creare un vuoto spinto per scongiurare che gli urti tra elettroni e molecole d'aria siano troppo frequenti, riducendo così considerevolmente l'intensità dei fasci. La pressione statica all'interno di tale involucro deve essere minore di 10−11 mmHg. In sei ore di funzionamento le 1012 particelle per fascio percorrono più di duecentoquaranta milioni di volte la circonferenza dell'acceleratore, che è di 27 km ca., coprendo una distanza pari a km 6,5×109, ossia maggiore di quella che separa la Terra da Nettuno (fig. 4).
Per esempio nel caso del LEP, costruito negli anni Ottanta, gli elettroni percorrono distanze pari a un terzo di anno luce prima di urtare contro una molecola d'aria.
Gli anelli di collisione, e gli acceleratori in generale, devono essere dotati di una strumentazione di grande sensibilità per determinare con precisione le posizioni dei fasci di particelle lungo la ciambella e intervenire su di essi nel caso le traiettorie descritte si allontanino troppo da quelle previste dai progettisti della macchina. Nel LEP, per esempio, le misure dei parametri più significativi hanno un'esattezza dell'1%: in alcuni casi le precisioni raggiunte nella determinazione dei parametri, tra questi in particolare l'energia del fascio di elettroni, sono di una parte su centomila (≈10−5).
Il fascio è composto di pacchetti di particelle di dimensioni tipiche, all'incrocio, di ca. 2×10−5 m di altezza, 2×10−4 m di larghezza e 2 cm ca. di lunghezza. Negli anelli di collisione, i fasci costituiti da particella e antiparticella ruotano in senso opposto.
Dinamica di particella singola (oscillazioni di betatrone)
La curvatura delle traiettorie descritte dagli elettroni dipende dall'intensità del campo magnetico lungo la circonferenza e dall'energia delle particelle. Siccome l'energia delle particelle aumenta di una quantità ΔE ogni qualvolta il fascio passa attraverso una serie di cavità risonanti, il cui campo elettrico è modulato a una ben determinata frequenza, occorre far variare il campo magnetico in modo che le particelle percorrano sempre le stesse traiettorie.
Il moto di una particella carica soggetta ai campi elettrici e magnetici che costituiscono, insieme al sistema di vuoto e alle cavità di radiofrequenza, gli elementi essenziali di un acceleratore può essere rappresentato come la somma del moto di un punto in equilibrio che ruota nell'anello con velocità angolare ω0 costante e delle oscillazioni che una particella di uguale impulso ma di diversa direzione descrive intorno al punto di equilibrio. Queste oscillazioni, dette 'di betatrone', avvengono rispettivamente nei piani orizzontale e verticale.
Uno dei problemi più importanti della dinamica dei fasci è evitare che gli elettroni e i positroni abbiano ampiezze di oscillazione trasverse più grandi delle dimensioni della camera a vuoto in quanto, in questo caso, le particelle del fascio sono perse a tutti gli effetti e il numero di particelle accumulate nell'anello diminuisce considerevolmente, come conseguentemente accade alla luminosità e alla frequenza con cui vengono prodotti i processi fisici che si esaminano.
Molti fenomeni fisici influenzano la dinamica delle particelle, riducendo la vita media del fascio e il numero di urti per unità di tempo. In generale tali fenomeni sono prodotti da non linearità introdotte nel sistema, quali, per esempio, i meccanismi di diffusione di particelle, di imperfezione dei campi elettrici e magnetici dell'acceleratore e così via. Nonostante la non linearità del sistema, si ottengono nei collider vite medie di parecchie ore nel caso degli elettroni e di parecchi giorni nel caso di sistemi non dissipativi, quali i fasci di protoni. Gli elettroni costituiscono un sistema dissipativo poiché perdono energia sotto forma di radiazione di sincrotrone.
La stabilità delle orbite è raggiunta impiegando, oltre ai dipoli, anche un altro tipo di magneti, i quadrupoli, che creano le forze di richiamo necessarie per rendere stabili le traiettorie delle particelle. Poiché l'ampiezza delle oscillazioni di betatrone è inversamente proporzionale alla loro frequenza angolare ωβ, quest'ultima è scelta in modo che il suo valore sia grande rispetto alla frequenza di rotazione del fascio nell'anello. Valori elevati del rapporto ωβ/ω0 si ottengono distribuendo opportunamente quadrupoli che focalizzano nel piano orizzontale e quadrupoli che focalizzano nel piano verticale. Va tenuto presente che un quadrupolo magnetico focalizza in un piano e defocalizza nel piano perpendicolare a esso.
Prima di concludere questo paragrafo, è opportuno soffermarsi sul nuovo concetto introdotto nel 1952 da Courant, Livingston e Snyder in analogia con un ben noto fenomeno dell'ottica geometrica. Se una coppia di lenti coassiali di lunghezza focale f1 e f2 è separata da una distanza d, la lunghezza focale F del sistema è data da
Se le due lenti hanno inoltre uguale lunghezza focale ma una è convergente e l'altra divergente, tale che sia f2=−f1, allora si ottiene F=f21/d; pertanto il sistema, avendo lunghezza focale positiva, è sempre convergente.
La prima applicazione di quest'idea a un sincrotrone consiste nel disporre lungo la circonferenza magneti di dipolo, con un grande valore radiale del gradiente, tali da focalizzare le particelle verticalmente e defocalizzarle radialmente. Questo insieme di magneti è seguito da un altro della stessa lunghezza azimutale nel quale il gradiente ha valore opposto, il cui effetto è focalizzare radialmente e defocalizzare verticalmente la traiettoria delle particelle. Le forze che fanno convergere le traiettorie sono sempre più intense di quelle che le fanno divergere e il risultato finale consiste nel far convergere le traiettorie verso la traiettoria nominale posizionata idealmente nel centro della ciambella. Le traiettorie sono stabili in entrambe le direzioni, radiale e assiale. Se l'indice di campo
è sufficientemente grande, le forze di richiamo che agiscono sulle particelle sono molto maggiori di quelle che agiscono su un sincrotrone a focalizzazione debole (acceleratore a gradiente costante) e le ampiezze delle oscillazioni di betatrone risultano molto ridotte. Un altro vantaggio consiste nel fatto che le aperture dei magneti sono notevolmente ridotte rispetto ai magneti a focalizzazione debole.
La tecnica che abbiamo brevemente descritto è denominata a gradiente alternato, o a focalizzazione forte.
Dinamica di particella singola (oscillazioni di sincrotrone)
Va premesso che una particella elettricamente carica, che descrive una traiettoria circolare in un campo magnetico, irraggia energia elettromagnetica; sotto l'effetto dell'irraggiamento le dimensioni trasverse dei fasci di particelle, specialmente se elettroni o positroni, diminuiscono in modo esponenziale nel tempo. La potenza media istantanea emessa sotto forma di radiazione elettromagnetica è data dalla formula
dove ϱ è il raggio di curvatura della traiettoria, E l'energia degli elettroni e dei positroni, o più generalmente della particella carica, c la velocità della luce e Cγ una costante che vale
La quantità re è il raggio classico della particella ed è inversamente proporzionale alla sua massa a riposo m. Per gli elettroni (e i positroni) Cγ=8,85∙10−5 m∙GeV−3, mentre per i protoni Cγ=7,79∙10−18 m∙GeV−3. Questa grande differenza numerica spiega perché la perdita di energia a causa dell'emissione di sincrotrone sia trascurabile, a parità di energia, nel caso dei protoni, mentre va presa in considerazione nel caso di macchine di elettroni. Come si vede dalla [3] il sistema di radiofrequenza deve, oltre che accelerare il fascio, anche restituirgli l'energia ceduta all'ambiente esterno sotto forma di luce di sincrotrone. Una volta fissata l'energia nominale E degli elettroni e scelto il sistema accelerante, la sola possibilità che resta al costruttore per ridurre la potenza emessa sotto forma di luce di sincrotrone è di aumentare il raggio di curvatura dell'anello. Questo è l'argomento che portò a scegliere le dimensioni del LEP.
La deviazione standard dell'energia del fascio rappresenta una situazione di equilibrio tra due fenomeni in competizione: l'energia media emessa dall'elettrone sotto forma di radiazione elettromagnetica tende a smorzare le oscillazioni, mentre l'emissione discreta dei fotoni a eccitarle.
Le particelle con energia diversa da quella nominale oscillano attorno a differenti orbite di equilibrio lungo la circonferenza. L'emissione stocastica dei fotoni introduce, perciò, un cambiamento istantaneo nelle oscillazioni radiali di betatrone e induce un valore di equilibrio nella emittanza orizzontale.
Le oscillazioni di sincrotrone possono essere descritte dall'equazione del moto di un oscillatore smorzato sottoposto a una forza di natura stocastica.
Ritornando alla dinamica del moto longitudinale, i fasci di elettroni e positroni sono distribuiti in piccoli pacchetti e il sistema di radiofrequenza, oltre a far aumentare l'energia delle particelle, ristabilisce il valore dell'energia che le particelle avevano prima dell'emissione della radiazione di sincrotrone; da esso si origina inoltre la 'focalizzazione della fase' (Veksler 1945; McMillan 1945).
Il sistema di accelerazione consiste, in linea di principio, di una o più cavità il cui campo elettromagnetico oscilla alla frequenza angolare ωRF, tipicamente alcune centinaia di MHz, scelta in modo da essere un multiplo della frequenza angolare di rivoluzione ω0 corrispondente a quella dell'orbita sincrona, la cui energia è uguale all'energia nominale E0.
Una particella che attraversa la cavità guadagna o perde energia a seconda del suo tempo di arrivo rispetto alla fase del campo elettrico. Una particella di impulso nominale p0 è in equilibrio se il tempo di entrata ts nella cavità è quello che corrisponde a un guadagno di energia uguale all'energia emessa sotto forma di radiazione di sincrotrone. Il moto delle particelle il cui impulso si discosta lievemente da quello corrispondente alla particella sincrona è anch'esso stabile, purché siano verificate certe condizioni. Supponiamo che una particella entri nella cavità all'istante t1 con l'energia nominale E0 precedendo di poco la particella sincrona. Essa acquista energia nell'attraversare la cavità e la sua velocità angolare, legata all'energia dalla relazione ω=eBc/E (dove E è l'energia, B il valore del campo magnetico, e la sua carica elettrica e c la velocità della luce), diminuisce. La stessa particella attraversa successivamente la cavità all'istante t2 con un ritardo inferiore nella fase rispetto alla fase della particella sincrona. Questo processo continua fino a che non si realizza l'attraversamento della cavità in corrispondenza del valore di campo uguale a quello della particella sincrona. Da questo istante in poi la particella tende a perdere energia e a guadagnare in frequenza, poiché attraversa la cavità quando il campo è decelerante. La particella esegue oscillazioni attorno alla particella sincrona; più esattamente la fase, la frequenza, l'energia e il raggio dell'orbita di una particella oscillano attorno alla traiettoria di equilibrio. Le particelle formano un pacchetto anche nella direzione longitudinale e percorrono traiettorie vicine alla traiettoria della particella sincrona. Ciascuna particella viaggia avanti e indietro all'interno del pacchetto e percorre molte rivoluzioni prima di compiere un ciclo.
Si può sfruttare questa proprietà della stabilità di fase per accelerare le particelle aumentando molto lentamente il campo magnetico e tenendo costante la frequenza. Nel caso di una particella relativistica, l'impulso aumenta mentre il raggio dell'orbita compie oscillazioni di piccola ampiezza attorno al valore di equilibrio che è mantenuto costante. Questo è il 'principio del sincrotrone'. Viceversa, si può mantenere costante il campo magnetico e diminuire lentamente la frequenza del campo accelerante; allora il raggio dell'orbita aumenta e con esso l'energia della particella. Questo è il 'principio del sincrociclotrone'. Si può anche mantenere costante il raggio e variare lentamente sia la frequenza sia il campo magnetico. Questo è il 'principio del protosincrotrone'.
L'equazione che descrive il moto longitudinale attorno alla particella sincrona è l'equazione di un pendolo. Nel piano definito dall'energia e dalla coordinata longitudinale si ottengono punti fissi, che non sono stabili, e curve che separano la zona di equilibrio stabile dalla zona in cui il moto non è più periodico. Tali curve sono le separatrici del moto. In condizioni particolari, da evitare nel caso del funzionamento degli acceleratori, si possono ottenere anche moti caotici.
Le oscillazioni di sincrotrone non sono generalmente lineari nella coordinata longitudinale. La regione stabile può essere aumentata se si accresce l'ampiezza del campo elettrico. Le oscillazioni di betatrone nel piano orizzontale sono accoppiate alle oscillazioni longitudinali del moto di sincrotrone, poiché la traiettoria curvilinea descritta dalla particella nel piano orizzontale dipende dall'energia totale. I termini non lineari accoppiano tra loro, in generale, i modi normali del sistema.
Il sistema di accelerazione è formato da più cavità opportunamente distribuite lungo la macchina, i cui parametri di funzionamento sono tali che la particella, percorrendo milioni di volte la traiettoria nell'anello, sia sempre in sintonia con il campo accelerante con grande precisione.
Il sistema di accelerazione a radiofrequenza svolge inoltre il ruolo importantissimo di concentrare longitudinalmente le particelle in pacchetti compatti. Questo sistema nel caso del LEP funziona alla frequenza di 352,21 MHz (un milione di cicli al secondo), il che significa che produce 31.320 oscillazioni ogni giro delle particelle. Ogni ciclo contiene una regione all'interno della quale un certo numero di particelle può oscillare stabilmente rispetto alla particella posta al centro del pacchetto. Questa regione stabile rappresenta l'accettanza longitudinale dello spazio delle fasi e ha proprietà tali da focalizzare le particelle in pacchetti distinti, di uno o due centimetri di lunghezza, nei quali tutte le particelle hanno la stessa energia a meno dello 0,1%.
Poiché in un giro del LEP vi sono 31.320 oscillazioni, vi sono anche 31.320 posizioni dove l'accettanza longitudinale è ben definita. Si può immaginare l'anello di accumulazione come una coppia di gigantesche ruote da luna park, ciascuna con 31.320 seggiolini, che girano in versi opposti. Se due amici vogliono stare su due ruote diverse e passare uno accanto all'altro in una particolare posizione devono sedersi sui seggiolini giusti. Allo stesso modo, affinché i pacchetti di elettroni e di positroni si scontrino al centro dei rivelatori, le particelle devono essere iniettate e accumulate solo nelle zone di accettanza corrette. A questo scopo è necessaria una sincronizzazione estremamente precisa tra il sistema a radiofrequenza e quello di iniezione.
Effetti non lineari
Nei grandi anelli di collisione il moto delle particelle è sottoposto a fenomeni non lineari, che vanno ridotti il più possibile per evitare l'instabilità del fascio.
Un parametro molto significativo per valutare tali effetti è la cromaticità del fascio, ξ, definita come la variazione del 'tune' della macchina, Q=ωβ/ω0, prodotta da una deviazione unitaria dell'energia relativa, ξ=δQ/(ΔE/E). La cromaticità dell'anello di collisione SPEAR, costruito a Stanford (USA), che ha un'energia per fascio di 2 GeV, una circonferenza di 0,2 km e un 'tune' verticale di 5,17, è ξ=−19. Nel LEP, la cui circonferenza è di 27 km, con energia tipica per fascio di 70 GeV e 'tune' di 78,20, la cromaticità è ξ=−170. La cromaticità può essere ridotta introducendo nel sistema magnetico speciali magneti, i sestupoli, nei quali il campo magnetico varia come il quadrato delle coordinate trasversali. Tale sistema di sestupoli, non lineare nelle coordinate trasversali, origina a sua volta risonanze parametriche del terzo ordine, che devono essere evitate, completamente o parzialmente, nelle coordinate trasversali. A volte occorre introdurre anche ottupoli magnetici il cui campo è cubico; l'introduzione di queste lenti magnetiche rende sempre più complessa l'analisi del moto di una particella singola. Sfortunatamente, per combattere le non linearità del sistema, si introducono sistemi non lineari che dovrebbero compensarle.
Lo studio di questi effetti sulla dinamica dell'acceleratore costituisce un interessante capitolo della teoria delle perturbazioni per sistemi hamiltoniani non integrabili. Nei grandi anelli di collisione adronici, si richiede per il moto di particella singola con grandi ampiezze betatroniche di varie centinaia di milioni di giri di macchina, una stabilità a lungo termine comparabile a quella del moto planetario nel Sistema solare.
Effetti collettivi
Uno dei più importanti effetti collettivi degli anelli di collisione deriva dall'interazione tra i fasci che si verifica quando essi si incrociano. La corrente dovuta alla carica elettrica associata a uno dei due fasci dà luogo a una considerevole forza di Lorentz sulle particelle dell'altro fascio. Questa forza è una funzione dispari e non lineare dello spostamento trasversale della particella.
Un secondo effetto collettivo è originato dalle inevitabili discontinuità presenti nella camera a vuoto, discontinuità dovute, per esempio, alle cavità di radiofrequenza, alle aperture di strumenti che consentono di controllare il fascio lungo la circonferenza, alle discontinuità tra i suoi diversi settori, ai giunti meccanici e così via. Quando una particella passa nelle vicinanze di queste discontinuità genera un campo elettromagnetico, detto 'campo di scia' (wakefield), che esercita una forza sulle particelle dello stesso fascio. Poiché le particelle sono distribuite in pacchetti e non riempiono l'anello in modo continuo, il campo elettromagnetico da esse generato all'inizio del pacchetto genera una forza che agisce sulle particelle di coda del pacchetto stesso. Questa forza è anch'essa una funzione non lineare delle coordinate della particella di coda ed è responsabile sia delle instabilità trasversali, sia delle variazioni delle dimensioni del fascio. I fenomeni collettivi associati ai campi di scia comprendono anche effetti di attraversamento multiplo, che sono la conseguenza di molti passaggi del fascio attraverso le cavità di radiofrequenza. Tali fenomeni dipendono dal fatto che le cavità hanno un fattore di merito molto grande, tipicamente di 1010 per cavità superconduttrici, che permette di 'ricordare' i valori del campo elettromagnetico indotto dal passaggio di un primo pacchetto quando è attraversato da un secondo pacchetto di particelle. Per intensità di fascio molto elevate, i campi originati dalle particelle circolanti nell'anello possono essere confrontabili con i campi esterni e i metodi perturbativi che generalmente si usano per calcolare la dinamica dei fasci possono dar luogo a errori.
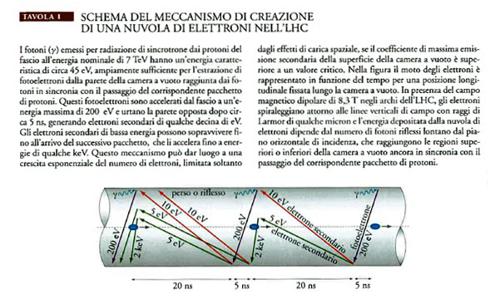
Nel caso di anelli di accumulazione per fasci di protoni o positroni di alta intensità, la carica positiva del fascio tende a essere neutralizzata dallo sviluppo di nuvole di elettroni. L'origine di questi elettroni può essere dovuta a diversi meccanismi, come la fotoemissione legata alla radiazione di sincrotrone (LHC e b-factories), la ionizzazione del gas residuo, oppure le perdite di piccole frazioni del fascio (Tav. I).
Una volta creati, questi elettroni sono accelerati nel potenziale del fascio e urtano contro le pareti della camera a vuoto con energie dell'ordine di 100÷1000 eV, generando elettroni secondari di bassa energia. Se questi sopravvivono fino all'arrivo del pacchetto successivo ci può essere una moltiplicazione ulteriore del numero di elettroni, come avviene nei fotomoltiplicatori. Questo fenomeno può indurre instabilità del fascio e deposito di energia sulle pareti della camera a vuoto. Tale ultimo aspetto è particolarmente rilevante per l'anello di collisione protone-protone, large hadron collider (LHC) in costruzione al CERN di Ginevra. La struttura magnetica di questo collider è costituita da circa 1300 dipoli superconduttori, ognuno della lunghezza di 14 m, che funzionano a una temperatura di 1,9 K. L'intensità dei fasci di protoni può essere limitata dal fenomeno della nuvola di elettroni se la potenza depositata per unità di lunghezza supera circa 1W/m ed eccede quindi la potenza criogenica installata.
Quando vari pacchetti successivi di particelle dei due fasci si trovano nella stessa camera a vuoto, si verificano anche interazioni fascio-fascio a lungo raggio che possono ridurre in maniera drastica la stabilità delle oscillazioni con grande ampiezza betatronica. Questo fenomeno è responsabile dei limiti attualmente incontrati nell'operazione ad alta luminosità del collider protoni-antiprotoni Tevatron, a Fermilab, e avrà un ruolo importante anche per l'LHC, dove due fasci di protoni si incrociano in un angolo che è limitato dalle dimensioni dei quadrupoli delle zone di interazione.
Una veduta d'insieme sulla dinamica dei fasci
Dalla descrizione precedente si deduce che gli acceleratori sono sistemi dinamici non lineari la cui evoluzione temporale dipende da forze elettromagnetiche generate sia da campi esterni sia dalle interazioni delle particelle tra loro e con l'ambiente. Queste forze hanno generalmente una componente di natura stocastica e le equazioni del moto, tante quante le particelle del fascio, sono equazioni differenziali stocastiche. Esse sono non lineari e i diversi gradi di libertà sono accoppiati l'un l'altro.
Trovare la soluzione di un siffatto sistema di equazioni è impossibile e, in quasi tutti i casi, lo si sostituisce con una singola equazione differenziale stocastica, che descrive il moto di una 'particella fittizia' soggetta all'azione delle forze originate dai campi esterni e di quelle generate dalle altre particelle. Questa equazione stocastica è del tipo:
dove abbiamo indicato con x=(q,p) il vettore delle coordinate e dell'impulso della particella, con ψ(x, t) la densità delle particelle nello spazio delle fasi al tempo t. Nel secondo membro della [5] compare la 'forza deterministica' K, che è di tipo hamiltoniano, e la somma delle forze di natura dissipativa e aleatoria, associate a sorgenti di rumore sia esterne sia interne al fascio. Poiché le correlazioni temporali delle corrispondenti variabili stocastiche ξα(t) sono, in generale, molto brevi rispetto ai tempi di rilassamento della funzione di distribuzione ψ(x, t), le variabili ξα(t) possono essere considerate come processi stocastici gaussiani e l'equazione [5] è equivalente a una equazione di Fokker-Planck per la densità di particelle ψ(x, t). Da un punto di vista stocastico, la ψ(x, t) si ottiene a partire dalla funzione di distribuzione di N particelle f(q1,…,qN;p1,…,pN;t) dopo aver integrato sulle coordinate q e p dello spazio delle fasi di (N−1) particelle. Determinata la ψ(x, t) si possono dedurre la densità di carica ϱ(q,t) e la densità di corrente j(q,t). Le ϱ e j costituiscono rispettivamente la densità di carica e la densità di corrente del fascio di particelle.
Le forze esterne sono originate dalle distribuzioni di cariche e di correnti esterne al fascio, mentre le forze interne sono generate dalle cariche delle particelle del fascio. Le prime sono indipendenti dalle densità di particelle nello spazio delle fasi e sono le sole forze che si prendono in considerazione per studiare le proprietà ottiche dell'acceleratore: per esempio, per determinare l'orbita di equilibrio. La stabilità delle traiettorie q(t)e p(t) descritte dalle particelle può essere studiata prendendo in considerazione le forze esterne in regime lineare, cioè per piccole deviazioni Δq(t) e Δp(t) rispetto all'orbita di equilibrio di coordinate q0(t) e di impulso p0(t).
Per determinare l'apertura dinamica o le dimensioni longitudinali del fascio è necessario tener conto degli effetti non lineari riconducibili alle forze esterne. Queste ultime possono avere una componente stocastica originata dalla diffusione delle particelle che urtano le molecole d'aria residue nella camera a vuoto, oppure dovute alle fluttuazioni dei campi esterni o ad altre sorgenti di rumore stocastico.
Le forze interne dipendono, invece, dalla funzione ψ(x, t) e originano fenomeni collettivi quali l'interazione fascio-fascio, l'interazione fascio-parete (mediante i cosiddetti 'campi di scia'), la diffusione delle particelle che interagiscono con quelle dello stesso pacchetto, denominata intra-beam scattering, o il rumore associato alla corrente elettrica generata dal moto degli elettroni (schottky noise). I valori dei campi elettrici e magnetici interni dipendono, in generale, dalla storia precedente del fascio attraverso una funzione di Green che tiene conto delle condizioni al contorno. La forza totale che in media agisce su una particella è la forza di Lorentz:
dove si è indicato con E e B rispettivamente la somma dei campi elettrici e magnetici medi, sia interni sia esterni. I campi esterni dipendono solo da q e t, mentre gli interni dipendono anche da ψ. Oltre ai campi medi occorre anche considerare i campi microscopici che descrivono i processi d'urto e d'irraggiamento. La distinzione tra questi ultimi e i campi medi è legata alla differenza tra processi irreversibili e reversibili. Le equazioni del moto in cui intervengono i campi elettrici e magnetici medi sono derivabili da una hamiltoniana e soddisfano il teorema di Liouville, cioè conservano il volume dello spazio delle fasi o, in altre parole, l'emittanza del fascio. I campi microscopici, invece, generano forze non conservative, il cui comportamento è aleatorio. Queste forze stocastiche, che includono anche le fluttuazioni delle forze esterne, sono all'origine dei fenomeni diffusivi e dissipativi, cioè irreversibili. Va considerato che anche i fenomeni deterministici possono dar luogo, se intervengono termini non lineari, a fenomeni il cui comportamento è stocastico.
Esempi di fenomeni dissipativi sono i processi fisici in cui si ha emissione di radiazione, raffreddamento stocastico, fluttuazioni di densità, e così via. La funzione di distribuzione ψ(x, t) soddisfa l'equazione di Fokker-Planck:
dove il vettore S(q,p,t;ψ) rappresenta il flusso irreversibile di particelle nello spazio delle fasi (q,p) all'istante t; nel caso di forze stocastiche indipendenti da ψ, S è un funzionale lineare di ψ, mentre per fenomeni come il raffreddamento stocastico la dipendenza di S da ψ è più complicata.
Uno dei principali processi irreversibili per acceleratori di elettroni è l'emissione incoerente di radiazione di sincrotrone. In questo caso il vettore S che compare nella [7] si può scrivere come di seguito indicato:
dove ϰ è una costante adimensionale dell'ordine dell'unità,
il valore medio istantaneo della potenza irraggiata dall'elettrone, εph l'energia critica dei fotoni emessi e p l'impulso della particella. La [7], con il flusso irreversibile S espresso dalla [8], può essere linearizzata rispetto alle deviazioni dall'orbita di equilibrio. Nella [8] il primo termine del secondo membro rappresenta la dissipazione associata alla radiazione di sincrotrone emessa secondo un'interpretazione classica, il secondo termine è dovuto al processo diffusivo associato all'emissione di natura quantistica della radiazione stessa. L'equazione [7], con il flusso espresso dalla [8], descrive nel modo più generale il comportamento del fascio nel collider, tuttavia è troppo complicata per poter essere risolta esattamente. L'interazione fascio-fascio accoppia inoltre le equazioni di Fokker-Planck per le distribuzioni di ciascuno dei due fasci in collisione, mentre l'interazione con nuvole di elettroni o di ioni accoppia l'evoluzione della distribuzione di ciascun fascio con quella degli elettroni o degli ioni stessi. Il metodo usuale che si segue è quello di linearizzare la [7] rispetto alle coordinate e all'impulso e di introdurre una funzione di dispersione della coordinata radiale, disaccoppiando il moto radiale di betatrone da quello longitudinale e procedendo allo studio matematico del moto.
Una procedura alternativa consiste nell'analisi dell'evoluzione temporale della funzione ψ con metodi approssimati e nelle simulazioni matematiche su un numero finito di particelle, tipicamente 103, partendo dall'equazione stocastica [5]. Tali simulazioni matematiche possono introdurre incertezze che non rispecchiano il comportamento reale del fascio di particelle nell'acceleratore. Soltanto il confronto con l'esperienza consente di acquisire le competenze necessarie per programmare correttamente il funzionamento di un acceleratore e di un collider. Da un punto di vista pratico, nel progettare un acceleratore si deve fare uso di strumenti che permettano di diagnosticare esattamente il comportamento dinamico del fascio di particelle e di correggere le eventuali anomalie, impiegando una sofisticata strumentazione che riporti il fascio a descrivere le traiettorie prestabilite.
La costruzione e il funzionamento di una macchina acceleratrice è il risultato dell'impegno congiunto di fisici, matematici, informatici, ingegneri e tecnici specializzati, ognuno dei quali contribuisce con le sue competenze specifiche. È importante avere una direzione centralizzata che prenda le decisioni finali.
Cronologia dei collider
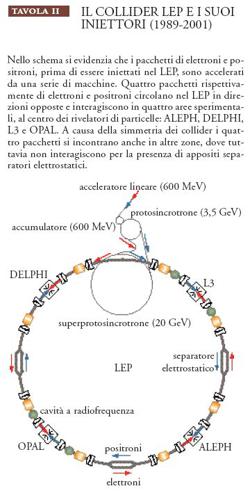
Nella descrizione precedente non si è accennato al fatto che per far funzionare un anello di collisione occorre avere un sistema di iniezione, che, in generale, è tanto più complesso quanto più è elevata l'energia che si vuole ottenere.
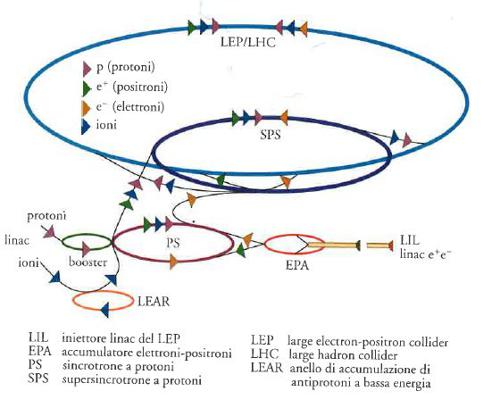
Il sistema di iniezione consiste, sovente, in un insieme di acceleratori in cascata l'uno rispetto all'altro. Nel caso del LEP, per esempio, esso consiste di un Linac (acceleratore lineare), di un anello di accumulazione e di due sincrotroni, in ognuno dei quali si raggiungono energie sempre più elevate. Il sistema di iniezione del LEP opera a energie di 20÷22 GeV e l'iniezione nell'anello finale avviene, quindi, a queste energie; nell'anello principale, poi, grazie a un sistema di cavità superconduttrici, le energie raggiungono i 100 GeV. Il progetto consiste nel far funzionare un insieme di acceleratori, ognuno dei quali ha le sue caratteristiche specifiche (Tav. II).
La storia dei collider inizia nel 1956, quando un gruppo della Midwestern University Research Association (MURA) negli Stati Uniti avanzò l'idea di costruire acceleratori circolari che accumulassero per tempi lunghi fasci di particelle (Nilsen 1956). L'idea in sé non era nuova, ed era stata discussa nell'ambiente dei fisici e degli ingegneri specializzati nella ricerca sugli acceleratori, ma all'epoca era considerata irrealizzabile a causa delle intensità troppo basse che si potevano ottenere. L'idea dei fisici di MURA era basata sulla possibilità di accumulare per lungo tempo fasci di particelle seguendo una nuova tecnica (particle stacking). Questo moderno metodo di accumulazione permette di ottenere luminosità tali da produrre molti eventi di alta energia facendo interagire due fasci di particelle tra loro.
Il metodo consiste nell'iniettare un fascio di protoni su una traiettoria (closed orbit) vicina alla parete interna della camera a vuoto e, quindi, nell'accelerare il fascio in modo tale che la sua traiettoria sia spostata verso una regione vicina alla parete esterna della ciambella. Questo ciclo di iniezione nell'anello viene ripetuto più volte, in modo da aumentare l'intensità del fascio accumulato nel collider. Dopo aver raggiunto l'intensità richiesta si porta il fascio nella zona centrale dell'anello, dove incontrerà l'altro fascio di protoni che ha subito lo stesso trattamento. Tale metodo richiede l'uso di un sofisticato sistema di radiofrequenza. Nello ISR (Intersecting storage ring), in cui è stato applicato, sono state ottenute correnti di protoni dell'ordine di 30÷40A per tempi di accumulo di 50÷60 ore. Il nuovo metodo ha reso così accessibili ai fisici sperimentali energie elevate a costi moderati.
Negli anelli di elettroni la radiazione di sincrotrone induce una riduzione delle dimensioni trasverse del fascio, permettendo di accumulare elevate intensità.
Gli anelli di collisione elettrone-positrone hanno una lunga storia alla cui origine, presumibilmente, si può collocare un seminario tenuto da Bruno Touschek ai Laboratori Nazionali di Frascati (Bernardini et al. 1962), nel quale il fisico austriaco mise in evidenza l'importanza di uno studio sistematico dell'urto elettrone-positrone. Egli, in quella occasione, propose la costruzione di un solo anello in cui i fasci di elettroni e positroni ruotano in direzioni opposte e si incontrano in più punti lungo la circonferenza. Lo studio di questi urti può fornire informazioni importanti sull'andamento delle leggi di Natura nella regione temporale (time-like region). ADA (anello di accumulazione) fu costruita a Frascati e permise di comprendere alcuni aspetti fondamentali dell'urto fascio-fascio. I primi risultati dell'interazione elettrone-positrone all'energia di 2×200 MeV furono riportati nel 1963.
Un'altra proposta più o meno dello stesso periodo fu avanzata da Gerard O'Neill e dai suoi collaboratori, tra i quali Burton Richter. Essi costruirono due anelli tangenti nei quali erano accumulati due fasci di elettroni ciascuno di 300 MeV (Barber 1966). Nel caso degli elettroni è conveniente far circolare i due fasci in due anelli separati e farli incontrare quindi in una sola regione dove le traiettorie sono tangenti. I primi risultati sperimentali furono riportati nel 1966. Altri anelli di collisione elettrone-positrone, VEPP I e VEPP II, furono costruiti a Novosibirsk (URSS) qualche anno più tardi; VEPP II rappresenta forse il primo anello di collisione a produrre i primi eventi di annichilazione, nel 1966, a una energia pari a 2×380 MeV (Budker e Skrinsky 1978). Nel 1967 entrò in funzione ACO (anneau de collision d'Orsay) a Orsay (Francia) alle energie di 2×550 MeV (Haïssinski 1998).
Da allora in poi gli anelli di collisione elettrone-positrone hanno avuto un ruolo sempre più importante nello studio della fisica delle particelle elementari. La semplicità dello stato iniziale dell'urto elettrone-positrone favorisce lo studio dei processi fisici in un ambiente privo, o quasi, di processi competitivi. L'esperienza in tutti questi anni ha mostrato che gli anelli di collisione elettrone-positrone sono potenti strumenti moderni per lo studio della fisica di alte energie.
Dopo ACO furono costruiti nel 1970 ADONE (2×1,5 GeV) a Frascati, nel 1973 un by-pass a Cambridge (USA), nel quale gli elettroni e i positroni riuscirono a raggiungere l'energia di 5 GeV nel centro di massa, e poi, nel 1974, SPEAR (Stanford positron electron asymmetric ring, 2×4,2 GeV) a Stanford, dove fu scoperta la particella J/ψ, (Pais 1986, cap. 21; ivi è descritta la scoperta della J/ψ avvenuta contemporaneamente a Brokhaven e a SLAC) e ancora DORIS (2×5 GeV) ad Amburgo, Germania; nel 1978 fu realizzato al DESY di Amburgo PETRA (2×19 GeV), e infine, nel dicembre 1979, CESR (Cornell electron storage ring, 2×8 GeV) a Cornell, negli USA. Gli anelli di collisione TRISTAN in Giappone, HERA al DESY di Amburgo, SLC allo Stanford linear accelerator centre di Stanford e il LEP al CERN di Ginevra sono stati gli ultimi anelli di collisione costruiti negli anni Ottanta. HERA a rigore è costituito da due anelli, dove si incontrano in più punti elettroni e protoni (Kohaupt e Voss 1983).
Riguardo agli anelli di collisione protone-protone e protone-antiprotone, il primo anello di collisione di protoni è stato lo ISR del CERN di Ginevra. Esso consisteva in due anelli magnetici che si incrociavano, sotto un angolo diverso da zero, in più zone, nelle quali avevano luogo gli esperimenti. I due fasci di protoni avevano una energia di 2×31 GeV e non erano formati da pacchetti, bensì da fasci continui, come 'nastri di particelle' (two ribbon-shaped beams crossing at an angle).
Lo ISR ha avuto un ruolo importante nello studio della fisica delle particelle, poiché ha insegnato, sia ai fisici degli acceleratori sia ai fisici sperimentali che costruiscono i rivelatori di particelle, come usare efficientemente un anello di collisione di protoni. Questo anello entrò in funzione nel 1971 migliorando continuamente la sua intensità, a volte in modo spettacolare, e terminò di funzionare nel 1984 (Briant e Johnsen 1993). Dopo lo ISR furono costruiti altri collider, per esempio UNK in Russia, fino ad arrivare all'LHC del CERN di Ginevra, che dovrebbe raggiungere energie di 14÷15 TeV nel centro di massa del sistema protone-protone.
Lo ISR servì come modello per gli anelli di collisione di protoni, sia per il funzionamento della macchina sia per la nuova concezione nel progettare gli esperimenti. Mentre oggi sembra ovvia la scelta degli anelli di collisione per ottenere alte energie, inizialmente esistevano molte perplessità nell'intraprendere la loro costruzione, essendo necessarie due enormi estrapolazioni nel progettarli: la prima consisteva nel fatto che la luminosità prodotta dai collider era di gran lunga minore di quella che si otteneva utilizzando gli acceleratori convenzionali; la seconda si basava sulla scarsa conoscenza della stabilità del fascio per tempi di accumulo molto più lunghi del tempo durante il quale un fascio di particelle rimane negli acceleratori a bersaglio fisso. Lo ISR dimostrò che queste preoccupazioni sono superabili e che esistono soluzioni in entrambi i casi.
Un significativo sviluppo portò alla costruzione dei collider protone-antiprotone. Con l'invenzione del raffreddamento stocastico, dovuto al lavoro di Simon van der Meer (1972) al CERN, è stato possibile ridurre le dimensioni dei fasci e aumentarne, quindi, la densità. Questo metodo è particolarmente efficiente se applicato a fasci di bassa intensità. Esso permise di realizzare il progetto proposto da Rubbia di accumulare antiprotoni per tempi lunghi in un 'anello di accumulazione' (AA), per poi iniettarli nel 'protosincrotrone' (PS) e infine nel 'superprotosincrotrone' (SPS), dove venivano accelerati all'energia di 270 GeV, interagendo successivamente con protoni della stessa energia (Cline et al. 1991). Questa conversione del superprotosincrotrone da acceleratore convenzionale a collider fu un grande successo sia dal punto di vista della fisica degli acceleratori sia per i risultati ottenuti: furono infatti prodotte per la prima volta le particelle W± e Z0. Una simile conversione fu realizzata successivamente a Fermilab (USA), dove il 'collider Tevatron' entrò in funzione nell'estate del 1985, con i due fasci operanti a 2×800 GeV (Lederman 1991). I primi risultati furono ottenuti nell'ottobre del 1985 e, da allora, il complesso ha funzionato all'energia di 2×900 GeV. A Fermilab fu identificato per la prima volta il quark top.
È opportuno accennare più in dettaglio alla tecnica del raffreddamento dei fasci di particelle. Nel 1966 Gersh Budker e Alexander N. Skrinsky a Novosibirsk proposero di ottenere alti valori della luminosità nell'urto di fasci di protoni e antiprotoni in un singolo anello, utilizzando la tecnica del raffreddamento di un fascio di antiprotoni per mezzo di un fascio di elettroni (Budker 1967; Budker e Skrinsky 1978). Questo metodo consiste nel far interagire un fascio di elettroni di alta intensità con uno di antiprotoni lungo una sezione dritta dell'anello. Facendo coincidere le velocità dei due fasci, l'azione della forza coulombiana fa sì che essi si trovino dopo un certo tempo alla stessa temperatura. Il fascio di elettroni, che ha un moto trasverso minore del fascio di antiprotoni, riduce il moto trasverso di quest'ultimo, aumentando, quindi, la densità degli antiprotoni.
Circa due anni dopo, nel 1968, van der Meer al CERN propose un metodo differente, che consiste in un raffreddamento stocastico del fascio di antiprotoni. Egli suggerì che sarebbe stato possibile misurare le fluttuazioni statistiche del centro di gravità di un fascio, causate dal numero finito di particelle, in un sistema costituito da un pick-up e da un amplificatore. Il segnale originato dalle fluttuazioni viene inviato con la fase corretta a uno strumento di compensazione, situato a valle rispetto alla posizione del pick-up e dell'amplificatore. Dopo qualche tempo, il circuito di controreazione (feedback loop) tra il pick-up e lo strumento di correzione riduce le fluttuazioni statistiche e aumenta la densità del fascio. Queste due tecniche di raffreddamento furono sperimentate a Novosibirsk (electron cooling) e allo ISR (stochastic cooling) e con entrambe si ottennero risultati promettenti. Nel 1976 Rubbia propose vari schemi, basati sui due metodi sopra accennati, per raffreddare un fascio di antiprotoni che avrebbe dovuto essere iniettato nel SPS del CERN, accelerato insieme al fascio di protoni fino a raggiungere l'energia di 270 GeV per fascio e ottenere, quindi, nel centro di massa l'energia di 540 GeV, maggiore di circa un fattore dieci rispetto a quelle che si potevano ottenere con gli acceleratori esistenti.
Al CERN si utilizzò lo schema basato sul raffreddamento stocastico e si ottennero energie nel SPS, ora modificato come anello di collisione protone-antiprotone, di 2×270 GeV, e successivamente di 2×315 GeV. I principî di funzionamento del SPS, in particolar modo i sistemi di iniezione, accumulazione e raffreddamento, formano un complesso di tecnologie che ha ispirato e guidato i successivi sviluppi.
HERA, realizzata nel centro DESY ad Amburgo, è un anello di collisione elettrone-protone; in realtà sono stati costruiti due anelli, uno di elettroni all'energia di 30 GeV e uno di protoni a 820 GeV. L'anello di elettroni fa uso di un sistema di cavità di radiofrequenza superconduttrici per accelerare gli elettroni (come nel LEP) mentre l'anello di protoni impiega magneti superconduttori.
La necessità di comprendere il fenomeno della violazione della simmetria CP (operatore di carica e parità) ha imposto lo sviluppo di specifici collider elettrone-positrone finalizzati a produrre alte luminosità a ben definite energie nel centro di massa. In particolare, due collider progettati per studiare tale violazione nei sistemi b_b sono stati costruiti uno al KEK di Tsukuba, in Giappone, e l'altro a Stanford. Per facilitare la rivelazione dei prodotti di decadimento, sono stati progettati anelli asimmetrici nei quali gli elettroni e i positroni hanno energie diverse.
La costruzione di anelli di collisione di fasci di ioni pesanti alle energie relativistiche fu motivata dalla convinzione che fosse possibile creare un volume di materia nucleare in estreme condizioni termodinamiche di temperatura, e densità di energia tali da indurre cambiamenti di fase dallo stato adronico a quello di un plasma di quark e di gluoni; queste transizioni di fase offrono la possibilità di studiare la teoria delle interazioni forti nell'estremo limite delle alte energie e delle alte temperature. Per esempio, le collisioni tra fasci di ioni di oro (197Au) all'energia di 100 GeV/u per fascio consentono lo studio delle proprietà della cromodinamica quantistica (quantum chromodynamics, QCD) applicate al meccanismo di confinamento dei quark. Le energie raggiunte nel collider di ioni pesanti sono equivalenti a quelle che raggiungerebbe un fascio di ioni di 22 TeV/u contro un bersaglio fisso.
Un collider di ioni pesanti, pur avendo in comune numerose caratteristiche con un collider di protoni e antiprotoni, presenta molte novità tecniche. L'obiettivo principale è raggiungere al minimo una luminosità di 1026 cm−2 s−1 per fasci di 100 GeV/u.
Un tale anello di collisione, denominato RHIC (relativistic heavy ion collider) ed entrato in funzione recentemente a Brookhaven negli Stati Uniti, è costituito da due anelli che possono funzionare con valori di campo magnetico diversi. L'ottica del sistema magnetico è molto complicata e richiede particolari attenzioni, specialmente nel punto dove avviene l'urto tra i due fasci. L'energia accumulata è circa 200 KJ per fascio (Foelsche et al. 1998).
Linear collider elettrone-positrone
Se si volesse costruire un anello di collisione, come il LEP, a 500 GeV, si dovrebbe aumentare la circonferenza dell'anello di circa un fattore dieci. Gli elettroni e i positroni a ogni giro perderebbero un'energia pari al 30% dell'energia nominale e la potenza dissipata dal fascio di particelle sarebbe di circa 100 MW. Tenendo conto delle varie perdite nel trasferire questa potenza al fascio, probabilmente la stazione di potenza necessaria dovrebbe essere di circa 500 MW. Questo strumento sarebbe certamente molto costoso e poco efficiente. L'idea fondamentale per evitare i problemi della radiazione di sincrotrone è quella di costruire due acceleratori lineari (Linac), i cui fasci di elettroni e positroni, giungendo da direzioni opposte, interagiscono in una zona ben precisa. Poiché le traiettorie descritte dagli elettroni sono rettilinee, la radiazione emessa è praticamente nulla. Lo svantaggio di un linear collider è che le particelle non vengono riutilizzate più volte, come invece si verifica negli anelli di collisione; inoltre la potenza da fornire necessariamente al fascio per accelerare con continuità nuove particelle è confrontabile con quella che occorre per compensare le perdite di potenza dovute all'emissione di luce di sincrotrone in un anello circolare. Il vantaggio principale consiste invece nelle dimensioni trasverse e longitudinali dell'acceleratore, che sono molto più piccole di quelle relative a un ipotetico acceleratore circolare di elettroni a energie dell'ordine del TeV. Inoltre gli acceleratori lineari hanno il vantaggio di non richiedere magneti di dipolo e, non ultimo, quello di poter usare cavità di radiofrequenza di dimensioni molto ridotte rispetto al LEP, e con un gradiente di campo molto più elevato.
Il primo linear collider, lo SLC, è per molti aspetti un prototipo di quelli che saranno i futuri linear collider.
Esso è costituito da un acceleratore lineare di elettroni lungo 3 km, che è in grado di fornire un'energia di 50 GeV ed è usato per accelerare in maniera alternativa pacchetti di elettroni e positroni, che sono iniettati in direzione opposta in due archi di circonferenza. Gli elettroni e i positroni si incontrano lungo una sezione dritta dove è disposto l'unico rivelatore di particelle. SLC aveva in principio due obiettivi: studiare sia la produzione del bosone intermedio neutro Z0 sia certi aspetti nuovi della fisica degli acceleratori, per esempio la possibilità di ottenere fasci molto intensi di particelle su dimensioni trasverse e longitudinali estremamente ridotte.
I linear collider futuri prevedono l'uso di due Linac. Esistono progetti con caratteristiche diverse per costruirne esemplari con fasci interagenti nella regione di posizionamento del rivelatore di particelle. Qui accenniamo brevemente al principio di funzionamento di un Linac, rimandando ad articoli specializzati per uno studio più dettagliato (Lapostolle 1987, 1998).
In un tubo a raggi catodici gli elettroni acquistano energia se sottoposti a una serie di differenze di potenziale in cascata. Il principio di funzionamento dei Linac moderni risale al 1924, tuttavia lo schema iniziale fu modificato e un prototipo fu realizzato da Wideröe nel 1928. L'obiettivo primario di questa macchina acceleratrice è mantenere la velocità della particella lungo tutto l'apparato, in fase rispetto a un'onda elettromagnetica che si propaga lungo gli elettrodi. Il primo acceleratore di protoni per esperimenti di fisica fu costruito da Luis Alvarez nel 1945. Egli introdusse la cosiddetta 'struttura di Alvarez', che consiste in una guida d'onda circolare nella quale si propaga l'onda elettromagnetica TM (transverse magnetic field; Alvarez 1946). La lunghezza degli elettrodi che formano la guida d'onda e la loro distanza sono scelte in modo tale da assicurare la condizione di sincronismo richiesto per accelerare le particelle, mantenendo fissa la frequenza di risonanza della cavità. Se l'onda ha una componente del campo elettrico nella direzione del moto, le particelle guadagnano o perdono energia a seconda della loro posizione istantanea rispetto al picco dell'onda.
In un acceleratore lineare le particelle sono sottoposte a forze radiali e assiali. I campi elettromagnetici che originano le forze radiali sono, generalmente, complicati nelle usuali strutture acceleranti. Fortunatamente il problema può essere semplificato eseguendo un'analisi di Fourier delle componenti del campo nella direzione della propagazione del fascio di particelle e nella direzione opposta. La componente del campo che viaggia alla stessa velocità e nella medesima direzione della particella in equilibrio è in grado di esercitare una forza radiale sul fascio, mentre l'altra componente produce alternativamente deflessioni di piccole ampiezze il cui effetto globale è trascurabile. Di conseguenza si studia solamente l'effetto del campo che viaggia con le particelle.
La componente assiale del campo è del tipo:
dove E0 è il valore del campo elettrico sull'asse della guida d'onda. La componente radiale, derivabile dalle equazioni di Maxwell, è:
La componente del campo magnetico perpendicolare al campo elettrico è:
dove v è la velocità della particella, ω/2π è la frequenza angolare del sistema di radiofrequenza e φ0 la fase iniziale.
Il moto delle particelle nella direzione radiale soddisfa l'equazione
Se per semplicità si considera solo la forza radiale che agisce sulla particella di equilibrio, per la quale
si ottiene:
Per energie tali che la massa delle particelle m non varia apprezzabilmente in funzione di v, ovvero per v minore di c, l'equazione precedente indica che la forza radiale è così intensa che l'orbita descritta dalla particella è instabile e lascia la struttura accelerante. Per energie relativistiche la forza radiale decresce rapidamente al crescere di v per valori prossimi a c.
Dall'equazione [14] si può dedurre una proprietà importante: supponiamo che v≃c e operiamo la seguente sostituzione:
L'equazione radiale si riduce alla seguente equazione
la cui soluzione è
dove in sta per condizione iniziale.
La quantità dz′ non è altro che la lunghezza del percorso fatto dalla particella, misurato nel sistema di riferimento della particella stessa. Se si assume, inoltre, che il campo elettrico del Linac sia indipendente da z, allora l'energia cinetica della particella è
dove W−W0 rappresenta l'energia acquistata dalla particella percorrendo il tratto z. Dalla [18] e dalla [15] dopo un'integrazione si ottiene
La [19] mette in evidenza che in un Linac l'apparente lunghezza dell'acceleratore nel sistema di riferimento della particella è notevolmente ridotta. Nel caso del Linac di elettroni, costruito all'Università di Stanford, la lunghezza effettiva era di 50 m, mentre quella apparente era di soli 38,5 cm all'energia di 1 GeV e di 35,3 cm a 2 GeV. La conseguenza di questo risultato è che lo spostamento radiale subito dagli elettroni è estremamente piccolo e il funzionamento del Linac richiede, quindi, una focalizzazione radiale molto modesta.
In tutti gli acceleratori lineari la configurazione del campo elettromagnetico che si usa è quella TM, in cui la componente del campo magnetico è nella direzione perpendicolare a quella del moto. In tutti i casi si utilizzano alcuni accorgimenti, che fanno sì che le particelle siano sottoposte all'azione di un'onda progressiva la cui velocità è quella della particella di equilibrio. In ogni acceleratore lineare è sempre presente un campo elettrico assiale, cioè un campo elettrico nella direzione del moto. La configurazione del campo elettromagnetico è una soluzione delle equazioni di Maxwell in coordinate cilindriche. Le componenti radiali e assiali del campo elettrico e la componente azimutale del campo magnetico sono date dalle equazioni seguenti:
dove r e z sono le usuali coordinate cilindriche, E0 l'ampiezza azimutale del campo elettrico sull'asse, v la velocità di fase dell'onda, (μ0/ε0)1/2 l'impedenza del vuoto (377 ohm),
e J0, J1 sono le funzioni di Bessel che hanno le seguenti proprietà:
Nel 1948 fu proposto un Linac di elettroni di 1 GeV che fu sottoposto per approvazione all'Office of Naval Research. Esso consisteva di una struttura di lunghezza complessiva di 50 m, la cui potenza acceleratrice era fornita da 16 Klystrons in serie, ciascuno dei quali produceva 30 MW di potenza di radiofrequenza applicata per tempi brevi (pulsed power). Questo acceleratore fu usato da Hofstadter e dal suo gruppo per studiare la struttura degli stati eccitati del nucleone, grazie alla diffusione degli elettroni sui nucleoni.
Nel 1956, dopo i successi ottenuti dal gruppo di Hofstadter, un gruppo di fisici dell'Università di Stanford progettò un Linac di elettroni lungo 3 km che poteva raggiungere l'energia di 20 GeV. Nel 1961 il Congresso degli Stati Uniti ne autorizzò la costruzione e nominò Direttore del progetto W. Panofsky. Esso, denominato SLAC, è un Linac di alta intensità, la cui struttura acceleratrice è fornita da elettrodi percorsi da onde elettromagnetiche progressive. La struttura magnetica che assicura la stabilità del fascio è costituita da campi magnetici quadrupolari opportunamente disposti lungo l'apparato. È bene notare che gli elettroni di 20 GeV, che percorrono 3 km nel laboratorio, in un sistema di riferimento solidale con gli elettroni risultano percorrere solo 1 m. Nel 1966 lo SLAC fornì alla comunità dei fisici elettroni di 17 GeV, nel 1967 elettroni di 20 GeV, nel 1975 fasci di elettroni di 33 GeV; infine, nel 1986, dopo diverse importanti modifiche, raggiunse l'energia di 50 GeV.
Tra gli esperimenti condotti con lo SLAC va ricordato il celebre SLAC-MIT del deep inelastic scattering, dove fu messo in evidenza per la prima volta che il nucleone è costituito da quark (Breidenbach et al. 1969). Lo SLAC ha fornito in seguito elettroni e positroni all'anello di collisione SPEAR (Stanford positron electron asymmetric ring), che iniziò a funzionare nel 1972 a 2,5 GeV e, dopo qualche modifica fu portato a 4 GeV. In questo anello fu messa in evidenza l'esistenza di una risonanza molto stretta centrata attorno a 3,1 GeV, la famosa risonanza J/ψ che indicava l'esistenza di stati legati del quark charm (Richter 1974; Pais 1986). Sempre allo SPEAR nel 1975 fu scoperto da Martin Perl e dai suoi collaboratori il leptone pesante 'tau'.
I nuovi progetti linear collider, molto più complicati dei Linac che abbiamo menzionato, sono però sostanzialmente improntati allo stesso principio di funzionamento.
Il tipo più semplice di linear collider prevede due Linac che dirigono fasci di particelle l'uno contro l'altro. Tuttavia, per molti aspetti è assai più difficile costruire un linear collider che un anello di collisione con le stesse prestazioni. In un anello di collisione, tipo LEP, le particelle seguono un percorso circolare e hanno circa diecimila possibilità al secondo di scontrarsi con le particelle che si muovono in direzione opposta. In un linear collider, invece, vi è una sola possibilità di urto a ogni accensione della macchina. Lo SLC può, per esempio, produrre circa cento impulsi al secondo e, per compensare la più bassa frequenza di collisione, i pacchetti di particelle devono essere cento volte più densi dei fasci prodotti in un anello di collisione. Nello SLC diventa possibile concentrare in ogni pacchetto circa cinquanta miliardi di particelle, con pacchetto focalizzato fino a ridurlo a un diametro di pochi micrometri.
Generalmente è facile produrre un fascio di elettroni fornendo un brevissimo impulso a un catodo di grandi dimensioni. La corrente di elettroni entra nell'estremità a monte di uno dei Linac, dove, sotto l'azione di opportuni campi elettromagnetici, gli elettroni vengono rapidamente riuniti in pacchetti di piccole dimensioni ma molto intensi. Il fascio di positroni è più difficile da produrre; a questo scopo si colpisce un bersaglio con un fiotto di elettroni ad alta energia e si selezionano i positroni separandoli dallo sciame di particelle che ne risulta, per mezzo di un sistema di magneti.
Per rendere i fiotti di particelle sufficientemente densi occorre ridurre la sezione trasversa del fascio in modo che le particelle si trovino molto più vicine tra loro. Questo processo viene eseguito all'interno di due piccoli anelli di accumulazione detti 'anelli di smorzamento' (damping storage ring). Nello SLC i fiotti di particelle vengono accelerati sino a un miliardo di elettronvolt e poi iniettati nei due anelli di smorzamento, dove la loro sezione viene ridotta considerevolmente: via via che le particelle emettono radiazione di sincrotrone, la loro distanza media diminuisce.
Gli elettroni e i positroni rimangono negli anelli di smorzamento per una frazione di secondo e poi i relativi pacchetti vengono reintrodotti nel rispettivo Linac, dove vengono accelerati a energie più elevate. Nel progetto Tesla di Amburgo si prevede di raggiungere, a tappe successive, energie di circa 1 TeV (mille miliardi di elettronvolt) per fascio. Questo ciclo di funzionamento dei linear collider viene ripetuto più volte al secondo.
Uno dei problemi più importanti da risolvere è fornire la potenza di radiofrequenza necessaria per accelerare i fasci. Nei Linac già costruiti, come lo SLAC, si fa uso di klystron, cioè di tubi elettronici di notevoli dimensioni, circa due metri, che producono l'energia necessaria per generare intensi campi elettromagnetici. Ogni klystron dello SLAC produce 67 MW. Altri progetti prevedono sistemi diversi per generare energia. Un altro problema di notevole rilevanza è produrre fasci di elettroni e positroni di densità mai raggiunte in precedenza. Nel punto di interazione il diametro dei fasci è, nello SLC, di pochi micrometri, ma potrà anche essere di nanometri nei futuri linear collider; la densità delle particelle è sempre nello SLC dell'ordine di quella di un gas a temperatura e pressione ambiente. Un terzo problema è mantenere compressi i fasci durante il percorso lungo i due Linac; le componenti del Linac tendono a perturbare i pacchetti del fascio attraverso campi di scia, come avviene in un collider circolare. Le particelle nella parte anteriore del pacchetto inducono campi elettromagnetici sulle pareti del tubo di accelerazione e questi campi a loro volta interagiscono con la parte terminale del pacchetto, provocando la diffusione laterale. Questo effetto è tanto maggiore quanto più il fascio si allontana dall'asse del tubo e dipende, inoltre, dalle dimensioni trasverse della sezione accelerante.
Da quanto brevemente accennato è evidente che la progettazione, la costruzione e il funzionamento di un linear collider costituirà nel futuro un impegno tecnico maggiore. È d'altra parte molto probabile che collisioni elettrone-positrone a energie maggiori di quelle del LEP si potranno ottenere soltanto attraverso la costruzione di linear collider.
Per studiare e approfondire ulteriormente la fisica delle particelle elementari, esplorando regioni di energia sempre più elevate, occorre senza dubbio ricorrere a nuove macchine acceleratrici.
Il CERN sta costruendo un nuovo LHC, il cui obiettivo è ottenere energie nel centro di massa di 14 TeV. In futuro è prevista anche la costruzione di collider lineari nei quali fasci di elettroni e positroni dovrebbero interagire a energie di vari TeV e permettere uno studio preciso dei fenomeni fisici messi in evidenza dagli anelli di protoni, o di fenomeni non incontrati nell'interazione fra adroni.
Bibliografia
Alvarez 1946: Alvarez, Luis W., The design of a proton linear accelerator, "Physical review", 70, 1946, pp. 799-780.
Amaldi 1981: Amaldi, Edoardo, The Bruno Touschek legacy, CERN 81-19, Yellow Report, Genève, 1981.
Barber 1966: Barber, Walter C. - Gittelman, Bernard - O'Neill, Gerard K. - Richter, Burton, Test of quantum electrodynamics by electron-electron scattering, "Physical review letters", 16, 1966, pp. 1127-1130.
Bernardini 1962: Bernardini, Carlo - Corazza, Gianfranco - Ghigo, Giorgio - Touschek, Bruno, Progress report on AdA (Frascati storage ring), "Nuovo cimento", 23, 1962, pp. 202-207.
Breidenbach 1969: Breidenbach, Martin e altri, Observed behavior of highly inelastic electron-proton scattering, "Physical review letters", 23, 1969, pp. 935-939.
Briant, Johnsen 1993: Briant, Philip J. - Johnsen, Kjell, The principle of circular accelerators and storage rings, Cambridge, Cambridge University Press, 1993.
Budker 1967: Budker, Gersh I., Status report of work on storage rings at Novosibirsk, Proceedings international symposium on electron and positron storage rings (Saclay 1966), Paris, Presses Universitaires de France, 1967, Sect. II, pp. 1-3.
Budker, Skrinsky 1978: Budker, Gersh I. - Skrinsky, Alexander N., The electron cooling and new possibilities in elementary particle physics, "Soviet Physics. Uspekhi", 21, 1978, pp. 277-296.
Christofilos 1956: Christofilos, Nicholas C., Unpublished report (1950), US Patent N° 2, 736, 799 filed March 10th, 1950; issued February 28th, 1956.
Cline 1991: Cline, David B. - Rubbia, Carlo - van der Meer, Simon, Alla ricerca dei bosoni vettoriali intermedi, in: Campi, forze e particelle, a cura di Luciano Maiani, Milano, Le Scienze, 1991, pp. 12-24.
Courant 1952: Courant, Ernest D. - Livingstone, Milton S. - Snyder, Hartland S., The strong-focusing synchrotron - A new high energy accelerator, "Physical review", 88, 1952, pp. 1190-1196.
Courant, Snyder 1958: Courant, Ernest D. - Snyder, Hartland S., Theory of alternating-gradient synchrotron, "Annals of physics", 3, 1958, pp. 1-48.
Foelsche 1998: Foelsche, Horst - Hahn, Horst - Harrison, Mike - Ozaki, Satoshi - Rhoades-Brown, M.J., The relativistic heavy ion collider, in: Advances of accelerator physics and technologies, edited by Herwig Schopper, (Advanced series on directions in high energy physics, XII), Singapore-London, World Scientific Publishing, 1998, pp. 104-130 (1. ed.: 1993).
Gareyte 1998: Gareyte, Jacques, Collective phenomena and instabilities, in: Advances of accelerator physics and technologies, edited by Herwig Schopper (Advanced series on directiones in high energy physics, XII), Singapore-London, World Scientific Publishing, 1998, pp. 67-103 (1. ed.: 1993).
Gintzon 1948: Gintzon, Edward L. - Hansen, William W. - Kennedy, William R., A linear electron accelerator, "Review scientific instruments", 19, 1948, pp. 89-108.
Haïssinski 1998: Haïssinski, Jacques, From ADA to ACO in: Bruno Touschek and the birth of e+e-, edited by G. Isidori (Frascati Physics Series, XIII), Frascati, 1998, pp. 17-31.
Hofsadter 1963: Hofsadter, Robert, Nuclear and nucleon structure, New York, Benjamin, 1963.
Jarlskog 1998: Jarlskog, Cecilia, What can we learn from experiments with accelerator and storage rings, in: Advances of accelerator physics and technologies, edited by Herwig Schopper (Advanced series on directions in high energy physics, XII), Singapore-London, World Scientific Publishing, 1998, pp. 3-27 (1. ed.: 1993).
KEKB B-factory design report, "KEK Report", 95/7, August 1995.
Kendall, Panofsky 1971: Kendall, Henry W. - Panofsky, Wolfgang Kurt Hermann, The structure of the proton and the neutron, "Scientific American", 224, 1971, pp. 61-77.
Kimura 1998: Kimura, Yoshitaka, The road to TeV electron positron Colliders, in: Advanced of accelerator physics and technologies, edited by Herwig Schopper (Advanced series on directions in high energy physics, XII), Singapore-London, World Scientific Publishing, 1998, pp. 249-281 (1. ed.: 1993).
Kohaupt, Voss 1983: Kohaupt, Rudolf D. - Voss, G.-A., Progress and problems in performance of e+ e- storage rings, "Annual review of nuclear and particle science", 33, 1983, pp. 67-104.
Lapostolle 1987: Lapostolle, Pierre, Introduction a la théorie des accélérateurs linéair, "CERN-Report", 87-09, Genève, 1987, pp. 1-114.
Lapostolle 1998: Lapostolle, Pierre, General aspects of linear accelerators, in: Advances of accelerator physics and technologies, edited by Herwig Schopper, (Advanced series on directions in high energy physics, XII), Singapore-London, World Scientific Publishing, 1998, pp. 163-193 (1. ed.: 1993).
Lawrence, Livingston 1932: Lawrence, Ernest O. - Livingston, M. Stanley, The production of high speed light ions without the use of high voltages, "Physical review", 40, 1932, pp. 19-35.
Lederman 1991: Lederman, Leon M., Il tevatron, in: Campi, forze e particelle, a cura di Luciano Maiani, Milano, Le Scienze, 1991, pp. 104-112.
LHC Large Hadron Collider: conceptual design, edited by P. Lefevre and T. Petterson, CERN/AC/95-05, October 20th, Genève, 1995.
Livingston, Blewett 1962: Livingston, Milton S. - Blewett, John P., Particle accelerators, New York, McGraw-Hill, 1962.
Livingston 1966: The development of high energy accelerators, edited by Milton S. Livingston, New York, Dover, 1966.
McMillan 1945: McMillan, Edwin Mattison, The synchrotron - A proposed high energy particle accelerator, "Physical review", 68, 1945, pp. 143-144.
van der Meer 1972: van der Meer, Simon, Stochastic damping of betatron oscillations in the ISR, CERN/ISR-PO/72-31, August 1972 (anche in: "Review of modern physics", 57, 1985, p. 689).
Möhl 1980: Möhl, Dieter - Petrucci, G. - Thorndahl, Lars - van der Meer, Simon, Physics and technique of stochastic cooling, "Physical reports", 58, 1980, pp. 75-119.
Möhl 1993: Möhl, Dieter, Cooling of particle beams, in: Advances of accelerator physics and technologies, edited by Herwig Schopper (Advanced series on directions in high energy physics, XII), Singapore-London, World Scientific Publishing, 1993, pp. 359-430.
Myers, Picasso 1990: Myers, Stephen - Picasso, Emilio, The design, construction and commissioning of the CERN large electron-positron collider, "Contemporary physics", 31, 1990, pp. 387-403.
Nilsen 1956: Nilsen, Nils Vogt, Attainment of very high energy by means of intersecting beams of particles, "Physical review", 102, 1956, pp. 590-591.
Pais 1986: Pais, Abraham, Inward bound of matter and forces in the physical world, Oxford, Clarendon Press, 1986.
Panofsky 1968: Panofsky, Wolfgang Kurt Hermann, Proceeding of the 14th international conference on high-energy physics, edited by J. Prentki and J. Steinberger, Genève, CERN, 1968, p. 23.
PEP-II: an asymmetric B factory. Conceptual design report, SLAC-418, Stanford (CA), 1993.
Perl 1975: Perl, Martin e altri, Evidence for anomalous lepton production in e+-e- annihilation, "Physical review letters", 35, 1975, pp. 1489-1492.
Picasso, Ruggiero 1988: Picasso, Emilio - Ruggiero, Francesco, Alcune considerazioni relative alla costruzione del LEP, "Il Nuovo saggiatore", 4, 1988, pp. 16-51.
Picasso 1998: Picasso, Emilio, Electron-positron storage rings from ADA to LEP, in: Bruno Touschek and the birth of e+ e-, edited by G. Isidori (Frascati Physics Series, XIII), Frascati, 1998, pp. 39-50.
Poth 1990: Poth, Helmut, Electron cooling: theory, experiment, applications, "Physics reports", 196, 1990, pp. 135-297.
Rees 1991: Rees, John R., Lo Stanford linear collider, in: Campi, forze e particelle, a cura di Luciano Maiani, Milano, Le Scienze, 1991, pp. 54-61.
Richter 1974: Richter, Burton, On research's personal account by Richter Burton, "Adventures in experimental physics", 5, 1974, pp. 143-161.
Ruggiero 1990: Ruggiero, Francesco - Picasso, Emilio - Radicati, Luigi, Kinetic description of the beam relaxation caused by incoherent synchrotron radiation in electron-positron storage rings, "Annals of physics", 197, 1990, pp. 396-438.
Rumolo, Zimmermann 2002: Proceedings of the mini-workshop on electron-cloud simulations for proton and positron beams (ECLOUD '02), CERN, 15-18 April 2002, edited by G. Rumolo and F. Zimmermann, CERN 2002-001, Yellow Report, Genève, 2002.
Schopper 1998: Advances of accelerator physics and technologies, edited by Herwig Schopper (Advanced series on directions in high energy physics, XII), Singapore-London, World Scientific Publishing, 1998 (1. ed.: 1993).
Seeman 1998: Seeman, John T., Accelerator physics of the stanford linear colider and SLC accelerator experiment towards the next linear collider, in: Advances of accelerator physics and technologies, edited by Herwig Schopper (Advanced series on directions in high energy physics, XII), Singapore-London, World Scientific, 1998, pp. 219-248 (1. ed.: 1993).
Symon, Sessler 1956: Symon, Keith R. - Sessler, Andrew M., Methods of radiofrequency acceleration in fixed field accelerators with applications to high currents and intersecting beam accelerators, in: Symposium on high energy accelerators and pion physics, Proceedings CERN, Genève, 1956, I, pp. 44-58.
Veksler 1945: Veksler, Vladimir I., A new method of acceleration of relativistic particles, "Journal of physics", USSR, 9, 1945, pp. 153-158.
Wideröe 1928: Wideröe, Rolf, A new principle for generation of high voltages, "Archiv für Elektrotechnik", 21, 1928, pp. 387-406.