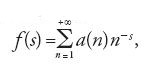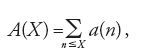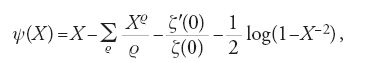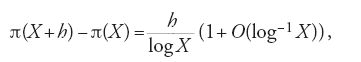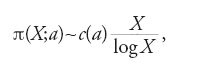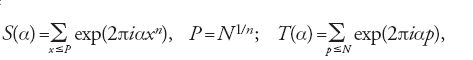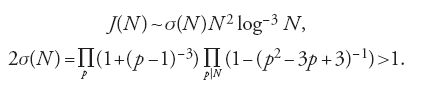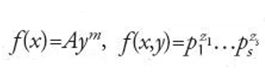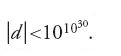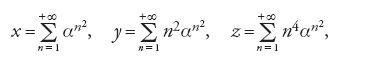La grande scienza. Teoria dei numeri
La grande scienza. Teoria dei numeri
Teoria dei numeri
La teoria dei numeri o, adottando una locuzione di Carl Friedrich Gauss (1777-1855), l'aritmetica superiore, è lo studio dei numeri interi. Egli, scrive nell'introduzione alle sue Disquisitiones arithmeticae:
Quel che viene comunemente chiamato aritmetica va difficilmente al di là dell'arte di numerare e calcolare (ossia rappresentare numeri in una ben determinata maniera, per esempio con la rappresentazione decimale, ed eseguire operazioni aritmetiche). Inoltre vengono spesso inclusi in essa argomenti che o non riguardano l'aritmetica affatto, come, per esempio, la teoria dei logaritmi o che valgono non solo per i numeri interi ma anche per una qualunque altra grandezza numerica. Sembra quindi appropriato distinguere due parti dell'aritmetica incorporando tutto ciò che è appena stato menzionato nell'aritmetica elementare e includendo le questioni più generali sui legami fra numeri interi nell'aritmetica superiore, che qui sarà la sola a essere trattata. (Gauss 1801, p. 5)
Nel XX sec. anche l'aritmetica elementare, alla quale Gauss fa riferimento, ha subito notevoli trasformazioni. Sistemi di calcolo evoluti esistono da non meno di seimila anni - i Sumeri 2000 anni a.C., per esempio, eseguivano complicate computazioni in un sistema di calcolo sessagesimale straordinariamente elaborato - ma negli anni Sessanta del XX sec. è stato sviluppato un nuovo metodo estremamente economico di moltiplicazione di numeri grandi che ha favorito a sua volta la revisione di tutti i metodi di calcolo dal punto di vista della velocità della loro esecuzione, dando vita alla teoria delle computazioni rapide.
Il concetto di numero intero è da sempre fonte di curiosità e già dagli albori della civiltà sono state formulate le prime domande riguardanti i numeri interi; i tentativi di risolvere tali questioni hanno condotto a nuove idee matematiche che a loro volta hanno fatto nascere nuove problematiche; a conclusione di questo sviluppo assistiamo alla creazione di una vera e propria teoria: la teoria dei numeri.
In essa, come in nessun'altra branca della matematica, si può chiaramente seguire l'evoluzione dei vari concetti nel corso del tempo; tuttavia spesso risulta difficile intravedere il legame tra i problemi moderni e quelli originali e a volte non si scorge subito il rapporto fra alcuni oggetti matematici comparsi con lo studio dei numeri interi e i numeri interi stessi.
Per esempio non è immediato comprendere quale sia il legame tra i numeri primi e la posizione degli zeri della funzione zeta di Riemann. Così anche non è certo evidente in quale modo sfruttare la periodicità delle funzioni trigonometriche elementari seno e coseno per lo studio delle proprietà dei numeri interi. Un progresso nell'ambito di una teoria dei numeri estesa e ramificata è ritenuto tanto più significativo e interessante quanto più è vicino al numero intero, a quell'oggetto, cioè, cui la teoria deve la sua comparsa, e la creazione di un metodo per affrontare una serie di problemi ha maggior valore della soluzione di un problema concreto.
Le prime formulazioni dei problemi della teoria dei numeri e le soluzioni di alcuni di essi risalgono a Pitagora e alla sua scuola e sono enunciate negli Elementi di Euclide.
In relazione alla nozione di divisibilità tutti i numeri naturali maggiori di 1 si dividono in due classi, una contenente quelli che hanno esattamente due divisori diversi (precisamente l'unità e il numero stesso), l'altra tutti i rimanenti numeri naturali. I numeri della prima classe si dicono primi, quelli della seconda composti.
Il numero 1 occupa un posto particolare tra i naturali visto che possiede un solo divisore e per questo motivo non appartiene né ai numeri primi né ai numeri composti. Il più piccolo divisore diverso da 1 di un numero naturale n>1 è un numero primo e di conseguenza n può essere scritto come il prodotto n=p1…pr, dove p1,…, pr sono numeri primi; in altre parole ogni numero naturale maggiore di 1 può essere fattorizzato nel prodotto di numeri primi.
Tale fattorizzazione è unica: comunque si fattorizzi il numero in fattori primi, si ottiene sempre lo stesso numero di fattori e ciascuno di questi compare sempre con la stessa molteplicità. Questa proprietà, a prima vista evidente, venne dimostrata rigorosamente solo da Gauss ed è indicata come 'teorema fondamentale dell'aritmetica'. I numeri primi costituiscono quindi una base moltiplicativa per i numeri naturali. È importante conoscere le proprietà di questa base e le prime problematiche della teoria dei numeri sono relative ai numeri primi: quanti sono, qual è la frequenza della loro distribuzione tra i numeri naturali, quali regolarità presenta tale distribuzione e così via. Euclide ha dimostrato l'infinità dei numeri primi con il metodo della reductio ad absurdum. Supponiamo che i numeri primi siano in numero finito e che p1,…, pr siano tutti i numeri primi. Considerando il più piccolo divisore p>1 del numero p1…pr+1, si può osservare che il numero p è primo e diverso da p1,…, pr, in contraddizione con l'ipotesi iniziale.
Il teorema di Euclide nella formulazione moderna si enuncia in questo modo: sia π(X) il numero dei primi non superiori a X, allora π(X)→+∞ quando X→+∞. Il comportamento della funzione π(X) è tuttora uno dei problemi basilari della teoria dei numeri.
Un altro problema è sin dai tempi più antichi quello della risoluzione di equazioni a coefficienti interi: Pitagora risolveva equazioni quadratiche legate ai triangoli rettangoli, Euclide utilizzava equazioni lineari per calcolare il massimo comun divisore di due numeri interi e Archimede studiava equazioni quadratiche, note oggi come equazioni di Pell. Successivamente si pose il problema più generale di determinare un algoritmo per stabilire se una data equazione a coefficienti interi ammetta soluzioni intere e in caso affermativo determinarle. Nei secoli III-IV d.C. a tali equazioni e ad altre più complesse, dedicò le sue ricerche Diofanto e in suo onore si parla oggi di equazioni diofantee.
A partire dal XVIII sec. la teoria dei numeri fiorisce rapidamente grazie alle opere di Pierre de Fermat, Leonhard Euler, Joseph-Louis Lagrange, Adrien-Marie Legendre e Gauss. Particolarmente feconde sono risultate le idee di Euler che introdusse l'uso dei metodi dell'analisi matematica per la soluzione dei problemi della teoria dei numeri, stabilendo una corrispondenza fra alcuni oggetti studiati e funzioni o classi di funzioni in modo che le relazioni fra gli oggetti si riflettessero sulle relazioni fra le funzioni, per applicare poi a queste ultime tutta la potenza dei metodi dell'analisi infinitesimale.
Uno sviluppo notevole ebbero due sue idee riguardanti i numeri interi e le equazioni diofantee.
Per s>1 Euler prese in esame la funzione definita dalla serie
Sfruttando l'unicità della fattorizzazione in primi dei numeri naturali, egli dimostrò l'identità di Euler:
dove a secondo membro il prodotto è esteso a tutti i numeri primi. Se si suppone ora che questi siano in numero finito, dalla [2] segue la limitatezza di ζ(s) per ogni s>1, mentre dalla [1] segue che ζ(s) cresce illimitatamente per s→1, (la serie armonica che si ottiene a destra per s=1 è divergente). Questa contraddizione fornisce un'altra dimostrazione, questa volta analitica, del teorema di Euclide.
L'altra idea di Euler è la seguente: siano a,b,…, c numeri naturali, n un numero intero non negativo, e R(n) il numero delle soluzioni dell'equazione ax+by+…+cz=n nelle incognite intere x, y,…, z. Usando la formula per la somma dei termini di una progressione geometrica, per ∣t∣⟨1 otteniamo:
Per calcolare R(n) è sufficiente derivare n volte F(t) e porre t=0. La grandezza R(n) può anche essere determinata usando la formula integrale di Cauchy. Indubbiamente le espressioni che in questo modo si ottengono per R(n) sono molto complicate, tuttavia questo metodo, noto come 'metodo delle funzioni generatrici' (la funzione F(t) 'genera' i numeri R(n) che si intende studiare), ha fornito un approccio generale all'analisi del numero delle soluzioni di equazioni diofantee.
Ai tempi di Euler vennero formulati anche 'problemi additivi' che caratterizzano proprietà di base, rispetto all'addizione, di particolari successioni di numeri interi.
Si dice che una successione di numeri naturali costituisce una 'base di ordine k' se ogni numero naturale (oppure ogni numero naturale maggiore di un certo numero naturale fissato) si esprime come somma di non più di k addendi appartenenti a tale successione. Per esempio i numeri dispari costituiscono una base di ordine 2. Euler e Christian Goldbach congetturarono che ogni numero pari ≥4 sia somma di due numeri primi (ogni numero dispari ≥7 sarebbe allora somma di tre numeri primi). Nel 1770 Lagrange dimostrò che i quadrati dei numeri interi costituiscono una base di ordine 4, cioè che ogni numero naturale è somma di non più di quattro quadrati.
Nello stesso periodo Edward Waring formulò la congettura che per ogni n≥2 le potenze n-esime dei numeri naturali costituiscano una base di ordine finito dipendente da n: esisterebbe cioè un intero k=k(n) tale che ogni numero naturale sia somma di al più k termini della forma an.
Si può trattare da un punto di vista additivo sia il problema dell'infinità dei primi gemelli, ovvero delle coppie di numeri primi della forma p, p+2, sia l'ultimo teorema di Fermat sulla non risolubilità dell'equazione Xn+Yn=Zn, n≥3, nelle incognite naturali X,Y,Z.
Vogliamo ora ricordare alcuni classici risultati ottenuti nell'Ottocento, che hanno avuto grande influenza sulle ricerche successive.
Sfruttando la prima delle due idee di Euler precedentemente citate, Peter Gustav Lejeune Dirichlet dimostrò il teorema sull'infinità dei numeri primi in una progressione aritmetica in cui il primo termine e la ragione sono coprimi.
Charles Hermite e Carl Louis Ferdinand Lindemann dimostrarono la trascendenza di e e π; risolvendo così il problema della quadratura del cerchio rimasto insoluto sin dai tempi di Pitagora.
Georg Friedrich Bernard Riemann sviluppò la teoria della funzione ζ(s) come funzione di variabile complessa e ricondusse il problema del comportamento asintotico di π(X) al problema della posizione degli zeri di ζ(s).
Ernst Eduard Kummer affrontò il problema di Fermat costruendo l'aritmetica dei numeri algebrici.
Pafnutij L´vovič Čebyšëv dimostrò con metodi elementari che π(X) è dell'ordine di X/logX.
Infine nel 1896 Jacques Salomon Hadamard e Charles De la Vallée Poussin dimostrarono che ζ(s) non ha zeri sulla retta Re(s)=1; deducendone la 'legge asintotica della distribuzione dei numeri primi': π(X)∼X/logX.
Nel 1900, al Congresso internazionale dei matematici, David Hilbert elencò una serie di problemi e in particolare alcuni di teoria dei numeri che "il diciannovesimo secolo lascia al ventesimo". Nello sviluppo della teoria dei numeri il XX sec. è caratterizzato dall'elaborazione di potenti metodi generali che hanno permesso di affrontare molte problematiche, gettando luce sui problemi originali e rivelando nuove proprietà dei numeri interi.
Nel XIX sec., grazie ancora all'idea delle funzioni generatrici di Euler, è stato scoperto che molti problemi della teoria dei numeri possono essere formulati come problemi del comportamento delle 'funzioni sommatoria' dei coefficienti delle corrispondenti 'serie di Dirichlet'. Per serie di Dirichlet si intende la somma formale
dove gli a(n) sono i coefficienti della serie, s=σ+it, σ e t numeri reali, i2=−1. Se la serie converge otteniamo una funzione f(s) della variabile complessa s che è anche detta funzione generatrice della successione numerica a(n).
Sotto determinate ipotesi per f(s) la funzione sommatoria A(X), cioè,
può essere espressa mediante l'integrale di f(s) lungo una particolare retta, ottenendo così la 'formula di Perron'. Studiando questo integrale con i metodi della teoria delle funzioni - in genere mediante la deformazione del contorno di integrazione - e conoscendo le proprietà analitiche di f(s), si riesce spesso a ottenere informazioni sul comportamento di A(X) quando X→+∞. Questo metodo è chiamato 'metodo di integrazione complessa' e la sua più brillante applicazione si ha nell'argomento dimostrativo della legge asintotica della distribuzione dei numeri primi. Dall'identità di Euler [2] segue che
dove λ(n) è la funzione di Mangoldt che assume il valore log(p) se n è una potenza di p, con p primo, ed è uguale a 0 altrimenti. Si vede così che la derivata logaritmica della funzione zeta di Riemann coincide con la funzione generatrice dei numeri λ(n), la cui funzione sommatoria è la funzione di Čebyšëv,
Lo studio del comportamento asintotico di π(X) è equivalente a quello del comportamento asintotico di ψ(X), dal momento che si può esprimere una funzione mediante l'altra grazie alla formula di sommazione per parti di Euler-Maclaurin; il resto nella formula asintotica per π(X) risulta essere log(X) volte più piccolo del resto nella formula asintotica di ψ(X) e viceversa. Solitamente si preferisce studiare ψ(X) dato che tale funzione è più semplice e il suo termine principale è uguale a X, mentre il termine principale di π(X) è uguale al logaritmo integrale di X; anche la formula approssimata corrispondente a ψ(X) prende il nome di 'legge asintotica della distribuzione dei numeri primi'.
Mediante integrazione complessa si ottiene per ψ(X), con X>1 non intero, la seguente formula:
dove i ϱ sono tutti gli zeri complessi di ζ(s), considerati nell'ordine crescente dei loro valori assoluti. È noto che essi giacciono nella 'striscia critica' 0≤Re(s)≤1. Per ottenere l'asintotica di ψ(X) bisogna conoscere la posizione delle loro parti reali: tanto più precisamente questa sarà individuata, tanto più accurata sarà la formula asintotica per ψ(X).
Nel 1896 De la Vallée Poussin dimostrò che le parti reali dei ϱ sono di poco più piccole di 1 e ottenne per ψ(X) la formula:
Questa e le sue successive precisazioni e generalizzazioni hanno permesso di progredire notevolmente nelle problematiche legate alla distribuzione dei numeri primi.
Nel corso di tutto il XX sec. sono stati compiuti notevoli sforzi per dimostrare 'l'ipotesi di Riemann' - tutti gli zeri complessi della funzione ζ(s) giacciono sulla 'retta critica' Re(s)=1/2 - nonché le sue generalizzazioni alle funzioni L di Dirichlet e alle funzioni zeta ζK(s) dei campi di numeri algebrici. L'ipotesi di Riemann e le sue generalizzazioni non hanno soltanto un interesse nella teoria delle funzioni. Dall'ipotesi di Riemann segue per esempio la stima del resto nella legge asintotica della distribuzione dei numeri primi: R(X)=√Xlog2X e, viceversa, da questa stima o dalla stima più debole R(X)=X0,5+ε, ε>0 arbitrario, segue l'ipotesi di Riemann. È noto inoltre che esistono due successioni numeriche X→+∞ e Y→+∞ per le quali:
Dunque, l'ipotesi di Riemann permette di stimare non soltanto il termine principale della formula approssimata [9] per ψ(X) ma anche l'esatto ordine del resto R(X). Risultati analoghi si deducono da ipotesi opportune per le generalizzazioni della funzione zeta e da molti altri interessanti risultati della teoria dei numeri. Al momento attuale l'ipotesi di Riemann e le sue generalizzazioni restano senza dimostrazione.
Sugli zeri della funzione ζ(s) sono state dimostrate - dagli studiosi e negli anni indicati nelle parentesi - le seguenti affermazioni:
1) sulla retta critica giacciono infiniti zeri di ζ(s) (Hardy, 1914),
2) se N0(T) è il numero degli zeri di ζ(s) della forma s= =1/2+it, 0⟨t≤T allora N0(T)>cT con c>0 costante (Hardy e Littlewood, 1921);
3) se N(T) è il numero di tutti gli zeri di ζ(s) contenuti nel rettangolo 0≤Re(s)≤1, 0⟨Im(s)≤T, allora N0(T)>cN(T), con c>0 costante (Selberg, 1942);
4) la costante c di Selberg non è inferiore a 1/3 (Levinson, 1974). Si può dimostrare che l'uguaglianza N0(T)=N(T) è equivalente all'ipotesi di Riemann;
5) in quasi ogni intervallo della retta critica Re(s)=1/2 della forma (t; t+h), con h=Φ(t)/log∣t∣, Φ(t)→+∞ per t→+∞, giace uno zero di ζ(s) (Selberg, 1942);
6) in quasi ogni intervallo della retta critica della forma (t; t+h) con h=tε, ε>0, giacciono non meno di c(N(t+h)−N(t)) zeri di ζ(s) (Karatsuba, 1984);
7) quasi tutti gli zeri di ζ(s) giacciono nel dominio ∣1/2− −Re(s)∣≤F(∣t∣)(log∣t∣)−1, dove F(∣t∣)=Φ(∣t∣)loglog∣t∣, Φ(∣t∣)→+∞ per ∣t∣→+∞ (Littlewood, 1924), e con F(∣t∣)=Φ(∣t∣) (Selberg, 1942);
8) la funzione ζ(s) non ha zeri nel dominio ∣t∣≥14, Re(s)≥ ≥1−c(log∣t∣)−α, α>3/4 (Chudakov, 1934), α>2/3 (Vinogradov, 1958);
9) se N(σ,T) è il numero degli zeri di ζ(s) nel rettangolo 1/2≤σ⟨Re(s)≤1, 0⟨Im(s)≤T, allora vale la stima ('teorema di densità'): N(σ,T)≤Tα(1−σ)(logT)c, T≥10, c>0 costante, a=8/3 (Ingham, 1940), a=5/2 (Montgomery, 1969); il caso a=2 costituisce l'ipotesi di densità (non ancora dimostrata).
Dal risultato di Vinogradov citato al punto 8) precedente segue la formula approssimata
mentre dal teorema di densità citato al punto 9) deriva la relazione
con h≥X1−1/a+ε, ε>0 arbitrario. Il risultato che si ottiene per a=2 è lo stesso che segue dall'ipotesi di Riemann e questo spiega il particolare interesse per l'ipotesi di densità.
Risultati analoghi sono stati dimostrati per le generalizzazioni di ζ(s) - anche se per questo argomento è stato necessario introdurre ulteriori parametri come il modulo del carattere, il discriminante del campo, ecc. - e da queste i corrispondenti teoremi sui numeri primi nelle progressioni aritmetiche, sulla distribuzione dei divisori primi, e così via.
Un ruolo fondamentale nella teoria additiva è ricoperto dai teoremi sui numeri primi nelle progressioni aritmetiche corte (short arithmetic progressions).
Assumendo valida per le funzioni di Dirichlet [4] un'ipotesi analoga a quella di Riemann, nel 1922 Godfrey Harold Hardy e John Edensor Littlewood ricavarono una formula approssimata per il numero delle rappresentazioni di un numero dispari N come somma di tre primi; da questo risultato seguiva la congettura di Goldbach per tutti gli N≥N1 (nel 1997 Jean-Marc Deshouillers, Gove Effinger, Herman J.J. te Riele e Dimitrii Zinoviev, con l'ausilio del computer, hanno ottenuto per N1 il valore 7). Con le stesse ipotesi Christopher Hooley risolse nel 1957 il problema di Hardy-Littlewood sulla rappresentabilità di un numero come somma di un primo e di due quadrati; successivamente una dimostrazione nella quale non si assumono ipotesi non provate venne fornita da Yurii Vladimirovich Linnik.
Da un'ipotesi analoga a quella di Riemann per la funzione zeta dei campi ciclotomici, Hooley ricavò nel 1967 la formula approssimata:
dove π(X;a) rappresenta il numero dei primi non superiori a X che ammettono come radice primitiva il numero a, diverso dal quadrato di un numero intero e da −1 (un numero intero a si definisce radice primitiva modulo un numero primo p se i numeri 1=a0, a, a2,…, ap−2 danno resti distinti nella divisione per p); c(a)>0 è una costante dipendente esplicitamente da a.
La formula approssimata di Hooley [13] è equivalente all'ipotesi di Emil Artin (1927), un caso particolare della quale è rappresentato dall'ipotesi di Gauss sull'infinità dei numeri primi che ammettono 10 come radice primitiva (nel 1984 Rajiv Gupta e Maruti R. Murty dimostrarono che, scelti tre arbitrari primi distinti a,b,c, almeno uno dei numeri aα,bβ,cγ, 0≤α,β,γ≤3, è una radice primitiva modulo p per infiniti numeri primi p; quest'affermazione rappresenta un 'avvicinamento' a una dimostrazione dell'ipotesi di Artin; inoltre Roger Heath-Brown (1986) ha dimostrato che esistono al più tre numeri che non si dividono per il quadrato di nessun numero primo, per i quali l'ipotesi di Artin non vale). Atle Selberg dimostrò, utilizzando l'ipotesi di Riemann, che quasi ogni intervallo del tipo (X;X+log2+εX) contiene un numero primo.
Oltre alla maggiorazione della differenza di due numeri primi vicini che segue dalla formula asintotica [12] per π(X+h)−π(X), è stato anche dimostrato (Paul Erdös, Robert Rankin) un teorema sull'esistenza di 'grandi differenze', considerevolmente superiori al valore medio, che per la legge asintotica ha ordine pari al logaritmo di uno dei due numeri.
La funzione zeta di Riemann e le sue generalizzazioni sono state studiate anche dal punto di vista della teoria delle funzioni e sono stati dimostrati (Alexander Ostrovskij, Dimitrii D. Mordukhai-Boltovskoi, Sergej Michailovič Voronin) teoremi relativi alla loro indipendenza differenziale in risposta a uno dei problemi posti da Hilbert nel 1900.
Nel 1975 S.M. Voronin dimostrò il teorema 'sull'universalità' di ζ(s): se f(s) è una funzione olomorfa nel cerchio K di raggio r, ∣3/4−s∣≤r⟨1/4, f(s)≠0, per ogni ε>0 esiste t tale che ∣ζ(s+it)−f(s)∣⟨ε, s∈K. Sono stati dimostrati teoremi sulla distribuzione dei valori ζ(σ+it) per σ∈(1/2; 1], t→+∞ (Harald August Bohr, Edmund Landau) e teoremi sulla distribuzione dei valori del vettore
[14] γ(t)=(ζ(σ+it), ζ(1)(σ+it),…,ζ(N-1)(σ+it)),
per σ∈(1/2;1], t→+∞, e di vettori analoghi in uno spazio complesso N-dimensionale (Voronin 1988).
Molti collegamenti fra ζ(s) e varie problematiche matematiche, fisiche e informatiche sono stati stabiliti da Jürgen Moser che ripropone una concezione dell'Universo ispirata alla filosofia pitagorica e così sintetizzata da Aristotele:
I cosiddetti Pitagorici si dedicarono per primi alle scienze matematiche; […] individuavano, inoltre, nei numeri le proprietà e i rapporti delle armonie musicali e, insomma, pareva loro evidente che tutte le altre cose modellassero sui numeri la loro intera natura e che i numeri fossero l'essenza primordiale di tutto l'universo fisico; e per tutte queste ragioni essi concepirono gli elementi dei numeri come elementi di tutta la realtà, e l'intero cielo come armonia e numero. (Metaphysica I, 5, 985b-986a)
Pertanto, dal momento che ζ(s) riflette le proprietà dei numeri primi, i numeri primi costituiscono la base della matematica, la matematica rispecchia le scienze naturali, ovvero il mondo che ci circonda, ζ(s) è strettamente 'legata al mondo circostante'.
Supponendo valida l'ipotesi di Riemann, Moser (1984) costruisce un'infinità di modelli dell'Universo sferico; più precisamente, per ogni intervallo (t1;t2), t1>1000, con t1 e t2 ordinate di due zeri vicini di ζ(1/2+it), è costruito un modello dell'Universo. Moser ha inoltre messo in luce il legame fra ζ(s) e il teorema fondamentale della teoria dell'informazione, il teorema di Kotelnikov-Whittaker-Nikewist, le formule di quadratura e i processi casuali. A loro volta Khalil Bitar, Nicola N. Khuri, Hai-Cang Ren (1991) hanno applicato il teorema di Voronin sull'universalità di ζ(s) al calcolo degli integrali d'azione di Feynman in meccanica quantistica.
Il metodo di integrazione complessa si utilizza molto spesso nello studio delle funzioni sommatoria f(s) delle 'successioni moltiplicative' a(n), ossia delle a(n) per le quali a(1)=1, a(mn)=a(m)a(n), se (m,n)=1. Le a(n), esprimibili in modo semplice attraverso la fattorizzazione in primi di n, si comportano in maniera bizzarra, mentre i loro valori medi hanno un comportamento regolare. Per esempio, se a(n)=τ(n), dove τ(n) è il numero dei divisori di n, allora f(s)=ζ2(s),
dove R(X)=Xα+ε, 0⟨α⟨1, ε>0 arbitrario.
Il problema della formula asintotica [15] per A(X) venne sollevato e risolto da Dirichlet (1837), che dimostrò con metodi elementari che α=1/2. È facile osservare che A(X) è uguale al numero delle coppie di numeri naturali (m,n) per cui mn≤X; in altre parole A(X) è uguale al numero dei punti (m,n) con coordinate intere positive che giacciono sotto l'iperbole mn=X. Il problema del calcolo del valore esatto di α nella formula di Dirichlet [15] è noto come 'problema dei divisori di Dirichlet', analogo al classico problema di Gauss sul numero dei punti interi interni al cerchio. Sia K(X) il numero dei punti a coordinate intere (m,n) ('punti interi') che giacciono nel cerchio m2+n2≤X. Gauss dimostrò che
[16] K(X)=πX+O(R1(X )), R1(X)=Xα+ε, α≤1/2.
Il problema di Gauss consiste nel calcolo del valore esatto di α nella [16].
Nel 1903 Georgii F. Voronoi dimostrò che α≤1/3 nella formula di Dirichlet [15], mentre Waclaw Sierpinski ottenne con il metodo di Voronoi lo stesso risultato per il problema di Gauss. Esiste un'ipotesi secondo la quale in entrambi i problemi α=1/4, che è tuttora non dimostrata; con il metodo delle somme trigonometriche si è riuscito a dimostrare soltanto che α è di poco inferiore a 7/22. Problemi generali sul numero dei punti interi in domini del piano e dello spazio, simili ai problemi di Gauss e Dirichlet, sono stati studiati e risolti nei primi decenni del XX secolo. Nel 1917 Ivan Matveevič Vinogradov ricavò la formula asintotica per il numero dei punti interi in un trapezio curvilineo della forma 0⟨y≤f(x), a⟨x≤b; per f(x) si richiede soltanto un determinato ordine di crescita della sua derivata seconda. Il resto nella formula di Vinogradov è simile al resto di Voronoi nel problema dei divisori di Dirichlet; come venne mostrato nel 1924 da Vojtech Jarnik, questo resto non può essere significativamente migliorato senza l'aggiunta di ulteriori condizioni per f(x).
Risultati di questo genere sono stati ottenuti per domini pluridimensionali; in alcuni casi di ellissoidi pluridimensionali e figure simili i problemi sono stati risolti del tutto; la soluzione completa del caso pluridimensionale del problema dei divisori di Dirichlet (si sommano i numeri τk(n), pari al numero delle rappresentazioni di n come prodotto di k fattori naturali) è equivalente alla dimostrazione dell'ipotesi di Lindelöf sulla crescita della funzione zeta di Riemann sulla retta critica. I punti interi possono essere trattati come punti di una 'griglia'. Questo tipo di trattazione è confluito nella 'geometria dei numeri'; le sue problematiche sono legate alla suddivisione dello spazio in figure regolari, al riempimento dello spazio (o di domini) con figure di diverso genere, alle applicazioni dei risultati ottenuti alla teoria algebrica dei numeri e alla cristallografia.
I problemi relativi alla somma di funzioni moltiplicative hanno portato Littlewood al teorema che afferma che il numero dei divisori primi distinti di un numero naturale è 'quasi sempre' asintoticamente uguale al doppio del logaritmo del numero considerato. Questo teorema si inquadra nell'ambito della 'teoria probabilistica dei numeri', che tratta le funzioni della teoria dei numeri come variabili aleatorie indagando le regolarità statistiche del loro comportamento.
Lo studio dei resti nelle formule asintotiche, come quella del problema dei divisori di Dirichlet [15], porta invece alla questione del valore assoluto della funzione zeta e delle sue generalizzazioni nella striscia critica e sulla retta critica. Nell'ambito di questa linea di ricerca troviamo 'l'ipotesi di Lindelöf', secondo la quale ∣ζ(1/2+it)∣ cresce al crescere di ∣t∣ meno velocemente di una qualunque potenza positiva arbitrariamente piccola di ∣t∣; finora si è solo dimostrato che la crescita è limitata da una potenza di ∣t∣ di poco più piccola di 9/56. Dall'ipotesi di Riemann segue quella di Lindelöf e da questa si deduce 'l'ipotesi di densità'.
Parallelamente alla teoria della distribuzione dei numeri primi si sviluppava la teoria additiva e nel 1909 David Hilbert risolse il caso generale del problema di Waring (i casi particolari n≤10 erano stati risolti in precedenza da altri matematici). Il metodo utilizzato da Hilbert è molto complicato e non ha trovato ulteriori applicazioni, ma il problema di Waring non fu abbandonato e in seguito, tra il 1918 e il 1922, vi rivolsero la loro attenzione Hardy, Littlewood e Srinivasa Ramanujan, sfruttando in modo innovativo nei loro lavori l'idea di Euler delle funzioni generatrici. Hardy, Littlewood e Ramanujan rappresentarono, utilizzando la formula di Cauchy, il numero delle soluzioni di un'equazione diofantea come integrale della corrispondente funzione generatrice, ottenendo in alcuni casi rappresentazioni asintotiche per tali integrali. A tal fine, essi suddividevano la circonferenza di integrazione in 'grandi' e 'piccoli' archi, evidenziando sui primi il termine principale della formula asintotica e stimando l'integrale lungo i secondi con una grandezza di ordine inferiore a quello del termine principale; la somma dei due addendi così ottenuti costituiva proprio la formula approssimata per il numero delle soluzioni dell'equazione e tale formula permetteva di stabilire non solo la risolubilità dell'equazione ma anche il comportamento del numero delle soluzioni al variare dei corrispondenti parametri.
Così, indicato con il simbolo J(N;k,n) il numero delle soluzioni dell'equazione di Waring
[17] xn1+…+xnk=N,
nelle incognite intere non negative x1,…,xk, Hardy e Littlewood dimostrarono che per k≥n2n vale la formula approssimata
[18] J(N;k,n)∼c(N;k,n)Nk/n-1, c(N;k,n)>c(k,n)>0,
cioè J(N;k,n)>0 per N≥N1(k,n). Hardy e Littlewood introdussero inoltre due funzioni g(n) e G(n); la prima esprime il più piccolo valore di k per il quale l'equazione di Waring [17] ammette soluzione per ogni N≥1, mentre la seconda rappresenta il più piccolo valore di k per cui la stessa equazione ammette soluzione per ogni N≥N1(n). È evidente che n⟨G(n)≤g(n), e il risultato di Hardy e Littlewood può essere anche formulato come segue: n⟨G(n)≤n2n. Ora, visto che il numero naturale N della forma N=2n([(3/2)n]−1)+2n−1 è più piccolo di 3n, per le sue rappresentazioni come somma di potenze n-esime sono necessarie [(3/2)n]−1 potenze del 2 e 2n−1 potenze dell'1, cioè g(n)≥2n+[(3/2)n]−2. È stata allora avanzata l'ipotesi che g(n) sia uguale all'espressione a secondo membro dell'ultima disuguaglianza; questa ipotesi è al momento attuale dimostrata per tutti gli n≤100 e per tutti gli n sufficientemente grandi.
Se indichiamo con il simbolo J(N) il numero delle soluzioni dell'equazione di Goldbach p1+p2+p3=N nei numeri primi p1,p2,p3, allora, supponendo vera 'l'ipotesi di Riemann generalizzata', Hardy e Littlewood dimostrarono che per N dispari
[19] J(N)∼σ(N)N2log-3N, 2σ(N)>1,
cioè J(N)>0 per N≥N1.
Parallelamente al metodo analitico si sviluppava nei problemi additivi anche il metodo puramente aritmetico, o come si dice ora, il 'metodo elementare'.
Viggo Brun elaborò nel 1919 il 'metodo del crivello' che risale a Eratostene e dimostrò che ogni numero pari ≥ 4 può essere rappresentato come somma di due addendi ciascuno dei quali è un prodotto di al più nove primi; verificò anche l'infinità delle coppie di numeri naturali (n,n+2), ognuno dei quali abbia al più nove fattori primi. Questi teoremi possono essere considerati come una variante debole della congettura di Goldbach e del problema dei primi gemelli.
Nel 1930 Lev G. Shnirelman introdusse il concetto di densità di una successione di numeri naturali; utilizzando la stima esatta dell'estremo superiore del numero delle soluzioni dell'equazione nei numeri primi x+y=z+u≤N, che si ottiene applicando il metodo del crivello di Brun, Shnirelman dimostrò che ogni numero naturale maggiore di 1 è somma di un numero limitato di addendi primi. Anche il teorema di Shnirelman può essere considerato come una versione debole della congettura di Goldbach.
Un contributo notevole alla teoria additiva dei numeri venne dal metodo delle somme trigonometriche di Vinogradov, il quale sostituì le serie infinite utilizzate da Hardy, Littlewood e Ramanujan con somme finite, nelle quali gli addendi sono seni e coseni di funzioni reali, semplificando la dimostrazione di molti teoremi e aprendo la strada alla soluzione di nuovi problemi. Alla base dell'introduzione delle somme trigonometriche c'è una semplice formula: l'integrale in α lungo un segmento di lunghezza unitaria di exp(2πiαm)= =cos(2παm)+isen(2παm) è uguale a 1 se m=0 ed è uguale a zero se m≠0, numero intero.
Le grandezze J(N;k,n) e J(N) definite dalle [18] e [19] si esprimono rispettivamente come integrali in α lungo un segmento di lunghezza unitaria delle espressioni
[20] Sk(α)exp(-2πiαN), T3(α)exp(-2πiαN),
dove
e la somma in T(α) è ristretta ai numeri primi.
Vinogradov suddivide l'intervallo di integrazione (0,1) in due insiemi: il primo costituito da intervalli analoghi ai grandi archi di circonferenza di Hardy, Littlewood e Ramanujan, il secondo dai rimanenti intervalli simili ai piccoli archi di circonferenza. L'integrale sul primo insieme fornisce il termine principale della formula asintotica, mentre per l'integrale sul secondo insieme si può fornire una maggiorazione.
Con questi metodi si può evidenziare il fenomeno della 'ternarietà' (ternarity): l'equazione ternaria del tipo x+y+z=N è risolubile, ed è possibile ricavare una formula approssimata per il numero delle sue soluzioni, se x e y assumono valori da successioni di numeri naturali di densità anche nulla, purché abbastanza 'ben distribuite' nelle progressioni aritmetiche con differenza 'lentamente' crescente e se z assume valori da successioni poco dense ma 'uniformemente distribuite' su [1;N].
Nel 1934 Vinogradov dimostrò con il suo metodo che per la funzione G(n) di Hardy-Littlewood è verificata la stima n⟨G(n)⟨6nlogn+10n, e nel 1937, dopo aver dato una stima non banale per T(α) sugli archi piccoli, dimostrò che per J(N) nel problema di Goldbach vale la formula approssimata:
In particolare, la [22] fornisce la soluzione completa del problema di Goldbach per gli N dispari, N≥N2 (logN2=3100, Lyu e Yuan Wang 2002).
Il problema relativo alla rappresentabilità di quasi tutti i numeri pari come somma di due numeri primi è ternario ed è stato risolto nel 1937 con il metodo di Vinogradov da Johannes Gualtherus Van der Corput, Chudakov, Theodor Estermann, Hans Arnold Heilbronn e Loo-Keng Hua indipendentemente l'uno dall'altro. Il metodo delle somme trigonometriche ha trovato molte applicazioni anche in altri campi della teoria dei numeri, rivelandosi uno dei più potenti metodi analitici del XX secolo. Sembra che le somme trigonometriche siano comparse per la prima volta in una delle dimostrazioni di Gauss della legge di reciprocità quadratica. Successivamente riapparvero all'inizio del XX sec. con Hermann Weyl che affrontò nel 1916 il problema della distribuzione delle parti frazionarie delle successioni f(n), dove f(x) è un polinomio con coefficiente del termine di grado massimo irrazionale, riconducendo il problema della distribuzione uniforme di {f(n)} alle stime di somme trigonometriche con il polinomio a esponente ('somme di Weyl') e fornendo un metodo per stimare il modulo di tali somme (una successione an è uniformemente distribuita se il numero delle parti frazionarie {ai}, i=1,2,…,P, che cadono in un qualunque intervallo (α;β), 0≤α⟨β⟨1, è pari a (β−α)P+o(P) per P→+∞).
Una variante del metodo di Weyl per somme trigonometriche con una funzione liscia a esponente è stata sviluppata da Van der Corput nel 1922. Nel 1934 Vinogradov elaborò un metodo per stimare le somme di Weyl - più preciso di quello dello stessoWeyl - che riduceva la stima della somma individuale alla stima del suo valore medio, portando a un considerevole progresso in tutte le problematiche relative alle somme di Weyl. La teoria delle somme trigonometriche multiple con un polinomio a esponente ha avuto molte applicazioni nei problemi pluridimensionali della teoria dei numeri (Arkhipov et al. 1987).
Negli anni Sessanta Hooley e Linnik elaborarono un metodo per la risoluzione di una serie di problemi additivi binari sui numeri primi, con il quale sono stati risolti il problema di Hardy-Littlewood sulla rappresentabilità di un numero naturale come somma di un numero primo e di due quadrati e il problema di Titchmarsh relativo alla formula approssimata per le somme di termini del tipo τ(p+a) primi, con a≠0 e p≤X. Questi problemi si riconducono ai problemi sulla distribuzione in media dei numeri primi nelle progressioni aritmetiche e fu trovata successivamente una soluzione più semplice sulla base del teorema di Bombieri-Vinogradov. Il numero π(X;k,l) dei primi non superiori a X e appartenenti a una progressione aritmetica con primo termine l e ragione k, con (k,l)=1, viene studiato con gli stessi metodi di analisi complessa utilizzati per π(X).
Le funzioni L(s,χ) di Dirichlet svolgono in questo caso un ruolo analogo a quello della ζ(s). Se la ragione della progressione k rimane costante, i risultati che si ottengono per π(X;k,l) e per π(X) sono simili.
La situazione cambia notevolmente se k=k(X)→+∞ per X→+∞, ovvero se vengono prese in considerazioni progressioni aritmetiche 'corte'; ed è proprio questo il caso che si presenta nel corso della risoluzione dei problemi additivi.
Al pari della questione degli zeri complessi delle funzioni L(s,χ) si presenta, nel caso di 'carattere reale' χ, il problema degli zeri reali, strettamente legato al problema di Gauss sul comportamento del numero h(−d) delle classi di forme quadratiche binarie a discriminante negativo −d (l'insieme delle forme quadratiche binarie del tipo aX2+bXY+cY2 a discriminante d=b2−4ac viene ripartito in h(−d) classi di forme equivalenti, in ciscuna delle quali le forme si ottengono l'una dall'altra mediante un cambiamento lineare di variabile del tipo X=αX1+βY1, Y=γX1+δY1, con α,β,γ,δ numeri interi tali che αδ−βγ=1.
Gauss ipotizzò che h(−d)→+∞ per d→+∞; questa congettura venne dimostrata nel 1934 da Heilbronn. Gauss calcolò inoltre il valore di nove discriminanti d per i quali h(−d)=1 (d=3,4,7,8,11,19,43,67,163) e congetturò che non vi fossero altri discriminanti con questa proprietà. Heilbronn e Edward H. Linfoot dimostrarono che ne potrebbe esistere al più uno e nacque così il 'problema del decimo discriminante'.
Nel 1935 Carl Ludwig Siegel dimostrò che h(−d)≥d1/2−ε, ε>0 per d≥d1(ε). Questo risultato permise di ottenere delle formule asintotiche per π(X;k,l), simili alle formule per π(X) anche nel caso in cui, al crescere di X, k cresce come un'arbitraria ma fissata potenza del logaritmo di X. Il risultato di Siegel è sufficiente per la risoluzione della maggior parte dei problemi additivi ternari sui numeri primi. Il teorema di Siegel è però non effettivo, non permette cioè di calcolare per un dato ε la grandezza d1(ε). Allo stesso modo questa disuguaglianza non permette di stimare il numero di quei d per i quali h(−d) è uguale a un numero fissato, per esempio a 1 o a 2. Per questo nelle applicazioni si utilizza spesso un teorema più debole ma di natura più costruttiva, il teorema di Le Paige su π(X;k,l) (in questo teorema k è poco più piccolo del quadrato del logaritmo di X).
Si è scoperto che per la risoluzione di una serie di problemi additivi sui numeri primi, come per esempio i problemi di Hardy-Littlewood e di Titchmarsh di cui si è parlato in precedenza, è sufficiente conoscere il comportamento di π(X;k,l) 'in media modulo k≤X1/2−ε'. Un teorema di questo genere venne dimostrato nel 1965 da Enrico Bombieri e Vinogradov.
Lo sviluppo del metodo elementare del crivello assieme ai teoremi analitici sulla distribuzione dei numeri primi (Bombieri, Alexander A. Buchstab, Alfred Renyi, Selberg, Van Iuan, Vinogradov) portarono Jing-Run Chen alla dimostrazione dei teoremi sulla rappresentabilità dei numeri pari come somma di un primo e del prodotto di due primi - 'problema quasi binario' di Goldbach - e sull'infinità delle coppie (p;p1p2) con la condizione p−p1p2=2 - un 'quasi' problema dei primi gemelli.
Infine, lo sviluppo del metodo del crivello (crivello asintotico, Bombieri 1976) e le stime di somme trigonometriche di tipo speciale (analoghe alle 'somme corte di Kloosterman', Karatsuba 1994) hanno consentito a Henryk Iwaniec e John B. Friedlander (1996) di dimostrare l'infinità dei numeri primi p rappresentabili nella forma p=a2+b4; essi dimostrarono inoltre la seguente formula approssimata: per x→+∞
dove γ(t) è la funzione gamma di Euler.
Un altro orientamento della teoria additiva è legato alla teoria dei numeri algebrici che si suddivide a sua volta nella teoria analitica, che considera le proprietà metriche dei numeri algebrici e in quella algebrica, che si basa sia sull'aritmetica dei numeri algebrici sia sulla geometria algebrica.
Un numero α si dice algebrico di grado n se è radice di un'equazione f(x)=axn+bxn−1+…+c=0, dove a≠0, e b,…,c sono numeri interi e il polinomio f(x) è 'irriducibile sul campo dei numeri razionali', cioè non si può rappresentare come prodotto di due polinomi di grado positivo a coefficienti razionali. Se a=1 allora α si definisce intero algebrico. I numeri non algebrici si dicono trascendenti. Già nel 1844 Joseph Liouville aveva dimostrato che se α è un numero algebrico di ordine n≥2 allora esiste una costante c=c(α)>0 tale che per ogni coppia di interi p,q>0 risulta verificata la disuguaglianza
[24] ∣α−p/q∣>cq-n.
Questa disuguaglianza mostra come i numeri algebrici 'si approssimino male' mediante i razionali e fornisce un criterio sufficiente per la trascendenza. Nasce così il problema della determinazione di una costante ϑ=ϑ(n) tale che per un numero algebrico α di ordine n la disuguaglianza ∣α−p/q∣>q−ϑ−ε con p,q>0 interi ammetta un numero finito di soluzioni se ε>0 e un numero infinito di soluzioni se ε⟨0. Nel 1909 Axel Thue dimostrò che ϑ≤(n/2)+1, e da ciò segue che se f(z)=azn+bzn−1+…+cz+d è un polinomio irriducibile nel campo dei numeri razionali, a coefficienti interi e di ordine n≥3, allora l'equazione diofantea
[25] ayn+byn-1x+…+cyxn-1+dxn=l
ammette un numero finito di soluzioni per ogni intero l≠0.
Il metodo di Thue è stato successivamente sviluppato da Siegel e altri studiosi e alla fine nel 1955 Klaus Roth dimostrò che ϑ=2.
Sono stati presi in considerazione casi particolari dell'equazione [25] di Thue, per esempio un analogo dell'equazione di Pell del tipo x3−Dy3=1; per questi casi particolari si è riusciti a determinare in modo effettivo le frontiere dell'insieme delle soluzioni (Boris N. Delone, Dimitrij Kostantinovič Faddeev). Inoltre, nel 1929 Siegel dimostrò che se f(x,y) è un polinomio irriducibile a coefficienti interi, allora l'equazione f(x,y)=0, a eccezione di due casi, ammette un numero finito di soluzioni intere.
Parallelamente ai miglioramenti della disuguaglianza di Liouville [24] si è sviluppata la teoria dei numeri trascendenti. I numeri algebrici costituiscono un insieme numerabile, dunque 'quasi tutti' i numeri sono trascendenti, tuttavia dimostrare la trascendenza di un particolare numero è spesso molto difficile.
Negli anni Trenta del XX sec. è stato risolto un problema proposto da Hilbert: il numero αβ, con α algebrico, α diverso da 0 e da 1 e β algebrico irrazionale, è trascendente. Già nel 1744 questo problema era formulato da Euler, anche se la definizione esatta di numero trascendente è stata introdotta più tardi. Casi particolari di questo problema (settimo problema di Hilbert) sono stati risolti da Aleksandr Osipovič Gel´fond e Rodion O. Kuzmin nel 1930; tali casi mostrano per esempio la trascendenza di eπ e di 2√2; la soluzione generale venne trovata nel 1934 da Gel´fond e da Thorald Schneider.
A metà degli anni Cinquanta si cominciò a studiare forme lineari dei logaritmi di numeri algebrici (Gel´fond, Linnik) e negli anni Sessanta questa direzione di studi venne coronata dal teorema di A. Baker: se α1,…,αm sono numeri algebrici, b1,…,bm numeri interi, B=max(∣b1∣,…,∣bm∣,3) e Δ=b1logα1+…+bmlogαm≠0 allora ∣Δ∣>B−c con c=c(α1,…,αm)>0 costante effettivamente calcolabile noti gli α1,…,αm.
Da simili stime A. Baker ottenne il primo rafforzamento effettivo della disuguaglianza di Liouville [24] (la costante c venne sostituita dalla grandezza effettiva λ(q) che cresce, al crescere di q, poco più lentamente di una potenza di q), nonché una serie di teoremi effettivi sulla risoluzione di equazioni diofantee. Successivamente Naum I. Feldman sostituì nella disuguaglianza di Baker λ(q) con la grandezza qδ, δ>0.
Eleganti risultati ottenuti con il metodo di Baker sono i seguenti teoremi: tutte le soluzioni intere dell'equazione y2=x3+k, k≠0 numero intero, soddisfano la disuguaglianza
mentre tutte le soluzioni 'dell'equazione di Catalan' xu−yv=1 soddisfano la disuguaglianza yv⟨xu⟨exp(exp(exp(exp(103)))).
L'applicazione dei numeri algebrici e dell'analisi p-adica ha permesso di dimostrare teoremi effettivi sulla finitezza del numero delle soluzioni di equazioni diofantee come
(Alan Baker, Vladimir Gennadievič Sprindžuk).
I teoremi di approssimazione sono stati applicati al problema del decimo discriminante (Chudakov, Harold M. Stark), anche se tale problema era stato già in precedenza risolto da Kurt Heegner (1952). Stark dimostrò anche che per il discriminante dei campi con due classi si ha la stima:
Sviluppando idee di Heegner, Benedict Gross e Don Zagier (1986) ottennero una minorazione effettiva per il numero h(−d) delle classi di forme quadratiche binarie a discriminante negativo −d: h(−d)>c(logd)1−δ, 0⟨δ qualsiasi. Con gli stessi metodi sono stati trovati tutti i d per i quali h(−d)≤3.
Con metodi algebrici e con metodi della teoria dei numeri trascendenti è stato quasi completamente risolto il problema dell'equazione F(x1,…,xm)=c, dove F è una forma riducibile a coefficienti razionali interi, ovvero un polinomio omogeneo in x1,…,xm che si fattorizza in fattori lineari in un'estensione del campo dei numeri razionali (Albert Thoralf Skolem, Wolfgang Schmidt).
Indipendentemente dalla teoria delle equazioni diofantee si sviluppava lo studio che proseguiva le ricerche di Hermite e di Lindemann sulla trascendenza o sull'indipendenza algebrica dei valori di particolari funzioni in punti algebrici o in punti prossimi a essi (Siegel, Kurt Mahler). Alla fine del XX sec. in questa direzione sono stati conseguiti notevoli risultati (Jurij V. Nesterenko, Daniel Bertrand). È stato per esempio dimostrato da Nesterenko, nel 1996 che: (1) i numeri π e eπ sono algebricamente indipendenti (se A(x,y) è un arbitrario polinomio in x e y a coefficienti interi e non identicamente nullo, allora il numero A(π,eπ) è trascendente; in particolare, il numero π+eπ è trascendente); (2) i tre numeri π, eπ, γ(1/4), ove γ è la funzione gamma di Euler, sono algebricamente indipendenti; (3) per ogni numero algebrico α, 0⟨∣α∣⟨1, i tre numeri x,y,z:
sono algebricamente indipendenti.
Il secondo indirizzo della teoria algebrica dei numeri è legato all'aritmetica dei numeri algebrici e all'approccio di Kummer all'ultimo teorema di Fermat. È stata sviluppata un'intera disciplina con molti risultati notevoli, che hanno permesso (assieme ai calcoli al computer) di dimostrare la validità del cosiddetto 'primo caso' dell'ultimo teorema di Fermat per tutti gli esponenti n≤6∙109 (l'esponente n non divide il prodotto XYZ).
Negli anni Trenta Leo Mordell congetturò che su una curva F(x,y)=0 di genere almeno 1, giace un numero finito di 'punti razionali' (punti le cui coordinate sono numeri razionali). In particolare, se n≥3 allora l'equazione di Fermat si trasforma in F(x,y)=xn+yn−1=0, e l'ultimo teorema stesso afferma che su questa curva giacciono esattamente due punti razionali, e più precisamente (0,1) e (1,0). L'ipotesi di Mordell venne dimostrata da Gerd Faltings nel 1983 con metodi di geometria algebrica, al cui sviluppo diedero un contributo notevole i lavori di Igor Rostislavovič Šafarevič, Jurij Ivanovič Manin, Aleksei N. Parshin.
All'inizio degli anni Ottanta Vadim A. Demjanenko e Gerhard Frey, studiando l'aritmetica delle curve ellittiche, cioè delle curve della forma y2=x3+ax+b, crearono un collegamento fra tali curve e l'ultimo teorema di Fermat. In quel periodo Jutaka Taniyama aveva già congetturato la modularità delle curve ellittiche 'semistabili'. Nel 1985 Frey ipotizzò che la curva ellittica corrispondente al controesempio dell'ultimo teorema di Fermat non potesse essere modulare e poco dopo Ken Ribet dimostrò che l'ultimo teorema seguiva dalla congettura di Taniyama. Infine, nel 1995 Andrew J. Wiles pubblicò un articolo in cui dimostrava l'ipotesi di Tanyiama.
In relazione ai problemi sulla risolubilità di equazioni a coefficienti interi è stato introdotto e considerevolmente sviluppato il cosiddetto 'metodo locale'.
Si dice che i numeri interi a e b sono 'congrui modulo m', con m>1 naturale, se a e b hanno lo stesso resto nella divisione per m, o, equivalentemente, se m divide a−b; la teoria delle congruenze è stata fondata da Fermat, Euler e Gauss. In analogia con le equazioni si può considerare il problema della risolubilità di congruenze. Se un'equazione ammette soluzione negli interi allora la corrispondente congruenza ammette soluzione modulo qualunque m. La proposizione inversa, in generale, non vale; per esempio, la congruenza
[27] (x2-13)(x2-17)(x2-221)≡0 (modm)
ammette soluzione modulo qualunque m, ma la corrispondente equazione non ammette evidentemente soluzioni intere. Il metodo locale è, essenzialmente, lo studio delle congruenze modulo m, e si riduce, come si capisce facilmente, allo studio di congruenze modulo una potenza di un primo.
È vero il seguente teorema di Minkowski-Hasse: sia F(x1,…,xn) una forma quadratica a coefficienti razionali; l'equazione F(x1,…,xn)=0 ammette soluzione intera non banale se e solo se ammette soluzione non banale nei reali e la corrispondente congruenza ammette soluzione non banale modulo qualunque m. Un analogo di questo teorema per forme di grado ≥3 e oltre non è generalmente valido: l'equazione 3x3+4y3+5z3=0 ammette soluzione nei reali e la congruenza corrispondente ammette soluzione modulo qualunque m≥0, tuttavia quest'equazione non ammette soluzioni intere non banali.
Si può osservare che lo studio dell'integrale lungo grandi archi di circonferenza nel metodo del cerchio altro non è che lo studio della risolubilità locale dell'equazione corrispondente. In una serie di casi tale equazione è relativamente semplice e la sua influenza sul risultato finale è evidente (per es., nel problema di Goldbach). In altri casi, come per esempio nel problema di Waring e nelle sue generalizzazioni, la risolubilità locale incide considerevolmente sul risultato finale. Per esempio nel problema di Hilbert-Kamke sulla rappresentabilità del vettore intero (N1,…,Nn) come somma di vettori del tipo (x,…,xn) con x intero, la risolubilità locale richiede un numero di addendi dell'ordine di 2n, mentre quella nei reali solo cn2logn (Gennadii Ivanovich Arkhipov).
In relazione alla risolubilità locale di equazioni Emil Artin costruì la teoria delle 'congruenze delle funzioni zeta' e ipotizzò che per queste funzioni fosse valida un'ipotesi analoga a quella di Riemann. Helmut Hasse nel 1934 dimostrò un caso particolare dell'ipotesi di Artin, e André Weil nel 1948 ne diede una dimostrazione completa. Questo ha permesso di risolvere completamente il problema del numero delle soluzioni della congruenza F(x,y)=0 (mod m), essendo F(x,y) un polinomio a coefficienti interi, nonché di determinare una stima di particolari somme trigonometriche. Le stime di Weil hanno trovato molteplici applicazioni negli studi che riguardano le distribuzioni dei valori dei caratteri additivi e moltiplicativi. La teoria pluridimensionale, simile alla teoria di Artin-Hasse-Weil, è stata sviluppata da Bernhard Dvork e Pierre Deligne.
Un gran numero di risultati particolari della teoria delle equazioni diofantee può essere spiegato con il teorema di Yuri Matyasevich (1970): non esiste un algoritmo che permetta, data un'equazione diofantea, di affermare se essa ammetta o meno soluzioni intere (questo teorema è la soluzione al decimo problema di Hilbert).
I metodi elementari della teoria delle congruenze hanno trovato numerose applicazioni in crittografia. Se p è un numero primo e g una radice primitiva modulo p allora per ogni numero naturale n, non multiplo di p, esiste un numero γ, 0≤γ⟨p−1, tale che gγ e n danno lo stesso resto nella divisione per p, cioè n≡gγ(mod p). Il numero γ si dice indice del numero n modulo p (con base g). L'indice è quindi un analogo 'discreto' del logaritmo. Il calcolo degli indici per p grandi è un'operazione molto complessa, e su questa complessità si fondano molti metodi di codifica 'sicura'. Proprio alla crittografia deve la sua comparsa la teoria 'computazionale' dei numeri che studia il 'riconoscimento' della primalità di numeri 'grandi', cioè la fattorizzazione di quelli composti.
Negli ultimi decenni è stata ottenuta una serie di risultati teorici con l'ausilio di calcoli al computer. In particolare Andrew Odlyzko e Herman J.J. te Riele confutarono la vecchia ipotesi di Franz Mertens (da cui segue facilmente l'ipotesi di Riemann) secondo la quale il modulo della somma dei valori della funzione di Möbius μ(n) non supera la radice quadrata del numero degli addendi (μ(n)=1 se n=1, μ(n)=0 se n è un multiplo del quadrato di un numero primo, μ(n)=(−1)ν se n è uguale al prodotto di ν numeri primi distinti), mentre Noam D. Elkies confutò l'ipotesi di Euler sulla non risolubilità nei numeri naturali dell'equazione:
[28] xn1+xn2+…+xnn-1=xnn, n≥4;
per n=4 l'equazione ammette la soluzione x1=95800, x2=217519, x3=414560, x4=422481; per n=5 l'equazione ammette la soluzione x1=27, x2=84, x3=110, x4=133, x5=144.
Alcuni problemi classici della teoria dei numeri, come il problema dell'esistenza di numeri dispari 'perfetti' (un numero si definisce perfetto se è somma di tutti i suoi divisori propri, per es., 6=1+2+3), il problema dell'infinità dei numeri primi di Fermat, di Mersenne e di Gauss (numeri primi della forma, rispettivamente, 22n+1, 2p+1, p primo, n2+1) e altri sono ancora 'irrisolti'.
Il XX sec. ha trasformato molto la teoria dei numeri, conservando tuttavia il suo orientamento aritmetico che mira allo studio dei legami interni fra numeri interi.
Al secolo successivo rimangono problemi profondi, sollevati dal precedente progresso scientifico.
Bibliografia
Arkhipov 1987: Arkhipov, Gennadii Ivanovich - Karatsuba, Anatolij Alekseevič - Čubarikov, Vladimir Nikolaevič, Teorija kratnych trigonometričeskich summ [Teoria delle somme trigonometriche multiple], Moskvà, Nauka, 1987.
Borevič, Safarevič 1985: Borevič, Zenon Ivanovič - Safarevič, Igor Rostislavovič, Teorija čisel [Teoria dei numeri], 3. ed., Moskvà, Nauka, 1985 (1. ed.: 1964; trad. ingl.: Number theory, New York, Academic Press, 1966).
Chandrasekharan 1970: Chandrasekharan, Komaravolu, Arithmetical functions, Berlin-Heidelberg-New York, Springer, 1970.
Davenport 1967: Davenport, Harold, Multiplicative number theory, Chicago, Markham, 1967.
Friedlander 1996: Friedlander, John B., Topics in analytic number theory, "Lecture note in pure and applied mathematics", 204, 1996, pp. 47-64.
Gauss 1801: Gauss, Carl Friedrich, Disquisitiones arithmeticae, Leipzig, Fleischer, 1801.
Gel´fond 1973: Gel´fond, Aleksandr Osipovič, Izbrannye trudy [Opere scelte], Moskvà, Nauka, 1973.
Hooley 1976: Hooley, Christopher, Applications of sieve methods to the theory of numbers, Cambridge-London, Cambridge University Press, 1976.
Karatsuba, Voronin 1992: Karatsuba, Anatolij Alekseevič - Voronin, Sergej Michailovič, The Riemann Zeta-function, Berlin-New York, de Gruyter, 1992.
Karatsuba 1993: Karatsuba, Anatolij Alekseevič, Basic analytic number theory, Berlin-Heidelberg-New York, Springer, 1993.
Karatsuba 1995a: Karatsuba, Anatolij Alekseevič, Complex analysis in number theory, Boca Raton-Ann Arbor-London-Tokyo, CRC Press, 1995.
Karatsuba 1995b: Karatsuba, Anatolij Alekseevič, Složnost' vyčislennj [Complessità dei calcoli], "Trudy MIAN", 211, 1995, pp. 186-202.
Landau 1927: Landau, Edmund, Vorlesungen über Zahlentheorie, Leipzig, Hirzel, 1927, 3 v.
Lidl, Niederreiter 1983: Lidl, Rudolf - Niederreiter, Harald, Finite fields, Reading (Mass.)-London, Addison-Wesley, 1983.
Manin, Pančiškin 1990: Manin, Jurij Ivanovič - Pančiškin, Aleksej A., Teorija čisel [Teoria dei numeri], "Itogi nauki i tekhniki. Serija: Sovremennye problemy matematiki", Moskvà, VINITI, 49, 1990.
Nečaev 1999: Nečaev, Valerij Jakovlevič, Elementy kriptografii [Elementi di crittografia], Moskvà, Vysšaja škola, 1999.
Prachar 1957: Prachar, Karl, Primzahlverteilung, Berlin-Göttingen-Heidelberg, Springer, 1957.
Prasolov, Solovëv 1997: Prasolov, Viktor Vasil´evič - Solovëv, Jurij Pavlovič, Elliptičeskie funkcii i algebraičeskie uravnenija [Funzioni ellittiche e equazioni algebriche], Moskvà, Faktorial, 1997.
Sprindžuk 1982: Sprindžuk, Vladimir Gennadievič, Klassičeskie diofantovy uravnenija ot dvuch neizvestnych [Equazioni diofantee classiche in due incognite], Moskvà, Nauka, 1982.
Titchmarsh 1986: Titchmarsh, Edward Charles, The theory of the Riemann Zeta-function, 2. ed., Oxford, Clarendon Press, 1986 (1. ed.: 1951).
Vinogradov 1985: Vinogradov, Ivan Matveevič, Selected works, Berlin-New York-Heidelberg, Springer, 1985.
Wiles 1995: Wiles, Andrew John, Modular elliptic curves and Fermat's last theorem, "Annals of Mathematics", 145, 1995, pp. 443-551.