La scienza bizantina e latina: la nascita di una scienza europea. Ottica, scienza dei pesi e cinematica
La scienza bizantina e latina: la nascita di una scienza europea. Ottica, scienza dei pesi e cinematica
Ottica, scienza dei pesi e cinematica
'Perspectiva': la scienza della luce, del colore e della visione
di Katherine Tachau
La scienza che gli Europei medievali chiamarono perspectiva ‒ dal verbo latino perspicere, 'osservare attentamente', e che oggi potremmo rendere col termine 'percettività' da intendere come 'scienza della percezione' (qui 'della luce e del colore' e, nell'insieme, 'scienza della visione') ‒ si formò come una disciplina ben definita, oggetto di veri e propri trattati e di lezioni nelle università nel corso del XIII sec.; dalla fine di questo secolo, infatti, agli studiosi apparve chiaro che la sua sfera d'azione nel suo insieme abbracciava, come un tutt'uno, parti della filosofia naturale e dell'epistemologia. Lo studio scientifico della luce e della visione non riguardava soltanto la fisica e la matematica della luce, del colore e della visione; se il suo punto di partenza ‒ parlando in senso stretto ‒ era l'irraggiamento da parte del Sole e delle stelle, insieme al suo effetto su tutti gli esseri viventi, la perspectiva doveva comprendere anche l'anatomia e la fisiologia dell'apparato visivo umano e del cervello, includendo la descrizione delle facoltà psicologiche e dei processi conoscitivi influenzati dalla luce e attuati o resi possibili dalla visione.
Questo insieme di questioni aveva radici che si estendevano fino all'Antichità greca, e che erano state trapiantate dapprima nel mondo islamico e poi nella Francia e nell'Inghilterra medievali. Da quando gli antichi filosofi greci cominciarono a tentare di capire come riusciamo a 'percepire' il mondo che ci circonda e come possiamo stabilire se ciò che percepiamo sia il mondo quale esso è 'realmente' oppure no, una sorta di 'contatto' tra gli oggetti nel mondo e i nostri organi corporei fu presto riconosciuto come essenziale, ma la vista fu trattata come il senso paradigmatico. A differenza del gustare o del toccare, il 'vedere' appare alla persona che 'vede' come un atto che non richiede alcun contatto con l'oggetto osservato; anzi, se vogliamo vedere un oggetto bisogna che esso non tocchi il nostro occhio. Così, il problema principale che ogni tentativo di spiegazione della visione deve risolvere in via preliminare riguarda il modo nel quale si realizza un contatto 'invisibile' tra un oggetto e gli organi della vista (ossia gli occhi e i nervi ottici).
Gli studiosi dell'Antichità hanno proposto parecchie soluzioni per questo problema, e tutte presupponevano o che l'occhio emettesse qualcosa verso l'oggetto osservato ‒ la cosiddetta 'estromissione' ‒ oppure che l'occhio ricevesse qualcosa dall'oggetto ‒ cosiddetta 'intromissione'. I platonici e gli stoici elaborarono teorie del primo tipo, mentre gli atomisti, gli epicurei e Aristotele ne proposero del secondo tipo, in particolare Aristotele, sostenendo che il ruolo del mezzo intermediario fosse quello di trasmettere le immagini visive ‒ o 'potere visivo' ‒ tra l'oggetto e l'osservatore (v. La scienza greco-romana, cap. XXVI). All'inizio del III sec. d.C., grazie a Galeno queste trattazioni filosofiche del modo di operare della luce nella visione entrarono a far parte dell'anatomia e della fisiologia del cervello, dei nervi ottici e degli occhi; le concezioni galeniche furono adottate, via via, da Plotino e dai primi neoplatonici (specialmente Nemesio), i quali tendevano a essere sincretisti, impegnati com'erano ad armonizzare il pensiero di Aristotele con quello di Platone, e a far proprie le opinioni di altre scuole filosofiche che fossero compatibili con le loro (Lindberg 1976, 1986).
Con l'eccezione delle teorie neoplatoniche della metafisica della luce e dei suoi ruoli epistemologici, nella cristianità latina dal VI al XIII sec. i risultati greci sull'ottica erano disponibili soltanto in frammenti. Le vedute di Plotino erano note soltanto indirettamente, in quanto trasmesse e ampliate da vari autori cristiani, specialmente lo Pseudo-Dionigi e Agostino di Ippona. Per quest'ultimo, la caratteristica fondamentale della visione che doveva essere spiegata era 'lo sforzo attivo' ‒ come dire l''iniziativa' ‒ dell'osservatore, il quale decide di fissare la sua attenzione su determinati oggetti o campi visivi, e non su altri; si tratta di un ruolo attivo realizzato in parte mediante i raggi 'estromessi', nozione che Agostino accettò da Plotino e da fonti stoiche. Oltre a ciò, Agostino, in accordo con loro, ammetteva che l'osservatore fosse anche un 'ricettore', non soltanto della luce esterna che era necessaria perché si avesse la visione, ma anche di un'immagine (species) dell'oggetto osservato che la memoria dell'osservatore potesse ricevere e conservare. Agostino era tuttavia interessato, come lo stesso Platone, alla visione 'corporea' degli oggetti fisici per mezzo dei raggi visivi che illuminano attraverso gli occhi e toccano tutto ciò che vediamo, principalmente come un modello per comprendere, in quale modo, lo sguardo della mente (acies mentis) potesse rivolgersi tutt'intorno e acquisire una conoscenza intellettuale o una comprensione spirituale di oggetti intelligibili ‒ compreso Dio, come Agostino sottolineava. Quando i teologi del XIII sec. volsero la loro attenzione agli studi matematici e scientifici della luce e della visione trovarono incoraggiamenti per la loro opera in frequenti allusioni di Agostino alle implicazioni spirituali della visione nel suo duplice aspetto sensoriale e intellettuale.
Entro il IX sec. gli studiosi nel mondo islamico acquisirono un più diretto accesso agli insegnamenti di Plotino e di Proclo, nonché di Galeno, attraverso le traduzioni in lingua araba delle loro opere (v. cap. XII). L''emanazionismo' neoplatonico si diffuse quindi ampiamente tra gli studiosi arabi, i quali a esso rimasero saldamente legati sino a che anche l'intero corpus delle opere di Aristotele divenne accessibile in arabo. Il medico e filosofo al-Kindī (m. 870 ca.) conosceva bene un gran numero di antichi studi greci appena tradotti in lingua araba ai suoi tempi; egli fu probabilmente il primo scrittore arabo ad apprezzare e a integrare il complesso delle trattazioni greche ed ellenistiche riguardanti da un lato la luce e la visione, e dall'altro lato la scienza delle stelle. Per al-Kindī coloro che si occupavano delle stelle e quelli che si occupavano della visione studiavano in realtà lo stesso fenomeno fondamentale, ossia il vero irraggiamento della potenza stessa, intesa anche come luce (v. cap. VII).
Almeno due delle opere di al-Kindī divennero disponibili in latino nel XIII sec. a Oxford e a Parigi, ossia il Liber de causis diversitatum aspectus, noto anche come De aspectibus, e il trattato De radiis stellarum, conosciuto anche come Theorica artis magicarum. Dopo al-Kindī numerosi altri savants nel mondo islamico incrementarono la crescente letteratura sulla luce e sulla visione; particolarmente influenti furono tre medici, Ibn Sīnā (Avicenna, 980-1037), Ibn Rušd (Averroè, 1126-1198) e Ibn al-Hayṯam (Alhazen, 965 ca.-1039 ca.), i quali trattarono il fenomeno della visione e i suoi aspetti psicologici ‒ in particolare, Alhazen scrisse il più importante trattato arabo di ottica conosciuto nell'Occidente latino, Kitāb al-manāẓir, tradotto in latino con il titolo De aspectibus (omonimo di un trattato di al-Kindī). Tutti e tre appartennero al gruppo di studiosi di medicina che propose i ventricoli cerebrali come sede dei vari sensi interni, ma ciascuno trovò una via differente per accordare l'anatomia di Galeno con altri risultati aristotelici e neoplatonici (Wolfson 1935; Lindberg 1976; Smith 1981; Tachau 1988).
Luce e visione nell'Occidente latino del XIII secolo
Sin dall'inizio del XIII sec., come si è detto, testi scientifici arabi furono tradotti in latino; nei loro primi lettori delle nascenti università europee questi trattati rafforzarono e incrementarono la ben consolidata visione neoplatonica del mondo, che già aveva assimilato aspetti del pensiero aristotelico. Tra i primi studiosi che tentarono una sintesi delle idee di questi nuovi autori con quelle ereditate dalla patristica neoplatonica troviamo l'inglese Roberto Grossatesta (1175-1253), vescovo di Lincoln, sul quale recentemente sono stati messi in evidenza nuovi fatti che hanno portato a modificarne profondamente il curriculum vitae. Prima di raggiungere l'Università di Oxford, alla quale il suo nome è indissolubilmente legato, Grossatesta visse per vari anni a Hereford, in un ambiente intellettuale all'avanguardia nel sapere scientifico e filosofico, dove poté facilmente accedere alle opere di fonte araba appena tradotte; già in possesso di alcune conoscenze di medicina, egli dedicò un certo tempo a studi di teologia, probabilmente a Parigi intorno al 1220 (Schulman 1997; Goering 1995). Sempre interessato a nuove idee e scoperte, e alla loro introduzione nel sapere cristiano, Grossatesta fu tra i primi studiosi latini a mettere insieme un'ampia lettura della letteratura patristica (comprendente lo Pseudo-Dionigi, la cui opera egli ritradusse dal greco in latino) con quella dei testi di Aristotele (traducendo anche l'Ethica Nicomachea) e quasi l'intero corpus di opere già da tempo tradotte dall'arabo. Egli fu così tra i primi autori medievali cristiani a mostrare un vero apprezzamento per i trattati De anima di Avicenna e di Averroè, e a continuare le linee di ricerca aperte da Albumasar (Abū Ma῾šar) e da al-Kindī.
Grossatesta conosceva il De speculis di Euclide (una traduzione della Catottrica), probabilmente anche il De visu dello stesso autore e il De aspectibus di al-Kindī, ma non l'Ottica di Tolomeo o il De aspectibus di Alhazen. Le sue letture lo portarono, in un piccolo trattato intitolato De lineis, angulis et figuris seu de fractionibus et reflexionibus radiorum, a proporre di applicare la geometria a questioni riguardanti la Natura: "l'utilità di considerare linee, angoli e figure è molto grande, dal momento che è impossibile capire la filosofia naturale senza di essi. [...] tutte le cause degli effetti naturali si devono esprimere per mezzo di linee, angoli e figure, poiché altrimenti è impossibile giungere alla loro spiegazione" (Roberto Grossatesta, De lineis, angulis et figuris, ed. Baur, pp. 59-60). Questa affermazione riconduce ad al-Kindī, la cui dottrina dell'irraggiamento universale della forza Grossatesta fece propria e propugnò come la "moltiplicazione delle specie". Ogni oggetto ‒ egli affermava ‒ per sua natura agisce sul suo ambiente mediante l'emanazione in tutte le direzioni di suoi simili o di sue specie. Nel preferire il termine 'specie' per ciò che era chiamato anche 'potenza' o 'forza' (vis o virtus) Grossatesta e i suoi seguaci sostenevano la nozione di "ciò che è visibile". Come la terminologia stessa suggerisce, l'irraggiamento della luce è il caso paradigmatico, non soltanto perché ‒ trattandosi di radiazione 'visibile' ‒ mostra il modo in cui si manifesta anche la radiazione che non si può vedere, ma ‒ cosa più importante, sostiene Grossatesta ‒ perché la diffusione della luce da un punto-origine per il tramite di questo moltiplicarsi ha generato l'intero Universo di sfere concentriche. Le origini plotiniane di questa tesi sono indiscutibili, anche se qualche volta trascurate a causa dei frequenti riferimenti di Grossatesta ad Aristotele allo scopo di avanzare argomenti specifici a sostegno di essa (McEvoy 1982; Lindberg 1986).
Secondo Grossatesta, ciò che percepiamo con gli occhi quando abbiamo davanti un oggetto è luce e un insieme di colori ‒ questi ultimi sono la luce da cui si originò l'Universo incorporatasi (nel significato letterale del termine) in corpi materiali trasparenti. Questi colori sulla superficie dell'oggetto sono i suoi aspetti o la sua 'forma visibile', come dire la sua 'specie' visibile, e quando sono soffusi dai raggi di luce generano a loro volta altri raggi, moltiplicandosi rettilineamente in tutte le direzioni. La visione richiede che questo irraggiamento dall'oggetto della sua 'specie visibile' interagisca con uno 'spirito visivo' che emana dall'occhio ed è costituito ‒ dice Grossatesta ‒ "dalla stessa natura della luce del Sole" (De iride, ed. Baur, pp. 72-73; Commentarius in Posteriorum analyticorum libros, ed. Rossi, p. 386). Quando l'occhio ha ricevuto come risultato questa 'specie', l'atto della visione è completo, ma l'opera dei sensi interni ‒ tramite i quali capiamo ciò che vediamo ‒ deve ancora cominciare. Grossatesta cita quattro di questi sensi, collocandoli nelle tre cavità, o 'celle', del cervello; una nozione, questa, derivata da Nemesio per il tramite di Avicenna. Nella prima di queste celle del cervello le forme di un oggetto, che sono state ricevute dai differenti sensi esterni, sono riunite dal senso comune e sono conservate dall'immaginazione. Nella cella di mezzo risiede il senso interno della estimativa, definito ‒ seguendo Avicenna ‒ come il potere che, per esempio, rende capace l'agnello di rendersi conto del pericolo che per lui rappresenta un lupo; le basi per il giudizio dell'agnello non sono le forme visive ma le intenzioni, e il cervello registra queste intenzioni nella memoria, che si trova nella terza cella, la più interna (Commentarius in Posteriorum analyticorum libros).
Grossatesta concordava anche con l'opinione neoplatonica secondo la quale la mente umana subisce le esperienze interne dell'intelletto riguardanti gli oggetti intelligibili ‒ quali oggetti matematici, forme, universali e verità ‒ per il tramite di processi che sono costitutivamente simili a quelli mediante i quali la visione corporea rende manifesti gli oggetti visibili. Rifacendosi ad Agostino (a volte senza menzionarlo) egli afferma nel suo importante commento agli Analytica posteriora di Aristotele:
Io dico che c'è una luce spirituale (lux spiritualis) che si diffonde sugli oggetti intelligibili (res intelligibiles) e sull'occhio della mente (oculus mentis), [una luce] che è in relazione con l'occhio 'interiore' e con gli oggetti intelligibili così come il Sole 'corporeo' si riferisce all'occhio 'corporeo' e agli oggetti 'corporei'. Perciò gli oggetti intelligibili che sono più capaci di ricevere questa luce 'spirituale' sono più visibili all'occhio 'interiore' […]. E così le cose che ricevono meglio questa luce sono meglio penetrate dallo sguardo della mente (acies mentis), che è come un'illuminazione spirituale, e questa più perfetta penetrazione si traduce in una maggiore certezza. (ibidem, pp. 240-241)
La diffusione delle teorie di Grossatesta fu agevolata dal suo ruolo di insegnante presso i francescani e di vescovo di Lincoln, incarichi che gli consentirono di diffondere le proprie idee e di riunire il sapere greco-arabo di recente acquisizione con la saggezza degli autori della patristica; a Parigi, inoltre, il suo amico ‒ e primo sostenitore di quest'apertura al pensiero greco-arabo (e della psicologia di Avicenna) ‒ Guglielmo di Alvernia divenne vescovo, riuscendo così a diffondere con maggiore facilità questa sintesi. Alla loro morte ‒ avvenuta per Guglielmo di Alvernia nel 1249, per Grossatesta nel 1253 ‒ Alberto Magno (1193 ca.-1280) e l'inglese Ruggero Bacone (1214 ca.-1294) erano già attivi e studiavano le fonti recentemente accessibili in latino sulla luce e la visione. Costoro furono i primi nella cristianità latina a fornire un'esauriente analisi e un'interpretazione della filosofia di Aristotele, che da allora divenne disponibile in latino quasi per intero.
Alberto, membro dell'ordine domenicano attivo nell'organizzazione dell'insegnamento sia a Colonia sia a Parigi, fu una figura chiave della cultura del XIII sec.; famoso per avere interpretato Aristotele, egli fu ammirato nel Tardo Medioevo anche per i suoi commenti sulle opere dello Pseudo-Dionigi, composti intorno al 1248-1252. La compilazione dei suoi commenti sull'intero corpus delle opere attribuite ad Aristotele lo obbligò, naturalmente, a commentare le teorie di Aristotele sulla luce e sul colore. Il suo studio sulla psicologia aristotelica fu influenzato in modo determinante dalla lettura di Avicenna, del quale condivise generalmente la classificazione per i cinque sensi interni e al cui Canone attinse ampiamente. Alberto lesse inoltre gli scritti sull'ottica di Euclide, di al-Kindī e di Alhazen e acquistò quanto meno una certa familiarità con essi.
Nessun autore, tuttavia, fu più importante di Ruggero Bacone per lo sviluppo della scienza latina della perspectiva. La sua convinzione che lo studio della luce fosse fondamentale per la comprensione di 'tutta' la filosofia naturale ‒ includendo la percezione umana dell'Universo ‒ era chiaramente dovuta alla sua familiarità con il De radiis stellarum di al-Kindī e con le opere di Grossatesta, la cui dottrina e il cui vocabolario della 'moltiplicazione delle specie' Bacone adottò apertamente. Nonostante si fosse in parte formato a Oxford, in realtà Bacone non studiò sotto la guida di Grossatesta, ma ebbe accesso alla sua biblioteca più tardi, tramite il convento francescano di Oxford, e ne fu chiaramente influenzato. Verso la metà del 1230 si recò a Parigi, dove ‒ come ebbe a dire in seguito ‒ fu tra i primi a introdurre nel suo insegnamento tutte le opere di Aristotele dopo la loro 'riscoperta' successiva all'annullamento delle proibizioni dalle quali erano state colpite.
Bacone discusse sommariamente questioni relative alla luce e alla visione in commenti composti per le lezioni su Aristotele, ma i suoi lavori specifici su questi argomenti comparvero all'incirca a partire dal 1267, dopo essere stato maestro all'università ‒ e lo fu per circa trent'anni ‒ e membro della locale comunità francescana di Parigi per oltre dieci anni. In una serie di trattati che egli scrisse a Parigi da allora sino quasi al termine della sua vita ‒ in particolare Opus minus, Opus maius, Opus tertium, De speculis comburentibus, Communia mathematica, Communia naturalia, Compendium studii theologiae ‒ Bacone elaborò proposte per la riforma di tutta l'istruzione universitaria cristiana, dando la precedenza proprio allo studio scientifico della luce e dei suoi effetti. Queste opere ‒ come il De multiplicatione specierum che delinea la propagazione universale delle 'forze' ‒ lo mostrano come il primo studioso europeo che si sia reso padrone dell'intero corpus delle opere tradotte in latino che avevano per oggetto la luce e la visione; tra queste ve ne erano alcune che non erano state accessibili a Grossatesta, quali i lavori sull'ottica di Tolomeo e di Alhazen.
Bacone pensava che pochi studiosi suoi contemporanei si rifacessero alle autorevoli fonti antiche e arabe sino ad allora disponibili in latino, e uno degli scopi di queste sue ultime opere fu di mostrare che cosa si poteva ottenere da una sintesi degli insegnamenti contenuti in quelle importanti opere. Egli sosteneva che tutti gli autori di esse ‒ Platone, Aristotele, Euclide, Tolomeo, Galeno, Agostino, Ḥunayn ibn Isḥāq, al-Kindī, Avicenna, Alhazen, Averroè ‒ possedessero una parte della verità. Peraltro, non era facile sintetizzare fonti così differenti tra loro: per lui la soluzione consisteva talvolta nel passare sopra alle differenze. Per esempio, si trattava di mettere a confronto parecchie vedute alternative sulla natura della luce, quali la nozione del 'fuoco visivo' di Platone, la teoria di Aristotele sulla trasformazione qualitativa del mezzo, quella di al-Kindī sulla propagazione universale delle forze, e quelle basate sulle 'forme' di Alhazen o sulle 'specie' di Grossatesta. Riguardo a queste ultime, Bacone assegnò alle 'specie' di Grossatesta tutte le proprietà e le funzioni delle 'forme' di Alhazen, sostenendo che questa fosse l'intenzione di Aristotele, e ribadì il fatto che esse si diffondevano in tutte le direzioni a partire da ciascun punto di ogni oggetto visibile, così come aveva affermato al-Kindī.
Ruggero Bacone si rendeva conto però che la filologia ‒ indipendentemente dalla sua importanza per interpretare la 'sapienza' acquisita dal passato ‒ era di per sé assolutamente insufficiente come base della scienza. Così, i suoi trattati del periodo 1260-1290 proponevano anche una metodologia propriamente scientifica, già suggerita da Grossatesta, che univa la convinzione neoplatonica ‒ secondo la quale l'Universo, essendo strutturato in forme geometriche, poteva essere interpretato per via matematica ‒ con una concezione, più aristotelica, secondo la quale ogni spiegazione scientifica doveva anche essere basata (o provata) empiricamente su quello che i sensi percepiscono. In tal modo Bacone ‒ ben più di Grossatesta ‒ sosteneva l'applicazione del metodo matematico quale "porta e chiave" per accedere a tutte le discipline scientifiche, affermando che "nessun'altra scienza può essere capita senza questa scienza [la matematica] e [...] nessuno può rendersi conto della sua ignoranza in altre scienze se non è ben informato su di essa. Né le cose di questo mondo possono essere conosciute, né l'uomo può comprendere gli usi del corpo e delle cose se non è imbevuto dei profondi lavori di questa scienza" (Opus maius, IV, 1, ed. Bridges, p. 97).
L'autorevolezza di quella che egli chiamò 'scienza sperimentale' (scientia experimentalis) fu sostenuta da Bacone in modo altrettanto caloroso: tra le molte affermazioni in proposito vi erano argomenti sulla sua importanza epistemologica, come una sorta di maestra alla quale le altre scienze, le sue ancelle, le dovevano obbedienza. Queste enfatiche affermazioni hanno costretto gli storici a un considerevole sforzo per capire esattamente quali aspettative fossero conseguenze delle affermazioni di Grossatesta e quali no. Basti qui sottolineare che il punto di vista di Bacone è che, in linea di principio, sia possibile con l'aiuto dell'illuminazione divina sviluppare una completa spiegazione matematica della luce e della visione, capace di tenere conto dell'esperienza sensibile (acquisita direttamente, o indirettamente tramite i testi). Pur non essendo mai riuscito a raggiungere questo obiettivo, egli andò ben oltre Grossatesta lungo questa strada, e l'ampiezza del suo programma matematico appare a prima vista da un semplice esame della Perspectiva (che contiene 51 diagrammi geometrici) o del De multiplicatione specierum (che ne contiene 39).
Bacone raggiunse una completa padronanza matematica dei fenomeni della riflessione e della formazione delle immagini con specchi sia piani sia convessi o concavi; egli conosceva, naturalmente, la legge dell'uguaglianza degli angoli nella riflessione e, giustamente, collocava le immagini degli oggetti visti per riflessione là dove il prolungamento rettilineo all'indietro del raggio riflesso che entrava nell'occhio intersecava la perpendicolare condotta dall'oggetto visibile alla superficie riflettente. Prese in considerazione con successo le questioni relative all'ingrandimento e alla riduzione, rispetto all'oggetto, delle immagini fornite dalla riflessione, nonché al capovolgimento alto-basso e al ribaltamento destra-sinistra di esse; inoltre, i concetti di 'punto focale' e di 'piano focale' sono impliciti nella sua analisi del funzionamento degli specchi sferici convessi.
Più insolito fu il tentativo di Bacone di introdurre considerazioni geometriche in questioni riguardanti l'anatomia dell'occhio e l'irraggiamento della luce al cervello tramite gli occhi e i nervi ottici. Egli argomenta che le membrane e gli umori dell'occhio (cornea, cristallino, umore acqueo, umore vitreo, retina e così via) sono tutti limitati e racchiusi da superfici sferiche i cui centri si trovano su una linea retta che va dal centro della pupilla all'apertura del nervo ottico. Seguendo Alhazen, Bacone sostiene che i raggi responsabili della visione sono principalmente quelli che cadono perpendicolarmente sull'occhio e penetrano in esso senza rifrangersi; l'insieme di questi raggi di 'specie visibili' moltiplicantesi dall'oggetto forma un cono (o una piramide) che ha la base sull'oggetto osservato e converge verso un apice (che peraltro non è mai raggiunto) situato nell'occhio dell'osservatore. I raggi costituenti questo 'cono visivo' attraversano, senza rifrangersi, la cornea e la superficie anteriore del cristallino (che è concentrica con la superficie della cornea, per cui un raggio che sia perpendicolare a una di esse è necessariamente perpendicolare anche all'altra); sulla superficie posteriore del cristallino i raggi sono rifratti in modo da essere proiettati verso l'apertura del nervo ottico, che li porta al punto di congiunzione con il nervo ottico dell'altro occhio (punto che noi chiamiamo 'chiasma ottico'). In esso la visione si attua nel ricongiungimento delle 'specie' raccolte dai due occhi in una sola immagine visiva coerente, e quest'ultima continua a moltiplicarsi nelle tre camere del cervello che ospitano i cinque sensi interni del De anima di Avicenna (Smith 1981).
In questo modo di trattare l'incidenza della luce sull'occhio, Bacone fu d'accordo con Aristotele, Avicenna e Alhazen nel sostenere che le specie intromesse sono necessarie per la visione e costituiscono la principale causa di essa; i sensi (come Aristotele aveva sostenuto in un passo citato da Bacone) partecipano inizialmente in maniera passiva, mentre la parte attiva è la specie dell'oggetto osservato. Tuttavia, convinto che i nostri sensi siano non soltanto passivi ma anche attivi, Bacone non volle trascurare le teorie di coloro che sostenevano il ruolo dell'estromissione, le quali potevano essere corroborate da argomenti persuasivi e da un'ampia evidenza basata sull'esperienza, quale, per esempio, la presunta capacità che hanno i gatti di vedere al buio.
Alhazen, Avicenna e Averroè, secondo Bacone, avevano provato la necessità, e perciò l'esistenza, dei raggi intromessi senza mai avere dimostrato l'inesistenza di quelli estromessi. Questo gli consentì di affermare che i raggi intromessi sono la causa immediata della visione, riconoscendo nel contempo che esistono anche i raggi estromessi; questi ultimi devono esistere se è vera la sua tesi fondamentale che "ogni oggetto naturale", quale è lo stesso occhio, "completa la sua azione soltanto [moltiplicando] il suo potere, o le 'specie'" (Perspectiva, ed. Lindberg, p. 104). Rifacendosi a Galeno, Bacone sostiene che i nervi ottici sono tubi vuoti che si dipartono dal cervello e che possono incanalare il flusso bidirezionale prodotto dall'accettare raggi sia estromessi sia intromessi; lungo questi nervi scorrono non soltanto lo spirito visivo, con il suo potere sensoriale che va dal cervello agli occhi, ma anche le specie degli oggetti visti, che giungono al cervello. Come minimo, le specie estromesse dall'occhio consentono allo stesso di vedersi in uno specchio; esplicano la funzione ausiliaria di 'nobilitare' il mezzo e le specie visibili incidenti, rendendo queste ultime capaci di "completare la loro azione" su un corpo vivente, qual è l'occhio.
Di importanza cruciale per Bacone, l'estromissione si rivelò fondamentale per sostenere che, in un Universo nel quale tutti gli oggetti moltiplicano le loro 'specie', non soltanto "le cose celesti influenzano quelle terrestri" ma, anche, le creature sulla Terra "agiscono reciprocamente sui cieli", e non soltanto per quanto riguarda la visione (De multiplicatione specierum, ed. Lindberg, pp. 72-75).
Colori e apparenze
Gli aspetti della teoria di Bacone riguardanti l'intromissione costituirono le basi per ciò che i filosofi di oggi chiamerebbero una 'epistemologia realistica', secondo la quale possiamo sapere com'è realmente il mondo in quanto le 'specie visibili' moltiplicantisi degli oggetti non sono prodotte dall'operato della mente umana, ed esisterebbero anche se non ci fossero esseri umani a recepirle. Tuttavia, si potrebbe costruire la base per un'epistemologia di carattere contrario, scettica sulla somiglianza fra ciò che percepiamo con la visione e il mondo effettivo al di fuori della nostra mente, a partire dalla difesa che Bacone fa dell'estromissione e dal suo insistere sull'idea che le facoltà di percezione e di valutazione della mente ‒ in particolare il senso della visione, il senso comune e il senso estimativo ‒ sono anche parte attiva nel fare sì che il mondo ci appaia come ci appare.
Sia le letture fatte sia l'esperienza acquisita avevano persuaso Bacone che alcuni fenomeni ottici, come le immagini virtuali, gli spettri cangianti e le differenti dimensioni apparenti della Luna quando è prossima all'orizzonte e quando invece è alta nel cielo, non siano completamente indipendenti dall'osservatore, e sembrino possedere un tipo di realtà debole rispetto a quello che generalmente consideriamo reale. Per esempio, quando la luce passa attraverso una finestra con un vetro colorato ‒ chiede Bacone ‒ il fascio di raggi colorati che ne risulta sulla parete opposta è 'realmente' colorato? Osservando che "se un debole raggio di luce solare passa attraverso una finestra non appaiono colori", Bacone deduce che "c'è, quindi, un'apparenza più che una esistenza di tali colori". Questa 'apparenza' ‒ prosegue Bacone ‒ è proprio la 'specie' moltiplicata dei colori della finestra e, anche se esiste in misura assai piccola, tuttavia esiste. Nell'Opus maius, utilizzando l'esempio dei mutevoli colori del collo delle colombe e dei piccioni, si osserva che "in funzione dei differenti [angoli secondo i quali] una data luce cade su un oggetto, l'aspetto di questo cambia e appaiono differenti colori" (Perspectiva, p. 62).
Per Bacone, come per altri studiosi di perspectiva e per il loro pubblico medievale, la sfida più significativa che veniva da questi fenomeni consisteva nella spiegazione dell'arcobaleno, simbolo della promessa divina a Noè dopo il diluvio. Attualmente gli storici generalmente valutano in modo positivo le conclusioni delle prime tre generazioni di studiosi latini medievali di perspectiva nello stabilire i ruoli causali della rifrazione e della presenza nell'aria di gocce di pioggia nel prodursi dell'arcobaleno. Primo fra tutti, Grossatesta ipotizzò che l'originarsi dell'arcobaleno implicasse in qualche maniera la rifrazione dei raggi solari su una nuvola tramite una nebbia intermediaria, tuttavia non disse in modo esplicito come l'arcobaleno risultasse visibile all'osservatore. In seguito, Ruggero Bacone, il quale eliminò totalmente il ruolo dei raggi rifratti della luce solare, nondimeno propose nell'Opus maius che questa luce, se riflessa da "un numero [quasi] infinito di gocce di pioggia" produce l''apparenza' di colori che costituisce l'arcobaleno; una seconda riflessione nei percorsi delle 'specie' visive moltiplicantisi le fa giungere ai nostri occhi.
Teodorico (Dietrich) di Vriberg (1240 ca.-1311), che si servì dell'Opus maius di Bacone, spiegò infine correttamente, nel 1304-1311, che il percorso della luce solare in ognuna delle gocce d'acqua subisce una rifrazione entrando nella goccia, poi una riflessione sulla superficie opposta e infine una seconda rifrazione nell'uscire dalla goccia dirigendosi verso l'occhio dell'osservatore (Lindberg 1976; Eastwood 1968; Wallace 1959).
Due delle questioni trattate da Ruggero Bacone ‒ e precisamente il cambiamento della posizione dell'arcobaleno in relazione al mutare della posizione dell'osservatore e la determinazione tanto del numero quanto della natura dei suoi colori ‒ ebbero una notevole influenza nei dibattiti epistemologici. Riguardo alla prima questione, Bacone riconobbe chiaramente le implicazioni epistemologiche del ruolo dell'osservatore:
è evidente, come sappiamo dall'esperienza, che ci sono tanti arcobaleni quanti sono gli osservatori. Poiché se due persone ferme osservano un arcobaleno che si produca verso il nord e una di esse prende a muoversi verso ovest, l'arcobaleno si sposterà parallelamente ad essa; se l'altra persona va ad est, l'arcobaleno si sposterà parallelamente a questa seconda persona; se una persona resta ferma, anche l'arcobaleno resterà fermo. è evidente, perciò, che, in quanto vi sono tanti arcobaleni quanti sono gli osservatori, è impossibile che due osservatori vedano lo stesso arcobaleno. (Opus maius, IV, 1, p. 187)
Ciò significa, conclude, che "dove c'è l'arcobaleno non ci sarà nulla più dell''apparenza' di colori", apparenza che è presente soltanto temporaneamente, finché dura l'arcobaleno. Poiché le posizioni di qualunque osservatore determinano come e dove appare l'arcobaleno ‒ egli continua ‒, così anche le colorazioni delle nubi sono soltanto fenomeni soggettivi. Qualunque osservatore può stabilire empiricamente da sé stesso che i colori dell'arcobaleno non sono indipendentemente "vividi" e stabili ("fissi"), ma sono apparenze dovute a una visione debole o difettosa. Osservando in ben determinate condizioni gocce di rugiada sul prato oppure la brillante luce del Sole estivo che entra in una stanza attraverso una piccola apertura, una persona, aprendo, chiudendo e rimettendo a fuoco gli occhi, dovrebbe vedere apparire i colori dell'arcobaleno. Facendo apparire e sparire tali raggi a piacere nel suo campo visivo l'osservatore dovrebbe scoprire che essi differiscono dai colori "veri", come lo spettro di colori che si vede quando si fanno passare i raggi solari attraverso un prisma di cristallo, i quali sono visibili allo stesso modo per tutti gli osservatori. Bacone afferma poi che questi colori veri sono causati naturalmente dalla struttura della superficie del cristallo e dagli angoli con i quali i raggi solari la colpiscono, purtroppo però separando la spiegazione causale dei colori dell'arcobaleno da quella dei colori irradiati da un prisma (ibidem, pp. 174, 190-191).
Al tempo in cui Bacone scriveva non si era comunque d'accordo su quanti colori esistessero, né su quanti fossero visibili nell'arcobaleno. Dal De sensu et sensibili di Aristotele si potrebbe ricavare una scala fotometrica dei colori, a partire dal 'nero', definito come completa oscurità, al 'bianco', completa chiarezza; tra questi due estremi Aristotele collocava sei 'tinte', o colori ‒ grigio, blu scuro, verde-porro, violetto, cremisi, giallo ‒ in base al rapporto tra nero e bianco (o tra scuro e chiaro) in ognuno di essi. Restava da interpretare una notevole discrepanza tra l'affermazione di Aristotele sull'esistenza di sette colori e la sua scala che, includendo gli estremi, ne contiene otto. Un'ulteriore difficoltà era costituita dall'esistenza di un'altra differente lista di Aristotele per colori da lui denominati 'irriducibili' e che noi chiameremmo 'primari': i suoi lettori, a fronte dell'affermazione ‒ contenuta sempre nel De sensu et sensibili ‒ che i quattro colori centrali tra il nero e il bianco (blu scuro, verde-porro, violetto e cremisi) sono 'irriducibili', leggevano invece nei Meteorologica che "i soli colori che i pittori non possono elaborare […] mischiandoli [ossia i colori irriducibili] sono il cremisi, il verde-porro e il violetto"; questi tre ‒ dice Aristotele ‒ sono quelli effettivamente presenti nell'arcobaleno e in fenomeni simili, nonostante che anche il giallo "si veda spesso tra il cremisi e il verde" (De sensu et sensibili, 442a 19-29; Meteorologica, 371b 34-372a 11; 375a 1-11).
Tanto l'enciclopedista francescano Bartolomeo Anglico quanto il domenicano Alberto Magno si basarono sul conteggio aristotelico dei colori irriducibili nel De sensu et sensibili. Nel De proprietatibus rerum, basato su quanto insegnato intorno al 1230 a Parigi, Bartolomeo cominciò con una scala di tre colori, collocando il rosso rubino (rubeus) a metà strada tra il nero e il bianco; forse, come più tardi Bacone, fu indotto a ciò dalla lettura di trattati recentemente acquisiti di alchimia che facevano derivare dall'osservazione dei procedimenti di combustione e di fusione i tre colori principali, vale a dire, andando dal freddo al caldo, rispettivamente il nero, il rosso e il bianco. Tra il bianco e il rosso Bartolomeo collocò il giallo pallido (pallidus) e lo zafferano (croceus), e tra il rosso e il nero collocò il violetto (purpureus) e il verde (viridis), eliminando quindi dalla scala di Aristotele il blu e il grigio.
Alberto, seguendo il suggerimento di Aristotele, dispose i sette colori principali (non nominandoli tutti) su una scala a intervalli regolari e armonici del rapporto bianco-nero, dallo scuro assoluto al chiaro assoluto; Vincenzo di Beauvais (1190 ca.-1264) ne seguì le orme. Nessuno di questi autori, quindi, tentò di conciliare gli otto colori citati da Aristotele con il suo elenco di sette, e probabilmente nessuno di essi era a conoscenza della soluzione di Grossatesta, consistente in un'estensione delle gradazioni tra i due estremi dell'oscurità totale e della chiarezza totale in modo da comprendere multipli sia di un ottavo sia di un settimo. Così, Grossatesta aveva sostenuto che ci sono esattamente sette tonalità di colore (non denominate) subito dopo il nero assoluto, la meno scura delle quali è contigua alla meno chiara di altre sette, la più chiara delle quali, in progressione, è contigua al bianco assoluto; dunque nel complesso ‒ continuava Grossatesta ‒ "ci sono sedici colori nell'Universo" e tra l'uno e l'altro di essi ci sono "[quasi] infinite gradazioni" di 'purezza', dalla più intensa fino alla più debole (De coloribus, pp. 78-79).
L'introduzione, da parte di Grossatesta, del concetto di 'intensità' della purezza dei colori è un'indicazione del fatto che egli, come Alberto, pensava al colore, in linea di principio, come a qualcosa di quantitativamente definibile. È interessante notare che riferendosi all'arcobaleno, entrambi affermino come l'osservazione degli arcobaleni sia resa difficile perché i loro colori sono instabili, fluttuanti (non 'fissi'), e hanno bordi talmente mal definiti "che i pittori non possono dipingerli" (Grossatesta, De iride, p. 77; Alberto Magno, Liber methaurorum, p. 674). Entrambi danno per scontato che i colori varino da un arcobaleno all'altro, e anche da una parte all'altra di uno stesso arcobaleno. Grossatesta attribuisce questa variabilità alla combinazione di sei fattori variabili nella disposizione che sia l'aria sia le nuvole sia, infine, qualunque altro mezzo trasparente interessato dal fenomeno presentano nel tragitto dei raggi solari tra il Sole e la zona dove l'arcobaleno si produce.
Due di questi fattori sono "la molteplicità o la pochezza", ossia il numero relativamente grande oppure piccolo dei raggi di luce solare che si automoltiplicano nel propagarsi attraverso i vari mezzi; essendo tutto il resto uguale, laddove arrivano più raggi "appare un colore più chiaro e luminoso", mentre si trova un colore più vicino al blu scuro (hyazinthinus) laddove arrivano meno raggi. I colori variano anche in base all'intensità ‒ o, per dirla con Grossatesta, in base "allo splendore o all'oscurità" ‒ della luce che si moltiplica su ognuno di questi raggi. I fattori finali che egli nomina sono "la purezza o l'impurità" di ogni mezzo attraversato dai raggi, perché più 'pura' è la trasparenza del mezzo, più vicino al bianco sarà il colore della luce che ne risulta, proprio come, più affumicata è l'aria, più scuro e meno brillante sarà il colore.
D'accordo con Grossatesta ‒ e con Aristotele ‒ sul ruolo dei suddetti fattori nel prodursi dei colori nei diversi mezzi, Bacone nondimeno propose una più dettagliata analisi del colore, che teneva conto anche della teoria e della pratica alchemiche. Nel suo commento giovanile al De sensu et sensibili di Aristotele, Bacone notò una certa confusione relativa a quali colori fossero indicati esattamente dai termini greci usati da Aristotele, poi ricostruì la sua scala aristotelica di sette colori secondo le proprie preferenze. Nella sua scala, come Bartolomeo Anglico, egli eliminò il blu scuro e il grigio, considerandoli come gradazioni dell'estremo colore nero, lasciò il rosso-rubino (rubedo) a metà strada tra il nero e il bianco, e inoltre ‒ ciò che si può considerare il suo contributo più significativo alla scala a intervalli uguali di Bartolomeo ‒ introdusse l'arancione (puniceus) collocandolo con il giallo (glaucus) a uguali intervalli tra il rosso-rubino e il bianco, e, analogamente, il violetto (purpureus) e il verde (viridis), nell'ordine, tra il rosso-rubino e il nero.
Queste sono dunque le sette "più evidentemente distinte" gradazioni fondamentali della scala cromatica di Bacone (estremi compresi), benché tra esse ‒ dice l'autore, rifacendosi ancora ad Aristotele, ad Averroè e a Grossatesta ‒ si potrebbero a ragione designare altri colori intermedi, meglio considerati come ulteriori sfumature dei sette colori fondamentali, andando dall'uno al successivo o al precedente per gradi (De sensu et sensato). Ritornando molti anni dopo, in modo specifico, sull'arcobaleno, Bacone sostenne però nell'Opus maius che ci sono cinque colori principali, e precisamente il bianco (chiarezza) e il nero (oscurità) alle estremità della scala dei colori, e il giallo (qui glaucitas), il rosso e il verde entro questi estremi. Numericamente, ciò significava ‒ e Bacone se ne compiaceva ‒ che il numero delle tonalità cromatiche corrispondeva ai tre umori e alle due tuniche dell'occhio che partecipano a generare questi colori apparenti. Tuttavia, adattando la sua idea alla enumerazione aristotelica dei sette colori visibili nello spettro ottico, Bacone riconobbe che il giallo e il verde potevano essere suddivisi in altre sfumature.
Quando Teodorico di Vriberg si chiedeva quanti colori fossero presenti nell'arcobaleno e se essi avessero un'"esistenza reale" oppure "soltanto apparente", erano disponibili sia la scala cromatica sia le considerazioni sull'arcobaleno di Bacone, insieme a ciò che sosteneva Aristotele. Teodorico riferisce che i due negano che il giallo (citrinus) visibile nell'arcobaleno tra il rosso e il verde sia un "colore vero", considerandolo piuttosto visibile soltanto "a causa di un errore di un inganno o di […] un'illusione della visione". Nel ribadire la realtà di questo giallo, esattamente come quella dei tre colori generalmente ritenuti presenti nell'arcobaleno, nel De iride Teodorico dice che sia il numero sia la realtà dei colori dell'arcobaleno possono essere confermati dalla nostra quotidiana esperienza di fenomeni più vicini; per esempio, possiamo vedere tutti questi colori quando la luce solare illumina un cristallo a sezione esagonale oppure gocce d'acqua presenti, come rugiada, su tele di ragno o sull'erba di un prato o che formano quella sorta di nebbia che si stacca dalla ruota di un mulino quando gira.
Questi erano i fenomeni 'accessibili' ai quali Bacone aveva indirizzato i lettori dell'Opus maius, ma utilizzandoli come evidenza in favore della conclusione opposta. Inoltre, mentre i colori nell'arcobaleno sono reali, secondo le opinioni di Teodorico esposte nel De colore, essi peraltro non sono presenti allo stesso modo dei colori 'fissi' in un corpo opaco, né come quelli che egli chiama i mutevoli "colori erranti" (colores peregrini) prodotti da un raggio di luce che passa attraverso una finestra dal vetro colorato.
Poco dopo la composizione del De colore e del De iride di Teodorico di Vriberg, questi concetti emersero nuovamente nelle lezioni sulle Sentenze di Pietro Lombardo tenute da Pietro Aureolo (m. 1322). Frate francescano originario della Linguadoca che sarebbe diventato vescovo di Aix-en-Provence, Aureolo insegnò a Tolosa intorno al 1314-1316, tra periodi di insegnamento a Bologna e a Parigi. Egli riconobbe che, nel momento in cui si accettava un'interpretazione intromissionistica della visione, si doveva ritenere che la realtà extramentale producesse i contenuti della mente e predisponesse la loro sistemazione. Gli studiosi convenivano sul fatto che apparizioni transitorie quali gli arcobaleni, i colori fluttuanti e le immagini virtuali, o illusioni ottiche, fossero eccezionali, essendo in parte il prodotto della posizione e dello sguardo dell'osservatore, in parte realtà indipendenti. L'originalità di Aureolo consistette nel considerare tutto ciò in modo diverso, per cui poteva affermare:
Coloro che si interrogano sui colori dell'arcobaleno, o sui colori che si vedono sul collo di una colomba o su un'immagine che appare in uno specchio o su una candela che appare in qualche parte diversa da quella in cui è effettivamente, se abbiano un'esistenza vera o soltanto intenzionale, vogliono chiedersi se questi fenomeni abbiano soltanto un'esistenza 'soggettiva' e fittizia o apparente, oppure abbiano un'esistenza reale e fissa [stabile] al di fuori della mente, nella Natura oggettiva, indipendentemente da ogni apprensione. (Tachau 1988, p. 96)
La risposta di Aureolo a queste domande divenne la fonte di molti dibattiti. Queste 'apparizioni' visive non hanno nessuna esistenza extramentale ma esistono nella mente di chi le vede. Esse non sono le 'specie visibili' che si moltiplicano dall'oggetto osservato e alle quali si deve il prodursi dell'apparizione; piuttosto, devono essere generate dalle facoltà cognitive, da quelle sensitive e da quelle intellettuali. Cosa più importante ‒ afferma Aureolo ‒ la produzione di tali fenomeni mostra ciò che succede anche in una percezione normale e veritiera. In altre parole, quello che Bacone e gli altri studiosi della perspectiva credevano che 'talora' fosse il frutto delle capacità percettive dell'osservatore, secondo Aureolo è 'sempre' nell'atto della visione (nella sua terminologia, "cognizione oculare" o "intuizione"), quando queste capacità percettive formano attivamente un'immagine concettuale e puramente soggettiva che somiglia all'oggetto, e quindi ne costituiscono una rappresentazione. Queste apparizioni mentali hanno ‒ insiste Aureolo ‒, un'esistenza reale, anche se più debole, "intenzionale" o "apparente" (ibidem).
Nel XIV e nel XV sec. molti studiosi conoscevano il pensiero di Aureolo, ma pochi di essi lo capivano bene, e meno ancora erano d'accordo con la sua convinzione che le nostre facoltà visive inevitabilmente creassero mentalmente la realtà. Un teologo francescano, Bernardo d'Arezzo, sembra aver adottato la teoria di Aureolo intorno al 1335, ma la maggior parte dei lettori temeva che accettare tale opinione significasse abbracciare uno scetticismo senza appello; dopo tutto, come ci si poteva mai accertare che il mondo fosse effettivamente quel quadro dipintoci dalle nostre facoltà? Perciò un noto oppositore di Bernardo, l'atomista Nicola di Autrecourt (attivo a Parigi nel 1327-1347, erroneamente considerato a lungo dagli storici come uno scettico), mantenne la terminologia di Aureolo basata sulle apparenze visive, ma ne stravolse lo scopo. Secondo Autrecourt, gli oggetti danno origine a immagini extramentali che, quando ci si presentano, posseggono l'evidenza necessaria per essere accettate come certezze. Nel giungere a tale conclusione, tuttavia, Autrecourt non difese la moltiplicazione delle 'specie' sostenuta dagli studiosi della perspectiva, che cercò di rimpiazzare con gli atomi. I lavori di Autrecourt, tuttavia, quasi cessarono di circolare dopo che furono condannati dal papa nel 1346 (Tachau 1988; Kaluza 1995).
La diffusione della perspectiva dopo Bacone
La maggior parte degli studiosi che si ispirarono inizialmente a Bacone per l'analisi della perspectiva era costituita da teologi, forse perché egli (seguendo Grossatesta, il suo modello) presentava questa scienza come essenziale per comprendere e realizzare il progetto divino del Creato. Bacone inviò alcune delle sue proposte per riformare l'insegnamento, che includono i suoi corposi trattati di perspectiva, a Viterbo per il papa Clemente IV, che aveva chiesto di vederle. Alla corte papale il religioso slesiano Witelo (1220/1230-1280 ca.), che aveva studiato nell'Università di Parigi e in quella di Padova, evidentemente venne a conoscenza delle opere di Bacone. Ciò che Bacone aveva soltanto accennato, Witelo lo acquisì a Viterbo intorno al 1270 e lo completò in un esauriente e sistematico resoconto sulla nuova disciplina, un'enorme Perspectiva contenente all'incirca 600 figure geometriche.
Seguendo Alhazen e Bacone, Witelo usa il "cono visivo", formato da raggi che incidono perpendicolarmente sull'umore cristallino dell'occhio, per analizzare la visione geometricamente; nondimeno rifiuta la teoria di Bacone dei raggi estromessi, e a differenza sia di Bacone sia di Alhazen sostiene che la luce si propaga istantaneamente. Affronta inoltre questioni che Bacone non aveva considerato, quali l'analisi della riflessione da specchi paraboloidici (tratta da Alhazen), una ricerca quantitativa per la legge della rifrazione (copiata da Tolomeo) e il principio della minima distanza di Erone di Alessandria (secondo il quale per avere il cammino più breve dalla sorgente allo specchio e di qui all'osservatore occorre che l'angolo di incidenza sullo specchio dalla sorgente e quello di riflessione verso l'osservatore siano uguali). Varie osservazioni nella sua Perspectiva fanno pensare che egli avesse accettato la teoria di Bacone della moltiplicazione delle 'specie' nella propagazione della luce (Lindberg 1976).
I trattati di Bacone suscitarono dall'inizio un interesse profondo anche a Parigi. Molti dei più alti ingegni dell'ordine francescano studiarono e insegnarono nel convento di Parigi nel periodo 1267-1278, quando Bacone vi abitò e vi scrisse sulla luce; non sorprende, perciò, che i suoi confratelli parigini siano stati tra i primi teologi a recepire la nuova perspectiva. Il primo critico di Bacone, Pietro di Giovanni Olivi (1248 ca.-1298; a Parigi nel 1266-1268), dimorò nello stesso convento per parte di quel periodo, e così fecero altri frati tra i più propensi ad accettare i principî della perspectiva nell'ambito delle loro lezioni e dei loro dibattiti teologici, come Ruggero Marston (a Parigi nel 1271-1272), Guglielmo de la Mare (m. 1298), Matteo di Acquasparta (1235/1240-1302) e soprattutto Giovanni Peckham (1240 ca.-1292). Dopo aver insegnato teologia a Parigi (1270 ca.-1272) Peckham ricoprì lo stesso incarico presso la corte papale di Viterbo (1277-1278), dove certamente incontrò Witelo. Scrisse un elementare trattato di perspectiva, basato principalmente su Alhazen e Bacone, che divenne il manuale più ampiamente usato per quella disciplina nelle università del Medioevo e del Rinascimento, con il titolo di Perspectiva communis. Insieme alle opere di Euclide, al-Kindī, Alhazen, Bacone e Witelo, esso gettò le basi della disciplina (specialmente nei suoi aspetti matematici) in generazioni di studenti e di studiosi, fino ai primi decenni del XVII sec. (Lindberg 1976).
Un percorso analogo attraverso gli scritti su questioni di ottica di studiosi dell'ordine domenicano collega fra loro Alberto Magno, Vincenzo di Beauvais, Teodorico di Vriberg e anche Witelo (che, pur non essendo membro di tale ordine, frequentò peraltro studiosi domenicani a Viterbo). La perspectiva era comunque diventata una sorta di proprietà comune dei teologi delle Università di Oxford, di Parigi e di Tolosa. Per trovare lettori di trattati sulla perspectiva non appartenenti a ordini mendicanti basta dare uno sguardo al Tractatus moralis de oculo di Pietro di Limoges, un libro per predicatori scritto a Parigi, o alle questioni teologiche discusse da Enrico di Gand (a Parigi nel 1272-1292) e da Goffredo di Fontaines (1250 ca.-1309 ca.).
Così, alla fine del secolo le lezioni sulle Sentenze di Pietro Lombardo servivano correntemente a precisare come si giunge a conoscere il mondo, e molti a tale scopo si riferivano alla teoria della 'moltiplicazione delle specie'. Il francescano Giovanni Duns Scoto (1274 ca.-1308) adottò le idee di base della perspectiva, e ciò ebbe un'importanza determinante per la loro diffusione, dal momento che le lezioni di Duns Scoto a Oxford e a Parigi durante gli ultimi anni del XIII sec. fino al 1308 furono spesso fra i presupposti della problematica dei teologi fino al XVI secolo. Questo fu il caso sia di Pietro Aureolo che del suo più famoso fratello francescano, Guglielmo di Ockham (1280 ca.-1347), il cui insegnamento a Oxford coincise esattamente con quello di Aureolo a Tolosa e a Parigi. Nelle letture sulle Sentenze tenute a Oxford nel 1317-1319, Ockham dedicò uno sforzo considerevole a confutare le posizioni della perspectiva sulle species moltiplicantisi sia in un mezzo di propagazione, sia nei sensi o, infine, nell'intelletto. Le argomentazioni di Ockham, che i suoi contemporanei trovarono poco efficaci, provocarono molte critiche in Inghilterra nei decenni successivi.
I teologi a Parigi erano convinti in maniera meno unanime che la moltiplicazione delle 'specie' fosse necessaria per spiegare gli effetti della luce, il processo della visione o i modi della conoscenza, ma in gran parte continuarono per il resto del XIV sec. a integrare la scienza della perspectiva nella loro opera teologica (Lindberg 1976; Tachau 1988). L'importanza di questa disciplina per i teologi attivi a Parigi in quel tempo è suggerita dalla loro possibilità di accesso a copie del De aspectibus di Alhazen, della Perspectiva di Bacone e della Perspectiva communis di Peckham nella biblioteca della Sorbona entro il 1338; inoltre, laddove le questioni esaminate avessero a che fare con la Natura e la vastità dell'influenza degli astri, l'opera che essi consultavano e citavano a tale riguardo era il De multiplicatione specierum di Bacone: così fecero, per esempio, Roberto Holcot a partire dal 1330 e Pietro d'Ailly all'inizio del XIV secolo.
In qualche modo la perspectiva entrò anche nel curriculum degli studi degli artisti a Parigi, ma è difficile stabilire quando ciò avvenne. Per il primo quarto del XIV sec. abbiamo la testimonianza del celebre maestro delle arti Giovanni di Jandun (1285/1289 ca.-1328), che nel suo trattato De laudibus Parisius incluse lo studio di "grandezze celesti, suoni armonici e raggi visivi" tra le discipline insegnate al vico Straminum (o rue de Fouarre), ossia tra quelle impartite nella Facoltà delle arti. Nel giro di pochi decenni, in ogni caso, le lezioni di Giovanni Buridano sulle due opere di Aristotele De sensu et sensibili e De anima confermano l'uso della perspectiva nell'insegnamento presso la Facoltà delle arti di Parigi (Lindberg 1976, 1978). Gli studenti delle arti liberali nelle nuove Università di Praga e di Vienna poterono frequentare i corsi sulla Perspectiva communis di Peckham entro la fine del XIV secolo. L'insegnamento di questa scienza fu particolarmente fiorente nell'Università di Cracovia, giustamente celebre per il suo impegno nelle discipline matematiche nel corso del XV secolo.
Proprio come gli autori di opere sulla perspectiva avevano utilizzato gli scritti medici greco-arabi, così nel XIV sec. i membri delle Facoltà di medicina cominciarono a interessarsi alla crescente letteratura sulla luce, sul colore e sulla visione. A Parigi, per esempio, Domenico di Chivasso, durante il suo insegnamento sulle arti e nei suoi studi di medicina agli inizi del 1350, tenne lezioni su problemi tratti da Alhazen e da Witelo; ne risultò un trattato, Questiones super perspectivam, probabilmente completato prima che Domenico entrasse a far parte della Facoltà di medicina di Bologna col titolo di dottore nel 1356, che ebbe una larga circolazione, raggiungendo, in particolare, anche Firenze. Da allora i docenti di arti e di medicina dell'Università di Bologna si occuparono sempre più di perspectiva. Alla fine del XIV sec., grazie alla loro integrazione con lezioni sulle opere di Aristotele, almeno alcuni dei principî della perspectiva si erano largamente diffusi in altre università italiane. Le lezioni sulle opere di Aristotele De anima e Meteorologica che Biagio Pelacani da Parma tenne a Pavia, Bologna, Firenze e Padova esemplificano bene questo processo di diffusione della cultura sulla perspectiva.
I numerosi lettori dell'Opus maius e del De multiplicatione specierum di Bacone, della Perspectiva communis di Peckham e dei testi più esaurienti di Alhazen e di Witelo dissentirono su aspetti particolari degli argomenti trattati estesamente in queste opere, quali, per esempio, il sito dell'occhio dove si formano le immagini, oppure la natura e il ruolo delle 'specie' che si moltiplicano. I trattati sulla perspectiva erano volti a incoraggiare la realizzazione di dispositivi e di strumenti di grande utilità pratica, come lenti di ingrandimento, occhiali da vista e telescopi. Inoltre, come gli storici dell'arte hanno recentemente apprezzato, una volta che Giotto e i suoi seguaci del XIV sec. incominciarono ad applicare la concezione geometrica nel rappresentare in maniera più realistica i paesaggi, gli edifici e gli esseri viventi, la perspectiva medievale divenne indispensabile (Lindberg 1976; Edgerton 1991).
Non sappiamo ancora dove e come si siano verificati i primi incontri determinanti tra artisti e studiosi di luce, colore e visione ma, date le pratiche dell'apprendimento artigianale caratteristiche dell'epoca, è probabile che gli scambi iniziali siano stati informali e personali e non mediati da libri. Chiaramente, alcuni studiosi ‒ come Grossatesta, Alberto Magno, Bacone e Nicola Oresme ‒ si interessarono alla relazione esistente tra la pratica artistica corrente e le loro teorie ottiche; significativamente, almeno Ruggero Bacone propose di servirsi della precisione della geometria nelle arti figurative a beneficio della fede (Perspectiva, pp. 210-212).
Motivati inizialmente da Bacone e da altri studiosi di perspectiva, entro il XV sec. gli artisti del Rinascimento cominciarono a usare il termine per indicare l'insieme delle tecniche geometriche che via via entrarono e si perfezionarono nella pratica del disegno, della pittura, dell'incisione, della scultura e dell'architettura. Tale uso era iniziato poco tempo prima, per opera di alcuni artisti e teorici eccezionali che, specialmente in Italia, avevano adottato, modificato e integrato la scienza della perspectiva chiamandola 'prospettiva' (presto foneticamente trasferito in altre lingue europee). Questo nuovo termine apparve anche in alcuni trattati: De pictura (1435) e Della pittura (1436), ambedue di Leon Battista Alberti; i Commentarii (della metà del Quattrocento) del pittore e incisore Lorenzo Ghiberti; De prospectiva pingendi (1474 ca.) del grande pittore Piero della Francesca; De divina proportione (pubblicato a Venezia nel 1509) di Luca Pacioli. Da questo momento la scienza dell'ottica risultò sistematizzata su basi matematiche e teoriche così certe che ne avrebbero assicurato lo sviluppo come una delle scienze fondamentali per l'indagine e la cultura filosofica fino all'era moderna.
La scienza dei pesi
di John D. North
La tradizione aristotelica
La 'scienza dei pesi' medievale (scientia de ponderibus) è oggi nota come 'statica', una materia che viene comunemente insegnata senza fare troppo riferimento alla sua posizione tra le scienze in generale; nel Medioevo, invece, alla geografia generale del 'territorio' intellettuale si prestava quasi altrettanta attenzione che ai suoi più raffinati particolari. Per quanto le 'mappe' che ne risultavano fossero diverse tra loro, quasi tutte avevano come antenato comune lo schema aristotelico della classificazione delle scienze, basata su due nozioni fondamentali: esistenza e cambiamento. La fisica, la matematica e la metafisica (o la teologia) erano distinte per i diversi tipi di enti che studiavano. Enti con una esistenza sostanziale separata? Enti soggetti a cambiamenti? Se la risposta a entrambe le domande è sì, allora ‒ secondo l'idea di Aristotele ‒ si studia la fisica; i teologi o i metafisici rispondono rispettivamente sì e no; il matematico risponde no a entrambe le domande: numeri e linee, per esempio, esistono solo in quanto si qualificano come realtà concrete. Aristotele sapeva perfettamente che la sua classificazione aveva bisogno di essere sviluppata ulteriormente, dal momento che la matematica può essere applicata a parecchie scienze sussidiarie, come l'ottica, la musica e la meccanica; tuttavia, sebbene abbia riconosciuto esplicitamente che gran parte della matematica fosse stata originariamente pensata ed elaborata nel contesto delle arti pratiche, egli era ben contento di convergere nella tradizione greca cancellando ogni traccia dei debiti nei riguardi del 'laboratorio'. La matematica greca e quasi tutte le sue più antiche derivazioni quando venivano affidate alla pagina scritta avevano un aspetto assolutamente "puro".
Gli studiosi medievali seguirono la strada tracciata dai Greci, dando alle loro opere un aspetto fortemente teoretico e non empirico, e ancora oggi i principî della statica e della dinamica sono insegnati senza un riferimento particolare alla loro base sperimentale; i fenomeni che esse trattano sono considerati in qualche modo semplici, perfino ovvi. È consueto ‒ ma fuorviante ‒ distinguere tra una tradizione aristotelica che cerca di "salvare i fenomeni" basando la teoria sull'osservazione del mondo fisico, e una tradizione platonica che non lo fa. È fuorviante perché quello che Aristotele desiderava innanzi tutto salvare non erano le scoperte avvenute attraverso gli esperimenti, ma le credenze e gli usi linguistici delle persone mediamente colte. È vero che il suo modo di procedere era fortemente sistematico e logico; quasi inevitabilmente mentre elaborava le proprie teorie scientifiche sviluppava quelle degli altri. Ma le sue erano teorie destinate principalmente a essere 'compatibili' con ciò che era noto dall'esperienza; e questo ideale fu condiviso dai suoi successori medievali: originariamente, nel Medioevo, la meccanica non fu una scienza sperimentale.
I seguaci della tradizione aristotelica non trovarono fra gli scritti del 'Filosofo' pagine illuminanti sui problemi della statica, ed è una questione molto controversa se si possa affermare che egli abbia sviluppato una teoria della dinamica. Nella Fisica e nel De caelo, compaiono solo affermazioni isolate, che mettono in relazione le forze, i movimenti che esse producono nel tempo e gli effetti che le forze producono su corpi grandi o piccoli, oltre che su corpi più leggeri o più pesanti. Aristotele non ha mai tracciato una chiara delimitazione tra la dinamica (intesa nel senso moderno di scienza che mette in relazione le forze con la massa e con il moto) e la statica; in realtà, si può dire che egli non abbia avuto in alcun modo una teoria della statica. Tuttavia, in un'antica opera pseudoaristotelica, i Problemi di meccanica (o semplicemente Mechanica), si trova un debole tentativo di dimostrare la legge della leva sulla base dei principî del moto. Quest'opera in sé stessa costituisce una interessante conferma del fatto che la statica non era vista come una scienza primaria. Come spesso succede, non possiamo dire con certezza che la Mechanica fosse nota in latino prima della fine del XV sec., sebbene siano noti alcuni riferimenti al suo titolo. Quelli che sembrano richiami a essa ‒ nei numerosi tentativi di dimostrare le leggi della statica mediante prove che si riferiscono ai corpi in caduta libera ‒ sono probabilmente idee che derivano da quest'opera attraverso un cammino tortuoso. Il trattato di Ṯābit ibn Qurra (836-901) Liber karastonis è uno dei casi in questione e sarà discusso più avanti; alcuni autori piuttosto ottimisti, infatti, hanno sostenuto di aver identificato il cosiddetto principio delle velocità virtuali sia nella Mechanica sia nell'opera di Ṯābit. Vero o falso che sia, il nostro problema in questo capitolo sarà dimostrare che è stato certamente possibile scoprire qualcosa di simile nel Medioevo.
Anche nella dinamica, i tentativi di Aristotele ‒ finalizzati a correlare la forza che agisce su un corpo in movimento con la velocità che ne risulta ‒ furono inconcludenti, e perciò, considerando che la statica era un soggetto secondario, bisogna riconoscere che essa non ha mai avuto molte opportunità di affermarsi. I principali concetti di forza utilizzati sono riferiti l'uno alla forza esterna e l'altro alla forza interna, e si tratta di forze di natura differente. La forza esterna muove una cosa; quella interna è una specie di opposizione a essa (questa non sembrerà un'idea strana a coloro che si sono formati nell'ambito della dinamica newtoniana, in cui è tracciata una distinzione tra una forza applicata e un'opposizione inerziale a essa). Ma allora, cosa sono le forze esterne? Lo studente di oggi cade facilmente nella tentazione di applicare ‒ come principio basilare per la composizione delle forze ‒ la regola che una forza direttamente opposta a un'altra produce una forza che è semplicemente la differenza tra le intensità delle due forze. Aristotele non aveva chiara neppure questa regola: così, nel Libro V della Fisica si dice che un uomo solo è assolutamente incapace di muovere una nave, mentre molti uomini possono muoverla. Il fatto che considerasse problemi di questo tipo come problemi di dinamica probabilmente spiega perché Aristotele non abbia neppure trattato la forza come una grandezza continua; senza tale presupposto non vi è mai stata una teoria della statica semplice e di successo.
Gli studenti medievali potrebbero essere stati ingannati dal fatto che mentre Aristotele trattava l'ottica, l'armonia e la meccanica come le più fisiche fra le scienze matematiche, e mentre forniva esempi presi dalle prime due, egli non avesse tratto esempi dalla meccanica ‒ dinamica o statica ‒ per supportare le sue argomentazioni. Quando gli autori medievali ripetevano pedissequamente che la meccanica era una scienza a metà strada tra la matematica e la fisica, la maggior parte di loro aveva una padronanza così approssimativa dei suoi principî che la loro concezione scientifica poteva essere considerata, al massimo, un abbozzo. Un 'abbozzo' di questo tipo aveva il piccolo vantaggio che vi si potevano aggiungere altri dettagli, tuttavia i suoi argomenti non potevano essere completati senza risalire, oltre le opere aristoteliche, alle dottrine di Euclide e di Archimede, evitando in tal modo un approccio di tipo dinamico a problemi di statica. Questo taglio con il passato avvenne, grosso modo, durante il XIII secolo.
La tradizione archimedea
Per comprendere la natura della 'mappa della conoscenza', si consideri ciò che scrive Domenico Gundisalvi, autorevole enciclopedista degli inizi del XII sec., sulla "divisione della filosofia" (De divisione philosophiae; v. cap. XV). Egli sottolinea l'"universalità" della matematica, che ‒ dice ‒ ha sette arti sotto di sé. Le prime quattro sono le arti tradizionali del quadrivio: aritmetica, geometria, musica e astrologia (non dice astronomia); poi nomina "la scienza delle apparenze", con cui intende l'astrologia nel senso che noi oggi diamo al termine; infine, aggiunge la scienza dei pesi (scientia de ponderibus) e la scienza delle macchine (scientia de ingeniis), dividendo la prima in due parti (v. cap. XV, tab. 4). Una riguarda la misurazione dei pesi e l'altra la misurazione delle cose mediante i pesi. Senza dubbio egli aveva in mente i clienti della piazza del mercato, e le semplici regole aritmetiche per graduare una serie di pesi. A tutto ciò, che sembra molto banale, fa seguito il riferimento ai principî degli strumenti utilizzati per sollevare i corpi pesanti e che determinano il loro cambiamento di posizione, vale a dire alla teoria dei congegni meccanici. È ancora un concetto piuttosto vago, ma Gundisalvi è confusamente consapevole di una tradizione non ancora affermata nell'Europa occidentale e il cui più illustre esponente era stato Archimede. Se nel lungo periodo questa tradizione sia stata di importanza superiore a quella aristotelica per la statica medievale è un punto sul quale si può discutere, ma gli studiosi che erano in grado di apprezzare la differenza sentivano che le due dottrine dovevano essere riconciliate.
Nell'opera di Gundisalvi c'è un passaggio piuttosto nebuloso, ma interessante, in cui egli espone le sue idee su quale potrebbe essere la scienza delle macchine. Si richiama l'attenzione sulle conseguenze pratiche dell'applicazione delle teorie matematiche dei numeri (razionali e irrazionali), della geometria, e persino dell'algebra, ai problemi pratici della misurazione delle pietre, del sollevamento dei corpi, della fabbricazione delle armi e della costruzione di congegni musicali e ottici. In breve, Gundisalvi rivela un interesse per l'aspetto pratico delle scienze che è tipico dell'epoca ‒ Ruggero Bacone, per esempio, nel XIII sec. espresse lo stesso concetto con parole molto energiche. Il fatto che Archimede fosse della stessa idea significò che quando le sue opere furono infine introdotte nell'Europa occidentale, esse incontrarono un clima favorevole. È mortificante pensare che tanta parte della scienza medievale dipendesse dalla riscoperta di tecniche che erano state così brillantemente sviluppate un millennio e mezzo prima.
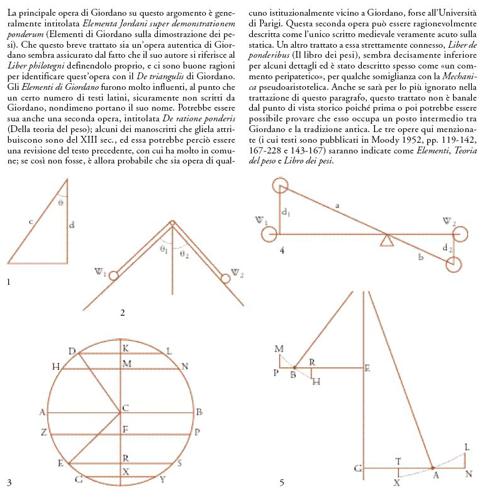
L'influenza di Archimede nel Medioevo (egli scriveva nel III sec. a.C., un secolo dopo Aristotele) è già stata trattata con una certa ampiezza (v. capp. XI e XIX); si è visto che egli aveva al suo attivo diverse invenzioni meccaniche. A torto o a ragione gli si attribuivano infatti, di volta in volta, la vite nota col suo nome, la puleggia composta, l'equilibrio idrostatico e un planetario meccanico, per fare solo qualche esempio. Non solo egli fu uno dei più abili matematici dell'Antichità, ma ebbe anche un talento notevole per la geometria applicata ai problemi della statica e dell'idrostatica. Sembra che Archimede avesse un'idea del peso simile a quella di Aristotele, vale a dire che lo considerava diretto verso il centro della Terra, ovvero il centro dell'Universo. Tuttavia, egli dimostrò la legge della leva (legge della bilancia) in un modo totalmente geometrico che deve ben poco, o nulla, ad Aristotele (si suppone qui che il lettore abbia familiarità con questa semplice legge della leva: senza calcolare il peso della leva stessa, qualunque esso sia, se i pesi W1 e W2 sono alla distanza a e b dal fulcro (fig. 5), allora W1a=W2b). Archimede rappresenta i pesi come grandezze geometriche; il momento di ciascun peso rispetto al fulcro è rappresentato da un'area (il prodotto della distanza dal fulcro per la grandezza del peso); l'equilibrio è così ridotto al problema di rendere uguali le aree poste ai due lati del fulcro, ed è ovvio che, in ultima analisi, verificare se questa rappresentazione funzioni o meno spetta all'esperienza. Si è discusso molto se l'analisi di Archimede di un caso reale (con un braccio che è pesante e pesi che sono di grandezza finita, a cui egli applica il concetto di centri di gravità) implichi un argomento circolare; quello che interessa in questa sede, tuttavia, è che Archimede aveva formulato una serie di principî generali con i quali poteva facilmente analizzare casi molto complicati sia nella statica sia nell'idrostatica, e che poteva applicarli ai problemi della realtà concreta delle macchine ‒ alle quali era estremamente interessato.
Le sue opere non erano molto diffuse nell'Antichità, e il fatto che siano divenute familiari a tutta l'Europa occidentale è dovuto in parte alla loro influenza sugli autori arabi (v. cap. XIX), e in parte allo studio di cui furono oggetto a Bisanzio tra il VI e il X secolo. Gran parte del merito di questa ultima fortunata coincidenza sembra essere di Eutocio di Ascalona (VI sec.), il quale ebbe accesso alle opere di Archimede nel periodo in cui studiava ad Alessandria, e più tardi scrisse dei commenti su tre di queste. Questi testi suscitarono grande interesse e provocarono, a loro volta, ulteriori commenti. Nel IX sec., Leone di Tessalonica ‒ uno studioso con interessi enciclopedici al quale si riconducono i congegni meccanici noti con il suo nome ‒ riunì in un'inestimabile raccolta i testi archimedei, e la sua fu una delle due raccolte di manoscritti greci delle opere di Archimede utilizzate dal domenicano fiammingo Guglielmo di Moerbeke (le cui traduzioni latine, risalenti al 1269 ca., sono state analizzate nel cap. XIX). La seconda raccolta di manoscritti comprendeva le opere meccaniche di Archimede ‒ Equilibrio dei piani (presente anche nell'altro manoscritto), Galleggianti e Quadratura della parabola (un'opera che usava metodi statici per scopi geometrici); questo secondo manoscritto è poi andato perduto, mentre il primo ci è rimasto.
Gli autori arabi che svilupparono alcune delle idee di Archimede sul finire del periodo bizantino, e che crearono una tradizione 'archimedea' alternativa, non sembrano essere stati molto fedeli ai testi originali; tuttavia, essi fecero buon uso dell'altro materiale greco che a sua volta era basato sugli originali di Archimede ‒ per esempio, la Mechanica di Erone, la Pneumatica di Filone, e un'opera pseudoeuclidea Sulla bilancia (in effetti tutte e tre queste opere sono note oggi soltanto attraverso i loro intermediari arabi). Dal Libro della bilancia della sapienza di al-Ḫāzinī apprendiamo che anche Menelao, il grande matematico alessandrino del I sec., scrisse un libro sulla meccanica; alcuni dei teoremi di Menelao sono infatti riprodotti da al-Ḫāzinī, il quale indirettamente, attraverso la lettura di Menelao, descrive anche la spiegazione della bilancia fornita da Archimede. Dalla stessa fonte apprendiamo come Menelao usasse una bilancia per misurare i pesi specifici, e analizzare in questo modo le proporzioni dei metalli nelle leghe.
In generale, gli autori arabi non solo tradussero l'antico materiale greco, ma ne fecero la revisione e diedero propri contributi originali. Purtroppo, gran parte del materiale arabo è andato perduto, e ci è noto soltanto per citazioni indirette; va notato, però, che gli argomenti della statica e dell'idrostatica sono stati affrontati da molti dei più importanti autori della scienza islamica, come Banū Mūsā, al-Ḫāzinī, Qusṭā ibn Lūqā, Ṯābit ibn Qurra e Ibn al-Hayṯam. Costoro erano seriamente interessati ai dettagli pratici della pesatura e del disegno delle bilance, eppure, con la notevole eccezione di un trattato di Ṯābit ibn Qurra, poche delle loro opere sono state tradotte in latino durante il Medioevo.
Quando nel Tardo Medioevo gli scritti di Archimede cominciarono gradualmente ad attirare l'attenzione dei dotti, nell'Europa occidentale si andava sviluppando uno stile piuttosto diverso nel trattare la scienza dei pesi, basato su un testo di Giordano Nemorario di cui si discuterà ampiamente tra breve. Quelle che oggi si possono considerare tradizioni distinte, tuttavia, non erano percepite nello stesso modo nel Tardo Medioevo, cosicché raramente Giordano è stato considerato alternativo ad Archimede. Ciò era forse dovuto anche alla mancanza di idee precise sulla paternità delle opere. Le teorie medievali sulla statica che si basavano sugli scritti di Archimede si rifacevano soprattutto a scritti di seconda o terza mano, e questo rimase vero anche dopo una seconda ondata di traduzioni latine del corpus archimedeo per opera di Giacomo da Cremona intorno al 1450. La doverosa correzione della traduzione di Moerbeke del Dei corpi galleggianti rimase un compito per il XVI sec.; dell'opera apparvero a intervalli alcune edizioni a stampa, ma basate sulla traduzione di Moerbeke, e il primo significativo progresso si ebbe nel momento in cui Federico Commandino la stampò (Bologna, 1565) senza avere avuto ancora accesso al testo greco (che a quell'epoca era perduto), ma apportandovi i suoi acuti emendamenti.
La 'bilancia romana'
Oltre ai testi di Archimede, nel Medioevo erano disponibili altri materiali di grande interesse, ma meno facilmente classificabili, alcuni dei quali risalgono apparentemente al mondo antico. Così vi era il libro De ponderoso et levi (Sul pesante e sul leggero), erroneamente attribuito a Euclide, e ‒ come già ricordato ‒ il Liber karastonis (Libro della bilancia romana) pubblicato da Ṯābit ibn Qurra nel IX secolo. Prima di considerare i più importanti scritti dell'autore latino del XIII sec. Giordano Nemorario e dei suoi seguaci, è necessario dire qualcosa della tradizione precedente e più empirica relativa al principio della leva.
La forma più semplice di bilancia, che risale ai tempi preistorici ‒ in realtà almeno al 5000 a.C. ‒ ha bracci di uguale lunghezza; il suo nome latino è trutina. La sua utilità in un mercato è evidente; la simmetria, da sola, assicura che ciò che si misura abbia un peso uguale al peso standard sull'altro braccio. Il suo uso, però, è poco pratico per oggetti molto pesanti, e così, fin dai tempi molto antichi, si usarono bilance con bracci disuguali. Queste sono spesso chiamate 'bilance romane' ('stadere'); l'oggetto pesante è a una distanza breve (che chiameremo d) dal punto di sospensione, mentre il contrappeso è a una distanza grande (D); tralasciando le complicazioni dovute al peso dei bracci della bilancia, l'oggetto pesante pesa D/d volte il contrappeso. In pratica, il braccio più lungo veniva graduato controllandolo con pesi standard, così che al momento dell'uso il peso della merce poteva essere letto direttamente. Se fatta teoricamente, questa gradazione avrebbe richiesto di prendere in considerazione anche il peso del giogo della bilancia stessa e la sua forma, e questo richiedeva troppo lavoro. C'è un'opera, Liber de canonio (Il libro della bilancia; Moody 1952, pp. 55-76), che è spesso citata oggi per le informazioni che fornisce su questa praticissima istituzione, ma occorre anche ricordare che essa è nota soltanto attraverso un manoscritto derivato da un originale greco.
Sullo stesso soggetto generale, ma di influenza di gran lunga superiore, fu il Liber karastonis (Moody 1952, pp. 77-118), apparentemente tradotto dal testo di Ṯābit. Esso è designato abitualmente in italiano come il Libro della bilancia romana, che è esattamente il significato della parola karaston (al-Qarasṭūn in arabo), sebbene l'etimologia sia oscura. Pierre Duhem sosteneva che derivasse dal nome di una persona altrimenti ignota alla storia, Charastion, che secondo lui sarebbe stato l'inventore della 'bilancia romana', ma ciò sembra improbabile. Ricordiamo che Ṯābit ibn Qurra fu uomo di grande talento e scrisse di matematica, astronomia, medicina e filosofia. Nato a Ḥarrān, in Mesopotamia, apparteneva alla setta dei Sabi, e sebbene la sua lingua madre fosse il siriano conosceva anche le lingue greca e araba. Fu portato a Baghdad e, grazie a ciò, fu introdotto nel mondo scientifico che più tardi avrebbe tanto arricchito con le sue traduzioni e con le sue ricerche. In gioventù era stato cambiavalute, e perciò era presumibilmente esperto nell'uso di una bilancia.
Nel Libro della bilancia romana si utilizza un concetto di forza (virtus, nella versione latina) ed è presente un'argomentazione sulla velocità che tale forza può produrre in un peso variabile in ragione inversa al peso (vi sono autori moderni ‒ a dir poco ambiziosi ‒ che hanno tentato di leggere in tutto questo l'idea newtoniana di forza). Certi passaggi nel libro richiamano molto da vicino la Mechanica pseudoaristotelica, con un procedimento che è stato anche descritto da alcuni autori moderni come una dottrina delle 'velocità virtuali' o dei 'lavori virtuali'. Questa descrizione può trarre in inganno, e per i lettori che non abbiano familiarità con tali termini tecnici è necessario fare qualche precisazione; per tutto il secolo scorso, e anche oltre, tali termini sono stati considerati attribuibili agli autori di statica dell'Antichità e del Medioevo, il che provava l'importanza di quegli autori per la scienza moderna, dal momento che molti autori di meccanica oggi affrontano il problema dell'equilibrio non mediante la risoluzione delle forze ma mediante il principio dei lavori (o velocità) virtuali. In breve, se il punto di applicazione di una forza viene spostato su una distanza breve, la parte dello spostamento indotta nella direzione della forza è chiamata la sua 'velocità virtuale' (notare che lo spostamento non possiede la dimensione della velocità). Il prodotto della forza per la proiezione lungo la direzione dello spostamento virtuale del suo punto di applicazione è chiamato 'lavoro virtuale' della forza. Il 'principio dei lavori virtuali' stabilisce che la somma dei lavori virtuali di tutte le forze in un sistema in equilibrio diventa zero per ogni spostamento infinitesimale (è una sfortunata coincidenza che gli autori che si riferiscono al 'principio delle velocità virtuali' normalmente intendano la stessa cosa). Dove questo principio abbia avuto origine nel corso della storia è oggetto di dispute senza fine, che però in questa sede non interessano (la prima persona a usarlo in uno stile riconoscibilmente moderno con grande generalità analitica fu Johann Bernoulli [1667-1748]; gli autori medievali di statica erano per la maggior parte interessati a un numero molto piccolo di cambiamenti facilmente misurabili in quella che noi oggi chiamiamo energia potenziale).
Ṯābit non presenta principî che meritino veramente questo nome. Egli pensa a un giogo di bilancia sul quale sono posti dei pesi, e si concentra su quanto accade quando il giogo ruota attorno a un perno. Noi sappiamo che per valutare cambiamenti di energia potenziale (per usare concetti moderni) dobbiamo trovare il prodotto dei pesi (forze orientate verso il basso) e delle 'componenti verticali' dei cambiamenti di distanza. Ṯābit invece di queste distanze verticali prende in considerazione archi circolari che si formano nel corso della rotazione. Per cambiamenti infinitesimali, quando la bilancia è vicina all'equilibrio, entrambi forniscono la stessa risposta, e con questo semplice caso Ṯābit può provare la legge della leva di Archimede. Egli può anche provare ciò che Archimede aveva soltanto supposto, cioè che il peso distribuito di un braccio (omogeneo) della bilancia è equivalente allo stesso peso posto al centro del braccio, e ottenne quest'ultimo risultato con il metodo dell'esaustione matematica e considerando le somme integrali superiori e inferiori.
Nonostante le sue carenze, il lavoro attribuito a Ṯābit ebbe un ruolo significativo nella scienza occidentale; con qualche aiuto del Liber de canonio, contribuì a persuadere gli studiosi occidentali del fatto che la 'scienza dei pesi' era una vera scienza, con una sua propria identità, e li stimolò efficacemente a basarsi su di essa; la persona che accolse la sfida con maggiore successo fu Giordano Nemorario.
Giordano Nemorario e i suoi postulati
Giordano rimane una figura vaga. Sulla base dei suoi scritti si concorda generalmente nel considerarlo un matematico e uno scienziato di grande originalità; Leonardo Fibonacci è forse il solo europeo del XIII sec. che gli è nettamente superiore come matematico. Si è anche suggerito che Giordano sia vissuto nel tardo XII sec., ma la migliore valutazione sembra essere quella che colloca la sua attività intorno al 1240, almeno una decade o due prima del 1260, quando morì Richard de Fournival, poiché le opere di Giordano sono elencate nel catalogo della sua biblioteca. Non c'è unanimità circa il luogo apparentemente indicato nel suo nome, 'Nemorario'; alcuni hanno suggerito che egli fosse di Nemi, e altri che 'Nemorario' ("de Nemore") non si riferisse a un nome di luogo ma al suo lavoro sui numeri (de numeris). Lo si è anche identificato con il famoso domenicano Giordano di Sassonia, ma tutte queste congetture sembrano improbabili. R.B. Thomson ha riproposto la vecchia idea che egli abbia insegnato a Tolosa (Thomson 1974, 1976). È probabile che Giordano provenisse da Nemours, a sud di Parigi. Pietro Apiano, suo editore nel XVI sec., è stato criticato per avergli dato un nome che equivaleva a chiamarlo 'abitante dei boschi' (da nemus), ma il nome romano di Nemours, 'Nemoracum', deriva dai boschi (latino nemora) che circondavano quella città. È meno probabile che fosse di Namur (sulla Mosa). Nel complesso, anche se sapessimo che una di queste ipotesi è vera, essa non fornirebbe indicazioni sull'influenza della sua formazione sulla sua opera; l'unica cosa certa che si può dire di lui è che fu un pensatore di grande originalità, per quanto sia un autore abbastanza oscuro.
Giordano riuscì a combinare lo spirito aristotelico della filosofia naturale, per quanto riguarda il movimento e l'organizzazione del Cosmo, con il rigore matematico di Archimede, sebbene fosse ben lontano dall'eguagliarlo. Da Euclide e da Aristotele prese l'idea di poter formulare la sua teoria in forma assiomatica, e fece lo stesso con le opere che scrisse sulla geometria e sulla geometria della sfera (la cosa non deve sorprendere, dato il precedente euclideo), e in un trattato sull'aritmetica che stabilì un nuovo modello per il Medioevo in forte contrasto con lo stile dell'aritmetica di Boezio. I suoi tre testi principali sulla scienza dei pesi (v. Tav. I, nella quale sono incluse le figure relative ad alcuni dei postulati e teoremi discussi in seguito) hanno in comune alcuni postulati di grande importanza storica. Sebbene gli assiomi debbano, in quanto tali, essere chiari ed espliciti, quelli di Giordano sono stati interpretati in modi molto diversi, e ciò potrebbe diminuirne in qualche modo l'importanza. L'ipotesi, a volte avanzata, che non siano autentici non è del tutto convincente: gli assiomi infatti non possono essere raccolti senza alcuna sistematicità; essi devono essere utili e coerenti.
Una ragione dell'importanza di questo sistema di assiomi è che alcuni commentatori moderni hanno sostenuto di trovarvi un'anticipazione della definizione attuale del lavoro di una forza in questa semplice forma: il lavoro necessario per sollevare un peso lungo una distanza verticale è dato dal prodotto del peso per la distanza. Più avanti si dirà come ciò sia una distorsione della verità; tuttavia, quello che Giordano fa è, sotto certi aspetti, ancora più sorprendente; egli discute infatti i problemi dell'equilibrio introducendo qualcosa di simile al principio del lavoro virtuale. Ancora una volta, però, è necessaria molta cautela, poiché soltanto in secoli recenti l'uso di parole come 'lavoro', 'potenza' (tasso di lavoro) e persino 'forza' o 'peso' (inteso come 'forza' e contrapposto a 'massa') è stato definito e standardizzato. Ci si imbatte in questo problema, per esempio, proprio nel primo postulato degli Elementi: "Post. 1. Il movimento di ogni peso (ponderosus) è verso il centro [del mondo]".
La Teoria del peso contiene postulati che sono quasi identici a quelli degli Elementi; al primo postulato sono aggiunti i seguenti termini, che hanno significati estranei ai loro corrispettivi moderni e il cui senso può essere analizzato correttamente soltanto riferendosi al loro uso successivo: "e la sua forza (virtus) è un potere (potentia) di tendere verso il basso e di resistere al movimento nella direzione contraria".
Uno degli ostacoli alla comprensione del pensiero di Giordano sui problemi della statica è l'uso molto frequente di un vocabolario per così dire 'in movimento'. Il secondo postulato sembra affermare chiaramente che quanto più pesante è una cosa, tanto più veloce è la sua caduta, e ciò, appare oggi fuori luogo: "Post. 2. Ciò che è più pesante discende più rapidamente". Giordano con questo secondo postulato rende quasi certamente omaggio alla trattazione dinamica del peso da parte degli aristotelici; sebbene sia possibile interpretare questo secondo postulato a prescindere da questa idea, tale interpretazione non sembra molto plausibile e qui si presumerà che il postulato 2 sia quello che sembra essere: un'inaccettabile legge del moto per i corpi in caduta libera. Gli altri postulati sono i seguenti:
Post. 3. [Ciò che è più pesante] è più pesante nella discesa (gravius in descendendo) quando il suo moto verso il centro [del mondo] è più diretto.
Post. 4. Esso è posizionalmente più pesante (gravius secundum situm) quando, in una data posizione, il suo [percorso di] discesa è meno obliquo.
Post. 5. Una discesa più obliqua è quella che, mossa lungo una distanza [reale] data, si muove meno in direzione verticale.
Post. 6. Un oggetto è posizionalmente meno pesante di un altro quando viene fatto risalire dalla caduta dell'altro.
Post. 7. La posizione di equilibrio ("uguaglianza") [di un giogo di bilancia] è il piano dell'orizzonte.
Da una prima riscrittura di questi postulati in termini simbolici risultano le seguenti formulazioni:
Post. 1*. La caduta libera è verso il centro del mondo.
Post. 2*. v (velocità di caduta) aumenta quanto aumenta G ("pesantezza nella caduta").
Post. 3*. G diminuisce quanto aumenta θ (l'angolo del moto con la verticale).
Post. 4*. P ("pesantezza posizionale") diminuisce quando aumenta θ.
Post. 5*. d/c decresce quanto θ aumenta. [Qui d è il movimento verticale corrispondente a un movimento obliquo c; v. fig. I.1].
Post. 6*. L'equilibrio è determinato dall'equivalenza dei valori di P per oggetti contrapposti.
Post. 7*. Un giogo di bilancia è in equilibrio quando è orizzontale.
Nel postulato 6* si parla di "oggetti contrapposti" coerentemente con le interpretazioni adottate in questa sede. Negli Elementi Giordano sembra avere in mente soltanto i pesi che tirano giù una bilancia nei sensi opposti. Il fascino di tali postulati è che possono essere interpretati in maniera molto generale, e nella Teoria del peso riescono a comprendere anche il caso di pesi contrapposti su piani inclinati, uniti da una corda che passa sopra lo spigolo centrale, secondo quello che da allora è diventato un dispositivo familiare nei laboratori (fig. I.2).
Il postulato 7* richiede un commento, poiché Giordano nel seguito del trattato mostra di ritenere che un giogo orizzontale in equilibrio se disturbato ritornerà nella posizione iniziale, il che non è necessariamente vero. Egli traeva questa convinzione dal caso del giogo di una bilancia, concepito per tornare alla posizione orizzontale quando è in stato di equilibrio, ponendo il centro di gravità del giogo e dei piatti ben al di sotto del fulcro. I termini da lui utilizzati non sono quelli adottati nella nostra formulazione, in cui si sono distinti i due concetti G e P. Egli potrebbe aver inteso diversamente; la forma verbale dei postulati rende difficile l'interpretazione. Se G e P devono essere identici, il significato dei postulati 3 e 4 è lo stesso; se devono essere distinti i postulati 2 e 3 sembrano aver poco a che fare col resto del trattato.
Va notato che i postulati non riportano indicazioni circa le precise relazioni matematiche che esistono tra le variabili citate come in crescita e in diminuzione. Non si può ritenere che siano tutte in proporzione semplice ‒ infatti, sapendo che alcune dipendono dal coseno dell'inclinazione con la verticale, certamente non lo sono. I postulati non sono presentati in modo abbastanza preciso perché Giordano ne potesse far derivare tutti i suoi teoremi in maniera rigorosa. Si possono fare solo delle ipotesi plausibili su cosa egli avesse in mente dal modo in cui sviluppa il suo sistema e ne trae le conclusioni. Le citazioni che seguono sono tratte dal resto del paragrafo e sono collocate qui soltanto per poterle paragonare con le loro versioni precedenti (non reinterpretate o minimamente interpretate). Esse si adattano bene al sistema completo quale si è venuto evolvendo dal tempo della stesura della Teoria del peso.
Post. 2**. V=kG, dove k è una costante.
Post. 3**. G=Wcosθ.
Post. 4**. P=Wcosθ.
Post. 5**. d/c=cosθ.
Post. 6**. Come i precedenti due postulati: i valori di P sono usati come verifica di equilibrio.
Si è ritenuto lecito introdurre i rapporti di coseno, almeno nel contesto della Teoria del peso, poiché in un punto di quel testo l'autore scrive: "per proporzione di inclinazioni io non intendo il rapporto degli angoli, ma delle linee prese nel punto in cui una linea orizzontale taglia un uguale segmento sulla verticale". Prima di poter introdurre il rapporto di coseno, tuttavia, si deve essere sicuri che l'autore intendesse considerare spostamenti minimi, o perfino spostamenti infinitesimali, in modo che, per esempio, la direzione istantanea di un moto circolare potesse essere giudicata da una tangente al cerchio piuttosto che da un lungo movimento sull'arco. Più avanti si dimostrerà che questa era effettivamente la sua intenzione.
Il primo teorema dell'equilibrio di Giordano
Il primo teorema degli Elementi, identico a quello della Teoria del peso, è fondamentale; viene usato come base per la prova di altri teoremi, in particolare per la legge della leva. Il teorema è presentato e spiegato in modi leggermente diversi, e qui ci si attiene agli Elementi, anche se è un testo in cui Giordano sembra limitarsi ai problemi della leva (la Teoria del peso, trattando un problema di piani inclinati, può fare uso del primo teorema interpretandolo in un modo nuovo, e sembra che la possibilità di quest'uso sia stata scoperta in maniera fortuita dopo che gli Elementi erano stati scritti). Di seguito si riporta l'enunciazione del teorema senza tentare di trascriverlo in termini moderni, sebbene si aggiunga una frase implicitamente compresa nel rozzo latino originale.
"Teor. 1. La proporzione della velocità di discesa tra corpi pesanti è la stessa di quella dei pesi presi nello stesso ordine; ma la stessa proporzione [quella tra i pesi, che si comprende ora essere collegati] è quella della discesa rispetto all'ascesa contraria, ma con l'ordine dei termini invertito" (il testo dell'originale latino è il seguente: Prop. 1. Inter quelibet gravia est velocitatis in descendendo et ponderis eodem ordine sumpta proportio, descensus autem et contrarii motus proportio eadem sed permutata).
Nella prima parte del teorema si eguaglia il rapporto delle velocità e il rapporto dei pesi semplici (non i pesi posizionali). Usando a e b sottoscritte per distinguere i due pesi si ha:
va/vb = Wa/Wb .
Segue un'affermazione che riguarda il caso di un equilibrio perturbato (alcuni autori hanno cercato di interpretare diversamente questo teorema, ma in maniera non convincente). Si tratta di un'uguaglianza del rapporto dei pesi semplici dei corpi con il rapporto inverso dei corrispondenti spostamenti verticali:
Wa/Wb = db/da .
La prima parte del teorema risulta dai postulati 2 e 3. La seconda parte risulta dai postulati 4, 5 e 6. Usando le nostre versioni dei postulati (per desiderio di chiarezza piuttosto che di autenticità storica) si avrà:
[1] Pa = Pb [la condizione per l'equilibrio, dal postulato 6**];
[2] Wacosθa =Wbcosθb [da (1) e dal postulato 4**];
[3] da = ccosθa e db = ccosθb [dal postulato 5**]; quindi
[4] Wada = Wbdb [da (2) e (3)].
Questo insieme di ipotesi sembra congruente con l'interpretazione dell'autore della Teoria del peso. Giordano potrebbe aver fatto queste stesse ipotesi fin dall'inizio. Come minimo, egli non poteva avere ottenuto una prova del suo teorema senza ipotizzare implicitamente le stesse relazioni funzionali [2] e [3], nonostante si debba ammettere che negli Elementi egli sembra avere ottenuto la sua prova in maniera semi-intuitiva.
Soltanto quando il risultato è applicato negli esempi appare chiaro quanto sia straordinario. La comprensione del testo non è facilitata dalle figure disegnate sui margini, che di solito sono soltanto due linee verticali contrassegnate con indicatori di direzione e che suggeriscono semplicemente dei moti verticali. L'intenzione, tuttavia, è di confrontare le 'componenti' verticali dei moti, producendo così quelli che sono i nostri valori d (il nostro approccio astratto, che non richiede diagrammi, è reso possibile dall'uso di una notazione algebrica, per non parlare di postulati che recano informazioni più esplicite di quelle di Giordano). Cominciamo con un esempio preso dalla Teoria del peso che è totalmente accettabile, cioè il caso di due corpi connessi in equilibrio su un piano inclinato. Il testo parla di due corpi, uno dei quali ha massa maggiore dell'altro. Il corpo che ha massa maggiore è mosso leggermente verso il basso (esso poteva altrettanto facilmente essere mosso verso l'alto, ma l'autore non aveva colto pienamente le possibilità del suo metodo). Si presume che i due pesi siano legati da una corda, cosicché il movimento di un peso verso l'alto su un piano è lo stesso dell'altro verso il basso sul suo piano. Per l'equilibrio, l'aumento della quantità Wd di un oggetto sarà controbilanciato dalla diminuzione della Wd dell'altro. Che vi sia o meno una consapevolezza della ramificazione del concetto di lavoro, questo per ora non ha conseguenze sul risultato, ed è meglio per il momento usare una descrizione neutra. Gli autori di questi trattati erano matematici sufficientemente bravi da trasformare questo risultato qualitativo in una relazione geometrica o trigonometrica equivalente a W1cosθ1 = W2cosθ2 (fig. I.2). Il risultato rimane valido non soltanto per moti di grandezza infinitesimale, ma anche per moti più ampi.
Diversamente avviene nel caso della leva. Supponiamo che il testo contenga soltanto problemi inerenti ai piani inclinati, e che si debba riflettere sul modo in cui Giordano è arrivato alla sua idea di far dipendere l'equilibrio dal "peso posizionale" (postulato 6). Con la nostra conoscenza su come risolvere il problema dell'equilibrio scomponendo le forze, si può facilmente vedere che la tensione della corda deve essere uguale e opposta al "peso posizionale" (Wcosθ) di ciascuno dei due singoli pesi. In altre parole, i due pesi posizionali devono essere identici. Questa ricostruzione è improbabile perché i "moti inclinati" prevalentemente trattati non sono affatto moti in linea retta, ma moti lungo archi circolari originati da punti su una leva che oscilla su un perno. C'è un'altra possibilità. Se si abbandona la distinzione tra "pesantezza discendente" (G) e "pesantezza posizionale" (P), si giunge esattamente alla stessa conclusione circa l'equivalenza dei due valori di Wd. Forse Giordano ha sviluppato la statica partendo da una base dinamica (aristotelica), come potrebbero far supporre i suoi tre primi postulati; il caso è lungi dall'essere risolto.
Applicazioni del teorema di Giordano Nemorario
Gli Elementi di Giordano sono un piccolo trattato, di poche pagine e lungo solo un quinto della Teoria del peso; eppure finora ne abbiamo analizzato solo poco più di una pagina, e ci sono altri otto teoremi. Il secondo teorema tratta della bilancia (o piuttosto della leva) che ha pesi uguali alle estremità dei bracci di uguale lunghezza. Ciò è provato dal fatto che quando il giogo è orizzontale è in equilibrio, e viceversa (l'inverso è però sbagliato, poiché anche un giogo di bilancia inclinato può essere in equilibrio). Il terzo teorema mostra che la lunghezza dei pendenti che reggono i pesi sullo stesso tipo di bilancia non ne influenza l'equilibrio (dimostrare geometricamente che i valori di d non dipendono dalla lunghezza del pendente è semplice, a meno che il pendente non sia attaccato rigidamente). Il quarto teorema riguarda una semplice bilancia a bracci uguali, e stabilisce essenzialmente che quanto più il braccio si avvicina all'orizzontalità, tanto più piccola diventa la pesantezza posizionale di ciascuno dei pesi. Ciò manifesta la propensione di Giordano ad accettare larghi archi di movimento sui quali le inclinazioni cambiano direzione, invece degli archi infinitesimali, corrispondenti ai valori "istantanei" dell'angolo che prima si è chiamato θ. La figura disegnata nel testo (fig. I.3) mostra un giogo di bilancia ACB con il fulcro in C. Tre archi uguali (DH, AZ, EG) sono tracciati sul cerchio disegnato dalle estremità del giogo. Questi archi sono quelli che decidono l'inclinazione della discesa nelle vicinanze di D, A ed E. I segmenti KM e RX sulla verticale centrale sono chiaramente più piccoli di CF, e perciò è affermato che il peso è posizionalmente più leggero in D e in E piuttosto che in A. Come si può vedere, con l'allontanarsi del peso da A lungo il cerchio, cosθ diventa minore di 1 e progressivamente più piccolo, così che il peso posizionale si riduce continuamente (di fatto fino a zero). Ma cosa sono quei grandi archi circoscritti nel diagramma? Giordano sembra pienamente consapevole del problema, poiché scrive, abbastanza esplicitamente, che gli archi possono essere "piccoli a piacere", e che essi determinano l'obliquità della discesa "nelle vicinanze più immediate". È vero che questi testi utilizzano spesso grandi archi per illustrare i teoremi, ma questo avviene anche nei moderni libri di testo; simili figure servono solo ad aiutare l'immaginazione. Le idee che esse rappresentano sono state padroneggiate con facilità soltanto dopo l'avvento del calcolo differenziale. L'esempio di un caso simile sarà fornito tra breve, tratto dalla Teoria del peso.
C'è un solo teorema negli Elementi (il numero 8) che mostra chiaramente come usare il concetto di pesantezza posizionale in un modo non banale (gli altri teoremi fanno semplicemente deduzioni sulla pesantezza posizionale relativa dei pesi nelle diverse circostanze). Si tratta del principio generale della leva, provato con successo da Archimede in modo completamente diverso, e in maniera insoddisfacente da Ṯābit ibn Qurra. Si è già dimostrato che quest'ultimo, come l'autore della Mechanica pseudoaristotelica, suppone che il peso minore su un braccio più lungo possa bilanciare il peso maggiore su un braccio più corto, in quanto deve compiere una distanza relativamente più grande lungo l'arco circolare che lui stesso disegna. Giordano sa che bisogna confrontare le "distanze verticali" di salita o di caduta (i nostri valori d). Procedendo in tal modo si ricava immediatamente la legge della leva: in triangoli simili, il rapporto dei valori d è lo stesso del rapporto delle corrispondenti lunghezze dei bracci, che è allora l'inverso del rapporto dei pesi (fig. I.4). Questa è la legge della leva.
Si è molto discusso, risalendo fino ad Appiano, sul fatto che Giordano abbia usato consciamente o meno il suo primo teorema nel senso spiegato sopra, ed è difficile capire perché questo punto sia stato così dibattuto. Il teorema non è espresso in modo particolarmente chiaro, ma nel Medioevo ci sono molti esempi di usi peggiori dell'algebra verbale. Il teorema è citato (ma senza indicarne il numero) nella dimostrazione del teorema 8, particolarmente interessante proprio per questo collegamento, per mezzo del quale ci si avvicina alla formulazione della nozione di lavoro più che in ogni altro passaggio di questi scritti. Giordano afferma che "ciò che è sufficiente a sollevare [un peso a una certa posizione] deve essere sufficiente a sollevare [un altro peso lungo una certa distanza]". Questa terminologia (in latino, quod sufficit attollere) sembra rivelare che Giordano sentisse di avere a che fare con una sorta di lavoro o di energia, poiché cos'altro "è sufficiente a sollevare un peso"?
Il teorema 9 dimostra un principio usato dall'autore del Liber de canonio ricordato sopra: l'equilibrio di una bilancia non verrà disturbato se i pesi uniformemente distribuiti lungo un braccio della bilancia sono sostituiti con un solo peso, uguale alla loro somma e sospeso nel punto mediano della loro distribuzione.
I teoremi 6 e 7 degli Elementi contengono degli errori. Entrambi fanno affermazioni sulla pesantezza posizionale dei pesi attaccati a bracci di bilancia piegati. Non è necessario discuterli in dettaglio, ma (dal momento che questo è stato talvolta negato) si deve registrare che il primo è corretto, mentre il secondo è corretto per molte anche se non per tutte le configurazioni; e ancora, che entrambi sono corredati da prove deboli, troppo basate sul diagramma e sull'istinto. È significativo che nella Teoria del peso essi siano sostituiti con teoremi corretti.
Per terminare l'analisi di questi due notevoli trattati, basta esaminare solo uno dei molti teoremi dell'ultimo lavoro (teorema 8, parte I), dove si discute la tecnica di utilizzazione dei differenziali. Una leva priva di peso curva verso il suo fulcro e con bracci diseguali, ma che hanno pesi uguali alle loro estremità, si inclina in modo che i pesi (A e B nella fig. I.5) siano a uguale distanza dalla verticale centrale (BE=GA). Il testo non dice che il sistema è in equilibrio (il che è vero), ma che i pesi saranno di uguale pesantezza (posizionale). Più avanti l'autore prende in considerazione anche un caso di pesi ineguali, ma questo semplice esempio è sufficiente per illustrare il metodo generale.
Si consideri un piccolo movimento che spinge la leva da un lato, così che A si sposta verso X e B verso M, essendo i movimenti sul fulcro necessariamente uguali. "B salirà verticalmente più di quanto A scenda verticalmente, il che è impossibile", dice il testo, "poiché essi sono di uguale peso" (fig. I.5: PM>TX). Con il termine 'impossibile' l'autore intende che la condizione iniziale di uguali pesi posizionali è stata violata. Inclinando la leva in modo che A si muova verso L e B verso H, il movimento verticale di A è maggiore di quello di B (LN>RH), il che è di nuovo "impossibile". L'eccedenza di B su A, che prima era positiva, ora è negativa. L'unica possibilità che rimane è perciò l'equilibrio nella posizione originale, in cui AG e BE sono uguali. Aggiungere i necessari dettagli geometrici a questa dimostrazione può essere un esercizio per il lettore che lo desideri; va notato che questo è un caso classico di problema variazionale dello stesso tipo di quelli in cui Archimede (nel contesto della geometria) era maestro.
Biagio Pelacani e la Scuola italiana
I vari trattati del tipo di quello di Giordano furono molto copiati nel XIV sec. e oltre; spesso furono citati in opere su soggetti correlati o furono commentati (Brown 1967). Uno di questi commenti fu pubblicato da Apiano nel 1533 insieme alla sua versione del Liber de ponderibus: egli lo definì semplicemente aliud commentum, "un altro commento". È il più lungo dei commenti del suo genere, ma sembra scritto nell'ignoranza della Teoria del peso. Il suo autore ha una buona comprensione della struttura del sistema assiomatico di Giordano, e richiama l'attenzione più chiaramente di quanto abbia fatto Giordano stesso sul principio legato alla quantità Wd, su cui si basa la legge della leva. Ma egli mostra anche il modo in cui la statica stava di nuovo volgendo in direzione della dinamica.
Nel 1328 Tommaso Bradwardine, nel Tractatus de proportionibus, III, 2 (Moody 1952, Appendice II), aveva commentato il secondo postulato di Giordano (quello che mette in relazione velocità e peso), e l'aliud commentum mostra la conoscenza delle riformulazioni di Bradwardine della legge aristotelica della caduta libera. Si sono fatte molte ipotesi circa la paternità di questo commento, perfino che potrebbe essere attribuito allo stesso Bradwardine. Esso mostra come molti aristotelici tardo-medievali pensassero alla scienza dei pesi come poco più che un'appendice della teoria della caduta libera, in cui la bilancia stessa era introdotta soltanto come una scomoda complicazione ‒ quando si esercita una pressione su un lato di una bilancia si sente la resistenza di cui parla la teoria di Aristotele sulla resistenza di caduta. Non tutti però presero la strada della dinamica; coloro che rifiutarono fermamente di farlo erano spesso i seguaci della tradizione archimedea.
Due altri commenti che documentano un interesse per la scienza dei pesi in generale furono composti da Biagio Pelacani intorno alla fine del XIV secolo. Nato probabilmente a Parma intorno al 1345, Biagio si spostò tra le Università di Pavia, Bologna, Padova e Firenze. Nei primi anni del XV sec., dopo aver ottenuto una certa fama in Italia, insegnò sia a Pavia che a Padova, ma già prima del 1388 si era addottorato a Parigi, dove aveva sviluppato una forte inclinazione per alcune delle idee scolastiche sul moto in circolazione a Parigi e a Oxford. Il suo primo scritto sui pesi risale al periodo successivo al soggiorno parigino. Si tratta di cinque quaestiones ispirate chiaramente ai postulati di Giordano. Il secondo trattato è un nuovo manuale scolastico che resta fortemente ancorato alla tradizione di Giordano Nemorario mescolandovi alcuni elementi archimedei, sebbene l'opera nel suo insieme abbia un'impronta decisamente aristotelica.
Il commento aristotelico era il genere privilegiato di Biagio, ed egli era attratto dal Libro dei pesi proprio per i suoi toni aristotelici. Fu una scelta infelice: Biagio ne ricavò infatti alcune idee destinate a non avere sviluppi significativi, che egli preferì talvolta a validi argomenti basati sull'idea di pesantezza posizionale. Nel suo calcolo della pesantezza potenziale, Biagio cerca con scarso successo di comprendere la curvatura di un cammino potenziale; in una parte usa le idee aristoteliche per dimostrare che la legge della leva non funziona bene in un mezzo resistivo. L'importanza storica di Biagio non è da ricercare nei coraggiosi ma imperfetti contributi alla statica, bensì nel fatto che egli diffuse in Italia le idee che aveva incontrato per la prima volta a Parigi.
Il trasferimento di queste idee in Italia fu casuale, anche se il pensiero scientifico del Rinascimento trattò con durezza, spesso addirittura con poca intelligenza, gli scritti di Giordano sulla statica. Ciò era in parte dovuto alla comprensibile ossessione di riscoprire le opere di Archimede. Quando nel 1577 Guidobaldo Dal Monte criticò Giordano per la sua mancanza di rigore e per la sua erronea teoria dell'equilibrio su un piano inclinato, egli si dimostrò inferiore all'uomo che criticava, perché sostituì una teoria sbagliata a una giusta (Drake 1969, pp. 46, 50). I testi di Giordano, come molti altri testi scientifici medievali, erano stati copiati da studiosi a volte poco attenti, così che si perpetuavano piccoli errori di enunciazione. Ci furono anche alcune redazioni intelligenti ‒ per esempio, quella anonima nel Corpus Christi College di Oxford, ms. 252 ‒ ma relativamente pochi furono gli scrittori che avevano la stessa sensibilità matematica di Giordano. La via più facile in proposito era quella della filosofia naturale di Aristotele. Come si comportava una bilancia, in equilibrio secondo la legge della leva, se un peso veniva sospeso più vicino dell'altro al centro del mondo? Come bisogna considerare il fatto che le linee passanti per i pesi sui bracci di una normale bilancia e dirette verso il centro del mondo, non sono esattamente parallele, ma convergono verso quel centro? Simili problemi, che sembrano campati in aria, non erano banali, ma non erano alla portata di menti di secondo piano, incapaci di ragionare lungo le linee tracciate da Giordano, che aveva fornito una chiave per la loro soluzione. Ciò che importava, tuttavia, era che 'la torcia' ormai passata all'Italia fosse tenuta 'accesa' fino a quando Galilei e i suoi seguaci ne avrebbero potuto nuovamente fare buon uso.
La cinematica nel XIV secolo
di Johannes M.M.H. Thijssen
È indiscusso che gli studiosi del XIV sec. abbiano dedicato un notevole impegno allo studio degli aspetti spaziotemporali del movimento, ambito che oggi chiameremmo 'cinematica'. Che si tratti del settore probabilmente più studiato della scienza medievale del moto lo si deve principalmente alle ricerche del fisico francese Pierre Duhem (1861-1916). Nei primi anni del XX sec. Duhem sostenne che i traguardi della scienza del XVII sec., qual è rappresentata da Galilei (1564-1642) e da Descartes (1596-1650), erano in qualche modo già stati raggiunti nel XIV secolo. Nel campo della meccanica egli individuò in particolare due elaborazioni dottrinali ‒ a suo avviso ‒ felici, ossia le teorie del moto dei proietti e dei corpi in caduta libera, e la dottrina della latitudine delle forme. Esse gli apparvero anticipare, o quantomeno condurre direttamente, al principio di inerzia e alle leggi della caduta libera.
Sebbene la tesi di Duhem sia oggi ritenuta unanimemente erronea, essa ha sortito comunque l'effetto di definire un nucleo di argomenti per la successiva storia della scienza medievale del moto. Secondo l'attuale interpretazione della cinematica tardo-medievale, gli studiosi del Medioevo si preoccuparono di problemi alquanto diversi da quelli affrontati agli esordi della scienza moderna. Tuttavia, alcune problematiche furono comuni agli autori del XIV e a quelli del XVII sec.; ciò comporta che, più che anticipare, la scienza del Tardo Medioevo pose le basi di quella moderna.
Oltre a prospettare alcuni fondamentali problemi ai primi pensatori moderni, la cinematica del Tardo Medioevo presenta anche un grado significativo di continuità terminologica con gli inizi della moderna fisica del moto; questa continuità si rivela, in particolare, nel linguaggio e nella matematica della cinematica, ossia nel vocabolario tecnico e nell'approccio matematico a determinati problemi della fisica del moto. Tale continuità cela però importanti cambiamenti concettuali (Grant 1996).
Fu la Fisica di Aristotele a fornire il quadro intellettuale entro cui si sviluppò la cinematica del XIV secolo. Infatti, dal XIII al XVII sec., non vi fu altro libro di filosofia naturale tanto influente da essere metodicamente letto e commentato nelle università per quasi cinquecento anni. Ciò non è vero soltanto per i commenti alla Fisica, ma anche per opere indipendenti dedicate alla filosofia naturale in generale, o alla cinematica in particolare. Poiché la cinematica tardo-medievale non era distinta chiaramente da altri aspetti del moto trattati nella Fisica ‒ quali, per esempio, la sua natura e le sue cause ‒ e poiché il problema del moto si inseriva in una più vasta discussione sul concetto generale di cambiamento, è opportuno prima di tutto delineare il contesto più ampio, per affrontare poi le tre più significative aree problematiche legate al concetto aristotelico di moto: la sua natura, le sue cause e le sue relazioni con il tempo e con la distanza.
Partiamo da quegli studiosi che appartennero ai due più importanti centri della filosofia naturale del XIV sec., cioè Parigi e Oxford. A seguito degli studi di Anneliese Maier, è consuetudine distinguere due scuole principali, quella di Giovanni Buridano (1290 ca.-1358 ca.) a Parigi e quella di Tommaso Bradwardine (1290-1349) al Merton College di Oxford. A Parigi, Giovanni Buridano fu seguito da Nicola Oresme (1320 ca.-1382), Alberto di Sassonia (1316-1390) e Marsilio di Inghen (1330 ca.-1396). I maggiori protagonisti del Merton College furono invece Richard Kilvington (m. 1561), Riccardo Swineshead (attivo tra il 1340 e il 1355), Guglielmo Heytesbury (m. 1372/1373) e Giovanni Dumbleton (attivo tra il 1338 e il 1348). Riccardo Swineshead (da non confondersi con i suoi omonimi e contemporanei John e Roger) fu designato dagli autori più tardi come Calculator ('il Calcolatore'), mentre il gruppo del Merton nel suo complesso fu chiamato Calculatores (la definizione di 'Mertoniani' è una creazione storiografica moderna; Sylla 1982). Le ricerche condotte nel corso dell'ultimo decennio hanno rivelato con maggiore precisione le connessioni ‒ già notate dalla Maier ‒ tra queste due scuole, che in realtà appaiono ora meno omogenee di quanto precedentemente era stato supposto (Caroti 1993; Sylla 1997).
Le Università di Padova e di Bologna furono importanti principalmente come centri di trasmissione della fisica 'francese' e 'inglese' del XIV secolo. I due iniziatori italiani furono Giovanni di Casale (attivo intorno al 1346) e Francesco da Ferrara (attivo intorno al 1352). Un altro studioso di rilievo fu Biagio Pelacani, che insegnò prima a Pavia, poi a Bologna e a Padova, per tornare infine, nell'ultima decade del XIV sec., a Pavia. Il suo interesse per la cinematica risulta evidente dai suoi commenti alla Fisica di Aristotele e a una delle opere di Bradwardine, così come da vari trattatelli separati. Altri due dottori padovani attivi al volgere del secolo furono Angelo da Fossambruno (attivo intorno al 1402) e Giacomo da Forlì (m. 1413). Le loro opere di fisica mostrano dimestichezza sia con le vedute degli studiosi del Merton College sia con quelle del gruppo di Parigi. È necessario però distinguere l'impatto storico dei contributi italiani dalla loro rilevanza scientifica. Gli storici hanno generalmente considerato la maggior parte delle opere italiane sulla cinematica come opere non originali o, secondo la recente definizione di uno storico, come 'azioni di retroguardia'; un'immagine che negli ultimi dieci anni non ha subìto cambiamenti significativi (Lewis 1980; North 1992).
Lo sfondo concettuale
La Fisica fu soltanto una delle diverse opere che Aristotele dedicò alla filosofia naturale, ma nella percezione medievale divenne la più importante. Essa infatti fu considerata come l'opera che forniva una definizione dei principî e delle proprietà più generali delle entità naturali, cioè delle sostanze che grazie a una causa interna sono in grado di cambiare. Dato che la trattazione aristotelica del cambiamento è formulata in termini di materia e di forma, queste divennero anche i più importanti principî esplicativi della fisica medievale. La forma è il principio che porta con sé le proprietà essenziali di una sostanza, e cioè di ogni oggetto reale, determinando 'che cosa' l'oggetto sia, o meglio quale sia la sua natura specifica. La materia riceve passivamente la forma.
Aristotele aveva introdotto la teoria della forma/materia in risposta ai dilemmi logici sollevati dai filosofi eleatici Parmenide e Zenone, i quali avevano sostenuto che, poiché nessuna cosa esistente viene in essere o perisce, ogni cambiamento è in realtà soltanto apparente. Infatti, secondo quanto Aristotele riferisce, essi avevano argomentato che quel che viene in essere deve farlo o da ciò che già esiste ‒ nel qual caso non vi è un autentico venire in essere ‒ o dal nulla assoluto, ipotesi considerata del tutto assurda. Partendo da queste basi logiche, Parmenide e Zenone erano arrivati a negare che il cambiamento fosse realmente possibile.
La teoria aristotelica muove dalla premessa che il cambiamento percepito attraverso i sensi sia reale. Infatti, secondo Aristotele, gli oggetti del mondo sono composti da una materia soggiacente e da una forma imposta. Mentre dal punto di vista della materia il cambiamento implica sempre una continuità, per cui il sostrato soggiacente non cambia, dal punto di vista della forma il cambiamento comporta una modificazione reale, che consiste in successive sostituzioni di una forma con un'altra. Per esempio, se un oggetto nero diviene bianco, la materia o il sostrato rimane, laddove la forma della nerezza è sostituita dalla forma della bianchezza. In modo simile, se una ghianda diventa una quercia, il cambiamento può essere descritto in termini di continuità del sostrato cui viene imposta una nuova forma. Tuttavia, nella visione di Aristotele, la sostituzione di una forma con un'altra non deve essere considerata una transizione dal non essere all'essere, come volevano Parmenide e Zenone, ma un passaggio dalla potenza all'atto. Il nero, o piuttosto il non bianco, è potenzialmente bianco; divenendo bianco, esso non fa altro che divenire in atto ciò che era già in potenza. Allo stesso modo, una ghianda è in potenza una quercia. In questa maniera, facendo appello alla potenza e all'atto, la dottrina aristotelica superava, risolvendoli, i dilemmi logici dei filosofi eleatici.
Aristotele e i suoi seguaci medievali consideravano materia e forma costituenti inseparabili di ogni singola cosa, naturale o creata artificialmente. Negli oggetti naturali, la natura specifica dell'oggetto lo predispone a determinati tipi di comportamento, in particolare a ogni sorta di cambiamento naturale. Il fuoco, per esempio, ha un impulso interno a trasmettere calore, attribuibile alla sua stessa forma. Allo stesso modo, è la forma della ghianda a determinare che le ghiande si sviluppino naturalmente in querce. Al contrario delle sostanze naturali, i manufatti, mancando di questa fonte interna, non possono cambiare in modo naturale; un vestito, per esempio, non avrà mai un impulso interno a cambiare. Partendo da queste premesse "non ci deve rimanere nascosto che cosa sia il movimento. È inevitabile, infatti, che, se questo si ignora, si ignori anche la natura" (Physica, 200b 10-15). Definire la natura del movimento fu quindi il compito intrapreso da Aristotele nella Fisica, per cui gli altri libri naturales, affrontando soltanto aspetti particolari degli oggetti naturali, furono sistemati attorno a essa; questa suddivisione dei libri naturales era di norma presentata nei prologhi dei commenti a una particolare opera aristotelica di filosofia naturale.
Esemplare per il contesto concettuale della Fisica è la divisione proposta da Giovanni Buridano. Nei libri naturales Buridano individua due tipi fondamentali di cambiamento, ossia il cambiamento locale (ad ubi) e il cambiamento rispetto alla forma sostanziale (ad formam). Al primo tipo appartengono i cosiddetti moti semplici, tra i quali si distinguono il moto rettilineo 'dal basso verso l'alto' o 'dall'alto verso il basso' nella regione sublunare, e il moto circolare dei corpi celesti, i cui principî basilari sono discussi nel De caelo. Una trattazione dei principî generali del cambiamento riguardante la forma è offerta invece dal De generatione et corruptione. Nello schema di Buridano, i cambiamenti relativi alla forma sono di tre tipi, cioè generazione e corruzione, alterazione, aumento o diminuzione. Il processo di generazione e corruzione comporta un cambiamento intrinseco della forma sostanziale. Così, per esempio, quando la sostanza del legno si muta nella sostanza della cenere, la forma del legno è sostituita da quella della cenere. L'alterazione è invece un cambiamento estrinseco secondo la forma, nel senso che predispone un oggetto al ritiro o all'imposizione di una forma sostanziale. Essa costituisce quindi un cambiamento qualitativo, come quando un oggetto bianco diventa nero o un oggetto freddo diventa caldo. L'altro tipo di cambiamento estrinseco secondo la forma riguarda i cambiamenti quantitativi che accompagnano quelli della forma sostanziale, ed è rappresentato dall'aumento o dalla diminuzione.
Gli altri libri naturales, come i Meteorologica o i Parva naturalia, furono considerati opere specialistiche, in quanto analizzavano singoli aspetti di quei tipi di cambiamento che ricevevano una trattazione più generale nella Fisica, nel De caelo o nel De generatione et corruptione. Da questa divisione emerge che nel quadro concettuale aristotelico ‒ così come esso fu interpretato dagli studiosi medievali ‒ il moto locale era considerato come uno dei quattro tipi di cambiamento, e che l'analisi del moto procedeva parallelamente all'analisi del cambiamento in generale.
La natura del moto
I primi tre capitoli del Libro III della Fisica fornirono il contesto per tutte le speculazioni su quale tipo di ente fosse il moto. Quando i pensatori tardo-medievali discussero le idee di Aristotele sulla natura del moto, sia nei commenti alla Fisica sia in altri lavori, essi concentrarono la loro attenzione su due problemi principali, il primo dei quali concerneva l'adeguatezza della definizione aristotelica di moto e il secondo il suo status ontologico.
Una questione che i commenti del XIV sec. abitualmente sollevavano all'inizio del Libro III della Fisica era se la definizione del moto aristotelica fosse da considerare valida (bona). Nella versione medievale latina della Fisica la definizione del moto data da Aristotele era di solito resa attraverso l'espressione 'l'atto dell'ente in potenza in quanto è in potenza' (actus entis in potentia secundum quod in potentia). Di essa, più tardi, Descartes avrebbe scritto che constava di 'parole magiche' tanto oscure che era preferibile lasciarle in latino. È interessante notare come i dubbi di Descartes riguardassero innanzi tutto la necessità stessa di definire il moto. In effetti, mentre nella concezione cartesiana il moto era un concetto basilare conosciuto attraverso l'esperienza, secondo Aristotele e i medievali esso doveva essere definito, in quanto la definizione ‒ che esprime ciò che una cosa è (quid est) ‒ era considerata uno dei requisiti fondamentali della conoscenza scientifica.
La definizione aristotelica del moto non poteva non sollevare un certo numero di questioni, in particolare rispetto alle nozioni di potenza e di atto; i commenti dei filosofi arabi Avicenna e Averroè fornirono il materiale per le discussioni trecentesche in merito al problema. Avicenna aveva osservato che un oggetto capace di movimento (mobile) possedeva la duplice potenza di passare dalla quiete al movimento e di continuare il suo movimento fino a raggiungere il suo obiettivo finale (terminus motus). Sotto questo profilo, il moto stesso avrebbe potuto essere considerato il primo atto dell'oggetto mobile, mentre il termine finale del moto ne costituiva il secondo. La distinzione di Avicenna suscitò nei pensatori medievali un dibattito volto a chiarire se la definizione di Aristotele concernesse la generica disposizione dei corpi al movimento, oppure la potenza di un corpo in movimento di raggiungere uno specifico obiettivo. In generale, essi conclusero che Aristotele aveva voluto indicare la potenza verso il termine finale del moto, sebbene lo stesso Avicenna non avesse assunto una posizione precisa a questo riguardo.
Un'altra importante distinzione introdotta da Avicenna fu quella tra moto come processo e moto come proprietà. Nel primo senso, il moto è visto come un essere successivo, non permanente in un corpo mobile. La mente, astraendo dal continuo cambiamento di posizione del corpo mobile, rappresenta il moto come un'unità simultanea. Nel secondo senso, il moto è considerato una proprietà dell'oggetto mobile, e precisamente la proprietà di essere in un dato momento in una certa posizione e immediatamente dopo in un'altra. La proprietà dell'essere in moto è tale che essa cambia di continuo. Come proprietà il moto inerisce al soggetto, cioè al corpo mobile, e ha un carattere permanente (esse stabile). Questa visione del moto fu ulteriormente sviluppata da Giovanni Buridano e Biagio Pelacani, che tuttavia non fecero esplicito riferimento ad Avicenna. In particolare, Biagio sostenne che il moto locale non è altro che una qualità intrinseca al corpo mobile, che ammette una varietà di gradi; Anneliese Maier giudicò questo concetto non distante dalla formulazione del principio di inerzia, secondo cui il moto è uno stato che non necessita di alcuna causa per la sua prosecuzione (Maier 1958).
Il principale contributo di Averroè alla discussione sulla definizione aristotelica del moto consistette nel considerare l'essere potenziale del moto (ens in potentia) come un passaggio successivo dalla potenza all'atto (exitus de potentia ad actum). In altre parole, nella visione di Averroè un corpo mobile non esiste in potenza, ma passa dall'essere potenziale all'essere attuale essendo già parzialmente in atto. Tuttavia, fintanto che il moto non raggiunge il suo obiettivo finale (terminus motus), esso è anche in potenza.
La maggior parte dei commentatori seguì l'interpretazione che Averroè diede della definizione aristotelica. Giovanni di Jandun e Giovanni Buridano, per esempio, ritennero opportuno evidenziare che un corpo mobile, che in quanto tale era in moto in potenza, possedeva una tendenza (tendentia) verso l'atto del moto. L'ens in potentia, o l'essere potenziale di un corpo mobile, non è semplicemente uno stato intermedio tra la potenza e l'atto (così come l'acqua tiepida potrebbe essere vista come un imperfetto stato intermedio tra il caldo e il freddo), ma contiene anche un aspetto dinamico, che è espresso precisamente dalla sua tendenza verso un ulteriore obiettivo.
Una linea completamente diversa fu adottata da Guglielmo di Ockham, secondo il quale la definizione di Aristotele deve essere interpretata nel senso che un corpo mobile è in atto in quanto si trova adesso in una posizione diversa da quella in cui era immediatamente prima, ed è in potenza in quanto immediatamente dopo si troverà in una posizione in cui non è ancora. Il mobile è in atto rispetto agli spazi già attraversati successivamente, è in potenza rispetto agli spazi che devono ancora esserlo. In tal modo, Ockham rifiuta l'idea che il moto sia un''attualità' distinta dal corpo mobile in sé.
Dal quadro fin qui delineato emerge chiaramente che, sebbene avessero vedute divergenti, i commentatori del XIV sec. concordavano sostanzialmente sul fatto che la definizione di Aristotele esprimesse adeguatamente la natura del moto, al punto che tutti se ne servirono introducendo nella definizione aristotelica originaria la propria interpretazione dei concetti di potenza e atto.
Il secondo problema principale legato alla natura del moto era il suo status ontologico, cioè se il moto fosse da considerare un ente distinto, oppure da identificare con la cosa mossa. Nel Libro III della Fisica Aristotele aveva sostenuto che il moto, nel senso di cambiamento, non costituiva una categoria separata ma si collocava in diverse categorie, proprio come la potenza e l'atto. Il moto quindi era un modo di essere pertinente all'ente cui accadeva di muoversi o cambiare. Poiché Aristotele aveva distinto quattro tipi di cambiamento ‒ e precisamente il cambiamento di sostanza, di qualità, di quantità e di luogo ‒ sembrò che il moto appartenesse a tutte e quattro le categorie. Tuttavia, altrove Aristotele aveva espresso altre considerazioni sui tipi di cambiamento e la loro categoria di appartenenza. Nelle Categorie, per esempio, aveva affermato che il moto ricadeva specificamente nella categoria della passio o affezione. Il tentativo di riconciliare questa apparente incompatibilità caratterizzò quasi tutte le successive discussioni sul problema.
Averroè tentò di riconciliare la Fisica con le Categorie, affermando che nella prima opera Aristotele aveva sostenuto l'idea più corretta, mentre nella seconda si era espresso seguendo la concezione più comune. Secondo la Fisica, il moto è la generazione progressiva, parte dopo parte, del suo termine finale e appartiene quindi alle categorie di esso, e cioè sostanza, qualità, quantità o luogo. Il moto differisce dal termine finale cui tende non secondo il genere, ma solamente rispetto al suo grado di attualità o perfezione (non differt a perfectione ad quam vadit nisi secundum magis et minus). D'altra parte, il moto può essere considerato come un processo verso l'atto o la perfezione (via ad perfectionem), il che implica che esso non possa coincidere con il suo atto, bensì debba appartenere a una categoria sua propria (genus per se).
Questa stessa distinzione ricorre nel commento di Averroè al Libro V della Fisica, dove però si cela sotto i termini di moto secundum materiam e moto secundum formam. Secondo la materia, il moto e il suo termine appartengono allo stesso genere; secondo la forma, si deve considerare il moto come una trasmutazione che ha luogo nel tempo e costituisce una categoria a sé. Nel XIV sec., queste opzioni alternative furono rispettivamente designate come forma fluens e fluxus formae, e gli autori trecenteschi solitamente attribuivano tale classificazione, insieme alla relativa terminologia, ad Alberto Magno. Nella teoria della forma fluens il moto non è altro che la successiva trasmissione della forma al corpo mobile. Nel caso del cambiamento qualitativo, la forma fluens è la perdita o l'acquisizione di vari gradi; nel caso del moto locale, essa corrisponde ai luoghi successivamente raggiunti dal corpo mobile. Nella teoria del fluxus formae, invece, il moto è il flusso di una forma, vale a dire il processo o la strada da percorrere verso l'attualità o la perfezione, sebbene essenzialmente diverso da questa.
Alcuni autori scolastici, quali Giovanni di Jandun e Guglielmo di Alnwick (attivo intorno al 1315), considerarono le teorie della forma fluens e del fluxus formae come concezioni complementari dello stesso fenomeno. Guglielmo di Ockham invece assunse una posizione differente. Egli rimarcò che il solo modo corretto di intendere il moto era di vederlo come una forma fluens, mentre la teoria del fluxus formae implicava che il moto fosse una cosa (res) realmente distinta dagli oggetti che cambiano o si muovono ("il moto è una cosa che differisce sia dal termine da cui il moto procede, sia dall'oggetto mobile, sia dal termine verso cui procede"; Adams 1987, p. 804). La discussione di Guglielmo sulla natura del moto portò alla ribalta le implicazioni ontologiche di questo dibattito. Aderire alla teoria del fluxus formae significava ammettere che il mondo fosse popolato, oltre che di cose permanenti, anche di cose successive. Gli oppositori di Guglielmo sostenevano che il moto non potesse essere una 'cosa permanente' (res permanens) ‒ non essendo il genere di cosa le cui parti possono esistere tutte contemporaneamente ‒ bensì 'successiva'. Ockham argomentò diffusamente contro l'esistenza di 'cose successive'. Probabilmente, il suo argomento più forte fu che era del tutto superfluo assumere l'esistenza di una 'cosa successiva' in quanto realmente distinta dalla 'cosa permanente' (il cosiddetto 'rasoio' di Ockham). Detto altrimenti, egli spiegava il fenomeno del moto esclusivamente nei termini dei singoli oggetti mobili, dei luoghi e delle forme che essi successivamente occupavano. A sostegno della propria teoria egli intraprese un'analisi semantica dei termini 'moto' e 'cambiamento', concludendo che essi non erano nomi cosiddetti 'assoluti', riferentisi cioè a singole cose concrete, ma astratti, in quanto abbreviavano espressioni più lunghe e complesse. Così, la frase 'il cambiamento è ciò che va da un prima a un poi' deve essere interpretata come 'quando qualcosa cambia, essa va da un prima a un poi'; e la proposizione 'il moto esiste' è in realtà un'abbreviazione della proposizione 'un oggetto mobile ora ha qualcosa che immediatamente prima non aveva, ma immediatamente dopo avrà qualcos'altro' (Adams 1987). In modo simile, Ockham sosteneva che ogni proposizione che contiene il termine 'moto' può riferirsi unicamente a cose singole.
Fu Walter Burleigh (1275-1337), uno dei primi fellows del Merton College, ad accusare esplicitamente Ockham di negare con le sue teorie la realtà del moto e, come conseguenza, di distruggere la filosofia naturale. Insieme a lui, anche altri contemporanei rigettarono le teorie di Ockham, ma per motivi diversi. Giovanni Buridano, per esempio, che generalmente concordava con Guglielmo nella predilezione per un approccio semantico alla scienza naturale, non aderì alla concezione del moto come 'forma fluente'. Sulla base di considerazioni teologiche, egli difese invece la teoria del fluxus formae. Un ruolo cruciale nelle sue argomentazioni fu svolto dalla condanna di 219 tesi da parte del vescovo Stefano Tempier nel 1277. La prop. 49 negava che Dio potesse muovere in linea retta il cielo più esterno, e dunque il mondo stesso, dal momento che tale moto avrebbe lasciato dietro di sé un vuoto dovuto all'allontanamento del mondo dalla sua presente posizione. Dopo la condanna di questa tesi, gli scolastici di norma ammisero che Dio potesse muovere il mondo in modo rettilineo (e circolare), se così gli fosse piaciuto fare.
Ma come si poteva immaginare il movimento dell'intero Cosmo come un unico corpo? Se nella concezione aristotelica il moto locale non è altro che un cambiamento rispetto al luogo ‒ come un 'essere prima in un modo e dopo in un altro rispetto a esso' (aliter et aliter se habere prius et posterius) ‒ e non vi è altro luogo al di fuori del Cosmo, a quale posto avrebbe dovuto riferirsi questo tipo di moto? Non esistendo luoghi che sono successivamente occupati dal Cosmo, si dovrebbe dedurre che il moto non esiste. Questa conclusione è però incompatibile con il punto di partenza espresso da Buridano, secondo il quale Dio può muovere il Cosmo se desidera farlo. Se quindi la successione deve essere conservata, allora il moto locale deve comportare qualcos'altro oltre al corpo mobile e ai luoghi raggiunti. Secondo Buridano, questo qualcos'altro è una cosa puramente successiva (res pure successiva), intrinseca all'oggetto mobile e tuttavia distinta da esso. In base all'idea di moto come flusso, il Cosmo è in una condizione di continuo cambiamento, che consiste precisamente di un aliter et aliter se habere prius et posterius. Partendo dal caso ipotetico del moto del Cosmo, ammesso sotto la pressione della condanna di Tempier, Buridano applicò le sue conclusioni a tutti i tipi di moto locale, anche a quelli che avvengono in casi naturali. L'esito di questa discussione fu che il moto è una proprietà o una disposizione (dispositio) intrinseca al corpo mobile.
La stessa teoria fu difesa sia da Biagio Pelacani sia da Alberto di Sassonia, ma il secondo fece alcune interessanti precisazioni. Egli distinse nettamente tra i casi naturali e quelli non naturali di moto, e considerò l'introduzione di un flusso aggiuntivo non necessaria a dar conto dei casi naturali. Nondimeno, il caso del possibile movimento del Cosmo a opera dell'onnipotenza divina poteva, secondo lui, essere spiegato soltanto ricorrendo a una concezione del moto come flusso intrinseco al corpo mobile. Ciò significa che, pur ritenendo le teorie della forma fluens e del fluxus formae egualmente valide, egli preferì la seconda solamente per ragioni teologiche (Sarnowsky 1989).
Una posizione diversa fu assunta da Nicola Oresme, che a prima vista sembrò aderire alla teoria del fluxus formae. Nel suo commento alla Fisica, Nicola sostenne che il moto era una cosa successiva, o un flusso, ma rigettò la visione di Buridano secondo la quale il flusso era una cosa distinta (res distincta) dall'oggetto mobile e a esso aggiunta. A questo riguardo, la sua posizione non differisce da quella di Ockham, ma se ne allontana in quanto non identifica il moto con il corpo mobile e i suoi luoghi successivi, ma introduce un ente ontologico distinto, vale a dire un modus rei, un modo di essere. Secondo Oresme, infatti, il moto, sebbene non sia una cosa separata successiva, possiede un carattere successivo che è espresso dal modo o condizione (modus seu conditio) dell'oggetto mobile; questi non sono altro che i continui cambiamenti interni dell'oggetto, espressi mediante la definizione ‒ ormai familiare ‒ di moto come 'essere in un altro modo che prima' (aliter se habere quam prius).
Le cause del moto
Aristotele distinse due tipi di moto locale, ossia naturale e non naturale o violento. Il moto naturale è quello verso il luogo naturale del corpo mobile, che è determinato dalla proporzione che i quattro elementi ‒ acqua, terra, aria, fuoco ‒ hanno in esso. I corpi in cui gli elementi acqua o terra predominano sono pesanti e, conseguentemente, si muovono verso il basso, mentre i corpi in cui predominano aria e fuoco sono leggeri e si muovono verso l'alto. I moti violenti sono rivolti verso qualsiasi direzione contraria al luogo naturale del corpo in movimento (per es., verso l'alto per i corpi che consistono principalmente dell'elemento terra). Aristotele spiegò il moto locale dei corpi inanimati, cioè dei corpi che non si muovono autonomamente, invocando il principio che il moto non è mai spontaneo, ma che tutto ciò che è in moto "è necessariamente mosso da qualcosa" (Physica 241b 34; 259a 29-31). Nella terminologia medievale questa proposizione era resa come 'ogni cosa che si muove è mossa da un'altra' (omne quod movetur ab alio movetur). Secondo il filosofo greco non è possibile l'azione a distanza, per cui la causa del moto e la cosa mossa hanno bisogno di essere in continuo contatto (ibidem 243a 3-4), essendo il motore e il mobile enti separati.
Quando i commentatori medievali si rivolsero a questi due fondamentali principî aristotelici con cui si spiegava il moto, fecero convergere le loro disquisizioni su due aree problematiche che sembravano offrire dei controesempi agli assiomi aristotelici, l'una nel campo del moto naturale, l'altra nel campo del moto violento.
Il moto naturale: la spiegazione della gravità e della caduta libera accelerata
Se è vero che nel moto violento è sempre coinvolta una forza motrice esterna, come si distingue invece nel moto naturale il motore dal corpo mobile?
Nel rispondere a questo interrogativo, la maggior parte degli studiosi medievali, seguendo Averroè, concluse che è il generans (generatore) a dare al corpo mobile la sua forma e tutto ciò che ne deriva, inclusa la forza motrice e la disposizione a muoversi, vale a dire la sua gravità (gravitas) o la sua leggerezza (levitas). Stando a tale teoria, il generans agisce nel moto naturale come una sorta di causa motrice remota, per cui il moto di un corpo naturale viene a essere la conseguenza della sua generazione originaria. Invece, nel caso di un corpo impedito a muoversi dopo essere stato generato, gli studiosi medievali ritenevano che la causa del suo moto naturale fosse da individuare in qualsiasi cosa avesse rimosso l'impedimento al suo moto (removens impedimentum). Per esempio, il moto naturale di una pietra appesa a una corda era causato dall'agente che recideva la corda. Tuttavia, rimaneva aperto il problema di come spiegare la prosecuzione del moto naturale di un corpo, nel caso in cui il generans e il removens dell'impedimento non fossero in continuo e simultaneo contatto con esso.
Una prospettiva originale fu quella adottata da Giovanni Duns Scoto. Egli pervenne alla conclusione che i corpi pesanti e i corpi leggeri fossero mossi dalla loro pesantezza e dalla loro levità, e che quindi, in un certo senso, si muovessero da soli. Tale idea derivava ovviamente da Aristotele, Averroè e i precedenti commentatori, secondo i quali il generans era la vera causa della caduta di un corpo, mentre forma sostanziale, pesantezza e leggerezza erano al massimo cause strumentali di ordine inferiore. Dopo Duns Scoto, autori come Giovanni di Jandun, Guglielmo di Ockham, Walter Burleigh, Giovanni Buridano, Marsilio di Inghen e Alberto di Sassonia abbracciarono l'idea che pesantezza e leggerezza fossero le cause immediate del moto non ostruito di un corpo, abbandonando definitivamente il principio aristotelico stando al quale il motore e il mobile sono enti separati. Pertanto il motore non fu più ritenuto una causa estrinseca (com'era stata il generans), ma un principio intrinseco, inerente al corpo mobile. Di conseguenza, venne meno l'importante distinzione aristotelica tra moto dei corpi animati e moto dei corpi inanimati.
Un'altra questione sollevata nel contesto dei corpi in caduta fu l'accelerazione; com'è generalmente noto, un corpo in caduta libera non si muove con una velocità uniforme, bensì è sottoposto ad accelerazione costante. La spiegazione causale della caduta libera, in termini di gravità e levità, ignorava il fenomeno dell'accelerazione, che era discusso separatamente. Il punto di partenza erano le regole del moto fornite da Aristotele nel Libro VII della Physica (249b 27-250a 9) e nel Libro I del De caelo (273b 30-275a 20), dove egli discuteva le nozioni di 'più veloce', 'più lento' e 'di eguale velocità'. Qui, utilizzando pochi esempi, Aristotele formulava le relazioni che si ottengono tra la velocità e le forze e resistenze che la determinano.
Relativamente al moto naturale, in cui il peso agisce come forza interna del moto e la densità del mezzo come resistenza, Aristotele stabilì che il tempo richiesto da due corpi per coprire una data distanza era inversamente proporzionale al loro peso. In altre parole, se si dimezza il peso dell'oggetto mosso, allora si raddoppierà la distanza o si dimezzerà il tempo, ossia giungerà due volte più lontano o si muoverà due volte più velocemente. Nel Libro IV della Physica, Aristotele diede una formulazione simile per il movimento naturale in un mezzo: un corpo attraverserà un mezzo doppiamente denso nel doppio del tempo, ossia nello stesso tempo ne attraverserà soltanto la metà (Physica 215a 24-216a 11). In altre parole, per corpi di uguale peso i tempi richiesti per attraversare una distanza data sono proporzionali alle densità dei rispettivi mezzi.
All'interno di questo quadro vi erano soltanto due possibilità di spiegare l'accelerazione di un corpo in caduta: l'una era supporre che essa fosse causata da un incremento della forza, l'altra da un decremento della resistenza. La maggior parte dei pensatori medievali scartò la seconda opzione per affermare invece che l'accelerazione era causata da un incremento di forza. La teoria che ebbe maggiore influenza fu quella proposta da Giovanni Buridano. Egli sostenne che il peso del corpo non soltanto dava inizio alla sua caduta verso il basso, ma generava anche una forza impressa sul corpo in caduta, forza che egli denominò impetus. Poiché il peso del corpo non si esauriva ma continuava ad agire come causa, esso continuava a produrre nuovi incrementi di impetus, che progressivamente aumentavano la velocità del corpo in caduta. Questa spiegazione fu sostanzialmente seguita da Nicola Oresme, Alberto di Sassonia e Marsilio di Inghen.
Il moto violento. La spiegazione del moto dei proietti
La teoria dell'impetus era stata inizialmente elaborata per affrontare un altro problema della fisica aristotelica, ossia quello riguardante il moto dei proietti (Clagett 1959; Maier 1968). Questo particolare tipo di moto violento sembrava contraddire i principî aristotelici su motori e corpi mobili. Il problema consisteva nello spiegare come il mobile continuasse il proprio moto dopo aver perso il contatto con la forza motrice (per es., la mano che scaglia una pietra). A questo riguardo Aristotele aveva affermato che era il mezzo circostante a far proseguire il moto del proietto; simultaneamente a esso, anche il mezzo riceveva una forza motrice dal proiciente, che continuava a trasmettere mediante le particelle del mezzo urtate, spingendo così in avanti il proietto. In questo modo, Aristotele poteva fare salvo il principio in base al quale la forza esterna rimaneva in continuo contatto con il corpo mobile, in quanto la funzione del proiciente era rilevata dal mezzo.
Nel XIV sec. questa spiegazione fu definitivamente rifiutata in quanto il ruolo del mezzo nella prosecuzione del moto del proietto fu considerato del tutto superfluo. Francesco di Marchia (attivo intorno al 1320) puntualizzò che se il proiciente originario poteva produrre qualche forza motrice nel mezzo, non vi era ragione perché non potesse farlo anche nello stesso proietto. Questa 'forza lasciata dietro' (virtus derelicta) o 'forza impressa' (vis impressa) permetteva al proietto di essere la vera causa immediata del proseguimento del proprio moto. In realtà, questa soluzione era stata anticipata intorno alla metà del VI sec. dal commentatore greco Giovanni Filopono, il quale aveva ritenuto inverosimile che il mezzo agisse, anziché come resistenza al moto del proietto, come forza motrice. Tuttavia, poiché la sua opera non era disponibile in traduzione, né lo erano le opere di vari pensatori islamici che avevano sviluppato le teorie della forza impressa (mail) nel moto dei proietti, sembrò che la versione di Giovanni Buridano fosse una creazione originale del Medioevo latino.
Fu probabilmente Buridano a introdurre il termine tecnico impetus per identificare questa forza impressa e a elaborarne una sofisticata teoria. Nella concezione di Buridano, l'impeto era una forza motrice che poteva agire in ogni direzione verso cui fosse stata trasmessa dal motore iniziale. Asserendo che la forza dell'impetus era determinata dalla velocità con cui il motore iniziale muoveva il proietto, Buridano fece il primo passo verso la quantificazione dell'impetus. Inoltre, considerò la forza dell'impetus proporzionale al peso del proietto, che a sua volta dipendeva dalla quantità di materia (quantitas materiae); per suffragare questa regola fece riferimento al fenomeno per cui un proietto di piombo può essere lanciato più lontano di un proietto di legno avente egual volume e forma, in quanto il primo ha una capacità maggiore di ricevere l'impetus.
Buridano non applicò la teoria dell'impetus unicamente alla spiegazione dell'accelerazione dei corpi in caduta, ma anche a quella dei moti celesti. Affermò infatti che al momento della Creazione, Dio aveva impresso ai cieli un impetus il quale, non producendo un moto violento, cioè contrario ai luoghi naturali, e dunque non incontrando alcuna resistenza, sarebbe continuato per sempre. Di contro, nella regione sublunare l'impetus era corrotto dalla tendenza del corpo mobile a muoversi verso il suo luogo naturale, nonché dalle resistenze (dovute, per es., al mezzo) agenti sul corpo. In sintesi, Buridano concepiva l'impetus come una qualità quasi permanente, intrinseca al corpo mobile, che nelle condizioni terrestri interagiva con il moto naturale dei corpi e, di conseguenza, era destinato a esaurirsi.
Alberto di Sassonia aderì alle teorie di Buridano, anche se evitò il termine impetus per parlare invece di 'forza motrice' (virtus motiva) o di 'qualità motrice' (qualitas motiva). Nicola Oresme e Marsilio di Inghen posero invece l'accento sul fatto che l'impetus si esaurisse da solo, come fa un raggio di luce emesso da una fonte luminosa distante. A ogni modo, tutte queste varianti dell'impetus, proprio come la nozione di peso (gravitas) come qualità intrinseca al mobile nel moto naturale, contraddicevano il principio aristotelico secondo cui il motore e il mobile sono enti separati in contatto tra loro. La teoria medievale dell'impetus rimase la spiegazione dominante del moto dei proietti fino al XVII sec., pur avendo poca influenza a Oxford. Una sua versione distorta fu ricusata da Giovanni Dumbleton.
Una diversa direzione nella spiegazione del moto dei proietti fu presa da Guglielmo di Ockham. Egli rifiutò l'idea che nel moto dei proietti fosse trasmessa una forza, in quanto tale supposizione avrebbe reso superfluo il primo proiciente del moto del proietto, oppure avrebbe portato a un regresso infinito delle cause. Se infatti si assume che il proietto sia mosso, dopo che il primo proiciente ha cessato di muoverlo, è lecito chiedersi se esso si muova da sé oppure grazie a una forza estrinseca. Se si muove da sé, allora non si ha necessità di un impetus per spiegare il moto del proietto; se si muove grazie a un corpo estrinseco, ci si deve chiedere ‒ come prima ‒ se esso sia mosso da sé stesso o da una causa esterna. Nel secondo caso, il primo proiciente sarebbe superfluo; nel primo caso, si dovrebbe ipotizzare un altro corpo estrinseco come causa del moto, e così via, all'infinito. Conseguentemente, Ockham arriva alla conclusione che la supposizione di una forza aggiuntiva esterna è del tutto superflua in quanto la prosecuzione del moto di un proietto non necessita di alcuna causa. Il proietto è mosso da sé grazie a una complessa interazione di momenti naturali e violenti nella sua traiettoria. In questo modo Ockham riesce a salvare il principio aristotelico per cui il moto violento richiede il contatto immediato tra il motore e il mosso, sebbene in una maniera decisamente differente rispetto a quella chiamata in causa dalla teoria dell'impetus (Goddu 1984).
La quantificazione delle cause del moto
Dopo aver discusso le relazioni tra motore e corpo mobile in due contesti particolarmente problematici, ossia le spiegazioni causali della caduta libera e del moto dei proietti, è opportuno menzionare un ulteriore aspetto. Le regole quantitative che Aristotele aveva formulato descrivendo i fattori della forza e della resistenza nell'interazione tra motore e mosso furono duramente criticate all'inizio del Trecento. Nel suo Trattato sulle proporzioni, scritto nel 1328, Tommaso Bradwardine fornì una trattazione generale di come il cambiamento di velocità di un mobile dovesse essere riferito a una variazione delle sue cause. Fra le teorie criticate nel secondo capitolo del trattato è annoverata anche quella di Aristotele secondo cui, quando la resistenza è uguale o maggiore della forza motrice, è ancora possibile una produzione di velocità. Quest'assurda implicazione si evidenzia in modo più chiaro riportando le affermazioni di Aristotele ‒ la velocità (V) è direttamente proporzionale alla forza (F) e inversamente proporzionale alla resistenza (R) ‒ in termini moderni: V=F/R. Questa funzione assegna un valore positivo a V anche se R è uguale o maggiore di F, laddove ‒ secondo gli assunti medievali ‒ V avrebbe dovuto essere uguale a zero.
Bradwardine sostituì le formulazioni di Aristotele ‒ e quelle delle altre tre teorie ‒ con una nuova 'legge', secondo cui "la proporzione tra le proporzioni delle potenze di moto e le potenze di resistenza è uguale alla proporzione tra le rispettive velocità di moto, e viceversa", specificando che "ciò deve intendersi nel senso di una proporzione geometrica" (Crosby 1961, p. 113). Gli esempi riportati da Bradwardine illustrano che cosa egli avesse in mente nel formulare questo teorema. Il teorema stabilisce che le velocità (V) variano aritmeticamente mentre i rapporti delle forze alle resistenze che determinano queste velocità (F/R) variano geometricamente. In altri termini, raddoppiare la velocità implicava che la proporzione della forza alla resistenza fosse 'duplicata'. Nella matematica medievale delle proporzioni, che a Bradwardine era ben nota, 'duplicare' o 'subduplicare' (cioè 'dimezzare') i rapporti corrispondeva rispettivamente a elevarli a potenza o a estrarne la radice. Così, per duplicare una data velocità si doveva elevare al quadrato il rapporto della forza alla resistenza F/R e, per dimezzare quella velocità, si doveva estrarre la radice quadrata di F/R. L'assunzione sottostante era che il rapporto iniziale F0/R0 doveva essere maggiore di 1 per mettere in moto un mobile (Tav. II).
La terminologia in cui Bradwardine formulò il suo teorema è certamente boeziana, mentre l'idea di applicare la dottrina delle proporzioni a problemi dinamici può essere fatta risalire ad al-Kindī, a Walter Odington e ad Arnaldo da Villanova (North 1992).
Il risultato conseguito da Bradwardine fu l'aver stabilito una relazione matematica che salvava il postulato scolastico secondo cui il moto è impossibile se il detto rapporto F/R è minore di 1, un postulato che era violato dalle 'leggi' del moto attribuite ad Aristotele. La relazione matematica di Bradwardine, come ha sintetizzato uno storico, "era compatibile con ‒ ma non logicamente derivata da ‒ un postulato per il quale i soli argomenti proponibili erano basati sulla correttezza intuitiva" (ibidem, p. 81).
L'approccio matematico di Bradwardine ebbe un'enorme influenza. A Oxford, Riccardo Swineshead sviluppò ulteriormente le intuizioni di Bradwardine applicandole a due nuovi problemi. Nel Libro dei calcoli, scritto intorno al 1350, Swineshead, oltre a specificare il teorema di Bradwardine per differenti tipi di cambiamento di velocità (uniforme, difforme, uniformemente difforme, e così via), applicò la sua funzione alla caduta di un corpo pesante al centro dell'Universo. Se si considera questo corpo come una sottile asticella e si assume che questa agisca come la somma delle sue parti, allora le proporzioni forza-resistenza che determinano la velocità dell'asticella diventano alquanto complesse; quelle parti dell'asticella che hanno superato il centro avrebbero un moto naturale opposto al moto originario, e cioè resisterebbero al moto dell'asticella. In questo modo Riccardo Swineshead riuscì a trattare gli aspetti matematici della questione, provando che l'asticella non avrebbe mai raggiunto il centro dell'Universo.
Il teorema del moto di Bradwardine fu incorporato nei commenti parigini alla Fisica. A partire da Giovanni Buridano, altri studiosi trecenteschi dell'Università di Parigi iniziarono a mostrare dimestichezza con le vedute di Bradwardine. Alberto di Sassonia e Nicola Oresme elaborarono la funzione di Bradwardine nei loro lavori, rispettivamente il Trattato sulle proporzioni e il Trattato sulle proporzioni delle proporzioni; essi si allontanarono dai problemi fisici che Bradwardine aveva discusso, concentrandosi invece sul calcolo delle proporzioni in quanto tale.
Gli effetti del moto
I problemi discussi fin qui riguardano l'ambito che gli studiosi medievali chiamavano la velocità del moto 'rispetto alla causa' (penes causam), da distinguere da quello del moto 'rispetto all'effetto' (penes effectum), vale a dire la descrizione del moto in termini di tempo e di spazio, senza alcun riferimento alla causa. Tale distinzione, resa esplicita da Riccardo Swineshead ‒ sebbene fosse già presente nel Trattato di Bradwardine ‒ coincide per sommi capi con la distinzione moderna tra dinamica e cinematica (North 1992).
La trattazione del moto da un punto di vista cinematico fu introdotta nel contesto della dottrina cosiddetta della 'latitudine delle forme' (latitudo formarum), elaborata per affrontare i differenti gradi attribuibili a una stessa qualità; per esempio, una banana può essere più gialla di un'altra, o un oggetto più caldo di un altro.
L'idea che le qualità in un soggetto possano esistere in diversi gradi fu espressa inizialmente da Aristotele nelle Categorie (10b 26 e segg.) e diede origine a due serie di problemi. La prima, chiamata nella terminologia medievale dell'intensio et remissio formarum, elaborava ulteriormente l'idea che le qualità potessero accrescersi o diminuire, vale a dire che fossero appunto soggette a intensificazione o remissione (intensio et remissio; Maier 1968). Tale teoria suscitava non poche perplessità; ci si domandava infatti se fosse la qualità stessa a modificarsi, oppure se il cambiamento dipendesse dalla maggiore o minore partecipazione di un soggetto a una qualità, e soprattutto ci si interrogava su come si intensificasse o si indebolisse una qualità. Le due alternative principali che emersero nel corso del XIV sec. furono la teoria della successione e quella dell'addizione. La teoria della successione ‒ rappresentata, tra gli altri, da Walter Burleigh ‒ attribuiva le variazioni di qualità alla successione delle forme di cui il soggetto era investito, in quanto ciascuna forma era distrutta e sostituita dalla successiva. Secondo la teoria dell'addizione, difesa da Duns Scoto e dalla sua scuola (scuola scotista), intensità maggiori o minori erano causate invece dall'addizione o dalla sottrazione di nuove parti di forma, le quali, in combinazione con la forma precedente, producevano gradi maggiori o minori di una data qualità. Giovanni Dumbleton, e probabilmente anche Bradwardine, Heytesbury e Riccardo Swineshead, aderirono a quest'ultima teoria.
Nelle discussioni intorno all'intensificazione e alla remissione delle forme si assumeva tacitamente che in un dato soggetto una qualità fosse uniformemente distribuita e che essa cambiasse uniformemente nel tempo. Tuttavia, proprio questo assunto fu ulteriormente indagato nella seconda area di problemi, quella della latitudine delle forme (latitudo formarum). Quest'area studiava il fenomeno dei cambiamenti qualitativi di un soggetto sotto il profilo del tempo e dello spazio. Il punto di partenza era costituito dal presupposto che in un soggetto dato le qualità potessero essere distribuite non uniformemente ‒ ossia difformemente (difformiter), secondo la terminologia medievale ‒ e che esse potessero cambiare in modo difforme. I mertoniani misero a fuoco il problema della misurazione di queste qualità, specialmente delle qualità uniformemente difformi, cioè quelle che si rafforzavano o si attenuavano in ragione costante da un'estremità all'altra del soggetto. Per analogia, essi si interrogarono sulle misure di altri tipi di cambiamento, e specialmente del moto locale. Fu in questo contesto di misurazione delle qualità e dei moti che il concetto di latitudine arrivò ad assumere un ruolo cruciale.
Il concetto medievale di latitudine fu inizialmente elaborato nell'ambito medico e farmacologico, nel quale era applicato alla gamma variabile di stati che nell'uomo vanno dalla salute alla malattia. Nel XIII sec. la latitudine era vista come un arco di valori astratto entro cui una qualità poteva variare, come una sorta di 'scala'. Nei lavori di Dumbleton, Bradwardine e Heytesbury la latitudine venne a essere equiparata a un grado di forma specifico. Nicola Oresme, che è oggi generalmente considerato l'ideatore del sistema più chiaro di misurazione delle qualità e dei moti, ritornò al significato geometrico originale di ampiezza. Egli applicò questo significato di latitudine nel suo sistema di rappresentazione geometrica bidimensionale delle qualità, dove la latitudine si riferiva all'intensità della qualità e la longitudine alla sua estensione. L'analisi filosofica dei gradi delle qualità contribuì a sviluppare l'idea di velocità come grandezza, alla quale poteva essere attribuito un valore numerico e mediante la quale poteva essere misurato il moto. L'idea era del tutto aliena da Aristotele, che aveva concepito la velocità come un concetto non quantificabile (Souffrin 1992).
Questi quattro autori, insieme a Riccardo Swineshead, rappresentano gli esempi più importanti dell'uso delle latitudini delle qualità e delle velocità. Essi combinano in modo tipico queste discussioni con i dibattiti sulle proporzioni delle velocità 'rispetto alla causa' e con altri aspetti del moto che qui non abbiamo trattato, come la sua misurazione in termini di limiti temporali iniziali e finali (incipit et desinit). Questo approccio si rinviene nelle Regole per la risoluzione dei sofismi di Guglielmo Heytesbury e nel Libro dei calcoli di Riccardo Swineshead. Per contro, il Trattato sulle configurazioni delle qualità e dei moti di Nicola Oresme si incentra sulla discussione della latitudine delle forme e della loro rappresentazione geometrica.
Eccellenti resoconti di questi lavori sono stati dati altrove; ci limiteremo così a discutere un teorema che si sviluppò nel contesto della latitudine delle forme e che Edward Grant ha indicato come il maggiore contributo individuale che il Medioevo abbia dato alla storia della fisica matematica, ossia il teorema della velocità media (Grant 1996). Questo teorema misura i moti uniformemente accelerati rispetto agli spazi attraversati mediante la comparazione con i moti uniformi; esso trova un'anticipazione nell'equazione del movimento di rotazione di un segmento con la velocità del punto medio del suo raggio, descritta nel Libro sul moto di Gherardo da Bruxelles. Il teorema della velocità media afferma che un mobile che si muove di moto uniformemente accelerato copre in un dato tempo lo stesso spazio che coprirebbe muovendosi a una velocità uniforme uguale a quella media, e cioè alla velocità nell'istante medio della durata dell'accelerazione. Se l'accelerazione inizia dalla velocità zero, allora la velocità media sarà uguale alla metà della velocità massima raggiunta, ma se l'accelerazione inizia a una velocità finita, allora la velocità media sarà maggiore della metà di quella massima.
Il teorema della velocità media ha suscitato grande attenzione negli studiosi perché è menzionato da Galilei nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze (Giornata terza, teorema I) e applicato alla caduta libera dei corpi, che è un esempio naturale di moto uniformemente accelerato (cioè difforme). I Calculatores fornirono molte prove del teorema, ma nessuna sofisticata come quella geometrica di Nicola Oresme, che fu impiegata anche da Galilei. Nicola notò che il triangolo rettangolo ha un'area equivalente a quella di un rettangolo la cui altezza è l'altezza media del triangolo (fig. 12). In tal modo egli comparò graficamente la quantità di una qualità uniformemente difforme a quella di una qualità uniforme di media intensità.
Oltre a Nicola Oresme, anche altri parigini erano al corrente delle discussioni dei Calculatores di Oxford sulla misura degli effetti del moto, com'è chiaro dalle loro trattazioni nei commenti alla Fisica (Sylla 1997).
Il ruolo della logica nella cinematica
Nelle sezioni precedenti abbiamo cercato di presentare le principali speculazioni tardo-medievali nel campo della cinematica. Tuttavia, ciò che si è detto su questi argomenti resta incompleto. Un tratto essenziale delle riflessioni cinematiche tardo-medievali, che non può non essere menzionato, è il coinvolgimento della logica. A Parigi come a Oxford le numerose discussioni dei vari aspetti del moto si inserivano in un quadro logico di riferimento. Gli studiosi di Parigi cercavano di fornire sempre analisi semantiche dei termini in cui formulavano i loro problemi di fisica. Termini come 'moto', 'Natura', 'cambiamento', 'alterazione', 'punto', 'spazio', 'tempo' e 'istante' erano sottoposti a un'analisi dettagliata che si avvaleva di tutte le tecniche logiche disponibili. In questo senso risultò fondamentale la teoria della suppositio ('supposizione'), strumento mediante cui si analizzava il significato di un termine nel contesto di una specifica proposizione, determinandone così il significato e la verità. La teoria della suppositio era in grado di offrire, per esempio, diverse analisi semantiche delle proposizioni 'l'uomo è una specie' e 'uomo è una parola di quattro lettere'. Un altro strumento semantico molto usato fu l'analisi della posizione di un termine all'interno di una proposizione, cioè l'ordine delle parole. Questo aspetto era espresso nel vocabolario tecnico dalla distinzione tra l'uso categorematico e sincategorematico di un termine (v. sopra). Gli aspetti semantici, riguardando in modo significativo il valore di verità delle proposizioni nelle quali si esponevano i problemi fisici, ebbero un peso influente nella soluzione di questi ultimi.
A Oxford, l'applicazione della logica alla cinematica si fuse con le tecniche descritte. In effetti, uno dei tratti distintivi più diffusi negli scritti dei Calculatores è proprio il fatto che essi ebbero origine da un contesto logico e disputativo. Questo è vero soprattutto per i Sophismata, collezioni di asserzioni controintuitive denominate 'sofismi', che servivano come esempi illustrativi di teorie semantiche. Spesso i Sophismata avevano un carattere puramente logico, ma al Merton College si originò anche un nuovo genere di sofismi, quello fisico-matematico. L'accento sulle tecniche logico-matematiche, piuttosto che sulla teoria fisica, è presente soprattutto nei trattati di Swineshead e Heytesbury e nei Sophismata di Richard Kilvington. Un tipico esempio del genere di problemi discussi in queste opere è la verità del sofisma 34: 'Platone può muoversi uniformemente per qualche tempo e alla velocità con cui si muove Socrate ora'.
I trattati del Merton combinavano complesse teorie semantiche con complessi calcoli. Come ha persuasivamente argomentato Edith D. Sylla, il fine di questi trattati era di insegnare agli studenti a pensare e ad argomentare chiaramente e correttamente (Sylla 1982). Tuttavia, la crescente complessità di applicazione delle tecniche matematiche e semantiche ci induce a dubitare che i mertoniani potessero conseguire il loro fine pedagogico con gli studenti del primo anno, ai quali erano destinati questi trattati.
Bibliografia
Adams 1987: Adams, Marilyn McCord, William Ockham, Notre Dame (Ind.), University of Notre Dame Press, 1987, 2 v.
Brown 1967: Brown, J.E., The Scientia de ponderibus in the Later Middle Ages, PhD diss., University of Wisconsin, 1967.
Burnyeat 1979: Burnyeat, M.F., Conflicting appearances, "Proceedings of the British Academy", 1979, pp. 69-111.
Caroti 1993: Caroti, Stefano, Oresme on motion, "Vivarium", 31, 1993, pp. 8-37.
Clagett 1959: Clagett, Marshall, The science of mechanics in the Middle Ages, Madison, University of Wisconsin Press, 1959.
Crosby 1961: Bradwardine, Thomas, Thomas of Bradwardine. His Tractatus de Proportionibus. Its significance for the development for mathematical physics, edited and translated by H. Lamar Crosby, 2. ed., Madison, University of Wisconsin Press, 1961 (1. ed.: 1955).
Damerow 1992: Damerow, Peter [et al.], Exploring the limits of preclassical mechanics. A study of conceptual development in early modern science, New York, Springer Verlag, 1992.
Drake 1969: Mechanics in sixteenth-century Italy. Selections from Tartaglia, Benedetti, Guido Ubaldo, & Galileo, transl. and annot. by Stillman Drake and I.E. Drabkin, Madison, University of Wisconsin, 1969.
Eastwood 1968: Eastwood, Bruce, Medieval Empiricism. The case of Grosseteste's Optics, "Speculum", 43, 1968, pp. 306-321.
Edgerton 1991: Edgerton, Samuel Y., The heritage of Giotto's geometry. Art and science on the eve of the scientific revolution, Ithaca (N.Y.), Cornell University Press, 1991.
Federici Vescovini 1965: Federici Vescovini, Graziella, Studi sulla prospettiva medievale, Torino, Giappichelli, 1965.
Fisher 1971: Fisher, N.W. - Unguru, Sabetai, Experimental science and mathematics in Roger Bacon's thought, "Traditio", 27, 1971, pp. 353-378.
Goddu 1984: Goddu, André, The physics of William of Ockham, Leiden, E.J. Brill, 1984.
Goering 1995: Goering, Joseph, When and where did Grosseteste study theology, in: Robert Grosseteste. New perspectives on his thought and scholarship, edited by James McEvoy, Turnhout, Brepols, 1995, pp. 17-52.
Grant 1996: Grant, Edward, The foundations of modern science in the Middle Ages. Their religious, institutional and intellectual contexts, Cambridge-New York, Cambridge University Press, 1996.
Hackett 1995: Hackett, Jeremiah, 'Scientia experimentalis'. From Robert Grosseteste to Roger Bacon, in: Robert Grosseteste. New perspectives on his thought and scholarship, edited by James McEvoy, Turnhout, Brepols, 1995, pp. 89-120.
Kaluza 1995: Kaluza, Zenon, Nicolas d'Autrécourt ami de la vérité, in: Histoire littéraire de la France, ouvrage commencé par des religieux bénédectins de la Congrégration de Saint-Maur et continué par des membres de l'Institut (Académie des inscriptions et belles-lettres), Paris, Imprimerie nationale, 1733-; v. XLII, t. 1, Paris, De Boccard, 1995.
Lewis 1980: Lewis, Christopher, The Merton tradition and kinematics in late sixteenth and early seventeenth century Italy, Padova, Antenore, 1980.
Lindberg 1976: Lindberg, David C., Theories of vision from al-Kindi to Kepler, Chicago, Chicago University Press, 1976.
‒ 1978: Science in the Middle Ages, edited by David C. Lindberg, Chicago, University of Chicago Press, 1978.
‒ 1986: Lindberg, David C., The genesis of Kepler's theory of light. Light metaphysics from Plotinus to Kepler, "Osiris", 2, 1986, pp. 5-42.
Maier 1952: Maier, Anneliese, An der Grenze von Scholastik und Naturwissenschaft. Die Struktur der materiellen Substanz; das Problem der Gravitation; die Mathematik der Formlatituden, 2. Aufl., Roma, Edizioni di Storia e Letteratura, 1952 (1. ed.: 1943; trad. it. parziale: Scienza e filosofia nel Medioevo. Saggi sui secoli XIII e XIV, Milano, Jaca Book, 1983).
‒ 1958: Maier, Anneliese, Zwischen Philosophie und Mechanik, Roma, Edizioni di Storia e Letteratura, 1958.
‒ 1968: Maier, Anneliese, Zwei Grundprobleme der Scholastischen Naturphilosophie, 3. erweiterte Auflage, Roma, Edizioni di Storia e Letteratura, 1968 (1. ed.: 1939).
Marshall 1981: Marshall, Peter, Two Scholastic discussions of the perception of depth by shading, "Journal of the Warburg and Courtauld Institutes", 44, 1981, pp. 170-175.
McEvoy 1982: McEvoy, James, The philosophy of Robert Grosseteste, Oxford, Clarendon Press, 1982.
‒ 1995: Robert Grosseteste. New perspectives on his thought and scholarship, edited by James McEvoy, Turnhout, Brepols, 1995.
Molland 1995: Molland, George, Mathematics and the medieval ancestry of physics, Brookfield (Vt.), Variorum, 1995.
Moody 1952: The medieval science of weights (Scientia de ponderibus). Treatises ascribed to Euclid, Archimedes, Thabit ibn Qurra, Jordanus de Nemore, and Blasius of Parma, ed. with introd., Engl. transl. and notes by Ernest A. Moody, Marshall Clagett, Madison, University of Wisconsin, 1952.
‒ 1978: Murdoch, John E. - Sylla, Edith, The science of motion, in: Science in the Middle Ages, edited by David C. Lindberg, Chicago, University of Chicago Press, 1978, pp. 206-265.
‒ 1989: Murdoch, John E., The involvement of logic in late medieval natural philosophy, in: Studies in medieval natural philosophy, edited by Stefano Caroti, Firenze, L.S. Olschki, 1989, pp. 3-29.
‒ 1991: Murdoch, John E., Pierre Duhem and the history of late medieval science and philosophy in the Latin west, in: Gli studi di filosofia medievale fra Otto e Novecento. Contributo a un bilancio storiografico, a cura di Ruedi Imbach e Alfonso Maierù, Roma, Edizioni di Storia e Letteratura, 1991, pp. 253-302.
Murdoch 1970: Murdoch, John E., Bradwardine, Thomas, in C.C. Gillispie (ed.), Dictionary of Scientific Biography, New York 1970, v. II, pp. 390-397.
Newman 1989: Newman, William R., Technology and alchemical debate in the late Middle Ages, "Isis", 80, 1989, pp. 423-445.
North 1992: North, John D., Natural philosophy in late medieval Oxford, in: The history of the University of Oxford, general editor Trevor H. Aston, Oxford, Clarendon Press, 1984-; v. II: Late medieval Oxford, edited by J.I. Catto and Ralph Evans, 1992, pp. 76-95.
Parkhurst 1990: Parkhurst, Charles, Roger Bacon on color. Sources, theories and influence, in: The verbal and the visual. Essays in honor of William Sebastian Heckscher, edited by Karl-Ludwig Selig and Elizabeth Sears, New York, Italica Press, 1990, pp. 151-201.
Rashed 1997: Rashed, Roshdi, L'Optique géométrique, in: Histoire des sciences arabes, sous la direction de Roshdi Rashed, avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.; v. II: Mathématiques et physique, 1997, pp. 293-318.
Rosier 1994: Rosier, Irène, La parole comme acte. Sur la grammaire et la sémantique au XIIIe siècle, Paris, J. Vrin, 1994.
Sarnowsky 1989: Sarnowsky, Jürgen, Die aristotelisch-scholastische Theorie der Bewegung. Studien zum Kommentar Alberts von Sachsen zur Physik des Aristoteles, Münster, Aschendorff, 1989.
Schulman 1997: Schulman, N. M., Husband, father, bishop? Grosseteste in Paris, "Speculum", 72, 1997, pp. 330-346.
Smith 1981: Smith, A. Mark, Getting the big picture in perspectivist optics, "Isis", 72, 1981, pp. 568-589.
Souffrin 1992: Souffrin, Pierre, Sur l'histoire du concept de vitesse d'Aristote à Galilée, "Revue d'histoire des sciences", 45, 1992, pp. 231-267.
Steneck 1980: Steneck, Nicholas, Albert on the psychology of sense perception, in: Albertus Magnus and the sciences. Commemorative essays. 1980, edited by James A. Weisheipl, Toronto, Pontifical institute of medieval studies, 1980, pp. 263-290.
Stroud 2000: Stroud, Barry, The quest for reality. Subjectivism and the metaphysics of colour, Oxford, Oxford University Press, 2000.
Sylla 1982: Sylla, Edith D., The Oxford Calculators, in: The Cambridge history of later Medieval philosophy. From the rediscovery of Aristotle to the disintegration of scholasticism, 1100-1600, editors Norman Kretzmann, Anthony Kenny and Jan Pinborg, Cambridge-New York, Cambridge University Press, 1982, pp. 540-564.
‒ 1986: Sylla, Edith D., Galileo and the Oxford 'Calculatores'. Analytic languages and the mean-speed theorem for accelerated motion, in: Reinterpreting Galileo, edited by William A. Wallace, Washington (D.C.), Catholic University of America Press, 1986, pp. 53-111.
‒ 1991: Sylla, Edith D., The Oxford Calculators and mathematical physics. John Dumbleton's Summa Logicae et Philosophiae Naturalis, Parts II and III, in: Physics, cosmology and astronomy, 1300-1700. Tension and accommodation, edited by Sabetai Unguru, Dordrecht-Boston, Kluver Academic Publishers, 1991, pp. 129-161.
‒ 1997: Sylla, Edith D., Transmission of the new physics of the fourteenth century from England to the continent, in: La nouvelle physique du XIVe siècle, études éd. par Stefano Caroti et Pierre Souffrin, Firenze, Olschki, 1997, pp. 65-111.
Tachau 1988: Tachau, Katherine H., Vision and certitude in the age of Ockham. Optics, epistemology and the foundations of semantics, 1250-1345, Leiden, E.J. Brill, 1988.
Thomson 1974: Thomson, Ron B., Jordanus de Nemore and the University of Toulouse, "British journal for the history of science", 7, 1974, pp. 163-165.
‒ 1976: Thomson, Ron B., Jordanus de Nemore: Opera, "Mediaeval studies", 38, 1976, pp. 97-144.
Wallace 1959: Wallace, William A., The scientific methodology of Theodoric of Freiberg, A case study of the relationship between science and philosophy, Fribourg, The University Press, 1959.
Williams 1994: Williams, Steven J., Roger Bacon and his edition of the Pseudo-Aristotelian 'Secretum Secretorum', "Speculum", 69, 1994, pp. 57-73.
Wolfson 1935: Wolfson, Harry A., The internal senses in latin, arabic, and hebrew philosophic texts, "Harvard theological review", 28, 1935, pp. 69-133.