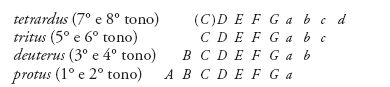La scienza bizantina e latina prima dell'influsso della scienza araba. La musica
La scienza bizantina e latina prima dell'influsso della scienza araba. La musica
La musica
Tarda Antichità
Secondo una divisione del sapere ereditata dalla Tarda Antichità, la musica era una delle quattro scienze fondamentali (il cosiddetto quadrivium) della conoscenza matematica del mondo delle essenze. La definizione sicuramente più rigorosa di queste scienze è stata formulata da Boezio (480 ca.-524/525) nel Proemio al De institutione arithmetica e ampiamente divulgata attraverso la sintesi lapidaria inserita nelle Institutiones di Cassiodoro (490 ca.-580 ca.), come epigrafe al De mathematica (II, 21): "l'aritmetica è la disciplina della quantità numerabile in sé; la musica è la disciplina che tratta dei numeri relativi alle componenti del suono; la geometria è la disciplina delle grandezze statiche e delle forme; l'astronomia è la disciplina delle orbite degli astri celesti".
Boezio, nel trattato De institutione musica, distingueva tre differenti generi di musica: la musica mundana, che concerneva le relazioni esistenti tra i corpi celesti nel Cosmo, il ciclo delle stagioni e gli elementi; la musica humana, legata alla raffinata armonia tra anima e corpo propria del genere umano, e, infine, la musica [...] instrumentis, "che si dice inerente agli strumenti" (De institutione musica, I, 2), più specificamente connessa alle strutture sonore prodotte dagli strumenti musicali. Da questo vasto campo di conoscenze, il mondo medievale, seguendo Boezio, escludeva la musica humana, costitutiva del microcosmo umano; alla musica mundana non era dedicato un interesse molto maggiore. A tale riguardo, il pensiero medievale si limitò a confermare, attraverso Boezio, i differenti sistemi di equivalenza, stabiliti da Platone e da Cicerone, tra i gradi della scala acustica e i pianeti (ibidem, I, 27).
Non siamo a conoscenza di nessun serio tentativo medievale di elaborare una rappresentazione globale e matematizzata delle relazioni tra la scala dei suoni e il movimento delle sfere celesti. Durante l'Alto Medioevo ci si accontentava di trascrivere le suddette equivalenze in diagrammi che rappresentavano la scala dei suoni e soltanto nel corso del XIII sec., col diffondersi dell'influenza delle teorie aristoteliche sui moti del cielo, si cessò di fare riferimento al principio dell''armonia delle sfere'. Restava così soltanto il terzo genere di musica, il cui oggetto era la costruzione matematica del sistema acustico. Allo studio di questo aspetto della musica, basato allo stesso tempo sui concetti fondamentali dell'aritmetica elaborati dall'Antichità greco-latina e sulla filosofia dei numeri, era dedicato tutto il trattato di Boezio.
La teoria della consonanza e, in definitiva, la costituzione del sistema acustico si basavano sulle proprietà inerenti alle progressioni dei numeri. Le più semplici erano quelle dei 'multipli' (ossia "quando il numero maggiore contiene il minore o totalmente o due volte o tre o quattro volte e via dicendo, e nulla manca, nulla avanza", ibidem, II, 4), dei 'superparticolari' (cioè "quando il numero maggiore contiene il numero minore totalmente più una qualche sua parte e questa è la sua metà, come tre a due o è la terza, come quattro a tre", ibidem) e dei 'superparzienti' (che si ha "quando il numero maggiore contiene totalmente in sé il minore, più alcune sue piccole parti; se ne contiene due di più, si chiama 'proporzione superbisparziente', come sono 5 a 3, se poi ne contiene 3 di più, si chiamerà 'supertriparziente', come 7 a 4, e negli altri casi può esserci la medesima somiglianza", ibidem). A un livello più complesso, esse erano la media aritmetica, la media geometrica e quella armonica (oggi, per questi casi, si preferirebbe dire 'successione' e non 'media'). La media aritmetica si stabilisce tra tre termini, a, b e c, in modo che b−a=c−b; la media geometrica richiede invece una proporzione tra questi stessi termini (b:a=c:b); infine, per ottenere la media armonica, le differenze tra i termini devono essere proporzionali al rapporto tra il più grande e il più piccolo termine della proporzionalità (c−b:b−a=c:a).
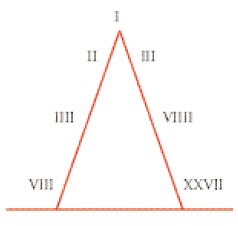
La serie paradigmatica dei numeri tridimensionali 6, 8, 9, 12 risponde esattamente alle condizioni poste da questi tre tipi di media; infatti, i rapporti 6/8, 9/12 e 6/9, 8/12 soddisfano le condizioni della media geometrica, 6, 9 e 12 quelle della proporzione aritmetica, mentre 6, 8 e 12 sono in proporzione armonica. L'importanza di questa serie che discende dal numero 6 ‒ primus perfectus (ossia un numero uguale alla somma dei suoi divisori) ‒ nella teoria della musica è dovuta alle sue proprietà acustiche; la media aritmetica divide infatti l'ottava (6:12) in intervalli di quarta (12:9) e di quinta (9:6), mentre la media armonica inverte questi rapporti (12:8:6, quinta e quarta). Essa pone così in evidenza gli intervalli strutturali del sistema acustico pitagorico: di ottava (12:6), di quinta (12:8 o 9:6), di quarta (12:9 o 8:6) e infine il tono (9:8).
La teoria della musica medievale confermava, sull'esempio di Boezio, la preminenza dell'ottava, che ottenne sul monocordo (mediante la bipartizione della corda) il primo multiplo (2:1) o, inversamente, il primo rapporto superparticolare (1:2). A partire da questo doppio rapporto esemplare, la progressione dei multipli da una parte e quella dei superparticolari dall'altra generavano due serie di intervalli, rispettivamente crescenti e decrescenti. Queste progressioni erano alla base di una gerarchia di consonanze (symphoniae) che opponevano, termine a termine, la dodicesima (quinta raddoppiata all'ottava, 3:1) alla quinta (3:2) e la doppia ottava (4:1) alla quarta (4:3) (ibidem, I, 20):
Il postulato pitagorico secondo cui le consonanze potevano essere costituite soltanto da un rapporto multiplo o superparticolare condusse ugualmente i teorici medievali a rifiutare, sull'esempio di Boezio, all'undicesima (ottava + quarta) lo status di consonanza. Questo intervallo, perfettamente consonante all'ascolto, corrispondeva in effetti al rapporto 8:3, vale a dire 2×(4/3), che non apparteneva a nessuna delle due classi in cui si dividevano i rapporti consonanti, ma rientrava nella classe dei multipli superparzienti. Il riconoscimento di questo postulato stabilì in questo modo permanentemente nella teoria della musica medievale il primato della ragione sull'esperienza sensibile.
Oltre a questi principî aritmologici, la scienza medievale della musica riprese da Boezio diverse osservazioni sulle relazioni tra i numeri e i suoni. Così, l'esperienza dimostrava che aumentando la tensione di una corda, aumentava il numero e la frequenza delle pulsazioni e si otteneva un suono più acuto (ibidem, I, 3). Sulla base di tale osservazione si formò il paradigma della proporzionalità dell'acutezza e della gravità del suono al numero e alla velocità delle pulsazioni che colpiscono l'aria; suo corollario fu inoltre l'idea di associare una quantità più grande a un suono più acuto e la diminuzione di questa quantità a un suono più grave.
In contrapposizione a questo modello, derivato da una rappresentazione fisico-acustica del fenomeno sonoro, la graduazione del monocordo ne introdusse un altro, di tipo geometrico; tendendo una corda, che poteva essere rappresentata da un segmento di retta, si poteva osservare che il suono più grave è prodotto dalle vibrazioni emesse dalla totalità della corda. Il tono superiore del suono fondamentale è ottenuto riducendo la porzione di corda vibrante di un nono della sua lunghezza, l'intervallo di quarta riducendola di un quarto, quello di quinta riducendola di un terzo e, infine, l'intervallo di ottava riducendola della metà. Questa rappresentazione spaziale ‒ conforme a un'impostazione di tipo geometrico e presente, con qualche correzione, nella struttura delle canne dell'organo ‒ fu alla base della nozione che a una quantità maggiore corrisponda un suono più grave e che, inversamente, un suono più acuto sia funzione di una diminuzione quantitativa. La scienza medievale della musica riprese dunque dal De institutione musica una rappresentazione spaziale dei suoni così come una scala acustica rigidamente strutturata.
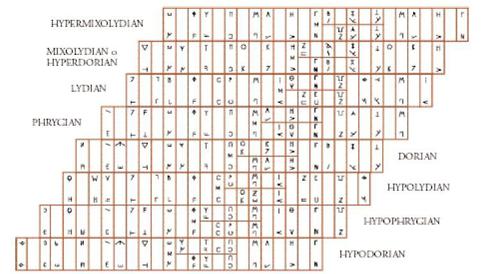
La dimostrazione del sistema acustico sul monocordo (ibidem, IV) non imponeva soltanto una nuova rappresentazione quantitativa del suono, ma anche una spazializzazione delle altezze del suono associando alla progressione grave-acuto l'orientamento sinistra-destra della scrittura e usando fondamentalmente la successione delle lettere dell'alfabeto per designare i suoni del monocordo, dai gravi agli acuti. Tra i diversi modi di indicizzazione dei suoni utilizzati da Boezio, la tradizione medievale conservò in particolare la notazione alfabetica continua, dalla lettera A alle lettere O, P (ibidem, IV, 14 e 17), nell'analisi della struttura interna degli intervalli di quarta, di quinta e di ottava. La scala dei suoni di Boezio si estendeva lungo una doppia ottava, articolata in cinque tetracordi discendenti, ciascuno dei quali costituito da due toni e da un semitono (fig. 2).
Questa concezione di disgiunzione e di congiunzione dei tetracordi conferiva al sistema acustico della Tarda Antichità un'instabilità strutturale (mobilità di grado b/h) a lungo oggetto delle discussioni dei teorici medievali. L'analisi degli "aspetti" degli intervalli fondamentali (di quarta, di quinta e di ottava) tentava di mettere in evidenza la serie delle similitudini interne al sistema eptatonico. La nozione di 'aspetto' (species) designava la struttura interna degli intervalli, differenziati secondo il principio della rotazione circolare dei toni e dei semitoni costitutivi; l'intervallo di quarta, composto da due toni (T T) e da un semitono (S), possiede così tre aspetti: T T S (in ordine discendente, che corrisponde alla forma 'tipica' del tetracordo strutturale), T S T e S T T; per lo stesso principio, l'intervallo di quinta ne possiede quattro (T T T S, T T S T, ecc.) e l'ottava sette (T T S T T S T, T S T T S T T, ecc.).
La proiezione di questi sette aspetti dell'ottava sulla doppia ottava del grande sistema perfetto fu all'origine dei 'toni di trasposizione' o 'toni d'altezza', definiti "tropi" (tropus) da Boezio, e interpretati dalla tradizione medievale in una prospettiva modale. Questi tropi derivavano da una configurazione astratta che prevedeva la trasposizione in successione, verso l'alto della scala, dell'insieme dei gradi del grande sistema perfetto, secondo l'ordine dei toni e dei semitoni che separavano i sette aspetti dell'ottava o, in altre parole, secondo l'ordine dei toni e dei semitoni che componevano il primo aspetto dell'ottava (T T S T T S T). Questo principio di trasposizione fu riassunto da Boezio in una tavola (fig. 3) che ebbe una notevole influenza sull'elaborazione della teoria medievale della modalità.
La ricezione medievale: trasformazioni e mutazioni concettuali
Il sistema acustico
Il ricco corpus di glosse che ha accompagnato la trasmissione del De institutione musica di Boezio testimonia l'attenzione rivolta dai chierici dell'Alto Medioevo alle nozioni teoriche in esso contenute. Il carattere prevalentemente esegetico di queste glosse rivela un pensiero orientato più verso la spiegazione e la comprensione del testo che verso la ricerca speculativa. L'originalità del pensiero scientifico medievale in campo musicale appare non tanto nella riformulazione e nel commento delle teorie boeziane quanto nell'elaborazione di un discorso inteso a imporre un metodo razionale alla prassi del canto liturgico. Così, negli scritti dei teorici medievali i concetti boeziani alla base dell'elaborazione e dell'analisi del sistema acustico s'integravano a un interesse che, nel corso di tutto il Medioevo, si distinse per il suo carattere teorico-pratico. Ci si proponeva, sulla scia delle riforme liturgiche e dei tentativi di unificazione intrapresi nell'età carolingia, di dotare di una base razionale la struttura modale dei canti intonati durante la celebrazione della messa e, soprattutto, dell'officio quotidiano. Nel quadro di una pratica vocale dominata, da una parte, dal canto monodico dell'officiante e dalle 'polifonizzazioni' omofoniche e, dall'altra, dal rispetto per l'intelligibilità del testo, questo sforzo di razionalizzazione fu prevalentemente diretto all'ordinamento delle altezze del suono.
La tradizione ereditata dalla Tarda Antichità conobbe così, sotto l'influenza di una volontà normativa tesa alla razionalizzazione di certe pratiche musicali, alcune sostanziali modifiche che condussero a profonde divergenze su alcune questioni, in particolare sulla struttura della scala dei suoni. Il tetracordo, concetto portante nella costruzione del grande sistema perfetto, e le symphoniae rimasero uno strumento fondamentale nella concezione della scala sonora riorganizzata a partire dalle finales (D E F G) del canto gregoriano. Così, Ubaldo di Saint-Amand (850 ca.-930 ca.), attento lettore di Boezio, proponeva una ricostruzione originale del grande sistema perfetto a partire dal tetracordo costituito da queste finales, ma secondo il principio di congiunzione e di disgiunzione dei tetracordi enunciato da Boezio. Questa costruzione imponeva una lettura 'ascendente' del grande sistema perfetto, dai gravi agli acuti, ma a partire da un tetracordo perfettamente simmetrico, composto da due toni separati da un semitono (fig. 2).
Il trattato teorico Musica enchiriadis, redatto verso la fine del IX sec., elaborava, a partire da questo stesso tetracordo, costituito dalle finales del canto liturgico, una scala acustica specifica. Il tetracordo di riferimento in questo caso, come per Ubaldo, seguitava a essere quello delle finales, tuttavia questo sistema privilegiava la quinta, che diveniva l'intervallo strutturale; così, contrariamente al grande sistema perfetto, che presentava due ottave quasi simmetriche e quindi favoriva i rapporti di ottava, la scala della Musica enchiriadis associava a ogni grado del sistema un grado, se non due, in rapporto di quinta. Questa costruzione, basata sul principio della giustapposizione di tetracordi disgiunti, favoriva in tal modo le trasposizioni alla quinta, le quali rispondevano evidentemente ad alcune esigenze inerenti alla specificità del canto liturgico monodico, ma anche alla prassi del canto polifonico per moto parallelo alla quinta.
Il sistema acustico pitagorico ‒ e la struttura eptatonica divisa in toni e semitoni che lo caratterizzava ‒ fu adattato anche agli strumenti musicali. Tuttavia, per alcune ragioni probabilmente inerenti ai processi di fabbricazione delle canne d'organo, questa scala si caratterizzava per la presenza, ai gradi inferiori, di due toni successivi, che formavano la base di un tetracordo ascendente del tipo T T S. Questa scala è documentata da diverse fonti risalenti al periodo che va dal IX al XII sec.: da Ubaldo di Saint-Amand, dalla Scolica enchiriadis (Tertia pars), commento alla Musica enchiriadis e, infine, da molte misure di canne di organo e di campane, così come dall'insieme delle misure cosiddette dell'organistrum. Questa scala propriamente strumentale coincideva inoltre con quella composta dalle proporzioni dell'"anima del mondo", descritta nel Timeo di Platone; la sua considerevole fortuna nella storia della teoria musicale, ma anche della pratica, rende opportuno dedicarle un esame più approfondito.
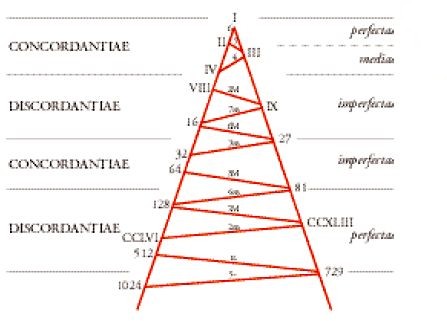
Benché i riferimenti espliciti al Timeo fossero rari, questo testo era senza alcun dubbio ben noto ai teorici altomedievali grazie alla traduzione e al commento di Calcidio, anche se l'apogeo della 'fortuna di Calcidio' coincise con la rinascita intellettuale del XII secolo. Così, l'anonimo autore della Musica enchiriadis, Gerberto di Reims, Abbone di Fleury (945 ca.-1004), o i glossatori del De institutione musica, dimostravano una conoscenza approfondita delle teorie platoniche. I teorici della musica prendevano in considerazione soprattutto il primo dei tre diagrammi contenuti nel commento di Calcidio, in cui era esposta la struttura fondamentale dell'"anima del mondo" (Timaeus a Calcidio translatus, XXXII-XXXIII). Questo diagramma a forma di lambda, il cui vertice coincideva con l'unità, presentava sulla gamba sinistra la serie delle prime tre potenze di 2 (2, 4, 8) e sulla destra quella delle prime tre potenze di 3 (3, 9, 27) (fig. 4). I primi sei numeri di questo diagramma indicano le proporzioni delle 'sinfonie' che costituivano il sistema acustico pitagorico: l'ottava (1:2), l'ottava più la quinta (1:3), la quinta (2:3), la quarta (3:4), il tono (8:9). Sviluppando, da un lato e dall'altro, le due serie di potenze (rispettivamente 16, 32, 64,… e 81, 243, 729) e seguitando a porle in relazione si ottenevano tutti i possibili intervalli tra i differenti gradi della scala eptatonica: la settima minore (9:16), la sesta maggiore (16:27), la terza minore (27:32), ecc. Questa notevole progressione‒ definita, nel XIV sec., dei "numeri armonici" ‒ ha avuto una profonda influenza sulla formulazione dei principî della polifonia occidentale; essa, in particolare, ha consentito di stabilire una classificazione razionale delle consonanze, divise in concordanze e discordanze perfette e imperfette, e di rafforzare in tal modo, in una prospettiva decisamente pitagorica, il primato della ragione sull'esperienza sensibile (fig. 5).
La subordinazione della sensibilità era sancita, in modo paradigmatico, dalla norma formulata da Giovanni di Garlandia: "le consonanze che derivano più direttamente dall'uguaglianza sono anche quelle che concordano di più sul piano sonoro. Quelle che se ne discostano di più sono anche meno concordanti e di conseguenza più dissonanti all'ascolto" (De mensurabili musica, ed. Reimer, p. 73).
I toni di trasposizione greci e le scale modali medievali
Una delle più importanti innovazioni della scienza medievale della musica è stata quella di aver ideato per un uso pratico ‒ e in una prospettiva normativa ‒ una scala acustica; mediante essa e i sistemi in cui era strutturata (gli aspetti di quarta, di quinta e di ottava) s'intendeva precisare le relazioni reciproche tra i gradi di altezza del suono all'interno di una data melodia. La teoria delle scale modali, che nel corso di tutto il Medioevo definì il quadro euristico della determinazione dei modi, derivava da una fusione tra la teoria degli aspetti delle sinfonie (in particolare di quelli dell'ottava) e la teoria dei toni di trasposizione, che in Boezio erano completamente separate. Il diagramma di tali toni ha svolto un notevole ruolo euristico fin dai primi tempi della ricezione del De institutione musica, durante la prima metà del IX secolo.
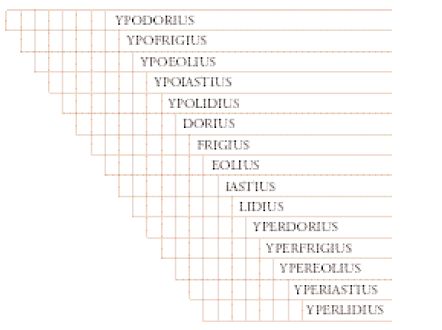
Molto prima della riscoperta del De institutione musica, avvenuta nel primo quarto del IX sec., i lettori del quadrivio conoscevano già, attraverso Marziano Capella (prima metà del V sec., De nuptiis Philologiae et Mercurii, IX, 935) nonché Cassiodoro (Institutiones, II, 5), la teoria dei quindici toni di trasposizione esposta da Aristide Quintiliano, scrittore greco di musica, vissuto secondo alcuni nel II sec. d.C., secondo altri nel III o anche nel IV secolo. Si pensò così di rappresentare questi toni utilizzando la tavola di Boezio, e questa rappresentazione ci è pervenuta attraverso numerosi esemplari dell'opera enciclopedica di Marziano Capella. Nel diagramma, i toni erano rappresentati sotto la forma di scale eptatoniche (fig. 6). Questa tavola dei toni di trasposizione ha anche ispirato la formulazione della teoria dei toni ecclesiastici di Ubaldo di Saint-Amand, che postulava l'equivalenza tra questi ultimi e i tropi di Boezio. Ubaldo stabiliva così per ciascun tono una scala di otto suoni (con l'eccezione del tetrardus, la cui estensione poteva essere ampliata di un tono supplementare ai gradi inferiori):
Così, a differenza dei toni di trasposizione di Boezio, che possedevano una struttura intervallare identica e che si distinguevano solamente per il grado di altezza, le scale modali si caratterizzavano sia per la differente distribuzione degli intervalli sia per le differenze di registro.
L'assimilazione delle scale modali ai toni di trasposizione fu definitivamente realizzata nel corso del IX sec., per opera dell'autore anonimo di un trattato divulgato con il titolo di Alia musica. L'autore identificava oramai esplicitamente i toni di trasposizione di Boezio (tropus o anche modus) con gli aspetti dell'ottava, e l'identificazione aveva origine nella confusione tra i concetti boeziani di constitutio e di species (cioè l'ordine invariabile dei toni e dei semitoni che costituivano la scala tipica del grande sistema perfetto rispetto alla disposizione variabile, attraverso la rotazione circolare dei toni e dei semitoni, su cui si basavano le differenti possibili strutture delle consonanze di quarta, di quinta o di ottava). Questa confusione concettuale ha comportato due conseguenze decisive per la storia medievale della teoria della modalità: essa è all'origine della toponimia greca dei toni ecclesiastici (dorico/ipodorico, frigio/ipofrigio, lidio/ipolidio, misolidio/ipomisolidio o ipermisolidio); inoltre, ha introdotto stabilmente una scala acustica strutturata da quarte, quinte e ottave attorno alle quattro finales del canto ecclesiastico.
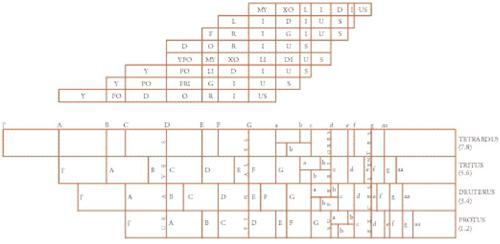
A margine di questa tradizione, i tentativi di adattare effettivamente i toni di trasposizione al sistema delle scale modali rimasero eccezionali. Un dispositivo di questo genere fu ideato da un certo Otker, monaco del convento di Saint-Emmeram a Ratisbona, nella seconda metà dell'XI secolo. Questo dispositivo, conosciuto col nome di quadripartita figura o theorema troporum, fu descritto e discusso da Guglielmo di Hirsau e da Aribone, due teorici attivi nella Germania meridionale durante la seconda metà dell'XI secolo.
Il diagramma ideato da Otker, destinato a essere applicato alla tavola del monocordo, si presentava (fig. 7) sotto la forma di quattro strisce, di cui quella superiore coincideva con le divisioni del monocordo; la scala rappresentata su questa striscia corrispondeva ai gradi del grande sistema perfetto di genere diatonico aumentato di un tono ai gradi inferiori. La striscia immediatamente inferiore recava la stessa scala trasposta un tono più in alto. Quella successiva presentava una nuova trasposizione di un mezzo tono. Infine, l'ultima striscia, operava una trasposizione al tono superiore. Le quattro strisce osservavano così un rapporto di trasposizione identico a quello del tetracordo delle finales (diviso in tono, semitono e tono). Tuttavia questo dispositivo era ambiguo; da un punto di vista propriamente ottico, il diagramma poneva in evidenza i tetracordi in cui era strutturato il sistema acustico (gravi, finali, superiori ed eccellenti), e i gradi costitutivi di questi tetracordi si trovavano in effetti distribuiti su quattro linee che attraversavano verticalmente il diagramma. Allo stesso modo, una lettura orizzontale poneva in evidenza i gradi caratteristici di ciascun tropo (A, D, a, d per il protus; B, E, #, e per il deuterus, ecc.). D'altra parte, applicando questo diagramma alla tavola del monocordo ‒ dato che, a quanto sembra, esso era stato ideato proprio per questo scopo ‒, si otteneva una rappresentazione acustica; così il protus, cioè il tropo più grave (che corrispondeva al primo e al secondo tono), era associato alla trasposizione più alta della scala e di conseguenza al registro più acuto del monocordo. Inversamente, il tropo più alto, cioè il tetrardus (il settimo e l'ottavo tono), si trovava paradossalmente trasposto alla quarta inferiore, verso il registro grave dello strumento.
Aspetti degli intervalli ed esacordi di solmisazione
I teorici della Tarda Antichità (Boezio, Macrobio, Cassiodoro) non attribuivano una realtà acustica alle symphoniae. Ciononostante, l'influenza di una teoria della musica indirizzata a organizzare la pratica vocale dotò i concetti fondamentali dell'acustica matematica di un carattere più concreto. Nel quadro della teoria dei modi, essi delimitavano e qualificavano la sezione della scala dei suoni al cui interno doveva evolversi la melodia. Allo stesso modo, nell'analisi dell'organum originario per moto parallelo delle voci, essi erano esplicitamente identificati come le consonanze fondamentali della polifonia.
La nozione di aspetto, inerente al concetto di symphonia, rimase tuttavia modello per l'elaborazione della nozione di intervallo melodico. Così, pur identificando le symphoniae con le consonanze (consonantiae) dell'organum parallelo, Ubaldo concepiva gli intervalli melodici del canto (modi) come la combinazione degli intervalli semplici (minora intervalla) dati dal tono (T) e dal semitono (S). Ubaldo distingueva così nove intervalli (dalla seconda minore alla sesta maggiore): S, T, S+T, T+T, S+T+T, T+T+T, S+T+T+T, T+T+T+T, S+T+T+T+T, che si riteneva esaurissero l'estensione naturale della voce umana. Questa costruzione architettonica a partire dall'XI sec. fu definitivamente sostituita dalla nomenclatura ideata da Guido d'Arezzo (992-1050), che ammetteva soltanto sei intervalli (modi): il tono e il semitono, la terza maggiore e minore, la quarta e la quinta, che rappresentavano le uniche congiunzioni possibili tra i suoni, per moto ascendente o discendente (Micrologus, IV). Il limitato numero di intervalli consentito da Guido d'Arezzo poteva trovare una spiegazione nel modello canonico delle sei symphoniae (4 5 8 11 12 15).
In Boezio, l'esame degli aspetti delle sinfonie era finalizzato soprattutto alla comprensione delle differenti possibili distribuzioni dei toni e dei semitoni all'interno della quarta, della quinta e dell'ottava. Ora, rapportati alla scala diatonica di un'ottava (per es., T T S T T T S), o alla scala diatonica dei suoni nella sua totalità, gli aspetti della quarta e della quinta ponevano soprattutto in evidenza l'impossibilità di sviluppare un sistema perfettamente simmetrico. Questa impossibilità derivava innanzi tutto dalla presenza, all'interno della scala eptatonica, di tre toni successivi, e come tali dunque irriducibili alle categorie strutturali della quarta e della quinta che rimanevano i concetti fondamentali dell'architettura modale. Così, le trasformazioni della teoria medievale della tonalità derivarono, in gran parte, dal tentativo di assimilare le nozioni di aspetto e di tonalità.
Anche se, indipendentemente da queste difficoltà, gli aspetti della quarta, della quinta e dell'ottava rimasero uno strumento indispensabile nell'analisi del sistema acustico, i teorici altomedievali elaborarono, nel corso dei primi decenni dell'XI sec., un concetto teorico-pratico originale che restò in uso sino alla soglia dei tempi moderni, ossia l'esacordo definito di 'solmisazione'. In opposizione all'ordine variabile dei toni e dei semitoni all'interno delle symphoniae in base al loro aspetto, l'esacordo si caratterizzava, al contrario, per la sua struttura inalterabile, formata da due coppie di toni disposte simmetricamente ai lati di un semitono (T T S T T). L'ideazione dell'esacordo discendeva certamente dall'esigenza di mettere in evidenza un certo numero di simmetrie all'interno della scala dei suoni. Questo concetto fu descritto in modo esemplare da Guido d'Arezzo (Micrologus, VII), che lo impiegava per mettere in evidenza le affinità strutturali di certi gradi della scala (i gradi delle finales dei toni); l'esacordo mostrava le loro trasposizioni virtuali nel seguente modo:
(si noterà che nella concezione modale di Guido d'Arezzo il grado G non tollerava la contiguità con D senza prestarsi a un'anfibologia). A prescindere dalle contiguità tra i gradi A e D, B ed E, C ed F, l'esacordo manifestava una serie di analogie strutturali nella distribuzione dei toni e dei semitoni all'interno dell'ottava.
La teoria dell'esacordo era inoltre strettamente associata alla teoria degli intervalli formulata da Guido d'Arezzo, secondo il quale i sei intervalli (tono, semitono, terza maggiore e minore, quarta e quinta) consentivano, in effetti, di costruire attorno a ogni nota della scala sonora uno spazio esacordale, attraverso la combinazione di un intervallo discendente e di un intervallo ascendente (semitono o tono + quinta; terza maggiore o terza minore + quarta). Questo dispositivo teorico era rigidamente subordinato alle tecniche didattiche del canto liturgico e probabilmente fu concepito come un metodo mnemotecnico destinato a guidare il giovane cantore nell'apprendimento e nel riconoscimento degli intervalli e della loro giustezza. Probabilmente un brano relativamente oscuro di una lettera di Guido d'Arezzo al monaco Michele (Epistola, redatta successivamente al 1028; cfr. Gerbert 1784), in cui l'autore riassumeva il suo metodo di insegnamento del canto, alludeva proprio a una tecnica simile. L'originalità di questo metodo derivava, molto probabilmente, dall'utilizzazione esemplare, a fini mnemotecnici, della melodia dell'inno a san Giovanni Ut queant laxis appositamente composto dallo stesso Guido d'Arezzo (fig. 9).
La memorizzazione del testo dell'inno con la sua melodia consentiva in tal modo di ottenere una struttura intervallare caratteristica, grazie ai melismi che iniziavano con le sillabe Ut, re, mi, fa, sol, la (3M=terza maggiore; 3m=terza minore):
Questa tecnica, simile, in definitiva, a un'arte della memoria, era verosimilmente già molto nota al tempo di Guido d'Arezzo. La vasta e rapida diffusione dei suoi scritti, a partire dalla seconda metà dell'XI sec. e nel corso di tutto il XII, introdusse stabilmente questa melodia nei metodi pedagogici dei cantori medievali. Sembra poi che un legame più sistematico tra la scala dei suoni e l'esacordo sia stato stabilito solamente nel corso del XII sec., quando gli fu attribuita una posizione di primo piano nelle rappresentazioni tabulari in cui erano distribuite su due o tre righe le sillabe ut, re, … opponendole alle lettere del monocordo (v., per es., Malibu, The J. Paul Getty Museum, Ludwig XII 5 [Phillips 12145], f. 35v):
Tuttavia, la teorizzazione definitiva dell'esacordo di solmisazione fu enunciata soltanto nel corso del XIII sec., probabilmente associata all'insegnamento svolto a Parigi da Giovanni di Garlandia. I testi che documentano le sue lezioni furono tra i primi a descrivere sistematicamente la tecnica della solmisazione. L'esacordo era ormai invariabilmente considerato una scala di trasposizione in grado di manifestare gli elementi isostrutturali della scala dei suoni; collocato in C, in F o in G esso determinava in effetti un'organizzazione rigorosamente identica dei toni e dei semitoni. Questa presentazione sistematica si accompagnava inoltre a una disposizione verticale della 'tavola di solmisazione' che evidenziava sette posizioni dell'esacordo e identificava con chiarezza tre posizioni tipiche: una posizione "naturale" (in C), una posizione "dura" (in G) e una "molle" (attraverso il bemolle, in F).
Grazie alla tecnica delle mutazioni esacordali (vale a dire il passaggio da un esacordo all'altro attraverso la sostituzione delle sillabe corrispondenti a uno stesso suono) sviluppata da Giovanni di Garlandia, vennero inoltre alla luce i vantaggi della strutturazione esacordale della scala dei suoni per la pratica musicale. La mutazione dell'esacordo 'naturale' o dell'esacordo 'duro' in esacordo in bemolle consentì di ridurre 'artificialmente' il tritono naturale (F-h) inerente alla scala eptatonica, sostituendo al grado 'h' il grado 'b'.
Bibliografia
AMIS = Antiquae Musicae Italicae Scriptores, a cura dell'Istituto di Studi Musicali e Teatrali, Sez. Musicologia dell'Università di Bologna, Bologna, 1966-1975.
Bernhard 1990: Bernhard, Michael, Rezeption des antiken Fachs im Mittelalter, Darmstadt, Wissenschaftliche Buchgesellschaft, 1990.
‒ 1993-: Glossa maior in institutionem musicam Boethii, hrsg. von Michael Bernhard und Calvin M. Bower, München, Verlag der Bayerischen Akademie der Wissenschaften, 1993-.
de Coussemaker 1864-76: Scriptorum de musica medii aevi nova series, primum edidit Charles E.H. de Coussemaker, Paris, Durand, 1864-1876, 4 v. (nuove edizioni critiche a partire dal 1950).
CSM = Corpus scriptorum de musica, [by] American institute of musicology, Neuhausen-Stuttgart, Hänssler, 1950-.
DMA = Divitiae Musicae Artis, Schola palaeographica Amstelodamensi conspirante collectae, auspice Josepho Smits van Waesberghe, Buren, Knuf, 1975-.
Eggebrecht 1984: Eggebrecht, Hans H., Die mittelaterliche Lehre von der Mehrstimmigkeit, Darmstadt, Wissenschaftliche Buchgesellschaft, 1984.
Gerbert 1784: Gerbert, Martin, Scriptores ecclesiastici de musica sacra potissimum. Ex variis Italiae, Galliae et Germaniae codicibus manuscriptis collecti et nunc primum publica luce donati a Martino Gerberto, St.-Blasien, Typis San Blasianis, 1784, 3 v.
GLMT = Greek and Latin music theory, Lincoln (Nebr.), University of Nebraska Press, 1984-.
Huglo 2000: Huglo, Michel, Die Lehre vom einstimmigen liturgischen Gesang, Darmstadt, Wissenschaftliche Buchgesellschaft, 2000.
Zaminer 1984-: Geschichte der Musiktheorie, hrsg. im Auftrag des Staatlichen Instituts für Musikforschung Preussischer Kulturbesitz Berlin von Frieder Zaminer, Darmstadt, Wissenschaftliche Buchgesellschaft, 1984-.