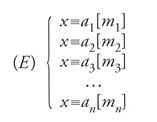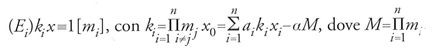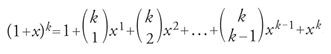La scienza in Cina: l'epoca Song-Yuan. La matematica
La scienza in Cina: l'epoca Song-Yuan. La matematica
La matematica
La rinascita della matematica e la tarda tradizione settentrionale
di Karine Chemla
Nessun documento cinese di matematica databile tra l'VIII e l'XI sec. è giunto fino a noi, se si prescinde da quelli trovati nell'Asia centrale, in particolare da quelli sepolti a Dunhuang intorno all'anno 1000. La prima testimonianza di ciò che ci sembra una ripresa dell'attività matematica è la composizione, nell'XI sec., dei Procedimenti dettagliati del Canone dell'Imperatore Giallo dei Nove capitoli sulla matematica (Huangdi jiuzhang suanjing xicao, che qui di seguito abbrevieremo in Procedimenti dettagliati) di Jia Xian. Tuttavia di questo libro, come di quello contemporaneo di Liu Yi, Discussione sulle fonti degli antichi [metodi] (Yi gu genyuan, che abbrevieremo in Discussione sulle fonti) restano soltanto le citazioni fatte da autori della seconda metà del XIII sec. (Guo Shuchun 1988; Te Gusi 1990; Xu Yibao 1990), ed è a questo periodo che risalgono i libri più antichi a noi pervenuti che testimoniano la rinascita dell'attività matematica. Infatti, a differenza dei secoli precedenti, la seconda metà del XIII sec. ci ha trasmesso molti scritti di argomento matematico. Ma se pensiamo alle quantità di titoli di opere in essi citati e che sono andati perduti, gli scritti in nostro possesso rappresentano probabilmente soltanto un pallido riflesso della produzione del tempo. Sono comunque libri che contengono nuovi e importanti sviluppi della tradizione matematica, rappresentata da una fonte principale, i Nove capitoli sui procedimenti matematici (Jiuzhang suanshu), cui fanno tutti riferimento. Dopo il XIV sec., le pubblicazioni che ci sono pervenute attestano un crescente oblio dei risultati più interessanti ottenuti nel XIII sec. ed è per queste ragioni che il periodo delle dinastie Song-Yuan è stato spesso indicato come un 'Rinascimento' e addirittura un'età dell'oro per la matematica in Cina.
In che senso si può parlare di 'Rinascimento'? L'aspetto più evidente sembra essere un rinnovato interesse per i testi del passato tramandati come Canoni, un fenomeno generale in quell'epoca e che non riguarda soltanto la matematica. Una delle prime indicazioni dell'importanza che veniva attribuita a quel lontano passato è che nel 1048 il Dipartimento della Biblioteca imperiale (mishu sheng) si impegnò a recuperare i Dieci canoni di matematica (Suanjing shishu), la raccolta di epoca Tang, e li stampò. In matematica, come in altri campi, la stampa da parte dello Stato favoriva il rinnovato interesse per i Canoni. Quando nel 1213 Bao Huanzhi ristampò la raccolta, la sua postfazione indicava i Nove capitoli come Canone principale, dal quale derivavano tutti i procedimenti presi in esame dagli altri. L'attribuzione della sua composizione al duca di Zhou, e quindi a una remota Antichità, e la convinzione che il Canone comprendesse tutta la matematica contrastano notevolmente con l'impressione espressa da Bao Huanzhi che, nella trasmissione, il libro, danneggiato, fosse stato restaurato, e che vi fosse una discontinuità nella tradizione. È interessante osservare come le attese riposte nel libro da Bao rispecchino quelle dei commentatori precedenti.
Un altro segno del grande valore attribuito dagli studiosi di matematica di epoca Song ai testi antichi è la ripresa dell'attività di commento ai Canoni, e più precisamente al testo considerato sempre come il più importante, i Nove capitoli. Il libro Procedimenti dettagliati di Jia Xian si presenta come un commento al Canone Han: quando Rong Qi stampò quest'opera nel 1148, la sua prefazione presentava la stessa enfasi della successiva postfazione di Bao Huanzhi. Vi si sottolineava l'origine sacra dei Nove capitoli, attribuiti a Huangdi, il quale li avrebbe composti sulla base dell'osservazione della Via (Dao), fonte di tutti gli esseri. Inoltre, dal confronto dei Nove capitoli con i Classici del confucianesimo, Rong Qi traeva la convinzione che il Canone avrebbe potuto spiegare tutti i fenomeni dei regni del Cielo, della Terra e dell'Uomo, e motivava la necessità di stampare il testo con la volontà di favorire il ripristino e l'ampia diffusione della conoscenza illuminata dei procedimenti suggeriti dai saggi, la comprensione dei quali era caduta nell'oscurità. L'ultimo commentatore del quale si ha conoscenza, Yang Hui, nella prefazione alla Spiegazione dettagliata dei 'Nove capitoli sui metodi matematici' (Xiangjie jiuzhang suanfa, 1261, che abbrevieremo in Spiegazione dettagliata), fortemente ispirata a Rong Qi, assume lo stesso punto di vista (v. par. 2). Le più antiche attività matematiche della dinastia Song a noi note si svolsero così intorno al corpus classico: gli scritti più antichi di quel periodo a noi pervenuti attribuiscono il massimo valore ai Canoni, esprimendo anche la necessità che i testi danneggiati venissero ripristinati senza aggiunte arbitrarie. In questo senso si può ben dire che a opera di alcuni personaggi dell'epoca Song si assiste a un vero e proprio 'Rinascimento'.
Il recupero dei Canoni e le relative ricerche: una nuova concezione delle equazioni algebriche
L'insistenza sul ritorno alle fonti della conoscenza matematica e la ricerca di una profonda comprensione degli elementi fondamentali trovano un'eco nel fatto che tutti gli autori del XIII sec. dei quali possediamo le opere mostrano una gran conoscenza e dimestichezza con i Nove capitoli. A differenza di quanto accadeva nei periodi precedenti, quando apparentemente gli eleganti algoritmi del Canone Han non erano più capiti né apprezzati, nel XIII sec. si assiste a un recupero di quanto sembrava scomparso. Un esempio è dato dalla 'regola della doppia falsa posizione' descritta nei Nove capitoli la cui portata non sembra essere stata completamente compresa dai Canoni più tardi e che torna in auge nel XIII secolo. Un altro esempio è l'algoritmo per la risoluzione dei sistemi di equazioni lineari, anch'esso contenuto nei Nove capitoli. Infatti, nonostante sia utilizzato nei Canoni successivi, vengono ignorati i numeri positivi e negativi introdotti nei Nove capitoli per estendere il suo campo di applicazione. Questi contrassegni si ritrovano invece in tutti gli scritti matematici del XIII sec., nei quali non soltanto sono utilizzati per la risoluzione dei sistemi di equazioni, ma vengono anche trasferiti al campo delle equazioni algebriche, e sempre allo scopo di ampliare il campo di applicazione dell'algoritmo (v. oltre). L'essere in grado di riprodurre un'analoga estensione di una tecnica pensata per un altro ambito dimostra una profonda conoscenza dei Nove capitoli. Gli scritti del XIII sec. presentano inoltre un nuovo aspetto che va molto oltre il problema della soluzione dei sistemi di equazioni lineari (v. oltre); in essi compaiono figure che rappresentano i sistemi di equazioni e le trasformazioni alle quali queste sono soggette nel corso dell'algoritmo.
Se si accetta il punto di vista secondo il quale la Spiegazione dettagliata di Yang Hui cita sistematicamente il contenuto dei Procedimenti dettagliati di Jia Xian (Guo Shuchun 1988), allora i due aspetti menzionati per quanto riguarda gli algoritmi di risoluzione di sistemi di equazioni forse erano già presenti nel commento dell'XI secolo. Siamo però nel campo delle congetture. Yang Hui fa invece esplicito riferimento al nome di Jia Xian per quanto riguarda i progressi nel problema dell'estrazione di radice, un argomento trattato anch'esso nei Nove capitoli e che ci offre l'immagine di un processo storico complessivo che è diverso da quello delle due questioni precedenti. Nei Nove capitoli si trovavano algoritmi per l'estrazione di radici quadrate e cubiche, e molti dei successivi Dieci canoni forniscono una nuova stabile descrizione di procedimenti che, se a prima vista sembrano gli stessi, considerati nella prospettiva dei valori della tradizione culturale racchiusa nei Nove capitoli rappresentano invece un progresso, in quanto i calcoli per l'estrazione di radice sono caratterizzati da una grande omogeneità. È quindi molto interessante che il contributo attribuito a Jia Xian, nel solco della pratica del commento di Liu Hui e di Li Chunfeng, si possa considerare un perseguimento di quei valori. Vediamo ora di chiarire meglio quanto affermato: la pratica matematica nella tradizione dei Nove capitoli rivela una forma di continuità.
Il primo fatto rilevante riguardo all'estrazione di radice nel periodo Song è che Yang Hui associa esplicitamente il nome di Jia Xian a questi ultimi procedimenti, per cui Jia Xian si trova a essere l'erede non soltanto dei Nove capitoli ma anche di alcuni sviluppi più recenti contenuti nei Dieci canoni. Inoltre, la descrizione che gli viene attribuita concorda con la formulazione del secondo tipo di procedimento per l'estrazione di radice presente nei Dieci canoni, un segno della persistente stabilità di questo secondo stato raggiunto dal procedimento. Il punto importante è però che Yang Hui associa il nome di Jia Xian a un altro procedimento, il 'metodo per estrarre radici mediante addizioni e moltiplicazioni' (zeng cheng kaifangfa), che presenta proprietà di notevole rilievo. Nell'estrazione della radice cubica, per esempio, ci accorgiamo che, attraverso l'algoritmo, viene utilizzata sempre la stessa routine, ossia moltiplicazione della cifra della radice considerata per il valore che si trova in una riga al di sotto, e addizione o sottrazione del prodotto dalla riga immediatamente superiore. Ciò comporta numerose conseguenze.
In primo luogo, il confronto di questo passo essenziale dell'algoritmo con la divisione o la moltiplicazione effettuate sulla superficie di calcolo permette di concludere che l'estrazione di radice viene ora effettuata alternando i passi essenziali di queste due operazioni: l'algoritmo è stato così ridotto alla ripetizione delle stesse due operazioni di base, la moltiplicazione e la divisione. Abbiamo così una prima prospettiva secondo la quale considerare la maggiore omogeneità dell'algoritmo ottenuta con questo modo di eseguire l'estrazione di radice. Ciò è in accordo con l'affermazione fondamentale di Yang Hui nella prefazione al suo commento, quando definisce la moltiplicazione e la divisione gli "strumenti fondamentali" della matematica. In secondo luogo, per tutta la durata dell'algoritmo la routine per il calcolo degli stati successivi del 'dividendo' è la stessa per tutti i divisori, fino al punto in cui si arriva all'inversione della sostituzione dell'addizione con la sottrazione: le righe si modificano nello stesso modo nel corso del calcolo. In terzo luogo, i calcoli associati alla prima cifra sono gli stessi di quelli per le cifre successive, e anche questa è una conferma dell'omogeneità del nuovo procedimento. Infine, ed è il punto più importante, volendo calcolare una radice cubica si lasciano due righe tra il 'dividendo' e il 'divisore' sottostante; se se ne lascia una sola, lo stesso algoritmo fornisce la radice quadrata, se se ne lasciano n−1, fornisce la radice n-esima. Sembra che in Cina l'introduzione del 'metodo per estrarre radici mediante addizioni e moltiplicazioni' sia contemporanea al fatto che fossero estratte radici di indice superiore a tre con questo stesso algoritmo. Divisione, estrazione di radici quadrate, cubiche ed n-esime si presentano ora come uno stesso algoritmo: quale operazione venga effettuata dipende dal numero di righe sulle quali esso si esegue. Anche da questo punto di vista siamo di fronte a una maggiore omogeneità. L'algoritmo, oggi noto come 'metodo di Ruffini-Horner', si trova anche, eseguito allo stesso modo, in un trattato del matematico arabo al-Samaw᾽al, completato nel 1174 (Chemla 1994). Un indizio che suggerisce che le relazioni scientifiche tra la Cina e il mondo arabo siano proseguite ben oltre la seconda metà del XII sec., anche se, stando alle fonti arabe medievali in nostro possesso, gli sviluppi cinesi tra i quali rientra questo algoritmo non sembrano avere equivalenti nel mondo arabo.
Da tutti i punti di vista sopra indicati, il 'metodo per estrarre radici mediante addizioni e moltiplicazioni' presenta gli stessi aspetti di omogeneità dell'algoritmo descritto nei Nove capitoli per sistemi di equazioni lineari e di quelli per le operazioni aritmetiche fondamentali. È quindi notevole che poco dopo la sua comparsa la nozione di equazione algebrica abbia subito una modificazione radicale e acquisito una notazione posizionale, in modo del tutto analogo alla modificazione che i numeri e le equazioni lineari avevano avuto almeno fin dalla formazione del Canone Han. Si può supporre che il nuovo algoritmo abbia avuto l'effetto di rimodellare l'oggetto matematico che ne era alla base: le equazioni di secondo e terzo grado erano state finora introdotte come operazioni numeriche che dipendevano dall'estrazione di radice e che avevano rispettivamente due e tre termini. A un certo momento, tra l'XI e il XIII sec., la concezione di queste equazioni subì una modifica; se nella tradizione dei Nove capitoli esse rimanevano operazioni aritmetiche, un'equazione di secondo grado aveva ora tre termini, corrispondenti a quelli che nella matematica moderna sono il termine noto e i termini in x e in x2, e una cubica un termine in più, in x3. Un cambiamento, in apparenza di scarsa importanza, ma invece molto significativo in quanto ora di un'equazione erano identificati ed espressi tutti i coefficienti. Questi erano scritti come una colonna di numeri, esattamente nel modo in cui le equazioni soggiacenti all'estrazione di radice emergevano regolarmente nel corso dei calcoli per effettuare l'estrazione. La potenza di x corrispondente, a cui era associato un dato coefficiente, era espressa dalla sua posizione nella colonna, così come in un numero la potenza di 10 a cui corrisponde una data cifra dipende dalla posizione che questa occupa nella successione delle cifre che rappresentano un numero. Inoltre, e parallelamente all'estensione del 'medesimo metodo di addizione e moltiplicazione' all'estrazione di radici n-esime, compaiono equazioni di grado superiore anch'esse espresse secondo il medesimo principio. E così, come un unico algoritmo serviva per radici di indice comunque elevato, che poi veniva adattato per la risoluzione di equazioni, le equazioni di qualunque grado erano presentate come un unico oggetto matematico. Il legame tra la nascita di un algoritmo generale e completamente omogeneo e lo slittamento nella direzione di una notazione completamente posizionale sembra indicare la possibilità che si tratti delle due facce di una stessa medaglia nella pratica matematica che segue la tradizione dei Nove capitoli. La superficie di calcolo è l'oggetto su cui questi due aspetti si articolano.
Il 'metodo per estrarre radici mediante addizioni e moltiplicazioni' di Jia Xian si può quindi considerare orientato da un valore di omogeneità. Tuttavia, il modo in cui Yang Hui lega esplicitamente l'algoritmo al nome di Jia Xian indica che può ben essere stato il tentativo di spiegare la correttezza degli algoritmi per l'estrazione di radice trovati nei Canoni a spingerlo a mettere in luce l'omogeneità e a produrre quindi un nuovo metodo.
Questa oscillazione tra il mettere in evidenza, da un lato, le operazioni fondamentali su cui si basano vari algoritmi, e dall'altro lato dimostrare la correttezza di questi ultimi può essere considerata come un segnale che Jia Xian, nel suo commento, continuando le ricerche sui Nove capitoli, persegue scopi simili a quelli di Liu Hui e di Li Chunfeng.
Un ultimo aspetto dell'estensione della nozione di equazione richiede di essere esaminato con attenzione. A un certo punto, tra l'XI e il XIII sec., la natura dei coefficienti cambia perché i numeri usuali adoperati fino a quel momento vengono sostituiti da numeri contrassegnati; i coefficienti possono così essere positivi, negativi o zero. In altre parole, i numeri con un contrassegno, tradizionalmente usati nella risoluzione di sistemi lineari, erano utilizzati in nuovi campi. Le equazioni venivano in ogni caso risolte con un algoritmo del tipo Ruffini-Horner, adattato però alla nuova situazione: l'operazione da eseguire era l'addizione o la sottrazione a seconda che, in un dato stadio del calcolo, in due righe contigue della colonna nella quale erano rappresentati i successivi stati in cui si trovava l'equazione nel corso dell'algoritmo, i numeri avessero contrassegni uguali o diversi. Nel corso dei calcoli richiesti dall'algoritmo continuava quindi a presentarsi, e in senso ancora più generale, un'alternanza di moltiplicazioni e divisioni a seconda della situazione che si incontrava sulla superficie di calcolo a ciascun passo. Come per i sistemi di equazioni lineari, i numeri contrassegnati conservavano il ruolo di contrassegni algoritmici e permettevano di estendere sia le possibilità di applicazione dell'algoritmo sia l'insieme delle equazioni permesse. Il libro di Liu Yi Discussione sulle fonti degli antichi [metodi] (Yi gu genyuan), che risale all'XI sec., dà alcune indicazioni su come sia maturata questa estensione. Questo nuovo modo di affrontare le equazioni algebriche, che si inscrive nella tradizione sviluppata in Cina almeno a partire dai Nove capitoli, segna uno dei capitoli più importanti dell'algebra del periodo Song-Yuan. I primi passi di questa tradizione si ritrovano nelle fonti arabe, ma questi sviluppi più recenti non si trovano nei testi occidentali a noi noti.
Non siamo in grado di stabilire con precisione quando ebbe luogo in Cina questa innovazione; la situazione generale della matematica nella Cina del XIII sec. ci fornisce però qualche indicazione in proposito. Dal 1127 e fino al 1279 il territorio corrispondente alla Cina odierna rimase diviso politicamente in Nord e Sud, divisione che si riflette nei testi matematici che il XIII sec. ci ha tramandato. Interi capitoli largamente sviluppati da autori del Sud (v. par. 2) non sono nemmeno menzionati in testi del Nord, almeno in quelli in nostro possesso, e viceversa (v. oltre). Gli argomenti che si trovano in entrambi i corpus e che appaiono essere ben conosciuti potrebbero allora appartenere a un retaggio comune che si può far risalire a prima del secondo quarto del XII secolo. L'equazione algebrica generale, risolta mediante la versione ampliata del 'metodo di addizione e moltiplicazione', ne è un esempio. Considerata da autori appartenenti alla tradizione meridionale come Qin Jiushao, ne viene data per scontata la conoscenza da parte di autori della tarda tradizione settentrionale come Li Ye (v. oltre), e ciò suggerisce gli inizi del XII sec. come possibile terminus ante quem per la sua elaborazione.
Tuttavia un'altra differenza tra scritti delle tradizioni settentrionale e meridionale riguardo a queste equazioni parla a favore di una fonte comune piuttosto remota. A differenza dei Canoni tramandati, questi scritti abbondano tutti di illustrazioni e di rappresentazioni di configurazioni di numeri come dovevano probabilmente apparire sulla superficie di calcolo. Nel nostro caso particolare, tutti questi testi includono tali rappresentazioni grafiche di equazioni, ma il modo in cui queste configurazioni sono inserite nel testo è diverso. Gli autori meridionali ‒ è il caso di Qin Jiushao ‒ rappresentano le equazioni come illustrazioni (tu) alle quali fa riferimento il discorso; ogni numero che compare nell'equazione è inoltre accompagnato da una menzione che ne indica la natura e il contrassegno. Nelle Misurazioni del cerchio sullo specchio del mare (Ceyuan haijing) di Li Ye, la colonna dei numeri che rappresenta un'equazione viene inserita come se fosse una parola di una frase del discorso matematico; compare nella colonna del testo senza interrompere il discorso, rispettando la sintassi della frase (Chemla 1996). Non vi è alcun carattere particolare accanto ai numeri, e per indicare un numero negativo si barra l'ultima cifra. Il fatto che autori delle due tradizioni condividano la nozione di equazione e gli algoritmi di risoluzione, mentre il modo di rappresentazione è così radicalmente diverso, sembra indicare che il retaggio comune riguardo a questi argomenti risalga a un periodo molto più antico.
In continuità con la tradizione di ricerca sulle equazioni algebriche che aveva ricevuto un ulteriore stimolo dall'opera di Jia Xian, nella Cina settentrionale si ebbero nuovi sviluppi, che non sembra siano stati trasmessi al Sud, riguardanti l'elaborazione di un'algebra dei polinomi rivolta a formulare equazioni algebriche per risolvere un problema. Esamineremo ora questo nuovo argomento attraverso il più antico testo in nostro possesso che se ne occupi: le Misurazioni del cerchio sullo specchio del mare di Li Ye.
Li Ye e l'algebra dei polinomi nel Nord della Cina
Tra il XII e il XIII sec., nelle regioni settentrionali dello Hebei e dello Shanxi, fa la sua comparsa un nuovo capitolo della matematica al quale saranno dedicate molte opere fino ai primi del XIV sec.: il 'procedimento del principio celeste', ovvero, in termini moderni, l'algebra dei polinomi. I due soli libri composti prima dell'unificazione della Cina a opera dei Mongoli nel 1279 che riguardano questo argomento e che sono giunti fino a noi sono opera dello stesso autore, Li Ye (1192-1279 ca., noto anche come Li Zhi): Misurazioni del cerchio sullo specchio del mare (1248, che abbreviamo in Misurazioni del cerchio) e Disporre i pezzi per la [Raccolta] che accresce gli antichi [metodi] (Yigu yanduan, completato nel 1259). Furono stampati intorno al 1282, e può essere stata proprio questa stampa a garantirne la trasmissione ai posteri. Il primo fu ristampato nel 1287, con una postfazione di Wang Deyuan. Altri due libri che trattano l'argomento, ampliandolo, furono scritti da Zhu Shijie poco più tardi, nel 1299 e nel 1303, e rappresentano in un certo senso una sintesi delle tradizioni settentrionale e meridionale a opera di un autore che aveva viaggiato a lungo per tutta la Cina (v. par. 3). Non abbiamo altri scritti sull'algebra dei polinomi, e poco dopo la loro stesura nessuno conosceva più l'argomento; esso fu riscoperto soltanto nel XVIII secolo.
La biografia di Li Ye è tipica di un certo tipo di intellettuale del suo tempo. Egli superò gli esami di Stato della dinastia Jin, ma qualche tempo dopo decise di ritirarsi dalla vita pubblica. Lasciò il posto di funzionario che occupava nel Nord della Cina, area costantemente destabilizzata dall'esercito mongolo, scegliendo una vita da eremita. Sostenuto finanziariamente da funzionari locali e da amici, prima nella regione dello Shanxi e quindi in quella dello Hebei, si dedicò a studi di vario genere, tra gli altri storia, poesia e matematica. Egli nomina e cita libri di matematica che sembrano risalire allo stesso periodo, e ciò può suggerire contatti con circoli che sviluppavano la nuova algebra nella regione: egli stesso afferma che erano numerosi quelli che andavano da lui a studiare matematica (ciò testimonia anche che questa disciplina veniva insegnata privatamente; Mei Rongzhao 1966). Le prefazioni ai suoi scritti di matematica mostrano come, a differenza dei contemporanei che disprezzavano la materia, egli aveva il sentimento di appartenere a un'antica e nobile tradizione cinese di studi di matematica che prendeva come modello e come fonte i Nove capitoli. Egli era convinto che la comprensione della matematica potesse essere ottenuta a partire dallo schema fondamentale (li) della Natura, e che, anche se si trattava soltanto di una tecnica, questa disciplina poteva agevolare il progredire verso la Via (Dao).
Le Misurazioni del cerchio si incentrano interamente sul nuovo metodo, e fanno uso costante del nuovo oggetto matematico, i polinomi in una indeterminata, nella notazione posizionale proveniente da quella usata per le equazioni, anche se le rappresentazioni distinguono chiaramente tra i due. Per simmetria con i numeri scritti orizzontalmente come successioni di cifre, i polinomi sono rappresentati come colonne di numeri corrispondenti ai coefficienti delle successive potenze, positive e negative, dell'indeterminata. Questi numeri possono essere contrassegnati come positivi o negativi, oppure essere nulli. È notevole che l'autore arabo del XII sec. al Samaw᾽al, già citato in relazione al 'metodo di Ruffini-Horner', sia il primo matematico occidentale conosciuto a introdurre polinomiali e a scrivere la notazione posizionale per i polinomi. Nell'Al-Bahir egli considera polinomi con coefficienti positivi e negativi di potenze positive e negative dell'indeterminata, un fatto apparentemente piuttosto isolato nel mondo arabo; i polinomi sono scritti però orizzontalmente.
Li Ye opera con i polinomi come se fossero numeri: li moltiplica, li divide, introduce frazioni e proporzioni (Chemla 1982). Sarà questo il metodo principale per ricavare equazioni atte a risolvere i 170 problemi raccolti nelle Misurazioni del cerchio. L'esame di quest'opera rivelerà i punti di continuità e quelli di rottura con la tradizione dei Nove capitoli, mostrando così quale influenza abbia avuto il Canone Han sulla matematica del periodo Song-Yuan. Il libro si apre con un disegno, al quale viene fatto continuamente riferimento, proposto indipendentemente da qualunque problema: già questo rappresenta una novità rispetto ai libri che conosciamo di epoca precedente. Li Ye introduce quindi i nomi per i segmenti che compaiono in questa figura e i valori che essi assumono in un esempio numerico particolare, nel quale le misure del triangolo più grande CQT sono rispettivamente 320, 600 e 680 per base (a), altezza (h) e ipotenusa (c). Seguono le due parti principali del libro: un formulario che raccoglie circa 700 formule riferite alla figura, il primo di questo genere nella letteratura matematica cinese, e 170 problemi che seguono tutti uno stesso modello.
Infatti, in questi problemi in generale viene data la lunghezza di due segmenti della figura, nel quadro dell'esempio numerico introdotto all'inizio, per poi chiedere sempre la stessa cosa: la lunghezza del diametro del cerchio. Poiché il risultato è virtualmente sempre lo stesso, l'interesse si concentra sul metodo per trovarlo mediante il 'procedimento del principio celeste'.
Si tratta quindi da più punti di vista di un libro su un argomento particolare, nel quale tutti i problemi riguardano il triangolo rettangolo. Vi si continua lo studio delle equazioni nella stessa branca della matematica nella quale questo studio era stato introdotto nei Nove capitoli e che Wang Xiaotong aveva proseguito.
La figura fondamentale delle Misurazioni del cerchio rivela forti legami con i Nove capitoli. L'apparenza esteriore contrasta tuttavia con le prime figure geometriche cinesi che conosciamo: qui infatti sono nominati i punti, non più le aree, anche se poi ci si serve di questi 'nomi' per individuare i triangoli rettangoli di cui è composto il disegno. Il cerchio occupa una posizione particolare rispetto a molti di questi triangoli: per esempio, è inscritto nel triangolo CQT. La figura rappresenta anzi un sistema di posizioni notevoli di un cerchio rispetto a un triangolo rettangolo, le cosiddette 'Nove inscrizioni' che Li Ye fa risalire a una delle sue fonti.
All'epoca in cui scriveva Li Ye, a un triangolo rettangolo venivano associate tredici quantità: a base, altezza e ipotenusa si aggiungevano tutte le possibili somme e differenze di queste, prese due a due e tre a tre. Da questo punto di vista, la figura di Li Ye presenta un altro aspetto notevole, in ragione del quale essa è un sistema anche in un altro senso: la somma dei tre lati di ciascuno dei tredici triangoli della figura dà una delle tredici quantità collegate al triangolo più grande CQT, di lati a, b e c. Ciò fornisce un possibile punto di vista dal quale considerare il legame di fondo che la figura ha con i Nove capitoli. La posizione del cerchio rispetto al triangolo maggiore CQT ci indirizza verso il problema che il Canone Han dedica a questa configurazione. Colpisce il fatto che nella dimostrazione della correttezza del procedimento data da Liu Hui intervengano due triangoli interni al triangolo grande, la somma dei tre lati dei quali vale rispettivamente b e a. La figura di Li Ye appare così un completamento, rispetto a quest'ultima proprietà, di quella introdotta da Liu Hui nel III sec. per fornire una dimostrazione. Inoltre, una conseguenza della proprietà della figura di Li Ye è che essa si può ingrandire di un fattore a+b+c in modo che tutte le quantità risultino numeri interi. L'esempio principale di Li Ye non è altro che il triangolo rettangolo di dimensioni 8, 15 e 17, ingrandito di un fattore 40, cioè di 8+15+17. Non sorprende allora che sia proprio questo il triangolo del problema 16 del cap. 9, intitolato 'Base e altezza', nel quadro del quale i Nove capitoli consideravano il diametro del cerchio inscritto.
Ciò indica che il Canone Han e i commenti a esso costituiscono l'inizio di una tradizione di ricerca alla quale le Misurazioni del cerchio appaiono collegate. Il lavoro che questa tradizione ha svolto su quella figura è notevole; non si tratta soltanto di un insieme di linee, bensì di una configurazione di triangoli opportunamente scelti che è in accordo con le figure utilizzate in tutti i commenti; questa figura sembra progettata proprio in questo modo. È interessante osservare che alcuni matematici del XIX sec., come Li Shanlan, continueranno a lavorare sul libro nello stesso spirito (Chemla 1982). Su questa base Li Ye fu nelle condizioni di produrre le centinaia di formule raccolte nelle Misurazioni del cerchio, utilizzando un linguaggio artificiale per esprimerle e uno letterario per lavorare su di esse e ordinarle. Su queste formule si basa la seconda parte del libro: esse costituiscono lo sfondo di carattere geometrico necessario per far intervenire i polinomi per risolvere i problemi con equazioni.
Il secondo libro di Li Ye, più elementare, sembra essere stato scritto per introdurre gli studenti a questo argomento. Disporre i pezzi per la [Raccolta] che accresce gli antichi [metodi] eredita la tradizione di stabilire un'equazione sulla base di un metodo fondato su un diagramma che ha lo stesso nome (disporre i pezzi, yanduan) e che sembra risalire a Discussione sulle fonti di Liu Yi (Te Gusi 1990; Horiuchi 2000). Esso sviluppa in modo sistematico questo metodo per i problemi del testo sul quale si basa: la Raccolta che accresce gli antichi [metodi] (Yiguji; Xu Yibao1990). Questi problemi poggiano su configurazioni di cerchi e di quadrati; Li Ye sviluppa quindi la propria ricerca sull'algebra dei polinomi su problemi di geometria piana. Più tardi Zhu Shijie generalizzerà il metodo a quattro indeterminate e amplierà sempre di più l'insieme dei campi della matematica nei quali esso troverà applicazione (virtualmente a tutti i campi; v. par. 3).
La tradizione meridionale: Qin Jiushao e Yang Hui
di Annick Horiuchi
Non si può che restare ammirati di fronte alla vivacità e alla ricchezza del sapere matematico nella Cina del XIII sec., nel momento in cui la corte imperiale, da poco insediata a Hangzhou nel Sud del paese, è esposta alla minaccia mongola; i trattati significativi di cui oggi siamo in possesso provengono dalla Cina libera dei Song meridionali (1127-1279) in numero quasi uguale a quelli prodotti nella Cina occupata dai Mongoli, a dimostrazione che in quel secolo il paese godeva nel suo insieme di un clima culturale, sociale ed economico favorevole allo sviluppo della matematica. Le due maggiori opere apparse durante la dinastia Song meridionale sono dovute a Qin Jiushao (1202-1261 ca.) e a Yang Hui (attivo nella seconda metà del XIII sec.). I testi di questi due autori sorprendono anzitutto per la loro diversità. Qin lasciò ai posteri una sola opera, concepita come una vera e propria summa: gli Scritti sui numeri in nove capitoli (Shushu jiuzhang, 1247), composti di 18 fascicoli (juan), testo che ha la malcelata ambizione di sostituirsi ai Nove capitoli. L'autore era figlio di un colto funzionario del Sichuan e usufruì, nonostante le agitazioni causate dalla guerra, di una preparazione di alto livello sia in matematica sia nella scienza del calendario; grazie alle numerose cariche amministrative che ricoprì ebbe occasione di fare molte esperienze sul campo, anche se si mise in luce più per l'abilità che per le qualità morali. Yang Hui fu invece un anonimo studioso che non ha lasciato traccia negli archivi ufficiali; si sa soltanto che era originario di Qiantang (non lontano dalla capitale). Tuttavia, il fatto che avesse potuto studiare la matematica antica e recente, insieme agli interessi pedagogici, ai riferimenti ad altri autori di trattati matematici, così come la buona conservazione e trasmissione della sua opera, fanno capire che apparteneva a un ambiente colto e ben inserito nella società urbana. Yang Hui, a differenza di Qin, ha lasciato trattati che sono in genere più corti e che mirano a obiettivi precisi: ristabilire il testo corrotto dei Nove capitoli, come nella già citata Spiegazione dettagliata dei 'Nove capitoli sui metodi matematici'; guidare i primi passi dei principianti nelle tecniche di moltiplicazione e divisione nei Metodi di calcolo per la vita quotidiana (Riyong suanfa, 1262); raccogliere 'i metodi rapidi per eseguire moltiplicazioni e divisioni' nel Compendio dei principi che regolano i vari modi di moltiplicare e dividere (Chengchu tongbian benmo, 1274); far conoscere l'opera del maestro Liu Yi (v. par. 1) nei Metodi rapidi di moltiplicazione e divisione per le superfici dei campi e problemi analoghi (Tianmu bilei chengchu jiefa, 1275); o ancora 'raccogliere le curiosità trovate nelle opere dei contemporanei' nella Scelta di curiosità nel solco della tradizione (Xugu zhaiqi suanfa, 1275). Gli ultimi tre testi sono stati riuniti e xilografati nel 1378 sotto il titolo Metodi matematici di Yang Hui (Yang Hui suanfa).
Le opere di Qin Jiushao e di Yang Hui differiscono anche per il profilo dei problemi affrontati e delle tecniche di risoluzione; i problemi di Qin sono in genere complessi, con abbondanza di dati numerici, mentre quelli di Yang sono semplici ed essenziali. Ciò lascia supporre che Qin si rivolgesse a un pubblico colto, già a conoscenza dei fondamenti del calcolo; quanto ai destinatari dei trattati di Yang, si può dire soltanto che sembra provenissero da ambienti più vari che nel passato. Le opere dei due autori non sono tuttavia prive di orientamenti comuni, risalenti verosimilmente all'epoca Song settentrionale (v. par. 1): i principali punti di riferimento procedono, infatti, per entrambi dai Nove capitoli. Le categorie fondamentali del Canone Han (v. cap. XII), come 'base e altezza' (gougu), 'piccola larghezza' (shao guang), 'misure in un quadrato' (fangcheng), 'discussione di opere' (shang gong) sono costantemente richiamate da Qin nelle sue soluzioni. Yang Hui si impegna invece in un'edizione dei Nove capitoli che raccoglie gli antichi commentari e che egli arricchisce con osservazioni personali. Tuttavia, per nessuno dei due i Nove capitoli rappresentano un orizzonte invalicabile; Yang Hui termina infatti l'edizione dell'opera proponendo di sostituire alle antiche classi di problemi categorie fondate sui metodi di risoluzione (zuanlei); Qin Jiushao si interessa invece a problemi che richiedono l'applicazione simultanea di più tecniche tradizionali.
Nel XIII sec. il quadro offerto dai Nove capitoli appare troppo rigido agli studiosi, che sono ora interessati a problemi rappresentativi di realtà concrete del loro tempo; nella maggior parte dei problemi di Qin Jiushao, infatti, le situazioni sono quelle che un funzionario può trovarsi a dover affrontare. E se il contributo teorico più importante degli Scritti sui numeri in nove capitoli, e cioè il metodo detto della 'grande espansione' (dayan) che oggi va sotto il nome di 'teorema cinese dei resti', ha origine in questioni legate al calendario, Qin Jiushao si affretta a trovarne numerose applicazioni nel campo dei problemi amministrativi. Nella prefazione, egli spiega la filosofia che ispira tutta la sua opera, sottolineando che nella matematica sono presenti due aspetti in continua interazione tra loro: la matematica per uso 'interno' (neisuan), che comprende le tecniche per la preparazione del calendario (zhui shu), campo riservato all'Ufficio astronomico della corte imperiale; e la matematica per uso 'esterno' (waisuan), suscettibile di una più larga diffusione, che si collega alla tradizione dei Nove capitoli.
Se negli Scritti sui numeri ogni problema è il risultato di una costruzione sapiente, l'interesse di Yang Hui pare invece rivolto soprattutto all'organizzazione e alla chiarificazione di problemi noti, antichi o moderni, appartenenti o meno alla tradizione colta. Hanno così spazio nelle sue opere i quadrati magici, che egli classifica tra le 'curiosità trovate nelle opere dei contemporanei', accanto alle somme di successioni finite e alle tecniche per semplificare le due operazioni fondamentali, la moltiplicazione e la divisione. L'opera di Yang Hui è piena di note esplicative, un segno della sua sollecitudine ad adeguarsi ai bisogni didattici e di divulgazione del tempo. Per questo aspetto essa rientra in quel gruppo di opere pubblicate a partire dalla fine dei Tang e sotto i Song allo scopo di facilitare il calcolo con le bacchette adattandolo al nuovo pubblico. Nessuna di queste opere ci è pervenuta; ne restano soltanto i titoli, consegnati agli annali di storia. Ci si riferisce di solito a esse in termini di 'matematica popolare' (minjian shuxue; Mei Rongzhao 1966), ma non vi è un confine netto tra questa matematica e quella praticata dalle classi colte. Si assiste a un fenomeno simile a quello dell'Europa del Rinascimento o del Giappone dell'epoca Edo; lo studio di opere di matematica si apre alle classi medie, e ciò provoca la produzione massiccia di opere di divulgazione, seguita da un aumento generalizzato del livello delle conoscenze. A questo proposito è interessante notare che sia Qin Jiushao sia Yang Hui ricordano nelle prefazioni delle loro opere i numerosi maestri di matematica attivi all'epoca.
Tra i punti di convergenza dei due autori va ricordato infine il ruolo fondamentale attribuito al calcolo numerico: in Yang Hui come in Qin Jiushao la risoluzione di un problema non si concepisce senza lo 'svolgimento' (cao), che riprende una per una le istruzioni date nel 'procedimento' (shu) e fornisce i risultati numerici corrispondenti. Esso comprende talvolta figure o tavole con complementi di informazione essenziali: questa importante evoluzione delle modalità di trasmissione del sapere (che presenta tratti diversi nelle tradizioni settentrionale e meridionale, v. par. 1) è collegata verosimilmente alle trasformazioni dell'oggetto 'libro' in seguito allo sviluppo delle tecniche di xilografia e alla conseguente espansione del mercato editoriale.
Congruenze ed equazioni negli Scritti sui numeri di Qin Jiushao
Di fronte a un'opera ricca di informazioni come gli Scritti sui numeri in nove capitoli si corre il rischio di perdere di vista il carattere teorico della riflessione di Qin Jiushao, che è particolarmente rilevante nel caso del metodo della 'grande espansione', il quale riguarda l'analisi indeterminata, ossia il problema detto modernamente 'dei resti' (i Cinesi parlano di 'numero totale'). Yang Hui, che è posteriore a Qin, enuncia il problema secondo uno schema già fissato risalente al Canone matematico del Maestro Sun (Sunzi suanjing); nella sua opera Scelta di curiosità nel solco della tradizione (Xugu zhaiqi suanfa), per esempio, si legge: "Ecco cose di cui si ignora il 'numero totale'. Si dice soltanto che contandole di 3 in 3, ne restano 2, contandole di 5 in 5 ne restano 3, contandole di 7 in 7 ne restano 2. Si domanda a quanto ammonta il numero totale di partenza" (Zhongguo kexue jishu dianji tonghui. Shuxue juan, I, p. 1100). Negli Scritti di Qin invece tale problema viene risolto all'interno di un quadro estremamente generale che lascia aperte numerose possibilità di applicazioni.
Il 'procedimento della grande espansione per il numero totale' (dayan zongshu shu), esposto subito dopo il primo problema del primo capitolo, permette di determinare un numero x (il 'numero totale') che, in termini moderni, soddisfa il seguente sistema di congruenze:
I problemi enunciati negli Scritti sui numeri riguardano tutti situazioni particolari, ma il procedimento con cui vengono affrontati si applica, conformemente alla tradizione dei Nove capitoli, in tutti i casi, senza restrizione sul numero di equazioni e nemmeno sui moduli m1, m2, ..., mn (detti yuanshu o 'numeri di base'), che possono quindi essere negativi, decimali o frazionari. Il primo passo dell'algoritmo prevede la riduzione dei moduli a una forma standard (dingshu, o 'numeri determinati') nella quale essi sono interi e a due a due relativamente primi (dopo una divisione per divisori comuni, se necessario). Questo passo usa tecniche di reciproca riduzione di numeri con divisori comuni. La presenza di una terminologia specifica, elaborata a questo proposito, ha costituito per lungo tempo per gli storici un ostacolo alla comprensione dell'algoritmo (Mo Shaokui 1987). Un esempio è dato dalla nozione di 'riduzione dispari' (yueqi), che indica la trasformazione della coppia d'interi (a, b) nella coppia d'interi relativamente primi (a/δ, b), dove δ è il massimo comune divisore di a e b: 'dispari' esprime in questo caso l'assenza di divisori comuni dei due numeri. Ulteriori esempi possono essere la nozione di 'riduzione pari' (yueou), che designa una trasformazione analoga e che conduce a una coppia (a/δ, b) di numeri non relativamente primi, nonché i 'numeri della categoria' (leishu), termine che designa i numeri che hanno un fattore comune.
Acquisito questo punto, il secondo passo, detto 'procedimento della grande espansione per determinare l'uno' (dayan qiuyi shu), viene eseguito per ognuna delle congruenze i cui moduli mi sono diversi da 1. Si cerca di esprimere la soluzione finale nella seguente forma x0, dove xi, detto 'coefficiente moltiplicativo' (chenglü), è una soluzione della congruenza Ei:
Il procedimento chiave è evidentemente quello che permette di risolvere la singola congruenza kx≡1[m], dove k e m sono interi dati; il calcolo raggiunge così un alto grado di generalità e di elaborazione. Questo metodo fu studiato alla fine del XVIII sec. da Euler e Gauss, i quali fornirono anche la dimostrazione della sua validità.
Qin non fa particolari commenti a proposito dell'infinità di soluzioni che problemi di questo tipo (problemi indeterminati) ammettono; dal nome dato al metodo si capisce però che questo aspetto stava molto a cuore a coloro che l'applicavano. Il termine 'grande espansione' ha infatti origine nel Classico dei mutamenti (Yijing), dove è associato a un insieme di riflessioni sulla capacità di certi sistemi finiti di tradurre o di rendere conto dell'infinito, dell'inesauribile: è il caso, per esempio, del sistema decimale di numerazione, degli esagrammi nella pratica della divinazione, o ancora dei cicli solari e lunari nell'osservazione dei movimenti degli astri. Sappiamo inoltre poco della giustificazione matematica del funzionamento del metodo che Qin aveva in mente. Per scoprirla occorre probabilmente leggere in filigrana la struttura dell'algoritmo, considerare l'analogia con altri algoritmi classici e studiare la terminologia utilizzata.
La scelta degli esempi di applicazione del metodo della 'grande espansione' rivela, infine, un'altra dimensione del lavoro di Qin Jiushao. Se il legame con i calcoli per il calendario (in due problemi) è senza dubbio ereditato da un'epoca precedente ‒ l'espressione 'grande espansione' fu usata in particolare per un calendario dall'astronomo Yixing (673-727, v. cap. XII, par. 5) ‒ il ruolo del metodo in problemi di carattere economico e amministrativo (sette problemi) è più originale, e sembra guidato dalla volontà di valutare e dimostrare le potenzialità del metodo. L'enunciato che segue (problema 1 del capitolo 2) riguarda tre contadini che all'inizio posseggono una medesima quantità di grano (N dou, ove il dou è una misura standard ufficiale) e che si recano da tre diversi clienti per venderlo. I tre clienti misurano il grano ciascuno secondo uno standard locale (il dou ufficiale corrisponde rispettivamente a 8,3, 11 e 13,5 misure locali); nell'enunciato del problema viene data la quantità di grano rimasta a ciascuno dei tre contadini dopo la vendita. L'ipotesi implicita che giustifica l'uso del metodo è che i clienti acquistano tutti e tre un numero intero di misure locali di grano.
Vi sono tre contadini della classe superiore. Il raccolto dei loro campi di grano misurato con il dou intero è uguale per tutti e tre. Lasciano i campi e vanno a vendere il grano. Il primo va al mercato ufficiale del proprio distretto e dopo la vendita gli restano 3 dou e 2 sheng di grano. Il secondo vende il grano a un privato del distretto di Anji, e gli restano 7 dou. Il terzo vende il grano a un esattore delle tasse [della prefettura] del Pinjiang, e gli restano 3 dou. Si vuole sapere quanto grano vi era in totale, quanto ne aveva ciascun contadino, e quanti shi sono stati venduti da ciascuno di loro. (Zhongguo kexue jishu dianji tonghui. Shuxue juan, I, p. 456)
La soluzione proposta permette di ricostruire i dati economici mancanti, e cioè il valore delle unità di misura locali rispetto all'unità ufficiale. Il problema si traduce nelle tre congruenze: N≡3,2[8,3], N≡7[11], N≡3[13,5].
Come si vede dall'esempio precedente, i problemi degli Scritti sui numeri presentano spesso situazioni complesse che un funzionario di livello culturale elevato potrebbe teoricamente trovarsi ad affrontare. La complessità può essere dovuta alla quantità di dati da considerare, oppure alla natura stessa del problema quando questo è costituito dalla sovrapposizione o dall'intreccio di più problemi particolari. In quest'ultimo caso la soluzione richiede l'applicazione successiva di due o anche tre tecniche diverse contenute nei Nove capitoli. Se rari erano i casi in cui la complessità obbligava a un rinnovamento delle tecniche di risoluzione esistenti, vi è tuttavia un campo che questo gioco di combinazioni sembra aver arricchito: il campo dell'algebra.
Sappiamo che la tecnica dell'incognita celeste (tianyuan) come la si incontra nell'opera di Li Ye (v. par. 1) è assente dagli Scritti sui numeri. Ciò non significa però che Qin non disponga di tecniche per dedurre le equazioni verificate dall'incognita e risolverle numericamente; queste tecniche però non sono espresse esplicitamente. Così, nel problema intitolato 'Determinare l'area di un campo a punte', nel quale si richiede di calcolare l'area di un campo formato da due triangoli isosceli a partire dai lati a e b dei triangoli e dalla loro base comune c, Qin si limita a dare l'espressione dei coefficienti, in funzione dei dati, dell'equazione di quarto grado soddisfatta dall'area richiesta.
Se questa fase delle operazioni di risoluzione è ancora oggi poco nota, la fase della risoluzione numerica non è mai stata tanto esplicita come nell'opera di Qin: per questo problema egli riproduce in particolare, sotto forma di tabella, le varie tappe del computo effettuato sulla superficie di calcolo. Il metodo utilizzato, che è poi quello di Ruffini-Horner, appare come un vero e proprio punto d'arrivo di contributi precedenti, in particolare quelli di Jia Xian e di Liu Yi (v. par. 1): vengono infatti stabilite convenzioni nel modo di rappresentare le equazioni (per es., il termine noto è sempre negativo) o per indicare e manipolare i segni dei coefficienti. Vi è una terminologia specifica per le operazioni dell'algoritmo: 'generare' (sheng) per una moltiplicazione di un coefficiente per il 'quoziente'; 'far entrare' (ru) per l'inserimento nel coefficiente di grado inferiore di un determinato prodotto ottenuto nel corso dei calcoli. Il procedimento di soluzione è suddiviso in parti dette 'trasformazioni' (bian), corrispondenti ciascuna alla determinazione di una nuova cifra del quoziente. Se non si può attribuire a Qin la paternità di questa tecnica (attestata nelle opere dei suoi contemporanei), il virtuosismo che egli dimostra nel farne uso per determinare le radici di un'equazione algebrica rappresenta in ogni caso, insieme al metodo della 'grande espansione', uno dei punti più alti degli Scritti sui numeri.
Yang Hui: una nuova classificazione della matematica dei Nove capitoli
Solo recentemente è stato messo in luce che dietro la facciata piuttosto banale della Spiegazione dettagliata dei 'Nove capitoli sui metodi matematici' si nascondeva una delle personalità più audaci e riformatrici della tradizione cinese (Kong Guoping 1993). Poiché il testo dei Nove capitoli era secondo lui corrotto e poco comprensibile, Yang Hui si accinse a una nuova classificazione dei problemi proposti nel Canone Han, secondo criteri più razionali. Una nozione che svolge un ruolo fondamentale in questo progetto è quella di categoria (lei), nozione che ritroviamo in particolare nel 'raggruppamento di categorie' (zuanlei), annesso alla sua edizione commentata dei Nove capitoli: viene abbandonato il vecchio criterio di classificazione basato sul 'principo delle cose' e si sceglie invece il criterio del metodo di risoluzione. I 246 problemi del Canone si trovano in tal modo suddivisi in nove 'nuove' categorie: (1) moltiplicazione e divisione (chengchu); (2) regola del tre (huhuan); (3) combinazione di lü (helü); (4) ripartizione dei lü (fenlü); (5) ripartizioni disuguali (cuifen); (6) volumi (dieji); (7) eccesso e difetto (ying bu zu); (8) misure in un quadrato (fangcheng); (9) base e altezza (gougu).
Alcune di queste categorie conservano la vecchia denominazione, anche se cambia il contenuto: per fare solo due esempi, sotto la voce 'moltiplicazione e divisione' si trovano ora riuniti tutti i problemi di misura delle aree, mentre la categoria 'base e altezza' comprende, oltre ai problemi tradizionalmente classificati sotto questa voce, anche i metodi di estrazione di radice quadrata e cubica che erano contenuti nella categoria 'piccola larghezza'. Un altro tratto caratteristico del lavoro di Yang Hui è rappresentato dai termini astratti con i quali si esprimono le 'regole' (fa) corrispondenti alle varie categorie. Nel caso della categoria 'base e altezza', le regole sono separate dal contesto dei problemi entro i quali erano state formulate e vengono presentate sotto forma di calcolo di una grandezza, se sono note altre grandezze (per es., 'regola per trovare il lato grande b, noti la somma b+c del lato grande e dell'ipotenusa e il lato piccolo a'). Si può dunque affermare che in questo capitolo ricorrono tutte le condizioni per la costituzione di un campo di studi di tipo algebrico.
Il quadro non sarebbe completo se non si ricordasse anche l''estensione della categoria', un compito intrapreso da Yang Hui per lanciare un ponte tra vecchi studi e interessi più recenti. Il termine denota il raggruppamento secondo criteri di analogia di problemi che a priori non rientrano nella definizione della categoria. Yang Hui scrive infatti nella prefazione alla Spiegazione dettagliata: "ho inventato problemi analoghi per spianare la strada ai compiti pratici". L''estensione della categoria' posta dopo determinati problemi offre l'occasione per introdurre nuovi problemi di carattere commerciale di vario tipo; ma non è questa la caratteristica più interessante dell''estensione': essa fornisce soprattutto il quadro concettuale per nuove ricerche, quadro che in seguito si svilupperà nei singoli campi autonomi della matematica. È il caso in particolare dei 'volumi di pile' (duoji), in pratica calcoli con serie di numeri, introdotti sistematicamente come estensione di calcoli di volumi solidi. La questione era già stata sollevata da Shen Gua nei Discorsi in punta di pennello dal Ruscello dei sogni (Mengxi bitan), ma questo argomento appare in forma compiuta solo nell'opera di Yang Hui ed è attraverso questa che i matematici la scopriranno nelle epoche successive (Kong Guoping 1993).
Ricordiamo, infine, che nelle numerose prefazioni e nei commentari che Yang Hui ci ha lasciato ritorna continuamente l'idea che la categoria 'moltiplicazione e divisione' sia alla base dell'insegnamento della matematica ("Le regole della matematica hanno origine nella regola delle 'moltiplicazioni-divisioni'" o "l'apprendimento della matematica si basa sulle 'moltiplicazioni-divisioni'" ne costituiscono due esempi). Questa categoria figura esplicitamente in due titoli delle sue opere (v. sopra); inoltre si suppone che i Metodi di calcolo per la vita quotidiana, oggi quasi del tutto perduti, fossero dedicati a questo tema. Ciò dimostra quanta attenzione avesse Yang Hui per i meccanismi del calcolo, dal punto di vista sia teorico sia pratico; scrive infatti nella prefazione al Compendio dei principi che regolano i vari modi di moltiplicare e dividere: "scegliere la regola in funzione dei problemi significa essere abili, prendere una regola per adattarla al problema significa essere maldestri" (Zhongguo kexue jishu dianji tonghui. Shuxue juan, p. 1057). Nel Compendio, più che altrove, l'oggetto di studio si scinde in una grande quantità di regole, alcune delle quali si rivelano molto utili, come la scomposizione del moltiplicatore in fattori semplici, la moltiplicazione per numeri che cominciano con la cifra 1, le regole di trasformazione del moltiplicatore in un altro che abbia come prima cifra 1 (jiuyi, 'ricerca dell'uno'), o l'utilizzazione delle tavole di divisione (jiugui). Tutte queste regole erano probabilmente già conosciute e applicate durante il periodo dei Song settentrionali e conosceranno un successo duraturo.
La sintesi delle tradizioni matematiche settentrionale e meridionale nell'opera di Zhu Shijie
di Andrea Eberhard-Bréard
Zhu Shijie: il maestro girovago e il girovagare dei suoi testi
Zhu Shijie (soprannominato Hanqing, pseudonimo Songting) è rappresentato dalla storiografia della matematica in Cina come uno dei personaggi maggiormente ignorati, benché si tratti, come oggi sappiamo, di una delle menti matematiche più brillanti. Vissuto nel XIII-XIV sec., egli non è menzionato né negli annali ufficiali della dinastia Yuan (1279-1368), né nella raccolta Biografie di matematici e astronomi (Chouren zhuan), compilata nel 1799 sotto la guida di Ruan Yuan (1764-1849). Le sue opere, Introduzione allo studio della matematica (Suanxue qimeng, 1299) e Specchio di giada delle quattro incognite (Siyuan yujian, 1303) rimasero incomprese per generazioni e a lungo introvabili. Solo dopo la riscoperta dei suoi lavori nel tardo periodo Qing (1644-1911), alcuni dati biografici, riportati nelle prefazioni, furono inseriti nel Supplemento alle 'Biografie di matematici e astronomi' (Chouren zhuan xu) di Luo Shilin (soprannominato Mingxiang, 1790-1853). Si apprese in tal modo che Zhu Shijie era originario di Yanshan (nella regione settentrionale dello Hebei, vicino alla capitale Pechino), che viaggiò per oltre vent'anni attraverso tutto il paese, e che quando "ritornò a Guangling [anch'essa nello Hebei], gli studenti si radunarono davanti alla sua porta come schiere di nuvole". Nel corso dei suoi lunghi viaggi e della sua attività di insegnante, Zhu Shijie dovette verosimilmente venire a conoscenza della tradizione matematica della dinastia Song meridionale, e soprattutto dell'opera di Yang Hui (v. par. 2), che rielaborò e sviluppò nei suoi scritti.
L'Introduzione allo studio della matematica, la prima opera di Zhu Shijie, è oggi disponibile in Cina solo in ristampe dell'edizione coreana del 1660, a partire dalla prima, pubblicata nel 1839 a cura di Luo Shilin. In Corea l'opera era stata stampata per la prima volta probabilmente nel 1433, durante il regno del re Sejong (al potere tra il 1418 e il 1450); la prima edizione critica fu curata da Kyong Son-jing (n. 1616), secondo quanto riportato nella prefazione dell'edizione coreana del 1660, curata da Kim Si-jin; in quest'ultima si affrontano anche due problemi di misurazione (lett. 'Procedimento per l'osservazione di un'isola in mare', Wang haidao shu) tratti dai Metodi matematici di Yang Hui (v. par. 2), opera passata anch'essa in Corea e utilizzata come manuale d'insegnamento. Sappiamo poco sulla diffusione dell'Introduzione in Cina durante la dinastia Yuan; soltanto dalla prefazione veniamo a conoscenza dell'esistenza di un discepolo di Zhu Shijie. In questa prefazione, dovuta a Zhao Cheng (detto Yuanzhen), Zhu Shijie viene lodato perché mostra in dettaglio i metodi di calcolo per i problemi trattati nell'opera con "parole perfette, spiegazioni delle figure e analisi dei solidi" (1B). La riscoperta dell'opera è dovuta a Ruan Yuan e a Luo Shilin; fu ricevuta in dono da due studiosi coreani loro ospiti intorno al 1809. Ma questa riscoperta ebbe minore risonanza del ritrovamento, avvenuto due decenni prima, dell'opera posteriore di Zhu Shijie, lo Specchio di giada delle quattro incognite. Solamente due commentari, uno di Wang Jian, intitolato Descrizione del significato dell''Introduzione allo studio della matematica' (Suanxue qimeng shuyi, 1884), e un altro di Xu Fenggao, Spiegazione completa dell''Introduzione allo studio della matematica' (Suanxue qimeng tongshi, 1886), furono dedicati a chiarire i procedimenti usati. Lavori recenti infine continuano a giudicare l'Introduzione un'opera scarsamente originale.
Nella prefazione dello Specchio di giada delle quattro incognite Zu Yi, amico di Zhu Shijie, spiega il significato di questo titolo: vuole esprimere attraverso una metafora l'ammirazione per i procedimenti utilizzati da Zhu Shijie, sostenendo che hanno le 'virtù della giada', espressione tratta da una conversazione tra Confucio e il suo discepolo Zi Gong. L'opera si apre con una premessa che consta di quattro illustrazioni e altrettanti problemi; seguono 24 capitoli con problemi le cui soluzioni sono date attraverso equazioni polinomiali sino a quattro incognite. La prima illustrazione riporta due diagrammi per la risoluzione di un'equazione algebrica, il secondo dei quali corrisponde all'ordinamento dei coefficienti nel 'triangolo di Pascal'. Seguono le rappresentazioni di tre superfici quadrate, ottenute a partire dalle quattro grandezze proprie di un triangolo rettangolo: l'ipotenusa (xian), i cateti (gou e gu) e il 'lato giallo' del quadrato (huangfang), che è il lato del quadrato circoscritto al cerchio inscritto nel triangolo.
Dopo i primi tre capitoli, dedicati interamente alle serie aritmetiche, si trova il capitolo Trasporto e scambio di sezioni di figure (Bohuan jietian), nel quale si affrontano 19 problemi riguardanti le trasformazioni e le suddivisioni di aree. Figure piane (triangoli isosceli, trapezi, triangoli rettangoli e cerchi) sono suddivise e trasformate in figure di uguale area (triangoli isosceli, trapezi obliqui) dette 'vicine'; si domandano una o due misure relative alle suddivisioni o alle figure vicine. Negli ultimi due problemi del capitolo sono trattate le sezioni di due cerchi. In altri problemi le varie sezioni di un oggetto geometrico sono considerate anche in relazione alla distribuzione tra più individui o al valore in argento o in moneta. Funzioni analoghe di oggetti matematici si incontrano anche in problemi di serie aritmetiche.
Numerose tracce dello Specchio di giada si ritrovano in opere del XV e del XVI sec.: esse tuttavia mostrano come l'opera fosse rimasta largamente incompresa. Il titolo veniva ancora citato all'inizio della dinasta Qing, ma affermazioni inesatte sulla mole e sul contenuto lasciano pensare che alla fine dell'epoca Ming essa fosse già poco considerata nella cerchia dei matematici. Solo dopo essere stata riscoperta fu inserita nell'enciclopedia Qing, Biblioteca completa dei quattro depositi (Siku quanshu). Lo stesso accadde per altre opere dell'epoca Song-Yuan che utilizzano il metodo dell''incognita celeste' (tianyuan). La riscoperta di queste opere sollevò un'ondata di commenti tra i matematici Qing che si divisero in due fazioni: la scuola Qian-Jia, di critica del testo, che vedeva nella ricostruzione dell'Antichità la ricreazione dell'intero campo dello scibile della Cina tradizionale, e altri studiosi che invece erano interessati soltanto al contenuto propriamente matematico e non esitavano a utilizzare anche la simbologia occidentale.
La trasmissione dell'opera matematica di Zhu Shijie
Luo Shilin descrive, nella prefazione dell'edizione da lui commentata dello Specchio di giada, la storia del ritrovamento del manoscritto da parte di Ruan Yuan, suo concittadino, durante una visita nella provincia del Zhejiang. La data di questa acquisizione è incerta: il manoscritto, copiato da He Yuanxi (detto Luohua), allievo di Zhu Shijie, giunse nelle mani di Ruan Yuan o di Li Rui (1765-1814) certamente soltanto dopo il 1799: infatti nella prima edizione delle Biografie di matematici e astronomi non viene menzionato. Luo Shilin venne a conoscenza del testo solo nel 1822, quando si recò nella capitale Pechino per sostenere gli esami imperiali. Dopo aver letto l'opera di Zhu Shijie, egli si rammaricò per aver sostenuto che gli antichi Canoni della matematica cinese potevano rinascere a nuova vita soltanto se reinterpretati alla luce dei metodi occidentali da poco introdotti in Cina. Studiò per dodici anni il metodo delle 'quattro incognite' (siyuan) contenuto nello Specchio di giada, e preparò un'edizione commentata dell'opera, nella quale la risoluzione dei problemi era descritta in dettaglio secondo il quadro concettuale della tradizione cinese, il calcolo con le bacchette e le tavole di coefficienti. Yi Zhihan, della stessa regione di Luo Shilin, vi aggiunse un'appendice, Esempi per spiegare le quattro incognite (Siyuan shili), nella quale indica con precisione come utilizzare le bacchette sui primi quattro esempi presentati all'inizio dell'opera di Zhu Shijie (v. sopra).
Un'altra versione dello Specchio di giada, senza commentario, è l'edizione curata da Ding Quzhong nell'Enciclopedia matematica della Sala del loto bianco (Baifu tang suanxue congshu) cui il curatore aggiunse, in un'edizione separata, Metodi di calcolo dettagliati (Xicao) per i primi quattro problemi, e un epilogo. Del commentario di Shen Qinpei (detto Xuebo), scritto nel 1821 a Zhengzhou, ci restano oggi soltanto sei fascicoli manoscritti, conservati nella biblioteca di Pechino. In un commentario manoscritto, completato nel 1844 da Dai Xu (1805-1860), recentemente scoperto a Taiwan, sono trattate soprattutto le relazioni sistematiche tra le serie aritmetiche che compaiono nei diversi capitoli del libro e la nomenclatura relativa. Si deve a un anonimo contemporaneo di Li Shanlan (1811-1882) un altro manoscritto (senza data), che si limita a due capitoli relativi alle serie aritmetiche. Oltre al commentario di Luo Shilin, l'unico a stampa e perciò quello più diffuso, fra il 1867 e il 1922 sono stati pubblicati anche lavori autonomi, dedicati soprattutto alla discussione e alla generalizzazione dei metodi con i quali venivano affrontate nello Specchio di giada le serie aritmetiche e la risoluzione delle equazioni algebriche a quattro incognite.
Grazie alla diffusione dell'Introduzione di Zhu Shijie in Corea, e alla fine del XVI sec. anche in Giappone, il metodo dell'incognita celeste, utilizzato in quest'opera (v. oltre), ricevette grande attenzione in tutta l'Asia orientale e fu oggetto di molti commenti. Nel 1658 vide la luce in Giappone una nuova edizione dell'opera, con l'aggiunta della punteggiatura, per iniziativa di Hisada Gentetsu, che l'aveva scoperta in un tempio. Un'altra edizione con il commentario di Hoshino Saneyoshi (1638-1699) apparve nel 1672 (Shinpen sangaku keimü chukai). Una versione commentata da Im Jun (nato tra il 1628 e il 1644) era già stata pubblicata nel 1662 in Corea, con lo stesso titolo. Zhu Shijie viene elogiato nella prefazione all'edizione coreana di Kim Si-jin del 1660 per la sua grande abilità nel penetrare a fondo i vari procedimenti e fornirne la corretta soluzione. Nel 1690 Takebe Katahiro (1664-1739) scrisse un Commentario completo all'Introduzione allo studio della matematica [in lingua giapponese parlata] (Sangaku keimü genkai taisei), che ebbe il merito di divulgare l'opera anche al di fuori della stretta cerchia di studiosi. Takebe adottò la nuova notazione, introdotta dal suo maestro Seki Takakazu (m. 1708), per la scrittura dei polinomi sulla carta, il metodo dello scrivere a fianco (bōsho-hō), che modificava dalle fondamenta il quadro concettuale del metodo dell'incognita celeste (tianyuan, in giapponese tengenjutsu). Gli studiosi si imbatterono anche in problemi che dimostravano i limiti di questo metodo, in particolare nel caso di un problema a due incognite non esprimibile con due equazioni indipendenti (Horiuchi 1994). In Cina, Zhu Shijie e i suoi predecessori sapevano già risolvere alcuni problemi di questo tipo, con un metodo che si applicava a equazioni sino a quattro incognite; le opere che descrivevano questo metodo non furono però trasmesse in Corea e in Giappone.
La generalizzazione del metodo dell'incognita celeste
Nell'Introduzione, Zhu Shijie utilizza il metodo dell'incognita celeste, cioè dell'algebra dei polinomi a una incognita nota nella tradizione settentrionale già nel XII sec. (v. par. 1), soltanto nell'ultimo capitolo, Sbloccare la serratura per aprire il lato del quadrato (Kaifang shisuo, riguardante l'estrazione della radice), per risolvere vari problemi di aree e, per la prima volta, di volumi. In questo capitolo, Zhu Shijie spiega l'origine del metodo dell'incognita celeste negli algoritmi per l'estrazione delle radici quadrate e cubiche. Nei primi due problemi descrive in modo particolareggiato la procedura per l''Apertura del lato quadrato o cubico' per il prodotto corrispondente all'area di un quadrato o al volume di un dado; nei successivi cinque problemi si richiede l'estrazione della radice n-esima (n>3) di un dato numero (come l'estrazione della radice quarta di 1.129.458 511/625), tuttavia senza descrivere l'algoritmo di risoluzione. Gli altri problemi del capitolo richiedono la rappresentazione dei coefficienti sulla superficie di calcolo, che permette la risoluzione con il metodo dell'incognita celeste.
Nello Specchio di giada, Zhu Shijie applica il metodo dell'incognita celeste per la risoluzione di oltre 200 problemi. I procedimenti però non comprendono più passaggi deduttivi delle tavole di numeri mediante argomenti di carattere geometrico, ma si dà soltanto la scelta dell'incognita celeste (tianyuan) e i coefficienti da ricavare dall'uguaglianza di due aree (ruji, prodotti di superficie uguali). è stato ipotizzato che Zhu Shijie sapesse risolvere equazioni della forma (A)1/2+(B)1/2=C, dove A, B e C sono espressioni razionali; non abbiamo però testimonianze su come Zhu Shijie potesse esprimere le equazioni che coinvolgono, come in questo caso, esponenti non interi. La disposizione dei coefficienti in forma di tavola utilizzata nei procedimenti di risoluzione dell'Introduzione mostra caratteristiche diverse rispetto a quella usata da Li Ye (v. par. 1): non sono segnati il termine noto e i coefficienti dei termini di primo grado; il coefficiente posto più in alto è sempre il termine noto (i polinomi hanno soltanto potenze positive); i coefficienti non interi sono poi dati nella notazione decimale, così come si trovano anche in Qin Jiushao (v. par. 2), senza la virgola, ma in posizione orizzontale rispetto ai numeri interi.
Per quanto riguarda le equazioni algebriche (la cui risoluzione numerica non presentava difficoltà per i matematici della dinastia Yuan), Zhu Shijie, sempre nel capitolo Sbloccare la serratura per aprire il lato del quadrato della sua Introduzione, spiega come esse compaiano negli algoritmi per 'separare i lati del quadrato e del cubo', cioè per l'estrazione delle radici quadrate e cubiche. In alcuni problemi Zhu Shijie definisce il metodo dell'estrazione come 'metodo inverso' (fanfa), ma si limita a suggerirne l'applicazione senza darne una descrizione precisa, descrizione che troviamo invece in Qin Jiushao. Nel caso di soluzioni non intere dell'equazione polinomiale egli rimanda al metodo di approssimazione descritto anch'esso da Qin Jiushao. Per tutti gli altri problemi Zhu Shijie dà soltanto i coefficienti per la risoluzione di equazioni algebriche, scrivendoli secondo un ordine che seguirà anche in opere più tarde. Il coefficiente più in alto nella tavola, il dividendo (shi), è il termine noto; seguono il coefficiente di x2 (fang); lo spigolo superiore (shanglian); il secondo spigolo (erlian); e così di seguito fino all'n-esimo spigolo o spigolo inferiore (xialian); infine l'angolo (yu) per il coefficiente di (n+1)-esimo grado. Per i coefficienti positivi si usano i termini cong o zheng, per i negativi yi.
In alcuni problemi dell'Introduzione, viene definita durante il calcolo una nuova incognita celeste. Il metodo dell'incognita celeste non permette, in quanto tale, la risoluzione di sistemi di equazioni a più incognite; tuttavia, la scelta di più incognite celesti, suggerita da Zhu Shijie, consente di ridurre la risoluzione di un dato problema a quella di una serie di equazioni a una sola incognita. Lo Specchio di giada è l'unica testimonianza che abbiamo di un metodo di risoluzione di sistemi non lineari sino a quattro incognite. Zu Yi, amico di Zhu Shijie, nella prefazione afferma che Zhu fu il primo a estendere il metodo dell'incognita celeste da tre a quattro incognite; prima di lui, infatti, Li Dezai aveva utilizzato due incognite nella Migliore raccolta dei massimi talenti dei due strumenti (Liangyi qunying jizhen), mentre Liu Dajian nel suo Comprendere mediante i trigrammi qian e kun (Qiankun kuonang) aveva utilizzato le tre incognite per risolvere due problemi.
La prima incognita è chiamata proprio 'incognita celeste' (tianyuan), la seconda è l''incognita terrestre' (diyuan), la terza è l''incognita umana' (renyuan) e la quarta l''incognita materiale' (wuyuan). Il trattamento di questo gruppo di quattro incognite è in stretta relazione con concetti taoisti; in questo senso deve essere interpretato il fatto che i primi quattro problemi dello Specchio di giada siano rispettivamente a una, due, tre e quattro incognite, e che nel titolo dei capitoli a essi dedicati compaia il numero delle incognite necessarie per la soluzione dei problemi in essi trattati: 'una' sostanza eterea (yiqi), 'due' strumenti, (liangyi), 'tre' potenze (sancai), 'quattro' fenomeni (sixiang). Non abbiamo però elementi per affermare un'eventuale appartenenza di Zhu Shijie a una delle scuole filosofiche del tempo. Così, il titolo del quarto capitolo è Tavole per la soluzione dettagliata di supposizioni con quattro incognite (Sixiang xicao jialing zhi tu): esso non si riferisce a una figura che descrive una situazione geometrica, bensì alle tavole dei coefficienti che sono via via compilate durante la risoluzione. Contrariamente a quanto si verifica per i problemi dei capitoli successivi, qui non viene dato soltanto un 'procedimento' (shu) di risoluzione riferito ai coefficienti dell'incognita celeste dell'equazione polinomiale da risolvere, bensì una traccia (cao) del metodo di risoluzione con l'indicazione dei passi principali. Luo Shilin, commentatore dell'epoca Qing, fornì poi i dettagli mancanti, spiegando in particolare le manipolazioni richieste per le tavole e 'reciprocamente nascoste' (huyin), l''unione delle parti' (tongfen) e l''eliminazione reciproca' (xiangxiao).
Negli altri capitoli, Zhu Shijie applica l'estensione a due, tre e quattro incognite a diversi problemi, dando luogo a equazioni che arrivano sino al 14° grado (il grado più alto nella storia della matematica dell'antica Cina). La disposizione dei coefficienti sulla superficie di calcolo nel caso di più incognite imponeva limiti evidenti alle possibilità del calcolo stesso. Da un lato non tutti i prodotti possibili possono essere rappresentati, dall'altro aumentando il numero delle incognite si rischia di finire in una impasse. Le possibilità della rappresentazione piana erano limitate dalle quattro direzioni celesti, e quindi si potevano avere al più quattro incognite. Oltre alle motivazioni sociali e politiche, a questa ragione di fondo va imputata l'impossibilità di estendere il metodo dell'incognita celeste oltre l'opera di Zhu Shijie.
L'incontro delle tradizioni settentrionale e meridionale
Aspetti di entrambe le tradizioni settentrionale e meridionale sono presenti nell'uso che Zhu Shijie fa di tavole numeriche all'interno del testo. In particolare, i coefficienti del binomio si trovano, nello Specchio di giada, all'interno dell'Illustrazione del metodo antico per la moltiplicazione fino alla settima potenza del lato del quadrato (Gufa qi chengfang tu) che apre l'opera; la (k+1)-esima riga della disposizione presentata, che corrisponde al 'triangolo di Pascal' dei coefficienti binomiali, fornisce i coefficienti binomiali:
Questa tavola numerica è una generalizzazione dell'Origine dei metodi per l'estrazione della radice quadrata (Kaifang zuofa benyuan), attribuita da Yang Hui a Jia Xian, che conteneva già i coefficienti per la risoluzione delle equazioni algebriche sino al sesto grado. Tuttavia, Zhu Shijie la utilizzò anche in relazione alle serie aritmetiche. Infatti, Zhu Shijie adoperava i coefficienti così disposti anche secondo le linee diagonali. Egli non si limitava a considerare solo le righe orizzontali e il significato dei coefficienti binomiali degli elementi che vi compaiono, ma vedeva anche un legame combinatorio lungo le diagonali: la somma di due elementi vicini è uguale all'elemento che si trova tra i due nella riga successiva, o più in generale, la somma dei primi k valori su una diagonale discendente da destra verso sinistra (o da sinistra verso destra) è il numero che si trova immediatamente sotto a destra (o a sinistra) del k-esimo valore. Queste relazioni secondo linee verticali e diagonali furono sfruttate in Cina negli algoritmi per determinare gli zeri delle equazioni algebriche. La nomenclatura relativa ai diversi tipi di fattorizzazione dei termini di una successione aritmetica è, inoltre, in stretta relazione con il passaggio da una diagonale della tavola alla successiva, così come la derivazione delle differenze divise per il calcolo della loro somma. Compaiono così in Zhu Shijie, per la prima volta, interpolazioni con differenze divise del quarto ordine, all'interno del quadro della risoluzione del 'problema inverso' per la somma di successioni aritmetiche di ordine superiore.
Nelle tre illustrazioni di superfici quadrate che seguono questa tavola, sempre nella parte iniziale dello Specchio di giada, si ritrova il metodo yanduan ('disporre i pezzi'). Il metodo risale a un certo Liu Yi della zona meridionale del Zhongshan, fu utilizzato da Li Ye nel quadro del metodo dell'incognita celeste, elaborato nella Cina del Nord, e anche Zhu Shijie se ne servì per la costruzione della tavola dei coefficienti dei polinomi.
Entrambe le tradizioni settentrionale e meridionale sono presenti nel rapporto fra rappresentazioni grafiche e testo negli scritti di Zhu Shijie. La sintassi, nel corso della descrizione dei procedimenti seguiti per risolvere i primi quattro problemi dello Specchio di giada, rimane corretta anche se dal testo si tolgono le figure; pure le tavole dei coefficienti dei sistemi di equazioni lineari sono fuori testo: un'analoga separazione tra testo e figure compare nell'opera di Qin Jiushao. Nell'opera di Li Ye invece, e nell'Introduzione di Zhu, le illustrazioni o tavole sono come le parole, sono cioè integrate nella struttura grammaticale della frase. Il procedimento di risoluzione dei sistemi di equazioni lineari, di cui fa uso Zhu Shijie, è anch'esso più vicino alla tradizione dei Dieci canoni di matematica, di quanto non lo sia quello usato da Liu Hui nel suo commentario ai Nove capitoli, che si ritrova piuttosto nella tradizione meridionale. Un'ulteriore indicazione dell'integrazione della tradizione meridionale nel quadro concettuale di Li Ye è l'interpretazione del capitolo canonico sui volumi, Discussioni di opere (Shanggong), che nell'opera di Li Ye manca del tutto. Nell'Introduzione, come nello Specchio di giada, si ritrova una separazione dei problemi sui volumi in un capitolo sui volumi continui e uno sui granai (ossia quantità misurabili di grano versate in recipienti aventi determinate forme geometriche), e l'estensione in un capitolo per 'accumulazione di oggetti discreti' (vale a dire, ai corrispondenti volumi non continui formati da oggetti numerabili): questa scelta è probabilmente influenzata dalla nuova classificazione della matematica introdotta nella Spiegazione dettagliata di Yang Hui.
Nel complesso, l'Introduzione di Zhu Shijie resta l'opera più vicina alla tradizione dei Nove capitoli, così come questa era proseguita nella Cina meridionale. Ciò è vero in particolare per quanto riguarda i procedimenti algoritmici di risoluzione e l'integrazione delle illustrazioni nella sintassi del testo. La sintesi con il metodo dell'incognita celeste della tradizione settentrionale si ha invece con la sua opera più tarda, lo Specchio di giada. L'integrazione nel quadro concettuale del metodo algebrico dei problemi trattati dai suoi predecessori andava di pari passo con una nuova articolazione dei capitoli classici della matematica e del problema della forma testuale dei commentari.
Bibliografia
Bai Shangshu 1987: Bai Shangshu - Li Zhaohua, 'Shushu jiuzhang' dui 'Jiuzhang suanshu' de jicheng he fazhan [Dal 'Shushu jiuzhang' al 'Jiuzhang suanshu'. Continuità e ampliamenti], in: Wu Wenjun, Qin Jiushao yu 'Shushu jiuzhang' [Qin Jiushao e il 'Shushu jiuzhang'], Beijing, Beijing Shifan daxue chubanshe, 1987, pp. 103-123.
Bréard 1999: Bréard, Andrea, Re-Kreation eines mathematischen Konzeptes im chinesischen Diskurs. Reihen vom ersten bis zum 19. Jahrhundert, Stuttgart, Steiner, 1999.
Chemla 1982: Chemla, Karine, Étude du livre 'Reflets des mesures du cercle sur la mer' de Li Ye, Diss., Université de Paris-Nord, 1982, 4v.
‒ 1990: Chemla, Karine, Du parallélisme entre énoncés mathématiques. Analyse d'un formulaire en Chine au 13e siècle, "Revue d'histoire des sciences", 43, 1990, pp. 57-80.
‒ 1993: Chemla, Karine, Li Ye 'Ceyuan haijing' de jiegou ji qi dui shuxue zhishi de biaoshi [Struttura dei testi ed espressione del sapere matematico nello 'Ceyuan haijing' di Li Ye], "Shuxueshi wenji", 5, 1993, pp. 123-142.
‒ 1994: Chemla, Karine, Similarities between Chinese and Arabic mathematical writings (I). Root extraction, "Arabic sciences and philosophy", 4, 1994, pp. 207-266.
‒ 1996: Chemla, Karine, Positions et changements en mathématiques à partir de textes chinois des dynasties Han à Song-Yuan. Quelques remarques, in: Disposer pour dire, placer pour penser, situer pour agir. Pratiques de la position en Chine, préparé par Karine Chemla et Michael Lackner, Saint-Denis, PUV, 1996, pp. 115-147.
Du Shiran 1966: Du Shiran, Zhu Shijie yanjiu [Studi su Zhu Shijie], in: Song Yuan shuxue shi lunwen ji [Raccolta di saggi di storia della tecnologia in epoca Song e Yuan], [a cura di] Qian Baocong, Beijing, Kexue chubanshe, 1966, pp. 166-209.
Guo Shuchun 1988: Guo Shuchun, Jia Xian 'Huangdi jiuzhang suanjing xicao' chutan. 'Xiangjie jiuzhang suanfa' jiegou shixi [Discussione sul 'Huangdi jiuzhang suanjing xicao'. Breve analisi della struttura del 'Xiangjie jiuzhang suanfa'], "Ziran kexueshi yanjiu", 7, 1988, pp. 328-334.
Hoe 1977: Hoe, John, Les systèmes d'équations polynômes dans le Siyuan Yujian (1303), Paris, Collège de France, Institut des Hautes Études Chinoises, 1977.
Horiuchi 1994: Horiuchi, Annick, Les mathématiques japonaises à l'époque d'Edo (1600-1868). Une étude des travaux de Seki Takakazu (?-1708) et de Takebe Katahiro (1664-1739), Paris, Vrin, 1994.
‒ 2000: Horiuchi, Annick, La notion de 'yanduan'. Quelques réflexions sur les méthodes 'algébriques' de résolution de problèmes en Chine aux Xe et XIe siècles, "Orient-Occident", 3, 2000, pp. 235-258.
Hu Mingjie 1989: Hu Mingjie, 'Siyuan xiaofa wenti' biejie [Spiegazione ulteriore del 'Siyuan xiaofa wenti'], "Beijing Shifan daxue bao. Ziran kexue ban", 25, 1989, pp. 91-96.
Kong Guoping 1988: Kong Guoping, Li Ye zhuan [Biografia di Li Ye], Tianjin, Hebei jiaoyu chubanshe, 1988.
‒ 1993: Kong Guoping, Xiangjie jiuzhang suanfa chutan [Ricerche preliminari sul 'Xiangjie jiuzhang suanfa'], "Shuxue shi yanjiu wenji", 4, 1993, pp. 36-41.
Lam Lay Yong 1977: Lam Lay Yong, A critical study of Yang Hui Suan fa. A thirteenth-century Chinese mathematical treatise, Singapore, Singapore University Press, 1977.
‒ 1979: Lam Lay Yong, Chu Shih-chieh's Suan-hsüeh ch'i-meng [Il 'Suanxue jimeng' di Zhu Shijie], "Archive for history of exact sciences", 21, 1979, pp. 1-31.
Libbrecht 1973: Libbrecht, Ulrich, Chinese mathematics in the thirteenth century. The Shu-shu chiu-chang of Chin, Chiu-shao, Cambridge (Mass.), M.I.T. Press, 1973.
Mei Rongzhao 1966: Mei Rongzhao, Tang zhongqi dao Yuan mo de shiyong suanshu [Matematica pratica dalla metà dei Tang alla fine degli Yuan], in: Song Yuan shuxue shi lunwen ji [Saggi sulla storia della matemati-ca in epoca Song e Yuan], [a cura di] Qian Baocong [et al.], Beijing, Kexue chubanshe, 1966.
‒ 1990: Mei Rongzhao, Song Yuan shuxue zhong de xin sixiang, fangfa he lilun [Nuove idee, metodi e teorie sulla matematica in epoca Song e Yuan], "Ziran kexueshi yanjiu", 9, 1, 1990, pp. 28-37.
Mo Shaokui 1987: Mo Shaokui, Qin Jiushao dayan qiuyi shu de xin yan jiu [Nuove ricerche sul procedimento 'dayan' per la determinazione di 'uno' in Qin Jiushao], in: Wu Wenjun, Qin Jiushao yu 'Shushu jiuzhang', Beijing, Beijing Shifan daxue chubanshe, 1987, pp. 183-203.
Qian Baocong 1966: Song Yuan shuxue shi lunwen ji [Raccolta di saggi sulla storia della matematica durante le dinastie Song e Yuan], [a cura di] Qian Baocong, Beijing, Kexue chubanshe, 1966.
Sha Na 1993: Sha Na, Yang Hui 'Xiangjie jiuzhang suanfa zuanlei' yanjiu [Ricerche sul 'Xiangjie jiuzhang suanfa zuanlei' di Yang Hui], "Shuxue shi yanjiu wenji", 5, 1993, pp. 38-41.
Te Gusi 1990: Te Gusi, Liu Yi ji qi yishi 'Yigu genyuan' [Liu Yi e il suo testo 'Yigu genyuan'], "Shuxue shi yanjiu wenji", 1, 1990, pp. 56-63.
Volkov 1994: Volkov, Alexei, Large numbers and counting rods, "Extrême-Orient, Extrême-Occident", 16, 1994, pp. 71-92.
Wu Wenjun 1987: Wu Wenjun, Qin Jiushao yu 'Shushu jiuzhang' [Qin Jiushao e il suo 'Shushu jiuzhang'], Beijing, Beijing Shifan daxue chubanshe, 1987.
Xu Yibao 1990: Xu Yibao, Dui 'Yiguji' de fuyuan yu yanjiu [Ricerche e recupero del testo del 'Yiguji'], "Shuxueshi yanjiu wenji", 1, 1990, pp. 64-73.
Yan Dunjie 1945: Yan Dunjie, Suanxue qimeng liuchuan kao [Trasmissione del testo 'Suanxue qimeng'], "Dongfang zazhi", 41, 9, 1945, pp. 26-28.
‒ 1966: Yan Dunjie, Song Yang Hui suanshu kao [Ricerche sulle opere matematiche di Yang Hui della dinastia Song], in: Song Yuan shuxue shi lunwen ji [Saggi sulla storia della matematica di epoca Song e Yuan], [a cura di] Qian Baocong, Beijing, Kexue chubanshe, 1966, pp. 149-165.