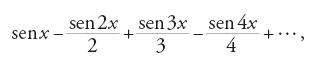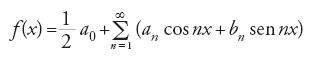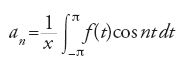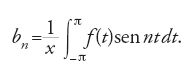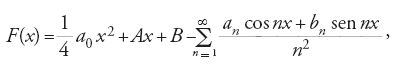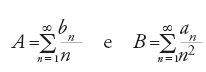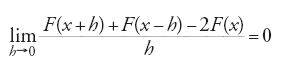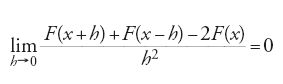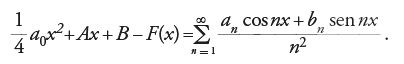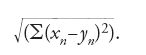La seconda rivoluzione scientifica: matematica e logica. La topologia degli insiemi di punti

La seconda rivoluzione scientifica: matematica e logica. La topologia degli insiemi di punti

La topologia degli insiemi di punti

La topologia generale o topologia degli insiemi di punti (point set topology) trae essenzialmente origine dai problemi dell'analisi del XIX secolo. Particolare rilevanza assumono i problemi legati alla rappresentabilità di una funzione come serie trigonometrica.

Come la denominazione stessa suggerisce, la topologia degli insiemi di punti si sviluppò in stretta relazione con la teoria degli insiemi di Georg Cantor (1845-1918). Come accadde per altre aree dell'analisi, anche la topologia generò propri problemi e tecniche svincolandosi sempre più dalle motivazioni per le quali era nata.

Limiti di funzioni continue

di Roger Cooke

Molti problemi che si sarebbero poi rivelati di interesse topologico sorsero come conseguenza dello studio della continuità. Per esempio Augustin-Louis Cauchy, nel Cours d'analyse (1821), sembrava sostenere che la somma di una serie convergente di funzioni continue era ancora una funzione continua. All'inizio del secolo si credeva che una funzione continua fosse derivabile, salvo in punti eccezionali, e André-Marie Ampère (1775-1836) aveva anche cercato di dimostrarlo. Quando si cominciarono a costruire funzioni continue non derivabili in insiemi sempre più grandi, la fiducia dei matematici in quel tipo di intuizione cominciò a venir meno. Bernhard Bolzano aveva costruito già nel 1817 una funzione continua non derivabile in un insieme di punti denso. Karl Theodor Wilhelm Weierstrass nel 1872 indicò un esempio di una funzione continua non derivabile in alcun punto. Anche la relazione apparentemente semplice tra differenziazione e integrazione fu messa in discussione nel 1881, quando Vito Volterra (1860-1940) costruì una funzione differenziabile la cui derivata non è integrabile (secondo Riemann). Il colpo di grazia all'intuizione fu dato da Giuseppe Peano (1858-1932) con la costruzione di un'applicazione continua da una retta a tutti i punti di un quadrato. L'affermazione di Cauchy secondo la quale la somma di una serie convergente di funzioni continue è ancora una funzione continua era stata ben presto messa in discussione da Niels Henrik Abel (1802-1829). Nel 1826, egli aveva fatto notare che la serie trigonometrica

converge a (1/2)x per -π<x<π e (ovviamente) a 0 per x=±π. Difficoltà di tale genere danno origine a due tipi di problemi, entrambi importanti in topologia: trovare condizioni sufficienti (e se possibile necessarie) affinché la somma di una serie di funzioni continue sia ancora una funzione continua; studiare le proprietà che deve avere una funzione per essere la somma di una serie convergente di funzioni continue. Il primo di questi problemi sarebbe stato risolto mediante uno studio attento della definizione di convergenza, che portò alla nozione di convergenza uniforme. Il secondo poté essere spiegato solo mediante la nozione topologica di categoria.

Cominciamo dal primo problema: dimostrare che il limite di funzioni continue è una funzione continua. Supponiamo, per esempio, che f(x) sia approssimata da una successione di funzioni continue {f_n(x)}, e che si voglia dimostrare che la differenza f(x1a)2f(x) è piccola per a piccolo. Il modo ovvio di affrontare il problema è di sfruttare la relazione

Con i termini raggruppati in questo modo si vede che il primo e l'ultimo termine tra parentesi quadra sono piccoli se n è grande per via dell'approssimazione, mentre il termine di mezzo è piccolo per a piccolo per via della continuità di f_n(x). Tuttavia, perché questo ragionamento sia valido, deve verificarsi una delle seguenti eventualità: o esiste un valore di n che rende l'approssimazione buona in tutti i punti x1a simultaneamente (convergenza uniforme), oppure esiste una maggiorazione di a che rende piccola la differenza f_n(x1a)2f_n(x) per tutti gli n simultaneamente (equicontinuità). Queste condizioni sono equivalenti per successioni convergenti di funzioni continue su un intervallo chiuso e limitato, e sono sufficienti, ma non necessarie, affinché la funzione limite sia continua.

La cosa più ovvia da fare era assumere la convergenza uniforme, soprattutto perché questa, oltre a garantire la continuità della funzione limite, permetteva anche l'integrazione termine a termine della serie o della successione approssimante. Nel 1848 Philipp Ludwig von Seidel (1821-1896) dimostrò che se la somma di una serie di funzioni continue è discontinua in un punto, allora in ogni intervallo contenente quel punto vi sono altri punti nei quali la convergenza è arbitrariamente lenta. Affermazione logicamente equivalente al fatto che la somma di una serie uniformemente convergente di funzioni continue è continua. Nel 1883 il problema fu studiato più da vicino da Cesare Arzelà (1847-1912), il quale stabilì una condizione necessaria e sufficiente per la continuità di una funzione limite di funzioni continue. Una condizione più utile, anche se solo necessaria, dimostrata da Ulisse Dini (1845-1918), afferma che una serie di funzioni continue positive la cui somma è continua converge uniformemente in ogni intervallo chiuso e limitato.

Anche se meno importante della convergenza uniforme, il concetto di equicontinuità doveva avere profonde implicazioni quando si sviluppò, agli inizi del XX sec., l'analisi funzionale. Nel 1883 Giulio Ascoli (1843-1896) scrisse un lavoro su spazi di curve, nel quale stabiliva che un insieme infinito, limitato ed equicontinuo di funzioni su un intervallo chiuso contiene una successione uniformemente convergente. In questo modo, alcuni dei concetti che, come vedremo fra breve, Cantor aveva appena sviluppato per gli insiemi di punti venivano applicati a insiemi di curve. Le idee di Ascoli furono sviluppate più tardi da Maurice-René Fréchet (1878-1973) e portarono al concetto di spazio metrico astratto, fondamentale per l'analisi funzionale e la topologia. Uno spazio metrico è uno spazio in cui è definita una distanza tra due punti, che gode di tre semplici proprietà: la distanza tra due punti distinti è positiva, e tra un punto e sé stesso è zero; la distanza è simmetrica (la distanza tra a e b è uguale alla distanza tra b e a); la distanza tra due punti a e c è minore o uguale alla somma delle distanze tra questi due punti e un punto b. Quest'ultima proprietà prende il nome di disuguaglianza triangolare, e la sua importanza topologica sta nel fatto che la distanza tra un punto variabile x e un punto fisso y è una funzione continua di x. Si può, per esempio, definire la distanza tra due curve piane come l'area compresa tra i loro grafici: un insieme di curve diventa così uno spazio metrico.

Il secondo problema, la determinazione delle proprietà di un limite di funzioni continue, non fu studiato pienamente fino al 1899, quando cominciò a occuparsene René-Louis Baire (1874-1932). Il caso particolare di una somma di una serie trigonometrica fu studiato da Georg Friedrich Bernhard Riemann (1826-1866) nella Habilitationsschrift, pubblicata dopo la sua morte, nel 1867. Questo scritto, nel quale viene tra l'altro sviluppato in due pagine l'integrale di Riemann, era destinato a fornire lo stimolo per la creazione di lì a poco sia della teoria degli insiemi sia della topologia.

Riemann chiedeva di stabilire quali proprietà dovesse avere una funzione per essere la somma di una serie trigonometrica. Egli era interessato in particolare alle condizioni sotto le quali una serie trigonometrica convergente

è la serie di Fourier della propria somma, ovvero alle condizioni che implicano

e

Più in particolare, può una serie a coefficienti non tutti nulli convergere a zero in ogni punto? Supponendo che i coefficienti tendano a zero (ipotesi rimossa poi da Cantor) Riemann mostrò che non era possibile.

La topologia era contenuta in germe in un'idea utilizzata da Riemann nella dimostrazione e per spiegarla occorre entrare nel dettaglio della dimostrazione stessa. Integrando due volte la serie per f(x), Riemann determinò una serie che converge uniformemente a una funzione continua

dove

Questa serie è quindi la serie di Fourier della propria somma. Per tornare da F(x) alla serie originaria f(x) occorre differenziare due volte, e in generale ciò non è possibile. Si può prendere però una derivata seconda generalizzata di F(x), e questa è la chiave della dimostrazione. Riemann dimostra che

in ogni punto x. Ne segue facilmente che il grafico della funzione F(x) non può avere 'angoli', non è possibile cioè che in un punto F(x) abbia derivate destra e sinistra distinte. Fu questo fatto cruciale che condusse Cantor, che lavorava appunto sulle serie di Fourier, alla scoperta del primo concetto propriamente topologico.

Riemann aveva anche dimostrato che

in ogni punto x nel quale f(x)50. Hermann Amandus Schwarz (1843-1921) dimostrò che se questo limite è zero in un intervallo (a,b), allora F(x) è una funzione lineare F(x)5cx1d in quell'intervallo. Ne segue che se una serie trigonometrica converge a zero in ogni punto, F(x) è una funzione lineare. Il polinomio quadratico (1/4) a₀x²1Ax1B2F(x) è allora somma di una serie trigonometrica uniformemente convergente:

Poiché il solo polinomio periodico è una costante, entrambi i membri di questa equazione devono essere costanti. La serie a secondo membro è uniformemente convergente e dunque è la serie di Fourier della propria somma, e perciò è la serie di Fourier di una costante. Ne segue che tutti i coefficienti della serie trigonometrica di partenza devono essere zero. Questo è il risultato più importante ottenuto da Riemann.

La generalizzazione di Cantor prevedeva alcuni punti isolati eccezionali nei quali la serie di f(x) non converge a zero. La funzione F(x) resta continua, e per il risultato di Schwarz deve essere lineare in un intervallo (x₀-δ, x₀) a sinistra e in uno (x₀, x₀+δ) a destra di un punto isolato x₀. Tuttavia, poiché il grafico di F(x) non può avere angoli, le due rette che costituiscono il grafico a sinistra e a destra di x₀ devono formare un angolo di zero gradi; in altri termini, il grafico deve essere lineare nell'intero intervallo (x₀-δ, x₀+δ). Ne segue che l'esistenza di punti isolati nei quali la serie non converge a zero non influisce sulla dimostrazione.

Si possono così avere punti eccezionali isolati senza che venga meno l'unicità; in particolare un insieme finito qualunque di punti eccezionali. Per un insieme infinito vi sarebbe un punto di accumulazione di punti eccezionali (teorema di Bolzano-Weierstrass), ma Cantor osservò che il teorema sussisteva ancora nel caso di un numero finito di punti di accumulazione: si è già visto come la linearità di F(x) non veniva alterata da un punto eccezionale isolato. Si potevano così rimuovere i punti eccezionali isolati lasciando solo quelli di accumulazione. Se questi erano a loro volta isolati (come nel caso di un numero finito) si poteva applicare di nuovo a F(x) il principio dell'assenza di angoli e la dimostrazione restava valida. Era quindi naturale considerare un insieme infinito di punti di accumulazione che avessero però a loro volta solo un numero finito di punti di accumulazione e così via.

Le serie trigonometriche avevano così dato luogo a una classe di figure molto più complicate dei classici poligoni e curve familiari ai geometri, dei quali si sapeva ben poco. Considerazioni di questo genere allontanarono Cantor dal problema delle serie trigonometriche, facendo sì che egli rivolgesse la propria attenzione allo studio del modo in cui i punti di una retta si accumulano l'uno con l'altro. Si trattava di una prospettiva veramente nuova dalla quale considerare le relazioni reciproche dei punti di una retta e che prometteva di illuminare di nuova luce lo studio degli insiemi connessi.

Le prime costruzioni della topologia generale

di Roger Cooke

Nell'impostazione di Cantor una figura geometrica astratta P contenuta in una retta era detta insieme lineare e a ogni insieme P restava associato l'insieme P' dei suoi punti di accumulazione, il cosiddetto derivato di P. L'introduzione stessa dell''insieme' (Punktmenge), rese il linguaggio matematico chiaro come non lo era mai stato in passato. Cantor mostrò che (P')' è contenuto in P'. Definì poi per induzione P⁽⁰⁾=P e P^(ν+1)=(P^(ν))'. La successione hP^(ν)j è decrescente, salvo il fatto che P=P⁽⁰⁾ può non contenere P'=P⁽¹⁾. Cantor definì chiuso l'insieme P se contiene P', usando per la prima volta questo fondamentale concetto topologico. Definì anche le operazioni fondamentali della teoria degli insiemi come l'unione e l'intersezione, il concetto di insieme aperto (un'unione di intervalli aperti) e l'intorno di un punto (un aperto contenente il punto). Il fatto che P^(ν+1)⊆P⁽ⁿ⁾ rese possibile la definizione di derivato di ordine infinito P^(∞) come l'intersezione dei P^(ν) per tutti gli interi positivi n. Cantor osservò che occorreva distinguere due eventualità: P^(ν) è finito per qualche n finito, per cui P^(ν+1) non contiene punti (o, nelle parole di Cantor, gar nicht vorhanden ist, introducendo così il concetto di insieme vuoto); P^(ν) è infinito per tutti i ν. Nel primo caso, Cantor parlava di insieme P di primo tipo e di specie ν; nel secondo, P era di secondo tipo. La generalizzazione di Cantor del teorema di unicità di Riemann per le serie trigonometriche giunse fino ad ammettere insiemi eccezionali del primo tipo. Egli svincolò la topologia dalle serie trigonometriche e fece della teoria degli insiemi una disciplina indipendente, malgrado l'opposizione di matematici come Leopold Kronecker e Jules-Henri Poincaré.

La svolta decisiva si ebbe quando Cantor osservò che una volta definito P^(∞) era possibile definire il derivato (P^(∞))'=P^(∞+1), e così via, dando quindi origine ai numeri ordinali infiniti. Questi ordinali infiniti risultarono nascondere anch'essi misteri, specie quando si considerava la classe di tutti gli ordinali infiniti numerabili, classe che, anche se non se ne poteva dare una descrizione, era seguita dal primo ordinale non numerabile. Cantor scoprì che si poteva definire il derivato P^(α) per ogni ordinale α. Accade però che raggiunto il primo ordinale non numerabile si ottiene sempre un insieme 'perfetto', cioè un insieme che coincide con il proprio derivato.

I numeri ordinali e le loro relazioni con i numeri cardinali attengono alla teoria degli insiemi. Nello sviluppare queste idee Cantor introdusse però concetti topologici, come quello di sottoinsieme denso E di un insieme F (tale cioè che F⊆E⋃E), di insieme separabile (un insieme che contiene un sottoinsieme numerabile denso), di insieme perfetto e altri.

L'opera pioneristica di Cantor fornì strumenti validissimi agli analisti francesi, i quali li utilizzarono per approfondire le proprietà dei numeri reali e nello studio dei concetti di derivata, integrale e funzioni di variabile reale o complessa. La topologia, con i concetti di punto di accumulazione e di insieme aperto, era esattamente ciò che permetteva di discutere il concetto di ampliamento del dominio di una funzione analitica o di attribuire in modo significativo una lunghezza a insiemi lineari più complicati degli intervalli. Il lavoro di Cantor, che aveva portato a studiare complicati insiemi di punti, e quelli di Riemann, Volterra e altri sull'integrabilità di funzioni discontinue avevano dimostrato la necessità di queste generalizzazioni. Nel 1892 Camille Jordan (1838-1922) aveva cercato di estendere la nozione di lunghezza ricorrendo a un ricoprimento dell'insieme da misurare mediante un numero finito di intervalli. Un ricoprimento di questo tipo non distingue però tra insiemi 'sottili', come l'insieme dei numeri razionali, e insiemi 'spessi', come un intervallo. Ogni ricoprimento finito dei razionali in [0,1] mediante intervalli deve avere lunghezza totale almeno uguale a 1. Ammettendo con Émile Borel (1871-1956) e Henri-Léon Lebesgue (1875-1941) ricoprimenti mediante famiglie numerabili di aperti, è facile dimostrare che i razionali possono essere ricoperti da una famiglia numerabile di aperti aventi lunghezza totale arbitrariamente piccola, per cui si può attribuire lunghezza zero all'insieme dei razionali contenuti in [0,1]. D'altra parte Borel dimostrò che da ogni ricoprimento con aperti dell'intervallo [0,1] si può estrarre un sottoricoprimento finito: gli intervalli di un tale ricoprimento devono allora avere lunghezza totale almeno 1. Questo famoso risultato sui ricoprimenti degli intervalli chiusi mediante intervalli aperti, noto come teorema di Heine-Borel, portò alla definizione del concetto fondamentale di compattezza: un insieme si dice compatto se da ogni suo ricoprimento aperto si può estrarre un sottoricoprimento finito. Come ricorda il nome dato al teorema, il fatto che un intervallo chiuso sia compatto era stato dimostrato (nel 1872) da Heinrich Eduard Heine (1821-1881), che lo utilizzò per dimostrare che una funzione continua in un intervallo chiuso è uniformemente continua.

La teoria della misura di Borel e quella dell'integrale di Lebesgue, presentavano, rispetto alla costruzione di Riemann, il vantaggio decisivo della facilità con la quale si potevano integrare termine a termine serie convergenti di funzioni continue. Analogamente, nel caso della lunghezza, un'unione numerabile di insiemi misurabili è misurabile e ha misura non superiore alla somma delle misure dei singoli insiemi (ciò è in evidente contrasto con la misura di Jordan, secondo la quale un insieme numerabile di singoli punti, ciascuno di lunghezza zero ‒ per es., l'insieme dei razionali in [0,1] ‒ ha lunghezza positiva). All'inizio Borel aveva osservato che i soli insiemi misurabili erano insiemi ottenuti prendendo unioni numerabili e intersezioni di intervalli, fermandosi dopo un numero finito di operazioni di tipo numerabile. In seguito, tuttavia, sia Borel sia Lebesgue costruirono una gerarchia di classi di insiemi ai quali si poteva attribuire una lunghezza e che partiva dagli insiemi aperti e chiusi, per passare alle unioni numerabili di insiemi chiusi ‒ insiemi F_σ ‒ e dei loro complementari ‒ insiemi G_δ ‒ alle unioni numerabili di insiemi G_δ e intersezioni numerabili di insiemi F_σ ‒ insiemi G_δσ e F_σδ, rispettivamente, ‒ e così via. Come nel caso del derivato, le classi di Borel si possono definire per ordinali infiniti e, sempre come nel caso del derivato, gli insiemi di Borel si stabilizzano quando si raggiunge il primo ordinale non numerabile, dando luogo a una classe chiusa rispetto a unioni e intersezioni numerabili (σ-algebra o σ-campo).

I lavori di Borel e Lebesgue si dimostrarono presto fondamentali per la difesa della teoria degli insiemi di Cantor. La versione ingenua di questa teoria aveva permesso la nascita di paradossi, come quello di Cesare Burali-Forti (1861-1931), che nel 1897 aveva osservato come la classe di tutti gli ordinali, essendo essa stessa un ordinale, ammetteva un successore, un ordinale che doveva allora essere più grande del più grande ordinale. Questo paradosso e altri che dovevano presto seguire avrebbero creato diffidenza e resistenze nei confronti della teoria degli insiemi difficili da superare, se non fosse stato per la portata delle implicazioni che Borel e Lebesgue avevano mostrato e per l'utilità dei risultati ottenuti in teoria dell'integrazione e nelle applicazioni alle serie di Fourier e alla probabilità.

Categorie topologiche

di Roger Cooke

Contemporaneamente a Borel, con la sua gerarchia di insiemi, Baire lavorava a un'analoga gerarchia di funzioni: si partiva da una classe 0 (le funzioni continue), per passare a una classe 1 (limiti di funzioni continue), e così via. Come nel caso degli insiemi di Borel, le classi di Baire si stabilizzavano al primo ordinale non numerabile, oltre il quale non nasceva niente di nuovo (come osservò più tardi Lebesgue, le due gerarchie di insiemi e di funzioni erano strettamente connesse). Nella sua tesi, discussa nel 1899, Baire dimostrò che il limite di funzioni continue è una funzione che se non è necessariamente continua in ogni punto, lo è in quasi tutti i punti, e così facendo introdusse la nozione di insiemi di prima e seconda categoria. Un insieme è di prima categoria se è unione di una famiglia numerabile di insiemi la cui chiusura non contiene intervalli; altrimenti è di seconda categoria. Baire dimostrò che un intervallo è di seconda categoria, mentre i punti nei quali il limite di una successione di funzioni continue non è continuo formano un insieme di prima categoria. Ne segue in particolare che il limite di una successione di funzioni continue non può essere discontinuo in ogni punto di ogni intervallo: i punti nei quali è continuo formano un insieme denso in ogni intervallo.

La nozione di categoria, che a prima vista non sembrava promettente come quelle di compattezza e connessione, doveva giocare un ruolo fondamentale nello sviluppo dell'analisi funzionale del XX secolo. I due teoremi principali dell'analisi funzionale, il teorema dell'applicazione aperta e il teorema del grafico chiuso, non si possono dimostrare senza utilizzare la nozione di categoria.

Gli inizi della topologia generale

di Brian Griffith

Curve

Allo sviluppo della topologia degli insiemi di punti contribuì la maggior parte dei pionieri degli studi topologici. Uno dei percorsi iniziali prese l'avvio dalla scoperta di Peano della celebre curva che riempie il piano. Era quindi naturale chiedersi quali proprietà dovesse possedere uno spazio metrico X per essere definito una curva. Innanzi tutto, X deve essere un continuo, vale a dire compatto e connesso (un insieme è connesso se non è unione di due aperti non vuoti). In secondo luogo, X deve essere localmente connesso, ossia dato un punto p e un intorno U di p, U deve contenere un intorno connesso di p. Se (come la curva di Peano) X ha entrambe le proprietà viene detto un 'continuo di Peano'.

Ognuna delle proprietà costitutive ‒ compattezza, connessione, connessione locale ‒ richiede uno studio separato. Gli spazi che si incontrano più comunemente sono continui di Peano, tuttavia, il teorema di Hahn-Mazurkiewicz, dimostrato intorno al 1913, afferma: se Y è un continuo di Peano, allora Y è un'immagine continua dell'intervallo unitario. Si tratta di un risultato difficilmente prevedibile e non molto utile per le applicazioni. Gli spazi localmente connessi (in cui ogni punto possiede un sistema di intorni connessi) vennero inizialmente introdotti in analisi per formulare problemi riguardanti il comportamento delle funzioni armoniche nel bordo di un dominio. I lavori contenuti nella rivista della scuola polacca, "Fundamenta mathematicae", hanno spesso un'impronta strettamente legata alla teoria degli insiemi e alle idee di Cantor. La scuola, il cui sviluppo coincise con il periodo tra le due guerre mondiali, venne brutalmente soppressa dai nazisti e dopo la sua ricostituzione non raggiunse mai il livello che l'aveva resa famosa.

Spazi astratti

Accanto ai problemi dell'analisi altre questioni più astratte suggerirono direzioni più generali in cui la topologia si sarebbe sviluppata. Sulla scia di David Hilbert, alcuni analisti pensavano già alle funzioni come punti di uno spazio metrico quale lo spazio di Hilbert, ossia l'insieme di tutte le successioni infinite di numeri reali x_n tali che la serie ∑x²_n converge con la distanza data dalla serie convergente

Questo portò Fréchet a considerare, nella sua tesi del 1906, insiemi di funzioni come l'insieme F(X) di tutte le funzioni continue in X∈R, con X spazio metrico. Se, per esempio, X è l'intervallo unitario I, il concetto di convergenza uniforme diviene molto più semplice da trattare in termini di una metrica su F(I) (la metrica dell'estremo superiore), nel qual caso F(I) è uno spazio metrico completo. La tesi di Fréchet diede origine alla teoria degli spazi metrici che altri utilizzarono per studiare oggetti come gli 'insiemi di Borel', introdotti da Borel per descrivere l'insieme delle discontinuità di una funzione continua in teoria della misura. In particolare, le dimostrazioni iterative di teoremi di esistenza per equazioni differenziali vennero considerate come interpretazioni specifiche di un unico risultato astratto ‒ il 'principio di contrazione' (Banach 1923) ‒ riguardante un'applicazione continua di uno spazio metrico completo S in sé stesso. In uno spazio completo vale anche il teorema di densità di Baire, utilizzato per mostrare che opportune funzioni di un certo tipo sono dense in spazi come F(I). Questi spazi sono più frequentemente completi piuttosto che compatti e gran parte del lavoro successivo fu diretto ad adattare in modo opportuno i risultati noti per gli spazi compatti. Se X è uno spazio qualsiasi, l'insieme F(X) ha una struttura non solo topologica ma anche di algebra reale. Le operazioni dell'analisi, come l'integrazione rispetto a una misura, portano a spazi di operatori lineari su F(X). Per studiarli Fréchet sviluppò una nozione astratta di successione convergente e i risultati condussero a interessanti teoremi in analisi. Queste strutture portarono a quel tipo di teorie topologicamente orientate come l'analisi funzionale, gli spazi di Banach e gli anelli normati, non più parte della topologia in senso stretto.