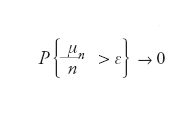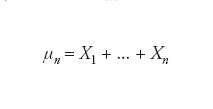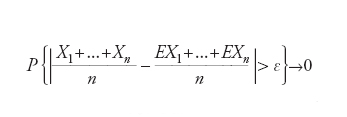legge dei grandi numeri

legge dei grandi numeri

Principio secondo il quale sotto condizioni molto generali l’azione simultanea di un grande numero di fattori casuali conduce a un effetto sostanzialmente deterministico (non casuale). Uno dei più importanti esempi di tale principio è la convergenza delle frequenze di occorrenza di un determinato evento (ossia del rapporto tra numero di eventi favorevoli e numero totale di eventi) alla sua probabilità con il crescere del numero di tentativi. Già alla fine del XVIII sec. Jakob Bernoulli dimostrava un teorema secondo il quale in una sequenza di eventi indipendenti, in ognuno dei quali la probabilità P{A} di un certo evento A di verificarsi è fissata nell’intervallo [0,1] (per es., una sequenza di lanci di una moneta), la relazione

è valida per ogni ε>0 al tendere di n∈ℕ a infinito; qui μ_n è il numero di occorrenze dell’evento considerato (per es. testa) nei primi n tentativi e μ_n/n è dunque la sua frequenza. Una naturale estensione del teorema di Bernoulli si ottiene osservando che la variabile casuale μ_n può essere rappresentata sotto forma della somma

di n variabili casuali indipendenti, con X_k=1 se A si realizza e X_k=0 altrimenti. Il valor medio o atteso E(μ_n/n) (coincidente con la media dei valori attesi EX_k, 1≤k≤n) vale allora p nel caso considerato da Bernoulli. In altra parole, abbiamo a che fare con le deviazioni del valore atteso delle variabili X_k dalla media dei loro valori attesi. Fu Chebychev a dimostrare sotto condizioni estremamente generali (limitatezza uniforme della varianza EX_k²) che

è valida per ogni ε>0 al tendere di n∈ℕ a infinito per variabili casuali indipendenti. Successivamente la legge dei grandi numeri è stata generalizzata anche al caso di processi markoviani da un lato, dall’altro si è proceduto a analizzare nozioni di convergenza differenti da quella considerata (convergenza in probabilità). Uno dei casi più importanti nei quali essa non è invece valida è quello del tempo di ritorno all’origine di una particella sottoposta a moto browniano.

→ Irreversibilità; Probabilità