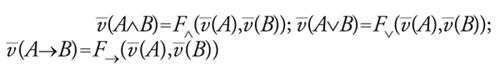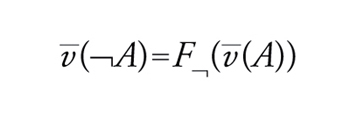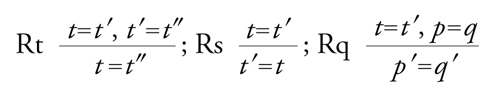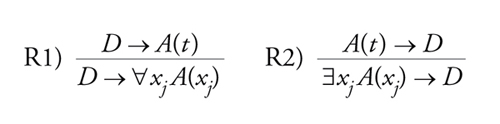Logica matematica
Logica matematica
Pur potendo vantare come erede della logica formale un'origine risalente almeno ad Aristotele, come disciplina scientifica la logica matematica è un acquisto recente. Possiamo far risalire la sua data di nascita al massimo alla metà dell'Ottocento, con i lavori di George Boole sull'analisi algebrica della sillogistica tradizionale (1847) e la costruzione da parte di Gottlob Frege di un linguaggio formale in grado di riprodurre e analizzare la struttura logica del linguaggio in uso nella pratica matematica (1879). Una doppia origine che sottolinea una duplice vocazione: da una parte l'indagine della struttura matematica sottostante ai metodi propri del ragionamento formale, dall'altra la ricerca di una fondazione per la matematica stessa che attraverso l'analisi logica ne ponga in luce i presupposti generali, giustificandone le definizioni e le procedure deduttive. Questo spiega la caratteristica più evidente che distingue la logica matematica dalla logica formale tradizionale: la coesistenza in essa di un livello dove si situano i linguaggi, le regole deduttive, le teorie costruite e nessuna nozione matematica specifica viene presupposta con un livello superiore in cui questi stessi linguaggi, queste regole e queste teorie vengono analizzate utilizzando eventualmente strumenti matematici specifici. Costante in ogni caso rimane la distinzione tra il piano teorico ‒ quello in cui si situano i linguaggi, le procedure e le teorie che vogliamo esaminare ‒ e il piano metateorico in cui appunto avviene questa analisi. Quanto ai metodi impiegati in questo studio, essi si sono andati precisando nel corso dei dibattiti susseguitisi a partire dai primi del Novecento tra sostenitori di una visione francamente infinitaria, che concepiva la teoria degli insiemi come la fondazione di una nuova matematica di carattere astratto, e quelli di una concezione che privilegiava l'aspetto costruttivo, legato a procedure dominabili, del pensiero matematico. Di qui l'articolazione dell'analisi delle teorie in due prospettive complementari: l'analisi sintattica, interessata alle teorie come sistemi formali, dispositivi di carattere appunto sintattico per costruire deduzioni, la cui importanza è stata sottolineata soprattutto da David Hilbert a partire dagli anni Venti; l'analisi semantica, rivolta all'aspetto interpretativo del linguaggio matematico e la cui indagine sistematica sarà Alfred Tarski a inaugurare negli anni Trenta. Centrale in entrambe le prospettive rimane il concetto di teoria, che costituisce sotto il duplice aspetto di calcolo logico e di teoria deduttiva l'oggetto fondamentale d'indagine.
Come disciplina in sé, la logica matematica non pone vincoli ai metodi impiegati. È chi intende utilizzare i suoi risultati in una data cornice filosofica che può eventualmente porne per ragioni fondazionali. Contrariamente a quanto si potrebbe pensare, questo tipo di vincolo è stato storicamente uno stimolo fondamentale per la ricerca, come mostrano gli esempi opposti della teoria della dimostrazione e della teoria dei modelli. Sono questi due dei settori centrali della moderna ricerca logica, accanto allo studio delle diverse logiche nate sin dagli anni Venti per motivi filosofici o per affrontare situazioni che si presentano in altre discipline (linguistica, informatica teorica, fisica e così via). Sullo sfondo, le indagini legate alla teoria degli insiemi e a quella della ricorsività, che tematizzano in generale le nozioni collegate alla costruzione di strutture astratte e alla definizione di procedure combinatorie. Di data più recente ma con promesse di grandi sviluppi i rapporti con la teoria delle categorie, che già ha fornito decisivi contributi all'unificazione dei diversi aspetti della ricerca logica.
In queste pagine ci limiteremo a presentare alcuni degli strumenti e dei risultati fondamentali riguardanti i linguaggi formali e le proprietà metamatematiche delle teorie formalizzate in questi linguaggi.
I linguaggi formali che la logica matematica utilizza hanno il ruolo di rendere esplicita la forma logica degli enunciati, in quanto è da questa forma che dipendono i loro rapporti (coerenza, incompatibilità, consequenzialità ecc.) che ci interessano dal punto di vista logico. Questa analisi può essere condotta a diversi livelli di profondità ed esiste una gerarchia di linguaggi di cui il logico si può servire per analizzare le teorie matematiche, dipendente da quali sono le componenti della forma logica degli enunciati che si prendono in considerazione. Ai livelli più elementari stanno due tipi di linguaggi, quelli enunciativi e quelli equazionali, oltre i quali stanno i linguaggi del primo ordine e di ordine superiore.
I linguaggi enunciativi
I linguaggi enunciativi considerano solo le connessioni tra enunciati date da sintagmi del tipo 'se … allora', 'e', 'oppure', 'non' ecc. così che per rendere sul piano sintattico la forma logica che risulta da questa analisi è sufficiente considerare vocabolari infiniti di simboli V=pii∈I ‒ le cosiddette lettere enunciative o enunciati atomici ‒ che potranno variare da un linguaggio all'altro e uno stock di connettivi C=c1,…,cn a ciascuno dei quali è assegnato un naturale, la sua arità, che ci dice quanti enunciati connette, e che supporremo comune a tutti i linguaggi enunciativi dello stesso tipo. Noi considereremo come connettivi , , →, ∉, tutti a due posti tranne l'ultimo unario. I connettivi con la rispettiva arità costituiranno il tipo del linguaggio proposizionale e simili saranno i linguaggi con lo stesso tipo. Come simboli ausiliari ‒ per rendere univoca la lettura ‒ utilizzeremo le parentesi ) e (. Possiamo così definire induttivamente l'insieme FormV delle formule del linguaggio LV ponendo che V⊂FormV e che se A,B∈FormV, allora anche (A B), (A B), (A→B) e (∉A)∈FormV.
I connettivi sono stati introdotti con l'idea di interpretarli in un modo preciso: come disgiunzione (inclusiva), come congiunzione, ∉ come negazione e → come condizionale. Dare questa lettura non significa ancora dare una semantica, perché per determinare una semantica è necessario fissare che cosa intendiamo come enunciato vero e come la verità di un enunciato dipende dalla verità dei suoi sottoenunciati. La storia della logica del Novecento ha mostrato che non solo sono possibili diverse alternative ma che è estremamente interessante indagare che logiche risultano se si sceglie una semantica piuttosto che un'altra. Rimandando ad altra sede l'analisi di alcune di queste, limitiamoci qui alla semantica classica, presentata per la prima volta da Ernst Schröder (1910) e Frege (1897). L'idea è che gli enunciati ‒ e quindi le formule del nostro linguaggio ‒ denotano valori di verità (il vero 1 e il falso 0) e che ai connettivi corrispondono funzioni che danno un valore di verità all'enunciato composto in dipendenza del valore degli enunciati componenti; la nostra è quindi una semantica denotativa o vero-funzionale. Così ‒ se indichiamo con W2 l'insieme 1,0 ‒ alla congiunzione faremo corrispondere la funzione F che assume come valore 1 se e solo se entrambi gli argomenti hanno valore 1, alla disgiunzione la funzione F che invece assume come valore 0 se e solo se entrambi gli argomenti hanno valore 0, alla negazione la funzione F∉ che dà valore 0 a 1 e 1 a 0. Quanto al condizionale ‒ posta l'ipotesi di base che i valori di verità sono solo 0 e 1‒ non rimane che fargli corrispondere la funzione F→ che assume valore 0 solo se il primo argomento è 1 e il secondo 0. Queste stipulazioni ci forniscono le cosiddette tavole di verità (classiche) dei connettivi, ovvero una rappresentazione tabulare del grafo delle funzioni di verità. Per definire il concetto di legge logica come enunciato vero in forza della sola forma, occorre isolare l'insieme dei valori di verità D che considereremo designati ‒ che nel nostro caso sarà l'insieme D=1 ‒ e definire la verità di una formula in un'interpretazione. Per noi le interpretazioni saranno valutazioni v: V→W2 che per ogni lettera enunciativa ci indicano se risulta vera o falsa. Il valore di A rispetto a v sarà il valore v_(A) rispetto alla estensione v_: FormV →W2 di v_ ottenuta ponendo che
e infine
Scriveremo v 'A per dire che A è vera in v, cioè che v_(A)=1, e definiremo infine tautologia ogni formula per cui v 'A per ogni valutazione v. Tutte queste nozioni si possono sistemare utilizzando il concetto di matrice, introdotto da Tarski e Adolf Lindenbaum negli anni Venti. Una matrice di tipo τ è un oggetto
[1] M = 〈Q, D〉
in cui Q=〈W,F1,…,Fn〉 è un'algebra di tipo τ dove W ‒ il dominio ‒ è un insieme non vuoto e ogni Fi è una funzione con argomenti e valori in W corrispondente al connettivo ci del tipo; D⊂W è l'insieme dei valori designati. Ragionando esattamente come sopra possiamo definire il concetto di M-valutazione e porre che è M-tautologia ogni formula che rispetto a ogni M-valutazione assume sempre valore designato. Più in generale, se Γ indica una classe di matrici con algebre dello stesso tipo possiamo definire Γ-tautologia ogni formula che sia M-tautologia per ogni matrice M in Γ. Altre nozioni semantiche fondamentali si possono definire su questa base: quella di conseguenza Γ-tautologica per cui T∣⊦ΓA se A ha valore designato in ogni valutazione in una matrice di Γ in cui abbiano valore designato tutte le formule di T; quella di Γ-soddisfacibilità per cui T è Γ-soddisfacibile se esiste una valutazione in una matrice in Γ che dà valore designato a tutte le formule in T, e così via. Questi concetti sono collegati tra loro; per esempio nel caso classico per cui K={M2}, se scriviamo T∣⊦KA per indicare che A è conseguenza tautologica di T, avremo che T∣⊦KA se e solo se T∪∉A non è Γ-soddisfacibile e A∣⊦KB se e solo se (A→B) è K-tautologia. Questo approccio generale si giustifica in quanto ci permette di confrontare la logica classica enunciativa con altre logiche (intuizioniste, polivalenti, modali, rilevanti, ecc.) che sono state introdotte. L'insieme W2 e le funzioni di M2 definiscono un'algebra di Boole e come Boole aveva supposto le W2-tautologie coincidono con le ΓB-tautologie, dove ΓB è la classe delle matrici booleane, con algebra un'algebra di Boole e insieme D quello costituito dal massimo dell'algebra. Questo è vero per il teorema di rappresentazione di Stone (1935) in base al quale ogni algebra di Boole è isomorfa a una sottoalgebra di un'algebra B(I) di insiemi i cui elementi sono i sottoinsiemi di I e le cui operazioni sono intersezione, riunione, complemento e complemento relativo. L'algebra B(I) d'altra parte è isomorfa all'algebra W2I delle funzioni caratteristiche e quindi a ogni valutazione in un'algebra di Boole che falsifica A ne corrisponde una in W2 che fa lo stesso. La logica enunciativa classica è quindi la logica delle interpretazioni su insiemi ed è questo che la differenzia da altre logiche. Per esempio, la logica enunciativa intuizionista LI è caratterizzabile come la famiglia delle H-tautologie, dove tutte le matrici in H sono algebre di Heyting e a loro volta le algebre di Heyting sono rappresentabili come algebre di aperti di uno spazio topologico. Come intuito da Hermann Weyl negli anni Trenta, la logica intuizionista è quindi la logica opportuna per interpretare predicati topologici. Discorso analogo si può fare per altre logiche e questo collegamento tra matrici su date classi d'algebre e logiche è alla base dello studio algebrico delle logiche enunciative iniziato da Tarski e Lindenbaum negli anni Venti e oggi particolarmente sviluppato in quegli studi di logica algebrica che costituiscono la forma moderna dell'approccio alla logica iniziato da Boole, Schröder ecc. nell'Ottocento.
Ma torniamo al caso classico. Quando una formula è tautologia? Per verificarlo basta costruire per ogni formula A la sua funzione di verità associata FA e controllare per tutte le possibili valutazioni quando prende valore designato. Poiché la verità dipende solo dal valore assegnato alle lettere enunciative occorrenti, se esse sono n 2n saranno i casi possibili, così che la complessità del problema di testare quando una formula è tautologia cresce esponenzialmente con la complessità di A. Poiché A non è soddisfacibile solo se ∉A è tautologia, lo stesso si può dire del problema di testare la soddisfacibilità. Molti sforzi sono stati dedicati al problema di indagare se il problema può essere ridotto al caso di complessità polinomiale. La cosa è particolarmente interessante in quanto Stephen A. Cook ha provato nel 1975 che il problema della soddisfacibilità enunciativa è NP-completo nel senso che a esso si riduce il problema generale P=NP di sapere se ogni insieme decidibile non deterministicamente in tempo polinomiale lo è anche deterministicamente. In ogni caso, diversi algoritmi sono stati proposti per testare tautologicità e soddisfacibilità di formule enunciative e diverse classi sono state isolate per cui i due problemi hanno complessità polinomiale. Un esempio è quello delle clausole di Horn del tipo
[2] D1 … Dn
dove ogni Dj è una disgiunzione di formule basiche, cioè formule atomiche o loro negazioni in cui al massimo una è una lettera proposizionale. Tanto l'algoritmo per le clausole di Horn che quello di risoluzione che si applica a formule qualsiasi, ma che non ha complessità polinomiale, si basano sul fatto che ogni formula è equivalente a una in forma normale ‒ forma normale disgiuntiva FND o congiuntiva FNC. Queste forme erano note fin dagli albori della logica matematica ma furono utilizzate per la prima volta a questo scopo da Émil Post nel 1921. Una FNC è una formula che è congiunzione di disgiunzioni di basiche mentre una FND è una disgiunzione di loro congiunzioni. Per le leggi di De Morgan, ogni negazione di una congiunzione è equivalente alla disgiunzione della negazione dei due congiunti nel senso che è tautologia l'equivalenza
[3] ∉(A B) ∣ (∉A ∉B)
dove (D∣C) è un'abbreviazione per (D→C) (C→D) e analogamente
[4] ∉(A B) ∣ (∉A ∉B).
Ne discende, sfruttando la distributività di su e di su come pure la legge della doppia negazione per cui è tautologia
[5] (A ∣ ∉∉A)
che la negazione di una FNC è equivalente a una FND e viceversa. Sulla base di questi fatti, è facile provare che ogni formula è equivalente tanto a una FNC che a una FND e fornire algoritmi che ci danno le forme normali. Se le FNC sono utilizzate nella dimostrazione automatica per definire procedure di risoluzione con le quali stabilire se una formula non è soddisfacibile, le FND ci offrono un controllo sulla varietà dei possibili modelli di una formula. Se infatti A contiene solo le lettere p1,…,pn è chiaro che a ogni valutazione v corrisponderà una congiunzione Cv
[6] ±p1 … ±pn
dove ±pj è pi se v(pi)=1 e ∉pi altrimenti. Ovviamente v′'Cv solo se v=v′, così che ogni formula A sarà equivalente alla FND i cui congiunti sono le varie Cv associate alle valutazioni che la rendono vera. In forza di questa associazione valutazioni/congiunzioni di basiche, non solo possiamo dimostrare il teorema di completezza funzionale di Post per cui ogni funzione di verità si ottiene per composizione dalle funzioni della nostra matrice M2 così che ogni connessione tra enunciati ‒ supposta la bivalenza dei valori di verità ‒ sarà esprimibile mediante i nostri connettivi, ma abbiamo un criterio per affrontare il problema della presentazione dell'insieme TautM2 delle tautologie classiche come teoria deduttiva fondata su assiomi e regole. È questo il versante sintattico della logica che storicamente è stato il primo a essere sviluppato, prima da Frege poi da Bertrand Russell e Alfred N. Whitehead nei Principia Mathematica e molti altri. Ci sono due strategie almeno che si possono seguire: quella dei calcoli di tipo logicista basata appunto sull'idea che la logica è una teoria deduttiva codificata da assiomi e regole di inferenza e quella ‒ inaugurata negli anni Trenta da Gerhard Gentzen ‒ basata sull'idea della logica come insieme di regole deduttive. I calcoli introdotti da Gentzen sono di due tipi: in primo luogo i sistemi di derivazione naturale o N-calcoli in cui viene massimizzato il ruolo delle regole, non si postulano assiomi e si dànno regole di introduzione ed eliminazione per ogni connettivo; in secondo luogo i calcoli di sequenti o L-calcoli, che formulano regole di derivazione per introduzione dei connettivi nell'antecedente o nel conseguente di sequenti del tipo
[7] A1, …, An ⇒ B1, …, Bk
letti come A1 … An→B1 … Bk. Se gli L-calcoli sono oggi lo strumento centrale della teoria riduttiva della dimostrazione, gli N-calcoli sono stati presentati in nuova veste negli anni Settanta da Dag Prawitz che ne ha fatto la base per la sua teoria generale della dimostrazione volta a classificare le dimostrazioni in funzione della loro complessità e reciproca convertibilità. Quale che sia il calcolo che si propone per la logica classica ‒ chiamiamolo genericamente CK ‒ i criteri di adeguatezza che deve soddisfare sono due: quello della validità e quello della completezza che riguardano entrambi la nozione di dimostrabilità associata, in base alla quale A è dimostrabile da T sulla base di CK ‒ e scriveremo T⊦CK A ‒ se esiste una dimostrazione A1,…,An tale che A=An e ogni Aj o appartiene a T o è ottenuto da formule precedenti nella dimostrazione utilizzando le regole del calcolo. Ci sono due modi di vedere il problema dell'adeguatezza, a seconda che si considerino solo le tautologie ‒ e si cerchi quindi un calcolo che ci permette di dimostrarle tutte ‒ o si voglia invece analizzare la più generale relazione di conseguenza tautologica cercando quindi un calcolo in base al quale dimostrare ‒ per ogni T ‒ tutte le sue conseguenze. Il primo problema è un caso particolare del secondo in quanto A è tautologia se →⊦CK A ed è facilmente risolubile con i metodi di Post. Il secondo coinvolge insiemi T di cardinalità arbitraria, quindi anche infinita, e si risolve ricorrendo al teorema di Lindenbaum (1931) che ci dice che se T è un insieme coerente rispetto al calcolo (cioè non ha tra i suoi teoremi sia A che ∉A per nessuna formula A), allora si estende a un insieme T′ non solo coerente ma completo (sempre rispetto al calcolo) nel senso che per ogni A avremo che T′⊦CK A oppure T′⊦CK ∉A. A partire da T′ possiamo definire una valutazione ponendo che v(pj)=1 solo se T′⊦CK pj. In base alla completezza possiamo dimostrare che v sarà modello di tutti i teoremi di T (e solo di quelli). Supponiamo ora che T ⊦CK A: avremo che T∪∉A è coerente e quindi ‒ per il teorema di Lindenbaum ‒ ci sarà un'estensione T′ di T la cui valutazione indotta sarà modello di T ma non di A. A non può essere quindi conseguenza tautologica di T. La relazione di dimostrabilità ha carattere finito, nel senso che T⊦CK A solo se esiste una parte finita Tf di T per cui Tf ⊦CK A; per la completezza anche ∣⊦K sarà di carattere finito e quindi avremo pure che condizione sufficiente affinché T sia soddisfacibile è che lo sia una sua parte finita. È questo il teorema di compattezza, che si può provare anche direttamente senza sfruttare la completezza e che ci mostra come siano collegate tra di loro la completezza rispetto alla conseguenza e la completezza rispetto alle tautologie.
Linguaggi equazionali
I linguaggi equazionali sono i più semplici accanto a quelli enunciativi e generalizzano la situazione dell'algebra elementare, in cui abbiamo a che fare con la manipolazione di equazioni. La loro introduzione si deve a Garrett Birkhoff, che negli anni Trenta ha introdotto lo studio delle classi d'algebre definibili equazionalmente e risolto il problema di fornire un'analisi della relazione di conseguenza tra equazioni mostrandone l'importanza nel contesto dell'algebra universale.
Sia τ un tipo di algebre, dato da una collezione Fτ di costanti per funzioni (ciascuna con la sua arità) e un insieme Iτ di costanti individuali. Il linguaggio equazionale associato LEτ, oltre alle costanti del tipo (che variano da linguaggio a linguaggio) avrà uno stock Var0=x1,x2,x3,… di variabili, le parentesi ), ( e il simbolo di identità = del linguaggio che sarà l'unico simbolo per relazione di LEτ. Le regole grammaticali del linguaggio ci forniscono le definizioni degli insiemi Termτ e Eqτ dei termini e delle equazioni di LEτ. Termτ è definito induttivamente ponendo che Var0⊂Termτ, Iτ⊂Termτ e che se t1,…,tn sono in Termτ e f è una costante funzionale n-aria di Fτ allora f(t1,…,tn)∈Termτ. Eqτ sarà l'insieme di tutte le equazioni t=t′ dove t,t′ sono termini. Sul piano semantico, termini ed equazioni si interpretano in algebre e le algebre di tipo τ sono strutture
[8] M = 〈DM, fMf∈Fτ, dMd∈Iτ〉
dove DM ‒ il dominio ‒ è un insieme non vuoto, per ogni f∈Fτ n-aria fM: DMn →DM è una funzione n-aria e per ogni d∈Iτ dM è un individuo in DM. La semantica per i linguaggi equazionali si basa sui concetti di denotazione e verità. Dati un termine t e un'algebra M, la sua denotazione tM ‒ che generalizza le funzioni polinomiali che associamo ai polinomi nell'algebra elementare ‒ è una funzione n-aria tM: DMn →DM che possiamo definire induttivamente una volta che specifichiamo come interpretare le variabili che occorrono nel termine e che non hanno un'interpretazione fissa come le costanti. Chiamiamo allora assegnazione ogni funzione a: Var0→DM e definiamo tM,a ‒ il denotato di t in M modulo a ‒ ponendo che se t è xj allora tM,a=a(j), se t è d allora tM,a=dM e infine che se t è f(t1,…,tn)
[9] tM,a=fM(t1M,a, …, tnM,a).
Possiamo ora definire la funzione tM dicendo che ‒ per ogni c1,…,cn in DM ‒ tM(c1,…,cn)=tM,a, dove a(xj)=cj. In altre parole definiamo la funzione su c1,…,cn dicendo che valore assume il termine che otteniamo da t sostituendo alla variabile xj l'oggetto cj. A questo punto possiamo definire il concetto di verità per le equazioni. Diremo che t=t′ è vera in M ‒ e scriveremo M't=t′ ‒ se per ogni c1,…,cn in DM si ha che
[10] tM(c1, …, cn) = t′M(c1, …, cn).
Immediata la definizione di conseguenza: se T è un insieme di equazioni, T∣⊦Et=t′ se ogni algebra in cui è vera ogni equazione di T (cioè ogni modello di T) rende vera anche t=t′. Anche per la conseguenza equazionale vale un risultato di compattezza per cui se E è conseguenza di T sarà conseguenza di una sua parte finita. La cosa si può dimostrare come nel caso proposizionale costruendo un calcolo equazionale CE completo nel senso che ‒ se CE indica la dimostrabilità nel calcolo ‒ si abbia
[11] T∣⊦EE se e solo se TCEE.
Basterà postulare come unico assioma il principio d'identità PI: xj=xj, la regola Rs di sostituzione ‒ per cui se è dimostrata un'equazione, è dimostrata anche ogni altra equazione che si ottiene da essa sostituendo uniformemente una variabile con uno stesso termine ‒ più
[12] formula
dove p′ e q′ si ottengono da p=q sostituendo occorrenze di t con occorrenze di t′. Il calcolo CE è ovviamente valido e la completezza ‒ come mostrato da Birkhoff ‒ si ottiene mediante la costruzione di un'algebra modello MT,X di T a partire da T stesso e da uno stock qualsiasi di costanti individuali aggiuntive X. Basterà considerare nel linguaggio esteso LE(X) l'insieme dei termini chiusi (in cui cioè non occorrono variabili) AX e definire la relazione:
[13] t ≈ t′ se e solo se T CE t=t′.
La ≈ è un'equivalenza per cui possiamo passare al quoziente AX /≈ e considerare le classi di equivalenza t^=t′∈AXt≈t′; si verifica pure per Rq che è corretto, per ogni f∈Fτ, definire:
[14] fM,X (t1^, …, tn^) = f(t1, …, tn)^.
Otteniamo così una struttura MT,X; è facile provare ora che MT,X⊦E se e solo se TCEE, così che se non TCEE avremo che non MT,X⊦E e quindi non T∣⊦E: se E non è teorema non è neanche conseguenza. Le algebre MT,X coincidono con le algebre libere su X nella classe dei modelli di T e sono d'importanza fondamentale ‒ come Birkhoff ha dimostrato ‒ nell'algebra universale; attraverso di esse lo studio delle teorie equazionali è oggi assorbito in quello delle varietà e quasi-varietà di algebre.
I linguaggi elementari
Molte proprietà significative di strutture algebriche importanti non sono di forma equazionale (per es., la proprietà di non avere divisori dello zero) e molte strutture della matematica coinvolgono non solo funzioni ma relazioni (prima fra tutte la relazione d'ordine). Inoltre, molti teoremi matematici hanno forma esistenziale (affermano cioè l'esistenza di oggetti che soddisfano date condizioni) e i nostri linguaggi enunciativi ed equazionali ‒ anche se combinati, considerando linguaggi enunciativi in cui le formule atomiche V sono le equazioni di un linguaggio equazionale ‒ non sono in grado di esprimere questo riferimento esistenziale. Per farlo occorre approfondire l'analisi della forma logica introducendo quelli che noi oggi chiamiamo i quantificatori, come mostrato nel 1883 da Oscar Mitchell ‒ un allievo di Charles Peirce ‒ e soprattutto da Frege con la sua Begriffsschrift (1879). Il sistema di Frege costituiva un'unica teoria ‒ la Grande logica ‒ con capacità espressive molto estese ed è stato solo successivamente ‒ soprattutto per opera di Hilbert e della sua scuola ‒ che sono stati isolati all'interno di questo sistema sottolinguaggi autonomi con sintassi e semantiche proprie. Base per questa frammentazione è stata la considerazione del tipo di oggetti su cui si ammette la quantificazione: individui, insiemi di individui, insiemi di insiemi, ecc.; dando così origine ai linguaggi del primo, del secondo ordine, e così via.
I linguaggi del primo ordine ‒ o linguaggi elementari ‒ sono associati a tipi di similarità τ che, oltre a contenere costanti funzionali e costanti individuali, hanno anche un insieme Rτ di costanti relazionali, ciascuno corredato da una sua arità. Naturali interpretazioni di questi linguaggi sono le strutture relazionali ‒ il concetto si deve a Tarski (1950) ‒ del tipo
[15] M = 〈DM, fM f∈Fτ, PMp∈Rτ, dMd∈Iτ〉
che sono come le algebre introdotte per i linguaggi equazionali salvo la clausola aggiuntiva che, per ogni P∈Rτ, PM è una relazione di opportuna arità su DM. Il linguaggio elementare associato Lτ avrà tra i simboli comuni a tutti i linguaggi elementari variabili individuali, parentesi, segno di =, connettivi e i quantificatori ∀ e ∃. Termini in Termτ saranno gli stessi del linguaggio equazionale corrispondente e formule gli elementi dell'insieme definito induttivamente Form ponendo: Eqτ⊂Formτ; per ogni t1,…,tn∈Termτ e ogni P∈Rτ n-aria, P(t1,…,tn)∈Formτ ; se A,B∈Formτ, anche (A B), (A B), (A→B), (∉A) sono in Formτ e se x è una variabile che occorre in A, (∀xA) e (∃xA) saranno in Formτ. La lettura delle formule è intuitiva; se diciamo che una variabile xj è libera in A nel caso non occorra nel raggio d'azione di un quantificatore contenuto in A, scriveremo A(x1,…,xn) per indicare le variabili libere in A e la formula denoterà una relazione n-aria; se invece A non contiene variabili libere ed è quindi una formula chiusa, rappresenterà un enunciato, vero o falso in una struttura relazionale. Estendendo quanto fatto nel caso equazionale, possiamo definire i concetti semantici di denotato e verità per formule. Per i termini la situazione è esattamente quella del caso equazionale e anche per le formule faremo uso del concetto di assegnazione, definendo quando una formula A con variabili libere x1,…,xn è soddisfatta in M dall'assegnazione a, il che scriveremo M'aA. Seguendo la falsariga della definizione dei concetti semantici data da Tarski nel 1935, procediamo per induzione sulla complessità di A distinguendo il caso atomico dal caso molecolare. Se A è atomica ed è un'equazione, allora la clausola è la stessa che per il caso equazionale; se A è P(t1,…,tk), porremo che M'aA se e solo se 〈t1M,a,…,tkM,a〉∈PM. Per i connettivi:
M'a(A B) se e solo se M'aA e M'aB
non M'a(A B) se e solo se non M'aA e non M'aB
non M'a(A→B) se e solo se M'aA e non M'aB
M'a∉A se e solo se non M'aA .
Per i quantificatori, diciamo che l'assegnazione a′ è un'alternativa su xj ad a ‒ e scriviamo a′Rja ‒ se a e a′ coincidono su tutti i valori che assegnano alle variabili xi con i≠j tranne che eventualmente su xj. Poniamo quindi:
M'a(∃xj A) se e solo se esiste a′ tale che a′Rj a per cui M'a′A
M'a(∀xj A) se e solo se per ogni a′ tale che a′Rj a si ha M'a′A.
Sulla base delle stipulazioni di sopra diremo che un enunciato A è vero in M e scriveremo M'A se A è soddisfatto da M rispetto a una (e quindi tutte) le assegnazioni; nel caso A sia una formula con libere x1,…,xn e a(xj)=dj diremo poi che la n-pla d1,…,dn soddisfa A in M e scriveremo M'A[d1,…,dn]. Il denotato di A in M sarà così la relazione
[16] AM = 〈d1,…,dn 〉M'A[d1,…,dn]
e definibile (senza parametri) in M sarà ogni relazione di questa forma. Da questi, altri concetti semantici si possono definire; se interpretiamo ogni A come la sua chiusura universale A∀ ‒ la formula che si ottiene quantificando le variabili libere universalmente ‒ A sarà conseguenza elementare di T ‒ e scriveremo T∣⊦1KA ‒ se A è vera in ogni M che sia modello di T, vale a dire, ogni M che rende veri tutti gli enunciati di T ‒ il che scriveremo M'T. Analogamente A sarà legge logica (elementare) se è vera in ogni struttura per il linguaggio e le leggi logiche coincidono con le conseguenze dell'insieme vuoto. Più in generale avremo che
[17] T∪B∣⊦1K A se e solo se T∣⊦1K B∀→A.
Anche nel caso elementare si pone il problema di analizzare in termini sintattici la relazione di conseguenza mediante un'adeguata relazione di deducibilità C1K indotta da un calcolo C1K. Un calcolo del genere si può ottenere da quelli per i linguaggi enunciativi ed equazionali, aggiungendo assiomi e regole riguardanti i quantificatori. Per esempio per i calcoli logistici aggiungendo gli schemi di assiomi
[18] A1) ∀xi A(xi) → A(t) A2) A(t) → ∃xj A(xj)
e le regole
[19] formula
per ogni formula A che contenga libera xi e non contenga t e ogni formula D in cui non occorra t.
Dato un calcolo valido per i linguaggi elementari, il problema è come provarne la completezza. La prima dimostrazione in questo senso risale a Kurt Gödel (1931) e la sua importanza storica sta nel fatto che mostrava come fosse possibile simulare sintatticamente una relazione quale quella di conseguenza definita in termini astratti e di natura infinitaria. Altre dimostrazioni seguirono, per esempio quella di Leon Henkin del 1945 che si basa sull'idea di utilizzare anche in questo caso estensioni di insiemi di cui si sa costruire un modello. Poiché è immediato che se T C1K A l'insieme T∪∉A sarà coerente rispetto al calcolo, ci basterà allora mostrare che ogni famiglia coerente di enunciati ha come estensione un insieme di questo tipo. Di tal fatta sono gli insiemi T* ricchi e completi, tali cioè che ‒ oltre a essere coerenti e completi nel loro linguaggio ‒ sono tali che per ogni enunciato ∃xj A per cui TC1K∃xjA esiste una costante d nel linguaggio tale che TC1K A(d). Data così T in L, passiamo a un ampliamento del linguaggio che contenga tante nuove costanti individuali d∈C quante le formule in L e in questo linguaggio L(C) costruiamo induttivamente una catena T1⊆T2⊆T3… di insiemi coerenti aggiungendo a ogni passo esempi A(d) per ogni ∃xj A dimostrabile al passo precedente utilizzando costanti distinte per formule distinte. Prendendo la riunione T§ degli insiemi della catena avremo così una teoria ricca e coerente. A questo punto basta ‒ rimanendo nel linguaggio L(C) ‒ utilizzare il teorema di Lindenbaum ‒ che nel caso di linguaggi più che numerabili richiede AC ‒ e passare a una estensione completa T* di T§ che sarà coerente ricca e completa. Associata a T* è una struttura ‒ la struttura canonica MT*,C di T* su C ‒ che è costruita esattamente come la struttura canonica per le teorie equazionali vista sopra ed è facile provare che per ogni A in L(C) avremo
[20] MT*,C 'A se e solo se T*C1KA.
Si noti che ‒ come nel caso enunciativo ‒ il teorema di Lindenbaum richiede il ricorso all'assioma di scelta AC se il linguaggio è più che numerabile. Corollario della completezza è ancora una volta il teorema di compattezza che ci dice non solo che se A è conseguenza di T lo sarà di una parte finita ma anche che condizione sufficiente affinché T abbia un modello è che ogni parte finita ne abbia uno. Questa proprietà è di fondamentale importanza nella teoria dei modelli. È naturale chiedersi quanto piccoli possono essere i modelli di una teoria coerente e se è possibile restringersi ‒ se non al finito ‒ almeno al numerabile se il linguaggio è numerabile anch'esso.
Così è per il modello canonico di una teoria coerente numerabile e questo ha come corollario il teorema di Löwenheim per cui A è legge logica se e solo se è vera in ogni struttura al più numerabile. Il problema si può approfondire se usiamo una tecnica introdotta da Thoralf Skolem negli anni Venti per analizzare il significato dei quantificatori. È possibile infatti provare che ogni formula A è equivalente a una formula A′ con le stesse variabili libere e del tipo:
[21] Q1x1, …, QnxnB
dove ogni Qi è un quantificatore e B è ottenuta dalle atomiche utilizzando solo i connettivi. Formule del genere si chiamano prenesse: la matrice B contiene condizioni su individui che non coinvolgono la totalità del dominio d'interpretazione mentre questi riferimenti sono tutti specificati dal prefisso la cui complessità è misurata dall'alternarsi di blocchi di quantificatori omogenei. L'idea di Skolem è di rendere esplicita questa complessità introducendo funzioni che esemplifichino i quantificatori esistenziali mostrando che individui devono esistere in funzione delle variabili precedenti nel prefisso quantificate universalmente. Consideriamo per esempio la formula
[22] ∃x1, ∀x2x3, ∃x4 B.
Perché sia soddisfatta in una struttura M è sufficiente che sia soddisfatta la formula
[23] ∀x2,x3 B(d1, x2, x3, f(x2, x3))
dove il denotato di d1 e quello di f siano definiti in modo tale che
[24] M'∀x2,x3 B(d1, x2, x3, f(x2, x3)).
Se assumiamo che tutte le formule di T siano prenesse e sostituiamo ogni A∈T con la formula AS ottenuta come sopra, avremo un insieme TS ‒ la teoria di Skolem associata a T ‒ che avrà un modello se e solo se lo ha T; questo si può provare semanticamente utilizzando AC o sintatticamente sfruttando il teorema dimostrato da Jacques Herbrand nel 1930 in base al quale una formula prenessa è legge logica se e solo se è tautologia una disgiunzione di esempi della matrice della trasformata di Herbrand AH. Si noti che questo fatto ‒ pur riconducendo la validità logica di enunciati elementari alla tautologicità di disgiunzioni associate ‒ non ci permette di trasferire il metodo di decisione per i linguaggi enunciativi a quelli elementari, in quanto il teorema non ci dà un confine superiore alla lunghezza della disgiunzione associata e quindi non sappiamo a priori quanti esempi della matrice considerare. Ricordando la dualità tra soddisfacibilità e dimostrabilità, possiamo verificare che, per ogni A, AH coinciderà con (∉A)S, il che significa che come modello di T possiamo prendere la struttura canonica di qualunque estensione enunciativamente completa della teoria T^ di tutti gli esempi chiusi delle matrici di formule in TS. Il dominio sarà dato dai denotati di questi termini. È questo il cosiddetto universo di Herbrand, divenuto centrale negli studi sulla dimostrazione automatica.
Nel caso elementare, la quantificazione ci impone la necessità di considerare strutture infinite (anche se solo numerabili, per il teorema di Löwenheim) e non deve stupire quindi che non siano disponibili metodi di decisione per la soddisfacibilità o la validità logica applicabili a formule arbitrarie; questo è possibile per classi di formule specifiche ed esiste una vasta letteratura sui problemi di decisione e sulla loro classificazione. Che un algoritmo generale per la validità logica non esista è il contenuto di un famoso teorema di Alonzo Church (1936), per il quale non è decidibile l'insieme delle leggi logiche di linguaggi elementari con un minimo di vocabolario. Il teorema si può vedere come corollario del teorema di indecidibilità di Gödel per una sottoteoria dell'aritmetica AP di Peano finitamente assiomatizzabile in cui siano rappresentabili i predicati ricorsivi. Un sottosistema del genere è il sistema Q di Raphael M. Robinson, costruito nel linguaggio con costanti 0, s, +, × e gli assiomi
A1) ∀x,y (s(x)=s(y) → x=y) A2) ∀y (0≠s(y))
A3) ∀x (x≠0 → ∃y (x=s(y))) A4) ∀x (x+0=x)
A5) ∀x,y (x+s(y) = s(x+y)) A6) ∀x (x×0=0)
A7) ∀x,y (x×s(y) = (x×y)+x).
Per il teorema di completezza, indicando con XQ la congiunzione dei sette assiomi di sopra,
[25] QC1K A se e solo se C1K XQ → A.
Ne segue allora ‒ poiché il teorema di indecidibilità di Gödel si applica anche a Q ‒ che se non esiste un algoritmo per testare la dimostrabilità in Q, non potrà esistere neanche un algoritmo per testare la dimostrabilità entro il calcolo. La situazione non cambia se ci si restringe alla verità nei modelli di cardinalità finita ma arbitraria. Come provato da Boris Trachtenbrot nel 1950, non esistono algoritmi neanche in questo caso: infinito o finito arbitrario non fa differenza. L'indecidibilità del calcolo non comporta d'altra parte che non esistano nei linguaggi elementari teorie decidibili. Tali sono tutte le teorie con insieme di assiomi decidibili (come si dice, ricorsivamente assiomatizzabili) che risultano complete. Possiamo infatti enumerare tutte le dimostrazioni di T e quindi anche i teoremi di T; la completezza d'altra parte ci dice che non TCKA se e solo se TCK∉A così che otterremo una enumerazione anche dell'insieme complementare dei non teoremi. Procedendo a zig-zag (secondo un metodo introdotto da Post) possiamo confrontare ogni formula con quelle delle due enumerazioni e concludere dopo un numero finito di passi se A è teorema o no. Decidibili sono molte teorie interessanti, come quella dei numeri reali o la geometria elementare, come provato da Tarski negli anni Venti; indecidibili quelle in cui una teoria come Q si può interpretare. È questo il caso della teoria degli insiemi Zermelo-Frenkel (ZF) o di quella dei gruppi, ma gli esempi in un senso o nell'altro sono tantissimi e coinvolgono alcuni dei risultati più interessanti della ricerca logica a partire dagli anni Quaranta.
Tra i risultati generali sui linguaggi elementari, fondamentali in quanto permettono di accedere alla soluzione di questioni più riposte, sono quelli che riguardano l'interpolazione e le sue applicazioni al problema della definibilità entro teorie (il cosiddetto criterio di Padoa) o la preservazione della verità rispetto a operazioni su strutture. Si tratta di teoremi originariamente dimostrati con metodi sintattici e che solo più tardi hanno trovato dimostrazioni semantiche contribuendo in modo decisivo a chiarire i rapporti tra le due tecniche, così che esistono oggi metodi che utilizzano il meglio delle due prospettive come quelli basati sul concetto di proprietà analitica di coerenza proposto da Raymond Smullyan nel 1963. Il teorema d'interpolazione ‒ dimostrato per la prima volta da William Craig (1957) ‒ afferma che se A e B sono due enunciati per cui A∣⊦1KB ‒ o sintatticamente AC1KB ‒ allora esisterà un enunciato D che contiene solo costanti extralogiche comuni ad A e B per cui AC1KD e DC1KB.
D è una formula interpolante e il risultato si può raffinare imponendo ulteriori condizioni su di esso. Per esempio ‒ è questo il teorema di Lyndon (1959) ‒ se nel linguaggio non ci sono costanti funzionali o individuali, possiamo fare in modo che la formula interpolante contenga solo le costanti che occorrono positivamente (sono precedute da zero o un numero pari di negazioni) tanto in A che in B. In base a questo risultato Lyndon poté dimostrare che le formule la cui verità è preservata passando da una struttura a una sua immagine omomorfa sono equivalenti a formule positive (in cui non compaiono ∉ e →). Dal teorema di Craig si ricava invece il teorema dimostrato nel 1953 da Evert W. Beth per rendere operante il criterio fornito da Alessandro Padoa (1900) sulla definibilità all'interno di teorie assiomatiche. Il teorema afferma che se T è una teoria in un linguaggio che contiene le costanti relazionali P, Q1,…,Qn esisterà una definizione D di P che contiene le sole costanti relazionali Q1,…,Qn per cui
[26] TC1K∀x (P(x)∣D(x))
se e solo se per ogni isomorfismo h: DM →DM′ rispetto ai predicati Q1,…,Qn, dove M e M′ sono modelli di T, c'è una sola interpretazione di P che lo trasforma in un isomorfismo anche rispetto a P. In altre parole, PM è univocamente determinato da Q1M,...,QnM in ogni M.
Estensioni dei linguaggi elementari
Già l'esempio degli assiomi per l'aritmetica di Peano ‒ quelli per Q più il principio di induzione ‒ ci mostrano che i linguaggi elementari hanno forti limiti espressivi. Il principio d'induzione infatti afferma che per ogni proprietà P, se P(0) e ∀x(P(x)→P(s(x)) allora ∀x(Px) quantificando sulla totalità dei sottoinsiemi di ℕ. I linguaggi del primo ordine non sono in grado di esprimere questo e si debbono limitare a postulare la formula
[27] A(0) ∀x(A(x) → A(s(x)) → ∀xA(x)
per ogni A(x) del linguaggio. Ciò significa che questo insieme di assiomi (questo schema) vincola solo i sottoinsiemi definibili di ℕ e non tutti i sottoinsiemi possibili. Stesso discorso per l'assioma di completezza per i numeri reali in base al quale ogni sottoinsieme di ℝ limitato superiormente ha un minimo confine superiore, o anche per la geometria sintetica dove il principio di Archimede richiede il riferimento a tutti i sottoinsiemi finiti di segmenti su una retta. I linguaggi elementari ci permettono di esprimere la condizione solo per i sottoinsiemi che sono definiti da formule e il discorso si potrebbe estendere alla teoria ZF degli insiemi considerando l'assioma di isolamento o quello di rimpiazzamento. Non è un caso quindi che i linguaggi proposti da Frege, Russell e Whitehead o Hilbert stesso nei loro lavori sulla fondazione della matematica a inizio secolo ammettessero la possibilità di quantificare anche su oggetti di tipo superiore: insiemi, relazioni, funzioni.
Per le teorie di sopra sono sufficienti linguaggi del secondo ordine anche se per altre (per es., la teoria degli spazi topologici dove si considerano famiglie di sottoinsiemi) sembrerebbe più naturale considerare anche altri tipi finiti.
Un linguaggio del secondo ordine di un dato tipo di similarità L2 avrà, oltre ai simboli per i linguaggi elementari, insiemi Varn=Xin dove i∈ℕ per le variabili che scorrono sulle relazioni n-arie. L'insieme dei termini sarà lo stesso del linguaggio L e per le formule allarghiamo l'insieme delle atomiche, aggiungendo per ogni Xin e ogni n-pla 〈t1,…,tn〉 la formula Xn(t1,....,tn), chiudendo poi anche rispetto alla quantificazione su insiemi e relazioni ponendo che se A è una formula con Xin, saranno formule anche (∀XinA) e (∃xinA). Le strutture naturali per simili linguaggi saranno del tipo
[28] M2 = 〈M, Dnn∈N〉
dove Dn=P(DMn) è la famiglia di tutte le relazioni n-arie su DM, cioè la famiglia di tutti i sottoinsiemi di DMn. La definizione di soddisfazione e di verità si ottiene facilmente da quella data per i linguaggi elementari e lo stesso vale per gli altri concetti semantici, in particolare per la relazione di conseguenza T∣⊦2K A. Esiste un calcolo C2K in grado di simulare la conseguenza al secondo ordine? La risposta è negativa e dipende ancora una volta dal teorema di indecidibilità di Gödel che ci dice che l'insieme degli enunciati elementari veri in ℕ non è generabile in modo effettivo (di più, non è neanche definibile nell'aritmetica, come provato da Tarski). Proprio per la loro potenza i linguaggi del secondo ordine sono in grado di darci assiomatizzazioni categoriche, teorie cioè i cui modelli sono tutti isomorfi. È questo il caso anche di AP2, l'aritmetica di Peano formulata al secondo ordine, i cui modelli ‒ come già provato da Richard Dedekind ‒ sono tutti isomorfi, cosa che non vale per la corrispondente teoria AP elementare. Ne segue che conseguenza di AP2 saranno tutte le formule vere in ℕ. D'altra parte, come osservato sopra, AP2 ha un numero finito di assiomi perché il principio d'induzione si riduce a una sola formula e ‒ se indichiamo con P la congiunzione degli assiomi ‒ avremo che
[29] AP2∣⊦2K A se e solo se ∣⊦2K P→A
per ogni formula A, così che, se esistesse un calcolo completo, enumerando le dimostrazioni delle leggi logiche avremmo una enumerazione delle formule vere in ℕ. Siamo così messi di fronte a un fatto fondamentale che riguarda in generale il rapporto tra linguaggi come dispositivi combinatori e strutture astratte: più i linguaggi sono espressivi e riescono a caratterizzare le strutture, meno possono essere dominabili e viceversa. Questo spiega l'importanza dei linguaggi elementari che costituiscono un vero e proprio punto di sella tra le opposte esigenze di dominabilità e di espressività sui linguaggi. Un modo per ridurre lo scarto è quello di indebolire il rapporto semantico di verità, e allargare la classe delle interpretazioni possibili per i linguaggi del secondo ordine lasciando cadere la condizione che i domini Dn su cui scorrono le variabili d'ordine superiore coincidano con P(DMn). Ci basterà prendere domini che contengano tutte le relazioni definibili. È questa la via proposta da Henkin nel 1945 con l'introduzione delle strutture generali contrapposte alle strutture piene in cui ogni Dn coincide con tutto P(DMn). Allargato il concetto di modello con queste nuove definizioni, la relazione di conseguenza si indebolisce ed è possibile costruire un calcolo completo. Si perde d'altra parte la categoricità per molte teorie e il secondo ordine così interpretato diviene un primo ordine con diverse sorta di oggetti: individui, insiemi, relazioni, ecc. L'importante è che ‒ considerando come domini famiglie significative dal punto di vista matematico (insiemi aperti, boreliani, insiemi finiti, ecc.) ‒ otteniamo linguaggi che ci permettono di studiare situazioni significative.
Altre soluzioni sono possibili se modifichiamo invece della semantica la sintassi. La situazione non cambia se ci restringiamo al frammento monadico di L2 che utilizza solo quantificazioni su relazioni unarie (ossia sottoinsiemi del dominio). Ben diversa è la cosa se consideriamo linguaggi che ammettano elementi infinitari; per esempio congiunzioni e disgiunzioni numerabili (i linguaggi infinitari Lω1,ω), congiunzioni infinite e quantificazioni simultanee infinite (i linguaggi Lk,λ). Non tutte le proprietà generali (compattezza, esistenza di un calcolo, teoremi di interpolazione, ecc.) che incontriamo nel caso elementare si ritrovano in questi linguaggi, il che ha portato alla elaborazione di nuovi metodi tanto nella teoria della dimostrazione che in quella dei modelli.
Bibliografia
Barwise 1993: A handbook of mathematical logic, 8. ed., edited by Jon Barwise, Amsterdam, North-Holland, 1993.
Boole 1993: Boole, George, L'analisi matematica della logica, Torino, Boringhieri, 1993.
Frege 1965: Frege, Gottlob, Logica e aritmetica, Torino, Boringhieri, 1965.
Gentzen 1969: Gentzen, Gerhard, The collected papers, edited by M.E. Szabo, Amsterdam, North-Holland, 1969.
Gödel 1986: Gödel, Kurt, Collected works, New York-Oxford, Clarendon Press, 1986.
Hedman 2002: Hedman, Shawn, A first course in logic, Oxford, Oxford University Press, 2002.
Hilbert, Ackermann 1928: Hilbert, David - Ackermann, Wilhelm, Grundzüge der theoretischen Logik, Berlin, Springer, 1928.
Lloyd 1986: Lloyd, John W., Fondamenti di programmazione logica. I suoi rapporti con la logica e la matematica, Milano, Muzio, 1986.
McCall 1967: McCall, Storrs, Polish logic 1920-1936, Oxford, Clarendon Press, I, 1967.
Mangione 1993: Mangione, Corrado - Bozzi, Silvio, Storia della logica, Milano, Garzanti, 1993.
Russell, Whitehead 1910-1913: Russell, Bertrand - Whitehead, Alfred N., Principia mathematica, Cambridge, Cambridge University Press, 1910-1913, 3 v.
Shoenfield 1980: Shoenfield, Joseph, Logica matematica, Torino, Boringhieri, 1980.
Skolem 1970: Skolem, Thoralf A., Selected works in logic, edited by Jens E. Fenstad, Oslo, Universitetsforlaget, 1970.
Tarski 1983: Tarski, Alfred, Logic, semantics, metamathematics. Papers from 1923 to 1938, 2. ed., Indianapolis, Hackett, 1983.
Van Heijenoort 1967: van Heijenoort, Jean, From Frege to Goedel: a sourcebook in mathematical logic, 1879-1931, Cambridge (Mass.), Harvard University Press, 1967.
Wojcicki 1988: Wojcicki, Riszard, Theory of logical calculi. Basic theory of consequence operation, Dordrecht-Boston, Kluwer, 1988.