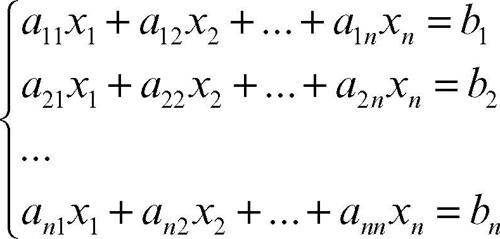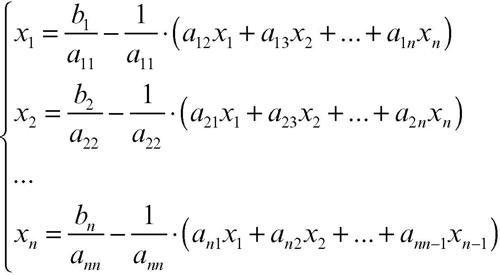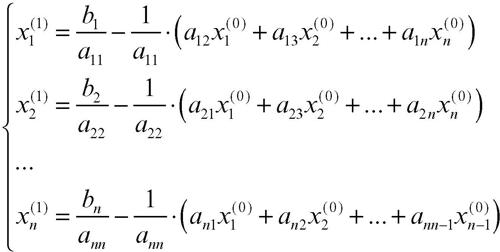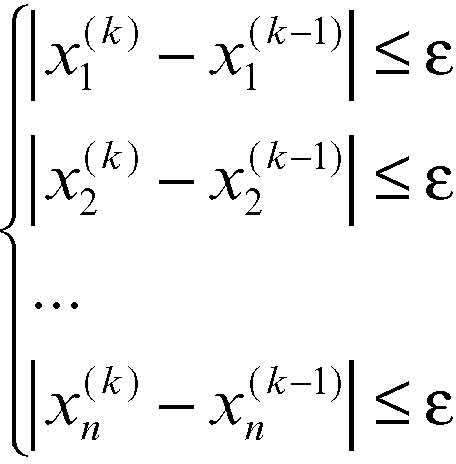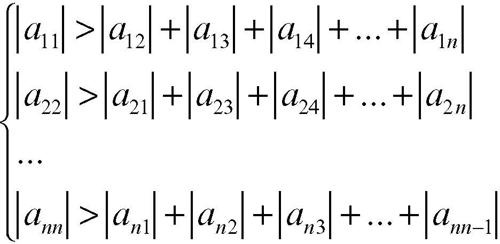Jacobi, metodo di

Jacobi, metodo di

Jacobi, metodo di metodo numerico per la risoluzione di un sistema di n equazioni lineari in n incognite. Oltre ai metodi cosiddetti diretti, come il metodo di → Cramer e il metodo di → Gauss, esistono infatti metodi iterativi che consistono nella ricerca delle soluzioni del sistema attraverso approssimazioni successive. Si consideri un sistema lineare di n equazioni in n incognite:

Il sistema può essere scritto in forma matriciale: A ⋅ X = B dove A è la matrice dei coefficienti

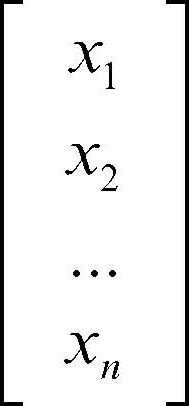
X è il vettore delle incognite

e B il vettore dei termini noti

Data una n-pla approssimata di soluzioni che si indica con

applicando un opportuno metodo iterativo si ottiene una nuova n-pla

Ripetendo l’iterazione si ottiene via via una successione di soluzioni approssimate:

Se la successione di soluzioni converge, cioè se esiste

tale limite è la soluzione del sistema. La prima n-pla può essere approssimata anche grossolanamente, per esempio scegliendo la n-pla nulla, perché, se il sistema è convergente, lo è per qualsiasi serie di valori iniziali: la n-pla, per così dire, si autocorregge durante l’iterazione del procedimento. Il metodo introdotto da C.G. Jacobi è anche detto metodo delle sostituzioni simultanee in quanto consiste appunto nel ricavare x₁ dalla prima equazione, x₂ dalla seconda e così via, ottenendo il seguente sistema:

Quindi, sostituendo nel secondo membro delle equazioni la n-pla iniziale X⁽⁰⁾ (scegliendo, per esempio, tutti i valori nulli) si ha:

La nuova n-pla ottenuta, X⁽¹⁾, si sostituisce nuovamente a secondo membro, ricavando X⁽²⁾ e così via. È necessario porre delle condizioni di arresto all’iterazione, perché è difficile che il metodo porti a ricavare le soluzioni esatte del sistema. Le condizioni di arresto dell’iterazione al k-esimo passo si ottengono quando la differenza tra i valori successivi di ciascun termine della n-pla è sufficientemente piccola:

con j = 1, 2, …, n. Quindi alla k-esima iterazione si deve avere:

Le difficoltà di applicazione del metodo di Jacobi non dipendono dal calcolo, ma dal determinare se la successione delle soluzioni approssimate converga o meno. È difficile dare delle condizioni generali, ma si possono fornire delle condizioni particolari sulla matrice A dei coefficienti:

• condizione necessaria per la convergenza è che tutti gli elementi della diagonale principale di A siano diversi da zero;

• condizione sufficiente è che A sia una matrice a predominanza diagonale, cioè che gli elementi della diagonale principale siano maggiori in valore assoluto della somma dei valori assoluti degli altri elementi della riga corrispondente:

È interessante notare come a volte sia possibile riscrivere ordinatamente le equazioni del sistema, trasformandolo in modo tale che sia soddisfatta la condizione di predominanza diagonale. Tale condizione è però solo sufficiente; possono esserci sistemi che non soddisfano la condizione di predominanza diagonale, ma che ugualmente convergono.