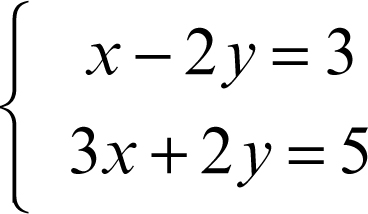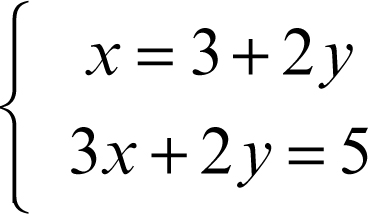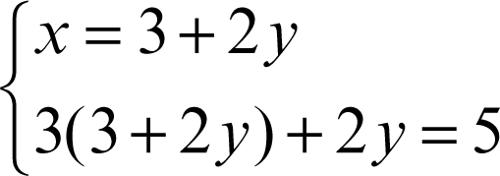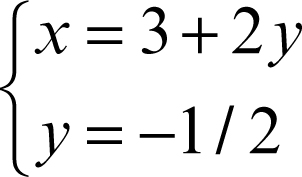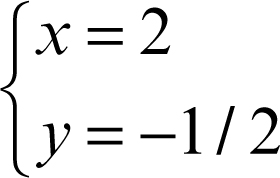sostituzione, metodo di
sostituzione, metodo di
sostituzione, metodo di metodo di risoluzione di un sistema di equazioni. Se le incognite sono x1, …, xn, il metodo consiste nel ricavare da un’arbitraria equazione del sistema (che per semplicità si può supporre essere la prima) il valore dell’incognita x1 (o di una qualsiasi altra) in funzione delle altre incognite del sistema: sostituendo tale espressione all’incognita x1 nelle rimanenti equazioni, l’incognita x1 scompare da tutte le equazioni del sistema tranne che dalla prima. Il sistema può allora essere risolto iterando il procedimento esposto al sistema costituito dalle rimanenti equazioni, ricavando a ogni passo il valore dell’incognita xi rispetto alle incognite successive xi+1, …, xn. Si sarà in questo modo trasformato il sistema iniziale in un sistema equivalente: se il numero delle equazioni è sufficiente e se il sistema ammette soluzione, dall’ultima equazione non banale di tale sistema sarà leggibile il valore dell’ultima incognita; il sistema potrà essere dunque risolto interamente “a cascata”, sostituendo via via nelle equazioni il valore delle incognite precedentemente calcolate. Il metodo è utile soprattutto per risolvere sistemi di equazioni di dimensione bassa.
Per esempio, si consideri il sistema di primo grado in due incognite
Esplicitando l’incognita x dalla prima equazione si ottiene il sistema equivalente:
sostituendo x nella seconda equazione si ottiene il sistema equivalente:
In questo sistema si può calcolare il valore di y dalla seconda equazione, che ora dipende solo da essa:
Sostituendo il valore di y trovato nella prima equazione si può adesso calcolare il valore di x, e il sistema è così risolto:
