Beltrami, modello di

Beltrami, modello di

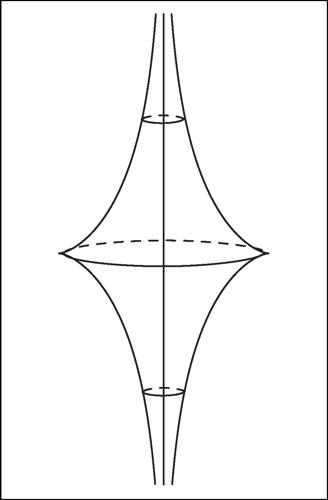
Beltrami, modello di superficie (detta anche pseudosfera di Beltrami) che, reinterpretando opportunamente il concetto di retta come linea di minima distanza, costituisce un modello euclideo di una geometria non euclidea. Tale superficie si ottiene ruotando una particolare curva piana, detta trattrice, intorno al proprio asintoto. Al pari di una superficie sferica ordinaria, essa ha la proprietà di avere curvatura costante, ma tale curvatura, a differenza di quanto accade per la sfera, risulta negativa. Per le sue proprietà, la pseudosfera fu proposta da Beltrami come modello del piano di Lobačevskij. Punti e rette di un piano euclideo corrispondono, sulla pseudosfera, rispettivamente a punti e linee geodetiche. In tal modo, sulla pseudosfera, similmente a quanto avviene nel piano ordinario, un segmento è costituito da un arco di geodetica, per due punti passa una e una sola retta (geodetica), tre punti non allineati (non appartenenti alla stessa geodetica) individuano un triangolo ecc. Avviene tutto esattamente come nel piano euclideo, tranne il fatto che la somma degli angoli interni di un qualsiasi triangolo risulta, in conseguenza della curvatura negativa, minore di un angolo piatto. Ciò equivale ad affermare che, sulla pseudosfera, per un punto P non appartenente a una retta r, passano infinite rette prive di punti comuni con r, cioè infinite parallele a r. Sulla pseudosfera non è perciò valido l’assioma della → parallela e la geometria su tale superficie è una geometria non euclidea, detta geometria iperbolica. Il punto debole del modello di Beltrami risiede nel fatto che esso rappresenta il piano non euclideo solo localmente. Infatti la cuspide della trattrice genera, nella rotazione, una circonferenza fatta di punti singolari così che la pseudosfera è una superficie non regolare e pertanto non può rappresentare interamente un piano.