negazione

negazione

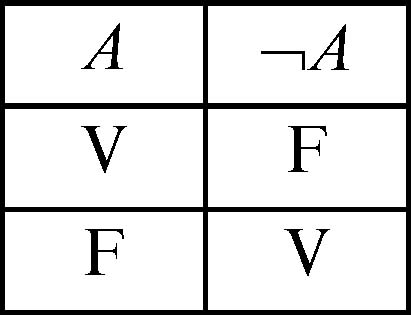
negazione connettivo logico, corrispondente nel linguaggio naturale all’avverbio «non», e indicato con il simbolo ￢ (a volte anche con il simbolo ∼). La negazione di un enunciato A si ottiene premettendo il simbolo ￢ all’enunciato stesso: ￢A (si legge «non A»). Se per esempio A indica l’enunciato «8 è un numero pari», allora ￢A indica l’enunciato «8 non è un numero pari»: se A è vero, come in questo caso, allora ￢A è falso; viceversa, se A è falso, allora ￢A è vero. La tavola di verità del connettivo della negazione è, quindi, la seguente:

Come è evidente dalla tavola, l’enunciato A e la sua negazione ￢A non possono avere lo stesso valore di verità, cioè non possono essere contemporaneamente veri o contemporaneamente falsi; ciò è espresso dal principio di non contraddizione, secondo cui una proposizione non può essere allo stesso tempo vera e falsa. Nella logica classica vale inoltre il principio del terzo escluso secondo il quale, dato un qualsiasi enunciato A, si possono avere solo due possibilità: A è vero oppure A è falso e quindi, in tale caso, è vera la sua negazione ￢A. Da ciò deriva che un enunciato A è logicamente equivalente alla negazione della sua negazione cioè all’enunciato ￢(￢A) (→ doppia negazione; → equivalenza logica). Questa equivalenza corrisponde all’affermazione secondo cui «la doppia negazione afferma» e trova riscontro nel fatto che l’enunciato A ⇔ ￢(￢A) (si legge «A se e solo se non non A») è una tautologia del linguaggio degli enunciati. L’equivalenza fra l’enunciato A e la sua doppia negazione ￢(￢A) è una prerogativa della logica classica, mentre non vale in altre logiche; in particolare nella logica intuizionista, dove la condizione A è considerata più forte della condizione ￢(￢A). Per comprendere questa maggiore forza si consideri un esempio non formalizzato, ma tratto dai ragionamenti d’uso comune: l’affermazione A: «è possibile trovare un motore più efficiente del motore a benzina». In logica intuizionista questa affermazione equivale ad avere a disposizione un motore, come potrebbe essere per esempio quello elettrico, che sia più efficiente del motore a benzina. L’enunciato ￢(￢A) corrisponde invece a «non è vero che è impossibile trovare un motore più efficiente del motore a benzina», affermazione che potrebbe essere sostenuta anche senza avere effettivamente a disposizione il motore in questione. L’effetto della negazione sui connettivi di disgiunzione e congiunzione è evidenziato dalle due leggi di → De Morgan, che possono essere espresse dalle seguenti equivalenze logiche (dove a e b sono due qualsiasi enunciati):

(«non (A o B)» se e solo se «non A e non B»);

(«non (A e B)» se e solo se «non A o non B»).

Nel modello insiemistico del linguaggio degli enunciati la negazione di un enunciato A corrisponde all’insieme complementare dell’insieme di verità dell’enunciato A, dove per insieme di verità di un enunciato si intende l’insieme di quegli elementi per cui l’enunciato è vero.