poliedro
poliedro
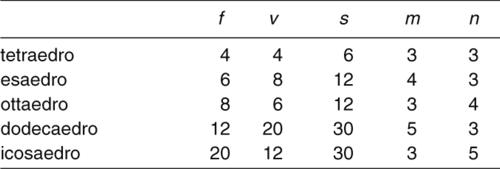
poliedro solido delimitato da un numero finito di poligoni in modo che ogni lato di ciascun poligono sia esattamente comune a due poligoni. I poligoni, i loro lati e i loro vertici sono detti, rispettivamente facce, spigoli e vertici del poliedro. Si suppone che due facce non siano mai complanari, e che ogni vertice appartenga ad almeno tre spigoli. Tra i poliedri più semplici sono da ricordare il → cubo, il → parallelepipedo, il → prisma, la → piramide. Il poliedro con il minor numero di elementi è il → tetraedro, che ha quattro facce triangolari. Si dicono diedri di un poliedro i diedri formati da due facce aventi uno spigolo in comune. Si dicono angoloidi di un poliedro gli angoloidi aventi per vertice un vertice del poliedro e per facce i poligoni che concorrono in quel vertice. Un poliedro tale che il segmento che congiunge due suoi qualsiasi punti gli appartenga interamente è detto poliedro convesso, altrimenti è detto poliedro concavo. Un poliedro convesso può essere definito anche come un poliedro tale che, considerato il piano contenente una sua faccia, tutti i vertici che non appartengono a tale faccia sono in uno stesso semispazio, rispetto al piano considerato. Un poliedro topologicamente equivalente a una sfera è detto poliedro semplice. Per i poliedri semplici vale la relazione di Eulero ƒ + v − s = 2, nella quale ƒ è il numero delle facce, ν il numero dei vertici, s il numero degli spigoli. Un poliedro le cui facce sono poligoni ordinari, ossia non intrecciati, e la cui superficie è bilatera è detto euleriano se soddisfa la relazione di Eulero.
Un poliedro concavo può essere ottenuto con l’operazione geometrica di → stellazione oppure considerando la possibilità di interpenetrazione delle sue facce: in entrambi i casi si ottiene un poliedro stellato che si presenta con alcuni vertici che sono vertici di un angoloide concavo e altri di un angoloide convesso.
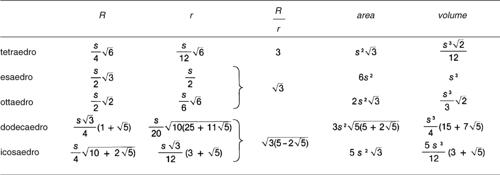
Un poliedro semplice avente per facce poligoni regolari tutti uguali e angoloidi regolari tutti uguali (un angoloide è detto regolare quando ha le facce uguali tra loro e anche i diedri uguali tra loro) è detto poliedro regolare o → solido platonico. Un teorema della geometria stabilisce che esistono solo cinque tipi di poliedri regolari: tetraedro, esaedro o cubo, ottaedro, dodecaedro, icosaedro, le cui facce possono essere solo poligoni con non più di cinque lati, cioè triangoli equilateri (tetraedro, ottaedro e icosaedro), quadrati (esaedro), pentagoni regolari (dodecaedro). Oltre ai cinque poliedri platonici, esistono altri quattro poliedri stellati che sono detti regolari stellati, e sono comunemente riportati come poliedri di Keplero-Poinsot (→ Keplero-Poinsot, poliedro di) per i quali le facce sono poligoni regolari tutti uguali, ma gli angoloidi appartengono a due distinti sistemi di angoloidi uguali, uno formato da angoloidi concavi e l’altro convessi. Un poliedro convesso le cui facce sono poligoni regolari, non necessariamente tutti uguali, e i cui angoloidi sono tutti uguali è detto poliedro archimedeo o poliedro semiregolare (→ solido archimedeo).
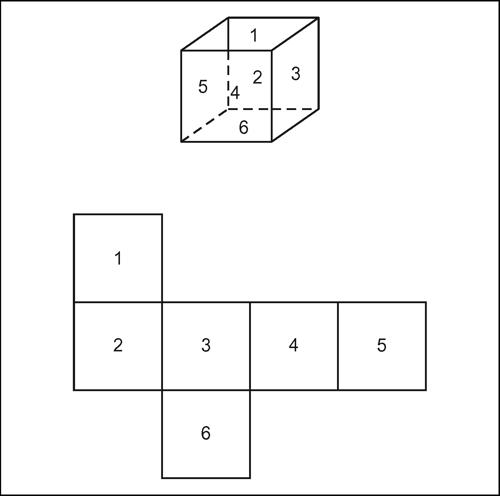
Il volume di un poliedro è la misura della sua estensione nello spazio. In taluni casi esistono formule che permettono di calcolare il volume di un poliedro a partire dalle misure di alcuni suoi elementi. Per esempio, il volume di un parallelepido rettangolo è dato dal prodotto delle misure dei tre spigoli, il volume di una piramide retta è uguale a un terzo del prodotto dell’area della base per l’altezza ecc. Poliedri aventi lo stesso volume sono detti poliedri equiestesi o poliedri equivalenti. L’equiestensione è una relazione di equivalenza nell’insieme dei poliedri. L’equivalenza tra due poliedri può essere stabilita utilizzando, per esempio, il principio di → Cavalieri. A differenza di quanto accade per due poligoni equivalenti, due poliedri equivalenti non sono necessariamente equiscomponibili (→ Dehn, teorema di). Si dice sviluppo di un poliedro sul piano ogni figura piana, connessa, ottenuta separando lungo opportuni spigoli alcune coppie di facce contigue. Viceversa, a partire da uno sviluppo piano, con opportune piegature, è possibile ricostruire un poliedro e tale tecnica è utilizzata per costruirne dei modelli. Ogni poliedro convesso ammette uno sviluppo piano. Possono esistere però differenti sviluppi piani di uno stesso poliedro. Alcuni poliedri possono essere utilizzati per la → tassellazione dello spazio tridimensionale. Poliedri regolari che tassellano lo spazio sono il cubo e il tetraedro regolare.