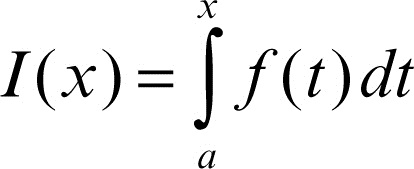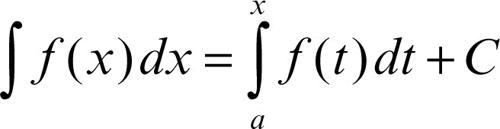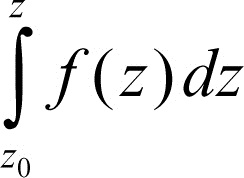funzione, primitive di una
funzione, primitive di una
funzione, primitive di una si dice primitiva di una funzione ƒ(x) in un intervallo [a, b], una funzione F(x) derivabile tale che F′(x) = ƒ(x). Per il teorema fondamentale del calcolo integrale, se per esempio ƒ è continua, una primitiva è data dalla funzione integrale
Per il teorema di → Lagrange, ogni altra primitive ha la forma I(x) + C, con C costante arbitraria. L’insieme di tutte le primitive di una funzione si dice → integrale indefinito di ƒ(x), e si designa con il simbolo
È pertanto
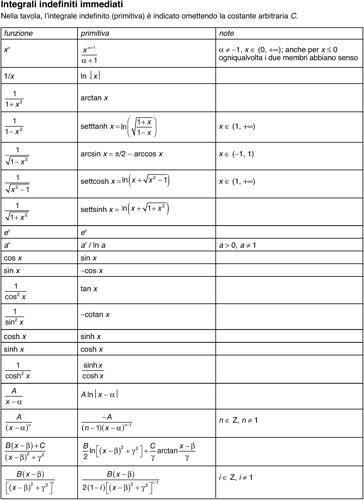
Per i metodi di calcolo delle primitive, si veda la voce → integrazione (e si veda anche la tavola degli integrali indefiniti immediati). Per il caso in cui ƒ non sia continua, ma integrabile in senso generalizzato, o nel senso di integrale di Lebesgue, l’uguaglianza F′ (x) = ƒ(x) vale solo quasi ovunque, e in particolare nei punti di continuità di ƒ(x) (→ integrale improprio).
La primitiva F(z) di una funzione ƒ: C → C è definite formalmente nello stesso modo, ma poiché l’esistenza della derivata F′ (z) implica che F sia una funzione analitica, tale deve essere pure la sua derivata ƒ(z). Supposto dunque che ƒ(z) soddisfi le condizioni di → Cauchy-Riemann, si potrà definire la funzione integrale
con l’avvertenza che l’integrale è in questo caso un integrale di una forma differenziale chiusa, esteso a una linea Γ che congiunga i punti z0 e z. In generale dunque la primitiva sarà una funzione F(z) che risulterà essere funzione polidroma; essa risulta monodroma solo se ƒ ha residuo nullo in tutte le sue singolarità al finito (supposte isolate). Per esempio, la primitiva di 1/z è la funzione polidroma log(z), mentre la primitiva di 1/z 2 è la funzione monodroma −1/z.