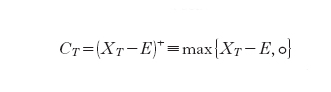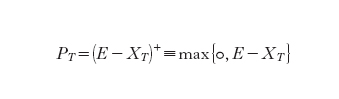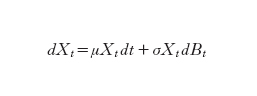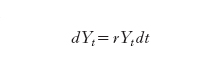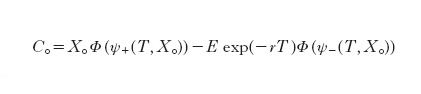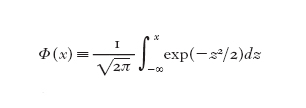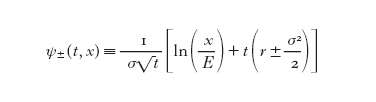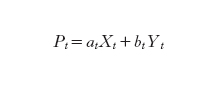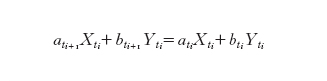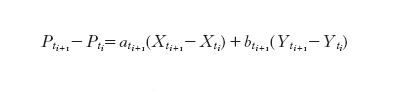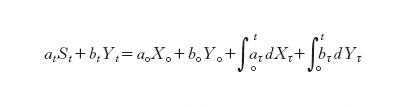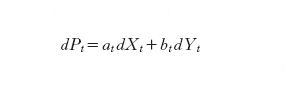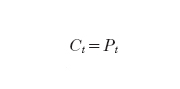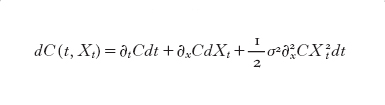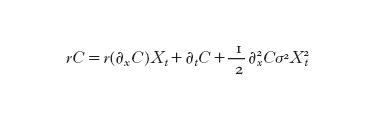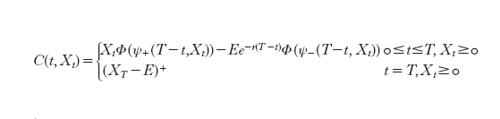Stocastici, processi
Stocastici, processi
(App. V, v, p. 275)
I p. s. hanno assunto sempre di più il ruolo di strumenti euristici anche al di fuori della fisica statistica, il contesto tipico in cui originariamente sono stati studiati per decenni. In particolare, in economia le grandezze che regolano i prezzi sono funzioni aleatorie descrivibili sia in modo 'locale', come innumerevoli sistemi elementari interagenti, sia come macrosistemi: i p. s. sono così divenuti un nucleo stabile delle teorie economiche e della finanza matematica e oggetto di una intensa ricerca che vede coinvolti fisici, matematici, economisti nel tentativo comune di formalizzare e raffinare modelli sempre più realistici degli andamenti del mercato finanziario. *
Processi stocastici in finanza matematica
di Luigi Accardi, Roberto Monte
Nella modellistica matematica di fenomeni economici l'uso di strumenti probabilistici sofisticati, quali le martingale, gli integrali stocastici, le equazioni differenziali stocastiche e le equazioni paraboliche a essi associate, ha una lunga storia la cui origine è in una tesi sottoposta nel 1900 da L. Bachelier all'Académie des sciences di Parigi. Questo lavoro contiene la prima descrizione matematica di quel p. s., noto in fisica col nome di moto browniano, che veniva proposto come modello delle fluttuazioni dei prezzi dei titoli.
Il moto browniano, già osservato nel 1827 e studiato come processo fisico per decenni, venne formalizzato solo intorno al 1905 da A. Einstein e da M. Smoluchowsky, e la teoria matematica fu ampiamente sviluppata a partire dai lavori di P. Levy, N. Wiener, A.N. Kolmogorov e molti altri. In economia, più di cinquant'anni dopo Bachelier, la ricerca di una teoria matematica della valutazione dei prezzi dei titoli con rischio fu portata avanti da P.A. Samuelson e da altri. Il fatto che tali prezzi non possono essere negativi motivò la sostituzione del moto browniano ordinario (o aritmetico) con il moto browniano geometrico. Queste teorie furono ulteriormente sviluppate tra il 1950 e il 1970, ma contenevano elementi ad hoc che lasciavano i loro stessi autori insoddisfatti. Una svolta si ebbe con il lavoro di F. Black e M.S. Scholes, che affrontarono il problema del prezzo delle opzioni.
Un'opzione è un esempio di titolo derivato, ossia di un titolo i cui rendimenti dipendono in qualche modo dai rendimenti di altri titoli. In particolare, con il termine di opzione europea si intende un contratto tra due parti, un titolare (holder) e un garante (writer), che sancisce l'acquisizione di un diritto e l'assunzione di un obbligo. Nel caso di un'opzione europea di acquisto (call option) il titolare, dietro corresponsione di un premio (prime), fa proprio il diritto, ma non l'obbligo, di acquistare dal garante (nel caso analogo di un'opzione europea di vendita - put option - di vendere al garante) un attivo finanziario rischioso, titolo sottostante (underlying risky asset o underlying security) a una scadenza (maturity) e a un prezzo (exercise o strike price) pattuiti all'atto della stipula del contratto. Il garante, in cambio del premio, si fa carico dell'obbligo di soddisfare il titolare. Un'opzione di vendita è quindi assimilabile a un'assicurazione con cui l'assicurato (holder) si garantisce almeno il prezzo d'esercizio e l'assicuratore (writer) incassa un premio per il rischio sopportato. Indicati con X il prezzo del titolo sottostante, con E il prezzo d'esercizio e con T l'istante di scadenza, il detentore di un'opzione d'acquisto sarà interessato a esercitare il proprio diritto solo se risulterà XT−E>0 (per un'opzione di vendita, XT−E⟨0). Pertanto, alla scadenza T, il valore CT di un'opzione europea d'acquisto è quantificato da
mentre il valore PT di un'opzione europea di vendita è quantificato da
.
È allora naturale porsi i seguenti problemi: 1) l'individuazione di una strategia finanziaria di copertura (hedging strategy) che consenta al garante dell'opzione di produrre dal premio incassato una ricchezza che alla scadenza sia almeno pari al valore dell'opzione; 2) la valutazione di un giusto premio (option pricing) che, fissato un prezzo di esercizio, consenta al detentore dell'opzione di realizzare un utile alla scadenza.
Le ipotesi sotto le quali Black e Scholes hanno risolto i problemi succitati sono le seguenti: 1) si considera un'opzione europea d'acquisto (o di vendita); 2) si considera il caso di un solo titolo rischioso e uno solo non rischioso; 3) si suppone che i prezzi del titolo rischioso seguano un modello lognormale (moto browniano geometrico), ossia che il loro valore al tempo t dipenda da quantità costanti, α,σ>0,X₀, e da fattori aleatori, descritti da un moto browniano Bt, secondo la formula Xt=X₀exp(αt+σBt) che equivale all'equazione differenziale stocastica
formula [
1]
con condizione iniziale X₀, essendo μ=α+½σ²; 4) si suppone che i prezzi del titolo non rischioso siano descritti dalla formula Yt=Y₀ert, che equivale all'equazione differenziale ordinaria
formula [
2]
con condizione iniziale Y₀, e corrisponde a un investimento iniziale Y₀>0, costantemente reinvestito al tasso di interesse istantaneo r>0 costante nel tempo; 5) si suppone che valga l'ipotesi di non arbitraggio; 6) si suppone che non vi siano costi di transizione o tasse.
Sotto queste ipotesi, il prezzo dell'opzione di acquisto è dato dalla seguente formula di Black e Scholes:
formula [
3]
dove Φ è la funzione di distribuzione della legge normale
e dove le funzioni ψ± sono esplicitamente date da
L'interesse di questa formula sta nel fatto che in essa il prezzo dell'opzione risulta indipendente dalla propensione al rischio dell'agente economico, che è difficile da valutare quantitativamente e che era presente nei precedenti approcci al problema.
L'idea che ha consentito questo progresso è l'introduzione del principio del pricing by simulation, che permette di costruire un portafoglio equivalente all'opzione e contenente solo opportune quantità del titolo rischioso sottostante l'opzione e del titolo non rischioso. Nelle notazioni introdotte sopra, chiamiamo strategia commerciale (trading strategy) una coppia di funzioni (at, bt) dove at e bt sono rispettivamente la quantità del titolo rischioso e del titolo non rischioso presenti nel portafoglio. Il valore del portafoglio è allora dato da
formula [
4]
La strategia (a, b) è detta autofinanziante (self-financing) se l'investitore, una volta noti i valori Xti e Yti, riaggiusta il suo portafoglio, facendolo passare dalla composizione (ati, bti) alla composizione (ati₊₁, bti₊₁), reinvestendo il valore totale del portafoglio senza togliere o immettere capitale. Ciò equivale all'uguaglianza:
formula [
5]
che include anche l'ipotesi di assenza di costi di transazione. Usando la [4] e la [5] il guadagno (netto), dovuto alla variazione del valore dei titoli tra gli istanti ti e ti₊₁, si esprime mediante la differenza
Ne segue che una strategia è autofinanziante se le variazioni del valore del portafoglio sono unicamente dovute alla variazione del valore dei titoli. Nel caso di tempo continuo un semplice passaggio al limite mostra che la condizione di autofinanziamento si esprime nella forma
per ogni t≥0. Osserviamo inoltre che, essendo i prezzi funzioni aleatorie (più precisamente p. s.), tali dovranno essere anche le strategie.
La condizione di autofinanziamento implica che il valore del portafoglio soddisfi l'equazione differenziale stocastica
formula [
6]
La proposta di Black e Scholes è di scegliere la strategia d'investimento in modo tale da riprodurre all'istante finale T il valore CT dell'opzione, strategia di copertura (hedging strategy). A questo punto entra in gioco l'ipotesi di non arbitraggio attraverso un teorema che asserisce che il sussistere di tale ipotesi comporta da parte di una strategia commerciale di copertura la necessità di riprodurre il valore Ct dell'opzione a ogni istante 0≤t≤T. Ciò consente di scrivere per il prezzo dell'opzione l'equazione
formula [
7]
per ogni 0≤t≤T. D'altra parte, se pensiamo al prezzo dell'opzione come a una funzione (incognita) C(t,Xt) del tempo e del prezzo del titolo rischioso, applicando la formula di Itō, si vede che questa funzione deve soddisfare l'equazione differenziale stocastica
formula [
8]
Dall'equazione [7] scritta in forma differenziale, tenendo conto delle [6] e [8], nonché delle [1] e [2], uguagliando separatamente tra loro i coefficienti del differenziale deterministico dt e di quello stocastico dBt, semplici calcoli mostrano che C deve soddisfare l'equazione parabolica
formula
[9]
completata con la condizione finale CT=(XT−E)⁺, che esprime il valore dell'opzione alla maturità T. Abbiamo quindi che il prezzo dell'opzione soddisfa una tipica equazione parabolica backward di Kolmogorov, il cui valore finale è noto (anche se soggetto ad aleatorietà) e il cui valore iniziale, incognito, rappresenta l'investimento iniziale che il writer deve fare per costituire il portafoglio autofinanziante che, al tempo T, riprodurrà il valore dell'opzione. È ragionevole quindi scegliere tale valore iniziale come ammontare del premio che l'holder deve pagare al writer per godere del diritto di opzione. Dato che l'equazione [9] è semplice, essa si può risolvere esplicitamente e la soluzione è
Il prezzo dell'opzione è quindi valore di questa funzione al tempo t=0, cioè la [3].
L'influenza della formula di Black-Scholes è stata enorme: migliaia di agenti finanziari e investitori la usano quotidianamente e le idee usate per la sua deduzione sono state estese oltre l'ambito puramente finanziario, includendo per es. la valutazione di contratti assicurativi o di progetti di investimento o di cespiti di tipo più generale. Data la sua importanza, una vasta letteratura è stata sviluppata nel tentativo di ampliarne la portata indebolendone le ipotesi e svincolandole, per quanto possibile, dal modello molto specifico definito dalle ipotesi 1)-6) elencate sopra. Il contenuto matematico dell'ipotesi di non arbitraggio è stato individuato nell'esistenza di una misura di probabilità rispetto alla quale i prezzi di tutti i titoli rischiosi associati all'opzione risultino martingale (misura martingala equivalente), mentre l'ipotesi di completezza del mercato, automaticamente soddisfatta nell'originale modello di Black e Scholes, in genere viene fatta corrispondere all'unicità della misura martingala equivalente (anche se su questo punto il dibattito teorico non si può ancora considerare concluso). Introducendo una terminologia usata in fisica, si può dire che l'ipotesi di non arbitraggio è una condizione di equilibrio, nel senso che, come i sistemi fisici isolati tendono all'equilibrio termodinamico, così un mercato in condizioni normali tenderà a utilizzare le eventuali finestre speculative facendole scomparire. Usando la stessa analogia si può dire che la condizione di completezza di un mercato è analoga a quella di assenza di transizioni di fase in un sistema fisico, nel senso che, come per la maggior parte delle temperature una condizione di equilibrio è compatibile con una sola fase di un sistema fisico, così ci si attende che in condizioni di non arbitraggio nella maggior parte dei casi i prezzi delle opzioni risultino univocamente definiti. D'altra parte, come l'acqua, in opportune condizioni di pressione e di temperatura, può trovarsi in più fasi, così non è escluso che la condizione di assenza di arbitraggio sia insufficiente da sola per una determinazione univoca dei prezzi. Su questi problemi è oggi in atto un'intensa attività di ricerca che coinvolge un numero di ricercatori sempre maggiore. L'attribuzione del premio Nobel per l'economia nel 1997 a R.C. Merton e a M.S. Scholes (F. Black è morto nel 1995 a meno di 60 anni) segna una data storica non solo nell'economia ma anche nella statistica. Per la prima volta, infatti, tecniche matematiche sofisticate (quali la teoria del moto browniano, le equazioni differenziali stocastiche, la formula di Itō) intervengono in economia non a livello di astratta speculazione teorica, ma nell'uso quotidiano di migliaia di operatori economici.
bibliografia
L. Bachelier, Théorie de la spéculation, in Annales scientifiques de l'École normale supérieure III, 1900, pp. 21-88.
K. Arrow, Le rôle des valeurs boursières pour la répartition la meilleure des risques, in Économétrie, 1952, pp. 41-47.
P.A. Samuelson, Rational theory of warrant pricing, in The random character of stock market prices, ed. P.H. Cootner, Cambridge (Mass.) 1964.
W. Sharpe, Capital assets prices. A theory of market equilibrium under conditions of risk, in Journal of finance, 1964, pp. 425-42.
R. Merton, Lifetime portfolio selection under uncertainity. The continuous time case, in Review of economics and statistics, 1969, pp. 247-57.
R. Merton, Optimum consumption and portfolio rules in a continuous time model, in Journal of economic theory, 1971, pp. 373-413 (Erratum 6, 1973, pp. 213-14).
F. Black, M. Scholes, The pricing of options and corporate liabilities, in Journal of political economy, 1973, pp. 637-54.
R. Merton, An intertemporal capital asset pricing model, in Econometrica, 1973, pp. 867-88.
R. Merton, The theory of rational option pricing, in Bell journal of economics and management science, 1973, pp. 141-83.
M. Rubinstein, The valuations of uncertain income streams and the pricing of options, in Bell journal of economics, 1976, pp. 407-25.
I. Karatzas, S. Shreve, Methods of mathematical finance, New York 1985.
L. Accardi, V. Mastropietro, Uniqueness of the prices in incomplete markets, in Chubu Forum in mathematics, 1988, 4, pp. 27-38.
E. Fama, Efficient capital markets II, in Journal of finance, 1991, pp. 1575-618.
R. Barsky, B. De Long, Why does the stock market fluctuate?, in Quarterly journal of economics, 1993, pp. 291-311.
A. Timmermann, How learning in financial markets generates excess volatility and predictability in stock prices, in Quarterly journal of economics, 1993, pp. 135-45.
D. Duffie, Dynamic asset pricing theory, Princeton 1996; E. Fama, Market efficiency, long-term returns, and behavioural finance, in Journal of financial economics, 1998, pp. 283-306.