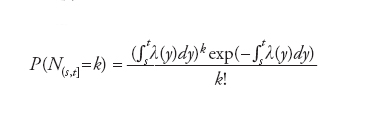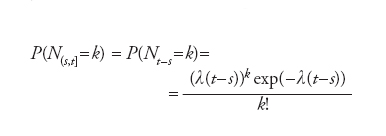processo stocastico di Poisson
processo stocastico di Poisson
Un processo di Poisson (dal nome del suo scopritore Siméon-Denis Poisson) può essere visto come un processo di conteggio indicizzato dal tempo: dato un intervallo di tempo (s,t], N(s,t]=Nt−Ns conta il numero di eventi occorsi in (s,t]. Nella sua forma più conosciuta, è caratterizzato dalle seguenti proprietà: (a) N è un processo di conteggio, ossia N(s,t] assume sempre valori interi non negativi; (b) N è un processo a incrementi indipendenti; (c) esiste una funzione non negativa λ, chiamata intensità del processo, sufficientemente regolare e limitata, tale che
Qualora l’intensità λ sia costante (λ>0), il processo di Poisson è detto omogeneo: l’ultima probabilità diventa
ossia la legge del numero del numero di eventi occorsi in (s,t] è una Poisson il cui parametro dipende dalla sola lunghezza dell’intervallo.