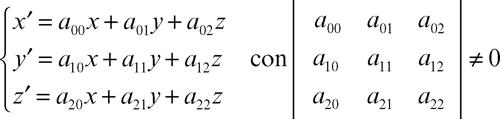proiettivita

proiettivita

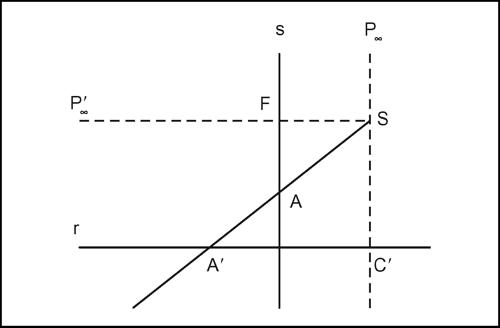
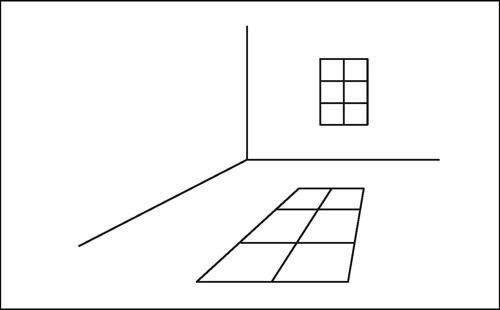
proiettività in geometria, corrispondenza biunivoca in sé dei punti di uno spazio proiettivo ottenuta come composizione di operazioni di proiezione e sezione (→ geometria proiettiva). Può essere definita anche come una → omografia tra due spazi sovrapposti. La proiettività è una trasformazione geometrica che conserva l’allineamento tra punti e ha come invariante il birapporto di quattro punti allineati (più in generale il birapporto di quattro elementi appartenenti a una forma di prima specie). In particolare una proiettività trasforma un gruppo armonico o quaterna armonica in un gruppo armonico e, viceversa, ogni corrispondenza biunivoca tra due forme geometriche di prima specie (ossia retta punteggiata, fascio di rette e fascio di piani) che trasforma gruppi armonici in gruppi armonici è ottenibile con operazioni di proiezione e sezione, cioè risulta una proiettività. Quando applicando a una forma di prima specie più proiezioni e sezioni si ritorna allo stesso sostegno, ossia stessa retta o stesso piano, si dice che le due forme sono sovrapposte (per esempio, due punteggiate proiettive sovrapposte su una medesima retta di sostegno). Due figure che si corrispondono in una proiettività sono dette figure proiettivamente equivalenti. Di norma una proiettività non mantiene né la forma, né le dimensioni di una figura, né il parallelismo tra piani e rette. In una proiettività tra due forme aventi entrambe per sostegno due rette oppure due piani si chiama elemento unito l’elemento necessariamente comune alle due forme il quale, pensato come appartenente a una delle due forme, abbia sé stesso come corrispondente nell’altra. Particolari casi di proiettività sono: l’identità, corrispondenza tra forme di prima specie sovrapposte in cui a ogni elemento corrisponde l’elemento stesso, e la → prospettività, proiettività che sussiste per esempio tra due punteggiate complanari non sovrapposte considerate come sezioni di uno stesso fascio di rette. Quando non si tratti d’identità, una proiettività può avere nessuno, uno o due elementi uniti e si dirà rispettivamente ellittica, parabolica o iperbolica. In quest’ultimo caso il birapporto dei due elementi uniti e di due qualsiasi elementi tra loro corrispondenti è costante e prende il nome di caratteristica o invariante assoluto della proiettività. Si dice proiettività involutoria o più semplicemente involuzione una proiettività tra due forme il cui quadrato è l’identità, cioè tale che il trasformato del trasformato di un qualsiasi elemento coincide con l’elemento stesso. Le locuzioni proiettività o trasformazione proiettiva sono a volte identificate con il termine omografia, a volte distinte da esso. Secondo il primo orientamento si usa definire omografia una proiettività in cui si corrispondono elementi dello stesso nome, mentre si definisce → reciprocità una proiettività in cui si corrispondono elementi di nome diverso. Un esempio di proiettività nello spazio ordinario tridimensionale è la corrispondenza tra i punti di un reticolato, per esempio, il telaio di una finestra e i punti della sua ombra sul pavimento, prodotta da una sorgente luminosa puntiforme S (→ proiezione centrale). Tale proiettività è definita mediante una prospettività, di centro S, tra il piano contenente la finestra e il piano contenente la sua ombra. È questa una corrispondenza proiettiva tra piani che può essere schematizzata attraverso una sezione in cui una retta s è la traccia della parete contenente la finestra, la retta r è la traccia del pavimento, il punto A′ è l’immagine (ombra) del punto A proiettato dal centro di proiezione S (sorgente luminosa). Per rendere biunivoca senza eccezioni la corrispondenza tra s e r occorre aggiungere a r il punto improprio P′_∞, in modo che il punto di fuga F abbia il suo trasformato proiettivo e occorre aggiungere a s il punto improprio P_∞ in modo che C′ risulti il trasformato di un punto (vedi figura):

Il completamento con gli elementi all’infinito comporta la necessità di utilizzare coordinate omogenee per esprimere analiticamente una proiettività. Una trasformazione proiettiva nel piano, dotato di un sistema di coordinate omogenee, ha equazioni:

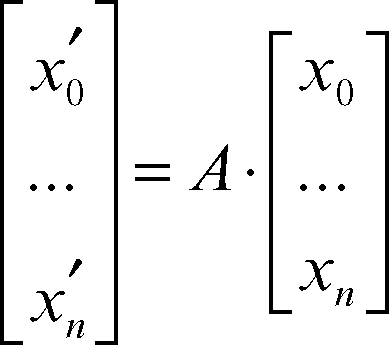
In generale, in uno spazio proiettivo n-dimensionale, le equazioni di una proiettività sono del tipo:

in cui A è una matrice quadrata di ordine n + 1, non degenere. In uno spazio proiettivo n-dimensionale una proiettività è univocamente individuata assegnando n + 2 punti arbitrari, tali che n + 1 di essi, scelti arbitrariamente, non appartengano a uno stesso iperpiano, e i loro n + 2 punti corrispondenti, anch’essi soggetti alla stessa condizione (→ Staudt, teorema di). Ciò vuol dire che, fissati nel piano quattro punti (A, B, C, D) a tre a tre non allineati, e quattro punti (A′, B′, C′, D′ ), a tre a tre non allineati, esiste una e una sola proiettività che trasforma A in A′, B in B′, C in C′, D in D′. Ne segue che tutti i quadrilateri sono proiettivamente equivalenti. Si definisce potenza di una proiettività tra due punteggiate, che non sia una similitudine, il prodotto, costante, delle distanze di due punti corrispondenti dai punti di fuga delle rispettive punteggiate (→ proiettività omologica).

Proiettività tra due forme di seconda specie o tra due forme di terza specie è una corrispondenza biunivoca tra gli elementi delle due forme che muta ogni forma di prima specie in una forma di prima specie e che definisce tra due forme di prima specie corrispondenti una proiettività.