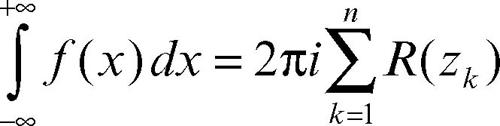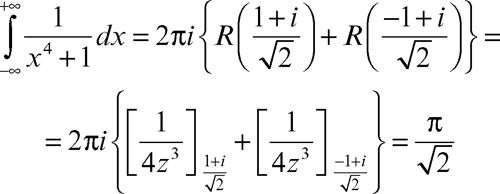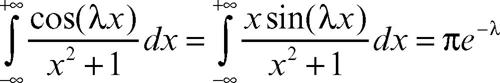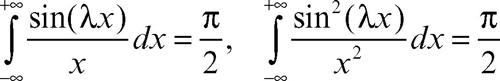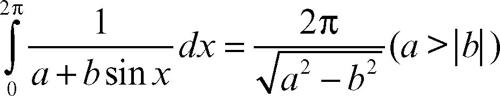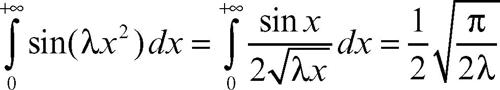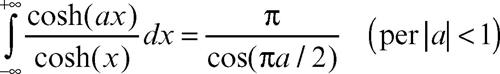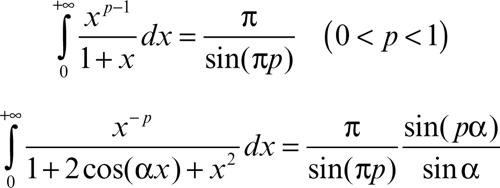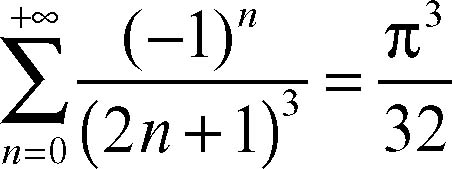residuo

residuo

residuo termine che assume significati diversi a seconda del contesto. Talvolta, in un contesto aritmetico e algebrico è utilizzato al posto del più comune → resto.

☐ In statistica, è così detto ognuno degli scarti e_i = y_i − ƒ(x_i) tra un valore y_i osservato e il valore teorico ƒ(x_i) ottenuto da una funzione di regressione semplice. Il metodo dei minimi quadrati per determinare la particolare funzione di regressione mira a minimizzare la somma dei quadrati di tali scarti, ma essi, in generale, non sono nulli.

☐ In analisi matematica, indica un concetto alla base di una tecnica estremamente potente e versatile per il calcolo di integrali definiti di funzioni analitiche. Il residuo R(z₀) di una funzione analitica in un suo punto singolare isolato z₀ è il coefficiente c₋₁ del termine (z − z₀)⁻¹ del suo sviluppo in serie di → Laurent. Dalla formula generale dei coefficienti si ricava che

dove σ è un ciclo (percorso in verso antiorario) che contorna il solo punto singolare z₀.

Residuo all’infinito è invece

in cui σ è ancora un ciclo antiorario che non lascia all’esterno alcun altro punto singolare. Può tuttavia essere R(z_∞) ≠ 0 anche se z_∞ non è un punto singolare per ƒ(z), in quanto il coefficiente c₋₁ appartiene alla parte olomorfa di ƒ all’infinito.

Il calcolo di un residuo è particolarmente semplice nel caso in cui ƒ(z) ammette un polo semplice in z₀: scritta infatti ƒ(z) come rapporto A(z)/B(z), con A(z₀) ≠ 0, B(z₀) = 0, ma B′ (z₀) ≠ 0, risulta R(z₀) = A(z₀)/B′ (z₀). Più in generale, se ƒ(z) = A(z)/B(z), con A(z₀) ≠ 0, B(z₀) = B′ (z₀) = ... = B⁽ⁿ⁾(z₀) = 0, ma B⁽ⁿ⁾(z₀) ≠ 0, per cui z₀ è un polo di ordine n per ƒ, posto B(z) = (z − z₀)ⁿB_n(z), risulta

Il teorema dei residui afferma che dato un ciclo σ al cui interno vi sia solo un numero finito di singolarità z_k risulta

Se invece vi è un numero finito di singolarità all’esterno di σ, risulta

Se ƒ ammette in totale un numero finito di singolarità, valgono entrambe le formule e di conseguenza la somma di tutti i suoi residui è nulla.

Per le applicazioni si considerano cicli di forma particolare, per esempio il ciclo σ formato dall’unione del segmento [−R, R] dell’asse reale e della semicirconferenza σ_R = {z : |z| = R, 0 ≤ arg(z) ≤ π}, per poi passare al limite per R → ∞. Si dimostra allora che se z_k sono i poli di ƒ(z) nel semipiano Im(z) > 0, e se (almeno per R > R₀):

• su σ_R risulta

con k > 1 si ha

• su σ_R risulta

con k > 0 e se λ > 0 si ha

dove R(z_k) è il residuo di eⁱλ^z ƒ(z) in z = z_k.

Questi risultati si applicano in particolare al caso di una funzione razionale ƒ(z) = A(z)/B(z), con A e B polinomi, grado(B) ≥ (2 + grado(A)) e B ≠ 0 sull’asse reale. Per esempio:

e, per λ > 0:

e, con calcoli più semplici:

Con qualche modifica del circuito indicato si ottengono risultati come

Usando una circonferenza con centro nell’origine si ottengono direttamente integrali di funzioni razionali di seno e coseno, come

mentre integrando su un settore di ampiezza π/4 si ricavano gli integrali di → Fresnel

(identici valori per il coseno).

Se si utilizza un opportuno rettangolo con lati paralleli agli assi si ottiene

Il metodo si può adattare al caso di funzioni polidrome, ottenendo risultati come

(0 < p < 1, 0 < |α| < π).

Infine, si possono ottenere, sotto ipotesi molto poco restrittive, somme di serie (→ serie bilatera) con le seguenti regole:

• somma dei residui di − πcot(πz)ƒ(z) nei poli di ƒ(z):

• somma dei residui di − πcsc(πz)ƒ(z) nei poli di ƒ(z):

• somma dei residui di π tan(πz)ƒ(z) nei poli di ƒ(z):

• somma dei residui di π sec(πz)ƒ(z) nei poli di ƒ(z):

Per esempio, se

i poli sono ±ai; il residuo di −πcot(πz)ƒ(z) in ai vale

e lo stesso valore si ha in −ai, per cui sommando si ha

da cui anche, spezzando la serie,

Passando al limite per a → 0, anche se con passaggi non banali, si risolve la forma indeterminata ∞ − ∞ e si ricava

Se ƒ(z) = 1/z ³ si calcola