formula

Enciclopedia on line

Chimica Notazione che utilizza simboli e indici per dare informazioni relative alla composizione atomica e alla struttura di una molecola. Infatti a seconda del grado di dettaglio utilizzato è possibile [...] sapere quali atomi sono presenti, i loro rapporti numerici e quali sono le relazioni topologiche e spaziali degli atomi costituenti la molecola stessa. Le più semplici sono le f. brute che indicano il numero degli atomi dei vari elementi che ... Leggi Tutto

CATEGORIA: CHIMICA GENERALE – MINERALOGIA – LOGICA MATEMATICA – TRIGONOMETRIA – DIRITTO CIVILE – STORIA E FILOSOFIA DEL DIRITTO – PRATICHE RITUALI E LITURGICHE

TAGS: RETICOLO CRISTALLINO – ETÀ DEL PRINCIPATO – LOGICA MATEMATICA – LEGIS ACTIONES – DIRITTO CIVILE

treccia

Enciclopedia on line

treccia Gruppo di tre ciocche di capelli lunghi che vengono tessute insieme passando alternatamente l’una sopra le altre così da riunirle in unico elemento dalla caratteristica forma ondulata; più genericamente, [...] di nastri, o strisce di cuoio, paglia o altri materiali, intrecciato per vari usi. In matematica, figura avente opportune proprietà topologiche. Su un telaio rettangolare si tendano più fili paralleli a due lati e con gli estremi sugli altri due; se ... Leggi Tutto

CATEGORIA: GEOMETRIA

TAGS: MATEMATICA

Geometria

Enciclopedia Italiana - VI Appendice (2000)

Geometria Ryoichi Kobayashi e Luigi Ambrosio Giovanni Bellettini (XVI, p. 623; App. III, i, p. 724; IV, ii, p. 39; V, ii, p. 391) Numerose voci dell'Enciclopedia Italiana trattano i vari oggetti e [...] del teorema dell'indice di Atiyah-Singer nella g. moderna. Esso appare in molti altri settori della ricerca, non solo nella parte topologica della g. ma anche in g. algebrica (il teorema di Riemann-Roch è un caso speciale del teorema di Atiyah-Singer ... Leggi Tutto

CATEGORIA: GEOMETRIA

TAGS: ACCADEMIA NAZIONALE DELLE SCIENZE DETTA DEI XL – EQUAZIONE DIFFERENZIALE ORDINARIA – SCUOLA NORMALE SUPERIORE DI PISA – CARATTERISTICA DI EULERO – FUNZIONI DIFFERENZIABILI

Nodi e fisica

Enciclopedia del Novecento II Supplemento (1998)

Nodi e fisica Louis H. Kauffman Sommario: 1. Introduzione. 2. Come fissare un nodo: le mosse di Reidemeister. 3. Invarianti di nodi e links: un primo passo. 4. Il polinomio di Jones. 5. Il polinomio [...] con il calcolo di bracket e f-polinomio per il nodo a trifoglio destrogiro T, il cui risultato dimostra che T non è topologicamente equivalente alla sua immagine speculare T*. Poiché l'immagine speculare di un nodo o link si ottiene, a partire da un ... Leggi Tutto

CATEGORIA: FISICA MATEMATICA – MECCANICA QUANTISTICA – GEOMETRIA

TAGS: TEORIA QUANTISTICA DEI CAMPI – FILOSOFIA DELLA MATEMATICA – EQUAZIONE DI SCHRÖDINGER – CALCOLO DELLE VARIAZIONI – RELAZIONE DI EQUIVALENZA

omeomorfismo

Dizionario delle Scienze Fisiche (1996)

omeomorfismo omeomorfismo [Der. di omeomorfo] [ALG] Corrispondenza biunivoca e bicontinua tra due spazi topologici, tale cioè che a ogni punto di uno corrisponda uno e un solo punto dell'altro (corrispondenza [...] dei punti di I (corrispondenza bicontinua); tali spazi (spazi omeomorfi) sono identici tra loro per quanto riguarda le proprietà topologiche; sono omeomorfe, per es., le curve che per deformazione continua siano riducibili l'una all'altra e, in ... Leggi Tutto

CATEGORIA: FISICA DEI SOLIDI – FISICA MATEMATICA – ALGEBRA

SMALE, Stephen

Enciclopedia Italiana - IV Appendice (1981)

SMALE, Stephen Matematico statunitense, nato a Flint (Michigan) il 15 luglio 1930. Dal 1961 professore alla Columbia University a New York e dal 1964 in quella di Berkeley. Per i suoi lavori di topologia [...] Veblen dell'American mathematical society. Si è anche interessato di equazioni differenziali utilizzando il complesso delle sue conoscenze topologiche; questa tecnica è nota col nome di "analisi globale". Ha studiato inoltre la teoria qualitativa dei ... Leggi Tutto

TAGS: EQUAZIONI DIFFERENZIALI – COLUMBIA UNIVERSITY – MATEMATICI – TOPOLOGIA – NEW YORK

Haar, Alfred

Enciclopedia on line

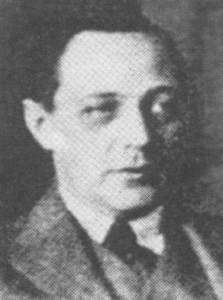Matematico ungherese (Budapest 1885 - Szeged 1933), allievo di D. Hilbert, prof. di fisica-matematica a Kolozsvár (1912) e quindi (dal 1920) di matematica a Szeged. I suoi contributi scientifici vanno [...] L. S. Pontrjagin la soluzione, per i gruppi compatti, del celebre "5º problema di Hilbert" che consisteva nel caratterizzare i gruppi di Lie mediante proprietà topologiche. Insieme con F. Riesz fondò (1922) la rivista Acta Scientiarum Mathematicarum. ... Leggi Tutto

CATEGORIA: BIOGRAFIE

TAGS: CALCOLO DELLE VARIAZIONI – EQUAZIONI DIFFERENZIALI – MISURA DI HAAR – GRUPPI DI LIE – MATEMATICA

La seconda rivoluzione scientifica: matematica e logica. La topologia algebrica all'inizio del XX secolo

Storia della Scienza (2004)

La seconda rivoluzione scientifica: matematica e logica. La topologia algebrica all'inizio del XX secolo John McCleary La topologia algebrica all'inizio del XX secolo Le radici della topologia algebrica [...] V; i numeri della successione P1,P2,…,Pm−1 sono i numeri di Betti di V. Nell'annunciare le proprie ricerche di topologia, nel 1892 Poincaré sottolineava che i numeri di Betti non sono sufficienti a distinguere le varietà e dava infatti un esempio di ... Leggi Tutto

CATEGORIA: GEOMETRIA

omologia

Dizionario delle Scienze Fisiche (1996)

omologia omologìa [Der. del gr. homolog✄ía, da homólogos "omologo"] [ALG] Particolare omografia (propr. o. piana) tra due piani coincidenti che ammette una retta di punti uniti (asse dell'o.) e, dualmente, [...] cui è definito il gruppo di omologia. ◆ [ALG] Teoria dell'o.: parte della topologia algebrica che si propone di esprimere proprietà geometriche e caratteri topologici di una varietà mediante gruppi abeliani (gruppi di o.), uno per ogni dimensione: v ... Leggi Tutto

CATEGORIA: ALGEBRA

nodo

Enciclopedia on line

Anatomia N. del seno (o n. seno-atriale) Formazione anatomica situata nell’atrio destro del cuore, in corrispondenza dello sbocco della vena cava superiore, importante nella regolazione del ritmo cardiaco. Astronomia Per [...] fatto che c1=c′1, c2≠c′2; infine, l’oscnodo dal fatto che c1=c′1, c2=c′2. Teoria dei nodi In topologia, studia le proprietà geometriche, in particolare i gruppi di omotopia dell’insieme complementare in R3, di un n. o circuito annodato, ossia di una ... Leggi Tutto

CATEGORIA: CORPI CELESTI – ANTROPOLOGIA FISICA – BIOINGEGNERIA – EMBRIOLOGIA – FISICA MATEMATICA – METEOROLOGIA – GEOMETRIA – ANATOMIA – STRUMENTI E TECNOLOGIA APPLICATA

TAGS: TEORIA QUANTISTICA DEI CAMPI – SCIENZA DELLE COSTRUZIONI – RELAZIONE DI EQUIVALENZA – FUNZIONE DI PARTIZIONE – MECCANICA QUANTISTICA