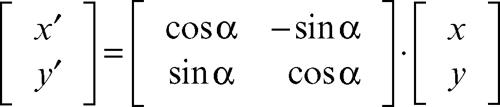rotazione

rotazione

rotazione nella geometria del piano, fissato nel piano un punto O (centro della rotazione) e un angolo di rotazione α (assegnato in ampiezza e verso), è la trasformazione che a ogni punto P(x, y) del piano associa il punto P′ (x′, y′ ) tale che OP′ = OP e inoltre PÔP′ = α. La trasformazione così definita è una isometria diretta le cui equazioni, nel caso in cui il centro di rotazione sia l’origine del riferimento, sono

Tutte le rotazioni con uno stesso centro formano un gruppo commutativo. Una rotazione nel piano con α = π è una → simmetria centrale. Ogni rotazione è individuata dal centro, dall’ampiezza e dal verso. La rotazione di ampiezza nulla è l’identità, quella di ampiezza π si dice opposizione o semigiro. Nella geometria dello spazio, fissata nello spazio una retta s e un angolo α (assegnato in grandezza e verso), si definisce rotazione di asse s e ampiezza α la trasformazione che a ogni punto P del piano associa il punto P′ ottenuto da P facendo ruotare il piano contenente P e s di un angolo α. Una rotazione nello spazio con α = π è una → simmetria assiale. Le rotazioni con uno stesso asse formano un gruppo commutativo. La geometria solida, o stereometria, studia le figure di rotazione, e precisamente le superfici di rotazione e i solidi di rotazione.