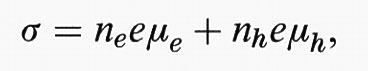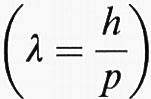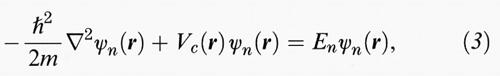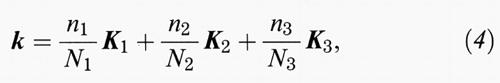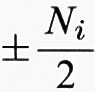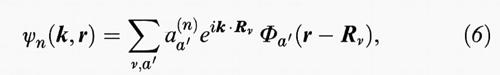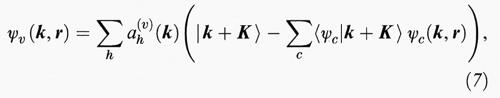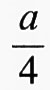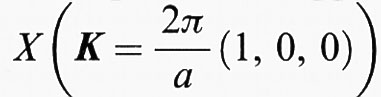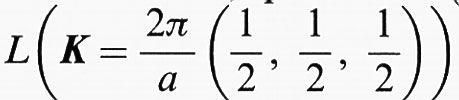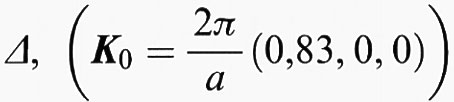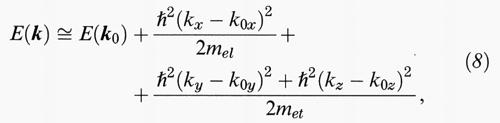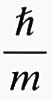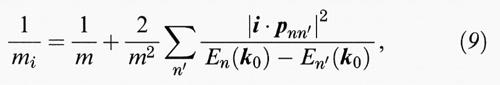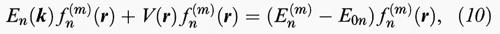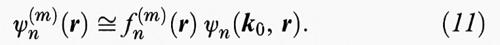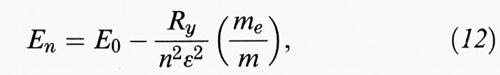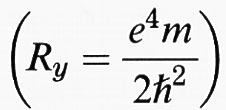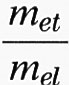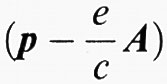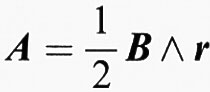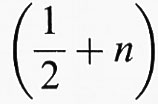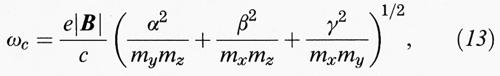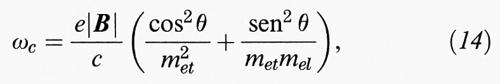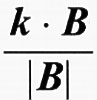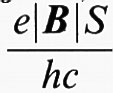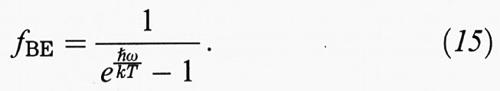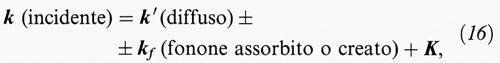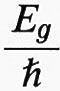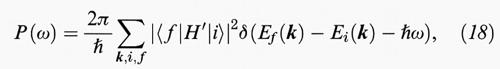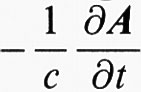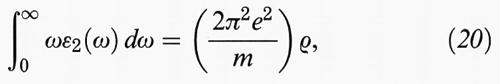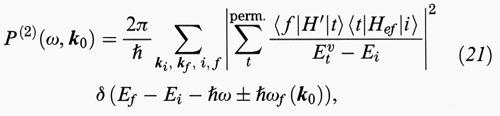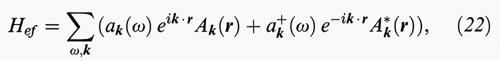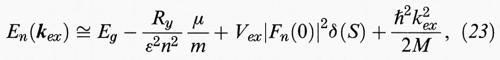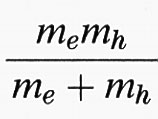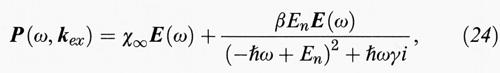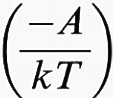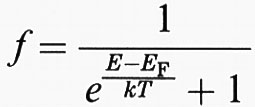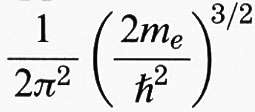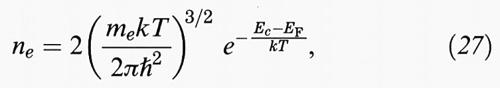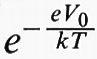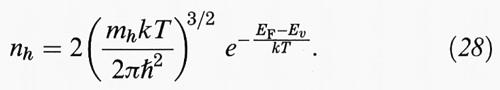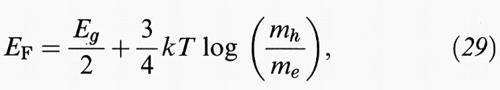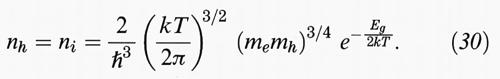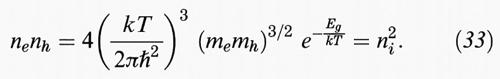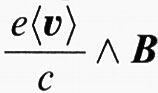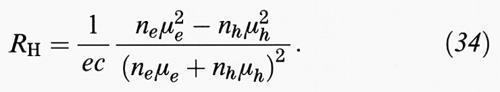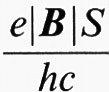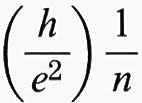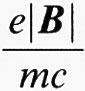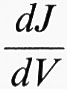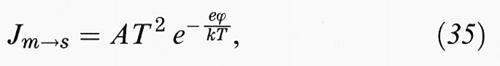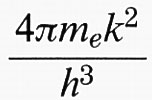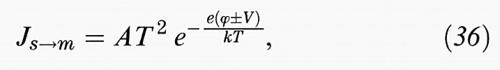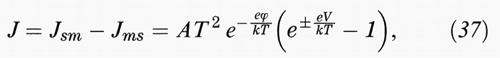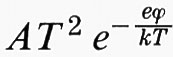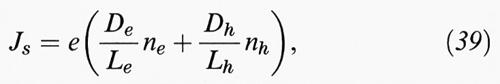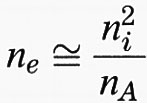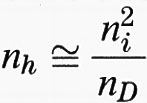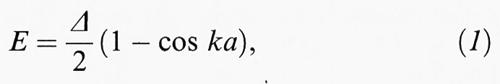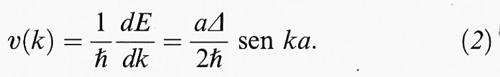Semiconduttori
Semiconduttori
Proprietà generali, di Franco Bassani
Superreticoli e microstrutture artificiali, di Federico Capasso
Proprietà generali di Franco Bassani
Sommario: 1. Introduzione e notizie storiche. 2. Teoria elettronica. 3. Bande di energia dei semiconduttori elementari e binari. 4. Stati localizzati, impurezze, livelli magnetici. 5. Stati vibrazionali: i fononi. 6. Proprietà ottiche: a) transizioni interbanda dirette; b) transizioni indirette; c) eccitoni diretti e indiretti; d) polaritoni; e) spettri di impurezze; f) luminescenza; g) effetti ottici non lineari. 7. Conducibilità elettrica e mobilità. 8. Numero di portatori, masse efficaci, proprietà statistiche: a) semiconduttore intrinseco; b) semiconduttore estrinseco; c) effetto Hall; d) effetto Hall quantistico; e) risonanze di ciclotrone. 9. Dispositivi a trasporto: raddrizzatori, transistor, circuiti integrati: a) oscillatori di Gunn come generatori di microonde; b) giunzione metallo-semiconduttore; c) giunzioni p-n ed eterogiunzioni; d) transistor; e) memorie; f) circuiti integrati. 10. Dispositivi optoelettronici: celle fotovoltaiche, laser: a) fotocelle e sensori di immagine; b) rivelatori fotovoltaici e celle solari; c) laser. 11. Nuovi materiali. Superreticoli e microstrutture: a) nuovi materiali; b) superreticoli; c) microcavità; d) pozzi quantici; e) fili quantici e punti quantici. □ Bibliografia.
1. Introduzione e notizie storiche
Essendo ormai prossimi alla fine del Novecento, è forse lecito chiedersi quale sia stata in questo secolo la scoperta scientifica che più ha influito sul progresso tecnologico in atto. La risposta a questa domanda non può che far riferimento al transistor e ai circuiti integrati al silicio; da essi ha avuto inizio l'elettronica a stato solido, che ha reso possibili i moderni calcolatori, la memorizzazione e l'elaborazione di quantità enormi di dati, il trasporto di informazioni con fibre ottiche, ossia gli strumenti - il cosiddetto hardware - per la rivoluzione informatica. Tali scoperte, e molte altre a esse correlate, hanno una storia interessante, legata da un lato allo sviluppo dei concetti della fisica moderna, in particolare della meccanica quantistica, e dall'altro lato allo studio delle proprietà di particolari cristalli, i semiconduttori, utilizzati già all'inizio del secolo per i dispositivi di rivelazione di onde radio.
In relazione alla loro attitudine al trasporto di elettricità, è conveniente dividere i materiali in due grandi categorie: i conduttori, con resistività elettrica inferiore a 10-4 Ω cm, e gli isolanti, con resistività elettrica superiore a 1010 Ω cm. Nei primi la resistenza elettrica aumenta linearmente all'aumentare della temperatura, nei secondi è indipendente dalla temperatura. Esistono peraltro sostanze di natura intermedia, che sono sia cattivi conduttori che cattivi isolanti, ma soprattutto hanno una resistività che diminuisce esponenzialmente all'aumentare della temperatura e, ad alte temperature, può raggiungere valori vicini a quelli dei buoni conduttori come i metalli. Tali sostanze sono state chiamate ‛semiconduttori'.
La prima osservazione di proprietà semiconduttrici risale al 1843, quando Faraday scoprì che il solfuro d'argento ha una resistività con coefficiente di temperatura negativo. In seguito, vennero scoperti molti altri materiali con questa proprietà e la famiglia dei semiconduttori si arricchì rapidamente. Sono semiconduttori un gran numero di sostanze solide: gli elementi del gruppo IV a struttura del diamante, C, Si, Ge e α-Sn; i composti binari III-V come il GaAs; i composti II-VI come CdTe e ZnS (blenda); i composti IV-VI come PbS (galena) e SnTe; alcuni composti I-VII come CuCl, o composti più complessi (molti ossidi e parecchi sali). Oltre al coefficiente di temperatura negativo per la resistività, successivamente vennero evidenziati altri effetti importanti che risultarono essere proprietà tipiche di tutti i semiconduttori. Nel 1873, W. Smith scoprì la fotoconducibilità, osservando che la resistività del selenio diminuisce quando il cristallo è esposto alla luce. È un fenomeno simile all'effetto fotoelettrico, ma gli elettroni vengono liberati all'interno del materiale. Nel 1874, F. Braun scoprì l'effetto rettificante del contatto metallo-semiconduttore: la resistenza non segue la legge di Ohm, ma dipende dalla grandezza e dal segno del potenziale applicato, in modo da favorire il passaggio di corrente in un verso e da inibirlo in quello opposto. All'inizio del secolo, e ancora negli anni venti, tali rettificatori furono utilizzati come rivelatori di onde elettromagnetiche, perché consentivano di usare trasduttori a cuffia; i radioamatori di una certa età ricordano il vasto impiego di tali rivelatori ottenuti mettendo a contatto i fili metallici del circuito con la galena (PbS) o con il carburo di silicio. Successivamente, l'avvento delle valvole a vuoto (i diodi), più affidabili anche se più costose e ingombranti, ridusse l'impiego dei semiconduttori, e la scoperta del triodo rese poi possibile l'amplificazione elettronica dei segnali e la costruzione di circuiti complessi da cui nacque l'elettronica moderna.
Come si sia passati dall'elettronica a vuoto all'elettronica dei semiconduttori, e in particolare ai circuiti planari a grande integrazione su silicio, è una storia lunga e affascinante, in cui i risultati di carattere puramente tecnologico sono strettamente collegati ai progressi nelle conoscenze di fisica fondamentale. La preistoria (v. Seitz, 1996) è legata alla necessità di rivelare efficientemente onde ultracorte (di lunghezza d'onda centimetrica), quali quelle riflesse da oggetti metallici quando sono investiti da tali onde generate da opportune sorgenti (i klystron e i magnetron a cavità multiple). Il problema sorse alla metà degli anni trenta con gli studi sulle microonde e già H. E. Hollmann (v., 1936) concludeva che il ricevitore migliore per tali onde era un diodo a cristallo. Ciò era dovuto, da un lato, alle proprietà raddrizzatrici del diodo che venivano mantenute alle altissime frequenze richieste, ≅ 100 MHz, dall'altro lato, alla proprietà delle giunzioni metallo-semiconduttore di essere fortemente nonlineari e quindi di poter agire come miscelatori di correnti a frequenza diversa in un circuito eterodina di rivelazione. Infatti, tale miscelazione produce una corrente di battimento di frequenza uguale alla differenza fra la frequenza fissa del circuito e quella dell'onda da rivelare; tale onda di battimento può essere opportunamente amplificata e quindi ragionevolmente utilizzata negli oscilloscopi, ed eventualmente resa udibile. L'importanza che tali applicazioni avevano per l'utilizzazione militare del radar si tradusse in uno sforzo tecnologico enorme, compiuto soprattutto in Inghilterra nel periodo immediatamente precedente la seconda guerra mondiale, e negli Stati Uniti durante la guerra, quando D. Robinson e H. W. Skinner al Radiation Laboratory di Cambridge, nel Massachusetts, ottennero i migliori risultati usando silicio purificato e contatti di tungsteno.
Gli studi sul silicio motivati dalla tecnologia radar vennero poi estesi al germanio e ad altri semiconduttori utilizzando metodologie più strettamente scientifiche, anche perché nel frattempo le conoscenze di meccanica quantistica avevano reso possibile la comprensione delle proprietà fondamentali dei solidi. Nel 1940 apparve il famoso testo di F. Seitz (v., 1940), che presentava lo studio dei fenomeni fisici dei cristalli alla luce della meccanica quantistica. Già precedentemente A. H. Wilson (v., 1936) aveva introdotto il concetto delle ‛bande di energia' per spiegare il comportamento degli elettroni nei metalli. I principî di base, definiti negli anni trenta, furono poi utilizzati per la comprensione delle proprietà elettroniche e ottiche dei semiconduttori. I concetti fondamentali sono essenzialmente due, ai quali se ne affiancano alcuni altri che ne sono una conseguenza.
Il primo concetto fondamentale è la quantizzazione dei livelli di energia degli stati elettronici in ‛bande di energia', En (k), dove il vettore k è un numero d'onda
Formula
legato alla lunghezza d'onda λ di de Broglie dell'elettrone (λ = h/p, dove h è la costante universale di Planck e p la quantità di moto dell'elettrone) e assume un numero discreto di valori uguale al numero di celle del cristallo. Ad ogni stato ∣n, k〉 corrisponde una funzione d'onda quasi-periodica
ψn (k, r) = eik • r un, k (r), (1)
dove un, k (r) ha la periodicità del reticolo cristallino. Le bande di energia En (k) e le funzioni di Bloch (1) sono le soluzioni dell'equazione di Schrödinger per gli elettroni nel potenziale medio cristallino, o le soluzioni dell'equazione di Dirac quando occorra tener conto di effetti relativistici.
Il principio di esclusione di Pauli è il secondo concetto fondamentale. Ogni livello di energia può essere occupato da un solo elettrone (due elettroni se non si tiene conto dello spin nell'enumerare i livelli). Perciò, in una banda totalmente occupata si hanno due elettroni per ogni cella elementare del cristallo. In tale caso non si ha corrente elettrica, perché per rendere l'impulso medio diverso da zero occorrerebbe uno spostamento medio di elettroni tra i livelli, il che non si può verificare se tutti gli stati sono occupati e se vale il principio di esclusione. Come conseguenza del principio di Pauli nasce anche il nuovo concetto di ‛buca' o ‛lacuna' (hole) di elettrone, particella con carica elettrica positiva e quantità di moto uguale a quella di un elettrone, che ha origine da una ‛banda' quando tutti gli stati sono occupati tranne uno. Il concetto di ‛buca' nei solidi, introdotto da R. Peierls nel 1929, ha consentito di capire i risultati di effetto Hall anomalo di K. Baedeker e di O. M. Corbino, noti dall'inizio del secolo, che rivelavano portatori di corrente con carica positiva.
I metalli sono conduttori perché le loro bande di energia non sono mai totalmente occupate. Il livello di Fermi, che separa gli stati occupati da quelli vuoti, cade all'interno di una banda di energia per gli elettroni. Gli isolanti non conducono la corrente perché le bande sono totalmente occupate o totalmente vuote, e tra le bande occupate e le bande vuote esiste un intervallo di energia proibita agli elettroni, il gap, entro cui si trova il livello di Fermi. I semiconduttori sono caratterizzati da un gap sufficientemente piccolo (inferiore a 2,5 eV) da consentire ad alcuni elettroni di passare per effetto statistico in una banda normalmente vuota, dove conducono la corrente elettrica come nei metalli. La conducibilità elettrica σ (inverso della resistività, tale che J = σE) è quindi nei semiconduttori
dove e è la carica dell'elettrone, ne e nh indicano, rispettivamente, le densità di elettroni e di buche nelle rispettive bande normalmente vuote (di conduzione) o normalmente piene (di valenza), e μe e μh indicano le loro mobilità medie (velocità in campo elettrico unitario).
Un ulteriore aspetto, di cui si venne affermando l'importanza nel dopoguerra durante gli studi sistematici sui semiconduttori, è l'enorme influenza delle impurezze sul numero e sul tipo di portatori di corrente. Impurezze con un numero di elettroni di valenza superiore a quello dell'atomo che sostituiscono (per esempio, P o As in Si e Ge) introducono elettroni nella banda di conduzione anche a temperature relativamente basse e generano conducibilità di tipo n (espressione convenzionale per indicare che è dovuta a elettroni, dove n sta per negativa). Impurezze con un numero di elettroni di valenza inferiore (per esempio, Al o Ga in Si e Ge) introducono buche e generano conducibilità di tipo p (espressione convenzionale per indicare conducibilità di buche, dove p sta per positiva).
Utilizzando questi concetti guida, nel corso di ricerche sulle proprietà fisiche del germanio, J. Bardeen, W. H. Brattain e W. Schockley inventarono nel 1948 il transistor, cioè un piccolo cristallo di germanio (base) con due contatti, uno per iniettare cariche (emettitore) e uno per raccoglierle (collettore); la base funziona come la griglia nelle valvole a vuoto, e pertanto una piccola variazione di potenziale o di corrente su di essa cambia di molto la corrente che passa al collettore. Il vantaggio rispetto alle valvole a vuoto è enorme: il transistor è molto più piccolo e maneggevole, può operare a potenze molto inferiori e non richiede un circuito ausiliario per produrre gli elettroni (i portatori sono già presenti nel cristallo ed è sufficiente la statistica di Fermi a regolarne la distribuzione). La scoperta del transistor ha dato luogo all'elettronica dei semiconduttori, che ha rapidamente sostituito l'elettronica convenzionale: circuiti anche complessi sono stati realizzati in poco spazio con componenti affidabili e di grande durata. A partire dagli anni cinquanta, ciò ha reso possibile lo sviluppo dei grandi calcolatori elettronici e dell'informatica moderna.
A cavallo tra gli anni cinquanta e sessanta nasceva anche il laser, un amplificatore di luce basato sull'emissione stimolata di radiazione coerente; pur essendo stato concepito per la fisica atomica, esso può essere realizzato anche utilizzando le proprietà di interazione della radiazione con la materia nei semiconduttori. Si svilupparono così i diodi emettitori di luce, i laser a semiconduttore e le celle fotovoltaiche, che trasformano la luce in corrente elettrica (v. laser e fotonica, vol. XI).
Negli anni sessanta sembrava che le possibilità di applicazioni tecnologiche dei semiconduttori fossero esaurite, quando Jack S. Kilby della Texas Instruments e Robert N. Noyce della Fairchild Camera and Instruments Company idearono i circuiti integrati. All'inizio l'obiettivo era quello di miniaturizzare i transistor con un deposito superficiale di ossido e un'incisione metallica per il contatto (transistor MOS, Metal Oxide Semiconductor) sulla superficie di un monocristallo di silicio. Usando i canali metallici come conduttori, le parti di silicio come diodi o triodi e le parti ossidate come isolanti necessari per la conduzione direzionale si ottennero complessi circuiti con elementi delle dimensioni di pochi micron. Il chip di silicio, con i suoi milioni di circuiti elementari sopra una superficie delle dimensioni di un'unghia, è l'elemento di base per la costruzione di quella che viene oggi chiamata ‛l'autostrada dell'informazione', percorsa dai giganteschi calcolatori e dai personal computers.
La tecnologia elettronica è ormai basata sul silicio, ma si sono rivelate possibilità interessanti e fenomeni nuovi nei tipi più vari di semiconduttori: dai composti III-V, quali GaAs, ai semiconduttori amorfi, alle leghe di semiconduttori diversi quali SixGe1-x, ai semiconduttori organici, quali il poliacetilene. Tutto ciò ha dato origine a quella che oggi viene chiamata ‛scienza dei materiali', che da un lato mira allo studio dei materiali esistenti, e dall'altro alla ricerca di nuovi materiali dotati di proprietà interessanti per la fisica fondamentale e per la tecnologia.
Nel corso della ricerca di nuovi materiali, Leo Esaki e R. Tsu realizzarono per primi negli anni settanta strutture ordinate stabili di tipo voluto, che non esistono in natura, depositando su un substrato cristallino atomi diversi in opportuna sequenza. Il controllo delle strutture può essere ottenuto a livello atomico, per cui si può parlare di nanostrutture artificiali. Le prime a essere realizzate sono stati i superreticoli, costituiti da strati di più piani atomici di un tipo di semiconduttore alternati a strati di un altro tipo di semiconduttore (v. semiconduttori: Superreticoli e microstrutture artificiali, vol. XI); nella direzione di crescita la struttura è periodica, ma la lunghezza di traslazione è un multiplo della distanza reticolare di base. Altre nanostrutture sono quelle a dimensionalità ridotta, in cui la periodicità è rotta in una, due o tre direzioni. Nel primo caso si hanno i cosiddetti ‛pozzi quantici' (QW, Quantum Wells), in cui nella direzione di crescita un semiconduttore è confinato in un semiconduttore diverso, con gap di energia maggiore. Nel secondo caso si hanno i ‛fili quantici' (QWW, Quantum Well Wires), in cui la struttura originaria è mantenuta in una sola direzione e gli elettroni sono confinati nelle altre due (v. cap. 11, § e). Si sono anche ottenuti i punti quantici (QD, Quantum Dots), in cui un semiconduttore di piccola dimensione è confinato all'interno di un semiconduttore diverso con gap maggiore. Tutte queste nanostrutture, e altre che possono essere costruite, realizzano effetti fisici importanti quali la quantizzazione da confinamento, l'effetto tunnel, il trasporto balistico, ecc. Le loro proprietà rendono possibili le costruzioni più diverse, nelle quali gli atomi non sono altro che i mattoni e le pietre di edifici di illimitata complessità. Si è coniata l'espressione ‛ingegneria della struttura a bande', per definire quello che oggi è il terreno più nuovo e promettente nello studio dei semiconduttori.
Nei capitoli seguenti verranno sintetizzati alcuni dei temi principali che sono stati menzionati in questo breve excursus storico, peraltro senza alcuna pretesa di completezza. Si seguirà un percorso logico che privilegia i livelli elettronici, in quanto essi sono la base per la comprensione di tutti i fenomeni.
2. Teoria elettronica
Il moto degli elettroni in un cristallo obbedisce alle leggi della meccanica quantistica (v. solidi, fisica dei, vol. VI), che in questo caso danno risultati diversi da quelli della meccanica classica perché la lunghezza d'onda di de Broglie
degli elettroni è confrontabile con la distanza tra gli atomi, la quale caratterizza le variazioni del potenziale cristallino, Vc (r). Il problema è di enorme complessità a causa del grande numero di particelle interagenti, ma si può affrontarlo con buoni risultati costruendo un potenziale medio Vc (r) al quale sono soggetti tutti gli elettroni. L'equazione di Schrödinger per la funzione d'onda ψn di ogni elettrone è allora:
e consente in linea di principio di calcolare l'energia En dei livelli. Naturalmente, il concetto di potenziale medio è una semplificazione (in realtà, il potenziale Vc (r) contiene termini di scambio non locali anche in prima approssimazione), però esso è sufficiente per ottenere le proprietà essenziali della struttura elettronica. Quando si considera esplicitamente l'interazione a molti corpi, tra gli elettroni insorgono effetti di correlazione che vanno valutati solo per scopi specifici, quali il calcolo delle energie coesive totali. Il moto dei nuclei produce un effetto addizionale di interazione tra elettroni e vibrazioni quantizzate (i fononi), che può essere considerato separatamente.
Anzitutto occorre notare che la simmetria di traslazione propria della struttura cristallina impone l'esistenza di un buon numero quantico, cioè il vettore d'onda k, che assume i valori:
dove K1, K2 e K3 sono i vettori della cella elementare del reticolo reciproco, e i numeri interi ni variano tra 0 e
,
Ni essendo il numero di celle elementari del cristallo in una direzione dello spazio reale. È pertanto evidente che il vettore k può essere definito in uno spazio racchiuso dai piani che bisecano i vettori del reticolo reciproco. Tale spazio è detto ‛zona di Brillouin' (BZ). Il numero dei vettori k è enorme quando il cristallo è abbastanza esteso, ed essi sono così vicini che la funzione ψ (k, r) e le bande E (k) possono essere trattate a tutti gli effetti pratici come funzioni continue di k, così come ipotizzato nella (1). Inoltre, per particolari valori di k (punti di alta simmetria), tali che
Rtnc;k = k + K, (5)
dove R denota un'operazione di simmetria spaziale del cristallo (per esempio, una rotazione di 90° attorno a tre assi perpendicolari nei cristalli cubici), e K un vettore del reticolo reciproco, bande diverse possono incrociarsi e richiedere degenerazioni aggiuntive oltre quella di spin. Per ogni valore di k i possibili stati sono classificabili in base alle proprietà di simmetria, proprio come negli atomi gli stati sono classificabili come s, p, d, ecc., a causa della simmetria sferica.
Dopo aver definito e classificato gli stati quantici, rimane il problema di calcolarne le energie e le autofunzioni (stati di Bloch), problema non facile a causa della complessità del potenziale. A partire dai primi tentativi degli anni trenta, si è sviluppata nella seconda metà del secolo una serie di metodologie che hanno consentito di ottenere la struttura elettronica dei solidi.
Nel caso dei semiconduttori conviene distinguere gli stati occupati, soprattutto quelli atomici più interni, dagli stati a energia maggiore, normalmente vuoti. Nel primo caso conviene sviluppare la funzione di Bloch in funzioni localizzate sugli atomi,
dove Φa′ (r - Rν è una funzione localizzata nella cella elementare che coincide con una funzione atomica per gli stati interni nei quali essa è diversa da zero solo vicino al nucleo, ed è una funzione atomica modificata per gli stati di valenza. Il metodo è utile per stabilire un collegamento tra stati atomici e stati cristallini e viene spesso utilizzato in forma semiempirica manipolando le funzioni localizzate di partenza o usando come parametri empirici gli integrali del potenziale cristallino Vc (r) tra funzioni Φa′ (r - Rν su atomi diversi.
Per gli stati di valenza, e soprattutto di conduzione, è più conveniente sviluppare le funzioni di Bloch in onde piane, con la condizione però che esse siano ortogonali agli stati interni del cristallo, ψc (k, r), del tipo descritto nella (6). Se si indicano le onde piane normalizzate sul volume col simbolo ∣k + K〉, e si usa la funzione di Bloch del tipo (6) per gli stati interni allo stato di valenza (di core), si ha per le funzioni di Bloch di valenza e conduzione
dove il simbolo 〈A∣B〉 indica l'integrale di sovrapposizione delle due funzioni d'onda ∣A〉 e ∣B〉. La (7), sostituita nell'equazione di Schrödinger (3), consente di determinare i coefficienti ah(v) (k) e le bande Ev (k) con il metodo variazionale. In tal modo gli stati convergono agli stati di valenza e di energie superiori, essendo automaticamente ortogonali agli stati interni, e si ottiene la convergenza con un numero ragionevolmente piccolo di onde piane.
Non è qui il caso di addentrarsi nella discussione riguardante la scelta del potenziale medio; basti ricordare che esso può essere collegato in modo univoco alla densità elettronica, e in tal modo si può superare l'approssimazione di campo medio e tener conto delle correlazioni, come è stato fatto da W. Kohn e P. Hohenberg nel 1983.
Uno sviluppo di grande importanza del metodo delle onde piane ortogonalizzate è il concetto di pseudopotenziale, forma diversa di un metodo introdotto per la prima volta da E. Amaldi ed E. Fermi per gli stati di valenza degli atomi. Esso consiste nel definire una funzione ausiliaria (pseudofunzione), ϕ (r, k), che è la parte della funzione di Bloch (7) sviluppata in onde piane, e aggiungere la parte rimanente, che coinvolge gli stati interni ψc (k, r) conosciuti, al potenziale Vc (r), in modo da ottenere un potenziale artificialmente costruito (pseudopotenziale). Le bande rimangono invariate e lo pseudopotenziale agisce solo lontano dai nuclei, dove non si sovrappongono le ψc (r) e le ϕ (r). Vicino ai nuclei, la parte che deriva dall'ortogonalità cancella il potenziale Vc (r), per cui lo sviluppo della ϕ (r, k) in onde piane è rapidamente convergente e il problema è risolubile. Il metodo dello pseudopotenziale ha consentito di calcolare il comportamento delle bande di energia in funzione di k in tutti i semiconduttori di interesse, e la combinazione con il metodo del legame stretto per gli stati interni e di valenza ha consentito di capire anche concettualmente la struttura a bande sulla base della simmetria e delle proprietà dei costituenti atomici.
Un ultimo accenno sulla struttura elettronica riguarda gli effetti relativistici che è necessario introdurre all'aumentare del numero atomico. Le correzioni sono di due tipi: la correzione massa-velocità combinata alla correzione di Darwin, che abbassa l'energia dei livelli quanto più grande è la componente a simmetria s (l = 0) della funzione di Bloch, e l'interazione spin-orbita che rimuove la degenerazione di spin nei cristalli senza simmetria di inversione e separa alcuni altri livelli degeneri.
3. Bande di energia dei semiconduttori elementari e binari
Con i metodi precedentemente descritti si è potuta calcolare, a partire dagli anni cinquanta, la struttura elettronica di C (diamante), Si, Ge, α-Sn, dei composti III-V, e di moltissimi altri elementi e composti semiconduttori. La conoscenza precisa delle bande di energia è la base per una comprensione microscopica di tutti i fenomeni elettronici.
Considerazioni basate sulla simmetria cristallina consentono di rendersi facilmente conto delle ragioni per le quali tutte le sostanze con la struttura cristallina della blenda possono essere semiconduttrici; le riassumiamo concisamente per poi esemplificare nei dettagli i risultati ottenuti per alcune strutture a bande. Mostriamo anzitutto la struttura della blenda (v. fig. 1): il reticolo di Bravais è cubico a facce centrate e la cella elementare è costituita da due atomi di tipo A e B, il primo localizzato all'origine della cella elementare, e il secondo lungo la diagonale nel punto
(1, 1, 1), a essendo la lunghezza dello spigolo della cella. Caratteristica di tale struttura è la proprietà di ogni atomo di essere al centro di un tetraedro ai cui vertici stanno atomi di tipo diverso. Quando i due atomi A e B sono uguali, come nel caso degli elementi del IV gruppo, il reticolo della blenda si trasforma in quello del diamante e si aggiunge al gruppo di simmetria l'operazione di inversione.
La zona di Brillouin, appropriata al reticolo cubico a facce centrate, è visualizzata nella fig. 2, dove sono indicati con simboli convenzionali i punti di maggiore simmetria, per es. Γ (K = 0),
Gli stati elettronici sono classificati in base alle proprietà di simmetria, mediante la ricerca delle rappresentazioni irriducibili dei gruppi spaziali, tenendo anche conto del fatto che la simmetria di inversione temporale implica En (k) = En (- k), e impone degenerazioni aggiuntive nei punti ad alta simmetria. Quando si tiene conto dello spin occorre considerare il gruppo doppio, perché l'operazione di rotazione R (2 π) non coincide con l'identità, ma cambia segno agli spinori; in tal caso la classificazione degli stati è diversa e si possono avere separazioni tra livelli altrimenti degeneri.
Nella tab. I viene riportata la classificazione dei livelli nel punto Γ per i reticoli della blenda e del diamante, prima trascurando l'interazione spin-orbita, e poi usando il gruppo doppio. Sono state utilizzate le notazioni tradizionali, e per ogni rappresentazione sono stati indicati anche gli stati atomici corrispondenti nella funzione di Bloch (6) e le onde piane di energia minore che compaiono nello sviluppo (7). Nella tab. II si presenta una simile analisi degli stati nei punti X e L; regole di compatibilità stabiliscono quali sono i collegamenti tra tali livelli e quelli che la simmetria consente lungo le direzioni Δ e Λ (v. fig. 2).
L'analisi di simmetria considerata è utile e significativa perché consente di capire la ragione per cui tutte le sostanze con la struttura cristallina della blenda o del diamante hanno strutture elettroniche simili. Anzitutto si può cercare quali sono gli stati che si possono ottenere con le funzioni atomiche di valenza s e p degli atomi che formano il cristallo e quali sono gli stati interni. Occorre ricordare che la sequenza dei livelli è correlabile con quella degli stati atomici corrispondenti e che soltanto gli stati della stessa rappresentazione irriducibile interagiscono fra loro a causa del potenziale cristallino. Nel caso della simmetria diamante si vede allora che le funzioni di valenza Γ¹1 (sA + sB) e le tre Γ³25′ (pxA - pxB, ...), che sono pari rispetto all'inversione, formano stati leganti con energia inferiore a quella degli stati antileganti, dispari rispetto all'inversione. Poiché gli elettroni di valenza nella cella elementare sono otto, gli stati leganti (quattro) sono completamente occupati ed esiste la possibilità di un gap che separi tutti gli stati occupati da tutti gli stati vuoti. I dettagli della struttura elettronica richiedono le soluzioni dell'equazione di Schrödinger negli altri punti della BZ ed è di grande aiuto il metodo dello pseudopotenziale prima descritto. Si vede infatti, già nei punti di simmetria X e L della BZ, che la sequenza dei livelli può essere determinata in modo perturbativo a partire dai livelli a energia inferiore con potenziale costante (reticolo vuoto), ed è la seguente: Γ1′ 〈 Γ³25′ 〈 Γ¹2', Γ³15′; X²1 〈 X²4 〈 X²1′ 〈 X²4, L¹1 〈 L¹2′ 〈 L²3 〈 L¹1, L²3, L¹2′.
I risultati numerici sono esemplificati con le bande di energia del silicio, mostrate nella fig. 3: il massimo della banda di valenza è Γ25′, mentre il minimo della banda di conduzione è nella direzione Δ,
con gap di circa 1,2 eV.
Simili risultati si ottengono per il diamante, con la differenza che tutte le separazioni tra i livelli sono maggiori perché la distanza interatomica è più piccola. Il gap è di oltre 5 eV, per cui il diamante è in realtà un isolante fino alla temperatura di fusione.
Situazione opposta è quella del germanio, in cui le separazioni tra i livelli sono inferiori a quelle nel silicio perché le distanze interatomiche sono maggiori. La presenza degli stati interni d respinge a energie più elevate gli stati di valenza Γ25' e di conduzione Γ15 rispetto al Γ2' di conduzione. Inoltre, l'aumento del numero atomico rende necessario considerare le correzioni relativistiche e, in particolare, le interazioni spin-orbita. Il risultato è mostrato nella fig. 4, dove si può osservare che il Γ2 (Γ6 con spin) è ora lo stato di conduzione di più bassa energia al punto Γ, e che il minimo della banda di conduzione è ora L6, con gap di energia ~ 0,72 eV. La separazione spin-orbita tra Γ+8 e Γ+7 al punto Γ è ≅ 0,3 eV (in confronto a 0,0044 eV nel silicio).
Nello stagno grigio (α-Sn) l'abbassamento del livello Γ2' (Γ6 con spin) per le correzioni relativistiche e la separazione spin-orbita sono sufficienti a sovvertire l'ordine dei livelli, così che Γ2' è inferiore a Γ8 e il semiconduttore diventa un caso limite a gap nullo.
Una trattazione simile può essere sviluppata per il caso dei composti che cristallizzano nella simmetria della blenda (per es., i composti III-V). Il massimo della banda di valenza è sempre lo stato di tipo p Γ15, ma il minimo della banda di conduzione può essere Γ1, X1 o L1. Si può osservare che l'assenza della simmetria di inversione produce interazione fra gli stati Γ1 e Γ15 pari e dispari, e che ciò allontana le bande di valenza dalle bande di conduzione rispetto al composto corrispondente del gruppo IV, producendo gaps di energia Eg maggiori. Questo si può vedere, per esempio, confrontando la struttura a bande di AlP (v. fig. 5) con quella del Si.
Gli effetti relativistici nei composti binari sono simili a quelli del gruppo IV e si possono notare nella struttura a bande del GaAs della fig. 6. Nel punto X l'interazione spin-orbita produce una separazione che si aggiunge a quella dovuta all'assenza di inversione. Nei punti generici della BZ si ha una separazione di spin che è molto piccola e che può essere apprezzata solo con esperimenti ad hoc di magneto-ottica. L'estremo di valenza Γ15 si separa in Γ48 e Γ²7, con Γ8 a energia superiore poiché corrisponde a J = 3/2 degli atomi costituenti. Nel caso dei composti I-VII con rame, la vicinanza degli stati d occupati produce un mescolamento di stati d e p nelle funzioni di Bloch di valenza e il contributo d tende a invertire l'ordine dei livelli Γ8 e Γ7. Questo effetto prevale nel CuCl, dove il massimo della banda di valenza è lo stato Γ7 (a degenerazione due). A scopo indicativo riportiamo nella tab. III alcuni dati relativi ai semiconduttori più comuni. È importante osservare che, mentre tutti i composti della simmetria descritta sono semiconduttori, le loro proprietà differiscono per i dettagli della struttura a bande (valore del gap, posizione degli estremi, ecc.) perché queste costituiscono lo spazio in cui si muovono elettroni e buche.
4. Stati localizzati, impurezze, livelli magnetici
Dalle bande di energia si ottengono anzitutto i livelli elettronici in presenza di perturbazioni interne, quali le impurezze o il disordine cristallino, o di perturbazioni esterne, quali il campo magnetico.
Si può osservare che il comportamento di elettroni e buche si ottiene sviluppando En(k) vicino agli estremi nelle rispettive bande. Fermandosi al termine quadratico dello sviluppo, si ottiene l'approssimazione della massa efficace, per cui elettroni e buche si comportano come particelle libere in uno spazio particolare definito dagli stati elettronici del cristallo, con masse efficaci determinate dalla curvatura delle bande nello spazio k. Vicino ai minimi di conduzione avremo, quando il minimo è lungo una linea di simmetria come nel caso di Si, Ge, GaP, ecc., che l'energia degli elettroni E (k) può essere espressa nella forma
dove mel e met indicano, rispettivamente, le masse efficaci longitudinale e trasversale. Quando il minimo è a k0 = 0, come in GaAs, InSb, ZnSe, CuCl, ecc., mel e met coincidono e la massa efficace è isotropa per simmetria. Se si suppongono noti gli stati di energia al minimo k0 della banda di conduzione, si può usare il metodo delle perturbazioni per livelli non degeneri vicini a k0, con operatore perturbativo
(k - k0) • p, e si ottiene l'espressione per le masse efficaci della banda n in funzione degli elementi di matrice pnn' (- iℏ ∇) tra stati al punto k0 nonché le loro differenze di energia En (k0) - En' (k0)
dove i è il versore che indica l'orientazione rispetto agli assi principali scelti per il calcolo della relativa componente (mi) della massa efficace nel punto k0. Nel caso k0 = 0 la massa è isotropa.
Vicino al massimo di valenza lo sviluppo non è così semplice a causa della degenerazione delle bande. In tal caso si utilizza la conoscenza vera o presunta dei livelli a Γ e si procede con la teoria delle perturbazioni, considerando esplicitamente i livelli degeneri. Si ottiene così una matrice 6 × 6 (con spin), detta matrice di Luttinger, da cui per diagonalizzazione si ricavano le bande di energia vicino a k = 0, quando si conservano i termini dello sviluppo di ordine più basso in k. Tale matrice contiene tre parametri (γ1, γ2, γ3) per lo stato Γ8 e uno per lo stato Γ7, separato da esso di Δs.o.; essi dipendono dagli elementi di matrice di p (- i ℏ ∇) tra stati a k = 0 e dalle differenze di energia tra essi. Si può osservare che, in approssimazione sferica, si ottengono espressioni per E (∣k∣) che corrispondono a tre sviluppi indipendenti, con due masse efficaci, una pesante e una leggera, per lo sviluppo a Γ8, e una massa per lo sviluppo a Γ7.
Come applicazione di questi concetti si può menzionare la possibilità di studiare semplicemente il comportamento di elettroni e buche quando nel cristallo si considerino potenziali aggiuntivi a Vc, siano essi esterni, quali campi elettrici e magnetici, o intrinseci, quali disordine cristallino o vibrazioni atomiche.
Un noto teorema mostra che il comportamento delle particelle in presenza di un potenziale aggiuntivo generico V (r) vicino a un estremo di banda E0n si ottiene dall'equazione
dove k è ora l'operatore (- i ∇), e l'autofunzione dello stato può essere espressa mediante la funzione inviluppo fn(m) (r) e la funzione di Bloch all'estremo
Nel caso della banda di valenza, quando l'approssimazione della massa efficace non è sufficiente, la (11) implica sei funzioni inviluppo (una per ognuno degli stati che costituiscono Γ8 e Γ7), e l'equazione (10) diventa un'equazione matriciale in cui al posto di En (k) si usa l'operatore matriciale di Luttinger.
Si può subito osservare che se il potenziale aggiuntivo è tale da localizzare gli stati, come quello dovuto a impurezze sostituzionali opportune, esso, oltre a diffondere le particelle ‛libere', produce livelli discreti nel gap delle bande. Consideriamo, per esempio, il caso di impurezze sostitutive donatrici (con un elettrone di valenza in più) o accettrici (con un elettrone di valenza in meno). Una buona approssimazione per V (r) è allora un potenziale coulombiano schermato dalla costante dielettrica statica ε, che nei semiconduttori è assai elevata (dell'ordine di 10), con una correzione di cella centrale che agisce solo a corta distanza. Il potenziale coulombiano produce livelli di tipo idrogenoide che possono essere immediatamente calcolati e che, nel caso degli elettroni con masse efficaci me isotrope, sono:
dove Ry è la costante di Rydberg
Per valori di ε dell'ordine di 10, il raggio di Bohr è così grande (≅100 aB) che il potenziale di cella centrale è poco influente. Nel caso di masse anisotrope, il calcolo è più complesso e i tre livelli (l = 1) non sono degeneri, mentre i livelli p0 sono separati dai p±1 di una quantità che dipende dal fattore di anisotropia γ =
La presenza di minimi equivalenti, tra i quali il potenziale ha elementi di matrice non nulli (6 nel Si e 4 nel Ge), fa sì che il livello fondamentale non sia semplice, ma suddiviso in più livelli di diversa simmetria (Γ1 + Γ15 + Γ12 in Si), separati di una quantità molto più piccola dell'energia di legame del livello.
Le impurezze accettrici producono stati legati per le buche, che si trovano anch'essi nel gap di energia ma al di sopra dello stato Γ8. I calcoli di tali stati sono di natura più complessa per la degenerazione delle bande a Γ8, e inoltre il massimo relativo Γ7 produce a sua volta stati localizzati per le buche, che però sono degeneri con il continuo della banda Γ8. Tali stati sono ‛risonanti', in quanto la particella in essi è localizzata per un certo tempo e poi diventa delocalizzata. Stati di questo tipo sono stati introdotti da G. Breit ed E. P. Wigner in fisica nucleare per il decadimento α, ma nel caso dei semiconduttori, più che alla forma del potenziale, essi sono dovuti alla struttura delle bande. Così, oltre agli stati di accettore a Γ7, anche in corrispondenza ai minimi secondari delle bande di energia (per esempio lo stato X in GaAs) esistono stati risonanti prodotti dal potenziale coulombiano di un donatore. Una schematizzazione dei livelli di impurezza è indicata nella fig. 7 per il caso di donatori e accettori.
Altri tipi di impurezze possono avere stati localizzati con energie di legame anche elevate a seconda della profondità del potenziale, perché la parte di potenziale che prevale è quella localizzata nella cella centrale. È questo il caso delle impurezze isoelettroniche: in alcuni casi (per esempio, C in Si) catturano gli elettroni e formano stati localizzati, in altri non hanno influenza che sulla diffusione perché il potenziale di cella centrale non produce stati legati.
Una sorgente di localizzazione degli stati è anche il disordine cristallino, che si ha quando molti atomi sono spostati dalle loro posizioni di equilibrio o se la presenza di dislocazioni modifica in media la regolare periodicità del cristallo, creando fluttuazioni nella distribuzione spaziale del potenziale. Quando tali fluttuazioni superano una soglia critica, come P. W. Anderson ha mostrato nel 1958, si creano nel semiconduttore stati localizzati in corrispondenza delle zone di disordine nei quali gli elettroni non sono più rappresentati da funzioni di Bloch e perdono la loro mobilità. Solo quando il numero di elettroni è sufficiente a colmare questi stati, e a lasciarne altri nella banda di conduzione, il semiconduttore riprende le sue proprietà di trasporto.
Un caso simile a quello del disordine si ha quando si producono leghe di semiconduttori diversi. In tal caso si può trattare il sistema come periodico, con un potenziale virtuale che è la media pesata dei potenziali dei componenti, e si ottengono bande di energia intermedia tra quelle dei componenti e funzione della concentrazione x, come indicato nella fig. 8 per il caso SixGe1-x. In aggiunta, si ha anche una fluttuazione di potenziale, che può essere sufficiente a produrre stati localizzati di Anderson, ma che in genere non lo è nelle leghe finora studiate.
Esiste un caso molto importante in cui la perturbazione che rompe la simmetria cristallina è introdotta dall'esterno e modifica tutti gli stati. È il caso di un campo magnetico costante B. Il potenziale aggiuntivo dell'equazione (10) si ottiene sostituendo l'operatore (p = ℏ k) con
con
Scegliendo B in una direzione arbitraria, ed estendendo i risultati ottenuti da Landau per le particelle libere, si ottiene che il moto delle particelle rimane libero nella direzione del campo B, mentre nei piani perpendicolari a esso è quantizzato in livelli di oscillatore armonico
ℏ ωc, separati della frequenza di ciclotrone
dove α, β e γ sono i coseni direttori della direzione di B rispetto agli assi principali che definiscono le masse efficaci. Nel caso isotropo mx = my = mz = me, la (13) si riduce alla solita espressione di ciclotrone, e nel caso di due tipi di masse met e mel (come in Si e Ge) diventa
dove θ è l'angolo che il campo B forma con l'asse principale (direzione di simmetria dove si trova l'estremo di banda). Ogni livello di Landau è degenere, perchéai tre numeri quantici k (kx, ky, kz) si sono sostituiti i due
e n. La degenerazione è
,
dove S denota l'area della superficie del campione ortogonale a B. Ogni livello è poi separato nei due stati di spin opposto dalla quantità gμB ∣B∣, dove μB è il magnetone di Bohr e g il fattore giromagnetico (g ≅ 2 negli elettroni liberi, dipendente dall'interazione spin-orbita nei livelli elettronici nei solidi).
5. Stati vibrazionali: i fononi
Una menzione speciale meritano quelle perturbazioni alla periodicità del cristallo che sono dovute agli spostamenti dei nuclei. Poiché il potenziale per piccoli spostamenti può essere considerato armonico, si hanno oscillazioni vicino alle posizioni di equilibrio, le cui frequenze possono essere calcolate classicamente risolvendo il problema dei moti armonici concatenati degli atomi in funzione delle variazioni di distanza tra gli atomi stessi.
Il potenziale che agisce sui nuclei e definisce la dinamica reticolare dipende dalle posizioni in un modo che è calcolabile dagli stati di Bloch della struttura elettronica. Non ci addentriamo nella discussione della determinazione di questo potenziale; il risultato di rilievo è che le frequenze proprie dei modi di vibrazione dei nuclei sono anch'esse definite nella BZ, ma gli stati sono classificati considerando le proprietà di simmetria degli spostamenti dei nuclei. Il numero di stati è limitato dal fatto che non è possibile avere stati con λ 〈 a. Si ottengono così, nel caso dei nostri semiconduttori, 6 modi vibrazionali per ogni valore di k: i 3 che tendono a frequenza nulla per k → 0 sono i modi acustici, perché tipici delle onde sonore; i 3 che coalescono nel Γ15 con gli atomi che vibrano in direzione opposta nel limite k → 0 sono modi ottici, perché nel caso di cristalli polari (atomi A e B con cariche diverse) sono assimilabili a un dipolo oscillante e producono una polarizzazione elettrica di frequenza ω e vettore d'onda k.
Un concetto molto importante per le vibrazioni deriva dal fatto che gli spostamenti ra e rb dalle posizioni di equilibrio possono essere espressi in coordinate normali mediante uno sviluppo in onde piane e che l'hamiltoniana totale è esprimibile in funzione di tali coordinate come somma di hamiltoniane di oscillatori armonici indipendenti, in modo del tutto analogo a quanto avviene per i campi della radiazione elettromagnetica. È perciò naturale associare una particella di campo a ogni modo vibrazionale caratterizzato da una frequenza ω e un vettore d'onda k, come si fa per la radiazione elettromagnetica con i fotoni. Tali particelle del campo vibrazionale, introdotte inizialmente da Einstein per spiegare il comportamento del calore specifico alle basse temperature, sono i fononi: essi obbediscono alla statistica di Bose-Einstein senza conservare il numero, per cui la probabilità di eccitazione di uno stato alla temperatura T è
Negli scambi di energia i fononi si comportano come i fotoni; sono particelle che possono essere distrutte o create, sempre con energia ℏ ω e impulso ℏ k.
Tra le molte proprietà dovute ai fononi, quali la diffusione anelastica della luce, ne segnaliamo una particolarmente importante che dimostra il loro carattere di particelle e consente di determinarne i modi ω (k): è la diffusione anelastica dei neutroni, per i cui studi applicati ai solidi C. Shull e B. N. Brockhouse hanno ricevuto il premio Nobel nel 1994. I neutroni che incidono su un cristallo vengono diffusi ai vari angoli per gli urti con i fononi, distruggendo o creando un fonone. In tale modo la loro quantità di moto, che definisce il vettore k mediante la relazione di de Broglie p = ℏ k, viene modificata nella diffusione in modo che sia
dove, al solito, la simmetria impone la presenza del vettore del reticolo reciproco K. L'energia cinetica del neutrone viene modificata in modo che si abbia
E (incidente) = E′(diffuso) ± ℏ ω (kf). (17)
Risolvendo le equazioni precedenti in corrispondenza dei picchi di diffusione anelastica si misurano tutti i modi fononici.
Riportiamo nella fig. 9, a scopo di esemplificazione, la struttura dei modi vibrazionali del silicio nelle direzioni di simmetria Δ e Λ della zona di Brillouin. Nella fig. 10 riportiamo invece, per confronto, la struttura dei modi vibrazionali lungo la direzione Δ per Ge e GaAs. Si può osservare che le frequenze sono tutte più elevate nel caso di atomi più leggeri (Si). I modi ottici cadono nella regione dell'infrarosso e i modi acustici si estendono con continuità dalla regione del suono al vicino infrarosso. I risultati sperimentali sono quelli ottenuti con la diffusione anelastica dei neutroni sopra descritta e, per piccoli valori di k, con la diffusione anelastica della luce (Raman per i rami ottici e Brillouin per i rami acustici). L'andamento dell'intensità dei picchi in funzione della temperatura consente anche di verificare la distribuzione statistica (15), perché il picco anti-Stokes associato alla distruzione di un fonone è proporzionale al numero di fononi presenti a quella temperatura.
6. Proprietà ottiche
Il modo più preciso di confermare e affinare la conoscenza degli stati elettronici dei semiconduttori descritta precedentemente è di studiarne l'interazione con la radiazione elettromagnetica. Le proprietà delle bande di energia possono essere verificate; per esempio il gap Eg produce una soglia di frequenza ω0 =
,
tale che per ω 〈 ω0 il materiale è trasparente e per ω > ω0 è fortemente assorbente. Vicino alla soglia sono tuttavia osservabili picchi discreti di assorbimento. Molto grande è pure la fluorescenza generata con eccitazioni varie o stimolata con radiazione.
a) Transizioni interbanda dirette
Per frequenze superiori a ω0, l'assorbimento ottico ha una struttura che riproduce la struttura a bande, in quanto è direttamente collegata alla probabilità per unità di tempo di una transizione di elettroni tra gli stati. Essa è calcolabile dalla regola d'oro di Fermi:
dove l'interazione elettromagnetica H′ che induce la transizione dello stato iniziale ∣i〉 nello stato finale ∣f〉 è al solito espressa in funzione del potenziale vettore A
e si usa la gauge di radiazione, per cui il campo elettrico è E =
Nella somma sui vettori k si tiene conto della regola di selezione ki = kf, perché il vettore d'onda della radiazione è trascurabile rispetto alle dimensioni tipiche (2 π/a) della BZ (transizioni dirette). Dalla definizione del coefficiente d'assorbimento α (ω) quale energia assorbita nell'unità di tempo e di volume (Pℏω), divisa per il flusso di energia incidente, si può poi ottenere la parte immaginaria ε2 (ω) della funzione dielettrica usando unicamente la struttura a bande. Il calcolo è numericamente complicato, ma può essere eseguito con il metodo a pseudopotenziale descritto nel cap. 2; esso rivela una struttura continua per ω > ω0, con picchi di assorbimento in corrispondenza dei punti di alta simmetria della BZ, dove si hanno singolarità nella densità degli stati elettronici; tale struttura si attenua alle alte frequenze seguendo la regola della somma di Thomas-Riche-Kuhn
dove ρ è la densità totale di elettroni.
È stato possibile rivelare sperimentalmente tale struttura solo a partire dagli anni sessanta, perché prima non si poteva procedere a una misurazione diretta del coefficiente d'assorbimento α, o di ε2 (ω), come avviene per i gas di atomi e di molecole, per il fatto che la grande densità di elettroni produce coefficienti di assorbimento così elevati (dell'ordine di 105 cm-1) da non avere trasmissione misurabile. Con lo sviluppo di tecniche appropriate per ottenere superfici pulite si è potuto risolvere il problema utilizzando la riflettività complessa R che si ottiene misurando in funzione della frequenza la riflettività a incidenza normale ∣R∣ e determinando la fase di R dalla relazione di dispersione di Kramers-Krönig, che collega la parte reale alla parte immaginaria di tutte le funzioni ottiche mediante un'integrazione sulle frequenze.
A scopo di esemplificazione si riporta nella fig. 11 il risultato della prima analisi di questo tipo, ottenuta nel 1962 sullo spettro ottico del germanio, con il confronto tra teoria ed esperienza e l'identificazione delle transizioni ai punti critici.
A partire dagli anni sessanta, le costanti ottiche sono state poi misurate per tutti i semiconduttori e ciò ha consentito di effettuare una verifica diretta della struttura elettronica.
b) Transizioni indirette
La regola di selezione kf = ki non permette tuttavia di spiegare le transizioni indirette che pure esistono quando il massimo della banda di valenza e il minimo della banda di conduzione non sono allo stesso valore di k (come nel Si e nel Ge). Nel silicio, per esempio, l'assorbimento ottico inizia a 1,2 eV, anziché alla transizione diretta Γ25' → Γ15 (~ 3, 8 eV).
Tale problema è stato risolto considerando processi del secondo ordine, in cui, oltre a essere assorbito un fotone, viene creato o assorbito un fonone di vettore d'onda opportuno k0. La regola d'oro di Fermi al secondo ordine diventa in tal caso la ben nota espressione:
dove Hef indica l'interazione tra fononi ed elettroni, e la somma si effettua su tutti i possibili stati intermedi t con permutazione di H′ e Hef, intendendo l'energia dello stato intermedio Evt come l'energia elettronica diminuita o aumentata dell'energia del fotone o del fonone assorbito o creato (stato virtuale).
Il termine di interazione elettrone-fonone Hef ha origine dal fatto che la separazione tra il moto degli elettroni e quello dei nuclei è soltanto un'approssimazione giustificata dalla grande differenza di massa tra tali particelle. L'interazione residua si può esprimere sviluppando il potenziale Vc (r) come funzione lineare degli spostamenti dall'equilibrio δ rν, ed esprimendo tali spostamenti in coordinate normali tramite operatori di distruzione ak (ω) e di creazione a+k (ω) di fononi:
dove gli operatori ak e a+k soddisfano le regole di commutazione bosoniche e Ak (r) denota la forza dell'interazione. L'elemento di matrice di Hef nella (21) fornisce l'impulso necessario k0, mentre il fotone dà impulso nullo e fornisce la quasi totalità dell'energia necessaria.
La struttura delle transizioni indirette è stata analizzata a partire dalla fine degli anni cinquanta. Mediante un accurato studio della soglia di assorbimento è stato evidenziato il contributo dei fononi in silicio e germanio, come mostrato nella fig. 12, e similmente in tutti gli altri semiconduttori a gap indiretto, confermando in tal modo le strutture elettroniche calcolate. La dipendenza dalla temperatura è essenziale, perché la creazione fornisce un fattore ak a+k = (Nk + 1) mentre la distruzione dà a+k ak = Nk, dove N è il numero di fononi presenti, funzione della temperatura secondo la (15).
Particolare menzione merita il caso dei sali di argento (per es., AgBr), dove la regione di transizioni indirette produce buche al massimo della banda di valenza Λ ed elettroni a Γ; tali particelle si possono ricombinare solo in modo indiretto, hanno lunghi tempi di vita e sono quindi responsabili dell'immagine fotografica.
c) Eccitoni diretti e indiretti
Tutti gli spettri ottici precedentemente descritti sono basati sul modello a particelle indipendenti per gli elettroni. In realtà, quando si va oltre l'approssimazione di potenziale medio si mette in evidenza un'interazione residua. Tale interazione risulta in un'attrazione tra l'elettrone e la buca prodotti dalla radiazione assorbita; essa genera stati legati di tipo idrogenoide, nei quali la coppia ha un'energia di legame e si muove con moto libero del centro di massa. Gli stati legati sono chiamati ‛eccitoni', hanno un momento di dipolo elettrico μex e possono essere considerati particelle indipendenti che seguono la statistica di Bose-Einstein perché di spin totale intero. La loro energia, misurata dal massimo della banda di valenza, è:
dove m è la massa dell'elettrone libero, Vex è il potenziale di scambio buca-elettrone (di un ordine di grandezza inferiore all'energia di legame) dovuto alla natura identica delle particelle di origine, la funzione Fn (r) è la funzione inviluppo della coppia di funzioni di Bloch agli estremi, ℏ kex è la quantità di moto del centro di massa della coppia di massa totale M = me + mh, μ =
è la massa ridotta e S lo spin totale.
Questo è l'eccitone trasversale (con kex perpendicolare alla direzione di polarizzazione data da μex (n)), ma esiste pure un eccitone longitudinale (kex parallelo a μex) con energia superiore alla (23) di ΔLT; esso non interagisce al primo ordine con la radiazione elettromagnetica. La separazione longitudinale-trasversale ΔLT è proporzionale alla forza d'oscillatore della transizione eccitonica, tramite l'elemento di matrice dipolare μex (n).
Un esempio di assorbimento eccitonico è mostrato nella fig. 13 per il caso di GaAs, dove il gap a transizione diretta favorisce l'osservazione. Sono stati osservati eccitoni anche sotto i gaps indiretti, i quali però richiedono partecipazione di fononi per essere eccitati, come nel caso delle transizioni indirette interbanda.
L'interazione spin-orbita crea un mescolamento tra stati di singoletto (S = 0) e stati di tripletto (S = 1), con una struttura interna di difficile risoluzione nella maggioranza dei semiconduttori, in quanto si deve considerare la struttura degenere della buca Γ8. Ben studiato è il CuCl a causa del piccolo valore della costante dielettrica ε e del raggio di Bohr, nonché per il fatto che, come si è visto, il massimo della banda di valenza è Γ7, solo doppiamente degenere, e quindi l'eccitone in quel caso è più semplice.
d) Polaritoni
Il fatto che la transizione eccitonica produca un momento di dipolo elettrico indica che, vicino alla frequenza necessaria per tale transizione, la radiazione che si propaga nel mezzo ha una dispersione anomala. Si vede allora che le vere particelle che si propagano nel solido sono un misto di radiazione e polarizzazione, quale si ottiene sostituendo nelle equazioni di Maxwell l'equazione costitutiva della polarizzazione vicino alla risonanza
dove E (ω) rappresenta il campo elettrico, γ è un termine di rilassamento, En (kex) l'energia dell'eccitone (23) e β un termine di accoppiamento legato alla forza d'oscillatore. Le soluzioni per gli autovalori del campo elettrico di propagazione sono i ‛polaritoni', con legge di dispersione schematicamente indicata nella fig. 14. Essi sono l'analogo dei fotoni all'interno dei semiconduttori e si comportano come i fotoni dal punto di vista delle proprietà statistiche. Nell'intervallo ΔLT, la radiazione del moto polaritonico è quasi totalmente riflessa (Rehstrahl). Inoltre, la dispersione spaziale permette la propagazione di due modi anziché uno, a frequenza superiore a ωL.
e) Spettri di impurezze
Oltre ai processi tipici dei cristalli perfetti, l'interazione con la radiazione elettromagnetica produce transizione di elettroni e buche tra gli stati delle impurezze, descritti nel cap. 4, dallo stato fondamentale agli stati eccitati e al continuo di ionizzazione. Tali transizioni producono picchi di assorbimento nell'infrarosso in tutto simili agli spettri atomici, ma influenzati dalla struttura a bande del cristallo. Essi consentono di verificare totalmente e in modo indipendente tutte le strutture elettroniche, le masse efficaci anisotrope degli elettroni e la degenerazione delle bande per le buche. Inoltre, dall'intensità degli spettri si possono misurare le concentrazioni di impurezze diverse, essenziali per tutte le proprietà elettroniche.
f) Luminescenza
Le proprietà sopra descritte riguardano il cristallo allo stato fondamentale, ma quando stati a energia superiore sono popolati con particelle, a causa di eccitazione elettrica, termica, o per un precedente assorbimento di radiazione, si hanno transizioni allo stato fondamentale con emissione di fotoni. Tale fenomeno di ricombinazione di elettroni e buche ha due componenti: una è la luminescenza spontanea, l'altra è una luminescenza stimolata dalla radiazione eccitatrice e coerente con essa.
La luminescenza spontanea ha un'intensità notevole solo per alcuni stati di eccitazione, perché gli stati a energia elevata hanno un tempo di vita brevissimo (≅ 10-13 s); a causa dell'accoppiamento del tipo (22), con le vibrazioni decadono agli stati eccitati di energia più bassa, che si annichilano solo per effetti radiativi e hanno tempi di vita piuttosto lunghi, dell'ordine del nanosecondo.
La luminescenza stimolata diventa molto importante quando si ha un'inversione di popolazione (elettroni nella banda di conduzione e buche nella banda di valenza). In tal caso si ottiene un guadagno rispetto alla radiazione incidente (un fotone produce un fotone aggiuntivo per transizione di ricombinazione elettrone-buca), che opportunamente utilizzato con riflessioni multiple produce radiazione laser.
g) Effetti ottici non lineari
Già si è accennato nell'introduzione alla grande importanza della risposta non lineare della corrente nei semiconduttori (silicio in particolare) nei circuiti di rivelazione delle microonde. Di enorme importanza sono anche le non linearità della risposta ottica dei cristalli semiconduttori, ora divenute di grande attualità anche se ancora non totalmente interpretate. Menzioniamone alcune brevemente.
Anzitutto va citata la generazione di seconda armonica 2 ω quando un fascio di luce di frequenza ω incide su un semiconduttore con la struttura cristallina della blenda, nel quale è assente la simmetria d'inversione. Similmente si ha produzione di battimenti ω1 + ω2 e ω1 - ω2 quando sono presenti due frequenze diverse. Questi processi producono polarizzazione al secondo ordine,
P(2) (ω1 ± ω2) = χ(2) (ω1, ± ω2) E (ω1) E (ω2), (25)
senza alcun assorbimento, perché la polarizzazione è sempre a frequenza ω1 ± ω2, diversa da quella dei campi.
Di grande utilità sono anche processi del terzo ordine in cui la suscettività è del tipo χ(3) (ω1, ± ω2, ± ω2); essi producono terze armoniche di frequenza ω1 ± 2 ω2, ma anche processi di assorbimento di due fotoni legati alla parte immaginaria di χ(3) (ω1, ω2, - ω2). Tali effetti sono misurabili con un esperimento in cui una radiazione di pompa, di frequenza ω2, incide sul semiconduttore e viene analizzato un fascio di prova di frequenza ω1. La parte non lineare è quella che risponde alle due sollecitazioni contemporanee.
A intensità molto elevate, il mezzo non lineare può produrre effetti di bistabilità, nei quali a una certa soglia di intensità la risposta ottica passa con discontinuità su una curva diversa e al diminuire dell'intensità si produce un ciclo di isteresi.
7. Conducibilità elettrica e mobilità
Quando gli elettroni o le buche si trovano in una data concentrazione vicino, rispettivamente, agli estremi delle bande di conduzione e di valenza, allora sono portatori di corrente come gli elettroni in un metallo.
Per quanto riguarda le proprietà di trasporto elettrico, nei semiconduttori esse sono date dalla (2), nella quale la mobilità può essere vista fenomenologicamente come la velocità media dei portatori di corrente nell'unità di campo elettrico. La mobilità dipende dai processi che diffondono il moto altrimenti libero delle cariche e può essere espressa nella forma:
dove il tempo medio τ tra le collisioni contiene tutti gli effetti microscopici; (1/τ) è la probabilità di diffusione dei portatori di carica, somma delle probabilità dovute agli urti con i fononi, le impurezze e le altre irregolarità del cristallo. Naturalmente, il calcolo microscopico di 1/τ è assai complesso e richiede di considerare non solo il campo elettrico applicato, ma anche il gradiente di temperatura dT/dx.
Tutto ciò è analogo a quanto avviene nel caso dei metalli e conduce a dipendenze simili della mobilità dalla temperatura, cioè proporzionalità a T-3/2 alle alte temperature per effetto fononico e indipendenza dalla temperatura a basse temperature, quando 1/τ è prevalentemente dovuto alle impurezze e al disordine reticolare. A campi elettrici elevati la mobilità dipende dal campo e insorgono effetti non lineari, dovuti a elettroni caldi con velocità che tende a saturare.
Analogamente ai metalli, si ha effetto Seebeck con formazione di differenza di potenziale agli estremi di un semiconduttore in presenza di gradiente termico, ed effetto Peltier con trasporto di calore in presenza di campo elettrico.
La caratteristica del trasporto nei semiconduttori consiste però nel fatto che i valori delle masse efficaci possono essere piccolissimi e quindi le mobilità possono assumere valori molto grandi. Inoltre, esse richiedono l'uso esplicito della statistica di Fermi solo quando il numero di particelle è sufficientemente grande da portare il livello di Fermi all'interno delle bande (semiconduttore degenere). È comunque il numero di portatori l'elemento che più influisce sul trasporto e al quale verrà dedicato qualche cenno nel capitolo seguente.
8. Numero di portatori, masse efficaci, proprietà statistiche
Il numero di portatori liberi in un semiconduttore varia con la temperatura secondo una funzione del tipo N exp
,
in cui l'energia di attivazione A e il coefficiente N dipendono dalla concentrazione e dal tipo di impurezze.
a) Semiconduttore intrinseco
In questo caso, per definizione, la concentrazione di impurezze è irrilevante. Allora l'eccitazione di ogni elettrone alla banda di conduzione produce una buca nella banda di valenza e pertanto ne = nh. In generale, il numero di elettroni può essere calcolato sommando tutti gli elettroni presenti al di sopra del gap Eg con la funzione di distribuzione di Fermi f =
e una densità degli stati disponibili che nell'approssimazione della massa efficace è g (E) dE =
E1/2 dE. Si ottiene una buona approssimazione trascurando il termine + 1 al denominatore della funzione di distribuzione f, che così coincide con la distribuzione di Boltzmann.
Calcolando gli integrali si trova per la densità di elettroni totale:
dove Ec è il minimo della banda di conduzione e, nel caso di massa anisotropa, me indica la media su tutte le direzioni e pesata sui minimi equivalenti. Se si vuole conoscere la densità di elettroni che hanno energia superiore a un certo valore eV0, basta aggiungere eV0 a Ec; di conseguenza, la (27) risulta moltiplicata per il fattore e-
Per la densità di buche, semplificando a una sola banda di valenza di massa efficace media mh e denotando con Ev il massimo della banda di valenza, si ottiene
Queste espressioni valgono sempre per i portatori liberi in equilibrio statistico, ma il valore del livello di Fermi distingue i vari casi. Tenendo conto dell'uguaglianza del numero di buche e di elettroni, si ottiene nel semiconduttore intrinseco
e
Il livello di Fermi del semiconduttore intrinseco è vicino alla metà del gap, ma spostato verso la banda di conduzione alle alte temperature, perché in generale me ≪ mh. Si può anche osservare che il prodotto ne nh è sempre una costante che dipende solo dal gap Eg e non dall'energia di Fermi (legge dell'azione di massa). A titolo di esempio, il valore di ne nh in silicio è 2, • 1019 cm-6 a 300 K.
b) Semiconduttore estrinseco
In questo caso si hanno impurezze che, come abbiamo visto, possono essere donatrici o accettrici; nel primo caso si introducono elettroni in eccesso nel semiconduttore, che viene detto di tipo n, nel secondo caso buche, e il semiconduttore è detto di tipo p. Gli stati legati di tali impurezze sono dati dalla (12) per il caso dei donatori, con la correzione aggiuntiva di cella centrale; le energie di legame sono in genere molto piccole (dell'ordine di 10 meV in Ge e di 50 meV in Si); si può perciò avere ionizzazione totale anche a temperature relativamente basse.
Con concentrazioni di impurezze anche piccole, dell'ordine di 1015 cm-3, il numero di portatori è dominato dalle impurezze in un largo intervallo di temperatura (regime estrinseco). Tale numero si ottiene allora trascurando i portatori intrinseci e considerando il numero di impurezze ionizzate calcolabili dalla funzione di distribuzione di Fermi, dalla densità di impurezze nd e dalle energie degli stati localizzati. Uguagliando tale numero all'espressione (27) si ottiene per il caso dei donatori
n ≅ (n0nd)1/2 e-Ed/2kT, (31)
dove
n0 = 2 (mekT/2 π ℏ2)3/2, (32)
ed Ed è l'energia di legame riferita al minimo della banda di conduzione.
Una simile espressione si ottiene per la densità di buche in un semiconduttore di tipo p con densità di impurezze accettrici na, energia di ionizzazione per le buche Ea riferita al massimo della banda di valenza e massa efficace media delle buche mh al posto di me.
Nel caso di semiconduttori con entrambi i tipi di impurezze, il calcolo dei due tipi di portatori è più complesso, ma prevale il tipo di portatori che corrisponde alle impurezze maggioritarie, perché esse compensano le altre. Si osservi che vale sempre, anche nel caso estrinseco, la legge dell'azione di massa
È anche importante valutare la posizione del livello di Fermi in un semiconduttore estrinseco. Nel caso di prevalenza di donatori, si può vedere subito dalla (27) che il livello di Fermi si sposta tanto più verso l'alto quanto più grande è il numero di impurezze ionizzate presenti, ossia che il livello di Fermi è tanto più vicino alla banda di conduzione quanto maggiore è la densità di elettroni. In modo simile si può mostrare che più diventa grande il numero di buche, più la posizione del livello di Fermi si sposta verso il massimo della banda di valenza.
In tutte le considerazioni svolte si prende in esame il caso in cui la concentrazione di impurezze è abbastanza piccola da non alterare le proprietà strutturali elettroniche del semiconduttore. Quando invece la concentrazione si avvicina al limite in cui le autofunzioni di impurezze diverse si sovrappongono (concentrazione dei portatori dell'ordine di 1018 cm-3), i livelli di impurezze si allargano a formare una banda, all'interno della quale si può avere conduzione. Per densità ancora più alte si mescolano i livelli di impurezze a quelli di banda. Il livello di Fermi entra nella banda e si ha un regime di degenerazione statistica con conduzione di tipo pseudometallico, in cui il numero di portatori non dipende più dalla temperatura.
Per verificare quanto detto e misurare il numero e il segno dei portatori, nonché le masse efficaci di elettroni e buche e la struttura elettronica degli estremi di banda, si possono citare due esperimenti fondamentali che nei semiconduttori hanno trovato importantissime applicazioni: l'effetto Hall e la risonanza di ciclotrone.
c) Effetto Hall
La forma tipica di un campione e i contatti necessari per effettuare misure di trasporto sono indicati nella fig. 15. I contatti sono ottenuti in modo tale da evitare le proprietà raddrizzanti del contatto metallo-semiconduttore e sono quindi contatti ohmici (in pratica, si interpone tra metallo e semiconduttore uno strato fortemente drogato con impurezze, che le cariche possono superare senza difficoltà). Tra i contatti A e B si applica un campo elettrico che produce una corrente che può essere misurata. La differenza di potenziale necessaria per ottenere la conducibilità del campione viene misurata tra i contatti C e D nel verso della corrente e tra i contatti E ed E′ in direzione perpendicolare. Si possono anche effettuare misure ottiche o a microonde con lo stesso campione incidendo con la radiazione in direzione opportuna e misurando la radiazione trasmessa o riflessa. Oltre alle misure standard, si può considerare l'effetto di un campo magnetico B perpendicolare al piano della fig. 15.
L'effetto Hall è dovuto al fatto che le cariche in moto con velocità media 〈v〉 = J/ne, in presenza di un campo magnetico vengono deviate dalla forza di Lorentz
,
e che tale forza deve essere compensata dal campo che si produce per accumulo di cariche sulle facce tra E ed E′ della fig. 15. Si ottiene: EHall = RHJ ∣B∣, con RH = 1/nec. Se le cariche sono positive, la costante cambia segno. In tal modo si può misurare la concentrazione e il segno dei portatori quando ne è presente un solo tipo. Quando sono presenti sia gli elettroni che le buche, si ottiene per la costante di Hall l'espressione
La misurazione simultanea della conducibilità e del coefficiente di Hall RH permette di conoscere le concentrazioni, se le mobilità sono note da misurazioni indipendenti sul materiale in esame. Dato che il numero dei portatori è molto più piccolo nei semiconduttori che nei metalli, l'effetto Hall è molto più grande e di facile misurazione nei semiconduttori. Da esso si sono ottenute misure di densità di portatori che confermano pienamente le considerazioni teoriche prima esposte. Riportiamo nella fig. 16 i risultati ottenuti per il silicio di tipo n debolmente drogato, in cui sono ben visibili le diverse regioni di temperatura, quella di comportamento intrinseco per T > 350 K, quella tra 350 K e 125 K in cui le impurezze sono tutte ionizzate, e quella sotto i 125 K in cui gli elettroni sono legati alle impurezze.
d) Effetto Hall quantistico
Un nuovo e inaspettato effetto è stato osservato nel 1980 da K. von Klitzing, G. Dorda e M. Pepper nel corso di misurazioni di effetto Hall in semiconduttori nei quali il moto degli elettroni era bloccato nella direzione del campo magnetico per effetto di un campo elettrico parallelo al campo magnetico all'interfaccia. In tal caso, se il campo magnetico è molto forte occorre tener conto della quantizzazione di Landau, e si osserva che quando il campo è tale da riempire totalmente un livello (cioè è un multiplo intero di
,
ricordando che la degenerazione dei livelli di Landau è
la resistività di Hall ρxy = Ex/Jy presenta un plateau, anziché aumentare linearmente al crescere di ∣B∣. Ciò è straordinario, perché la resistività mantiene il valore fisso di
con l'accuratezza di una parte su 107 per tutto l'intervallo in cui essa è costante al variare di ∣B∣, come se gli elettroni che formano uno stato incompleto fossero congelati e non contribuissero alla conducibilità. Altri plateaux sono poi stati trovati per n = 1/3, 2/3, 2/5 ..., il che ha presentato una problematica nuova per il gas di elettroni in due dimensioni: l'esistenza di stati di condensazione in corrispondenza di valori particolari della densità.
e) Risonanze di ciclotrone
La quantizzazione di Landau è stata osservata con grande precisione nei semiconduttori per mezzo di esperimenti di risonanza di ciclotrone. Questi consistono nel misurare l'assorbimento di una sorgente di microonde polarizzata perpendicolarmente al campo magnetico.
La transizione avviene tra il più alto livello occupato e il successivo livello vuoto, alla frequenza angolare data dall'espressione (14). L'osservazione richiede basse temperature e campioni puri, perché l'allargamento della transizione deve essere minore della separazione tra i livelli. In tal caso si osserva un picco di assorbimento nelle microonde alla frequenza opportuna, o a data frequenza con valore opportuno del campo magnetico. Se la massa efficace m è isotropa, come nel caso degli elettroni in GaAs, la frequenza della risonanza è ωc =
,
e non cambia al variare della direzione del campo magnetico. Se la massa ha due componenti mel e met, al variare della direzione rispetto all'asse principale dell'ellissoide cambia la frequenza di risonanza secondo la (14). Inoltre, poiché in tali casi l'estremo di banda non è al centro della BZ, come si vede per esempio dallo schema di bande di Si e Ge (v. figg. 3 e 4, rispettivamente), l'esistenza di diversi estremi, equivalenti in energia, per simmetria produce situazioni in cui θ è diverso con un'unica direzione del campo magnetico, e per un tipo di estremo si osservano più risonanze a direzione fissata. Tutto ciò consente di individuare le masse efficaci al massimo della banda di valenza e al minimo della banda di conduzione, e le rispettive posizioni nello spazio k. A titolo di esempio, si mostra nella fig. 17 una tipica curva di assorbimento in Ge, osservata per la prima volta nel 1953 da G. Dresselhaus, A. F. Kip e C. Kittel per una direzione fissata del campo magnetico. I valori misurati delle masse efficaci di elettroni e buche in Ge, Si e GaAs sono riportati nella tab. III, e concordano con i risultati dei calcoli descritti nei capp. 3 e 4.
9. Dispositivi a trasporto: raddrizzatori, transistor, circuiti integrati
Tra le innumerevoli proprietà che sono state usate nei più vari dispositivi dell'elettronica, ne menzioneremo qui soltanto alcune storicamente importanti e particolarmente significative.
a) Oscillatori di Gunn come generatori di microonde
Nel discutere la dipendenza delle proprietà di trasporto dalla mobilità e dal numero dei portatori, si è supposto che gli elettroni fossero vicini al minimo della banda di conduzione in base alla distribuzione statistica. In realtà, si può osservare che nelle bande di energia di molti semiconduttori si hanno diversi minimi con piccola separazione di energia rispetto al minimo assoluto. Nel caso del GaAs della fig. 6, per esempio, accanto al minimo principale Γ6 si hanno 3 minimi secondari X6, la cui energia supera quella del minimo di appena 0,1 eV. Con un campo elettrico sufficientemente elevato (o una compressione uniassiale) è possibile produrre una situazione in cui anche i minimi secondari sono popolati con elettroni. Poiché le mobilità nel minimo principale e quelle nei minimi secondari sono molto diverse (in generale quella nei minimi secondari è molto minore, perché le me sono maggiori e le collisioni con fononi più probabili), anche la conducibilità e le pendenze
risultano diverse. Pertanto, al di sopra di un campo elettrico critico si ha una brusca variazione di conducibilità, caratterizzata da una frequenza di modulazione, che per una lunghezza media di 100 µm e una velocità tipica di 107 cm/s è di circa 109 s-1.
Se il cristallo è inserito in un circuito risonante a frequenza uguale a quella propria, esso genera microonde a quella frequenza, in quanto dipolo oscillante. Se si fa in modo che il campo a radiofrequenza del circuito esterno abbia frequenza maggiore della frequenza propria, il dispositivo segue il circuito risonante e irradia alla frequenza voluta.
b) Giunzione metallo-semiconduttore
Sono i dispositivi più antichi, già menzionati nell'introduzione, che consentono di raddrizzare la corrente alternata e danno una risposta non lineare. Il loro funzionamento è immediatamente comprensibile mediante i concetti esposti precedentemente, a patto di tener conto del fatto che il livello di Fermi del gas di elettroni coincide con il potenziale chimico μ. Infatti, il potenziale chimico è l'energia libera che si deve fornire per aggiungere una particella al sistema che, nel caso del gas di elettroni, per il principio di esclusione, si porrà in uno stato la cui energia corrisponde all'energia di separazione fra stati vuoti e occupati, che è appunto l'energia di Fermi. Inoltre, si può dimostrare che il livello di Fermi coincide con il potenziale chimico anche nel caso in cui cada in una regione vuota di stati. Quando due cristalli vengono posti a contatto è essenziale, affinché si abbia equilibrio, che i potenziali chimici coincidano, altrimenti si produrrebbe uno spostamento di cariche per minimizzare l'energia. Nella fig. 18 si mostra lo schema di un contatto tra un metallo e un semiconduttore di tipo n; il contatto è stato stabilito attraverso un circuito esterno o per trasferimento tunnel di elettroni dal semiconduttore al metallo e i livelli di Fermi sono allineati. Il fatto che la superficie del semiconduttore sia carica positivamente produce una curvatura delle bande che crea una barriera locale (di Schottky) - in prima approssimazione corrispondente alla differenza di potenziale per gli elettroni - uguale alla differenza tra i due livelli di Fermi iniziali (se riferiti entrambi al livello di vuoto) ϕ = (Λ0 - χ), dove Λ0 è l'affinità del metallo e χ quella del semiconduttore (minimo della banda di conduzione), che all'incirca coincide con il livello di Fermi nei semiconduttori.
La spiegazione della proprietà raddrizzatrice della giunzione (v. Frova e Perfetti, 1977) si ottiene osservando che la corrente che va dal metallo al semiconduttore è data dall'equazione di Richardson e non dipende dalla tensione locale, ma solo dalla barriera ϕ:
dove A =
dipende dalle masse efficaci e da costanti universali. In condizioni di equilibrio una corrente uguale procede in senso opposto. Con un campo esterno, per quanto si è detto nel capitolo precedente, se il minimo della banda di conduzione del semiconduttore viene abbassato, il numero di portatori che può passare dal semiconduttore al metallo viene alterato del fattore e±eV/kT (dove la scelta del segno del potenziale definisce la polarizzazione diretta o inversa). Per la corrente dal semiconduttore al metallo si avrà quindi
e la densità di corrente totale sarà perciò
per un semiconduttore di tipo n.
Si vede in tal modo che solo in polarizzazione diretta si ha un apprezzabile passaggio di corrente (la risposta è ohmica per V piccolo e poi diventa non lineare), mentre in polarizzazione inversa il passaggio di corrente è minimo, e satura subito al valore AT2 e-
c) Giunzioni p-n ed eterogiunzioni
La spiegazione della funzione raddrizzatrice della giunzione p-n - costituita da due semiconduttori a contatto, uno con conducibilità n e l'altro con conducibilità p - è in linea di principio simile a quella che spiega la giunzione metallo-semiconduttore. In questo caso, però, è la diversa posizione nel gap del livello di Fermi per semiconduttori p e n a produrre per allineamento un dislivello di energia tra i minimi della banda di conduzione nei due tipi di materiale quando ha luogo il contatto. Questo implica un gradino di potenziale che gli elettroni devono superare per andare da n a p circa uguale alla differenza tra i due livelli di Fermi EF (n) - EF (p). Il numero di elettroni (e di buche) sempre presenti nella banda di conduzione n (e p) produce una corrente anche in assenza di campo esterno da n a p, a causa del gradiente di concentrazione alla giunzione (corrente di diffusione). A essa si oppone una corrente uguale e contraria di elettroni minoritari dal lato p al lato n (di campo o di generazione) dovuta al gradiente di potenziale elettrico e legata alla velocità con cui il semiconduttore p genera le cariche per ristabilire l'equilibrio statistico.
Se ora al sistema viene applicata una differenza di potenziale esterna, essa si stabilizza all'interfaccia (perché lì è la zona di massima resistenza) modificando la barriera, con il risultato di introdurre un fattore e±eV/kT nel numero dei portatori che hanno energia sufficiente a superare la barriera. Come conseguenza, la corrente di diffusione dei portatori che va contro la barriera aumenta dello stesso fattore e quindi la corrente nella direzione n → p risulta Js e±eV/kT. La corrente in direzione opposta non viene modificata e perciò la corrente alla giunzione sarà
J = Js (e±eV/kT - 1). (38)
Un esempio di corrente in funzione della tensione, per il caso di una giunzione p-n nel silicio, è riportato nella fig. 19. Da considerazioni più accurate delle equazioni di diffusione con campo elettrico nella giunzione si può ricavare la celebre relazione di Schottky per la corrente di saturazione
dove De e Dh denotano i coefficienti di diffusione, Le e Lh i cammini liberi medi di diffusione, e ne e nh le concentrazioni all'equilibrio di elettroni e buche (con forte estrinsecità si può scrivere
e
,
dove nA e nD sono le concentrazioni di impurezze). Per le applicazioni è importante che la corrente di saturazione inversa Js sia la più piccola possibile per evitare rumori, e quindi conviene mantenere a un basso valore la concentrazione di portatori intrinseci. Per questo il Si, che ha gap più grande, è superiore al Ge come rivelatore di microonde. D'altra parte, all'aumentare del gap aumentano le me (v. eq. 9) e quindi diminuiscono le mobilità. La scelta tecnologica richiede di ottimizzare gli effetti contrastanti.
Risultati del tutto simili si ottengono per le eterogiunzioni, nelle quali i semiconduttori sono intrinseci ma di tipo diverso; l'allineamento dei livelli di Fermi implica che il semiconduttore con gap maggiore è a potenziale più alto e agisce come il semiconduttore di tipo p nella giunzione p-n. La varietà di diodi è enorme e ne esistono versioni molto sofisticate: per esempio, il diodo p-i-n ha uno strato intrinseco (i ) che risulta svuotato di portatori e pertanto assicura una capacità costante. Inoltre, i campi sono molto più deboli perché la tensione V cade nella regione i di spessore elevato, il che consente di misurare tensioni molto grandi per le quali si avrebbe rottura dielettrica nei diodi normali.
In tutti i casi si produce comunque iniezione di portatori nelle regioni di carica spaziale (agli estremi della regione di contatto tra i semiconduttori). Gli studi dettagliati del fenomeno, influenzato dalle condizioni superficiali di contatto, sono molto complessi; tuttavia, i parametri rilevanti possono essere misurati sperimentalmente con risultati perfettamente riproducibili. Un effetto molto importante dal punto di vista applicativo è la costante di tempo con cui il diodo risponde al cambiamento di polarità da diretta a inversa, ovvero il tempo necessario perché i portatori minoritari in eccesso spariscano e si stabilisca la nuova distribuzione statistica. Questo tempo caratteristico dipende da molte circostanze e dal tipo di materiali, e per le applicazioni è importante che sia il più piccolo possibile (inferiore al nanosecondo per le microonde).
d) Transistor
Il più semplice dei transistor è una doppia giunzione p-n-p (oppure n-p-n), come quella indicata nello schema della fig. 20. La giunzione p-n funge da ‛emettitore': in essa elettroni e buche passano in condizione di polarizzazione diretta; si considera un drogaggio elevato che garantisca un gran numero di buche nello strato p, il quale pertanto viene denotato p+. La giunzione n-p all'estremo opposto funge da ‛collettore' e in essa si diffondono soltanto le buche per caduta diretta, essendo in polarizzazione inversa. Il contatto al semiconduttore centrale di tipo n ha funzione analoga alla griglia delle valvole a vuoto e costituisce la ‛base'.
In presenza del potenziale applicato e del potenziale di base le tre correnti IE = IEh (buche) + IEe (elettroni), IC = ICh e IB fluiscono nelle direzioni indicate nella fig. 20 e si può ottenere amplificazione, in quanto una piccola corrente di elettroni nella base controlla la ben maggiore corrente di buche al collettore.
La ragione fisica per cui il transistor bipolare descritto è un amplificatore per IB sta nel fatto che si richiede neutralità nella regione base del transistor, e quindi se si aumenta il flusso di elettroni in essa aumenterà anche il flusso di buche dall'emettitore al collettore in modo da mantenere la neutralità di carica nella base. Il fattore di guadagno viene espresso in funzione del fattore che governa la percentuale di corrente γ =
,
dovuta alle buche nella giunzione emettitrice, e della percentuale di buche che arriva al collettore per diffusione IC = BIEh. Essendo IB = IEe + (1 - B) IEh, si ottiene:
Scegliendo una base sottile e semiconduttori con impurezze ben controllate si ottengono valori tipici di β dell'ordine di 100. Semiconduttori a gap indiretto come il Ge e il Si sono per questo favoriti, in quanto la ricombinazione indiretta di elettroni e buche nella base è meno probabile e il tempo di vita è lungo, mentre semiconduttori a bassa massa efficace come GaAs hanno il vantaggio di una maggiore mobilità. È importante che il tempo di transito dei portatori attraverso la base sia breve, non solo per ottenere un grande guadagno, ma soprattutto per rivelare campi di alta frequenza (radiofrequenze e microonde). Vengono impiegati vari artifici per accelerare i portatori con un gradiente di impurezze o con una lega a concentrazione variabile nello spazio (semiconduttori a composizione graduata), e questo è un campo in fase di costante evoluzione (v. semiconduttori: Superreticoli e microstrutture artificiali, vol. XI).
Anziché amplificare la corrente di base IB è possibile modulare la corrente IC con un campo applicato sulla base e in tale caso si ottiene rivelazione di campi molto deboli. Questi transistor sono detti ‛a effetto di campo' perché si controlla la conducibilità di un canale con un debole campo elettrico applicato. Mostriamo, come esempio, nella fig. 21 un tipico transistor a effetto di campo, costruito sulla superficie di un semiconduttore, utilizzando come contatti dei canaletti metallici scavati nell'isolante (ossido) che ricopre la superficie. Tali nozioni sono racchiuse nella sigla MOSFET (Metal Oxide Semiconductor Field Effect Transistor), e i vantaggi che questo tipo di transistor offre sono già evidenti a un esame della fig. 21. Tra l'altro, quando il campo elettrico applicato localizza gli elettroni nella direzione del campo, il moto delle cariche è bidimensionale vicino alla superficie di separazione ossido-semiconduttore.
e) Memorie
Una variante del MOSFET particolarmente utile nei microprocessori può essere usata come dispositivo di memoria. Uno strato metallico, separato dalla porta da un sottilissimo strato isolante, può trovarsi in due stati: uno stato vuoto di cariche elettriche che non influisce sulla conducibilità tra la sorgente (emettitore, source) e il collettore (drain) e uno stato in cui cariche elettriche sono state intrappolate dal semiconduttore di base (porta, gate) per effetto tunnel stimolato. Nel secondo stato il transistor non funziona più perché il campo che si produce sposta le bande in modo da opporsi al passaggio di corrente nella base.
Il passaggio dal primo al secondo stato è la ‛scrittura', che avviene con un breve impulso di campo il quale stimola l'effetto tunnel dalla base alla piastrina metallica. La ‛lettura' viene fatta controllando la corrente nel circuito source-drain e verificando l'assenza di amplificazione. La memoria si può cancellare inviando un impulso di polarità opposta a quella usata per la scrittura, o togliendo gli elettroni intrappolati dalla piastrina metallica per effetto fotoelettrico con l'illuminazione. Nella fig. 22 è presentato un reale elemento di memoria tecnologicamente avanzato che funziona sulla base del principio descritto.
f) Circuiti integrati
La tecnologia di fabbricazione dei MOSFET e delle memorie descritte consiste nel ricoprire la superficie del semiconduttore con uno strato di ossido e nel tracciare incisioni in tale strato secondo linee opportunamente disegnate con un pennello di elettroni o un'immagine ottica. Sulle incisioni si fanno diffondere impurezze opportune, dove si vuole creare il semiconduttore di tipo opposto a quello del substrato (impurezze pentavalenti in Si, se il supporto è di tipo n, come nella fig. 21). Facendo evaporare un metallo conduttore nelle scanalature si producono transistor dove sono state diffuse le impurezze, come nella fig. 21, o memorie con deposizione e ossidazione successiva, come nella fig. 22. Il metallo conduttore agisce da gate, source e drain e viene poi collegato mediante un circuito elettronico opportuno.
L'idea del circuito integrato, che Robert N. Kilby e Jack S. Noice realizzarono per primi negli anni sessanta, è semplice ma geniale. Consiste nel costruire l'intero sistema di circuiti elettronici (conduttori, diodi, transistor, memorie ed elementi capacitativi) sulla superficie del semiconduttore, usando i canali metallici come elementi conduttori. Ciò consente una miniaturizzazione dei circuiti su una scala impensabile con fili conduttori tradizionali. Il limite attuale è quello delle tecniche fotolitografiche (incisione su un photoresist che poi viene eliminato con attacco chimico); esse oggi consentono di costruire circuiti con elementi a distanze dell'ordine di 1 µm. La minima distanza teorica utilizzabile è però mille volte inferiore, dell'ordine delle distanze interatomiche nei cristalli, e progressi nella miniaturizzazione sono ancora possibili. I problemi da affrontare nel mondo dei circuiti integrati sono soprattutto di carattere tecnologico: richiedono la conoscenza degli stati superficiali che alterano localmente le bande di energia in modo spesso non controllabile e la conoscenza delle impurezze, con livelli profondi che catturano elettroni e buche e ne limitano il tempo di vita; inoltre, la risoluzione nei processi litografici che permettono la costruzione dei circuiti alla superficie è limitata dalla lunghezza d'onda della radiazione. Al momento attuale, la tecnologia del silicio sembra insuperabile, anche per ragioni economiche, dato che il silicio è facilmente disponibile a bassissimo costo. Per questo si definisce ‛autostrada al silicio' il nuovo modo di convogliare informazioni. Un esempio di chip su base di silicio, contenente molte migliaia di componenti e transistor interconnessi, è mostrato nella fig. 23.
10. Dispositivi optoelettronici: celle fotovoltaiche, laser
Parallelamente agli sviluppi nel campo dell'elettronica, i semiconduttori hanno profondamente contribuito alla conoscenza e all'utilizzazione dei processi di conversione della luce in energia elettrica, e viceversa. Vengono descritti nel seguito i dispositivi più importanti e gli effetti fisici di base.
a) Fotocelle e sensori di immagine
I dispositivi più antichi e familiari, perché usati da ogni fotografo, sono basati sul fatto che l'esposizione a radiazioni con frequenza superiore al gap (hgr;n > Eg) produce transizioni di elettroni alla banda di conduzione, con creazione di elettroni e buche liberi nelle rispettive bande di energia. Tali particelle conducono la corrente quando al cristallo viene applicata una differenza di potenziale, e la misura di tale fotoconducibilità consente di rivelare l'intensità dei fotoni incidenti e la loro frequenza. Naturalmente, l'intensità della fotocorrente dipende dalla mobilità e dal numero di portatori generati, che è legato ai processi fondamentali di assorbimento di radiazione sopra la soglia descritti nel cap. 6, ma dipende anche dal tempo di vita dei portatori prima della ricombinazione o della cattura da parte di impurezze.
Vicino alla superficie si hanno anche processi di fotoemissione di elettroni, analoghi ai processi di fotoemissione nei metalli. In questo caso si hanno fotocelle convenzionali con correnti di elettroni nei tubi a vuoto. Le fotocelle utilizzano i più diversi semiconduttori, in relazione alla lunghezza d'onda della luce da rivelare, dall'InSb per l'infrarosso lontano al CdS per il visibile. Una variante è costituita dai rivelatori di particelle elementari con alta energia, nei quali i portatori di corrente sono prodotti da una singola ionizzazione per urto e da successive ionizzazioni a valanga.
Un'applicazione molto utile dei processi descritti è la trasduzione di un'immagine bidimensionale in impulsi elettrici alla superficie di un tubo a raggi catodici. Quando il pennello di elettroni esplora la superficie coperta da un semiconduttore, le zone illuminate diventano fotoconduttrici, determinando localmente una scarica elettrica la quale modifica la riflessione di elettroni del pennello, che nelle zone illuminate non è più totale. Il segnale video viene così registrato come segnale elettrico della corrente in corrispondenza a una posizione sullo schermo. Il processo opposto, in cui è il campo elettrico prodotto dagli elettroni incidenti a popolare gli stati eccitati e produrre luce per ricombinazione, consente di trasformare l'informazione elettrica in luce emessa da punti specifici dello schermo del fototubo.
b) Rivelatori fotovoltaici e celle solari
Lo schema di un rivelatore fotovoltaico con il suo circuito equivalente è mostrato nella fig. 24. Le coppie elettrone-buca in eccesso, prodotte dalla radiazione in una parte del cristallo, migrano in direzioni opposte a causa della caduta di potenziale descritta precedentemente per le giunzioni di vario tipo. Si ha passaggio di corrente anche senza applicazione di un potenziale esterno, con trasformazione di energia luminosa in energia elettrica. I materiali più comunemente usati sono Ge e Si, essendo il Ge più efficace all'infrarosso perché di gap minore. Si usa anche amplificare la corrente introducendo un potenziale esterno che accelera i portatori in eccesso nella direzione di facile caduta e produce un aumento nel numero dei portatori per ionizzazione a valanga.
Una variante utilissima dei principî esposti si ha nelle celle solari, che consentono un'utilizzazione pratica dell'energia della radiazione solare. Perché tale utilizzazione sia efficiente occorre utilizzare un semiconduttore che abbia gap di energia vicino al massimo dello spettro di emissione solare (circa 5.400 Å); in tal modo, gli elettroni vengono prodotti dalla transizione ottica in prossimità del minimo della banda di conduzione e perdono poca energia per produzione di fononi mentre conducono la corrente. Questa è la ragione per cui il GaAs è di gran lunga il materiale più adatto, con efficienze superiori al 25%; anche il Si è assai utilizzato, con efficienze ideali vicine al 20% ed efficienze reali vicine al 10%.
Un limite insuperabile all'efficienza della conversione sta nel fatto che lo spettro solare è esteso su un ampio intervallo di frequenze e che necessariamente molte transizioni hanno luogo a frequenze molto più elevate del gap, con dissipazione dell'energia in eccesso. Un modo possibile di ovviare a tale inconveniente consiste nel produrre leghe di semiconduttori a concentrazione graduata spazialmente. In tal modo la caduta di potenziale tra i valori Eg del semiconduttore a gap maggiore è distribuita su tutto il campione, anziché essere localizzata all'interfaccia, e ogni frequenza inizia a essere assorbita in una zona diversa del cristallo, in corrispondenza di ℏω = Eg (z). Facendo incidere la luce sulla faccia con gap massimo si assorbono le frequenze più elevate, e via via che la luce penetra nel campione gli assorbimenti hanno luogo in prossimità della soglia, minimizzando le perdite di energia per creazione di fononi. Naturalmente le difficoltà tecniche sono notevoli, perché la lega produce disordine e diminuisce il tempo di vita dei portatori, ma potrebbero essere superate con cadute di potenziale a gradino (v. semiconduttori: Superreticoli e microstrutture artificiali, vol. XI).
c) Laser
La luminescenza stimolata produce un'emissione di luce nei diodi emettitori LED (Light Emitting Diodes), che può essere amplificata in condizioni particolari e generare luce laser (v. laser e fotonica, vol. XI).
Occorre subito osservare che in questo caso, contrariamente a quanto vale per le proprietà elettroniche, è molto utile avere una probabilità di transizione elevata, perché si utilizza la ricombinazione elettrone-buca anziché il trasporto di cariche. I semiconduttori utili sono perciò quelli a gap diretto, in particolare l'arseniuro di gallio (GaAs), il cui schema a bande è quello della fig. 6, con gap diretto a ~ 1,5 eV a 77 K, di cui si mostra nella fig. 25 lo spettro di emissione. È anche possibile usare leghe contenenti Al se si vuole aumentare il gap (AlAs ha gap diretto molto maggiore, 2,4 eV), oppure In se si vuole diminuire il gap (InAs ha gap diretto molto minore, ~ 0,1 eV). È evidente che, se si riesce a ottenere una situazione in cui si abbiano in permanenza elettroni al minimo della banda di conduzione che popolano l'intervallo ΔEc e buche che popolano l'intervallo ΔEv al massimo della banda di valenza, si ha la cosiddetta inversione di popolazione per le frequenze che corrispondono all'intervallo ΔE + ΔEv al di sopra del gap Eg, e si può avere guadagno laser utile per l'amplificazione.
Tale inversione di popolazione è facilmente ottenibile, per esempio in una giunzione degenere, con un elevato drogaggio di impurezze sia nel lato p che nel lato n, come mostrato nello schema della fig. 26. Per polarizzazione diretta con campo esterno, nella regione p vicino alla giunzione, la distribuzione statistica produce inversione di popolazione, come indicato in fig. 26B, e si ha passaggio di corrente per effetto tunnel (il valore della corrente dipende dalla barriera superficiale da superare) e per iniezione. La corrente che attraversa la giunzione crea le condizioni per emissione stimolata, con conversione di energia elettrica in energia ottica a ogni ricombinazione elettrone-buca.
La regione attiva deve essere limitata nelle direzioni perpendicolari ai piani della giunzione, in modo da avere riflessione totale alla superficie e da non perdere radiazione. Per l'uso pratico del laser occorre inoltre limitare il campione nella direzione dell'emissione di luce con specchi o con le stesse superfici del cristallo rese riflettenti e poste a distanza opportuna, in modo da realizzare le condizioni Fabry-Perot (percorso multiplo della lunghezza d'onda) e da esaltare enormemente il fattore di guadagno per i modi risonanti della cavità ottica.
Da quanto abbiamo visto, l'effetto laser si verifica su tutto il piano della giunzione, il che provoca perdite nella direzione normale alla direzione di emissione stimolata prescelta. Questo può essere evitato quasi totalmente limitando l'estensione della zona attiva nella giunzione anche nella direzione normale alla direzione di propagazione del fascio luminoso, in modo che si abbia una geometria praticamente unidimensionale, in cui la direzionalità del materiale attivo coincida con la direzione di propagazione della luce laser. Nella fig. 27 si mostra, per esemplificazione, una struttura unidirezionale costruita con eterogiunzioni di GaAs, o Ga1-xInxAs per l'infrarosso più lontano, confinate da strati di Ga1-xAlxAs, con gap di energia maggiore, e attivate in una regione ristretta per effetto del campo applicato su un canale metallico della larghezza di pochi µm, dal quale la corrente passa al metallo di supporto alimentando l'emissione stimolata. La radiazione si propaga soltanto nella direzione del piano perpendicolare alla corrente perché è confinata nel GaAs, o nel GaInAs, da riflessione totale sulle pareti ed è mantenuta nella direzione voluta dal confinamento laterale della zona attiva.
I vantaggi dei laser a semiconduttori rispetto ai laser a gas sono la compattezza e il basso costo, e ciò ne ha reso possibili le applicazioni più disparate anche nelle attività quotidiane (rilevamento di distanze, livellamento dei terreni, in particolare dei campi di riso, lettura di dischi, ecc.). Di grande interesse è la possibilità di generare la radiazione laser e trasportarla in fibra ottica, allo scopo di trasmettere otticamente una quantità altrimenti impensabile di informazioni.
11. Nuovi materiali. Superreticoli e microstrutture
a) Nuovi materiali
Nell'ultimo decennio del secolo ci si è dedicati alla ricerca di un'immensa varietà di materiali nuovi, che sviluppando le nozioni e le tecnologie dei semiconduttori descritte precedentemente riescono a produrre effetti nuovi che per varie ragioni non sono osservabili nei semiconduttori tradizionali.
Anzitutto sono da menzionare i materiali amorfi, o costituiti da microcristalli così piccoli da non potersi applicare a essi i concetti di bande di energia generalmente associati all'ordine cristallino. I procedimenti tecnici di preparazione sono vari: raffreddamenti rapidi dal fuso, deposizione da plasma, deposizione da vapore, bombardamento ionico. Tra tali materiali sono di particolare interesse il silicio amorfo, il silicio poroso e vari tipi di vetri e sostanze ceramiche (isolanti con piccoli aggregati di atomi metallici al loro interno). Il loro uso in elettronica è ostacolato dalla scarsa mobilità dovuta alla diffusione delle cariche da parte delle fluttuazioni del potenziale, anche se nuovi effetti sono stati trovati proprio grazie a tali fluttuazioni del potenziale dovute al disordine; in particolare, è da menzionare la localizzazione dei portatori introdotta da P. W. Anderson, che produce stati legati nel gap e consente di definire un livello di mobilità che separa gli stati che non conducono (a causa del disordine o per la presenza di impurezze) dagli stati delocalizzati responsabili delle proprietà di trasporto. Nella fig. 28 si riporta, per esempio, lo schema della densità di stati in un semiconduttore amorfo, con l'indicazione degli stati di conduzione e degli stati localizzati per disordine e per impurezze. Ciò implica anche il passaggio da uno stato di resistività elevata a uno stato di bassa resistività sopra un valore critico del campo elettrico, con possibilità di utilizzazione come interruttore. Le proprietà ottiche dei materiali amorfi sono particolarmente interessanti, perché il disordine strutturale migliora l'efficienza dell'assorbimento in quanto si può violare la regola di selezione Δk ≅ 0 per le transizioni ottiche. Questo fa sì che si possano avere buoni assorbimenti di luce su strati sottilissimi di silicio amorfo, e ottenere come applicazione conversione diretta dell'energia solare con efficienza superiore al 15%.
Un'altra possibilità interessante è costituita dai semiconduttori organici, non molto usati in elettronica per la scarsa mobilità dei portatori e il loro forte accoppiamento con le vibrazioni reticolari. Ma ora che la tecnologia consente di ottenere deposizioni di materiale organico su semiconduttori inorganici, l'accoppiamento tra le eccitazioni nei due materiali consente effetti nuovi all'interfaccia (eccitoni ibridi, bistabilità ottica, ecc.).
Ma i nuovi materiali più comunemente usati nella fisica dei semiconduttori e nei dispositivi sono le microstrutture, costruite controllando a livello atomico la crescita epitassiale di semiconduttori di tipo diverso (per esempio, con fasci atomici o con deposizione chimica di vapori). È forse utile parlarne brevemente per rilevare alcuni punti di interesse, anche per la novità dei processi fisici realizzati.
b) Superreticoli
Si tratta di strati con un numero controllato di piani atomici di un tipo di semiconduttore, alternati a strati di un semiconduttore di tipo diverso, come indicato nella fig. 29.
In tale caso la periodicità di traslazione nella direzione di crescita non è più fissata dai valori delle distanze interatomiche, ma è un suo multiplo prefissato e grande a piacere. Ciò consente di produrre superreticoli con anisotropia controllata; le bande di energia sono bande normali nelle direzioni dei piani di crescita, ma hanno carattere di bande unidimensionali di piccola larghezza per le onde di Bloch nella direzione di crescita (minibande).
Tra i nuovi effetti quantistici di tali superreticoli è importante il fatto che in essi è possibile ottenere oscillazioni di Bloch. È cioè possibile, in conseguenza della diminuzione dello spessore della BZ, che gli elettroni attraversino tutta la BZ senza essere diffusi da vibrazioni o impurezze, e al confine di zona invertano la quantità di moto per aggiunta di un vettore del reticolo reciproco di segno opposto. Un campo elettrico applicato genera così oscillazioni elettroniche di tipo balistico, più controllabili delle oscillazioni Gunn descritte nel cap. 9, § a.
c) Microcavità
Un'altra possibilità interessante dei superreticoli è la capacità di creare specchi di Bragg nelle regioni otticamente trasparenti, mediante l'alternarsi di strati, a e b, di diverso indice di rifrazione e di lunghezza uguale a un quarto della lunghezza d'onda della luce che attraversa il campione. Questo ha suggerito la possibilità di produrre cavità per le radiazioni ottiche, in qualche modo analoghe alle cavità a microonde che tanta importanza hanno avuto nel concentrare energia elettromagnetica e nel realizzare radar e televisione. Riportiamo nella fig. 30 alcuni risultati preliminari per tali microcavità. Si apre concettualmente la possibilità di concentrare una sufficiente quantità di radiazione infrarossa, prodotta, ad esempio, da un laser a semiconduttore, in modo da consentire la trasmissione di informazioni ad altissima frequenza (1015 Hz) mediante fibre ottiche.
d) Pozzi quantici
Un effetto interessante si osserva quando gli strati confinati di semiconduttore b sono così lontani fra loro che ognuno di essi può essere considerato come un sistema separato, in cui la simmetria di traslazione è completamente interrotta nella direzione di crescita da un potenziale ‛a pozzo', come indicato nella fig. 29B. Un classico esempio è il GaAs (gap 1,42 eV a T = 300 K), con spessori dell'ordine di 80 Å, confinato da Ga1-xAlxAs (x ≅ 0,3, gap ≅ 1,9 eV). Tale sistema è il più comunemente utilizzato perché GaAs e AlAs hanno lo stesso parametro reticolare e sono miscibili senza creare tensioni interne.
Le bande di energia si hanno soltanto nello spazio bidimensionale perpendicolare alla direzione di crescita. Lungo la direzione di crescita, il potenziale della fig. 29B crea stati discreti, che per gli elettroni sono in prima approssimazione (quando si supponga infinito il potenziale di confinamento):
se riferiti al minimo della banda di conduzione del materiale che costituisce il pozzo.
Il calcolo per le buche è particolarmente complesso, perché occorre tenere conto della matrice di Luttinger al massimo della banda di valenza. Tuttavia, si può osservare che il potenziale a pozzo nella direzione z produce anche a k = 0 una separazione per simmetria tra le buche a massa pesante e le buche a massa leggera e, usando una formula simile alla (41) con le masse appropriate alle buche, l'energia delle buche pesanti risulta essere più vicina al massimo della banda di valenza di quella che si riscontra nelle buche leggere.
Una prima conseguenza della distribuzione dei livelli indicati è che sia gli elettroni che le buche vengono attirati nelle posizioni dello spazio che definiscono i pozzi quantici (QW).
Per quanto riguarda le proprietà elettroniche di trasporto, l'accumulazione di elettroni e buche in eccesso nelle regioni dei pozzi rende possibile aumentare enormemente le mobilità, perché le impurezze che donano elettroni o buche possono essere poste nelle barriere (modulation doping); i portatori sono attirati nei pozzi e nel loro moto planare non vengono diffusi dai potenziali delle impurezze ionizzate, come accade invece nei semiconduttori drogati.
La spaziatura tra le sottobande bidimensionali può inoltre essere verificata in base alla (41), mediante il controllo della larghezza dei pozzi e anche del potenziale di confinamento, e ciò è utile per la rivelazione di radiazione nel lontano infrarosso.
Nel campo delle proprietà ottiche nel vicino infrarosso e nel visibile assumono un ruolo rilevante gli eccitoni bidimensionali. La loro energia di legame è maggiore che nel cristallo tridimensionale e anche la loro forza di oscillatore è molto maggiore a causa del confinamento di buca ed elettrone. Per questo la luminescenza emessa per ricombinazione elettrone-buca ha dei picchi molto intensi in corrispondenza a eccitoni di buche pesanti e di buche leggere. Come esempio viene riportato nella fig. 31 uno spettro di fotoemissione stimolata a bassa temperatura in un pozzo quantico, che si può confrontare con la fluorescenza di GaAs della fig. 25. Al crescere della temperatura il picco si sposta e aumenta il contributo del picco a buche leggere e delle transizioni interbanda.
Le possibilità che i pozzi quantici offrono in conseguenza di un tale guadagno nella probabilità di ricombinazione elettrone-buca sono già state utilizzate nella produzione di laser a semiconduttori, con il vantaggio della migliore risoluzione spettrale e il controllo della frequenza di emissione mediante la scelta della larghezza dei pozzi.
e) Fili quantici e punti quantici
A partire dagli anni novanta, è stato possibile costruire microstrutture in cui il materiale semiconduttore a gap minore viene confinato anche lateralmente, o con attacco chimico di pozzi quantici lungo righe nel piano di crescita, o con crescita controllata di semiconduttori che introducono sforzi interni (per es. GaxInxAs in GaAs di diverso parametro reticolare). In tal modo si producono pozzi quantici filiformi, a simmetria di traslazione in una sola dimensione, i cosiddetti fili quantici (QWW).
In questo caso le particelle intrappolate per confinamento quantico hanno mobilità elevata solo in una direzione prescelta. Tale direzionalità è particolarmente importante negli effetti optoelettronici, perché anche i modi di propagazione delle onde elettromagnetiche (i polaritoni) sono unidirezionali e conferiscono ai fili quantici proprietà di guide di luce. Inoltre, le probabilità di transizione dipendono fortemente dalla direzione del campo elettrico rispetto ai fili, con rilevanti effetti di polarizzazione.
Un'ulteriore possibilità di grande interesse si è concretizzata negli anni novanta con il confinamento di un semiconduttore da parte di un altro semiconduttore a gap maggiore in tutte e tre le direzioni. Si ottengono in tal modo i punti quantici (QD), che catturano le particelle in livelli discreti, perché il confinamento in tutte le direzioni produce stati localizzati ben definiti. Ad essi si possono applicare tutte le proprietà della spettroscopia atomica, con il vantaggio che la posizione dei livelli può essere controllata variando le dimensioni dei punti quantici.
Queste, naturalmente, sono solo le prime e più evidenti possibilità offerte dalle microstrutture (per una più dettagliata discussione di questo argomento, v. semiconduttori: Superreticoli e microstrutture artificiali, vol. XI). Una possibilità che è opportuno menzionare è l'esaltazione degli effetti non lineari che queste strutture rendono possibile per la loro simmetria ridotta. A titolo di esempio, viene mostrata nella fig. 32 una risposta bistabile ottenuta con fili quantici.
BIBLIOGRAFIA
Bassani, F., Methods of band calculations for III-V compounds, in Semiconductors and semimetals (a cura di R. K. Willardson e A. C. Beer), New York-London 1966, vol. I, pp. 24 ss.
Bassani, F., Pastori Parravicini, G., Electronic states and optical transitions in solids, Oxford 1974.
Dalven, R., Introduction to applied solid state physics: topics in the applications of semiconductors, superconductors, and the nonlinear optical properties of solids, New York 1980.
Fiorani, D., Sberveglieri, G. (a cura di), Fundamental properties of nanostructured materials: proceedings of the National School of the Condensed Matter Group, Rimini, Italy, September 20-25, 1993, Singapore-River Edge, N. J., 1994.
Frova, A., Perfetti, P., Semiconduttori: proprietà e applicazioni elettroniche, Roma 1977.
Hollmann, H. E., Physik und Technik der ultrakurzen Wellen, 2 voll., Berlin 1936.
Kittel, C., Introduction to solid state physics, New York 1953, 19967 (tr. it.: Introduzione alla fisica dello stato solido, Torino 1971, 19934).
Mathieu, H., Physique des semiconducteurs et des composants électroniques, Paris 1987, 19963.
Seitz, F., The modern theory of solids, New York-London 1940.
Seitz, F., The tangled prelude to the age of silicon electronics, in ‟Proceedings of the American Philosophical Society", 1996, CXL, pp. 289-337.
Sze, S. M., Physics of semiconductor devices, New York 1969 (tr. it.: Fisica dei dispositivi a semiconduttore, Milano 1973).
Weisbuch, C., Vinter, B., Quantum semiconductor structures: fundamentals and applications, Boston 1991.
Wilson, A. H., The theory of metals: based on an essay awarded the Adams prize in the University of Cambridge, 1931-1932, Cambridge 1936.
Yu, P. Y., Cardona, M., Fundamentals of semiconductors: physics and materials properties, Berlin-New York 1996.
Superreticoli e microstrutture artificiali di Federico Capasso
Sommario: 1. Introduzione: ingegneria della struttura elettronica a bande e suoi elementi costitutivi. 2. Lanciatori balistici. 3. Microstrutture a gap graduato. 4. Microstrutture a effetto tunnel risonante. 5. Trasporto nei superreticoli. 6. Laser a cascata quantica. 7. Pozzi quantici pseudomolecolari con forti proprietà ottiche non lineari. 8. Ottica elettronica: filtri Fabry-Perot e stati legati al di sopra della buca di potenziale. 9. Modulazione artificiale delle discontinuità di banda. 10. Conclusioni. □ Bibliografia.
1. Introduzione: ingegneria della struttura elettronica a bande e suoi elementi costitutivi
Durante lo scorso decennio, lo sviluppo di una nuova e potente tecnologia ha consentito di progettare strutture di semiconduttori con interessanti proprietà elettroniche e ottiche. Questa ingegneria del gap, o più in generale della struttura a bande, ha prodotto una nuova generazione di materiali semiconduttori e di dispositivi elettronici e fotonici (v. Capasso, 1983 e 1987). Alla base dell'ingegneria del gap vi è la possibilità di variare a piacere la composizione e il contenuto di impurezze (drogaggio) di un semiconduttore su distanze che possono variare da pochi micrometri fino a circa 2,5 Å, valore tipico di uno strato monoatomico; ciò consente di modellare a piacere (in maniera quasi continua) la struttura elettronica a bande di un materiale. Possono così essere prodotte, anche in vista di applicazioni specifiche, strutture artificiali con nuove proprietà elettroniche e ottiche.
In questo capitolo si riassumono le tappe fondamentali nello studio delle eterostrutture di semiconduttori, dagli anni cinquanta fino agli anni ottanta, mentre nei capitoli successivi cercheremo di fornire una descrizione intuitivamente comprensibile dell'ingegneria del gap e delle sue applicazioni mediante l'uso sistematico di diagrammi di energia. Molti degli esempi specifici sono presi da risultati ottenuti ai Bell Laboratories nel campo delle proprietà elettroniche, ottiche, fotoniche e di trasporto di semiconduttori strutturati artificialmente.
Una rappresentazione schematica dell'energia degli elettroni negli elementi costitutivi essenziali dell'ingegneria del gap è fornita dai diagrammi della fig. 1, che mostrano le variazioni degli estremi della banda di valenza e di conduzione al variare della posizione all'interno del materiale; tali diagrammi sono di grande aiuto per visualizzare il moto di elettroni e buche in queste strutture artificiali, nonché le loro proprietà ottiche e il funzionamento dei dispositivi. Nella fig. 1A è rappresentato il diagramma per il semiconduttore omogeneo; Ec ed Ev indicano gli estremi della banda di conduzione e di valenza, rispettivamente; Eg è il gap, cioè l'intervallo di energia proibita per gli elettroni, ed è in genere compreso tra il centinaio di MeV e alcuni eV, a seconda della natura del semiconduttore. La freccia ondulata indica la transizione ottica di un elettrone dalla banda di valenza alla banda di conduzione con assorbimento di un fotone di energia hν maggiore di Eg; nella banda di valenza si forma allora una buca con carica positiva e+. Se si applica un campo elettrico al semiconduttore, gli estremi di banda si inclinano e gli elettroni e le buche si separano; la forza che agisce sulle due cariche è data dalla pendenza delle bande nel diagramma.
Essenziali allo sviluppo dell'ingegneria del gap sono state le eterogiunzioni di semiconduttori (v. fig. 1B) e la crescita epitassiale mediante fasci molecolari (MBE, Molecular Beam Epitaxy). Suggerimenti per migliorare le prestazioni dei dispositivi a semiconduttore attraverso l'uso di eterogiunzioni si trovano già nel famoso brevetto di W. B. Shockley per il transistor (1951). La fig. 1B dà il diagramma dell'eterostruttura doppia non drogata, costituita da uno strato semiconduttore a gap più piccolo confinato tra due strati a gap più grande. Con ΔEv e ΔEc si denotano, rispettivamente, le discontinuità nelle bande di valenza e di conduzione alle interfacce tra i due materiali.
Nel 1957 Kroemer avanzò l'idea di un semiconduttore a composizione variabile (v. Kroemer, 1957; v. fig. 1C): variando spazialmente la composizione x di un semiconduttore, per esempio AlxGa1-xAs, si produce un gap tra banda di valenza e banda di conduzione dipendente dalla posizione (gap di banda graduato). In questo esperimento, che rappresenta uno dei più semplici e dei primi esempi di ingegneria di gap di banda, si introducono artificialmente ‛forze quasi-elettriche' (v. fig. 1C) che agiscono sugli elettroni e sulle buche a causa del gradiente rispetto alle variabili spaziali degli estremi delle bande. Contrariamente al caso di campi elettrici applicati esternamente, queste forze spingono elettroni e buche nello stesso verso: a ciò si deve il nome di ‛forze quasi-elettriche', nonostante che esse abbiano in realtà origine chimica.
Dopo la realizzazione di un laser a iniezione, ottenuto nel 1963 con omogiunzioni di semiconduttori, Kroemer (v., 1963) suggerì che in strutture con eterogiunzioni il confinamento di elettroni e buche in una regione a piccolo gap inserita tra due regioni barriera a grande gap (v. fig. 1B) avrebbe prodotto inversione di popolazione e azione laser a densità di corrente molto inferiori a quelle necessarie nelle omogiunzioni. La realizzazione del laser a eterogiunzione, a temperatura ambiente e con bassa soglia di corrente, ottenuta contemporaneamente da Alferov e altri (v., 1970) e da Hayashi e altri (v., 1970), fu resa possibile dalla crescita epitassiale in fase liquida di eterogiunzioni AlGaAs/GaAs con interfaccia ben definita. Ciò aprì la strada alla produzione di laser di alta qualità per le comunicazioni con onde luminose.
Il passo successivo fu l'invenzione, avvenuta nei Bell Laboratories a opera di Cho e Arthur (v., 1975), della crescita epitassiale a fasci molecolari, che segnò l'inizio di una stagione straordinaria per la scienza delle superfici. Questa tecnica di crescita permette di ottenere sequenze di eterogiunzioni con interfacce definite a livello atomico, con composizione e contenuto di impurezze ben controllati su distanze dell'ordine della decina di Å. Tra tali strutture sono inclusi i cosiddetti ‛pozzi quantici' (QW, Quantum Well), che rappresentano gli elementi fondamentali dell'ingegneria del gap (v. fig. 1D). I pozzi quantici sono costituiti da uno strato di materiale, per esempio GaAs, a gap piccolo e assai sottile (di spessore più piccolo o prossimo alla lunghezza dell'onda di de Broglie associata all'elettrone termico, circa 250 Å in GaAs), confinato tra due semiconduttori a grande gap, per esempio leghe AlxGa1-xAs. Il profilo del potenziale individua una buca nella direzione di crescita; tale profilo produce livelli, indicati con E0 ed E1 in fig. 1D, con energie discrete i cui valori dipendono dalla larghezza della buca e dalla profondità del potenziale. Quest'ultimo parametro è determinato dal contenuto di Al nella lega. Gli stati quantici prodotti dal confinamento sono stati osservati per la prima volta da Dingle e altri (v., 1974) ai Bell Laboratories, e da Chang e altri (v., 1974) ai Laboratori IBM.
Crescendo molti pozzi quantici in sequenza, a distanze fisse, con barriere di spessore abbastanza piccolo (tipicamente inferiore a 50 Å) da ottenere un significativo effetto tunnel tra pozzi contigui, si producono i cosiddetti ‛superreticoli' (v. fig. 1E). I superreticoli sono nuovi materiali, ipotizzati e prodotti negli anni settanta (v. Esaki e Tsu, 1970), nei quali la periodicità artificiale introdotta produce nuove proprietà ottiche e di trasporto. Fino a ora abbiamo sempre citato il caso più comune di GaAs e AlAs, che hanno gap diversi ma costanti reticolari uguali. A partire dagli anni ottanta (v. Osbourn, 1982) è stato possibile ottenere la crescita di superreticoli composti da materiali aventi costanti reticolari diverse (per es., InAs e GaAs), che possono essere utilizzati come componenti di nuovi dispositivi. Altri superreticoli con proprietà interessanti possono essere ottenuti alternando periodicamente strati ultrasottili dello stesso semiconduttore drogato n e drogato p; essi sono pertanto chiamati superreticoli nipi (tipo n-intrinseco-tipo p-intrinseco; v. Esaki e Tsu, 1970; v. Doehler, 1972).
Occorre infine menzionare le cosiddette eterostrutture con modulazione di drogaggio, ottenute depositando in sequenza strati senza impurezze e strati di barriera con impurezze donatrici (o accettrici). In tal caso gli elettroni (le buche) in eccesso si trasferiscono dalle barriere negli strati a gap inferiori. Nella fig. 1F è schematizzata la situazione in cui l'eterostruttura è ottenuta introducendo intenzionalmente impurezze donatrici soltanto nel materiale alla sinistra dell'interfaccia. Gli elettroni ceduti dai donatori passano attraverso l'eterogiunzione nella regione a destra che ha energia minore per gli elettroni, e lì costituiscono un gas approssimativamente bidimensionale di elettroni, bloccato sull'interfaccia dall'attrazione elettrostatica tra i donatori, positivi perché ionizzati, e gli elettroni. Questa attrazione produce una buca di potenziale all'incirca triangolare, che ha un'energia E0 per lo stato fondamentale e un livello di Fermi EF, mostrato nella figura con una linea tratteggiata orizzontale. Parallelamente agli strati, gli elettroni hanno una mobilità molto maggiore che in un semiconduttore omogeneo di tipo n, drogato con la stessa densità di donatori. Ciò dipende dal fatto che in questa eterostruttura gli elettroni sono spazialmente separati dai donatori ionizzati, e questo riduce fortemente la sezione d'urto di diffusione degli elettroni sulle impurezze cariche positivamente, particolarmente a bassa temperatura. La modulazione di drogaggio in eterogiunzioni opportune ha condotto a nuovi transistor a effetto campo con alta mobilità elettronica.
È soltanto dagli anni ottanta, però, che l'epitassia a fasci molecolari ha consentito di produrre materiali di qualità sufficientemente buona da realizzare dispositivi adatti per usi commerciali, rendendo inoltre possibile controllare spazialmente la composizione e il drogaggio di semiconduttori nel modo desiderato (v. Cho, 1983 e 1991). Le strutture costruite sulla base di tali materiali hanno portato a una grande varietà di nuovi dispositivi; tra questi si può ricordare il laser a GaAs operante nella regione spettrale del vicino infrarosso, in uso nei lettori di compact disc (v. Cho, 1994; v. anche laser e fotonica, vol. XI).
Le interfacce fra due eterogiunzioni cresciute con MBE hanno il vantaggio di essere atomicamente ben definite, con un brusco salto di potenziale; tali caratteristiche risultano evidenti nella fig. 2, in cui è mostrata l'immagine al microscopio elettronico a trasmissione (TEM, Transmission Electron Microscopy) di una sezione di due eterogiunzioni InP/GaInAs a identico parametro reticolare, cresciute con MBE, in modo da formare un pozzo quantico. Questa combinazione di materiali è comunemente usata in laser e rivelatori per sistemi di comunicazione che operano nella regione infrarossa di 1,3-1,55 µm di lunghezza d'onda, e in transistor bipolari ultraveloci.
2. Lanciatori balistici
Le brusche discontinuità alle interfacce cresciute con MBE danno luogo a gradini di potenziale nella banda di conduzione e in quella di valenza, indicati con ΔEc e ΔEv, rispettivamente, come mostrato in fig. 3; le strutture illustrate consentono di usare le brusche eterogiunzioni come basi di lancio per elettroni balistici con il risultato di ottenere dispositivi di qualità migliore. Un elettrone che attraversa tali discontinuità di potenziale è sottoposto a un'accelerazione balistica per una distanza pari allo spessore dell'interfaccia e guadagna un'energia cinetica uguale al dislivello nelle bande di conduzione. L'uso di una discontinuità di banda come trampolino di lancio fu realizzato sperimentalmente per la prima volta per aumentare la probabilità di ionizzazione degli elettroni (v. Capasso e altri, 1982). Poco dopo venne proposto di usare questi gradini di potenziale per ottenere alte velocità in condizioni di non equilibrio (v. Cooper e altri, 1982) e anche per migliorare le prestazioni ad alta velocità dei transistor bipolari a eterogiunzione (HBT, Heterojunction Bipolar Transistor), come illustrato nella fig. 3A. Gli elettroni penetrano nella base (fatta per esempio di una lega di InGaAs) dall'emettitore (fatto di InP nel caso di una base di InGaAs) con un'energia cinetica di qualche centinaio di meV, corrispondente a una velocità di quasi 108 cm/s. Il trasporto elettronico nella base, e in parte nel collettore, avviene perciò in un tempo di transito più breve del normale attraverso il transistor, il che conduce a un dispositivo con frequenza di taglio più elevata. Sono state ottenute in questo modo frequenze di taglio superiori a 160 GHz.
Se il valore di ΔEc supera l'energia della soglia di ionizzazione del materiale della base (tipicamente superiore al gap per ragioni di conservazione di energia e quantità di moto), gli elettroni entrano nella base con un breve tempo di transito creando coppie elettrone-buca per ionizzazione da urto. Questo fu proposto originariamente da Kroemer ed è stato recentemente realizzato usando la struttura riportata in fig. 3B (v. Vengurlekar e altri, 1990). In questo dispositivo ΔEc = 1, eV, un valore che supera largamente l'energia di ionizzazione in InAs. Nella configurazione a base comune l'incremento della corrente di base a campo nullo tra collettore e base diviene negativo in corrispondenza di un incremento positivo della corrente all'emettitore, fornendo la prova della ionizzazione da urto dovuta alla discontinuità degli estremi delle bande nella base.
La ionizzazione da urto provocata dalla discontinuità degli estremi di banda può essere usata per realizzare un dispositivo a stato solido che è l'analogo di un fotomoltiplicatore (PMT, Photomultiplier; v. Capasso e altri, 1983). In questa struttura (v. fig. 3C) viene utilizzato un materiale a composizione graduata per creare un diagramma di banda a dente di sega, che con l'applicazione di un campo elettrico opportuno acquista una forma a scala. Gli elettroni ionizzano per urto poiché ΔEc, nella regione dopo ogni gradino, supera l'energia di ionizzazione. Le buche create dalla ionizzazione o fotoiniettate non possono produrre ionizzazione perché i gradini della banda di valenza hanno il segno sbagliato e il campo esterno applicato è mantenuto sufficientemente debole da impedire che i portatori producano ionizzazione per effetto del solo campo elettrico. Poiché un solo tipo di portatori produce ionizzazione e l'effetto valanga è spazialmente localizzato, il rumore di valanga è minimo e la struttura imita un fotomoltiplicatore; sebbene questo fotomoltiplicatore a scala non sia stato realizzato, l'aumento della probabilità α di ionizzazione da elettroni rispetto alla probabilità β di ionizzazione da buche quando ΔEc supera ΔEv è stato verificato in fotodiodi a valanga (APD, Avalanche Photodiode) costituiti da una molteplicità di pozzi quantici (MQW, Multiquantum Well) del tipo GaAs/AlGaAs. Questo porta a una riduzione del rumore di valanga, poiché tale rumore è massimo quando α = β, come dimostrato recentemente in strutture MQW del tipo GaAs/AlGaAs e InGaAs/AlInAs. Fotodiodi a valanga a basso rumore di questo tipo, da utilizzare nelle fibre ottiche per comunicazioni a grande lunghezza d'onda, sono in fase avanzata di realizzazione presso alcune ditte produttrici.
3. Microstrutture a gap graduato
Un altro potente elemento dell'ingegneria del ‛gap di banda' è rappresentato dalla possibilità di graduare la composizione del semiconduttore, che consente di modellare separatamente le proprietà di trasporto di elettroni e buche (v. Capasso, 1986). Una di tali applicazioni, originariamente suggerita da Kroemer (v., 1957), è esemplificata nella fig. 4. Il gap graduato produce una forza che agisce sugli elettroni che attraversano la base di tipo p nel cammino verso il collettore, in modo simile a quello prodotto da un campo elettrico applicato. L'origine di questa forza è chimica anziché elettrostatica, da cui il nome di campo ‛quasi-elettrico'. L'effetto finale è che, a causa di questa forza, gli elettroni si muovono per deriva piuttosto che per diffusione, quindi con velocità significativamente maggiori e tempi di transito nella base più brevi. Questo fenomeno venne dimostrato con misure impulsate in un fototransistor a base graduata di AlGaAs/GaAs. Tutte le misure ottiche, ottenute con tecniche di luce di ‛pompa' e luce di ‛prova', della velocità degli elettroni minoritari in semiconduttori AlGaAs a gap graduato, fortemente drogati con accettori, con un campo quasi-elettrico di 8 • 103 V/cm hanno dato velocità degli elettroni fino a 2 • 107 cm/s (v. Capasso, 1986). Il concetto del transistor a base con composizione graduata fu originariamente applicato in AlGaAs/GaAs ed è poi stato utilizzato con successo in dispositivi ultraveloci di AlGaAs/GaAs in transistor bipolari a eterogiunzioni di Si-Ge, con frequenze di taglio superiori a 100 GHz e a 50 GHz, rispettivamente.
Va sottolineato che l'emettitore a grande gap negli HBT delle figg. 3A e 4 produce una barriera per le buche nella base. Questa caratteristica cruciale degli HBT consente di ottenere simultaneamente un forte guadagno, una bassa resistenza di base e una capacità del sistema base-emettitore utile per operazioni ad alta velocità.
Nella fig. 5 viene illustrata l'applicazione del gap graduato a dispositivi di memoria (v. Capasso e altri, 1988). La struttura è del tipo a gate flottante; dispositivi di questo tipo vengono usati commercialmente come memorie permanenti nell'elettronica basata sul silicio. Nella struttura della fig. 5, uno strato graduato viene usato come iniettore di elettroni in una buca di potenziale (gate flottante) dove sono accumulate le cariche. Le cariche negative accumulate impoveriscono il canale sottostante il gate flottante, producendo così una caduta nella corrente che fluisce attraverso il canale. Il dispositivo rimane in questo stato fino a quando gli elettroni rimangono nel pozzo, il che dipende dalla probabilità di emissione termoionica attraverso le barriere di AlAs. Le nostre misure indicano che questo tempo varia da pochi secondi a una temperatura di 300 K a un valore estrapolato di 700 anni a 77 K. L'eterogiunzione tra un materiale a gap diretto (GaAs) e indiretto (AlAs) sopprime l'emissione termoionica molto più efficacemente di un'interfaccia diretta/diretta, grazie all'assenza di conservazione laterale della componente della quantità di moto nella transizione. La principale differenza tra il funzionamento di questi dispositivi e quello delle memorie a gate flottante basate sul Si è che gli elettroni sono iniettati dal contatto di gate piuttosto che dal canale, il che conferisce maggiore funzionalità e flessibilità alla configurazione del circuito.
Un'applicazione delle strutture a gap graduato come nuovi materiali fotorifrattivi (v. Ralph e altri, 1989) è illustrata nella fig. 6, nella quale un fascio di luce di pompa genera otticamente elettroni e buche che, in pochi picosecondi, vengono spazialmente separati dai diversi campi quasi-elettrici nella banda di conduzione e nella banda di valenza. Il campo elettrico creato da questa separazione persiste fino a quando le buche si riuniscono agli elettroni nel pozzo, cioè per un tempo di circa 50 ps, corrispondente al tempo di attraversamento della regione graduata. Nel caso che un secondo impulso linearmente polarizzato venga inviato nella struttura entro un tale intervallo di tempo, il campo della carica spaziale fotoindotta determinerà una rotazione della polarizzazione del fascio di prova a causa della modulazione dell'indice di rifrazione per effetto elettro-ottico. Tale struttura si comporta quindi come un nuovo tipo di materiale fotorifrattivo che può essere usato come un interruttore ottico quando inserito tra due polarizzatori incrociati. Il fascio di pompa attiva l'interruttore e consente la trasmissione del più debole impulso di prova. Questo effetto è stato recentemente dimostrato in una struttura a 50 periodi di AlGaAs/GaAs, con pozzi di 50 Å e regioni graduate di 500 Å. Si noti che in questi nuovi materiali fotorifrattivi, a differenza di quelli convenzionali, sono necessari solo due fasci ottici e non è richiesta la presenza di difetti.
4. Microstrutture a effetto tunnel risonante
Altri fenomeni e applicazioni molto interessanti nascono dalla buona definizione delle interfacce in corrispondenza delle eterogiunzioni. Gli elettroni possono formare onde stazionarie nella direzione perpendicolare all'interfaccia e in questo caso la loro energia cinetica è quantizzata come quella di una particella in una buca di potenziale. Naturalmente, il moto parallelamente all'interfaccia è libero, così che l'effetto finale della quantizzazione di dimensione è che la banda di conduzione viene suddivisa in molte sottobande il cui valore di fondo banda è rappresentato dai livelli di energia indicati nella fig. 7A. L'effetto quantistico del confinamento spaziale è alla base del funzionamento dei laser a pozzi quantici, in cui può essere usato per spostare nel visibile la lunghezza d'onda della luce emessa o per ridurre la minima corrente necessaria per ottenere l'emissione laser. Si può avere effetto tunnel negli stati quantizzati del pozzo se l'energia cinetica degli elettroni in direzione perpendicolare ai piani uguaglia quella dei livelli di energia della buca e le barriere sono sufficientemente sottili. Nel limite di una diffusione (ad es., di impurezze) trascurabile nella regione della doppia barriera, tale processo tunnel risonante è concettualmente simile a quello che dà origine alle risonanze nella trasmissione attraverso una cavità ottica a lunghezze d'onda ben definite. In pratica, i processi di diffusione tendono a distruggere l'interferenza coerente, così che in molte situazioni pratiche il processo è meglio descritto in termini di una sequenza di processi tunnel entro e fuori dal pozzo (v. Capasso e Datta, 1990).
Dalle proprietà sopraindicate segue che le barriere doppie che utilizzano come strati di contatto regioni fortemente drogate hanno un comportamento analogo a quello dei diodi a resistenza differenziale negativa (v. fig. 7A), come mostrato per primi da Chang e altri (v., 1974): si riscontra una rapida caduta della corrente quando il campo esterno viene aumentato e il livello di energia dello stato confinato nel pozzo si abbassa sotto il minimo della banda di conduzione nello strato emettitore. In questa condizione il processo tunnel risonante degli elettroni dall'emettitore entro il pozzo è inibito a causa dell'impossibilità di conservare la quantità di moto laterale. Diodi tunnel risonanti di AlGaAs/GaAs sono stati utilizzati come miscelatori fino a circa 2 THz, e come oscillatori fino a frequenze di oltre 400 GHz. Più recentemente, diodi tunnel risonanti con barriere di AlSb e pozzi di InAs hanno funzionato con frequenze di oscillazione di circa 700 GHz.
Anche se i diodi tunnel risonanti possono trovare applicazione negli oscillatori, i circuiti logici richiedono dispositivi con isolamento tra la corrente entrante e quella uscente per poter ottenere un guadagno senza eccessivo carico nello stadio iniziale. L'uso di un transistor permette di raggiungere tale condizione di isolamento nella maniera più efficace. In termini generali, un transistor a effetto tunnel risonante è un dispositivo che usa un voltaggio esterno di controllo per modulare la differenza tra i livelli di energia del pozzo quantico e l'energia degli elettroni incidenti. In tal modo si può far sì che la corrente tunnel risonante attraverso la doppia barriera abbia un massimo a uno o più valori del voltaggio di controllo, in corrispondenza dei diversi livelli di energia. Si noti che un transistor con una tale caratteristica corrente-voltaggio presenta una molteplicità di stati di risposta (on) e di non-risposta (off), in corrispondenza dei picchi e degli avvallamenti della curva corrente-tensione (curva I-V). Sebbene la logica a più valori on/off sia stata oggetto di considerevole ricerca teorica, fino a ora tutte le architetture circuitali realizzate sono basate sui convenzionali dispositivi a due possibilità (sì o no), o su diodi tunnel. La logica a più valori potrà un giorno ridurre la complessità delle interconnessioni dei circuiti integrati.
Concettualmente, il modo più semplice di costruire un transistor a effetto tunnel risonante è quello di produrre un contatto con il pozzo quantico pesantemente drogato di una doppia barriera. Questo contatto a bassa resistenza dovrebbe servire come terminale di controllo. Tale procedimento, tuttavia, presenta notevoli difficoltà tecniche e tentativi di questo tipo non hanno ancora avuto successo.
Un procedimento simile ma tecnologicamente più semplice, originariamente suggerito da Capasso e Kiehl (v., 1985) consiste nell'incorporare la doppia barriera nella base di un transistor bipolare. Nella fig. 7B è illustrato il diagramma a bande di energia di un transistor bipolare a effetto tunnel risonante. Se si aumenta il voltaggio tra base ed emettitore, la corrente tunnel attraverso ogni sottobanda prima raggiunge un massimo e poi si annulla quando il minimo della sottobanda (il livello di energia mostrato nella buca della fig. 7B) scende sotto il minimo della banda di conduzione dell'emettitore. Questo deve produrre una molteplicità di picchi nella corrente del collettore, cioè una molteplicità di transconduttanze negative.
Nel 1986 si è per la prima volta riusciti a far funzionare un transistor bipolare a risonanza tunnel (v. Capasso e altri, 1986). La prova, eseguita a temperatura ambiente, ha mostrato l'esistenza di un picco nella curva I-V, con un rapporto 3:1 tra il picco e la valle. Con la struttura a bande della fig. 7B è tuttavia difficile ottenere una molteplicità di picchi con altezze confrontabili, caratteristica utile, invece, nelle applicazioni circuitali.
Per risolvere questo problema fu introdotta la nuova struttura mostrata nella fig. 7C (v. Capasso e altri, 1989), nella quale due o più doppie barriere sono poste nell'emettitore anziché nella base. Per ottenere una molteplicità di picchi nella corrente di collettore in funzione del voltaggio tra base ed emettitore si sfrutta il fatto che nei pozzi quantici vengono a formarsi delle cariche spaziali. L'effetto di schermo elettrostatico rende il campo attraverso le due barriere doppie spazialmente non uniforme, e maggiore nel pozzo più vicino alla base. Così, quando si aumenta il potenziale esterno, la corrente di tunnel risonante attraverso le buche viene soppressa a due voltaggi diversi, producendo due picchi nella caratteristica curva I-V. (Quando la corrente di tunnel risonante è soppressa in un solo pozzo, la continuità della corrente è assicurata da processi tunnel anelastici). Tali strutture sono state costruite con Al0,48In0,52As e Ga0,47In0,53As cresciuti con tecniche MBE, situando due doppie barriere nell'emettitore. A temperatura ambiente il dispositivo ha mostrato due picchi di corrente, con eccellenti rapporti tra i picchi e le valli, guadagni di corrente superiori a 60 e una frequenza di taglio al di sopra dei 24 GHz (v. Capasso e altri, 1989).
Il tipo di caratteristiche di trasferimento illustrato in precedenza consente di realizzare una classe di circuiti di complessità fortemente ridotta che richiedono, per una data funzione logica, un numero molto inferiore di transistor rispetto ai circuiti convenzionali. Per esempio, è stato costruito un controllore di parità per parole a quattro bit con un singolo transistor a più stati. Tali circuiti sono comunemente usati nei sistemi di comunicazione digitale per verificare l'esistenza di errori di trasmissione, controllando se vi è un numero dispari o un numero pari di uno (o zero) nella parola binaria. I convenzionali controllori a 4 bit richiedono 24 transistor. I transistor a più stati sono utilizzabili anche come moltiplicatori di frequenza; ad esempio, con il dispositivo mostrato nella fig. 7B è stata moltiplicata per cinque una frequenza di alimentazione di 350 MHz. Altre possibili applicazioni sono i convertitori veloci da analogico a digitale e le celle di memoria.
5. Trasporto nei superreticoli
Consideriamo ora una struttura periodica con molti pozzi quantici e barriere abbastanza sottili da consentire una corrente tunnel significativa. L'energia degli elettroni nella direzione perpendicolare ai piani si separa in bande di energia permessa separate da gap proibiti (v. fig. 1E), proprio come ci si aspetta in ogni struttura periodica (v. Esaki e Tsu, 1970). Si tratta di una situazione del tutto analoga alla formazione di bande di energia nei solidi per effetto della periodicità del reticolo cristallino.
Vi sono tuttavia importanti differenze tra il reticolo cristallino naturale e il ‛superreticolo', come viene chiamata una siffatta struttura artificiale. Anzitutto, il periodo spaziale del superreticolo è tipicamente nell'intervallo 30 ÷ 100 Å, mentre il periodo del cristallo naturale è di pochi ångström; pertanto le bande di energia del superreticolo, che sono prodotte dall'accoppiamento tra i livelli di energia delle buche di potenziale, sono necessariamente molto più strette (nell'ordine di 10 meV) e per questo sono chiamate ‛minibande'. In secondo luogo, il profilo di banda del superreticolo è in genere unidimensionale, contrariamente al caso del reticolo cristallino tridimensionale. (Sono stati studiati anche superreticoli bidimensionali con strutture laterali ed elettrodi metallici opportunamente disposti).
La relazione che intercorre tra l'energia e il numero d'onda k in una minibanda di larghezza Δ è del tipo
in conseguenza della periodicità del superreticolo di periodo a e quindi la velocità di gruppo dell'elettrone oscilla in funzione di k secondo l'espressione
Questo implica riflessioni di Bragg agli estremi della minibanda, ed è molto diverso da quanto accade nel caso di elettroni liberi la cui velocità aumenta linearmente con k. Naturalmente il rappresentare la velocità degli elettroni con la (2) vale soltanto se Δ è sensibilmente maggiore dell'allargamento delle energie per le collisioni ℏ/τ (dove τ è l'intervallo di tempo tra due collisioni successive), ossia se il loro libero cammino medio è sensibilmente maggiore del periodo reticolare.
L'applicazione di un campo elettrico di intensità F produce un aumento lineare del numero d'onda k secondo la relazione, analoga a quella di Newton tra forza e quantità di moto,
Per elettroni liberi questa relazione produrrebbe un aumento illimitato della velocità, mentre in un superreticolo la velocità diminuisce quando k passa attraverso π/2a, come si vede dalla (2). Esaki e Tsu, nel loro lavoro pionieristico del 1970, mostrarono che la velocità di spostamento in condizioni stazionarie diminuisce anche a causa delle collisioni quando l'intensità del campo elettrico supera il valore di soglia ℏ/eaτ. Per tali campi la distribuzione degli elettroni si sposta verso le regioni dello spazio k in cui la loro velocità di gruppo diminuisce all'aumentare di k secondo la (2). Per periodi tipici dei superreticoli, dell'ordine di 100 Å, e per tipici tempi tra collisioni τ di circa 3 • 10-12 s, si ottiene un campo di soglia di 3 • 103 V/cm per lo stabilirsi di una conduttanza differenziale negativa. Per molto tempo non è stato possibile ottenere una conferma sperimentale di questo effetto a causa di due difficoltà: una consiste nella non uniformità del campo elettrico, con zone di campo elevato nel superreticolo, dovuta alla produzione di carica spaziale durante l'iniezione dai contatti; l'altra è la presenza di conduttanza differenziale negativa dovuta al trasferimento di elettroni nelle valli satelliti, fenomeno che nella maggior parte dei semiconduttori III-V compare a valori del campo elettrico confrontabili con quelli attesi per il superreticolo.
Le difficoltà descritte possono essere superate usando una struttura proposta recentemente (v. Beltram e altri, 1990; v. fig. 8A), nella quale gli elettroni possono essere introdotti nel superreticolo, posto nel collettore di un transistor bipolare poco drogato, a densità arbitrariamente basse controllando il potenziale esterno applicato alla base emettitrice. In queste condizioni il campo elettrico in tutto il superreticolo si mantiene uniforme. Inoltre, in questa struttura di transistor bipolare non si rilevano fenomeni di conduttanza differenziale negativa per trasferimento di elettroni ad altre valli in condizioni di iniezione di corrente costante dall'emettitore, perché la diminuzione di velocità media dovuta ai minimi con masse efficaci pesanti è compensata da un aumento del numero di portatori, e pertanto la corrente al collettore non varia. È invece possibile osservare il meccanismo di Esaki e Tsu poiché gli elettroni che hanno subito riflessione di Bragg nella regione di massa negativa della minibanda producono un flusso in direzione opposta, e pertanto la corrente al collettore diminuisce, mentre aumenta la corrente alla base in modo da mantenere una corrente costante di emettitore. La struttura descritta è stata realizzata usando un emettitore di AlInAs, una base quaternaria di AlInGaAs, e un superreticolo di materiale senza impurezze di 14 periodi di AlInAs(17Å)/GaInAs(36Å) seguito da uno strato di InGaAs pure intrinseco nel collettore. È stata osservata conduttanza differenziale negativa nella corrente al collettore misurata in funzione del potenziale esterno alla base del collettore, in condizioni di corrente di iniezione costante all'emettitore (v. Beltram e altri, 1990). Questa rappresenta la prima chiara dimostrazione della conduttanza differenziale negativa per riflessione di Bragg prevista da Esaki e Tsu.
Se il campo è molto più grande di ℏ/eaτ, ci si può aspettare che il numero d'onda k aumenti fino a un multiplo elevato di π/2a prima che l'elettrone sia diffuso. Di conseguenza, la velocità dovrebbe assumere un comportamento oscillante nello spazio reale, oltre che nello spazio delle quantità di moto. Le oscillazioni di questo tipo, chiamate oscillazioni di Bloch, suggeriscono la possibilità che, usando un dispositivo appropriato, si riescano a ottenere radiazione coerente di lunghezza d'onda desiderata.
In un recente esperimento di grande importanza Waschke e altri (v., 1993) hanno osservato emissione coerente di onde submillimetriche da elettroni oscillanti, eccitati otticamente in un superreticolo di AlGaAs/GaAs. La frequenza di oscillazione viene calibrata nell'intervallo da 0,5 a 2 THz variando il campo elettrico in modo da variare la frequenza delle oscillazioni di Bloch ωB =
Nei superreticoli con debole accoppiamento tra le buche (barriere di lunghezza ≥ 100 Å), le proprietà di trasporto sono descritte meglio considerando la diffusione tunnel tra gli stati localizzati dei pozzi individuali (v. fig. 8B). Questo processo tunnel risonante da una buca all'altra è stato osservato con misure di fotocorrente in un superreticolo di 35 periodi di AlInAs/GaInAs, con buche e barriere dello spessore di circa 140 Å.
Stati quantici si formano anche nel continuo classico al di sopra delle barriere, a causa delle interferenze nelle riflessioni quantiche. Tali stati risonanti sono stati usati per un nuovo tipo di rivelatore nell'infrarosso (v. Levine e altri, 1988; v. fig. 8C), sensibile nella regione di lunghezza d'onda 8-12 µm. Immagini termiche di grande qualità, con una differenza di temperatura al limite del rumore, sono state ottenute con un piano di 128 × 128 di tali rivelatori inseriti in un sistema circuitale di C-MOS in Si. Il potenziale vantaggio di tali rivelatori rispetto ai convenzionali dispositivi a HgCdTe è dovuto alla migliore tecnologia dei composti GaAs/AlGaAs. Questo sistema, che comprende il substrato, offre una migliore qualità di prodotto e una maggiore affidabilità. Inoltre, anche l'elettronica per la lettura potrà in futuro essere integrata sullo stesso substrato.
6. Laser a cascata quantica
Laser basati su transizioni tra stati confinati che hanno origine dalla stessa banda (transizioni intersottobanda) furono proposti 25 anni fa da Kazarinov e Suris (v., 1971). Recentemente è stato ottenuto un laser a sottobande a iniezione (laser a cascata quantica) basato su un progetto significativamente diverso (v. i contributi di Faist e altri, 1994); tale dispositivo fa uso di un solo tipo di portatori (è un laser a semiconduttore unipolare) e di transizioni elettroniche tra livelli di energia della banda di conduzione di pozzi quantici accoppiati; esso opera a una lunghezza d'onda di 4,26 µm, ma poiché la lunghezza d'onda dipende solo dal confinamento spaziale, si può variarla dal medio infrarosso alla regione submillimetrica usando eterostrutture dello stesso materiale. Gli elettroni che si propagano lungo un potenziale a scala emettono fotoni in sequenza, uno a ogni gradino. Questi ultimi consistono in pozzi quantici accoppiati in cui l'inversione di popolazione tra gli stati eccitati discreti della banda di conduzione è ottenuta in uno schema di laser a quattro livelli simile al caso atomico, nel quale l'iniezione è basata sull'effetto tunnel (v. fig. 9). La struttura AlInAs/GaInAs è ottenuta con MBE e comprende 25 gradini tra due strati di confinamento ottico, ognuno dei quali è costituito da uno strato a iniezione con gap graduato di tipo n e una regione attiva con tre pozzi quantici accoppiati. La regione attiva non drogata include buche di potenziale GaInAs di 8 Å e 3,5 Å di spessore, separate da barriere di AlInAs dello spessore di 3,5 Å. La ridotta sovrapposizione spaziale tra gli stati responsabili della transizione laser e il forte accoppiamento tunnel a una vicina buca di spessore di 2,8 Å di GaInAs garantiscono l'inversione di popolazione. I campioni sono stati fabbricati con tecniche di attacco chimico e le facce per le riflessioni laser sono state ottenute per sfaldamento. Potenze di circa 20 mW in regime impulsato (impulsi di 20 ns con un ciclo di lavoro di 10-3 s) sono state raggiunte alla temperatura di 80 K. Il funzionamento laser è stato ottenuto fino alla temperatura di 125 K con 5 mW di potenza. Un drastico restringimento dello spettro di emissione fornisce conferma diretta dell'azione laser. Un importante aspetto di questo laser è che il guadagno è molto meno influenzato dalla temperatura dei convenzionali laser a semiconduttori. Inoltre, la larghezza di riga intrinseca di questi laser in operazione continua a singolo modo appare limitata soltanto dall'effetto Schawlow-Townes, come nel caso di laser atomici, senza il fattore di accrescimento della larghezza di riga tipico dei diodi laser. Modi longitudinali ben definiti vengono osservati nello spettro ad alta risoluzione a due diverse correnti. La separazione tra i modi è in buon accordo con il valore calcolato. La larghezza di riga del modo dominante ha attualmente un limite inferiore dovuto agli effetti di riscaldamento e a salti del modo durante gli impulsi.
7. Pozzi quantici pseudomolecolari con forti proprietà ottiche non lineari.
Le due strutture che discuteremo ora possono essere viste come ‛quasi-molecole' con grandissimi elementi di matrice di dipolo e livelli di energia all'incirca equidistanti (v. fig. 10); è a queste caratteristiche che si devono le loro grandi suscettività ottiche non lineari (v. Capasso e altri, 1994). Entrambe le strutture sono cresciute nel sistema AlInAs/GaInAs, con concentrazioni di In tali da produrre una costante reticolare uguale a quella di InP, e solo la buca di maggiore spessore è drogata con impurezze di tipo n. La scelta di questo sistema di materiali non solo facilita l'accoppiamento tunnel tra gli stati grazie alla piccola massa efficace nella regione delle barriere in confronto a quella in AlGaAs, ma fornisce anche una grande discontinuità nelle bande, essenziale per confinare nella struttura a tre buche quattro stati separati da un'energia corrispondente a quella del fotone di un laser a CO2 (≈ 130 meV). Per eccitare otticamente il moto quantizzato nella direzione normale all'interfaccia occorre usare luce con una componente della polarizzazione normale ai piani di crescita. Nel nostro esperimento questa condizione era ottenuta usando luce linearmente polarizzata in una guida d'onda a molti passaggi inclinata a 45°. Nell'esperimento di generazione di seconda armonica (SHG, Second Harmonic Generation) viene creata una polarizzazione coerente a una frequenza doppia della frequenza dell'onda di pompa ω (un fascio laser di CO2) a causa dell'assenza di simmetria di riflessione nella nostra struttura a due buche asimmetriche (v. fig. 10A; v. Capasso e altri, 1994). Questa polarizzazione coerente irraggia un'onda di frequenza 2ω colineare con la luce di pompa. La vicinanza dell'energia del fotone di pompa a E2 - E1 e del fotone di seconda armonica a E3 - E1 produce un forte effetto di risonanza nella suscettività non lineare χ2(%²ω)associata alla SHG. La suscettività massima corrisponde a risonanze esatte, cioè ℏω = E2 - E1 = E3 - E2. Questa condizione può essere ottenuta usando il grande effetto Stark lineare tipico di questa struttura mediante l'applicazione di un campo elettrico di polarità opportuna. In queste condizioni si è misurato un valore χ2(%²ω) = 10-7 m/V, che è circa trecento volte il valore di ∣χ2(%²ω)∣ in GaAs massivo a λ = 10 µm.
La struttura a tre buche della fig. 10B con la quasi uguale separazione tra i suoi quattro livelli di energia è appropriata per la generazione di terza armonica (THG, Third Harmonic Generation) in condizioni di tripla risonanza (v. Capasso e altri, 1994). Il processo è quello di una frequenza di pompa ω che produce una polarizzazione non lineare a frequenza 3ω alla quale viene prodotta un'onda coerente. La suscettività non lineare χ2(%³ω), che interviene nell'espressione della polarizzazione, aumenta sensibilmente quando è verificata la condizione ℏω = E2 - E1 = E3 - E2 = E4 - E3. È importante osservare che una buca di potenziale parabolica (cioè un oscillatore armonico per gli elettroni) non è adatta a questo scopo, poiché in tale sistema la risposta al campo esterno è sempre lineare. Esperimenti di THG nella struttura della fig. 10B hanno prodotto un valore ∣χ2(%³ω)∣ = 10-14 (m/V)2 a 300 K. A temperature molto più basse (≈ 4 K), ∣χ2(%³ω)∣ è quattro volte maggiore. Queste sono le suscettività del terz'ordine più elevate ottenute in qualsiasi sistema materiale noto. La struttura di tre buche accoppiate è stata usata anche per studiare l'effetto fotoelettrico multifotone da un pozzo quantico, l'analogo della ionizzazione multifotone di un atomo (v. Capasso e altri, 1994). In questo fenomeno gli elettroni nella buca cui è applicato il campo sono fotoeccitati nel continuo, dando così luogo a fotocorrente, da luce laser a CO2 mediante assorbimento simultaneo di tre fotoni. La sezione d'urto di questo processo si rivela molti ordini di grandezza maggiore di quella che si produce in atomi e in molecole.
8. Ottica elettronica: filtri Fabry-Perot e stati legati al di sopra della buca di potenziale
Nel capitolo precedente abbiamo visto come gli stati confinati del pozzo quantico siano importanti per numerosi fenomeni ottici e di trasporto. Stati fortemente localizzati possono essere creati nel pozzo quantico anche a energie che superano il potenziale di barriera a causa dell'interferenza costruttiva (v. Capasso e altri, 1992; v. Sirtori e altri, 1992).
Consideriamo per esempio una semplice buca rettangolare (v. fig. 11A). Per energie sopra la barriera vi è un continuo di stati di diffusione; a valori discreti dell'energia corrispondenti a un numero semi-intero di lunghezza d'onda degli elettroni uguale alla larghezza della buca si hanno risonanze nella trasmissione. Sebbene a queste energie le ampiezze delle funzioni d'onda nella regione della buca siano accresciute, esse non decadono esponenzialmente nella barriera, come fanno gli stati confinati nella buca, ma si comportano come onde piane. Questi stati possono però essere localizzati nella buca usando come barriere successioni di strati di spessore λ/4 ognuno, dove λ è la lunghezza d'onda di de Broglie degli elettroni nello strato (all'energia della risonanza di trasmissione selezionata; v. figg. 11, B e C). L'interferenza costruttiva tra le onde parzialmente riflesse dalle eterointerfacce degli strati a λ/4 conduce alla formazione di uno stato quasi-legato sopra la buca centrale (v. fig. 11B). Questo effetto restringe considerevolmente la risonanza di trasmissione, analogamente a quanto avviene in un filtro ottico di Fabry-Perot, nel quale vengono prodotte strette risonanze ottiche usando come specchi ad alta riflettività successioni a quarto d'onda. Il grado di localizzazione aumenta con il numero di periodi; nella struttura con due periodi la funzione d'onda è già praticamente confinata (v. fig. 11B). Nel limite di superreticolo e a basse temperature gli strati diventano riflettori di Bragg: si apre un ‛mini-gap' (v. fig. 11C) e lo stato localizzato diventa uno stato legato con energie superiori all'altezza delle barriere. La previsione che certi potenziali oscillanti potessero produrre stati legati nel continuo per effetto dell'interferenza quantistica fu avanzata da von Neumann e Wigner già nel 1929.
Il campione di riferimento aveva venti pozzi quantici costituiti da strati di InGaAs di 32 Å, drogati con impurezze di tipo n, separati da barriere di AlInAs di 150 Å non drogate. Nelle altre tre strutture le buche di 32 Å, drogate allo stesso modo, erano confinate rispettivamente da uno, due, o sei periodi di strati a quarto d'onda, consistenti in barriere di AlInAs di 39 Å e buche di GaInAs di 16 Å, costruiti come precedentemente descritto. La lunghezza di coerenza di fase nella struttura a superreticolo della fig. 11C viene stimata in circa 300 Å a 10 K.
Lo spettro di assorbimento del campione di riferimento è allargato, con un taglio alle grandi lunghezze d'onda determinato dall'altezza della barriera. Nella struttura con un periodo λ/4 il picco è considerevolmente più stretto e centrato su un valore dell'energia corrispondente alla transizione tra lo stato fondamentale della buca di potenziale e lo stato localizzato risonante all'energia E6 (v. Sirtori e altri, 1992). Quando il numero degli strati a quarto d'onda viene raddoppiato, il picco di assorbimento non si sposta ma si stringe considerevolmente, come succede in un filtro Fabry-Perot. In effetti il restringimento osservato (16 meV) si può spiegare quantitativamente con l'aumento di riflettività degli strati λ/4 (v. Sirtori e altri, 1992). Nella struttura con sei periodi, alle temperature criogeniche, lo stato fortemente localizzato diviene uno stato legato confinato da riflettori di Bragg del superreticolo (v. Capasso e altri, 1994). Lo spettro di assorbimento mostra un picco isolato a 360 meV con una larghezza di circa 10 meV, corrispondente alla transizione dello stato E1 allo stato E2 della fig. 11C. È ineressante notare che la larghezza della transizione allo stato confinato sopra il pozzo nella struttura a due e a sei periodi è identica a quella di una transizione tra stati legati misurata in un pozzo quantico convenzionale di GaInAs dello spessore di 55 Å con barriere di 300 Å, il che dimostra che lo stato al di sopra della buca è uno stato legato.
9. Modulazione artificiale delle discontinuità di banda
La capacità di controllare le discontinuità delle bande all'interfaccia aggiungerebbe un importante grado di libertà all'ingegneria del gap. Alcuni anni fa proponemmo e dimostrammo la possibilità di controllare le altezze delle barriere all'interfaccia e le discontinuità di banda (v. Capasso e altri, 1985). La tecnica consiste nell'inserire tramite MBE strati ultrasottili (pochi piani reticolari) di donatori e di accettori ionizzati entro poche decine di ångström dall'interfaccia a eterogiunzione (drogaggio planare, δ; v. fig. 12). Il potenziale elettrostatico di questo ‛dipolo da drogaggio all'interfaccia' si aggiunge o si sottrae al potenziale di dipolo della discontinuità. Nel limite di pochi piani atomici di separazione tra i piani con carica elettrica, gli elettroni che attraversano l'interfaccia ‛vedono' una nuova discontinuità di banda ΔEc ± eΔϕ, dove eΔϕ è il potenziale del doppio strato aggiunto (v. fig. 12). Usando questa tecnica, è stato possibile ottenere una riduzione artificiale dell'altezza della barriera alla banda di conduzione dell'ordine di 0,1 eV in un'eterogiunzione Al0,25Ga0,75As/GaAs (v. Capasso e altri, 1985). Questo abbassamento della barriera produce un aumento (di un ordine di grandezza) dell'efficienza di raccolta di fotoportatori attraverso la giunzione rispetto a eterogiunzioni identiche senza dipoli di drogaggio alle interfacce.
Queste tecniche di modifica delle discontinuità di banda offrono grandi potenzialità nei dispositivi a eterogiunzione. L'efficienza di alcuni dei dispositivi descritti in questo articolo (v. figg. 3A e 4) e di altri dispositivi dipende esponenzialmente dal valore della discontinuità di banda. Per tale motivo una variazione artificiale di questa grandezza di 1 o 2 kBT (dove T è la temperatura e kB la costante di Boltzmann) può già alterare in modo significativo il loro funzionamento.
10. Conclusioni
In sintesi, abbiamo illustrato lo scopo, la potenzialità e l'uso dell'ingegneria del gap di banda. Da un punto di vista fisico, le strutture con gap di banda controllato hanno mostrato una grande ricchezza di nuovi fenomeni, sia elettronici sia ottici, associati alle proprietà della struttura a bande controllata artificialmente e alla dimensionalità ridotta. L'ingegneria del gap comincia ad avere un impatto importante anche sull'elettronica e sulla fotonica. Dispositivi commerciali che ne fanno uso comprendono i laser a pozzi quantici multipli, transistor a elevata mobilità elettronica, e fotodiodi a valanga. Dispositivi in fase di sviluppo avanzato e di prossima probabile commercializzazione comprendono i transistor bipolari a eterogiunzione, fotodiodi a pozzi quantici multipli a valanga e rivelatori di raggi infrarossi a pozzi quantici (v. laser e fotonica, vol. XI).
Le ricerche in questo settore interdisciplinare, in cui la scienza dei materiali, la fisica e la tecnologia si incontrano e si integrano, produrranno probabilmente sviluppi ancora più importanti nel prossimo futuro.
BIBLIOGRAFIA
Alferov, Z., Andreev, V. M., Portnoi, E. L., Trukan, M. K., AlAs-GaAs heterojunction injection lasers with a low room-temperature threshold, in ‟Soviet physics. Semiconductors", 1970, III, pp. 885-887.
Beltram, F., Capasso, F., Sivco, D. L., Hutchinson, A. L., Chu, S. N. G., Cho, A. Y., Scattering controlled transmission resonances and negative differential conductance by field induced localization in semiconductor superlattices, in ‟Physical review letters", 1990, LXIV, pp. 3167-3170.
Capasso, F., Band-gap engineering via graded gap, superlattice and periodic doping structures: applications to photodetectors and other devices, in ‟Journal of vacuum science and technology" (Part B), 1983, I, pp. 457-461.
Capasso, F., Compositionally graded semiconductors and their device applications, in ‟Annual review of materials science", 1986, XVI, pp. 263-291.
Capasso, F., Band-gap engineering: from physics and materials to new semiconductor devices, in ‟Science", 1987, CCXXXV, pp. 172-176.
Capasso, F., Beltram, F., Malik, R. J., Walker, J., New floating gate memory devices with graded-gap electron injectors and long retention times, in ‟IEEE electron device letters", 1988, IX, pp. 377-379.
Capasso, F., Beltram, F., Malik, R. J., Walker, J., Quantum functional devices: resonant tunneling transistors, circuits with reduced complexity and multiple valued logic, in ‟IEEE transactions on electron devices", 1989, XXXVI, pp. 2065-2082.
Capasso, F., Cho, A. Y., Mohammed, K., Foy, P. W., Doping interface dipoles: tunable heterojunction barrier height and band edge discontinuities by molecular beam epitaxy, in ‟Applied physics letters", 1985, XLVI, pp. 664-666.
Capasso, F., Datta, S., Quantum electron devices, in ‟Physics today", 1990, XLIII, pp. 74-82.
Capasso, F., Kiehl, R. A., Resonant tunneling transistor with quantum well base and high energy injection: a new negative differential resistance device, in ‟Journal of applied physics", 1985, LVIII, pp. 1366-1368.
Capasso, F., Sen, S., Gossard, A. C., Hutchinson, A. L., English, J. H., Quantum well resonant tunneling bipolar transistor operating at room temperature, in ‟IEEE electron device letters", 1986, VII, pp. 573-576.
Capasso, F., Sirtori, C., Cho, A. Y., Coupled quantum well semiconductors with giant electric field tunable nonlinear optical properties in the infrared, in ‟IEEE journal of quantum electronics", 1994, XXX, pp. 1313-1326.
Capasso, F., Sirtori, C., Faist, J., Sivco, D. L., Chu, S. N. G., Cho, A. Y., Observation of an electronic bound state above a potential well, in ‟Nature", 1992, CCCLVIII, pp. 565-567.
Capasso, F., Tsang, W. T., Hutchinson, A. L., Williams, G. F., Enhancement of electron impact ionization in a super lattice: a new avalanche photodiode with a large ionization rates ratio, in ‟Applied physics letters", 1982, XL, pp. 38-40.
Capasso, F., Tsang, W. T., Williams, G. F., Staircase solid-state photomultipliers and avalanche photodiodes with enhanced ionization rates ratio, in ‟IEEE transactions on electron devices", 1983, XXX, pp. 381-390.
Chang, L. L., Esaki, L., Tsu, R., Resonant tunneling in semiconductor double barriers, in ‟Applied physics letters", 1974, XXIV, pp. 593-595.
Cho, A. Y., Growth of III-V semiconductors by molecular beam epitaxy and their properties, in ‟Thin solid films", 1983, C, pp. 291-317.
Cho, A. Y., Advances in molecular beam epitaxy, in ‟Journal of crystal growth", 1991, CXI, pp. 1-13.
Cho, A. Y., Molecular beam epitaxy, Woodbury, N. Y., 1994.
Cho, A. Y., Arthur, J. R., Molecular beam epitaxy, in ‟Progress in solid-state chemistry", 1975, X, pp. 157-193.
Cooper, J. A., Capasso, F., Thornber, K. K., Semiconductor structures for repeated velocity overshoot, in ‟IEEE electron device letters", 1982, III, pp. 407-408.
Dingle, R., Stormer, H. L., Gossard, A. C., Wiegmann, W., Electron mobilities in modulation-doped semiconductor heterojunction superlattices, in ‟Applied physics letters", 1978, XXXIII, pp. 665-667.
Dingle, R., Wiegmann, W., Henry, C. H., Quantum states of confined carriers in very thin AlxGa1-xAs/GaAs/AlxGa1-xAs heterostructures, in ‟Physical review letters", 1974, XXXIII, pp. 827-830.
Doehler, G. H., Electron states in crystals with ‛nipi' superstructure, in ‟Physica status solidi. B. Basic research", 1972, LII, pp. 70-92.
Esaki, L., Tsu, R., Superlattice and negative differential conductivity in semiconductors, in ‟IBM journal of research and development", 1970, XLIV, pp. 61-65.
Faist, J., Capasso, F., Sivco, D. L., Sirtori, C., Hutchinson, A. L., Cho, A. Y., Quantum cascade laser, in ‟Science", 1994, CCLXIV, pp. 553-556.
Faist, J., Capasso, F., Sivco, D. L., Sirtori, C., Hutchinson, A. L., Cho, A. Y., Quantum cascade laser: an intersubband semiconductor laser operating above liquid nitrogen temperatures, in ‟Electronics letters", 1994, XXX, pp. 865-866.
Hayashi, I., Panish, M. B., Foy, P. W., Sumski, S., Junction lasers which operate continuously at room temperature, in ‟Applied physics letters", 1970, XVII, pp. 107-109.
Kazarinov, R. F., Suris, R. A., Possibility of the amplification of electromagnetic waves in a semiconductor with a superlattice, in ‟Soviet physics. Semiconductors", 1971, V, pp. 707-709.
Kroemer, H., Quasi-electric and quasi-magnetic fields in a non-uniform semiconductor, in ‟RCA review", 1957, XXVIII, pp. 332-340.
Kroemer, H., A proposed class of heterojunction lasers, in ‟Proceedings of the IEEE", 1963, LI, pp. 1782-1783.
Levine, B. F., Bethea, C. G., Hasnain, G., Walker, J., Malik, R. J., High detectivity D* = 1 × 1010 cm (Hz/W)1/2 GaAs/AlGaAs multiquantum well λ = 8.3 μm infrared detector, in ‟Applied physics letters", 1988, LIII, pp. 296-298.
Osbourn, G. C., Strained-layer superlattices from lattice mismatched materials, in ‟Journal of applied physics", 1982, LIII, pp. 1586-1589.
Ralph, S. E., Capasso, F., Malik, R. J., New photorefractive effect in graded-gap superlattices, in ‟Physical review letters", 1989, LXIII, pp. 2272-2275.
Sirtori, C., Capasso, F., Faist, J., Sivco, D. L., Chu, S. N. G., Cho, A. Y., Quantum wells with localized states at energies above the barrier height: a Fabry-Perot electron filter, in ‟Applied physics letters", 1992, LXI, p. 898.
Vengurlekar, A. S., Capasso, F., Chiu, T. H., Impact ionization in the base of a hot-electron AlSb/InAs bipolar transistor, in ‟Applied physics letters", 1990, LVII, pp. 1772-1774.
Waschke, C., Roskos, H. G., Schwedler, R., Leo, K., Kurz, H., Köhler, K., Coherent submillimeter-wave emission from Bloch oscillations in a semiconductor superlattice, in ‟Physical review letters", 1993, LXX, pp. 3319-3322.