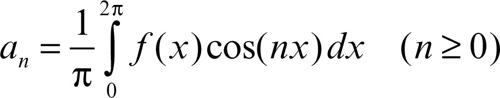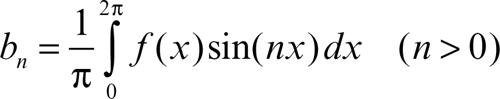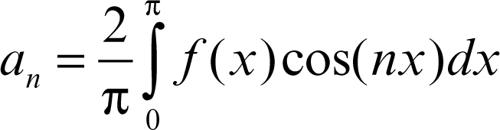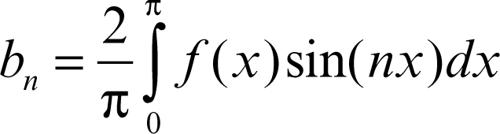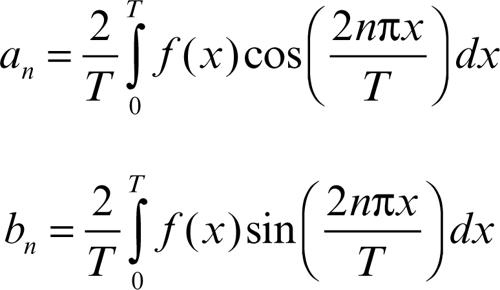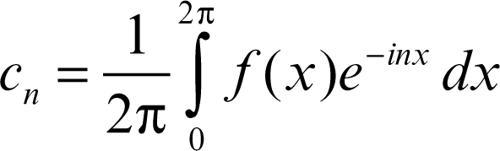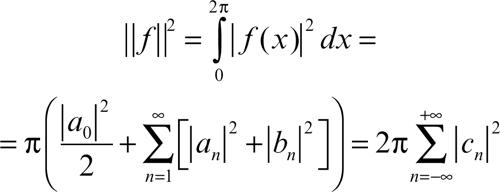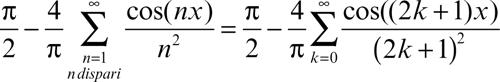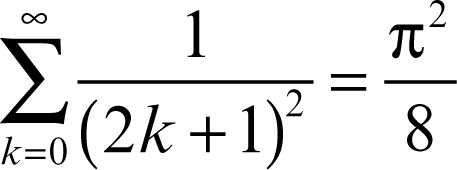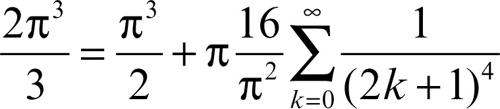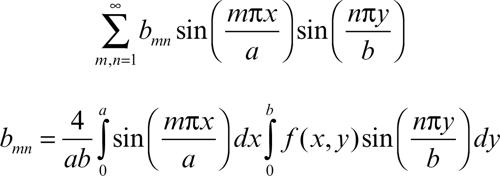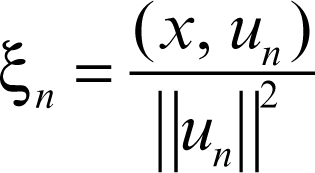Fourier, serie di

Fourier, serie di

Fourier, serie di in analisi, serie di funzioni goniometriche associata a una funzione periodica, di cui costituisce il cosiddetto sviluppo, nel senso che la funzione data è la somma di tale serie qualora sia convergente ed è questo il caso per funzioni sufficientemente regolari. Questi sviluppi di una funzione periodica in serie di funzioni, pur se già in parte noti a Eulero e d’Alembert, ebbero la loro prima utilizzazione nell’opera di J.-B. Fourier (1822) dedicata alla trasmissione del calore. Essi si presentano in modo naturale quando si cerca di risolvere un’equazione differenziale alle derivate parziali con il metodo di separazione delle variabili, ma hanno anche un interesse del tutto indipendente.

Si consideri ƒ(x), funzione periodica di periodo 2π e assolutamente integrabile; si supponga dunque che ƒ appartenga allo spazio L¹(0, 2π). È allora possibile associare a essa i coefficienti di Fourier, dati dalle formule

e

e associare a ƒ(x) la serie di Fourier

Per la periodicità, gli integrali possono essere valutati su qualsiasi altro intervallo di lunghezza 2π, per esempio [−π, π]. La costante a₀/2 rappresenta il valor medio di ƒ(x) in [0, 2π], il termine a_ncos(nx) + b_nsin(nx) rappresenta invece la n-esima armonica. Usualmente ƒ è una funzione reale e quindi anche i coefficienti a_n, b_n lo sono, ma tutte le formule riportate valgono anche se ƒ assume valori complessi, fermo restando che la variabile indipendente x è reale. Si dimostra che i coefficienti a_n e b_n sono infinitesimi per n tendente a infinito (→ Riemann-Lebesgue, lemma di); l’ordine di infinitesimo è tanto maggiore quanto più regolare è la funzione ƒ. Per esempio, se ƒ è continua a tratti, ammette solo discontinuità di prima specie (salti) e ha altrove derivata limitata, i coefficienti sono O(1/n); se ƒ è continua e ammette al più punti angolosi, i coefficienti sono O(1/n²) ecc.

La serie di Fourier associata a una funzione ƒ è detta sviluppo in serie di Fourier della funzione ƒ; con un termine proveniente dall’acustica è anche detta analisi armonica della funzione ƒ. Sviluppare in serie di Fourier la funzione corrisponde a vedere la funzione stessa come risultato del sovrapporsi di infiniti fenomeni periodici con periodi e ampiezze sempre minori.

Tuttavia, il problema di stabilire delle condizioni sotto le quali una serie di Fourier converga, e a quale valore essa converga, è piuttosto complesso. Condizioni sufficienti sono state date da L. Dirichlet, che espresse le somme parziali nella forma detta integrale di → Dirichlet, da U. Dini, R. Lipschitz e altri. Se ƒ ammette solo discontinuità di salto e soddisfa nei restanti intervalli una condizione di → Lipschitz in ogni punto x, la serie converge a ƒ(x) nei punti di continuità, alla semisomma [ƒ(x⁺) + ƒ(x⁻)]/2 dei limiti destro e sinistro nei punti di salto. Un esempio dovuto al matematico tedesco P. Du Bois-Reymond nel 1876 mostra che la continuità non basta a garantire la convergenza. In questo senso, il cosiddetto teorema di Fourier, per cui una funzione continua sarebbe sempre sviluppabile in serie di Fourier, non vale senza ipotesi supplementari. In realtà, la convergenza in un punto x dipende solo dal comportamento di ƒ in un intorno di x (teorema di localizzazione di Riemann). Per esempio, se, per opportune costanti δ > 0, L > 0 e 0 < α ≤ 1, nel punto di salto x valgono, per 0 < t < δ, le disuguaglianze

la serie di Fourier di ƒ converge a [ƒ(x⁺) + ƒ(x⁻)]/2. La convergenza uniforme di una serie di Fourier, sviluppo di una funzione continua ƒ, è garantita per esempio se la derivata ƒ(x) è continua a tratti (→ Fejér, integrale di; → Gibbs, fenomeno di).

Anche se la serie non converge uniformemente, tuttavia, è sempre lecita la sua integrazione per serie, e la serie ottenuta converge uniformemente in R (si noti che la primitiva di una funzione periodica ƒ(x) è periodica solo se il valor medio a₀/2 è nullo).

Si danno i seguenti casi particolari:

• ƒ pari: tutti i coefficienti b_n sono nulli e

• ƒ dispari: tutti i coefficienti a_n sono nulli e

• ƒ di periodo T ≠ 2π, allora

con

Nelle applicazioni alle equazioni differenziali alle derivate parziali, la funzione ƒ(x) non è periodica, ma è definita in un intervallo limitato, che si può pensare sia (0, 2π), e viene estesa per periodicità quando se ne calcoli lo sviluppo mediante le formule sopra riportate. Si noti che se una funzione è definita solo nell’intervallo (0, π), è possibile prolungarla a una funzione di periodo 2π in più modi: in particolare si può considerarne il prolungamento pari, ponendo ƒ(x) = ƒ(−x) in (−π, 0), o quello dispari, ponendo ƒ(x) = −ƒ(−x), o quello di periodo π, ponendo ƒ(x) = ƒ(x + π), e quindi estendendone la definizione da (−π, π) a tutto R per periodicità. Questi tre prolungamenti danno naturalmente luogo a serie differenti, tutte convergenti a ƒ(x) nell’intervallo originario (0, π). La scelta del prolungamento dipende in genere dalle condizioni ai limiti imposte per l’equazione differenziale.

Importante è poi la forma esponenziale delle serie di Fourier. Mediante le formule di Eulero si può scrivere una serie di Fourier nella forma

I coefficienti c_n sono legati ai precedenti coefficienti a_n, b_n dalle formule

e sono calcolabili direttamente da

La serie deve essere intesa nel senso del valore principale, cioè come

(→ serie bilatera). Analoghe formule valgono se il periodo è T ≠ 2π.

Se ƒ è assolutamente integrabile insieme al suo quadrato (basta chiedere che ƒ ∈ L²(0, 2π) ⊆ L¹(0, 2π); si veda → spazio L^p(Ω)), vale l’uguaglianza di Parseval (→ Parseval, identità di):

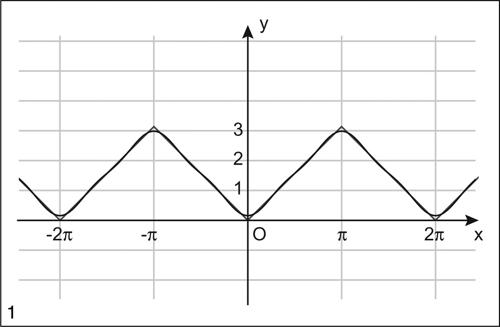
cioè le successioni {α_n}, {b_n}, {c_n} ∈ l ² (sono cioè a quadrato sommabile; si veda → spazio l ^p) e viceversa, se tali successioni sono in l ², ƒ ∈ L²(0, 2π). Questa uguaglianza ha un importante significato energetico: se ƒ rappresenta una funzione periodica, come per esempio una tensione, la sua norma L² è proporzionale alla sua energia media e gli addendi a secondo membro forniscono, a meno della stessa costante di proporzionalità, l’energia delle singole armoniche. Per esempio: sia ƒ(x) = |x| in [−π, π] e T = 2π. La funzione è pari, quindi ∀n, b_n = 0. Risulta a₀ = π, a_n = −4/(πn²) per n dispari, a_n = 0 per n pari. La serie di Fourier associata a ƒ(x) è dunque:

che converge a ƒ(x) uniformemente su R. Per x = 0 si ottiene

da cui

L’uguaglianza di Parseval dà

da cui

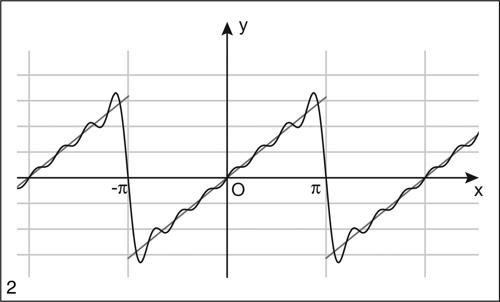
Si noti che la funzione data si può considerare anche come il prolungamento pari della funzione definita da ƒ(x) = x in (0, π). Se si fosse voluto eseguire il prolungamento dispari di x, si sarebbe ottenuto lo sviluppo

valido in (−π, π), convergente più lentamente del precedente, e per cui l’uguaglianza di Parseval darebbe la famosa somma

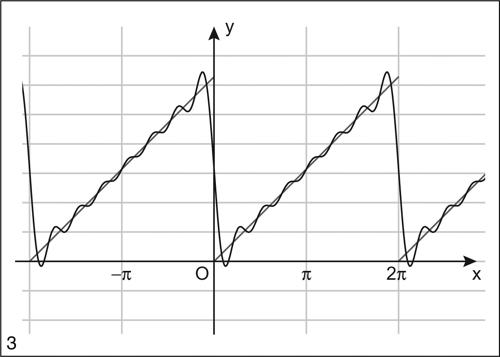
Un terzo tipo di prolungamento con periodo 2π, in cui ƒ(x) = x in (0, 2π), darebbe infine lo sviluppo

La scelta dipende dal problema da risolvere, che in genere specifica quali funzioni si debbano prendere in considerazione e su quale intervallo (per un altro esempio, si veda → Gibbs, fenomeno di).

Si possono considerare serie di Fourier multiple, per sviluppare funzioni di più variabili. Per esempio, una funzione ƒ(x, y) definita in un rettangolo R = [0, a] × [0, b] si può sviluppare in una serie della forma

Molte altre serie di funzioni hanno la stessa struttura formale delle serie di Fourier; in particolare le serie di → polinomi ortogonali e le serie di funzioni di Bessel (→ Bessel, equazione di; si vedano per queste serie le tavole delle funzioni speciali). Si veda anche → Fourier, serie generalizzata di.

Tale struttura si può inquadrare nella teoria degli spazi di Hilbert. Sia X uno spazio di Hilbert, in generale complesso, sia {e_n}, con 0 ≤ n, una base di versori ortogonali in X (o, come pure si dice, di versori ortonormati): risulti cioè (e_n, e_m) = δ_nm, con δ_nm simbolo di Kronecker e (e_n, e_m) il prodotto scalare dei versori e_n e e_m, che nel contesto di uno spazio di Hilbert sono indicati in corsivo e non in grassetto. Se un elemento x ∈ X ammette lo sviluppo

il suo coefficiente di Fourier generalizzato ξ_n si calcola mediante il prodotto scalare ξ_n = (x, e_n) e risulta {ξ_n} ∈ l ² con

Più in generale, se anche il vettore y ammette lo sviluppo

risulta

Viceversa, dato un generico elemento x ∈ X, se si costruiscono i coefficienti ξ_n = (x, e_n) si ha

Se la disuguaglianza si riduce all’uguaglianza per ogni x, la successione {e_n} si dice completa (o chiusa); in tal caso essa costituisce una base di X, cioè genera l’intero spazio. Affinché {e_n} sia completa, è necessario e sufficiente che se (u, e_n) = 0 per ogni n, allora u = 0. In caso contrario la successione {e_n} genera un sottospazio V di X, e ogni vettore x ammette la decomposizione unica x = ν + h, con ν ∈ V (proiezione di x su V) e h ∈ V^⊥, dove V^⊥ è il sottospazio ortogonale a V in X. Per esempio, se in una serie di Fourier classica si utilizzano solo le funzioni sin(nx), non si ricostruisce tutta la funzione generatrice ƒ. Infatti, la successione {sin(nx)} genera il sottospazio V di L²(−π, π) formato dalle funzioni dispari e quindi la serie

ha come somma la parte dispari di ƒ(x), cioè ν(x) = [ƒ(x) − ƒ(−x)]/2; mentre la parte pari, h(x) = [ƒ(x) + ƒ(−x)]/2, che ha sviluppo

e appartiene a V^⊥, non può essere recuperata. È dunque importante garantirsi che la successione {e_n} utilizzata sia completa, e a tale scopo esistono dei criteri dovuti a G. Vitali e a D.P. Dalzell.

Nelle applicazioni si usano successioni {u_n} di vettori ortogonali che non sono versori. Le stesse serie di Fourier classiche utilizzano i vettori corrispondenti alle funzioni {1, sin(nx), cos(nx)} anziché i versori

Il motivo, oltre che storico, è di praticità, per evitare fattori irrazionali scomodi nelle formule e dannosi nel calcolo numerico. Se

risulta allora

e l’uguaglianza di Parseval diviene