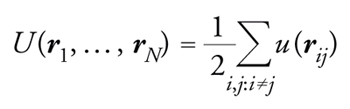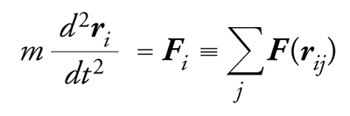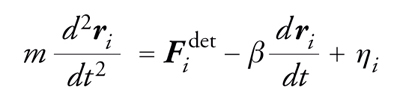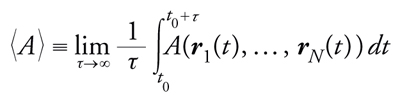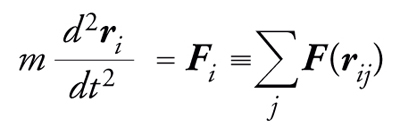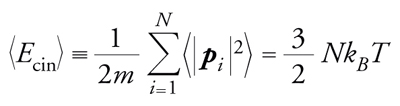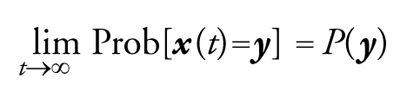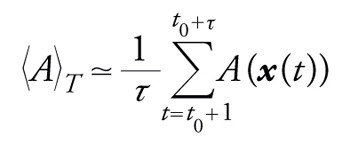Simulazioni di processi fisici mediante calcolatore

Simulazioni di processi fisici mediante calcolatore

Per simulazione di un processo fisico si intende la rappresentazione, eventualmente approssimata, di tale processo mediante la risoluzione di equazioni e modelli matematici al calcolatore. Il metodo numerico è stato uno strumento fondamentale nello studio dei fenomeni fisici e ha permesso di ottenere risultati difficilmente raggiungibili per altra via. L'uso di simulazioni numeriche assume sempre maggiore importanza con l'aumento della potenza di calcolo a disposizione. Si potrebbe credere che una simulazione numerica, soprattutto se condotta a partire direttamente dalle forze fondamentali, possa riprodurre esattamente il fenomeno fisico che si intende studiare. È importante tuttavia osservare che una simulazione numerica si limita a studiare il modello di un sistema fisico, ossia a fornire una descrizione approssimata dei fenomeni. Un modello è realistico se gli aspetti del processo fisico che esso ignora sono irrilevanti, o molto poco influenti, per il valore delle grandezze che interessa studiare. Una simulazione numerica è valida se, a meno delle inevitabili indeterminazioni statistiche e indipendentemente dal grado di realismo di un modello, ne riproduce il corretto comportamento. D'altra parte tale comportamento può in alcuni casi essere calcolato mediante una teoria analitica sufficientemente accurata, il cui studio numerico permette di verificare la validità di una simulazione numerica. Qualora non esistano risultati analitici attendibili, la compatibilità dei risultati numerici ottenuti mediante diverse simulazioni può essere verificata ricorrendo eventualmente ad algoritmi differenti.

Negli anni Settanta del XX sec., quando le simulazioni numeriche iniziarono a svolgere un ruolo importante nello studio dei processi fisici, fu naturale domandarsi se queste dovessero essere considerate uno studio teorico o una sorta di esperimento. Esistono argomenti a favore di entrambe le ipotesi: da un lato, una simulazione numerica è basata su un modello e non fornisce misure relative ad alcun sistema fisico reale, per cui essa non può essere considerata un vero esperimento; dall'altro i risultati di una simulazione numerica sono utilizzati per convalidare o confutare teorie, ed è difficile immaginare una teoria che ne confuti un'altra. La soluzione più facile consiste nel definire le simulazioni numeriche come una vera e propria terza via nello studio scientifico, parallela e interposta a quella teorica e a quella sperimentale.

Una simulazione numerica studia un modello teorico in modo analogo a quello con il quale uno studio sperimentale indaga un processo fisico reale. Il ruolo delle simulazioni numeriche in relazione alle teorie e agli esperimenti si manifesta classicamente nei due usi più riduzionistici: verificare unateoria confrontandone le predizioni con le 'misure' ottenute dai modelli e convalidare i modelli confrontandone il comportamento con quello del sistema fisico, studiato mediante esperimenti. Grazie alla creazione di nuovi e più potenti algoritmi numerici e alla crescente potenza di calcolo delle macchine, si sta tuttavia sviluppando un differente uso delle simulazioni numeriche, alternativo al riduzionismo classico. In questo nuovo modo di fare scienza, si considerano spesso modelli con una fenomenologia molto complessa, per la cui descrizione non esistono ancora teorie adeguate: li si studia con procedimenti di tipo numerico, alla ricerca di quelle proprietà peculiari che permettano alla fine la costruzione della teoria. L'uso esplorativo delle simulazioni numeriche è considerato alternativo a quello riduzionistico, perché studia in tutta la sua complessità un modello, senza ridurlo a priori.

La scelta del modello

In una simulazione numerica, attraverso la quale è possibile studiare solamente un modello della realtà, è di fondamentale importanza approssimare al meglio il processo fisico in esame, per esempio scartando tutti quei dettagli che risultano irrilevanti in quanto corrispondono a fenomeni che avvengono su scale di tempo (o di energia) molto più grandi o molto più piccole rispetto a quelle del processo fisico che si sta studiando. Supponiamo di voler studiare la viscosità di un fluido, e in particolare l'origine microscopica dell'aumento rapidissimo di viscosità che si osserva sperimentalmente abbassando leggermente la temperatura in alcuni liquidi (i cosiddetti glass-former liquids). Un modello minimale per questo studio è quello composto da N molecole sferiche, che interagiscono a coppie con una forza intermolecolare F(r) che dipende solamente dalla distanza relativa. Una buona scelta per F(r) è che la forza sia intensamente repulsiva a brevi distanze, così che le molecole non possano compenetrarsi, attrattiva a medie distanze e nulla a grandi distanze. Definendo la corrispondente energia potenziale intermolecolare u(r), tale che F(r)=−∇u(r), e il vettore distanza r_ij≡r_i−r_j, si può scrivere l'energia potenziale totale del sistema come una sommatoria su tutte le coppie di molecole:

[1] formula.

A seconda della densità delle molecole, questo modello può descrivere un liquido oppure un gas.

Nella definizione di questo modello sono stati trascurati tutti i dettagli relativi alla struttura interna delle molecole, il che permette una simulazione assai più veloce; tali dettagli sarebbero stati invece fondamentali se si fossero voluti studiare processi di altro tipo, per esempio la dissociazione molecolare. Spesso i dettagli mancanti sono aggiunti a un modello in un momento successivo, qualora emerga che l'approssimazione trascuri elementi rilevanti. Senza considerare ancora le forze intramolecolari, e approssimando quindi come un corpo unico e indissociabile la molecola, potrebbe però essere importante assumere per quest'ultima una forma non sferica: nel caso della molecola d'acqua, la forma triangolare è cruciale per la formazione della struttura cristallina del ghiaccio. Viceversa, se volessimo studiare la formazione di zone turbolente intorno al profilo di un'ala, la descrizione a livello molecolare sarebbe troppo dettagliata e dispendiosa. In questo caso sarebbe sufficiente un'approssimazione del fluido come un mezzo continuo con proprietà statistiche medie, quali la densità, la temperatura, la compressibilità, la viscosità, le quali si possono misurare sperimentalmente o calcolare mediante un'altra simulazione numerica a livello molecolare.

La scelta dell'algoritmo

Nel progettare una simulazione numerica, una scelta cruciale riguarda l'algoritmo da usare in relazione a ciò che si vuole misurare nel modello. Nel modello di fluido molecolare introdotto sopra, per esempio, se si vogliono studiare esattamente le traiettorie delle molecole non si può far altro che integrare numericamente le equazioni del moto. Al contrario, se si è interessati soltanto ad alcune proprietà statistiche medie del fluido, quali le funzioni termodinamiche o le caratteristiche dinamiche (per es.,i coefficienti di trasporto), allora si possono scegliere algoritmi basati su principî molto diversi. Senza pretendere di essere esaustivi, presentiamo una prima grande classificazione degli algoritmi basata sul loro grado di determinismo oppure di stocasticità, intesa come la caratteristica di far uso di valori aleatori per descrivere il processo.

La dinamica molecolare è un metodo perfettamente deterministico, in cui le posizioni delle particelle si calcolano risolvendo le equazioni del moto del sistema

[2] formula

dove F_i è la forza agente sulla i-esima particella ed è data dalla somma delle interazioni intermolecolari.

Se non si presenta la necessità di seguire la traiettoria di ogni singola molecola, la simulazione può essere resa più rapida integrando alcuni gradi di libertà del modello descritti soltanto a livello statistico. Per esempio, nel modello di una particella mesoscopica che si muove entro un fluido molecolare, quest'ultimo si può approssimare come un continuo che esercita sulla particella una forza di intensità e direzione aleatorie, dovuta agli urti con le molecole a livello microscopico. In quest'approssimazione, la simulazione numerica risolve un'equazione stocastica nota come equazione di Langevin:

[3] formula

in cui il primo termine rappresenta le forze deterministiche, per esempio l'interazione tra due particelle mesoscopiche, il secondo termine è dato dall'attrito e l'ultimo termine esprime la forza aleatoria, di cui è nota soltanto la distribuzione di probabilità.

Si ha infine il metodo Monte Carlo, il quale, basato fondamentalmente su un processo stocastico, ha lo scopo di generare in modo casuale le configurazioni più probabili del sistema, quelle che sarebbero raggiunte da una tipica traiettoria delle particelle. La differenza principale rispetto ai metodi precedenti, basati sull'integrazione delle equazioni del moto, è che la sequenza temporale delle configurazioni generate potrebbe anche non corrispondere a una vera traiettoria, per esempio perché due configurazioni generate consecutivamente potrebbero essere molto distanti tra loro.

Supponendo di voler studiare il modello a una temperatura T stabilita, le configurazioni delle N molecole devono essere generate con una probabilità pari a quella che hanno nell'ensemble statistico canonico:

[4] P_T(r ₁, ╝, r_N) ∝ e^{−U(r 1}, ^╝, ^rN)/T.

L'equivalenza tra i risultati che si ottengono con la dinamica molecolare, integrando esplicitamente le equazioni del moto, e quelli che si ottengono dal metodo Monte Carlo, generando le configurazioni con una certa distribuzione di probabilità, non è affatto ovvia e deve essere controllata caso per caso. La media di una generica quantità osservabile A(r₁,…,r_N) nell'insieme canonico è data dall'espressione

[5] 〈A〉_T ≡ ∫A(r ₁, ╝, r_N)P_T(r ₁, ╝, r_N)dr ₁╝dr_N

mentre nella dinamica molecolare la media di A(r₁,…,r_N) è calcolata lungo la traiettoria ottenuta dall'integrazione delle equazioni del moto, vale a dire

[6] formula

dove t₀ è il tempo necessario a raggiungere il regime asintotico stazionario; il limite di tempo infinito corrisponde in pratica al tempo totale della simulazione, che è limitato per ovvie ragioni. L'equivalenza tra le medie 〈A〉 e 〈A〉_T si basa sull'ipotesi ergodica, che corrisponde, in parole semplici, alla possibilità che una generica traiettoria della dinamica raggiunga tutte le configurazioni del sistema che hanno una probabilità P_T(r₁,…,r_N) non nulla. Il problema della rottura dell'ergodicità, ossia l'impossibilità di raggiungere con un dato algoritmo, deterministico o stocastico che sia, alcune configurazioni del modello che hanno probabilità non nulla, è uno degli aspetti più delicati in una simulazione numerica: è estremamente importante, sebbene talvolta difficile, riconoscere i 'sintomi' di una simulazione numerica che non sta raggiungendo tutte le configurazioni a probabilità non nulla. In questi casi è necessario risolvere il problema scegliendo un algoritmo migliore o modificando alcuni parametri del modello: tipicamente, negli algoritmi stocastici gli effetti della rottura dell'ergodicità possono essere ridotti aumentando la temperatura o diminuendo il numero di gradi di libertà del sistema (per es. il numero di particelle). In generale, la dinamica molecolare soffre maggiormente di problemi legati alla rottura dell'ergodicità, in quanto due configurazioni consecutive sono necessariamente vicine nello spazio delle configurazioni, mentre nel metodo Monte Carlo si può proporre di scambiare particelle assai lontane o muovere collettivamente molte particelle, purché l'energia del sistema non cambi troppo. Questa ampia libertà nel tipo di mosse con cui cambiare la configurazione del sistema rende i metodi stocastici facilmente adattabili a problemi anche molto diversi.

Dinamica molecolare

Nel metodo della dinamica molecolare si devono integrare le equazioni del moto dei singoli gradi di libertà del modello (quelli delle particelle, nel caso del modello di fluido molecolare):

[7] formula.

Il problema si riconduce quindi a quello, ben più generale, di risolvere numericamente un'equazione differenziale ordinaria. Esistono diversi algoritmi per l'integrazione numerica delle equazioni differenziali: di Eulero, Verlet, Gear, Runge-Kutta, ecc. Si basano tutti sulla discretizzazione dei tempi in intervalli Δt e sull'uso delle differenze finite al posto delle derivate, ma si distinguono per il numero di derivate cui fanno ricorso, per i tempi a cui queste sono calcolate e per la rapidità con cui la differenza tra la traiettoria vera e quella discretizzata tende a zero al diminuire del passo Δt. Va poi considerata la stabilità di un algoritmo di integrazione, ossia se e quanto la traiettoria calcolata numericamente rimanga vicino a quella esatta nel limite di tempi molto grandi. In generale, gli algoritmi d'integrazione che producono traiettorie migliori richiedono il calcolo di un maggior numero di derivate; in considerazione del fatto che il calcolo delle forze è l'operazione più onerosa in una simulazione di dinamica molecolare, si opta spesso per una soluzione di compromesso: le forze sono calcolate una sola volta per ogni passo, ma l'errore d'integrazione è ridotto mediante il ricorso ad alcuni stratagemmi. Per esempio, nel metodo di Verlet le posizioni e le velocità sono calcolate a tempi sfalsati di mezzo passo (Δt/2), mentre negli algoritmi di predizione-correzione (Gear) le posizioni, inizialmente predette, sono successivamente corrette a un valore migliore.

In una simulazione di dinamica molecolare, quanti-tà termodinamiche come temperatura e pressione non compaiono esplicitamente nell'equazione, ma si possono dedurre da relazioni del tipo

[8] formula

che lega l'energia cinetica alla temperatura, dove p_i è il momento della i-esima particella e k_B è la costante di Boltzmann.

Metodo Monte Carlo

Con la denominazione Monte Carlo si indica in generale qualsiasi metodo numerico che faccia uso di variabili aleatorie. Tale metodo trova una naturale e ovvia applicazione nel descrivere tutti i processi fisici in cui si verificano eventi casuali; sia se questi sono conseguenza del principio di indeterminazione quantistica, come nell'effetto fotoelettrico, sia se derivano da una nostra incapacità a descrivere in dettaglio le forze che li originano, come nel moto browniano. Un altro importante campo di applicazione delle tecniche Monte Carlo è il campionamento casuale di una distribuzione di probabilità P(x₁,…,x_N) definita in uno spazio a N dimensioni (con N che assume valori grandi); questo problema è rilevante, per esempio, per l'integrazione multidimensionale, l'analisi dei dati, l'inferenza bayesiana e la stima delle medie in un insieme statistico, come si vede dalla definizione di 〈A〉_T data sopra.

È bene osservare che un calcolatore è una macchina completamente deterministica e non contiene alcun dispositivo per la generazione di numeri realmente aleatori. Esistono tuttavia molti algoritmi, i generatori di numeri pseudocasuali, che forniscono sequenze di numeri che, se sottoposti a qualsiasi analisi statistica, risultano del tutto scorrelati e sono pertanto adatti a essere usati dagli algoritmi stocastici. Dato il problema di generare un gran numero di configurazioni della variabile N-dimensionale x=(x₁,…,x_N) con distribuzione di probabilità P(x), l'usuale metodo Monte Carlo consiste nel costruire un processo stocastico in tempo discreto {x(t)}_t=1,2,…, una sorta di sequenza nello spazio N-dimensionale, con le seguenti proprietà: (a) il processo stocastico in questione è un esempio di una struttura matematica molto comune, detta catena di Markov, in cui la probabilità che il valore di x(t+1) sia pari a y dipende, oltre che da y, solamente dal valore di x(t), ossia dal valore della variabile aleatoria al tempo immediatamente precedente, e non da tutta la sequenza:

[9] Prob[x(t+1)=y] =W(y, x(t))

(b) per tempi grandi, la probabilità che nella sequenza compaia il valore y è pari a P(y); vale a dire che, assumendo che non vi sia periodicità nella sequenza {x(t)} ‒ nel qual caso la proprietà sarebbe ancora vera, ma la formulazione leggermente più complicata ‒ si può scrivere:

[10] formula.

La seconda di queste proprietà permette di stimare la media 〈A〉_T mediante la seguente espressione:

[11] formula

dove il tempo t₀, detto di termalizzazione, deve essere sufficientemente grande affinché le proprietà statistiche della sequenza {x(t)} siano stazionarie e la media 〈A〉_T non dipenda più da t₀. La proprietà di Markov semplifica molto la generazione della sequenza e l'analisi teorica del processo. Grazie a quest'analisi è possibile scegliere la funzione W(y,x(t)) affinché la sequenza converga per tempi grandi verso la distribuzione di probabilità voluta, la P(x). Tra le molteplici scelte, una delle più comuni è quella dell'algoritmo di Metropolis, in cui il singolo passo, cioè la generazione di x(t+1) dato il valore di x(t), si compone di due fasi: (a) si propone una nuova configurazione z, scelta con una distribuzione di probabilità V(z,x(t)) che sia simmetrica sotto lo scambio del punto di partenza e di quello di arrivo, cioè

[12] V(y, z) = V(z, y)

(b) si accetta la nuova configurazione z come elemento successivo della sequenza, ossia x(t+1)=z, con una probabilità pari a min[1,P(z)/P(x(t))]; altrimenti, con probabilità complementare, si rigetta la nuova configurazione e si assegna x(t+1)=x(t).

In pratica, in una simulazione Monte Carlo si conserva nella memoria del calcolatore non tutta la sequenza, bensì soltanto l'ultima configurazione, che è aggiornata solamente allorquando la nuova configurazione proposta sia accettata. Nel caso della simulazione del modello di fluido molecolare descritto sopra, la nuova configurazione potrebbe differire da quella attuale nella posizione di una sola particella, alla quale si aggiunge un piccolo spostamento casuale estratto da una distribuzione gaussiana di varianza δ. Per piccoli valori di δ‚ la nuova configurazione è molto simile a quella precedente, il rapporto delle probabilità P(z)/P(x(t)) è molto vicino a 1 e la nuova configurazione è accettata quasi sempre; l'evoluzione del sistema tuttavia è molto lenta. La probabilità di accettare la nuova configurazione diminuisce aumentando il valore di δ; un buon compromesso consiste nel regolare δ in modo che la nuova configurazione sia accettata circa la metà delle volte.

La raccolta dei dati in una simulazione numerica è molto simile a quanto avviene in un esperimento. Si cerca prima di tutto di eliminare qualsiasi fonte di errori sistematici, quale la presenza di errori di programmazione e di arrotondamento, l'uso di cattivi generatori di numeri pseudocasuali, ecc. Quindi si calcolano le indeterminazioni e le correlazioni statistiche sulle grandezze misurate; per esempio, nella sequenza {x(t)}, generata con l'algoritmo di Metropolis, due configurazioni consecutive sono fortemente correlate e inducono forti correlazioni nelle grandezze.

Bibliografia

Barone 2006: Barone, Luciano Maria e altri, Programmazione scientifica: linguaggio C, algoritmi e modelli nella scienza, Milano, Pearson education, 2006.

Newman, Barkema 1999: Newman, Mark E.J. - Barkema, Gerard T., Monte Carlo methods in statistical physics, Oxford, Clarendon; New York, Oxford University Press, 1999.

Rapaport 2004: Rapaport, Dennis C., The art of molecular dynamics simulation, 2. ed., Cambridge, Cambridge University Press, 2004.