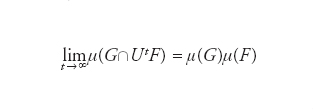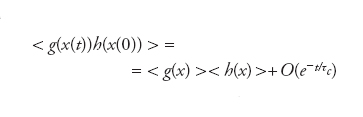sistema mescolante

sistema mescolante

La proprietà di ergodicità può essere verificata anche in sistemi molto regolari (come la rotazione sul toro). Nell’ambito della meccanica statistica è naturale aspettarsi che in tempi ragionevoli un sistema perda il ricordo dello stato iniziale per raggiungere l’equilibrio statistico. Un modo per caratterizzare la perdita di memoria della condizione iniziale si ottiene mediante la nozione, risalente a Willard Gibbs, di mescolamento. Si può considerare un insieme di sistemi identici, copie mentali di uno stesso sistema, i cui punti rappresentativi inizialmente siano concentrati in una piccola regione F della ipersuperficie con energia costante. È naturale aspettarsi che, dopo un certo tempo, in seguito all’evoluzione i punti rappresentativi vadano a distribuirsi in modo praticamente uniforme sulla ipersuperficie, secondo la misura microcanonica. Da un punto di vista generale un sistema dinamico (Ω,U^t,dμ(x)) è mescolante se per ogni coppia di regioni G e F dello spazio delle fasi si ha

dove U^tF indica l’insieme nel quale si è evoluto F dopo un tempo t e μ(G)=∫_G dμ(x). Se il sistema è mescolante allora si ha un rilassamento di un’arbitraria misura iniziale verso la misura invariante. Il tempo caratteristico di rilassamento τ_c è dato dal comportamento asintotico delle funzioni di correlazione temporali

dove le medie sono da intendere rispetto alla misura invariante.

→ Caos deterministico