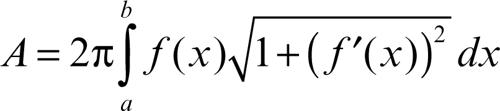solido di rotazione

solido di rotazione

solido di rotazione solido ottenuto, nel modo più semplice, facendo ruotare di 360° una figura piana (sezione) attorno a un asse che giaccia nel suo piano e non abbia punti interni alla sezione. Nei casi elementari in cui si considerano un triangolo rettangolo o un rettangolo che ruotano attorno a un loro rispettivo lato (nel caso del triangolo, attorno a un cateto) che è, quindi, l’asse di rotazione, si ottengono come rispettivi solidi di rotazione un cono (finito) e un cilindro (finito); la superficie descritta, nel caso del triangolo rettangolo, dall’ipotenusa e, nel caso del rettangolo, dal lato parallelo all’asse è detta superficie laterale del solido di rotazione. Dalla rotazione completa di un semicerchio intorno a un proprio diametro si genera una sfera; la semicirconferenza associata al semicerchio genera invece, nella rotazione completa attorno al diametro, la superficie sferica.

Se un solido di rotazione è delimitato da una superficie ottenuta attraverso la rotazione del grafico di una funzione derivabile y = ƒ(x), in un intervallo [a, b], attorno all’asse delle ascisse, l’area della sua superficie laterale è:

essendo ƒ′ (x) la derivata della funzione ƒ. Nel caso generale, se si considera una figura piana che ruota attorno a un asse e si assumono come piano il piano (x, z) e come asse di rotazione l’asse z, e se il contorno della figura, giacente nel semipiano x > 0, è dato dall’equazione ƒ(x, z) = 0, la superficie del solido ha equazione

Per il calcolo della superficie e del volume di un solido di rotazione sono utili i teoremi di Pappo-Guldino (→ Guldino, teoremi di).