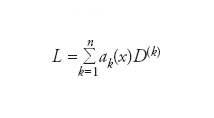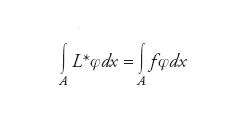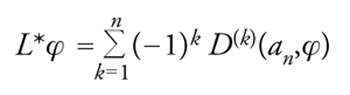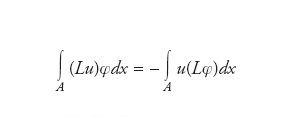soluzioni deboli
soluzioni deboli
Consideriamo un operatore differenziale lineare
definito su un aperto connesso A di ℝn, dove le ak(x) sono funzioni su A sufficientemente regolari (per es. differenziabili infinite volte, ovvero C∞) e i simboli D(k) indicano diverse combinazioni di derivate parziali (o ordinarie nel caso di operatori su funzioni di una singola variabile). Per es., Di=∂/∂xi con xi componente i-esima del vettore x. Si dice allora soluzione debole dell’equazione differenziale Lu=f una funzione (localmente integrabile) u che soddisfi l’equazione
per tutte le funzioni φ sufficientemente regolari (per esempio C∞) con supporto chiuso e limitato nonché contenuto in A. Il simbolo L* indica qui l’aggiunto formale dell’operatore L, definito tramite la
Per es., nel caso L=∂/∂xi, la definizione precedente si riduce a un’applicazione formale della formula di Green (o della formula dell’integrazione per parti nel caso di una variabile reale)
dove l’assenza di termini di bordo (definiti cioè sul bordo di A) è dovuta al fatto che per definizione φ(x)=0 per x∈A. Notiamo che la formula precedente può essere anche guardata come definizione del concetto di derivata della funzione generalizzata (o distribuzione) u. In altre parole, la derivata parziale generalizzata f=Diu di una distribuzione (localmente integrabile) può essere definita come come quella funzione localmente integrabile f tale che u è una soluzione debole dell’equazione f=Diu. Uno dei più importanti problemi della teoria delle equazioni differenziali (alle derivate parziali) consiste nel determinare quando una soluzione debole sia anche soluzione in senso proprio (forte). Questo equivale a dimostrare che la soluzione debole stessa, in linea di principio solo localmente integrabile e dunque potenzialmente molto irregolare, è in realtà derivabile un numero sufficiente di volte. Per es., nel caso delle equazioni cosiddette ellittiche ogni soluzione debole è anche forte.
→ Equazioni differenziali: problemi non lineari; Matematica: problemi aperti