Banach, spazio di

Banach, spazio di

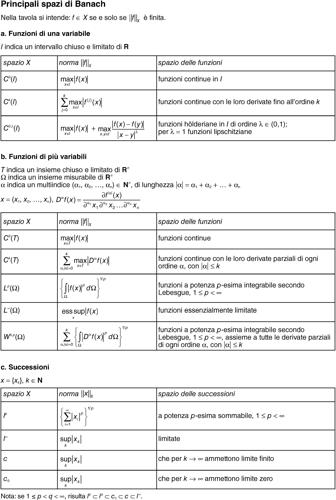
Banach, spazio di spazio vettoriale (definito sul campo dei numeri reali o complessi), in cui è definita una → norma che induce una → metrica rispetto alla quale ogni successione di Cauchy è convergente a un elemento dello spazio. È dunque uno spazio vettoriale e completo (X, ‖...‖). Importanti spazi di Banach sono:

• gli spazi di → Hilbert;

• gli spazi C^k(T), formati dalle funzioni continue con le loro derivate fino all’ordine k in T, dove T è un insieme chiuso e limitato di Rⁿ e k è un intero non negativo;

• gli spazi di funzioni hölderiane C^k,α(T), con T e k come sopra e α ∈ (0, 1) esponente di Hölder delle derivate di ordine k;

• gli → spazi L^p(Ω), formati dalle funzioni a potenza p-esima integrabile secondo Lebesgue in Ω, con Ω insieme misurabile di Rⁿ e 1 ≤ p < ∞;

• lo spazio L^∞(Ω), formato dalle funzioni essenzialmente limitate in Ω;

• gli spazi di → Sobolev W^k,p(Ω);

• lo → spazio l ^p delle successioni x = {ξ_k} a potenza p-esima sommabile, cioè tali che la serie

è convergente per p ∈ [1, ∞), e lo spazio l ^∞ delle successioni limitate.

Per le norme corrispondenti, definite in ognuno di tali spazi, si rimanda alla tavola degli spazi di Banach. L’importanza applicativa degli spazi di Banach sta nel fatto che essi costituiscono l’ambiente naturale in cui cercare le soluzioni di equazioni differenziali o integrali, per esempio mediante metodi di punto fisso, la cui esistenza e unicità è assicurata dal teorema delle contrazioni (→ Banach-Caccioppoli, teorema di).