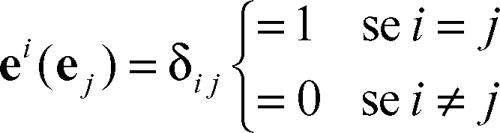spazio duale

spazio duale

spazio duale di uno spazio vettoriale V_K, su un campo K è lo spazio vettoriale V* i cui elementi sono i funzionali lineari su V* (→ funzionale). L’insieme V* viene dotato di struttura di spazio vettoriale su K definendo una operazione interna, detta addizione di funzionali, e una operazione esterna, detta moltiplicazione di un funzionale per uno scalare (elemento di K), che godono delle seguenti proprietà:

• (ƒ + g)v = ƒ(v) + g(v), ∀ƒ, g ∈V*, ∀v ∈ V*

• (kƒ)(v) = k ⋅ ƒ(v), ∀k ∈ K, ∀ƒ ∈ V*, ∀v ∈ V*

Uno spazio vettoriale di dimensione finita e il suo duale hanno la stessa dimensione. Se V* ha per base la n-pla di vettori (e₁, …, e_n), lo spazio duale V* possiede una base duale (e¹, …, eV*ⁿV*) così definita:

In altri termini, base duale dello spazio duale V* di uno spazio vettoriale V* è l’insieme degli n funzionali e_j che a ogni x di V* associano, rispettivamente, la sua coordinata j-esima nella base fissata di V*. Essendo elementi di uno spazio vettoriale, tali funzionali sono più correttamente indicati con e_j.

Se RV*ⁿV* è lo spazio dei vettori colonna con n componenti, lo spazio duale (RV*ⁿV*)* è lo spazio dei vettori riga con n componenti e ciascun vettore riga v può essere interpretato come un funzionale che fa corrispondere al vettore colonna u lo scalare dato dal prodotto righe per colonne dei vettori u e v.

Se V* è uno spazio vettoriale topologico, il suo duale, detto spazio duale topologico o spazio duale continuo, è costituito da tutti i funzionali lineari e continui su V*.