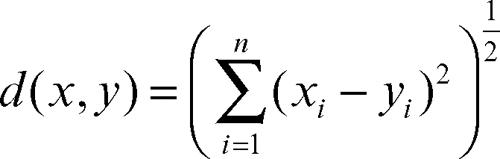spazio metrico

spazio metrico

spazio metrico insieme X in cui è definita una → metrica, cioè una applicazione d: X × X → R che, per ogni x, y, z ∈ X, soddisfa le seguenti proprietà:

• d(x, y) ≥ 0

• d(x, y) = 0 ⇔ x = y

• d(x, y) = d(y, x)

• d(x, y) ≤ d(x, z) + d(z, y) (disuguaglianza triangolare)

Il numero reale non negativo d associato a una coppia di punti qualsiasi in tale metrica è detto distanza tra i due punti.

Uno spazio euclideo è un particolare spazio metrico, ma la nozione è più generale. Per esempio, tutti i sottoinsiemi di uno spazio euclideo sono spazi metrici, ma non tutti, a loro volta, sono spazi euclidei. In uno spazio possono infatti definirsi metriche differenti da quella euclidea o pitagorica (generalizzazione a n dimensioni del teorema di Pitagora), quali per esempio la taxi-distanza (→ distanza). Uno spazio metrico può essere dotato della struttura di spazio topologico definendo intorno di un punto x di raggio r > 0 l’insieme di tutti gli elementi di X che hanno distanza minore di r da x e aperto un sottoinsieme A di X contenente un intorno di ogni suo punto. È quindi possibile introdurre la nozione di limite di una successione: la successione {x_n} di elementi di X ha per limite l’elemento x di X se per ogni ε > 0 risulta d(x_n, x) < ε almeno da un certo indice in poi. Lo spazio metrico si dice completo se è convergente ogni successione di Cauchy, ossia ogni successione tale che per ogni ε > 0 risulta d(x_n, x_m) < ε almeno per tutti gli indici n, m sufficientemente grandi.

Sono esempi di spazi metrici l’insieme Rⁿ delle n-ple ordinate di numeri reali, x = (x₁, ..., x_n), con la distanza euclidea

l’insieme delle funzioni continue sull’intervallo [a, b], con la distanza del massimo (detta distanza lagrangiana):

e in generale tutti gli spazi normati. Costituisce tuttavia uno spazio metrico, per esempio, anche un insieme qualsiasi dotato della metrica discreta, data da d(x, y) = 1 se x ≠ y e d(x, y) = 0 se x = y.

Uno spazio metrico di dimensione finita si dice compatto se è chiuso (contiene cioè tutti i suoi punti di accumulazione) e limitato (esiste cioè una massima distanza, espressa da un numero reale, tra i suoi elementi). In R, un segmento è un esempio di spazio metrico compatto, mentre non lo è né R stesso né l’insieme dei punti a coordinata razionale compresi tra due estremi reali.