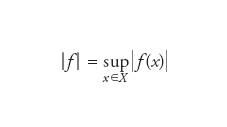spazio non commutativo
spazio non commutativo
L’oggetto di studio della geometria non-commutativa. Il fondamento concettuale della nozione di spazio non-commutativo è fornito dal teorema di Gelfand, che stabilisce una corrispondenza biunivoca tra C*-algebre commutative con identità e algebre C0(X,ℂ) di funzioni continue a valori complessi su opportuni spazi topologici (compatti di Hausdorff) dotate della norma
Una fondamentale proprietà degli spazi di Hausdorff è che le funzioni continue su di essi separano i punti, ovvero se f(x1)=f(x2) per ogni f∈C0(X,ℂ) (naturalmente x1,x2∈X) allora x1=x2. Dunque l’algebra delle funzioni continue su uno spazio di Hausdorff X permette di distinguerne i punti e possiamo considerare X assegnato una volta nota l’algebra C0(X,ℂ). Per analogia, le C*-algebre non commutative sono allora considerate come ‘algebre di funzioni’ associate a uno spazio non-commutativo. Per estensione, spesso per spazio non commutativo s’intende in ogni modo semplicemente una C*-algebra non commutativa. È tuttavia chiaro dalla discussione precedente che le C*-algebre sono in generale uno strumento adatto allo studio delle sole proprietà topologiche di un dato spazio non commutativo. Il riferimento al caso commutativo chiarisce che al fine di sviluppare una teoria della misura e quindi dell’integrazione su tali spazi è necessario, per così dire, passare dallo studio delle ‘funzioni’ continue a quello delle ‘funzioni’ misurabili: in termini di algebre questo significa sostituire le C*-algebre con algebre di von Neumann. Una misura su uno spazio non commutativo sarà allora definita come un funzionale sull’algebra di von Neumann (o W*-algebra) non commutativa a esso associata (o meglio che lo definisce) continuo rispetto alla topologia naturale dell’algebra stessa. In contesti più generali, talvolta la nozione di spazio non-commutativo coincide con quella di algebra non commutativa (non necessariamente C* o W*).