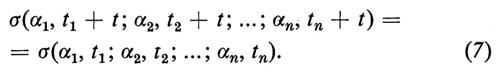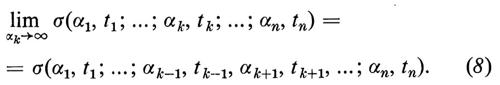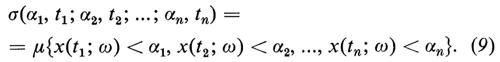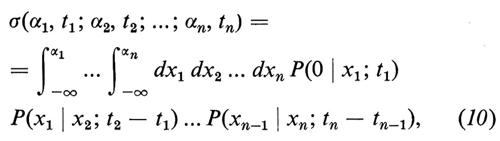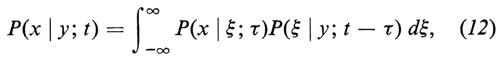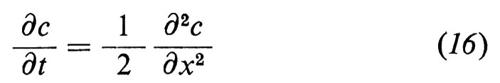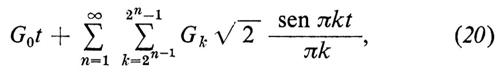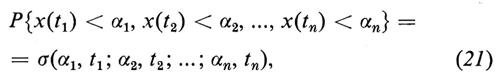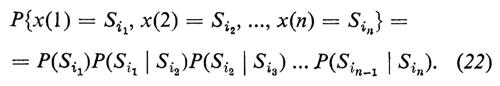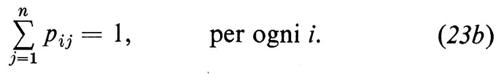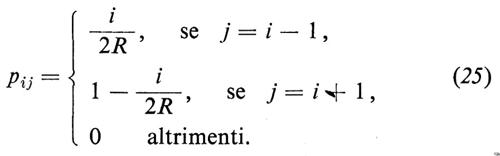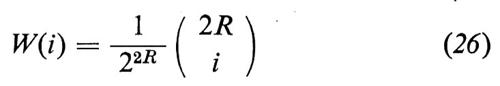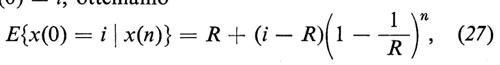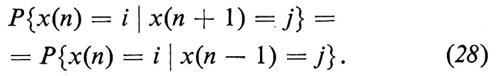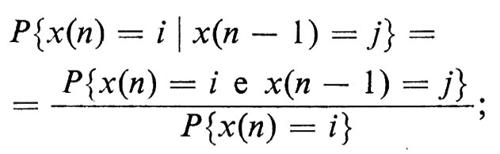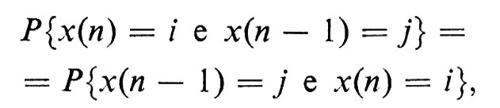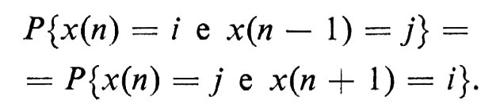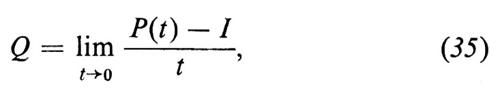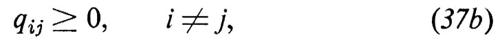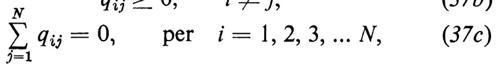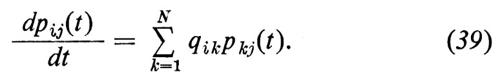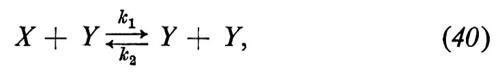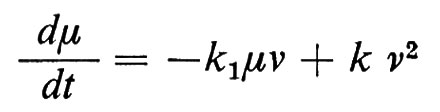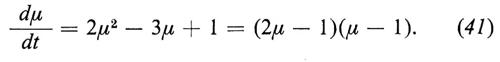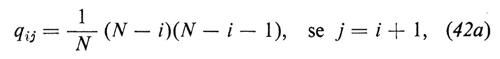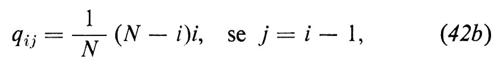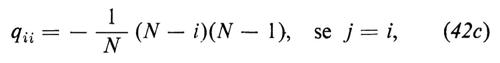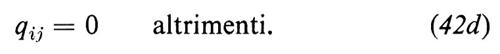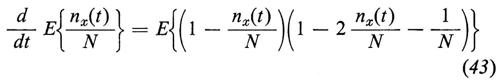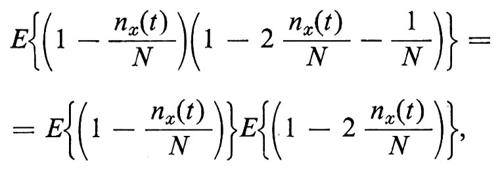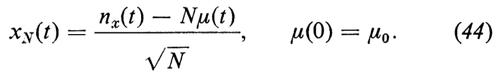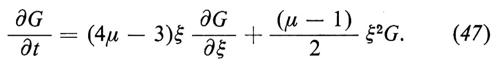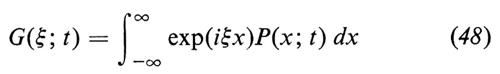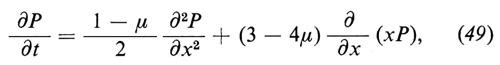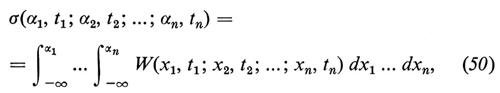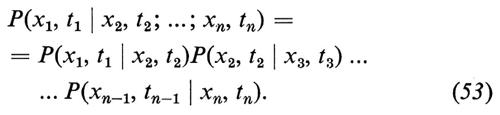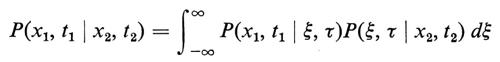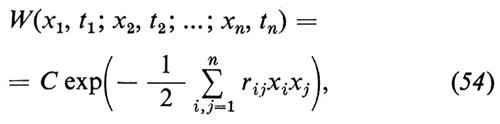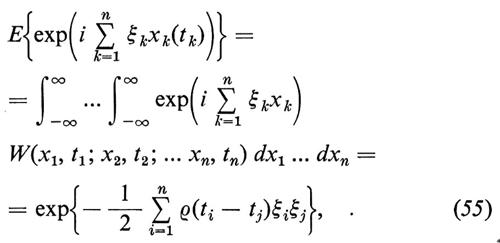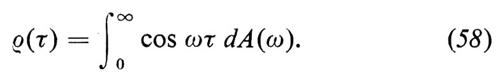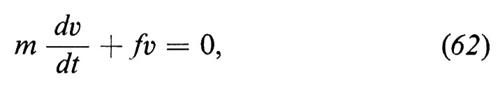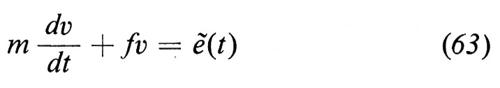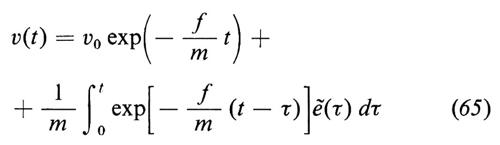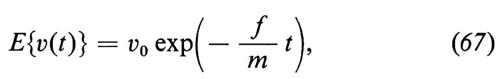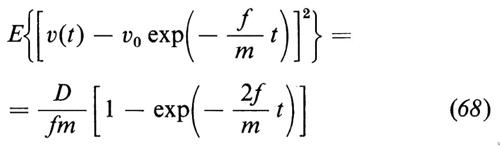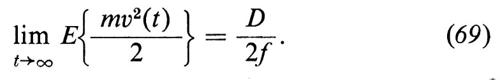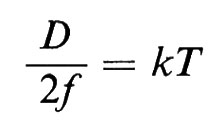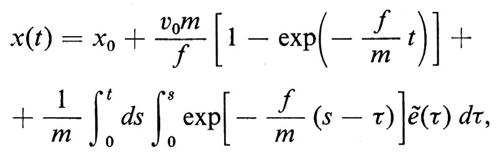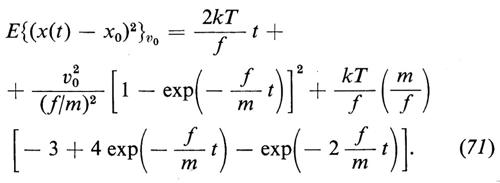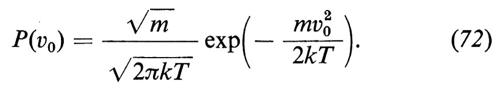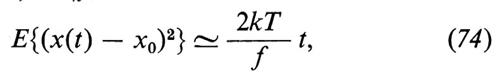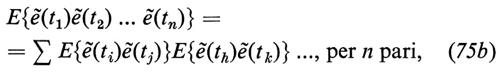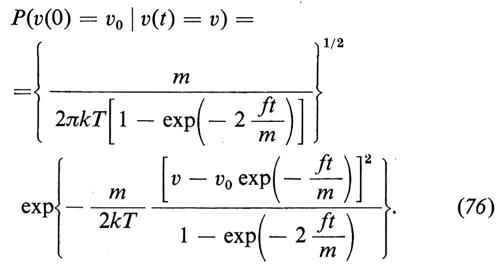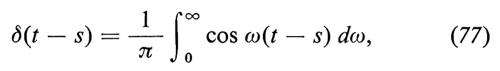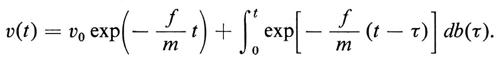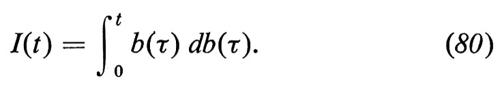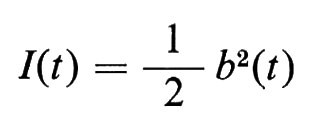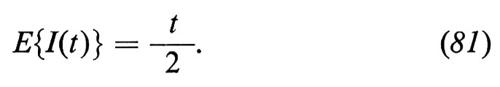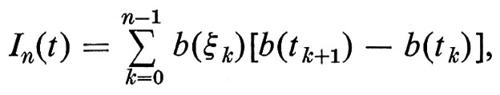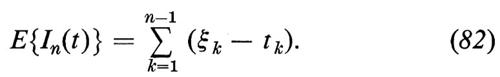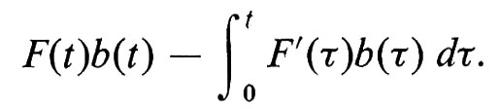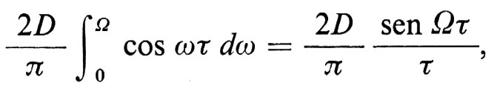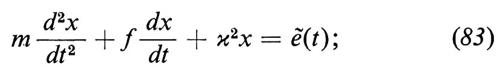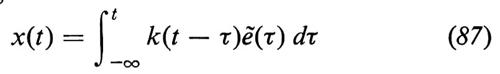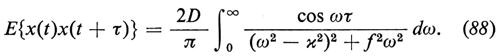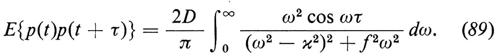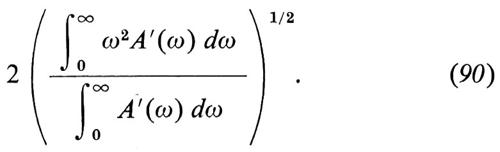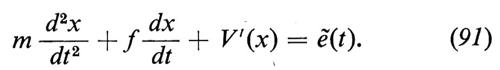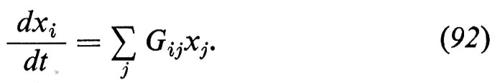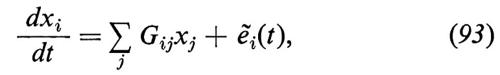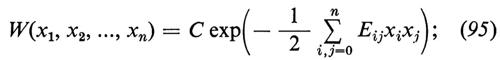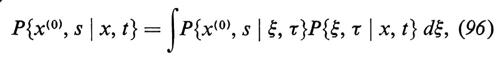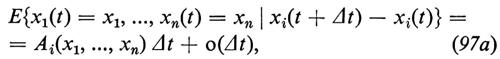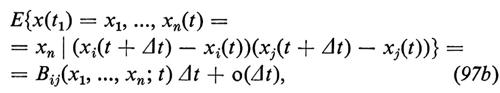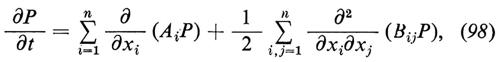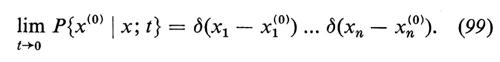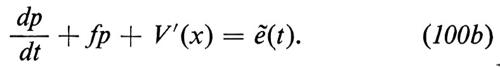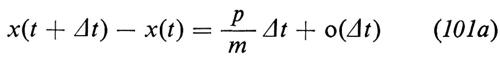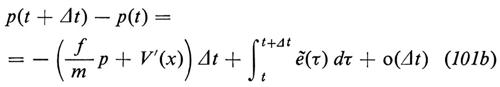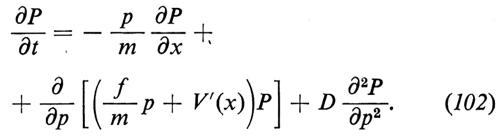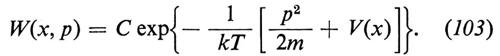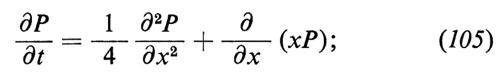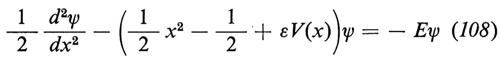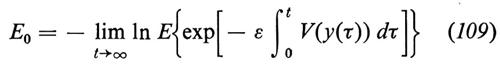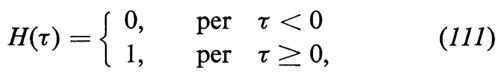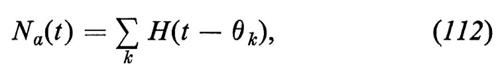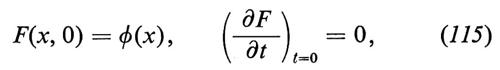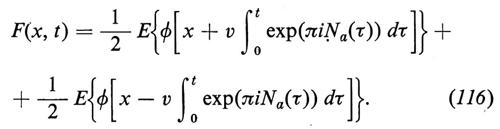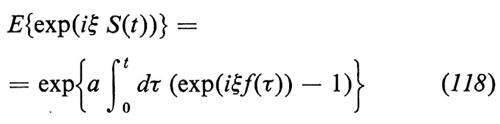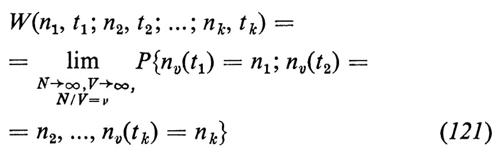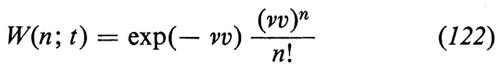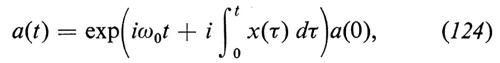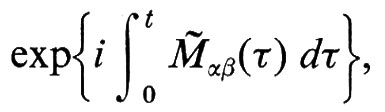Stocastica

di Mark Kac

SOMMARIO: 1. Preliminari. □ 2. Alcune sottigliezze matematiche. □ 3. Alcune classi generali di processi stocastici con esempi: a) processi di Markov con spazio degli stati finito e tempi discreti (catene di Markov); b) processi di Markov con spazio degli stati finito e tempo continuo; c) processi di Markov con un continuo di stati. □ 4. Processi stocastici definiti da equazioni differenziali. □ 5. L'equazione di Fokker-Planck. □ 6. Alcuni importanti processi stocastici: a) il processo di Poisson; b) il processo di Smoluchowski; c) processi di diramazione; d) processi moltiplicativi. □ Bibliografia.

1. Preliminari.

Un processo stocastico x(t) è una famiglia a un parametro di variabili aleatorie. Una variabile aleatoria è, in termini puramente matematici, una funzione misurabile su uno spazio Ω sul quale è definita una misura additiva μ: dovremmo quindi scrivere x(t; ω), ω∈Ω, invece di x(t). (L'omissione abituale della variabile ω è ciò che rende la teoria della probabilità incomprensibile ai principianti).

Dato un processo stocastico a valori reali e i valori t₁, t₂, ..., t_n, definiamo le distribuzioni congiunte

σ(α₁, t₁; α₂, t₂; ...; α_n, t_n) (1)

di x(t₁), x(t₂), ..., x(t_n) mediante la relazione

dove P (probabilità) indica la misura μ su Ω, cioè:

Secondo questa definizione,

x(t)=sen 2π(νt+ω) (3)

è un processo stocastico, se si sceglie, per esempio, per Ω l'intervallo (0, 1) e per μ la ordinaria misura di Lebesgue.

Consideriamo, per esempio, un sistema dinamico a n gradi di libertà governato dall'hamiltoniana H(p₁, ..., p_n; q₁, ..., q_n) e vincoliamo il sistema ad avere energia totale E. Allora la i-esima coordinata generalizzata del sistema, che al tempo t=0 aveva coordinate (p1⁽⁰⁾, ..., pn⁽⁰⁾; q1⁽⁰⁾, ..., qn⁽⁰⁾),

q_i(t)=q_i(t; p1⁽⁰⁾, ..., pn⁽⁰⁾; q1⁽⁰⁾, ..., qn⁽⁰⁾) (4)

è, per la nostra definizione, un processo stocastico e Ω è, in questo caso, la superficie

H(p₁, ..., p_n; q₁, ..., q_n)=E, (5)

sulla quale possiamo scegliere una ‛qualsiasi' misura μ, normalizzata a 1, completamente additiva.

È ben noto, dalla meccanica statistica, che la misura ‛naturale' da scegliere in questo caso è la cosiddetta misura ‛ergodica' o ‛microcanonica', che assegna a ogni elemento do della superficie Ω la misura

Questa misura è l'unica che renda stazionari i processi q_i(t) (e, più in generale, ogni processo F(p_i(t), ..., p_n(t); q_i(t), ..., q_n(t)), con F funzione misurabile), intendendosi per ‛stazionario' un processo le cui distribuzioni (1) siano invarianti per traslazioni temporali, tali cioè che per ogni α₁, ..., α_n, t₁, ..., t_n e t reali (e anche per ogni intero positivo n) si abbia

Gli esempi precedenti non sono affatto tipici e anzi è probabile che né l'uno né l'altro vengano riportati nei testi standard sui processi stocastici. Il motivo è che storicamente i processi stocastici furono introdotti nel mondo della scienza (e più tardi della matematica) sotto una forma assai diversa da quella derivante dalla definizione formale che abbiamo dato all'inizio di questo capitolo. Senza entrare nei dettagli storici, basterà dire che, molto prima che fossero introdotti Ω e μ, i processi stocastici non erano definiti, ma solamente ‛descritti' assegnando un insieme di distribuzioni (1) soggette soltanto alla seguente condizione di ‛compatibilità', per k=2, 3, ..., n:

Nel 1933 Kolmogorov dimostrò il suo famoso teorema di ricostruzione, secondo cui, assegnato un qualunque insieme di funzioni di distribuzione (1) che soddisfino la (8), è possibile costruire un insieme Ω, una misura μ e una famiglia di funzioni a un parametro x(t; ω) misurabili su Ω tali che

L'astrattezza e, diciamo pure, l'‛oscurità' di Ω e μ, ‛costruite' per mezzo del teorema di ricostruzione di Kolmogorov, contrastano in maniera così netta con la concretissima superficie di energia costante e la relativa misura ergodica e così pure con l'intervallo (0, 1) e la misura di Lebesgue, che siamo propensi a non considerare questi due esempi come processi aleatori. Ma una definizione è una definizione e un senso di disagio è il prezzo che si deve pagare per guadagnare in generalità.

2. Alcune sottigliezze matematiche.

Per un economista che si occupi di serie temporali, per un ingegnere che lavori su problemi di segnale e rumore, per un fisico che studi il moto browniano, un processo stocastico è definito quando tutte le funzioni di distribuzione (1) sono note. Un matematico necessita del teorema di ricostruzione per sapere di cosa sta parlando. Ma il teorema di ricostruzione non è la sottigliezza matematica più profonda fra quante stanno alla base del concetto di processo stocastico.

Per illustrare l'insufficienza del teorema di ricostruzione esaminiamo brevemente la teoria del moto browniano di una particella libera, limitandoci al caso unidimensionale.

Era noto dalla teoria di Einstein-Smoluchowski che le funzioni di distribuzione (1) di una particella dotata di moto browniano (per 0〈t₁〈t₂〈...〈t_n), avendo scelto le coordinate in modo tale che per t=0 sia x=0, sono date dalla relazione

con

Nella teoria fisica la varianza della densità gaussiana (11) è una quantità D che dipende, in maniera semplice, da certe proprietà fisiche della particella e del mezzo fisico circostante e dalla temperatura assoluta T che compare nella formula moltiplicata per la costante di Boltzmann k. È possibile determinare sperimentalmente D e dunque k e il numero di Avogadro. Benché questo sia di fondamentale importanza dal punto di vista fisico, non è affatto rilevante per lo sviluppo matematico della teoria, per cui abbiamo scelto le unità di misura in modo che risulti D=1.

Si vede facilmente che la condizione di compatibilità è contenuta nella relazione

spesso detta equazione di Chapman-Kolmogorov, oppure, più giustamente, di Smoluchowski o, meglio ancora, di Einstein-Smoluchowski.

Il teorema di ricostruzione garantisce l'esistenza dello spazio Ω (che può essere lo spazio di tutte le funzioni a valori reali x(t), o≤t〈∞, tali che x(0)=0) e di una misura additiva μ su Ω tale che, per 0〈t₁〈t₂〈...〈t_n, si abbia:

dove σ è data dalla (10).

Supponiamo ora di voler calcolare la probabilità che la particella rimanga alla sinistra di x=a(a>0) fino al tempo t, cioè di voler calcolare

P{x(τ)〈a, 0≤τ≤t}. (14)

La risposta a questo problema è ben nota ed è stata data per la prima volta da Smoluchowski nel suo lavoro pionieristico sul moto browniano; essa è basata sull'importante osservazione che la diffusione è la manifestazione macroscopica del moto browniano e dunque le probabilità legate al moto aleatorio di una particella browniana possono essere identificate con quantità approssimate di materia in un processo di diffusione.

Consideriamo un grande numero N di particelle browniane identiche e indipendenti (cioè non interagenti), che siano in x=0 al tempo t=0, e supponiamo poi di porre in x=a una barriera assorbente, così che le particelle che raggiungono x=a siano annichilate. La frazione di particelle che ‛sopravvivono' fino al tempo t, per N→∞, per un verso è la probabilità (13) che cercavamo; per l'altro è la quantità di materia in diffusione che si trova alla sinistra della barriera assorbente al tempo t. È quindi

dove c_a(x; t) è la soluzione dell'equazione di diffusione

soggetta alla condizione iniziale

c(x; 0)=δ(x) (17)

e alla condizione al contorno

c(a; τ)=0 per ogni τ≥0. (18)

Vi sono molti modi per giustificare questa conclusione, ma il più semplice è basato sull'‛approssimazione' del moto browniano con una ‛passeggiata aleatoria' discreta.

Fu pertanto assai sorprendente la scoperta fatta da Doob negli anni trenta che l'insieme dei cammini definito dalla condizione

{x(τ)≤a, 0≤τ≤t} (19)

non è misurabile rispetto alla misura μ.

Ancora più sorprendente e interessante è il fatto che anche il sottoinsieme C₀ delle funzioni continue (che, come tutte le funzioni in Ω, si annullano per t=0) non è misurabile. Se la teoria matematica rispecchiasse la realtà fisica, gli insiemi (19) e C₀ dovrebbero avere misura (15) e 1 rispettivamente. L'assegnazione del valore 1 alla misura di C₀ è in accordo con l'osservazione sperimentale che le traiettorie browniane sono continue. Si può rimediare a questo, come fece Doob, sfruttando il fatto che, benché C₀ non sia misurabile, esso ha misura esterna eguale a 1. Si può dunque modificare la misura μ ottenuta dal teorema di ricostruzione e imporre che C₀ sia misurabile e abbia misura 1, lasciando nello stesso tempo immutata la proprietà fondamentale (13).

Esiste una maniera molto più concreta per definire il moto browniano x(t) (x(0)=0), che fu introdotta per la prima volta da Wiener.

Restringendosi all'intervallo 0≤t≤1, Wiener mostrò che la serie

dove G₀, G₁, G₂, ... sono variabili aleatorie indipendenti, ciascuna con distribuzione normale (gaussiana), media nulla e varianza 1, converge uniformemente con probabilità 1 e che, ponendo x(t) uguale a (20), si verifica che, per 0〈t₁〈t₂〈...〈t_n,

dove σ è data dalla (10) e dalla (11).

In questa maniera la maggior parte delle difficoltà teoriche sulla misura spariscono e per Ω possiamo scegliere lo spazio prodotto ???OUT-R???×???OUT-R???×... (???OUT-R??? indica la retta reale) sul quale fissiamo la misura prodotto gaussiana.

L'estensione alla semiretta 0≤t〈∞ non presenta alcuna difficoltà.

3. Alcune classi generali di processi stocastici con esempi.

a) Processi di Markov con spazio degli stati finito e tempi discreti (catene di Markov).

Un processo markoviano con tempi discreti e con spazio degli stati finito è una famiglia di variabili aleatorie x_n=x(n), con n=1, 2, ..., ciascuna delle quali può assumere un numero finito di simboli (non necessariamente numerici) S₁, S₂, ... (‛stati'), tale che

In questa relazione P(S_i) indica una distribuzione iniziale arbitraria assegnata e P(S_i∣S_j)=p_ij indica la probabilità di transizione vincolata dalle condizioni ovvie

p_ij≥0 (23a)

e

È facile vedere che 1 è un autovalore della matrice P=((p_ij)) delle probabilità di transizione e che tutti gli altri autovalori hanno modulo minore o uguale a 1. Sotto condizioni piuttosto generali, l'autovettore sinistro della matrice P, (W(1), W(2), ..., W(n)) ha tutte le componenti non negative e possiamo normalizzarlo imponendo che sia

Se poniamo P(S_i)=W(i), il processo x(n) diventa stazionario, come accadeva al processo q_i(t) (si veda la 4) rispetto alla misura ergodica (6).

Dovrebbe essere ora chiaro che la matrice P caratterizza il processo x(n) e dunque la teoria delle catene di Markov con spazio degli stati finito si riduce alla teoria delle matrici che soddisfano le (23, a e b) (le cosiddette ‛matrici stocastiche'). Il carattere probabilistico di questa teoria (e di altre parti della teoria dei processi stocastici) emerge dagli esempi.

Probabilmente l'esempio più noto e istruttivo è il modello della ‛pulce del cane' proposto da P. e T. Ehrenfest nel 1907 per illustrare che un approccio a condizioni di equilibrio può essere conciliato con l'inversione del tempo e con la ricorrenza quasi periodica degli stati.

Si considerino due scatole (i cani) nelle quali siano distribuite 2R palline (le pulci) numerate da 1 a 2R. Estraiamo i numeri 1, 2, ..., 2R ‛a caso' (cioè in modo che ciascun numero abbia la stessa probabilità di essere estratto e che le estrazioni siano indipendenti) e trasferiamo la pallina il cui numero corrisponde a quello estratto dalla scatola in cui si trova nell'altra. Se si indica con x(n) il numero delle palline nella prima scatola, si vede facilmente che x(n) è una catena di Markov con probabilità di transizione

È anche facile verificare che

è la distribuzione stazionaria.

Se calcoliamo il valore medio condizionato di x(n), indicato con E{x(0)=i∣x(n)} (E da expectation), posto che sia x(0)=i, otteniamo

che mostra che ‛in media' si tende a uno stato di equipartizione (un ugual numero di palline in ciascula scatola) in maniera monotona (esponenziale). Questo risultato è in qualche maniera analogo al teorema H di Boltzmann.

Si osservi, però, che il modello è reversibile nel tempo, nel senso che

Ciò equivale a dire che, se ci si trova nello stato i al tempo n, la probabilità condizionata di raggiungere lo stato j al tempo (n+1) è uguale alla probabilità condizionata di essere partiti dallo stato j al tempo (n−1).

Per dimostrare la (28) dovremo esaminarne separatamente i due membri: il primo risulta uguale a p_ij, il secondo presenta alcune difficoltà. Ritornando alla definizione di probabilità condizionata, abbiamo

poiché è ovvio che è

abbiamo, in virtù della stazionarietà del processo,

Infine, sfruttando ancora la definizione di probabilità condizionata, si ha

P{x(n)=i}p_ij=P{x(n)=j}p_ji,

ovvero

W(i)p_ij=W(j)p_ji, (29)

che è equivalente alla (28) ed è banalmente verificata nel nostro caso.

Poiché il processo è stazionario ed ergodico, segue (v. probabilità) che ogni stato si ripresenta con probabilità 1 (in analogia col teorema di ricorrenza di Poincaré nella dinamica) e il tempo medio di ricorrenza (misurato dal numero di estrazioni) è 1/W(i). Quindi, per stati lontani dall'equilibrio, il tempo di ricorrenza medio diventa enorme, per esempio per i=2R il tempo medio di ricorrenza è 2^2R.

Processi di Markov a tempi discreti con un insieme numerabile di stati conducono a matrici stocastiche infinite che sono molto più difficili da studiare, perché la teoria spettrale per questo tipo di matrici è ancora in buona parte sconosciuta. Un'importante eccezione si presenta nel caso di processi reversibili nel tempo (nel senso della 29), poiché in questo caso le matrici sono simmetrizzabili e si dispone quindi della teoria degli spazi di Hilbert.

b) Processi di Markov con spazio degli stati finito e tempo continuo.

Un processo markoviano con tempo continuo e con spazio degli stati finito è una famiglia a un parametro di variabili aleatorie x(t), 0≤t〈∞, ciascuna delle quali indica uno degli stati S₁, S₂, ..., S_N nei quali il sistema può trovarsi, per la quale è assegnata una famiglia di matrici stocastiche P(s, t)=((p_ij(s, t))), s≤t, tali che, per 0≤t₁〈t₂〈...〈t_n, è

Chiaramente le matrici P(s, t) devono soddisfare la condizione di compatibilità

P(s, t)=P(s, τ)P(τ, t), (31)

per ogni τ tale che s≤τ≤t, e l'ovvia condizione iniziale

P(s, s)=I (matrice unità). (32)

La condizione di compatibilità (31) è chiaramente l'analoga della (12).

Nella maggior parte delle applicazioni si suppone che il processo sia omogeneo nel tempo, che cioè sia P(s, t)=P(t−s), s≤t; pertanto noi ci limiteremo a considerare processi di questo tipo.

La condizione di compatibilità (31) diventa

P(s+t)=P(s)P(t), s, t≥0, (33)

e la condizione iniziale (32) diventa

P(0)=I. (34)

È chiaro che abbiamo a che fare con semigruppi di matrici: infatti la teoria dei processi di Markov omogenei nel tempo (anche quelli a stati continui) è sotto molti punti di vista equivalente alla teoria dei semigruppi di operatori lineari.

Se supponiamo che esista il limite definito da

esso è detto ‛generatore infinitesimo' e si ha

P(t)=e^tQ. (36)

La matrice Q=((q_ij)) gode evidentemente delle seguenti tre proprietà:

e, inversamente, ogni matrice che gode di queste tre proprietà è il generatore infinitesimo di un semigruppo P(t).

Dalla (36) segue

o, equivalentemente,

Nella letteratura matematica le equazioni (39) sono note col nome di equazioni di Kolmogorov; nella forma (38) sono note ai fisici col nome di master equations. Non è necessaria praticamente alcuna modifica, almeno dal punto di vista formale, per estendere la teoria al caso N=∞, cioè al caso di un insieme numerabile di stati.

Anche in questo caso sono gli esempi che vivificano la teoria. Noi ne discuteremo uno nei dettagli, tratto da una teoria molto semplificata delle reazioni chimiche, teoria che è stata discussa diffusamente negli ultimi tempi in relazione all'estensione della termodinamica irreversibile a situazioni lontane dall'equilibrio.

La reazione, assolutamente irrealistica, è la seguente:

dove k₁ e k₂ indicano le velocità di reazione. Indicando con μ(t) e ν(t) le concentrazioni delle specie X e Y, rispettivamente, dalla legge dell'azione di massa segue

e

Poiché μ(t)+ν(t)≡1, supponendo per semplicità k₁=k₂ =1, abbiamo

Fin qui la teoria elementare. Ora, la μ(t) rappresenta chiaramente soltanto la concentrazione media della specie X; a causa della natura atomica, e dunque discreta, del processo, ci possiamo attendere fluttuazioni, anche osservabili, attorno al valor medio. Per analizzare queste fluttuazioni, si postulano modelli stocastici, detti a volte ‛modelli di McQuarrie', del tipo dei processi di Markov.

Nel nostro caso particolare supponiamo di avere N molecole, delle quali n_X(t) appartenenti alla specie X e n_Y(t)=N−n_X(t) alla specie Y. Due tipi di reazione sono possibili: dalla collisione di una molecola X con una molecola Y si formano due molecole Y, dalla collisione di due molecole Y si formano una molecola X e una molecola Y. La natura stocastica di questo processo è contenuta nell'ipotesi che si tratti di un processo di Markov e nel postulare la matrice corrispondente al suo generatore infinitesimo Q.

Gli elementi della matrice Q sono suggeriti dalla legge dell'azione di massa e sono dati dalle equazioni

Possiamo ora scrivere le equazioni di Kolmogorov (39) e da queste derivare un'espressione per la media E{n_x(t)/N}. Si ottiene in effetti facilmente

e, trascurando le fiuttuazioni, cioè ponendo

si ottiene (identificando E{n_x(t)/N} con μ(t)) l'equazione (41). Per studiare le fiuttuazioni intorno alla media introduciamo il processo

La scelta di √-N come fattore di normalizzazione diventerà chiara nel seguito. Consideriamo ora la funzione caratteristica

G_N(ξ; t)=E{exp(iξx_N(t))}; (45)

per essa, dalle equazioni di Kolmogorov, otteniamo

dove i puntini stanno per termini che sono o(1), cioè che tendono a zero per N→∞ (in realtà sono di ordine 1/√-N, (1/√-N)², ecc.). Si vede che i termini di ordine √-N si elidono in virtù della (41) e, se supponiamo che G_N(ξ; t) tenda a G(ξ; t) per N→∞, è chiaro che G(ξ; t) verifica formalmente l'equazione

Se inoltre supponiamo che G(ξ; t) sia la trasformata di Fourier di una funzione di densità, cioè che sia

(poiché G è una funzione caratteristica, essa è per definizione la trasformata di Fourier-Stieltjes di una funzione di distribuzione), si vede che P(x; t) verifica formalmente la relazione

che è un'equazione del tipo di Fokker-Planck, ma con coefficienti dipendenti dal tempo.

Si deve osservare che il fattore di normalizzazione √-N dell'equazione (44) è l'unico in grado di generare una distribuzione limite non degenere e dunque l'unico che conduca a una teoria compatibile. Vi è in realtà una questione più delicata che viene raramente messa in luce, cioè che la teoria che conduce alla (49) dipende da certe ipotesi sulla distribuzione di X_N(t) al tempo t=0. Senza entrare in dettagli, basterà osservare che ci è necessario un teorema che affermi che, se, per t=0, x_N(0)−Nμ(0) è dell'ordine di √-N, cioè se (x_N(0)−Nμ(0))/√-N tende a una distribuzione non degenere per N→∞, allora questa proprietà si mantiene nel tempo (propagazione del fattore di scala √-N). Per un'ampia classe di processi simili a quelli che abbiamo discusso, un teorema di questo tipo fu dimostrato da T. Kurtz (‟Journal of chemical physics", 1972, LVII, pp. 2976-2978).

È possibile che per reazioni più complicate, nelle quali intervengano più di due specie di molecole, debbano essere usati altri fattori di normalizzazione e che nelle equazioni corrispondenti alla (49) compaiano derivate rispetto alla x di ordine più elevato. Non vi è nulla di misterioso in fenomeni matematici di questo tipo, sebbene costituiscano una prova della grande varietà di comportamenti limite che si possono presentare in processi di Markov anche relativamente semplici.

Concludiamo questo paragrafo con due osservazioni.

1. L'esempio contenuto in questo paragrafo, come pure il modello di Ehrenfest della ‛pulce del cane', sono esempi di processi di ‛nascita e morte', cioè di processi per i quali p_ij o q_ij sono 0 tranne quando ∣i−j∣ è 0 o 1. Le relative matrici sono tridiagonali e, nel caso di processi reversibili nel tempo, diventano, per simmetrizzazione, matrici di Jacobi. Le proprietà spettrali delle matrici di Jacobi conducono a polinomi ortogonali e, in particolare, l'espressione di P(i∣j; n) per il modello di Ehrenfest (la probabilità che vi siano j palline nella prima scatola dopo n estrazioni, data la condizione che al momento iniziale ve ne fossero i) conduce ai cosiddetti polinomi di Krawtchuk. Esiste un'elegante teoria generale applicabile anche ai processi di nascita e morte non reversibili nel tempo.

2. A causa della scelta degli esempi, il lettore può aver avuto l'impressione che i processi, e le catene, di Markov siano usati soprattutto in fisica e in chimica. Questo non è affatto vero. Vi sono esempi interessanti e molto significativi di processi di Markov in altri campi della scienza; il più importante fra questi è la genetica delle popolazioni, nel cui ambito R. A. Fisher e Sewell Wright hanno introdotto, negli anni venti e trenta, modelli di Markov che conducono a processi di diffusione singolari. Successivi importanti contributi in questo campo sono stati dati da Karlin e McGregor (v., per es., la loro rassegna On some stochastic models in genetics, in Stochastic models in medicine and biology, a cura di J. Gurland, Madison, Wis., 1964, pp. 245-271) e da Kimma (v., per es., Diffusion models in population genetics, in ‟Journal of applied probability", 1964, I, pp. 177-232). Karlin e McGregor sono stati estremamente abili nell'uso di polinomi ortogonali per ottenere formule esplicite per parecchi modelli.

La psicologia è un altro campo nel quale i processi di Markov svolgono un ruolo importante (v., per es., M. Frank Norman, Markov processes and learning models, New York 1972).

Possiamo anche ricordare la teoria dell'informazione; in verità è probabile che, almeno in parte, problemi oggi collegati a questa teoria abbiano indotto A. A. Markov a introdurre le catene che portano oggi il suo nome: a riprova parziale di ciò ricordiamo un lavoro pubblicato in russo da Markov nel 1913 nei Proceedings of the Imperial Academy of Sciences di St. Petersburg, inteso a stabilire se la successione delle vocali nel testo del famoso poema di Puškin, Evgenij Onegin, potesse essere considerata un campione di catena di Markov a due stati: vocale, consonante.

c) Processi di Markov con un continuo di stati.

Nella prima parte ci limiteremo a considerare processi x(t) a valori reali e per evitare complicazioni tecniche supporremo che tutte le funzioni di distribuzione abbiano densità continue. Sarà pertanto

dove con W si indicano funzioni continue nelle x. Le densità condizionate sono definite nella maniera usuale, cioè

Si noti che, contrariamente alla convenzione adottata nella maggior parte della letteratura matematica, abbiamo scritto, come in altre parti di questo articolo, la condizione a sinistra anziché a destra. Scriveremo dunque la probabilità condizionata che x(t) si trovi tra a e b, data la condizione x(0)=x₀, così: P{x(0)=x₀∣a〈x(t)〈b}; mentre in molti altri testi matematici viene scritta P{a〈x(t)〈b∣x(0)=x₀}.

Il processo è di Markov se, per t₁〈t₂〈...〈t_n, è

P(x₁, t₁; ...; x_n-1, t_n-1∣x_n, t_n)=P(x_n-1, t_n-1∣x_n, t_n), (52)

Questa eventualità viene spesso descritta, imprecisamente, dicendo che il futuro è indipendente dal passato una volta assegnata la situazione attuale.

Dalla definizione (51) di probabilità condizionata segue immediatamente che, per un processo di Markov, si ha, per t₁〈t₂〈...〈t_n,

Questa relazione viene spesso usata come definizione di processo di Markov.

La relazione di compatibilità (8) diventa ora l'equazione di Chapman-Kolmogorov (o di Einstein-Smoluchowski)

per qualsiasi τ tale che t₁〈τ〈t₂.

L'estensione delle definizioni precedenti a processi di Markov ‛vettoriali' è immediata; in questo caso si indicherà con x_i l'insieme ordinato di numeri reali (xi⁽¹⁾, xi⁽²⁾, ..., xi^(k)) e i cambiamenti necessari sono solo notazionali. Il termine processo ‛vettoriale' in realtà è improprio, dal momento che la questione dell'invarianza per trasformazioni di coordinate non svolge alcun ruolo in questa teoria: più corretto sarebbe dire processo ‛a più componenti'. L'esempio più noto di un processo di Markov a più componenti è la coppia (x(t), p(t)), dove x e p indicano, rispettivamente, la posizione e il momento di una particella legata armonicamente che compie un moto browniano.

L'esempio più noto di processo di Markov a una sola componente, con un continuo di stati, è il processo di Ornstein-Uhlenbeck, che, oltre a essere di Markov, è anche stazionario e gaussiano. Come abbiamo già osservato prima, un processo è stazionario se le W sono invarianti per traslazioni temporali, è gaussiano quando le W sono della forma

dove C indica una costante di normalizzazione e le r_ij sono funzioni di t₁, t₂, ..., t_n. Se un processo gaussiano è anche stazionario, le r_ij dipendono solamente dalle differenze t_k−t_l e si vede facilmente che, in termini di funzioni caratteristiche, la definizione prende la forma

dove, se si suppone di aver scelto la normalizzazione, E{x²(t)}=1, ρ(s−t) indica il coefficiente di correlazione, cioè

ρ(s−t)=E{x(s)x(t)}. (56)

La ρ è chiaramente una funzione pari:

ρ(−τ)=ρ(τ); (57)

per semplicità supporremo anche che sia continua. Per un noto teorema di Wiener e Khintchine, basato su un altrettanto noto teorema di Bochner, segue che esiste una funzione non decrescente A(a) tale che

La derivata A′(ω) (che in alcuni casi deve essere intesa nel senso delle distribuzioni di Schwartz) è detta ‛spettro di potenza' del processo. Osserviamo che i concetti di funzione di correlazione e di spettro di potenza possono essere introdotti anche nel contesto di processi stazionari non gaussiani. In effetti non è neppure necessario che il processo sia strettamente stazionario: basta che lo sia in senso lato, secondo la definizione deducibile dalla formula (56).

Per il processo di Ornstein-Uhlenbeck, di cui si è detto sopra, si dimostra facilmente quello che va sotto il nome di teorema di Doob:

ρ(τ)=exp(−γ∣τ). (59)

In modo analogo (anche se in verità la dimostrazione è un po' meno semplice) per un processo di Markov stazionario e gaussiano a più componenti la matrice di correlazione

R(τ)=(ρ_ij(τ))=(E{x_i(0)x_j(τ)})

è della forma

R(τ)=exp(τQ), τ>0 (60)

e

R(τ)=exp(−τ Qè), τ〈0, (61)

dove si è indicata con Qè la trasposta di Q e Q è una matrice i cui autovalori hanno parte reale negativa.

L'applicazione più importante dei processi di Markov a più componenti si ha nella formulazione della termodinamica irreversibile, che discuteremo brevemente nel capitolo seguente.

4. Processi stocastici definiti da equazioni differenziali.

L'origine dell'argomento svolto in questo capitolo risale al 1908, anno in cui P. Langevin propose un metodo per trattare il moto browniano di una particella libera in un fluido.

Il moto lento unidimensionale di una particella libera di massa m in un fluido è descritto con sufficiente precisione dall'equazione

dove v indica la velocità (in effetti una componente della velocità) ed f un coefficiente di attrito che dipende dal fluido (per es., in un gas denso o in un liquido, f è dato dalla formula di Stokes). Langevin tratta la (62) come una equazione per il valor medio e la modifica aggiungendovi una forza ‛fluttuante' aleatoria ẽ(t) per rappresentare l'effetto del bombardamento delle molecole non incluso nel termine lineare di attrito. Alla (62) sostituisce dunque l'equazione, che porta il suo nome,

e interpreta ẽ(t) come un processo stocastico stazionario con valor medio nullo, la cui covarianza singolare è data dalla formula

E(ẽ(t)ẽ(s))=2D δ(t−s), (64)

nella quale D è un termine da determinare in un secondo momento. Procedendo come se la (63) fosse un'equazione differenziale ordinaria, otteniamo

e, poiché, per ipotesi, è

E{ẽ(t)}=0, (66)

si ottiene immediatamente

che non è un risultato sorprendente.

Più interessante è calcolare la varianza di v(t) attorno al valor medio; per essa si ottiene

e, al limite, per t→∞,

Per il teorema dell'equipartizione dell'energia, poniamo

ovvero

D=2kTf, (70)

una formula già ricavata da Einstein in un modo diverso.

Per ricollegarsi ad Einstein bisogna considerare lo spostamento di una particella browniana, dato dalla formula

dalla quale si ottiene, utilizzando la (64),

Abbiamo aggiunto v₀ per ricordare che il valor medio è condizionato e che la condizione è v(0)=v₀. In modo equivalente avremmo potuto usare la notazione E{v(0)=v₀∣ (x(t)−x₀)²}.

Per ottenere il valor medio non condizionato si deve mediare sui possibili valori di v₀; si pone allora il problema della scelta della densità di probabilità P di v₀. Se supponiamo che la particella browniana sia stata ‛spinta qua e là' abbastanza a lungo da aver raggiunto l'equilibrio col fluido circostante, se cioè si pensa immersa in quel che si chiama un ‛bagno di calore', P deve essere una maxwelliana alla temperatura assoluta T del bagno, cioè

Calcolando la media rispetto a questa densità maxwelliana, si ottiene

e dunque, per t≫m/f,

che è la formula di Einstein.

Einstein e, indipendentemente, Smoluchowski mostrarono inoltre che, per t≫m/f, lo spostamento x(t)−x₀ assume una distribuzione gaussiana con varianza data dalla (74) e che il processo x(t)−x₀ è anche markoviano, ma non stazionario.

Per ottenere questo risultato non è sufficiente supporre soltanto la validità della (64): è necessario anche supporre che ẽ(t) sia un processo stazionario, gaussiano, la cui covarianza singolare sia data dalla (64). Tutto ciò è equivalente alla seguente legge formale per calcolare le varianze di ordine più elevato:

E{ẽ(t₁)ẽ(t₂)...ẽ(t_n)}=0, per n dispari, (75a)

e

dove la sommatoria è estesa a tutte le decomposizioni in coppie completamente disgiunte di tempi. Per esempio, per n=4 si ha

Se consideriamo ancora l'equazione (63) si può allora mostrare formalmente che v(t) è un processo di Markov gaussiano con densità di transizione

Se imponiamo che v₀ abbia la distribuzione maxwelliana data dalla (72), v(t) diventa stazionario, oltre a essere markoviano e gaussiano, ed è dunque un processo di Ornstein-Uhlenbeck (v. cap. 3, È c).

Ora, il processo ẽ(t), detto ‛processo puramente aleatorio' o ‛rumore bianco', chiaramente non è un oggetto matematico ben definito. E neppure è ben definito dal punto di vista fisico; infatti, a causa dell'identità formale

lo spettro di potenza del processo è costante su tutto l'intervallo di frequenze (di qui il nome di rumore bianco) e questo ha come conseguenza assurda che la potenza totale è infinita.

È istruttivo paragonare i diversi modi in cui questa difficoltà è trattata dai matematici e dai fisici. In matematica si osserva che ẽ(t) è formalmente identico a √-2-D db/dt, dove abbiamo indicato con b(t) il processo di Wiener, discusso nel cap. 2. Poiché quasi ogni traiettoria b(t) del processo di Wiener è ovunque non differenziabile (risultato notevole, dimostrato per la prima volta da Wiener), il termine db/dt è privo di senso. Possiamo però riscrivere la (63) nella forma seguente:

mdv+fvdt=√-2-D db(t), (78)

dalla quale segue che

La difficoltà consiste ora nel definire l'integrale di Stieltjes

Bisogna procedere con cautela nell'effettuare l'integrazione per parti, poiché con probabilità uno le traiettorie b(τ) non sono a variazione limitata. Le difficoltà che si incontrano si possono illustrare esaminando l'integrale

Saremmo tentati di concludere che è

e dunque

Tuttavia, se approssimiamo I(t) con somme del tipo

dove t_k≤ξ_k≤t_k+1 e t_n=t, abbiamo

Questa equazione è compatibile con la precedente se si sceglie ξ_k=(t_k+t_k+1)/2, ma questa scelta è assolutamente arbitraria: scegliendo, per esempio, ξ_k=t_k si ottiene 0 e scegliendo ξ_k=t_k+1 si ottiene t.

Tutto si semplifica notevolmente per gli integrali del tipo (79) se, per esempio, F(τ) è differenziabile ed è possibile sostituire la (79) con

Esiste una teoria sugli integrali stocastici atta a trattare in maniera sistematica integrali nei quali compaia db(τ).

In fisica è chiaro fin dall'inizio che vi è un taglio nello spettro delle frequenze e in molti casi esso può essere stimato a priori dalla teoria; di conseguenza la covarianza di ẽ(t) non è una funzione delta, ma è del tipo

dove Ω è la frequenza di taglio. Tutto è perfettamente giustificato, si tratterà poi di calcolare il limite per Ω→∞ a uno stadio opportuno del calcolo. Questo punto di vista può essere riassunto nella maniera seguente: si tratta il processo aleatorio ẽ(t) come se fosse un processo ben definito e si usano le equazioni (64) e (75) per calcolare tutte le distribuzioni e le medie necessarie. Fin tanto che non vi sono divergenze i risultati sono corretti e possono essere ottenuti o sfruttando il ‛trucco' di riscrivere le equazioni differenziali nella forma (78), basandosi poi sulla teoria degli integrali stocastici, oppure introducendo un taglio che si fa poi tendere all'infinito.

A volte si incontrano situazioni che appaiono a prima vista paradossali; qui discutiamo uno di tali casi che è particolarmente interessante. L'idea di Langevin di trattare il moto browniano di una particella libera per mezzo di un'equazione differenziale stocastica fu estesa e approfondita da Ornstein e Uhlenbeck, che furono i primi a mettere in evidenza che ẽ(t) è gaussiano; essi applicarono poi l'idea di Langevin al moto browniano di un oscillatore armonico. In questo caso l'equazione differenziale stocastica è

per semplificare le formule, scegliamo le unità di misura in modo che sia m=1. Se per t=t₀ la posizione e il momento iniziali sono x₀ e p₀, abbiamo

+ termini che contengono i dati iniziali x₀ e p₀,

dove

con

Per t₀→−∞,

è il processo ‛stazionario' che descrive la posizione del nostro oscillatore armonico. Il processo è anche gaussiano, poiché è una funzione lineare del processo gaussiano ẽ(t), e si verifica facilmente che la covarianza di x(t) è data dalla

La covarianza del processo stazionario p(t)=dx/dt (si ricordi che m=1) è data dalla

Ora, se un processo gaussiano stazionario ξ(t) ha uno spettro di potenza A(ω), si può mostrare che il numero medio di zeri della ξ(t) per unità di tempo è dato dalla formula (detta a volte di Rice-Kac)

A questo punto ci si può domandare quante volte per unità di tempo x(t) cambi mediamente direzione. Questo numero coincide evidentemente col numero medio, per unità di tempo, degli zeri di p(t); poiché per p(t) che tende all'infinito A′(ω) è dell'ordine di cost./ω², dalla (90) risulta che questo numero è infinito.

D'altra parte, esistono delle esperienze sul moto browniano di un piccolo specchio la cui teoria è basata sull'equazione (84), dove la x indicherà un angolo, m il momento d'inerzia dello specchio ed ẽ(t) il momento puramente aleatorio delle forze. Sperimentalmente si osserva solo un numero finito di massimi e minimi e questo sembra essere in contrasto con la teoria, che ne prevedrebbe invece un numero infinito. La spiegazione è semplice: la traccia luminosa osservata ha una larghezza non nulla e l'occhio umano non è in grado di percepire oscillazioni molto brevi e rapide; vi è dunque un taglio nella gamma di frequenze e questo porta a un numero finito. Un'analisi più dettagliata, nel caso per esempio che lo specchio sia immerso in un gas di Knudsen, mostra che il numero medio di massimi e minimi per unità di tempo è dell'ordine di grandezza del numero di collisioni per unità di tempo che avvengono tra lo specchio e le molecole del gas circostante.

Nel cap. 3, È c abbiamo affermato che il processo a due componenti (x(t), p(t)) è di Markov: possiamo ora verificare questa affermazione con un calcolo esplicito basato sull'equazione di Langevin (83). La verifica ci mostra quanto sia essenziale che ẽ(t) sia un processo puramente aleatorio e soprattutto che sia gaussiano. Se l'oscillatore non è armonico, con forza di richiamo derivante da un potenziale non quadratico V(x), l'equazione di Langevin non è lineare:

Il processo a due componenti (x(t), p(t)) è ancora markoviano, ma non saprei dove si possa trovare nella letteratura una dimostrazione rigorosa di questo fatto.

Infine, discutiamo brevemente la formulazione di Onsager-Machlup della termodinamica lineare lontana dall'equilibrio (termodinamica irreversibile).

Si suppone che lo stato termodinamico di un sistema sia descritto da un insieme (completo) di n variabili estensive x₁, x₂, ..., x_n i cui valori di equilibrio x1⁽⁰⁾, x2⁽⁰⁾, ..., xn⁽⁰⁾ supponiamo nulli per semplificare le notazioni. Le variabili x_i(t) sono funzioni del tempo e in assenza di fluttuazioni il loro decadimento verso condizioni di equilibrio sarebbe descritto dalle equazioni lineari

Queste equazioni sono analoghe alla (62) e per tener conto delle fluttuazioni le sostituiamo, seguendo l'idea di Langevin, con le

dove le ẽ_i(t) sono processi puramente aleatori la cui matrice di covarianza Q_ij è data dalla

E{ẽ_i(s)ẽ_j(t)}=2Q_ijδ(t−s). (94)

La densità stazionaria W(x₁, x₂, ..., x_n) è gaussiana:

la forma quadratica a secondo membro è l'approssimazione quadratica di S/k, dove S≡S(x₁, x₂, ..., x_n) indica l'entropia come funzione di x₁, x₂, ..., x_n e k la costante di Boltzmann. La (95) è dunque l'inversione di Einstein della famosa formula di Boltzmann S=k log W. Si tratta di una generalizzazione, a più componenti, del processo di Ornstein-Uhlenbeck. La teoria dipende da tre matrici: G (corrispondente al coefficiente di attrito f), Q (corrispondente alla costante di diffusione D) ed E (corrispondente a M/kT). Si ha quindi un'equazione matriciale, corrispondente all'equazione (70) di Einstein, che racchiude il significato fisico della termodinamica irreversibile.

Questa teoria può essere estesa al caso in cui l'indice i vari su un insieme continuo (per es. v_x(r; t), la componente nella direzione x della velocità di un fluido al tempo t e nel punto r: in questo caso r corrisponde all'indice i) e si hanno importanti applicazioni nello studio delle fluttuazioni idrodinamiche.

5. L'equazione di Fokker-Planck.

Un processo di Markov a più componenti (x₁(t), x₂(t), ..., x_n(t)) è determinato dalla densità di transizione condizionata

Come abbiamo più volte osservato, la P soddisfa l'equazione di Chapman-Kolmogorov (o di Einstein-Smoluchowski)

per qualunque τ compreso tra s e t; x⁽⁰⁾, x e ξ indicano le rispettive n-ple. Ci limiteremo in questa sede a studiare uno spazio euclideo; le modifiche necessarie per trattare uno spazio curvo sono ovvie.

Una classe importante di processi stocastici comprende quelli per i quali gli spostamenti infinitesimi soddisfano le equazioni

Sotto queste condizioni, P soddisfa l'equazione di diffusione di Fokker-Planck

con le condizioni iniziali ovvie

L'equazione (98) è detta a volte ‛equazione forward'. Se consideriamo la P come funzione delle x1⁽⁰⁾, x2⁽⁰⁾, ..., xn⁽⁰⁾, P soddisfa l'aggiunta della (98), detta anch'essa ‛equazione forward'. L'equazione (98) e la corrispondente ‛equazione backward' furono ottenute per la prima volta da Kolmogorov nel 1931 e nel 1933 (‟Mathematische Annalen", vol. CIV e CVIII) e furono in seguito analizzate e discusse da Feller nel 1936 (‟Mathematische Annalen", vol. CXIII).

Un'indicazione della quasi completa mancanza di contatto fra matematici e fisici è data dal fatto che H. A. Kramers derivò, in un importante lavoro pubblicato su ‟Physica" nel 1940, un caso particolare della (98), ora universalmente detta ‛equazione di Kramers', senza essere al corrente del precedente lavoro di Kolmogorov.

Kramers considera il processo di Markov a due componenti (x(t), p(t)) generato dall'equazione di Langevin (91). Le condizioni infinitesime, mentre nel lavoro di Kolmogorov appaiono un po' costruite ad hoc, nel lavoro di Kramers sono derivate dalla (91), che viene riscritta nella forma

Possiamo ora scrivere

e

e derivare le A e le B dalle (101) e dalle proprietà statistiche di ẽ(t). Otteniamo dunque per P(x₀, p₀∣x, p; t) l'equazione

Se imponiamo ∂P/∂t=0, otteniamo la relazione per la distribuzione stazionaria W(x, p), che, se exp(−V(x)/kT) è integrabile, risulta essere (in modo univoco) la densità di Maxwell-Boltzmann

Non è ancora stato dimostrato in maniera soddisfacente, se si eccettua il caso armonico per cui V(x)=k²x²/2, che sia

benché nessuno dubiti che ciò sia vero.

Nel cap. 3, È b abbiamo ottenuto l'equazione (49), che, per t→∞, diventa

si tratta dell'equazione di Fokker-Planck associata al processo di Ornstein-Uhlenbeck (con f=1, D=1/2, m=1). Questo è un esempio, benché artificiale, del principio di Onsager-Machlup, che abbiamo discusso alla fine del cap. 4; in prossimità dell'equilibrio le fiuttuazioni decadono secondo processi di Ornstein-Uhlenbeck.

6. Alcuni importanti processi stocastici.

Abbiamo già discusso nei dettagli il processo di Wiener e il processo di Ornstein-Uhlenbeck: i due processi sono strettamente collegati, in maniera che, se x(t) è un processo di Wiener (x(0)=0), il processo

y(t)=e^-t x(e^2t) (106)

è il processo di Ornstein-Uhlenbeck di covarianza exp(−∣t∣).

Ambedue i processi furono introdotti per studiare il moto browniano, ma la loro importanza trascende questa origine. Nell'articolo probabilità si è già accennato al fatto che la cosiddetta formula di Feynman-Kac esprime la soluzione fondamentale dell'equazione parabolica

come valor medio di un funzionale del processo di Wiener, permettendo così di studiare questioni di analiticità delle soluzioni della (107) con metodi probabilistici.

Accenniamo adesso a un'applicazione del processo di Ornstein-Uhlenbeck a un problema di meccanica quantistica. Il minimo autovalore E₀ dell'equazione di Schrödinger

è dato dalla formula

(non si confonda il simbolo E, per expectation, che compare nella (109) con l'autovalore E della (108)), dove y(t) è il processo di Ornstein-Uhlenbeck di covarianza exp(−∣t∣). (Per ulteriori dettagli, v., per es., B. Simon, Functional integration and quantum physics, New York 1979).

Vi sono molte altre applicazioni dei processi di Wiener e di Ornstein-Uhlenbeck (per es., alla teoria del potenziale), a riprova dell'importanza che rivestono tali processi nella matematica e nella fisica.

Diamo ora una breve descrizione di alcuni processi che, sebbene forse non essenziali nello sviluppo della teoria, sono tuttavia di grande interesse e importanza.

a) Il processo di Poisson.

Il processo di Poisson probabilmente è il processo stocastico più elementare; poiché è già stato discusso in dettaglio nell'articolo probabilità, ci limiteremo qui a fare alcune osservazioni al riguardo.

Può essere comodo usare per il processo di Poisson N_a(t), 0≤t〈∞, una rappresentazione in termini di somme di variabili aleatorie indipendenti. Se Y₁, Y₂, ... sono variabili aleatorie indipendenti non negative aventi tutte la stessa legge di distribuzione e tali che

P(Y_i〈τ)=1−exp(−aτ), a〈0, (110)

allora N_a(t) è il numero delle somme Y₁, Y₁+Y₂, Y₁+Y₂+Y₃, ..., minori di t; in altre parole, è N_a(t)=k (k=0, 1, 2, ...) se e solo se Y₁+Y₂+...+Y_k〈t〈Y₁+Y₂+...+Y_k+1. Per esempio, se le Y sono i tempi aleatori fra l'emissione di una particella α e la successiva, allora, evidentemente, N_a(t) rappresenta il numero totale di particelle emesse fino al tempo t.

Se H(τ) è la funzione di Heaviside, definita da

allora è

dove

θ_k=Y₁+Y₂+...+Y_k. (113)

Vale la pena di osservare che il processo di Poisson può essere usato per ottenere una soluzione probabilistica dell'equazione detta ‛del telegrafista'

la quale è in parte di tipo parabolico e in parte di tipo ellittico. In effetti, la soluzione dell'equazione (114), con le condizioni iniziali

è

Non è difficile modificare la (116) per avere la soluzione per condizioni iniziali più generali (per ulteriori dettagli, v. M. Kac, A stochastic model related to the telegrapher's equation, in ‟Rocky Mountain journal of mathematics", 1974, IV, pp. 497-509).

Strettamente collegato al processo di Poisson è il processo dello shot noise, definito dalla

con f(t)=0 per t〈0 e con opportune condizioni di integrabilità sullaf.

L'origine fisica è la seguente. Se in un circuito elettrico l'unica sorgente di forza elettromotrice è un diodo, la tensione agli estremi di una resistenza è data dalla somma delle tensioni prodotte nel circuito dagli elettroni emessi dal catodo. Se f(t) rappresenta la tensione dovuta a un elettrone emesso al tempo t=0, allora S(t) è la tensione al tempo t, purché si supponga, evidentemente, che l'emissione degli elettroni sia governata da un processo di Poisson, cioè che i tempi che intercorrono fra due emissioni successive siano indipendenti e seguano una legge di distribuzione esponenziale del tipo dato dall'equazione (110). Per lo shot noise è f(t)=0, per t>Δ, dove Δ è il tempo di transito di un elettrone. È facile calcolare la funzione caratteristica di S(t): si ottiene

come generalizzazione della ben nota formula

E{exp(iξN_a(t))}=exp{a(exp(iξ)−1)}. (119)

Se f(t) tende a 0, per t→∞, e se f è integrabile (o, meglio ancora, se f(t)=0, per t>Δ, come nello shot noise), abbiamo che, per tempi sufficientemente grandi, E{exp(iξS(t))} è indipendente da t. In realtà, si può dimostrare addirittura che S(t) può essere considerato un processo stazionario. Questo non si verifica invece per N_a(t), poiché H(t) non è integrabile.

In un limite opportuno S(t) diventa un processo gaussiano stazionario la cui covarianza è un funzionale semplice di f. (Per ulteriori dettagli, si veda l'articolo di S. O. Rice, Mathematical analysis of random noise, in Wax, 1954). Il processo shot noise si incontra anche in elettrofisiologia come modello di scariche neurali.

b) Il processo di Smoluchowski.

Consideriamo un recipiente di volume V contenente N particelle colloidali indipendenti, non interagenti, in moto browniano. Sia n_v(t) il numero di particelle che al tempo t si trovano in una porzione di volume v del recipiente. Per V→∞ e N→∞, con v costante, posto

le distribuzioni limite

possono essere calcolate esplicitamente. Esse definiscono un processo ideale ò_v(t) che chiameremo processo di Smoluchowski. Smoluchowski in realtà calcolò solamente

e

P{n(0)=n₀∣n(t)=n}. (123)

Il processo, tuttavia, non è di Markov e sono necessarie tutte le funzioni W che compaiono nella (121). Smoluchowski introdusse questo processo per interpretare i risultati sperimentali di Svedberg, i cui dati usò poi per giustificare la conciliazione statistica dell'approccio all'equilibrio con l'inversione del tempo e con la ricorrenza periodica degli stati. In particolare, per n non troppo grande (rispetto a νv), l'espressione per il tempo medio di ricorrenza poteva essere verificata sperimentalmente (e rispecchiava la realtà in maniera eccellente) e questo rendeva più facile accettare la validità dell'espressione per valori di n molto più grandi di νv, per i quali la verifica sperimentale è impossibile. È però l'enorme tempo medio di ricorrenza in questa gamma di valori che fornisce una spiegazione di come si possano conciliare la ricorrenza e l'apparente irreversibilità.

Vi sono altri esempi di processi di Smoluchowski; forse il più divertente è quello relativo al numero di pedoni che si trovano su un certo tratto di marciapiede (dal numero dei pedoni, usando le formule di Smoluchowski, è possibile ricavare la velocità media dei pedoni, oppure, data la velocità, si può ottenere la lunghezza del tratto di marciapiede). Per ulteriori dettagli, fra cui un cenno sull'uso del processo di Smoluchowski per calcolare la velocità media degli spermatozoi, si vedano gli ultimi tre paragrafi del cap. 3 in M. Kac, Probability and related topics in physical sciences, New York 1959.

c) Processi di diramazione.

Questa è una classe importante di processi che ha molte applicazioni in diversi campi della scienza. L'applicazione più nota riguarda la moltiplicazione di neutroni nei processi di fissione nucleare.

Il più semplice processo di diramazione è N(nΔ), con N(0)=1, che rappresenta il numero totale di particelle dopo n generazioni, ciascuna di durata Δ, con la condizione che in ciascuna generazione ogni particella generi 0, 1, 2, ... particelle con probabilità p₀, p₁, ... (0 significa che la particella ‛madre' muore senza lasciare discendenti). Si suppone che gli eventi di riproduzione siano indipendenti da una generazione all'altra. È facile mostrare che, se è

si ha

E{exp(zN(n Δ))}=f_n(z),

dove f_n(z) è l'n-esima ‛iterata' di f. Per tempo continuo vi sono delle ovvie modifiche da fare.

Accenniamo a un altro processo di diramazione, per l'interesse fisico che suscita e perché è strettamente collegato a ciò che abbiamo discusso nel cap. 3, È b. L'esempio riguarda il cosiddetto modello di Furry, introdotto in relazione alla teoria degli sciami di raggi cosmici. Nella collisione con la materia una particella può dividersi in due particelle, la somma delle cui energie coincide con l'energia della particella originaria. La probabilità che, nell'attraversare uno spessore dx di materia, una particella di energia E si suddivida in due particelle, una delle quali con energia compresa fra u e u+du, è definita dalla formula

q(u, E) du dx.

Il problema consiste nel descrivere le proprietà statistiche di N(x, E) dE, che rappresenta il numero di particelle in x con energia compresa fra E ed E +dE. Consideriamo una rappresentazione discreta del problema, come fecero Nordsieck, Lamb e Uhlenbeck (‟Physica", 1940, VII, pp. 344-360); supponiamo cioè che le particelle possano avere solo energie discrete, ε, 2ε, 3ε, ...; denotiamo con q_ij dx la probabilità che una particella di energia iε si scinda, nell'attraversare uno spessore dx di materia, in due particelle di energia jε e (i−j)ε, con j〈i; possiamo allora trattare questo problema come una catena di Markov con spazio degli stati infinito (x svolge qui il ruolo del tempo). Gli stati del sistema sono ‛vettori' (n₁, n₂, ...), dove n_k denota il numero di particelle di energia kε; possiamo scrivere l'equazione di Kolmogorov per W(n₁, n₂, ...; x), che rappresenta la probabilità che, dopo aver attraversato uno spessore x, vi siano n₁ particelle di energia ε, n₂ di energia 2ε, ecc. Nordsieck, Lamb e Uhlenbeck hanno chiamato questa equazione master equation, nome ormai familiare nella letteratura fisica.

Accenniamo infine al fatto che si ottengono degli interessanti processi combinando moti browniani (liberi) e processi di diramazione: questo tipo di processi conduce a equazioni paraboliche non lineari (si vedano, per es., i paragrafi 5.12 e 5.13 del libro Diffusion processes and their sample palhs di Ito e McKean, Berlin-New York 1965).

d) Processi moltiplicativi.

Questi processi sono relativamente recenti e il più semplice fra essi è

dove x(τ) è un processo gaussiano stazionario. Esso fu introdotto da Kubo nel 1962 e nel 1963 (si veda a questo proposito, la rassegna di R. F. Fox, Gaussian stochastic processes in physics, in ‟Physics reports", 1978, XLVIII, 3, pp. 179-283).

Se si scrive la (124) nella forma

si vede facilmente che si ha a che fare con un oscillatore armonico la cui frequenza è la somma di una frequenza fissata ω₀ e di una parte aleatoria x(τ), descritta da un processo gaussiano stazionario (l'oscillatore di Kubo). Più in generale, si possono avere processi moltiplicativi a valori nello spazio delle matrici,

dove ogni elemento della matrice Mè è la somma di un termine non aleatorio M_αβ e di un termine aleatorio ϕ_αβ(τ). Anche in questo caso si suppone che le ϕ_αβ siano processi gaussiani stazionari le cui covarianze a quattro indici sono

R_{αβα′β′} (t−s)=E{ϕ_αβ(t)ϕ_α′β′ (s)}.

I processi nello spazio delle matrici sono molto più complicati a causa della non commutatività di Mè (t) e Mè (s).

(L'autore intende dedicare questo articolo a George Eugene Uhlenbeck - dal quale ha imparato la maggior parte delle cose che conosce circa i processi stocastici -, in occasione del suo ottantesimo genetliaco).

Bibliografia.

Chung, K. L., Markov chains with stationary transition probability, Berlin-New York 1967.

Doob, J. L., Stochastic processes, New York 1963.

Harris, T. E., The theory of branching processes, Englewood Cliffs, N. J., 1963.

Kac, M., Logan, J., Fluctuations, in ‟Studies in statistical mechanics", 1979, VII, pp. 3-60.

Kampen, N. G. van, Stochastic differential equations, in ‟Physics letters. Section C: physics reports", 1976, XXIV, pp. 171-228.

Nicolis, G., Prigogine, L., Self-organization in non-equilibrium systems, New York 1977.

Wax, N. (a cura di), Selected papers on noise and stochastic processes, New York 1954.