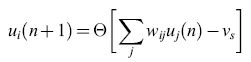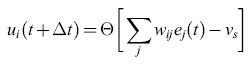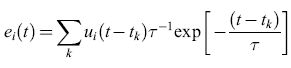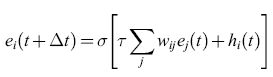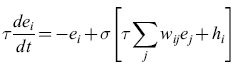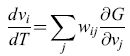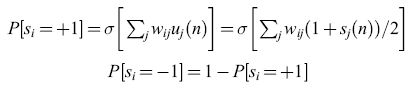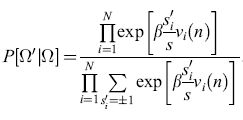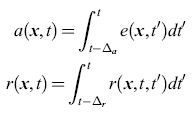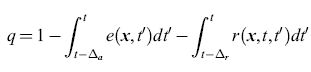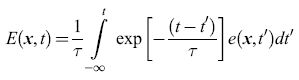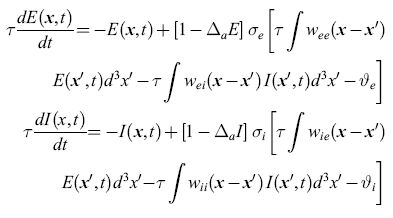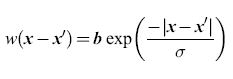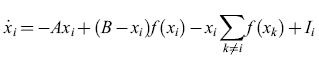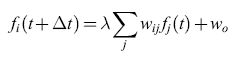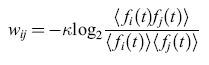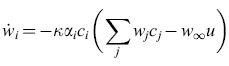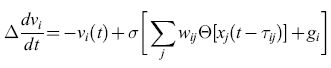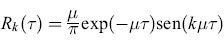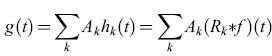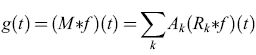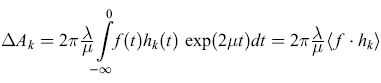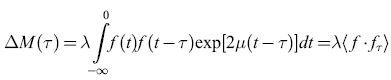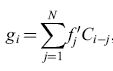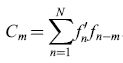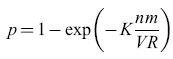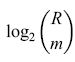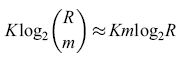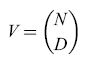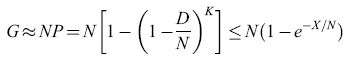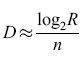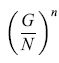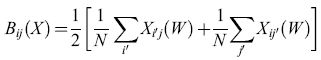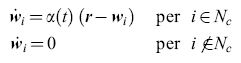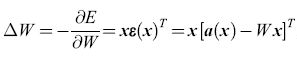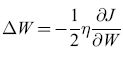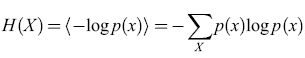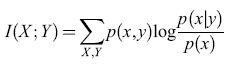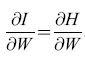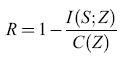Storia dei concetti e delle tecniche nella ricerca sulle reti neurali
Storia dei concetti e delle tecniche nella ricerca sulle reti neurali
In questo saggio descriveremo diverse ricerche sulle reti neurali, intese come elementi fondamentali costitutivi dei sistemi intelligenti, partendo dal lavoro classico di W.S. McCulloch e W. Pitts. Passeremo in rassegna i primi lavori sulla neurodinamica e sulla meccanica statistica, sulle analogie con le sostanze magnetiche, sulla tolleranza rispetto ai difetti dovuta alla elaborazione parallela distribuita, sulla memoria, sull'apprendimento e sul riconoscimento dei pattern. Descriveremo poi brevemente i lavori recenti sull'apprendimento supervisionato e non supervisionato nelle reti neurali, e i loro punti di contatto con i metodi statistici tradizionali per l'analisi dei dati. Le relazioni tra statistica e reti neurali, già chiare ai primi ricercatori, sono state formalizzate solo in epoca relativamente recente e rappresentano uno degli aspetti più promettenti per questo tipo di studi.
Introduzione
L'era moderna nello studio delle reti neurali e dell'intelligenza artificiale iniziò con il lavoro di W.S. McCulloch e W. Pitts (1943). Nel 1942 erano già passati venti anni da quando McCulloch, che era uno psichiatra e un neuroanatomista, aveva iniziato a riflettere sulla rappresentazione degli eventi nel sistema nervoso. Tra il 1941 e il 1951 egli lavorò a Chicago, che in quel periodo era il centro più attivo nella ricerca sulle reti neurali, grazie al lavoro di N. Rashevsky e del Committee on Mathematical Biology (Comitato di biologia matematica) dell'Università di Chicago. N. Rashevsky, H.D. Landahl, D. Rapaport e Shimbel svolsero molti studi pionieristici sulla dinamica delle reti neurali. Nel 1942 Pitts, che era allora uno studente diciassettenne di Rashevsky, fu presentato a McCulloch. Pitts stava già lavorando da qualche tempo sugli aspetti algebrici delle reti neurali, e colse rapidamente la problematica fondamentale insita nella ricerca della 'incarnazione' della mente che McCulloch perseguiva. In uno dei suoi ultimi saggi McCulloch (1961) ricorda i suoi sforzi con queste parole: "Il mio obiettivo, come psicologo, era quello di concepire un evento psichico elementare, o 'psicone', che avesse le seguenti proprietà. Primo: doveva essere così semplice da avere solo l'alternativa tra verificarsi o meno. Secondo: doveva verificarsi solo se si era verificata la sua causa (il che ci ricorda Duns Scoto!), doveva cioè implicare il suo antecedente temporale. Terzo: doveva comunicare la sua esistenza agli psiconi successivi. Quarto: tali eventi dovevano combinarsi in modo da produrre gli equivalenti di proposizioni più complesse sui loro antecedenti [ ... ] Nel 1921 mi apparve chiaro che questi eventi potevano essere considerati come gli impulsi 'tutto o niente' dei neuroni, che si combinano convergendo sul neurone successivo per produrre complessi di eventi rappresentanti una proposizione".
Le reti di McCulloch e Pitts
Le reti di McCulloch e Pitts (che chiameremo nel seguito reti MP) sono degli automi a stati finiti che realizzano la logica delle proposizioni con quantificatori, e consentono di formulare ipotesi precise sulla natura dei meccanismi cerebrali, in una forma equivalente ai programmi per computer. Questo fu un risultato notevole, in quanto stabilì una volta per tutte la validità dei modelli formali dei meccanismi cerebrali, se non la loro veridicità. Stabilì anche la possibilità di sviluppare una teoria rigorosa della mente, in quanto reti neurali con retro azione possono mostrare un comportamento funzionale a uno scopo. Come dicono McCulloch e Pitts: "Tutti gli aspetti dell'attività che siamo abituati a definire mentale sono deducibili in modo rigoroso dalla neurofisiologia attuale e nelle reti concepibili non è più vero che "la Mente è più evanescente di un fantasma"".
La tolleranza agli errori e l'elaborazione distribuita
Le reti MP furono le prime progettate per svolgere compiti logici specifici, e naturalmente la logica può essere posta in corrispondenza con l'aritmetica, cosicché qualsiasi calcolo aritmetico (finito) si può realizzare attraverso una rete MP. Ma cosa può succedere se di tanto in tanto una rete di questo genere funziona male, o se viene danneggiata? Fu questo problema ad attrarre l von Neumann. All'inizio degli anni Cinquanta, in seguito a conversazioni con McCulloch, Bruckner e Gell-Mann, von Neumann affrontò il problema della progettazione di reti MP in grado di funzionare in modo affidabile nonostante mal funzionamenti o guasti dei neuroni che le compongono, fili mal collegati, o danni subiti da una porzione della rete (von Neumann, 1956).
Von Neumann risolse il problema dell'affidabilità in due modi diversi. La sua prima soluzione consisteva nello sfruttare le proprietà di correzione di errori degli elementi logici 'a maggioranza'. Questi elementi realizzano la funzione logica m(a,b,c)=(a AND b) OR (b AND c) OR (c AND a). La procedura consiste nel triplicare ogni funzione logica da eseguire, cioè eseguire in parallelo ogni funzione logica tre volte, e inviare quindi gli output ad elementi logici a maggioranza. La sua seconda soluzione al problema dell'affidabilità consisteva nel multiplex. Ciò significa utilizzare N circuiti MP per svolgere il compito di uno solo. In reti di questo tipo un bit di informazione (la scelta tra un 1 e uno 0) non viene segnalata dall'attivazione di un neurone MP, ma dall'attivazione sincrona di molti neuroni MP. Poniamo che ∆ sia un numero tra 0 e 1; viene segnalato un 1 se ξ, la frazione di neuroni MP attivati coinvolti in un compito qualsiasi, è maggiore di ∆; in caso contrario viene segnalato uno O. Evidentemente, una rete MP con multiplex funzionerà in modo affidabile solo se ξ è prossima a 0 o 1. Von Neumann realizzò tale condizione usando reti composte interamente da elementi logici NAND, e mostrò che, per computazioni di profondità logica elevata, il metodo basato sul multiplex è superiore, rispetto alla decodifica basata sulla logica a maggIOranza.
Questa soluzione al problema dell'elaborazione affidabile effettuata con elementi inaffidabili risulta generale, poiché l'elemento logico NAND è universale. Ma è plausibile dal punto di vista biologico? La risposta sembra essere negativa, poiché i neuroni reali hanno migliaia di contatti sinaptici, per cui non è necessario concatenare molti elementi NAND in circuiti di grande profondità logica per realizzare funzioni logiche di molte variabili. Ciò induce a pensare che i neuroni reali possano realizzare funzioni logiche di molte variabili con una probabilità di errore, s, non molto più grande rispetto a quella degli elementi NAND. Tale osservazione spinse S. Winograd e ID. Cowan (Winograd e Cowan, 1963) a studiare il caso limite, in cui S è indipendente dalla complessità logica della funzione da realizzare. In questo caso è possibile usare codici a correzione di errore, proprio come viene fatto nei canali di comunicazione in presenza di rumore (Shannon, 1948). In tali canali un messaggio che contiene K simboli viene trasmesso attraverso un segnale che contiene, a sua volta, N segnali, dei quali N - K sono utilizzati dal ricevente per rilevare e correggere gli errori.
Nel caso della computazione questo approccio implica che K elaborazioni si possono realizzare mediante una rete MP che contiene un numero di elementi N / K volte superiore rispetto al numero necessario in assenza di errori. L'effetto complessivo di questo schema di codifica consiste nel distribuire le funzioni logiche da realizzare sull'intera rete MP. Questo schema funziona in modo più efficiente per K e N grandi, di fatto in un'architettura parallela e distribuita. Lo schema di Winograd e Cowan è dunque un primo esempio di elaborazione parallela distribuita (PDP, Parallel Distributed Processing). Si può naturalmente argomentare che tale schema non è realistico, in quanto si ipotizza che tutto il dispositivo di codifica aggiuntivo sia esente da errori. Come abbiamo già notato, per elementi logici semplici ciò potrebbe non essere vero, ma per i neuroni reali potrebbe essere più plausibile.
Queste soluzioni al problema della tolleranza agli errori hanno fornito elementi per capire meglio il modo in cui le reti neuronali nel cervello siano in grado di funzionare in modo affidabile, nonostante possano subire danni. Fin dagli studi neurologici classici di H. Jackson su pazienti con lesioni cerebrali e dalla dimostrazione, dovuta a K.S. Lashley, che topi con lesioni cerebrali conservano delle capacità cognitive, si è compreso che, malgrado regioni del cervello diverse siano specializzate per funzioni diverse, la scala alla quale è presente questa localizzazione di funzioni non si estende necessariamente ai singoli neuroni. In termini delle analisi sopra descritte, la rappresentazione di un bit d'informazione non è necessariamente unaria, e può essere invece ridondante, o anche distribuita. Su questo punto c'è stato un vivace dibattito. Lashley, per esempio, ha ipotizzato che regioni diverse del cervello siano equipotenti dal punto di vista funzionale (Lashley, 1950): qualsiasi regione può realizzare il compito dato. Si tratta di una posizione antitetica a quella della localizzazione. Più recentemente, H.B. Barlow (1972) ha affermato che il livello di ridondanza nel funzionamento del cervello si riduce sempre più quando ci si sposta dalle regioni periferiche a quelle centrali, fino ad arrivare a una rappresentazione unaria dell'informazione nelle regioni profonde del cervello. Nella terminologia d'uso comune, si parla di neuroni (o cellule) della nonna, che si suppone si attivino appunto solo alla percezione associata alla nonna.
Neurodinamica
Insiemi di neuroni e sinapsi di Hebb
La nozione, introdotta da Lashley, dell'equipotenzialità delle regioni cerebrali, si riflette nel lavoro di D.O. Hebb (1949). Hebb ha proposto l'ipotesi che le connessioni presenti nel cervello cambino continuamente via via che l'organismo apprende diversi compiti funzionali, e che questi cambiamenti creino insiemi organizzati di cellule. Hebb sviluppò ulteriormente una vecchia idea di S. Ramon y Cajal, e propose il suo famoso postulato: l'attivazione ripetuta di un neurone da parte di un altro, attraverso una particolare sinapsi, aumenta la conduttanza di questa. Ne segue che gruppi di cellule debolmente interconnesse, se attivate simultaneamente, tenderanno a organizzarsi in insiemi più fortemente connessi. Qui, di nuovo, la rappresentazione di un bit d'informazione è distribuita. Il lavoro di Hebb ha avuto una notevole influenza sulle ricerche successive. La teoria degli insiemi di cellule ha dato il via a numerosi studi sull' apprendimento in reti neurali, e sul modo in cui si genera e si propaga un'attività neurale sincronizzata. Gli studi su questo argomento, noti oggi come neurodinamica, iniziarono grazie a Rashevsky (1938). Rashevskye collaboratori rappresentarono l'attivazione e la propagazione nelle reti neurali in termini di equazioni differenziali, e cercarono nessi con teorie dello stesso tipo usate nel contesto di applicazioni alla fisica.
Analogie con sistemi di spin su reticolo
In seguito al lavoro di Hebb, la proposta più stimolante sulle proprietà degli insiemi di neuroni fu quella di B.G. Cragg e H.N.V. Temperley (1954). Essi notarono che, proprio come i neuroni possono essere attivati (emettendo potenziali d'azione) o quiescenti (a riposo), così gli atomi appartenenti a un certo insieme, o reticolo, possono trovarsi in uno di due stati energetici (per esempio, con lo spin verso l'alto o verso il basso). Inoltre, proprio come i neuroni si eccitano o si inibiscono reciprocamente, così un atomo esercita sui suoi vicini forze di tipo magnetico, che tendono a orientare gli altri spin nella stessa direzione, oppure nella direzione opposta. Quindi le proprietà dei neuroni in una rete densamente connessa dovrebbero essere analoghe a quelle degli atomi in un reticolo. l sistemi di spin che manifestano diversi tipi di ordinamento forniscono buoni modelli per le proprietà dei materiali magnetici. Per esempio, un ferromagnete, cioè un materiale in cui gli spin tendono ad allinearsi nella stessa direzione, è ordinato su grande scala; analogamente, un antiferromagnete, nel quale gli atomi tendono ad allinearsi in direzioni opposte, possiede un ordine su grande scala; invece un paramagnete è un sistema disordinato. È plausibile che le reti neurali esibiscano proprietà analoghe. Cragg e Temperley proposero quindi in primo luogo che l'organizzazione in domini (ognuno dei quali include insiemi di spin in su o in giù), caratteristica onnipresente nei ferromagneti, possa essere presente nelle reti neurali (dove i domini consistono in insiemi di neuroni eccitati o quiescenti), e, in secondo luogo, che le reti neurali manifestino, nelle transizioni tra gli stati disordinati e quelli ordinati, effetti simili all'isteresi ferromagnetica. Di conseguenza i domini neurali, una volta che sono stati attivati da stimoli esterni, dovrebbero essere stabili rispetto all'attività spontanea, casuale, e potrebbero quindi costituire una memoria dello stimolo.
Reti di neuroni integrate and fire
A.M. Uttley (1956) fu forse il primo a tener conto, nel costruire un modello di rete, del fatto che la membrana neuronale agisce come un integratore con perdita. Indichiamo con Ui(t) una variabile binaria che rappresenta lo stato del neurone i-esimo al tempo t, e e la funzione a gradino di Heaviside. lpotizziamo che il tempo sia misurato in passi ∆t: t = n∆t . L'attivazione di un neurone MP si può quindi esprimere con l'equazione:
formula [1]
dove wij è il peso della connessione (j → i), e Vs è il potenziale di soglia. Alternativamente, possiamo supporre che sia
formula [2]
dove
formula, [3]
τ è la costante di tempo di membrana, e tk indica il tempo di arrivo di un impulso di corrente in ingresso. Questo modello rappresenta il cosiddetto neurone integrate and fire con perdita (LlF, Leaky Integrate and Fire).
Reti neurali analogiche
l neuroni MP e LlF costituiscono una rappresentazione molto semplificata (ma matematicamente complicata) delle proprietà di un neurone reale. Fu per questo motivo che Cowan (1967) introdusse la curva caratteristica di emissione sigmoide σ(v) = (l +e-V)-1, e la condizione regolarizzata di emissione:
formula [4]
In questa relazione ei(t) è la frequenza di emissione dell'elemento i-esimo, una versione mediata nel tempo di Ui(t), t è misurata in unità di τ, hi(t) è uno stimolo esterno, e σ(x) è la funzione logistica. L'equivalente di questa condizione in termini di equazioni differenziali è:
formula. [5]
Neuromeccanica statistica
Cowan (1968) osservò anche che se wij = -wji' Wii = 0, e τ è grande, l'equazione [5] si può riscrivere nella forma:
formula [6]
in cui
Nella [6] la grandezza
,
è una costante del moto della rete, ovvero non varia con il tempo. Il contenuto fisico di questo risultato è che una rete di elementi simili a neuroni, con costanti di accoppiamento antisimmetriche, può generare oscillazioni neutralmente stabili. Inoltre, poiché G è una costante del moto, possiamo introdurre una meccanica statistica di equilibrio, in cui la probabilità che il sistema sia nello stato {Vl,V2, ... ,VN} prende la forma Z-le-βG, con Z = Σ(v) exp(-βG). Si possono quindi calcolare varie medie statistiche del comportamento di queste reti.
Poco tempo dopo questi sviluppi, W.A. Little (1974) continuò il lavoro di Cragg e Temperley e stabilì la connessione tra reti di neuroni MP sincroni ma rumorosi (o stocastici), e sistemi di spin su reticolo. Al posto della notazione Ui( n) = 0 o 1, Little introdusse la codifica standard che i fisici usano per lo spin, si(n) = ±1, in cui + 1 denota lo spin in su e -1 lo spin in giù, per cui ui(n) = [1 +si(n)]/2. La condizione di emissione data dall'equazione [4] era sostituita da:
formula [7]
dove P [Si = + l] è la probabilità che, al tempo n + l, l'i-esimo elemento sia attivo, mentre P[Si = -l] è quella che esso sia quiescente. La relazione tra questo schema di aggiornamento e la condizione di emissione dell' equazione [4] è ovvia: ei (t) è una media temporale del numero di occupazione Ui (t), mentre P[Si = + l] è una media su molte ripetizioni (o media sull'ensemble) della stessa quantità, Ui (n).
Consideriamo ora lo stato Ω= {S1, S2, ... , SN }. Qual è la probabilità che questo stato possa evolvere nello stato Ω' = = {s'1,s'2, ... ,s'N}? La risposta può essere messa nella forma
formula. [8]
Tale probabilità ha un'espressione molto simile a quella della funzione di partizione degli spin su un reticolo, in meccanica statistica. In effetti, se identifichiamo il tempo n con l'indice spaziale j, e se i pesi wij sono simmetrici (wij = wji), ritroviamo proprio la funzione di partizione per una variante del modello di Ising bidimensionale per gli spin su reticolo. Little usò tale analogia per dimostrare che, nel caso di pesi simmetrici, in una rete di questo tipo si può sviluppare un ordine temporale su larga scala, cioè possono realizzarsi correlazioni temporali.
Modelli basati su popolazioni di neuroni
Fu R.L. Beurle (1956; 1962) a fornire per primo un'analisi dettagliata del modo in cui funzionano l'attivazione e la propagazione dell'attività cerebrale su grande scala. Beurle non si concentrò però sull'attivazione dei singoli neuroni, ma sulla frazione di neuroni attivati per unità di tempo in un fissato elemento di volume di una porzione di tessuto cerebrale modello, composta da neuroni con connessioni casuali. In termini moderni, questa è l'approssimazione al continuo dell'attività neurale. Il lavoro di Beurle diede l'avvio a molte simulazioni al calcolatore di reti neurali con connessioni casuali. B.G. Farley e W.A. Clark (1961), per esempio, simularono il comportamento di 1024 neuroni modello con connessioni casuali, abbastanza più complicati e realistici rispetto ai neuroni di McCulloch e Pitts. Questi autori confermarono le conclusioni di N. Wiener e Beurle sulla esistenza di onde che si propagano e ruotano attraverso il tessuto nervoso.
Le equazioni di Wilson e Cowan
I risultati che abbiamo descritto forniscono informazioni interessanti sulle proprietà statistiche di equilibrio delle reti neurali (con il vincolo che i pesi siano simmetrici, antisimmetrici o casuali). Che cosa si può dire degli effetti transienti, o di quelli che si manifestano lontano dall'equilibrio? Il lavoro di Beurle può essere considerato un primo passo in questa direzione, ma esso trattava solo reti con neuroni eccitatori, e non considerava l'esistenza di un periodo refrattario del neurone dopo una scarica. Furono H.R. Wilson e Cowan (1972; 1973) a estendere il lavoro di Beurle includendo neuroni sia eccitatori che inibitori, e tenendo conto del periodo refrattario. Descriveremo ora brevemente questo lavoro.
Supponiamo che in un istante di tempo t qualsiasi i neuroni si trovino in uno di tre (soli) stati possibili: quiescente (sensibile), attivato o refrattario. Chiamiamo le frazioni di neuroni che si trovano in questi stati q(x,t), a(x,t) e r(x, t), rispettivamente. Chiaramente varrà l'eguaglianza q+a+r= l. Indicando con r(x,t,t')dt' la frazione di neuroni, attivati durante l'intervallo (t',t' + dt'), che sono ancora refrattari, si ha
formula [9]
in cui ∆a è la durata dello stato attivo, mentre ∆r è la durata dello stato refrattario relativo, e quindi:
formula. [10]
Wilson e Cowan si sono concentrati sul caso ∆r = 0, cioè quello in cui non ci sono stati refrattari relativi. Questi autori hanno introdotto le variabili temporali mediate sul tempo (time coarse-grained variables)
formula [11]
come approssimazione regolarizzata a e(x, t). Si procede in maniera simile per i neuroni inibitori, arrivando a definire una funzione I (x, t) che è l'analoga di E(x,t). Le equazioni che si ottengono sono:
formula [12]
in cui le funzioni Wee, Wei, Wie e Wii forniscono i pesi di tutte le sinapsi che connettono le cellule a distanza Ix - x'l, e i pedici indicano il tipo di popolazione (eccitatoria o inibitoria). Le variabili ϑe e ϑi rappresentano le soglie per l'eccitazione dei neuroni, e le funzioni σe e σi sono delle sigmoidi.
Dinamica ad attrattori
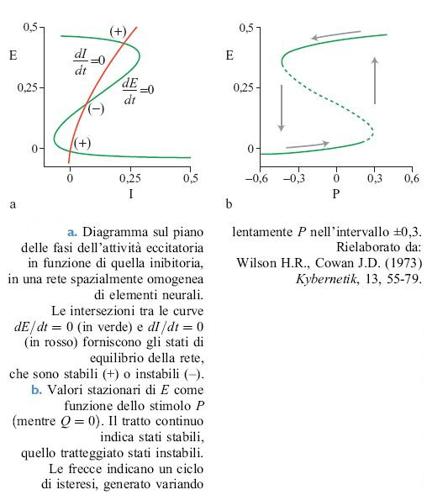
È istruttivo esaminare le soluzioni delle equazioni [12] per il numero totale di neuroni eccitatori e inibitori attivati, rispettivamente E(t) = ∫ E(x,t)d³x e I(t) = ∫ I(x,t)d³x. Si possono analizzare le equazioni ridotte risultanti attraverso metodi basati sul piano delle fasi, in cui i due luoghi di punti determinati dalle equazioni dE / dt = O e dI/ dt = O si riportano in un grafico sul piano (E,l).
La figura (fig. 2) illustra la situazione che si presenta nel piano delle fasi quando Wee è grande e non vi sono stimoli esterni. Si può dimostrare che lo stato stazionario E = I = 0 è stabile, e che c'è un altro stato stabile per E≈0,4, I≈0,23. Tale stato si può realizzare attraverso opportune condizioni iniziali o mediante una stimolazione di intensità appropriata. La figura 2b mostra i valori di E corrispondenti a uno stato stazionario al variare dell'intensità P di uno stimolo esterno applicato ai neuroni eccitatori. Si può notare che si ha una transizione da E = 0 e E≈0,4 quando P varia da -0,3 a +0,3, e viceversa. Il ciclo di isteresi associato è caratteristico dei sistemi noti come eccitabili. A questi stati stabili si dà ora il nome di attrattori stazionari.
Secondo questa analisi, dunque, una porzione di tessuto neuronale può manifestare un comportamento di riposo (attività in media nulla) o un comportamento eccitato (in cui, in media, circa il 40% delle cellule è attivato). Se anche ai neuroni inibitori viene applicato uno stimolo esterno Q ≠ 0, esiste un terzo attratto re stazionario corrispondente a E = I = 0, 23 (cioè circa il 23% delle cellule è attivato).
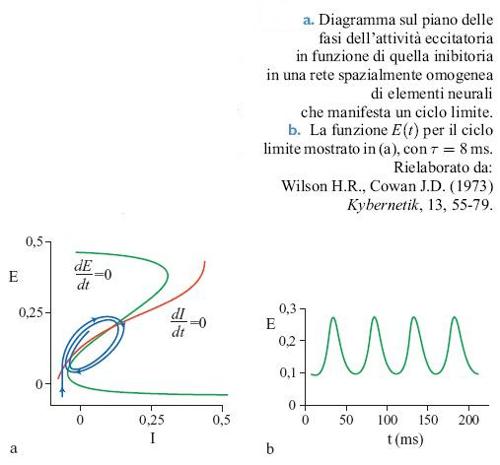
Oltre agli attrattori stazionari, nelle reti con inibizione forte possono manifestarsi attrattori stabili di tipo periodico o oscillatorio, noti in termini tecnici come cicli limite. La figura (fig. 3) mostra il piano delle fasi e il ciclo corrispondente per uno stato di questo tipo. Queste proprietà sono dipendenti dallo stimolo; una qualsiasi rete in cui esistono dei cicli limite per un insieme di stimoli mostrerà transizioni e isteresi per un diverso insieme di stimoli.
Attività localizzata e attività che si propaga
L'esistenza delle proprietà sopra descritte si può dimostrare in modo più generale. In effetti si possono avere transizioni con isteresi, transizioni e cicli di attività in un 'tessuto' neurale con struttura di tipo lineare, a forma di lamina o esteso nelle tre dimensioni. In presenza di interazioni dipendenti dalla posizione, però, emergono fenomeni nuovi. Consideriamo la funzione w(x-x'), e poniamo che questa sia della forma ipotizzata da Beurle, cioè:
formula [13]
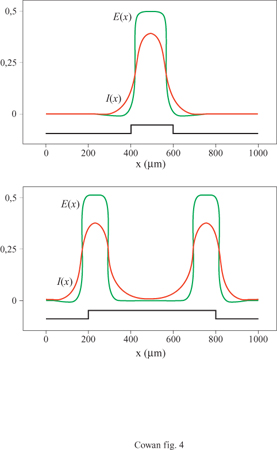
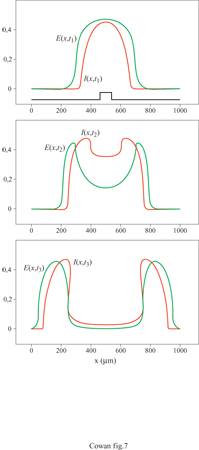
dove b è la densità delle connessioni sinaptiche e σ è la costante spaziale che regola il decadimento di w(x-x') con la distanza. Ne segue che, nel caso unidimensionale, il peso sinaptico totale è ∫+∞-∞ w(x - x')dx' = 2bσ. Con riferimento alle equazioni [12], supponiamo ora che σie > σeo cioè che le connessioni tra neuroni eccitatori e neuroni inibitori abbiano un raggio d'azione maggiore rispetto a quelle tra neuroni eccitatori. Questa condizione sulle costanti spaziali porta alla cosiddetta inibizione laterale, poiché l'eccitazione locale provoca inibizione, anziché eccitazione, a distanze ∣x - x'∣≥ σie. Sotto questa condizione gli stati stazionari o i cicli periodici possono rimanere localizzati nello spazio, se l'inibizione laterale è abbastanza forte.
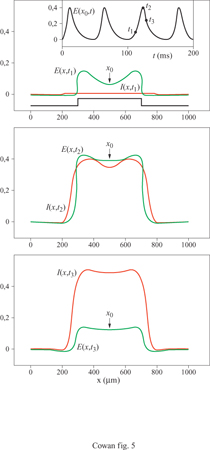
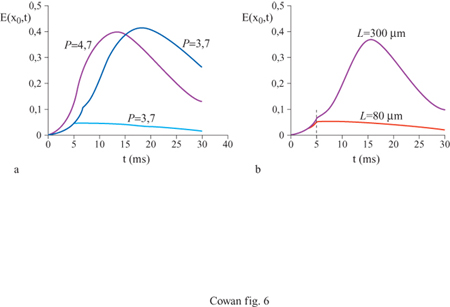
La figura (fig. 4) mostra, per esempio, gli attrattori stazionari localizzati nello spazio generati in un tessuto neurale con struttura lineare da due stimoli unidimensionali di diversa larghezza. Il più lungo produce effetti di accrescimento ai bordi, caratteristici dell'inibizione laterale. Analogamente, la figura seguente (fig. 5) mostra un ciclo limite localizzato nello spazio, generato in risposta a uno stimolo unidimensionale costante. C'è inoltre una terza possibilità: uno stato metastabile chiamato transiente attivo. In questo stato, la risposta a uno stimolo breve e localizzato continua a crescere anche dopo la fine dello stimolo, raggiunge un massimo e poi decade nuovamente nello stato di riposo. La figura (fig. 6) mostra due esempi di transiente attivo. In entrambi i casi P(x,t) è un'onda quadra nello spazio, di larghezza L e ampiezza P, applicata per un tempo ∆t. Per ipotesi P(x, t) eccita soltanto i neuroni eccitatori, all'interno della porzione di tessuto considerata. Se L è abbastanza piccolo, la risposta E(x, t) sviluppa un solo massimo nello spazio, situato al centro della regione di stimolazione, e rimane localizzata all'interno di questa. La figura indica che c'è una soglia per la generazione dei transienti attivi, nella quale sono coinvolte sia una somma spaziale che una somma temporale: uno stimolo P(x, t) genera un transiente attivo solo se il prodotto P x ∆t x L è abbastanza grande. Questo mostra che la soglia per il transiente attivo è una soglia 'di carica', simile a quella presente per il potenziale d'azione, nel caso degli assoni stimolati da una breve scossa.
Infine, se l'azione dei neuroni inibitori è bloccata, per esempio attraverso un contributo costante Q(x, t) di ampiezza -Q, in modo da privare la rete dell 'inibizione, un nuovo stato emerge da quello di ciclo limite: l'onda viaggiante. La figura (fig. 7) illustra questo effetto. La velocità di propagazione è una funzione di Q e dei parametri di connettività bij e σij, mentre la lunghezza d'onda dipende da P. Per Q = - 30 e σie = 50 μm la velocità di propagazione è pari a 4 cm/s.
Wilson e Cowan hanno utilizzato questi risultati nel tentativo di spiegare numerose osservazioni sperimentali sulle reti neuronali presenti nella corteccia e nel talamo di diversi vertebrati. Questi autori hanno proposto l'ipotesi che gli attrattori stazionari siano alla base della memoria a breve termine (STM, Short Term Memory). Cragg e Temperley avevano precedentemente suggerito che alla base della STM ci fossero effetti di isteresi, mentre Hebb aveva proposto la sua teoria degli effetti riverberanti. Gli attrattori stazionari che abbiamo descritto sono riverberanti: l'attività circola tra i neuroni delle regioni eccitate in modo tale che l'attività totale in ogni punto della regione rimanga costante e, come abbiamo visto, mostra effetti di isteresi. Wilson e Cowan suggerirono che i neuroni della corteccia frontale mostrassero effetti di questo tipo. Riguardo la modalità oscillatoria, o di ciclo limite, questi autori proposero l'idea che l'intensità persistente dello stimolo potesse essere codificata dalla frequenza delle raffiche di impulsi che verrebbero emessi in questa modalità. Gli stessi autori ipotizzarono anche che l'attività oscillatoria osservata in vari nuclei del talamo abbia le caratteristiche dei cicli limite, portando a sostegno di questa ipotesi le osservazioni sperimentali di neuroni del nucleo ventrolaminare. Tali neuroni, sotto certe condizioni, se sottoposti a una lunga sequenza di stimoli rispondevano solo ogni due stimoli: mostravano cioè una demoltiplicazione in frequenza. Wilson e Cowan ipotizzarono anche che la modalità con transienti metastabili attivi fosse rilevante ai fini dell'interpretazione delle risposte corticali a stimoli brevi (per esempio, a pattern visivi). Essi notarono che le risposte di tipo transiente attivo manifestano sia effetti di latenza (ci vuole più tempo a sviluppare l'accrescimento ai bordi in risposta a uno stimolo debole che in risposta a uno stimolo intenso), sia effetti legati alla dimensione e all'intensità (uno stimolo più intenso appare più ampio di uno debole), e che questi effetti necessitano non solo di inibizione laterale, ma anche di eccitazione laterale. Perciò è necessario che nella corteccia avvenga un'amplificazione degli effetti iniziali prodotti da brevi scariche di attività provenienti dalla retina o dal nucleo genicolato laterale. Di conseguenza, la modalità di transiente attivo caratterizzerebbe le risposte della corteccia visiva primaria.
Le equazioni di Grossberg
S. Grossberg (1973) raggiunse conclusioni molto simili, analizzando la dinamica delle reti neurali. Le equazioni di Grossberg sono della forma:
formula [14]
dove Xi≤B è l'attività media dell'i-esima popolazione,f(xi) (nella notazione di Wilson e Cowan) è una funzione sigmoide di Xi, e li è lo stimolo indirizzato all'i-esima popolazione. Le interazioni differiscono in modo notevole da quelle delle equazioni di Wilson e Cowan. Il termine (B -xi)f(xi) viene interpretato come una forma di autoeccitazione dell'i-esima popolazione, e il termine -xi ∑k≠if(xk) come una forma di inibizione laterale dell'i-esima popolazione da parte di tutte le altre. Grossberg notò che queste interazioni moltiplicative costituiscono un esempio del fenomeno detto shunting. Anche Grossberg trovò degli attrattori stabili, e li utilizzò per la formulazione di modelli di STM. Egli notò che interazioni sinaptiche moltiplicative di questo tipo consentono di controllare con più precisione il funzionamento di un sistema di memoria di questo genere. Inoltre l'autore suggerì l'ipotesi che le crisi convulsive e le allucinazioni fossero una conseguenza di instabilità dinamiche, e diede l'inizio a molte applicazioni alla neurobiologia. Tra i miglioramenti di questi modelli figura la sostituzione della costante B, l'attività massima (indipendente dalla popolazione), con una Bi' che ha l'effetto di creare dei sottoinsiemi delle popolazioni.
Apprendimento e memoria associativa
Sinapsi modificabili
La proposta, avanzata da Hebb, della modificazione sinaptica durante l'apprendimento, diede un ulteriore impulso all'attività sulle reti neurali e, in particolare, su reti adattative in grado di imparare a svolgere compiti specifici. l primi tentativi in questa direzione furono compiuti da Uttley (1954), il quale dimostrò come reti neurali con sinapsi modificabili potessero classificare semplici insiemi di sequenze binarie in classi di equivalenza.
La prima proposta avanzata da Uttley assegnava ai pesi sinaptici il ruolo di probabilità condizionate. Consideriamo il modello LlF introdotto precedentemente, descritto dall'equazione [2]. Secondo l'ipotesi di Uttley
wij = -klog₂p(i∣j) [15]
dove
è la probabilità condizionata che si verifichi l'evento i-esimo essendosi verificato il i-esimo e
è la frequenza di emissione, una versione mediata su tempi brevi di ui(t). Uttley costruì un 'computer idraulico' per calcolare tali probabilità condizionate, e dimostrò che un simile apparato poteva effettuare, dopo un periodo di addestramento, una semplice classificazione di pattern. Egli dimostrò inoltre come elementi di questo tipo, all'interno di reti con dei ritardi tra gli elementi (ritardi che potrebbero rappresentare, per esempio, la velocità finita di propagazione degli impulsi), possano imparare a immagazzinare e richiamare pattern sia spaziali che temporali. In una rete così fatta, quindi, si possono immagazzinare e richiamare sequenze. Uttley scoprì inoltre una proprietà molto importante, quella del completamento dei pattern temporali, per la quale i primi elementi di una sequenza erano sufficienti a richiamare anche il resto. Questa proprietà fornisce la base per una memoria indirizzabile a partire dal contenuto.
Nei lavori successivi Uttley introdusse una semplice versione del neurone analogico integrate and fire, nella quale la condizione di emissione (sulla scala temporale determinata da una costante di tempo TL" T) è rappresentata dalla formula:
formula [16]
in cui λ è una costante. L'equazione [16] si può considerare come un 'precursore' lineare dell'equazione [4], non lineare. Uttley introdusse anche un nuovo meccanismo di modificazione sinaptica, definito da:
formula [17]
in cui <fi (t)> è la media su scale di tempo lunghe di fi (t).
Il peso wij è connesso alla grandezza nota, in teoria dell'informazione, come informazione mutua fornita dai pattern di emissione i e j. Uttley denominò informoni gli elementi neurali con questi pesi. Egli mostrò come reti composte da informoni possano fungere da modelli dell' elaborazione dell'informazione nell'ippocampo e nella corteccia, e come possano essere addestrate utilizzando le procedure standard del condizionamento pavloviano. Da questo punto di vista, Uttley dimostrò la stretta relazione esistente tra gli informoni e un ben noto modello del condizionamento. Tale modello è espresso dalle equazioni di Rescorla-Wagner (RW) , che forniscono una descrizione semplice ma molto utile di molti aspetti della risposta condizionata (Rescorla e Wagner, 1972). Ne riassumeremo perciò il contenuto.
Supponiamo che u e ci siano variabili binarie che rappresentano, rispettivamente, la presenza o l'assenza dello stimolo incondizionato e dell'i-esimo stimolo condizionato. Indichiamo con Wi l"accoppiamento associativo' di ci, con αi il suo guadagno, con k un parametro che regola la velocità di apprendimento e con W∞ il livello asintotico di l"accoppiamento associativo' che u può sostenere. Le equazioni RW si scrivono:
formula [18]
Qual è la relazione tra l'equazione [18] e le equazioni di Uttley? Dopo qualche passaggio algebrico le equazioni di Uttley [16] e [17] possono essere riscritte, sotto opportune ipotesi, nella forma di RW. Le equazioni così ottenute non sono esattamente quelle di RW, ma le differenze sono piccole e poco rilevanti. Il lavoro di Uttley, anche se poco noto, è importante, poiché stabilì in certa misura la bona fides dei modelli di modificazione sinaptica basati su misure di informazione nello studio del condizionamento e dell'apprendimento associativo.
Campi di embedding
Grossberg (1969) introdusse un approccio più formale ai problemi sopra esposti e chiamò le reti modificabili che abbiamo descritto campi di embedding. Grossberg formulò un insieme di equazioni strettamente legate all'equazione per il potenziale, introdotta trattando le reti integrate and fire. Poniamo
formula. [19]
Questa è essenzialmente l'equazione [5], in cui con gi si indica lo stimolo esterno, ma con due differenze: la frequenza di emissione fj(t+∆) è data in questo caso non dalla funzione sigmoide σ[Xj(t)], ma dalla funzione lineare a soglia (nulla per x <xs)
Θ(x) =x per x≥xs [20]
il cui argomento è ritardato di un tempo τij a causa dei tempi di transito. C'è inoltre una modificazione del peso sinaptico rappresentata da:
formula. [21]
Questo è un primo esempio di una sinapsi basata puramente sulla correlazione, in quanto si ipotizza che il peso wij sia proporzionale alla funzione di correlazione incrociata (cross correlation) tra la frequenza di emissione presinaptica Θ[xj(t - τij)] e il potenziale postsinaptico Vi(t). Grossberg sviluppò un'analisi matematicamente approfondita di queste equazioni e, al pari di Uttley, fu in grado di correlare le loro proprietà a un'ampia varietà di esperimenti sul condizionamento.
Memoria associativa
Un altro interessante problema, quello della memoria associativa, fu studiato già negli anni Cinquanta, a partire dal lavoro di W.K. Taylor (1956). La rete originale di Taylor è strutturalmente simile a un perceptron elementare privo di unità nascoste. La principale differenza tra i due sistemi consiste nel fatto che le unità non sono neuroni MP, ma dispositivi analogici. Anche la procedura di addestramento usata in questo contesto è diversa da quelle caratteristiche dei perceptron e degli ADALlNE (che tratteremo in dettaglio nel seguito): è semplicemente la regola di Hebb. La rete impara ad associare tra loro diversi pattern sensoriali mediante la presentazione ripetuta di coppie di pattern, uno dei quali suscita all'inizio una risposta motoria. Alla fine, anche l'altro pattern provoca la risposta. La rete di Taylor manifesta quindi un condizionamento pavloviano semplice, e la memoria associativa è immagazzinata in modo distribuito nell'insieme dei pesi. In alcuni lavori successivi Taylor ha costruito reti più elaborate, in cui le unità motorie di output si inibiscono vicendevolmente: in termini moderni, un circuito winner take all (letteralmente, il vincitore prende tutto).
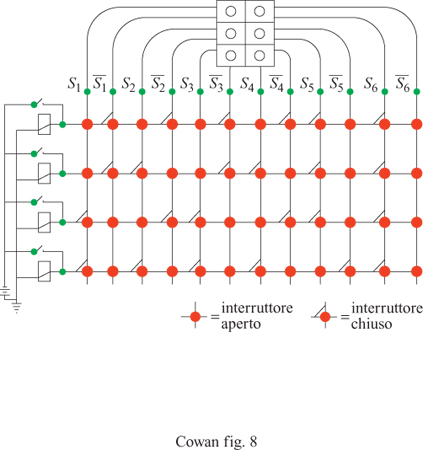
Il circuito winner take al! è in grado di formare associazioni con stimoli accoppiati in modo più controllabile e affidabile rispetto alle reti precedenti, e riesce anche a effettuare la discriminazione tra pattern, alla maniera dei perceptron e degli ADALlNE. Taylor avanzò l'ipotesi che le aree associative della corteccia cerebrale e del talamo contengano reti di questo tipo. Matrici di apprendimento Poco tempo dopo questi sviluppi, K. Steinbuch (1961) introdusse la matrice di apprendimento (fig. 8), che consiste in una rete planare di interruttori interposti tra griglie di recettori ed effettori. Gli interruttori sono controllati da pesi Wij il cui valore è proporzionale a una misura delle correlazioni tra i pattern di recettori e lo stimolo incondizionato. Usando la notazione di Uttley,
formula [22]
dove i e i si riferiscono ora a linee attive di input, provenienti rispettivamente dallo stimolo condizionato e incondizionato, ī a una linea di stimolo condizionato inattiva e σ è una funzione di tipo sigmoide, ripida ma regolare. La formula precedente costituisce una vera e propria regola associativa. l pesi diventano non trascurabili solo se p(i∣j) ≫ p(ī∣j). Ne segue che gli interruttori si chiudono solo se vi sono associazioni statisticamente significative, e la rete impara ad associare pattern. Di nuovo, la rappresentazione della memoria corrispondente risiede nel pattern dei pesi.
Olofonia e ologrammi
A partire dalla metà degli anni Sessanta molti altri ricercatori hanno sviluppato reti associative simili a quelle che abbiamo descritto. Possiamo suddividere i loro contributi in due categorie: da un lato, evoluzioni del lavoro di Uttley sulla memorizzazione temporale e sul richiamo; dall'altro, evoluzioni del lavoro di Taylor e Steinbuch sull'apprendimento associativo. Il lavoro di DJ. Willshaw e H.C. Longuet-Higgins sull'olofonia (1969) fornisce un buon esempio della prima categoria. La loro tecnica consiste nell'utilizzare un banco di filtri a banda stretta, connessi in parallelo, mediante amplificatori con guadagno variabile, a un canale di output. Si utilizza anche un insieme di integratori. La memoria olofonica è formata dai guadagni dei diversi amplificatori. Chiamiamo f(t) un segnale di input, e hk(t) l' output del k-esimo filtro, uguale a
∫∞0 Rk(τ)f(t-τ)dT= (Rk*f) (t), [23]
cioè alla convoluzione (*) del segnale con la risposta impulsiva di un oscillatore smorzato:
formula. [24]
La quantità μ rappresenta sia la larghezza di banda di ogni filtro, che la separazione tra i picchi (corrispondenti alle frequenze di risonanza) di filtri tra loro vicini, in modo che tutto l'intervallo di frequenze dato sia coperto. Il segnale di output g(t) si ottiene quindi dalla combinazione lineare
formula, [25]
dove il peso Ak è il guadagno del k-esimo amplificatore. Il dispositivo funziona in maniera analoga a processi fotografici quali l'olografia. In primo luogo si misura la potenza trasmessa da ogni filtro durante il passaggio del segnale f(t); ciò corrisponde alla formazione di un'immagine latente. Quindi si regolano i guadagni Ak in modo da rispecchiare la potenza di ciascun filtro; ciò corrisponde allo sviluppo fotografico.
In termini matematici, tale processo si può formulare nel modo seguente. Riscriviamo la risposta globale del dispositivo olofonico come
formula. [26]
Ne segue che M(T) = ∑kAkRk(Τ), per cui la variazione della risposta del dispositivo è semplicemente
formula, [27]
e la variazione di Ak è data dall'integrale
formula, [28]
in cui À è una costante. Dunque ∆Ak è proporzionale alla media pesata sul tempo del prodotto tra i segnali di input e di output del k-esimo filtro: questa è chiaramente la potenza trasmessa dal k-esimo filtro, e viene assegnato un peso maggiore agli eventi più recenti.
Nel limite in cui il valore di JL (cioè la larghezza di banda e la separazione tra i filtri) è piccolo, si dimostra facilmente che
formula, [29]
cioè che la variazione della risposta è in sostanza la funzione di auto correlazione, pesata col tempo, del segnale registrato f(t). Ne segue che se la durata dif è breve rispetto a μ-1, possiamo trascurare il termine esponenziale nell'integrando, mentre se è molto più lunga, si può ignorare la prima parte del segnale. Chiaramente μ-1 fissa un limite superiore alla lunghezza del segnale che si può registrare. Consideriamo ora la situazione in cui all'inizio tutti i guadagni dei filtri sono zero, cosicché M(T) ≡ 0, e si registra un segnale f. Un successivo segnale di input f' genererà un segnale di output g' = λ (f ·fr) *f'. In generale si tratterà solo di una debole eco dii'. Se peròfè un segnale complicato, e i' ne è un estratto, si può dimostrare che g' (t)∝f(t - θ), dove e è un certo intervallo di tempo fissato. In altri termini il segnale di output g' (t) è approssimativamente una continuazione del segnale registrato f(t) dal momento in cui scompare l"indizio' i'(t). Questo è l'effetto di completamento dei pattern temporali: il dispositivo olofonico può svolgere le funzioni di memoria indirizzabile a partire dal contenuto. Inoltre, come hanno notato Willshaw e Longuet-Higgins, l'operazione di richiamo di un segnale registrato mediante la presentazione di un suo estratto è analoga alla presenza di immagini virtuali nell'olografia. Tali immagini vengono prodotte quando si illuminano due oggetti con una sorgente di luce coerente, e i fronti d'onda diffusi si combinano in modo da produrre una figura di interferenza su una lastra fotografica. Se, in seguito, si rimuove uno degli oggetti, si illumina di nuovo l'altro oggetto mediante la stessa sorgente, e lo si visualizza attraverso la figura di interferenza, oltre all'oggetto realmente presente si vede l'immagine (virtuale) di quello assente. Nel caso temporale, il segnale registratofrappresenta entrambi gli oggetti, mentrei' corrisponde all'oggetto che non viene rimosso durante la seconda visualizzazione. Tuttavia, per i vincoli imposti dalla causalità,f' può evocare solo porzioni difche sono temporalmente successive.
Willshaw e Longuet-Higgins hanno anche affrontato il problema del possibile utilizzo dei dispositivi olofonici nel riconoscimento dei pattern temporali. Supponiamo che sia f che i' siano segnali 'rumorosi', senza alcuna periodicità, e che il nostro problema sia quello di riconoscere i' all'interno del segnale f, di cui esso è un estratto. In pratica, al tempo t = O, si registra i' seguito immediatamente da un forte impulso. Si può dimostrare che M(T) = λδ(T)+ λ exp(-2μτ)f'(-τ), per cui
formula. [30]
Il primo termine nell'output del dispositivo olofonico non riveste interesse, si tratta semplicemente di una ripetizione di f stesso. Il secondo termine è invece una correlazione incrociata, pesata sul tempo, di f ed f', e fornisce un notevole contributo al segnale di output ogni volta che l'ultimo segmento ricevuto di f coincide con f'. In questo caso il dispositivo emette un impulso. Questa proprietà di rivelazione è esattamente analoga all'utilizzo dell'olografia per il riconoscimento di pattern spaziali. Infine, Willshaw e Longuet-Higgins hanno studiato l'entità del rumore che accompagna la riproduzione di un messaggio registrato, indotta da un indizio tratto dal messaggio stesso. Per affrontare questo problema gli autori hanno introdotto un formalismo discreto, al posto di quello continuo che abbiamo descritto, nel modo seguente. Supponiamo che tutti i segnali siano abbastanza brevi da permetterci di trascurare il termine esponenziale. Riscriviamo f(t) come fi, con i che varia tra l e N, e ipotizziamo per comodità che fi sia periodica con periodo N. Supponiamo che fi possa assumere solo i valori ± l. Allora f ed f' si potranno rappresentare mediante i vettori N-dimensionalif = [fì1,f2, ... ,fN] e f'=[f'1,f'2, ... ,f'M,0, ... ,0], rispettivamente, con M<N. Per tempi t successivi alla fine dello stimolo di indizio i' l'output g(t), che nel formalismo discreto indicheremo con gi, si può scrivere come
formula [31]
essendo
formula. [32]
La somma a secondo membro di questa equazione comprende N termini, uno dei quali (con coefficiente C0 = M, in corrispondenza di i = j) si potrebbe ritenere dominante. Ogni altro coefficiente α-i' però, è la somma di M elementi, ognuno dei quali vale ±l con uguale probabilità (sefe/, sono sufficientemente casuali). La varianza di questi coefficienti vale (N -l)M, mentre quella di C0 è M². Il rapporto segnale-rumore è perciò M²/ (N - l )M, che si riduce a M/N se N è grande. Questo ragionamento euristico fa pensare che il rapporto segnale-rumore sia approssimativamente uguale alla durata di /' divisa per quella di f, per segnali lunghi. Le simulazioni al computer confermano queste ipotesi. Si potrebbe quindi concludere che i dispositivi olofonici possano fungere da memorie indirizzabili a partire dal contenuto, anche se tali memorie risultano abbastanza rumorose. D'altra parte, per il riconoscimento dei pattern temporali il rapporto segnale-rumore è molto più favorevole.
Il dispositivo olofonico resta un contributo importante allo studio delle memorie indirizzabili a partire dal contenuto e dei dispositivi distribuiti per il riconoscimento di pattem. Si è trattato forse del primo studio che ha fornito una teoria semiquantitativa degli effetti del rumore nella memorizzazione e nel richiamo di pattern, oltre che nel riconoscimento di pattern in un'architettura parallela e distribuita.
Correlogrammi
L'analogia tra i dispositivi olofonici e gli ologrammi ha portato Longuet-Higgins e i suoi studenti a effettuare anche uno studio della memoria associativa, sul modello di Taylor e Steinbuch (Longuet-Higgins et al., 1970).
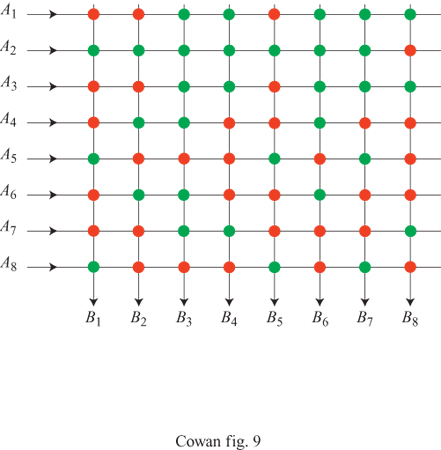
La figura (fig. 9) illustra la rete elaborata da questi autori. La relazione tra questa rete e quelle di Taylor e Steinbuch (in particolare le matrici di apprendimento) è evidente. La rete possiede V linee A di input, R linee B di output, e VR interruttori. Supponiamo che un tipico pattern A corrisponda all'attivazione di n linee A scelte a caso, e un tipico pattem B a quella di m linee B scelte a caso. Ci saranno dunque, in totale, nm interruttori attivati. Supponiamo che questi vengano accesi, se non lo erano già. Dopo che K coppie di pattern sono state associate in questo modo, una frazione p degli interruttori risulterà accesa. Se i pattern sono casuali, si potrà approssimare p con
formula. [33]
Richiamare un pattern è semplice. Si presenta un pattem A, in modo che si attivino n interruttori di ogni linea B appartenente al pattern B associato (le linee appartenenti al pattern B sono attive per ipotesi). Però anche le linee B che non appartengono al pattern B associato saranno attivate. La probabilità che una di queste linee B venga attivata attraverso tutte le sue n intersezioni con le linee A attivate è semplicemente pn. Se quindi la soglia di attivazione di ogni linea B è n, non si attiveranno solo le linee che comprendono il pattem B associato, ma probabilmente anche altre mpn linee. Se questo numero è minore di uno, non ci saranno errori, perciò il valore critico è
mpn = 1. [34]
Per specificare un singolo pattern B occorre un numero di bit pari
formula [35]
se dunque si possono richiamare accuratamente K pattern B, la quantità di informazione immagazzinata disponibile è
Klog₂ (β) βKmlog2R [36]
bit. Combinando queste equazioni otteniamo un'espressione per il numero di bit immagazzinati nella rete:
formula. [37]
Questa quantità raggiunge il valore massimo, pari a 0,693 VR, per p = 0, 5. In questo caso n ≈log2R, cioè, affinché la rete sia un deposito efficiente di informazione, il numero di linee per ogni pattern A deve essere piccolo. Questo è un primo esempio del tipo di ragionamento che porta alla codifica sparsa. Willshaw e Longuet-Higgins hanno successivamente dimostrato che si possono far funzionare le memorie associative in modo accurato anche se i pattern A sono rumorosi, e anche se la rete è danneggiata, aumentando n, e memorizzando quindi un minor numero di associazioni. La conseguente, marcata diminuzione della densità di informazione immagazzinata è coerente con i teoremi di Winograd-Cowan che abbiamo descritto in precedenza.
Codifica sparsa
L'analisi svolta mostra come la necessità di richiamare pattem senza errori ponga un severo limite al numero di linee per ogni pattem A utilizzabili per codificare informazione sugli elementi da memorizzare. Se vi sono V linee di input, questo vuoI dire che vi sono al più
formula [38]
pattem A diversi, o descrittori, che si possono immagazzinare. Poiché n deve essere piccolo, il solo modo per aumentare il numero possibile di descrittori, cioè il vocabolario, consiste nell' aumentare V. Ma questo ha senso? Già nel 1965 apparve un articolo, scritto da P.H. Greene, che trattava, in stretto parallelismo con l'analisi di Willshaw-Higgins, questo problema e quello del meccanismo di richiamo (Greene, 1965). L'articolo di Greene è particolarmente interessante in quanto, sebbene ciò non risulti chiaro a una prima lettura, dal punto di vista concettuale è praticamente identico al ben noto lavoro di D. Marr (1969), che a sua volta è strettamente collegato all'analisi di Willshaw e Longuet-Higgins.
Riassumeremo brevemente il contributo di Greene. Egli basava la sua analisi su un lavoro precedente di C.N. Mooers (1949) sulla memorizzazione e il richiamo dell'informazione su un mazzo di schede perforate. Il metodo è ben noto: si praticano dei fori in un certo numero di posizioni su ogni scheda del mazzo. Questi fori (o la loro assenza) realizzano delle descrizioni booleane espresse da una stringa di variabili Xi (con i che va da 1 a N), le quali possono essere vere o false a seconda che la stringa rientri o meno in diverse categorie: per esempio, persone di sesso femminile, sposate, caucasiche, e così via. Grazie ai fori, questi mazzi di schede si possono ordinare in modo automatico, con procedimenti meccanici o elettrici. Consideriamo ora l'aspetto combinatorio. Se vi sono N diversi fori, 2N pattem binari sono utilizzabili come descrittori. Supponiamo che a ogni descrittore siano assegnate D categorie, e che non vi siano sovrapposizioni. Ci sono quindi M = N/D sottocampi possibili, e il vocabolario è costituito da V = M . 2D descrittori indipendenti. Se dunque D = N, V = 2N; se D=N/2, V =2N/2+1; e se D= l, V =2N. Il contributo di Mooers (che l'autore brevettò con il nome di Zatocoding) consiste nel migliorare queste caratteristiche utilizzando come descrittori sottocampi sovrapposti a caso. Questa procedura genera un vocabolario di
formula [39]
descrittori indipendenti. Supponiamo ora che vi siano in media K descrittori per ogni scheda. Il numero massimo totale di descrittori è quindi
formula. [40]
Si può dimostrare che il numero totale di posizioni dove può essere praticato un foro, usate per formare i K descrittori, è
formula [41]
dove X = KD e P è la probabilità che una qualsiasi delle N posizioni sia in uno dei K descrittori. Questo numero raggiunge il valore massimo, G ≈ N /2, per X ≈ Nln2, con P ≈ 1/2. Questo è un risultato importante. Mooers ne dimostrò infatti la connessione con la teoria dell'informazione: la massima capacità si ottiene quando ogni posizione sulla scheda può trasmettere un bit di informazione, e questo succede quando si usa circa la metà delle posizioni. Questa conclusione, naturalmente, è simile a quella raggiunta più tardi da Longuet-Higgins e collaboratori seguendo un ragionamento leggermente diverso.
Finora abbiamo considerato il processo di codifica. Che cosa possiamo dire di quello di decodifica, cioè del recupero delle informazioni dal mazzo di schede? Supponiamo di avere R schede e che, come prima, sia necessaria la presenza congiunta di n descrittori per selezionare una scheda. Allora si possono decodificare in modo univoco circa 2nD schede diverse, cioè R ≈2nD, O ancora:
formula [ 42]
Inoltre, la frazione di schede selezionate per errore non supera la quantità
formula [43]
Tale quantità si può rendere piccola a piacimento variando G, N o n. Nel caso ottimale, in cui G≈N /2, essa risulta minore di 2-n.
Ne segue che, dato R, si dovrebbe prima scegliere D, e poi fissare un valore di N abbastanza grande da generare un numero sufficiente di descrittori, in media K per scheda. Fissiamo, per esempio, n = 3 eR = 4000. Allora D ≈log24000/n≈4. Se scegliamo N = 40, X ≈ 40 ln 2≈28, e quindi K =X /D≈7. Ciò dimostra che la codifica a sovrapposizione casuale è vantaggiosa quando il numero di descrittori è elevato, e ognuno di essi si presenta con frequenza relativamente bassa. Questo è un altro argomento a favore della codifica sparsa. Invece il metodo non è vantaggioso nel caso in cui vi siano uno o due descrittori su tutte le schede, oltre agli altri descrittori. Per indicare questi due descrittori sarebbe più conveniente utilizzare in ogni scheda un campo fisso a posizione singola, invece delle D posizioni diverse richieste dalla codifica a sovrapposizione casuale. Questo è in sostanza l'argomento a favore delle 'cellule della nonna' rispetto alla codifica distribuita sparsa.
Greene fece seguire alla sua analisi alcune proposte per un'implementazione su reti neurali. Facciamo corrispondere ogni scheda a uno degli R neuroni di output, e immaginiamo che vi siano N linee di input. Selezionando a caso gruppi costituiti da D linee di input si genereranno V linee secondarie, ognuna delle quali è connessa a tutti i neuroni di output. Supponiamo che tutti questi neuroni abbiano una soglia di eccitazione comune pari a n unità, e che, attraverso un processo di condizionamento classico, tra tali neuroni si formino delle sinapsi eccitatorie, in media K per neurone. Come notò Greene, si può fare in modo che tale procedura, che naturalmente è alla base dell'architettura standard per le reti con funzione di memorie associative, corrisponda alla selezione di una scheda tramite l'attivazione di n descrittori su K. Greene non realizzò questo schema in termini circuitali, né sviluppò in dettaglio i diversi meccanismi inibitori che aveva riconosciuto necessari per controllare il funzionamento del sistema. Va sottolineato che tutti questi meccanismi furono realizzati da Marr (1969) in un sistema praticamente identico da lui proposto (a quanto pare, senza conoscere il lavoro di Greene) come modello circuitale del cervelletto e dell'ippocampo.
Le reti di Hopfield
Nel lavoro di Il Hopfield (1982; 1984) troviamo un approccio completamente diverso alla memoria associativa. Egli dimostrò l'analogia formale tra una rete neurale con connessioni simmetriche, ora detta rete di Hopfield, e un materiale scoperto nel decennio precedente, chiamato vetro di spin (Sherrington e Kirkpatrick, 1975). Tale sistema consiste in una miscela casuale di spin con interazioni sia ferromagnetiche che antiferromagnetiche, che non manifesta una magnetizzazione netta. l vetri di spin godono di proprietà molto interessanti: in particolare, al loro interno si possono immagazzinare pattern disordinati di spin variando opportunamente la temperatura e le interazioni tra gli spino Le reti di Hopfield godono di proprietà simili, e rivestono un interesse considerevole come reti neurali, in particolare per quanto riguarda la memorizzazione.
L'idea fondamentale è semplice: chiamiamo βi lo stato (o lo spin) dell'i-esimo elemento, pari a + l se l'elemento è attivo, e a -l altrimenti. Consideriamo la coppia di elementi con indici i e j; βiβj rappresenta allora lo stato della coppia, e vale + 1 se i due elementi sono nello stesso stato, e - 1 altrimenti. Supponiamo ora che l'intensità, o peso, delle connessioni tra i due elementi sia wij = wji' Si ha allora Wijβiβj = wij se i due elementi sono nello stesso stato; altrimenti Wijβiβj = -wij. Sommiamo ora i contributi di tutte le coppie di elementi connessi della rete e cambiamone il segno; formiamo cioè la somma E = - ∑ Wijβiβj su tutte le coppie diverse di elementi (i,j). Se tutte le wij sono positive (sinapsi eccitatorie), il valore minimo di E si ottiene quando tutte le coppie (i,j) sono nello stesso stato. Se tutte le wij sono negative (sinapsi inibitorie), il valore minimo di E si ha invece quando tutte le coppie sono in stati opposti. Queste due configurazioni corrispondono rispettivamente al comportamento dei materiali ferromagnetici ed antiferromagnetici, in cui E è l'energia del sistema, e βi = ±l corrisponde all'orientazione (su o giù) dell'i-esimo spino In un vetro di spin, però, le wij (che sono simmetriche) hanno valori casuali, e si ha all'incirca lo stesso numero di interazioni ferromagnetiche e antiferromagnetiche, cosicché il minimo dell' energia si ottiene per una miscela di zone localmente ferromagnetiche e antiferromagnetiche. Perciò, a differenza del caso ferromagnetico e antiferromagnetico, in cui esiste una sola configurazione stabile, per un vetro di spin ne esistono molte. Approssimativamente possiamo dire che, dati N spin, vi sono non più di M ≤ N configurazioni stabili. Indichiamo con βi(S), con s = 1,2, ... ,M, lo stato dell'i-esimo elemento in una di tali configurazioni. Hopfield ha dimostrato che, se i pesi wij delle connessioni sono proporzionali ai prodotti βi(S)βj(s) sommati su tutte le M configurazioni stabili, cioè se wij = ∑sβi(s)βj(s), allora βi tendβ a βi(s): la rete raggiunge una delle configurazioni stabili. E importante notare che in una rete di N elementi, ognuno dei quali si possa trovare in due stati (in questo caso ±l), ci sono 2N configurazioni possibili. Nello schema di Hopfield questo insieme viene suddiviso in M sotto insiemi, o gnuno dei quali corrisponde a una configurazione stabile, cosicché qualsiasi configurazione iniziale (βj, β2, ... ,βN) porterà la rete nella configurazione stabile più vicina (ββ (s'),β;(s'), ... ,ββ(s')). Perciò in una rete di Hopfield, malgrado le fluttuazioni casuali, si possono immagazzinare e richiamare circa M configurazioni di spin.
Si può dimostrare che, se si richiede un funzionamento esente da errori, M vale al più N j4log₂N, mentre se si accetta un tasso di errore dell' l÷ 2%, M vale circa 0,14N. La tabella (tab. I) mostra la relazione tra N, M =N j4log₂N e M = 0, 14N. Le reti di Hopfield rappresentano, sul piano concettuale, un importante passo in avanti della teoria delle reti neurali: il principio su cui si basano, cioè l'immagazzinamento dell'informazione in configurazioni dinamicamente stabili (gli attrattori stazionari) è profondo. Una notevole applicazione recente di questo principio è contenuta nel lavoro di DJ. Amit e collaboratori (Amit et al., 1994) su un modello della memoria attiva a breve termine.
Rappresentazioni unarie e distribuite
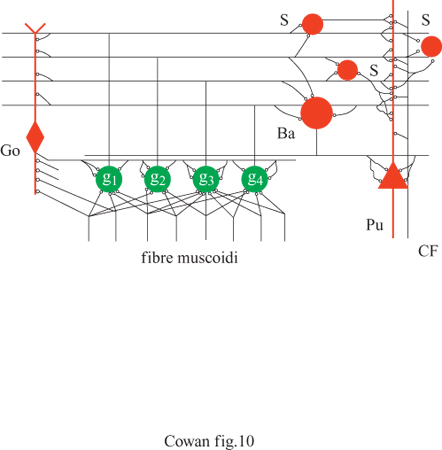
Come si rapportano le capacità di immagazzinamento e richiamo di informazione delle reti di Hopfield con quelle delle matrici di apprendimento e delle ACAM? A questa domanda hanno risposto dettagliatamente E.E. Baum e collaboratori (1988). Questi autori hanno dimostrato che, in assenza di malfunzionamenti o guasti, il modo più efficiente per immagazzinare informazione si ottiene utilizzando 'cellule della nonna', una per ogni informazione da memorizzare. In presenza di malfunzionamenti o guasti, però, le 'cellule della nonna' compiono troppi errori, e l'informazione si deve immagazzinare in modo distribuito, secondo la proposta di Winograd e Cowan. Si trova che uno schema particolarmente efficiente si avvicina molto al modello del cervelletto come ACAM proposto da Marr. In questo schema (fig. 10), supponiamo che vi siano N fibre muscose di input, N cellule di Purkinje di output e G cellule granulari. Chiamiamo s la frazione di fibre muscose attive in un qualsiasi istante, e c il numero corrispondente di cellule granulari attive (G è approssimativamente uguale al numero di modi in cui si possono scegliere c linee in un insieme di N linee). Baum e collaboratori hanno dimostrato che il numero di informazioni memorizzabili e richiamabili con un tasso di errore del 5%, in un sistema di questo tipo, è limitato dalla funzione 0,05 G / s (l - s). Qui s è una misura di quanto sia sparsa l'attività delle fibre muscoidi. Chiaramente il dispositivo di memoria è più efficiente se le linee di input sono in gran parte attivate o inattivate, proprio come nello schema originale di von Neumann (1956). Per facilitare il confronto con le reti di Hopfield, prendiamo c = 3. La tabella (tab. 2) mostra la capacità di questo dispositivo per s=0,06 e s=0,008. È chiaro che in un sistema di questo genere si possono immagazzinare e richiamare molti più pattern, rispetto a una semplice rete di Hopfield con circa G elementi. D'altra parte tecniche di questo tipo, volte alla creazione di una rappresentazione sparsa, possono aumentare notevolmente anche la capacità delle reti di Hopfield. Connessioni tra occhi e cervello Il cervello è un 'computer' biologico immensamente complicato, con neuroni e circuiti altamente specializzati. I neuroni sono interconnessi con elevata precisione in molte regioni del cervello, se non in tutte. Da dove viene una simile organizzazione? Consideriamo, per esempio, la struttura delle connessioni tra retina e corteccia. Queste connessioni sono topo grafiche, cioè si può dire che esse formano mappe, in cui punti vicini sulla retina vengono posti in corrispondenza con punti vicini nella corteccia. Come si sviluppano queste mappe? Inizialmente lungo questo percorso c'è un disordine considerevole: le cellule gangliari della retina si mettono in contatto con un gran numero di neuroni molto sparsi. Giunto alla maturità, però, il percorso visivo mostra un grado elevato di ordine topografico. In che modo è organizzata questa mappa? Un modello per la formazione delle mappe Nel seguito illustreremo le idee alla base di molti dei modelli proposti per rispondere alle domande poste in precedenza. Seguiremo la formulazione di A. Hiiussler e C. von der Malsburg (1983), basata a sua volta su lavori precedenti di Willshaw e von der Malsburg (1976). Chiamiamo r l'attività in una fila di cellule retiniche, e t l'attività corrispondente in una fila di cellule corti cali. Sia W la matrice dei pesi dei contatti sinaptici tra le fibre retiniche e le cellule corticali. Allora l'attività corticale si può esprimere in termini dell'attività retinica mediante la semplice equazione lineare:
t= Wr [44]
e la variazione di W è espressa dall'equazione matriciale di aggiornamento:
formula [45]
dove l rappresenta una matrice composta da tutti l. Questo è un sistema di equazioni cubiche in N² variabili. La costante ex rappresenta il tasso di formazione delle sinapsi, e la funzione C(W) il tasso di cooperazione tra sinapsi vicine. L'operatore lineare B è dato da:
formula. [46]
Si può notare che il primo termine nell'equazione [45] spinge Wa convergere allo stato omogeneo W = 1 (tutti i pesi uguali a 1), con un tasso ex. Il secondo termine spinge W a convergere ad uno stato in cui c'è un peso uguale a N (il numero di neuroni retinici e corticali) in ogni riga e colonna della matrice dei pesi W, e tutti gli altri pesi sono uguali a zero. Queste configurazioni corrispondono a mappe biunivoche. La maggior parte di tali configurazioni è però instabile. Chiaramente è la combinazione dei due termini, insieme alle condizioni iniziali, che dà luogo a mappe topografiche stabili.
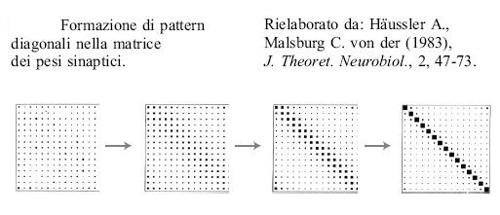
Si può analizzare ulteriormente questo processo utilizzando la teoria delle biforcazioni. Come hanno notato A Hiiussler e C. von der Malsburg, i risultati ottenuti sono simili a quelli di AM. Turing (1952). Il punto chiave è che mediante una scelta opportuna del parametro rx si possono far crescere solo i pattem diagonali nella matrice dei pesi (che corrispondono alle mappe topo grafiche), deprimendo tutti gli altri. La figura (fig. 11) illustra questo processo.
Mappe di caratteristiche (feature maps) e reti elastiche
Un approccio più astratto, ma sempre strettamente legato a quanto detto sopra, fu introdotto da T. Kohonen (1982). Una variante di tale approccio, alla base delle cosiddette reti elastiche, fu proposta da R.M. Durbin e D. Willshaw (1987), e suscitò a sua volta ricerche successive da parte di Durbin e G. Mitchinson (1990) sul problema della generazione delle mappe. In modo indipendente, K. Obermayer e collaboratori (Obermayer et al., 1990) pubblicarono uno studio simile. In quanto segue descriveremo in breve alcune di queste ricerche.
Modelli alla Turing. - La connessione tra l'apprendimento hebbiano competitivo e il lavoro di Turing sulla formazione dei pattem, implicita nel lavoro di Hiiussler-von der Malsburg, si trova anche nei lavori di N.V. Swindale (1980; 1982). Il primo modello di Swindale tratta della formazione delle strisce di dominanza oculare nelle mappe binoculari sovrapposte del campo visivo dei vertebrati superiori. Quali interazioni neuronali generano questi pattern di strisce? Swindale propose le seguenti regole: due fibre vicine che provengono dallo stesso occhio cooperano, mentre quelle che provengono da occhi diversi competono; se due fibre non sono vicine, le regole precedenti si invertono. In altri termini, queste regole equivalgono alla presenza di eccitazione e inibizione laterale, proprio come nel modello di Wilson e Cowan. Un'analisi matematica simile a quella di Hiiussler e von der Malsburg mostra che questo insieme di regole porta alla formazione di strisce su una superficie bidimensionale, e si può quindi utilizzare come modello per la formazione delle colonne di dominanza oculare. Nel suo secondo articolo, Swindale applicò queste regole alla formazione della sensibilità e della capacità di adattamento rispetto all'orientazione che i neuroni della corteccia visiva mostrano rispetto a linee e contorni presenti nel campo visivo. Una decina di anni dopo S. Tanaka (1989) e, indipendentemente, Cowan e A.E. Friedman (1991) hanno dimostrato che si possono riprodurre i risultati di Swindale attraverso un semplice modello di spin.
Mappe di caratteristiche. - Kohonen riformulò il modello di Willshaw-von der Malsburg in modo da mettere in evidenza il ruolo delle correlazioni tra vicini. Pensiamo la matrice W che compare nell'equazione [44] come una colonna di vettori di pesi Wi, con i = l, ... ,N. Kohonen osservò che la caratteristica essenziale di qualsiasi mappa autoorganizzata consiste nel fatto che i vettori dei pesi si adattino in modo da fornire una corrispondenza (match) con i vettori di input r(t).
L'equazione di adattamento (o aggiornamento) adeguata al caso è
formula [47]
dove α(t) è una funzione del tempo, e Ne(t) un 'intorno topologico' della posizione c della migliore corrispondenza con r(t). Di solito sia α(t) che Ne(t) sono funzioni lentamente decrescenti del tempo. Inoltre, se la mappa è bidimensionale, si può scegliere l'intorno Ne(t) di forma quadrata o esagonale. Si trova che il processo di formazione delle mappe è duplice. Alla rapida formazione di una mappa iniziale (in cui sia α(t) che Ne(t) sono grandi) segue una lenta convergenza all'equilibrio in cui sia α(t) che Ne(t) sono piccole e decrescenti. Per quest'ultimo processo serve di solito un tempo 10÷100 volte più lungo. L'unità corticale che realizza la migliore corrispondenza con i dati retinici di input viene trovata per prima, e quindi si ha una corrispondenza migliorata per questa unità e per quelle vicine. L'effetto complessivo è che la distribuzione dei vettori dei pesi P( Wi) converge essenzialmente fino a stabilire la corrispondenza con la distribuzione di probabilità dei dati di input P(r). Inoltre i Wi vengono ordinati rispetto alla loro reciproca somiglianza.
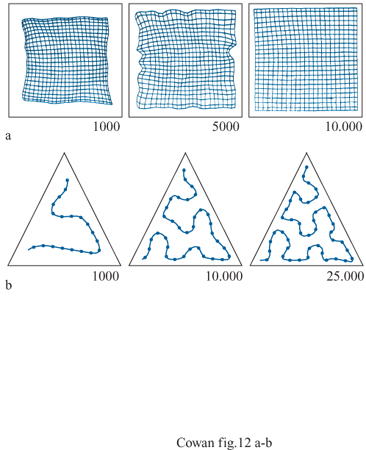
Una conseguenza importante è che caratteristiche simili in input si pongono in corrispondenza con unità vicine. Questo fatto viene indicato come creazione di una mappa di caratteristiche (jeature mapping). Poiché le interazioni locali tendono a preservare la continuità delle sequenze dei vettori Wi, si possono ottenere effetti diversi a seconda della dimensionalità e della varianza di P(r). La figura (fig. 12), per esempio, mostra stadi di sviluppo successivi della P( Wi) in risposta a vettori di input bidimensionali r distribuiti in modo uniforme rispettivamente su un quadrato e su un triangolo, campionati in modo casuale da un insieme di unità di elaborazione che formano una rete bidimensionale (nel primo caso) e unidimensionale (nel secondo caso).
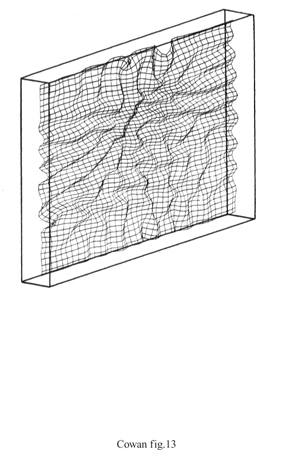
È chiaro che le dimensioni dell'input sono tra le caratteristiche rappresentate nelle mappe di caratteristiche. Ciò si può osservare chiaramente nei casi in cui la dimensionalità dell'input è maggiore di quella dettata dalla topologia della rete. La figura (fig. 13) mostra un esempio di tale circostanza. Qui una distribuzione tridimensionale è posta in corrispondenza con una topologia rettangolare bidimensionale. Il risultato è sorprendente: se la varianza nella terza dimensione di input è abbastanza grande, P(w;) diventa ondulata, la mappa retinotopica si distorce, e si sviluppano delle strisce. Ne emerge una possibile spiegazione elegante della formazione delle strisce di dominanza oculare.
Reti elastiche. - In una rete elastica, una mappa topografica si considera come una superficie, o una rete, elastica (con i bordi fissati). L'algoritmo prevede che le unità siano connesse agli input, e che unità vicine siano connesse tra loro. L'aggiornamento delle unità viene effettuato cercando di avvicinarle agli input, mantenendo la condizione che unità vicine si comportino in maniera simile. Tale procedura è strettamente connessa alle mappe di caratteristiche. Durbin e Mitchinson hanno proposto l'ipotesi che i principi alla base delle reti elastiche abbiano un ruolo nella formazione delle mappe corticali, e che lo sviluppo di tali mappe avvenga in modo da minimizzare la lunghezza complessiva della rete di connessioni. Gli stessi autori hanno osservato, però, che l'estensione di questa procedura di minimizzazione a mappe di dati multidimensionali sulla corteccia, bidimensionale, sarebbe impraticabile dal punto di vista computazionale, e quindi hanno utilizzato in sostanza una mappa di caratteristiche, con un metodo diverso per imporre la continuità. Indichiamo con y = (x,y, r, Θ) un vettore di input che codifica la posizione e la preferenza rispetto all'orientazione di un campo recettivo corticale, e con x un vettore scelto a caso in questo spazio quadri dimensionale; si assume che x e y siano distribuite uniformemente in [0,1], che e abbia distribuzione uniforme in [0,π/2] e che r sia pari a 0,17. Per ogni vettore di input x si calcola la risposta corticale, utilizzando campi recettivi gaussiani, e poi la si normalizza. La risposta della j-esima unità corticale è quindi
formula, [48]
dove K è l'ampiezza del campo recettivo di ciascuna unità, e la relativa equazione per l'aggiornamento è
formula, [49]
dove l'indice di sommatoria kvaria nell'insieme N dei primi vicini dell'unità j nella matrice corticale. È chiaro che questo schema è molto simile alla mappa di caratteristiche, in quanto utilizza l'apprendimento competitivo hebbiano insieme a un vincolo che favorisce la continuità. La figura (fig. 14) mostra la mappa risultante. Si può osservare che vi sono distorsioni della topografia retinica, e che tali distorsioni sono connesse con proprietà funzionali della mappa.
Computazione neuronale
I perceptron e gli ADALINE
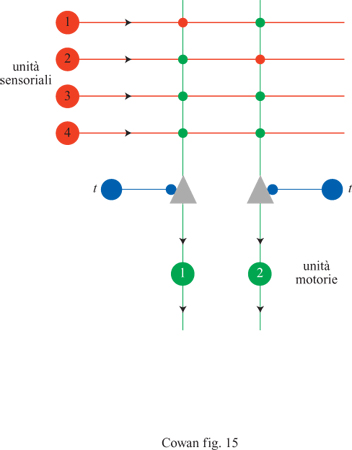
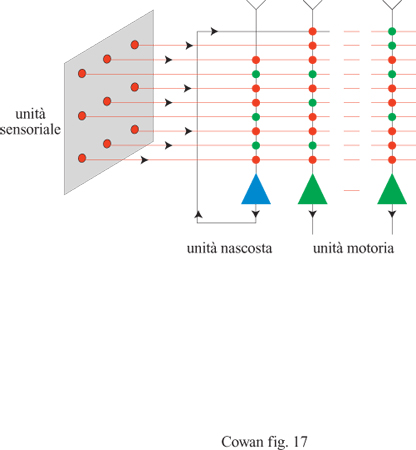
Circa quindici anni dopo la pubblicazione dell'articolo di McCulloch e Pitts, F. Rosenblatt (1958) propose un importante approccio al riconoscimento dei pattern con il suo lavoro sul perceptron. La figura (fig. 15) mostra l'architettura di un tipico perceptron elementare, che consiste in un insieme di recettori connessi, attraverso un solo strato di neuroni MP, a un insieme di effettori. All'inizio, le intensità delle connessioni (o sinapsi) della rete sono fissate a valori arbitrari, e dunque la stimolazione genera risposte arbitrarie. Per ottenere dalla rete le risposte desiderate bisogna modificare i pesi sinaptici. Rosenblatt ottenne tale scopo utilizzando la seguente procedura di addestramento. Anzitutto si annota la risposta di un'unità MP a uno stimolo dato. Alcune risposte saranno corrette (corrisponderanno cioè a quelle desiderate), mentre altre saranno sbagliate. Quindi si modificano i pesi seguendo il criterio di non effettuare nessun cambiamento se l'unità ha fornito la risposta giusta. Se la risposta è sbagliata, si aumenta il peso di tutte le sinapsi attivate (se l'unità doveva essere attivata) o (nel caso opposto) lo si diminuisce. Tale procedura si ripete per tutte le possibili coppie stimolo-risposta desiderata. Si può dimostrare che, dopo un numero finito di presentazioni delle coppie stimolo-risposta, i pesi convergono a un insieme di valori che rappresentano l'elaborazione o la classificazione contenuta in questi esempi, qualunque essa sia.
Poco tempo dopo i primi articoli di Rosenblatt apparvero delle varianti del perceptron inventate da B. Widrow e M.E. Hoff (1960) e denominate ADALINE (ADAptive Llnear NEuron, neurone lineare adattivo). La sola differenza tra i perceptron e gli ADALlNE risiede nella procedura di addestramento.
Nel seguito useremo una notazione vettoriale, per cui x indica un vettore colonna a N componenti, e xT è il suo trasposto, cioè un vettore riga. Chiamiamo W la matrice dei pesi, e(x) = Wx l'eccitazione indotta da un dato pattern di stimolo x nelle unità recettrici e a(x) il pattern di attivazione che lo stimolo dovrebbe innescare. Poniamo ε(x) = = a(x) - e(x). Un ADALINE fa in modo di minimizzare la funzione di errore E= (1/2)ε(x)Tε(x) mediante il metodo di apprendimento basato sulla discesa di gradiente. A tale scopo i pesi vengono modificati secondo la regola
formula, [50]
dove ΔW indica il cambiamento di W, e x lo stato dei recettori (ognuno uguale a ±l). Questa regola implica che Wik aumenta se Xi è attiva (uguale a +1), con ek(x) minore di ak(x); decresce se Xi è attiva con ek(x) maggiore di ak(x). Se Xi è quiescente (uguale a -1), avviene il contrario. Vedremo che questa regola ha una stretta corrispondenza con quella usata nel perceptron, poiché se un'unità MP non viene attivata da un dato recettore, quando invece dovrebbe esserlo, il peso della sinapsi coinvolta aumenta (e viceversa). In molte situazioni le prestazioni degli ADALINE sono simili a quelle dei perceptron.
Limitazioni dei perceptron elementari e degli ADALINE
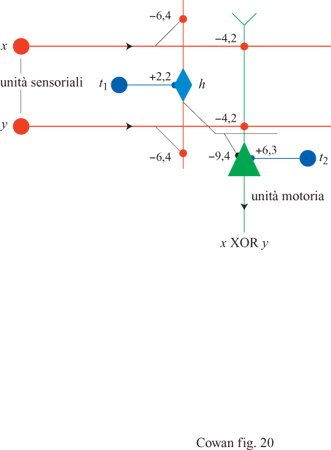
Le capacità dei perceptron elementari e degli ADALINE hanno comunque dei limiti. M. Minskye S. Papert (1969) dimostrarono che i perceptron elementari non riescono a distinguere immagini semplici, come una T o una C. La difficoltà risiede nella natura del neurone MP. Come abbiamo già visto, unità semplici di questo tipo possono valutare solo funzioni logiche semplici, come X AND y, X OR y, e NOT x. La funzione X XOR y e la sua negazione richiedono però diverse unità MP. Il motivo è semplicemente che X XOR y = (x AND NOT y) OR (y AND NOT x).
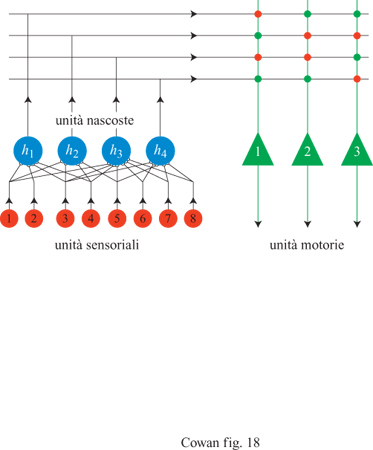
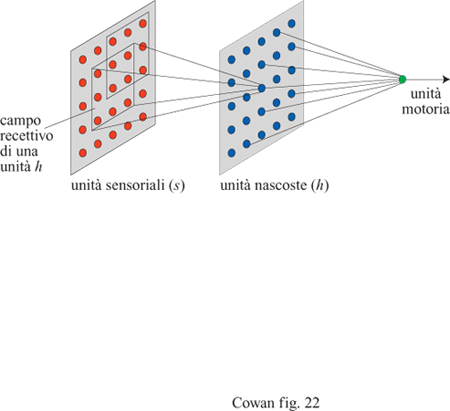
Questo è un peccato, perché la funzione NOT(x XORy) è universale dal punto di vista computazionale: ogni funzione si può esprimere come una stringa di (x XOR y) e NOT(x XOR y). Papert e Minsky dimostrarono che un perceptron elementare o un ADALlNE, che hanno un solo strato di unità MP, non sono universali dal punto di vista computazionale, anche se si usano connessioni modificabili. Questi autori ipotizzarono anche che non si possano addestrare le eventuali unità interne, o nascoste, in estensioni a più strati dei perceptron o, in altre parole, che il problema dell' attribuzione dei meriti (credit assignment) alle unità nascoste sia insolubile. Invece si è trovato che le limitazioni dei perceptron semplici e degli ADALlNE si possono superare utilizzando architetture più complesse, che incorporano unità nascoste con connessioni modificabili. Descriveremo queste soluzioni nel seguito.
Elaborazione con reti di Hopfield
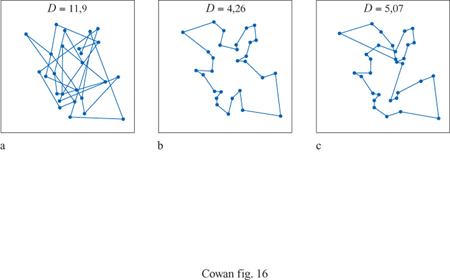
Le reti di Hopfield si sono rivelate utili nella risoluzione di problemi computazionali di ottimizzazione. Un esempio ben noto è il problema del commesso viaggiatore, in cui un commesso viaggiatore deve visitare una sola volta ogni città di un certo elenco, secondo l'ordine che minimizza la lunghezza totale del suo viaggio. Questo è un esempio di un cosiddetto problema di ottimizzazione vincolato. S. Kirkpatrick e collaboratori dimostrarono che le configurazioni di equilibrio di un vetro di spin forniscono una soluzione a questo problema (Kirkpatrick et al., 1983). In seguito Hopfield e Tank (1985) dimostrarono che anche certe reti di Hopfield riescono a trovare buone soluzioni allo stesso problema. La figura (fig. 16) mostra un esempio con 30 città. Sebbene la rete di Hopfield non riesca a individuare il percorso più breve, non sfigura nel confronto con l'algoritmo di Kernighan-Lin, uno dei migliori per la risoluzione di questo tipo di problemi. Durbin e Willshaw (1987) hanno sviluppato un'altra rete neurale, basata sul principio di una rete elastica, che riesce a trovare percorsi più brevi, e funziona meglio su problemi più complessi.
Le macchine di Boltzmann
Uno dei limiti delle reti di Hopfield risiede nella loro incapacità di trovare la migliore soluzione nei problemi di ottimizzazione vincolata. Esse possono rimanere prigioniere di minimi locali della funzione energia E, essenzialmente a causa del fatto che il loro funzionamento è deterministico, fissato da regole ben precise. Per trovare il vero minimo globale bisogna che la rete effettui, di tanto in tanto, dei salti di configurazione casuali, che aumentano il valore della funzione energia, anziché diminuirlo, permettendo così una fuga dai minimi locali. Questa è in sostanza una variante ben nota dell'algoritmo Monte Carlo. In tale algoritmo si calcola la variazione di energia ∆E prodotta da un'inversione casuale di uno degli spin della rete. Se ∆E è negativa si accetta la nuova configurazione, poiché ha un' energia minore della precedente; altrimenti la configurazione viene rigettata, cioè l'inversione dello spin viene annullato, con una probabilità che dipende da ∆E. Tale procedura, per quanto lenta, troverà alla fine il minimo globale dell'energia. G.E. Hinton e T.J. Sejnowski (1983) impiegarono l' algoritrno Monte Carlo per minimizzare l"energia' di una rete di Hopfield, utilizzando in effetti il metodo con le stesse modalità seguite da Kirkpatrick e collaboratori in problemi relativi ai vetri di spino Questi ricercatori scoprirono così un procedimento attraverso il quale la rete, che chiamarono macchina di Boltzmann, può modificare le sue connessioni in modo tale da risolvere il problema dell'attribuzione dei meriti.
Il procedimento si può descrivere nel modo seguente. Consideriamo la rete mostrata in figura (fig. 17), che è una macchina di Boltzmann, cioè una rete di Hopfield adattiva con unità nascoste, che realizza un algoritmo Monte Carlo per trovare la configurazione di unità attive e inattive che minimizza E. Come abbiamo già notato, il perceptron e l'ADALlNE non possono risolvere il problema dell'attribuzione dei meriti, cioè cambiare l'intensità delle connessioni da e verso le unità nascoste, in modo tale da migliorare le prestazioni. La macchina di Boltzmann non utilizza però semplici neuroni MP, ma neuroni con curva di attivazione sigmoide. Hinton e Sejnowski dimostrarono che con questi dispositivi si può massimizzare una misura opportuna delle prestazioni se i pesi sinaptici si modificano secondo la seguente regola. Chiamiamo Pij la probabilità media che due unità (la i-esima e laj-esima) siano attivate simultaneamente (direttamente o indirettamente) da un pattern di stimolo, e Pβ la probabilità corrispondente in assenza di stimoli. Ricordiamo che wij è il peso della connessione tra i e j. La regola per cambiare wij è molto semplice: se Pij > P'ij, si incrementa wij di una piccola costante K,; se Pij <pij, si sottrae K, da wij. Con questa regola le macchine di Boltzmann sono capaci di risolvere una serie di problemi di ottimizzazione vincolata, molti dei quali si presentano negli approcci computazionali alla visione. Apprendimento delle rappresentazioni Le macchine di Boltzmann forniscono anche una soluzione al problema dell'attribuzione dei meriti per unità nascoste, anche se nel caso particolare di reti di Hopfield adattive. La regola sopra enunciata risolve tale problema usando solo informazioni disponibili localmente. La modificazione del peso della connessione tra i e j, ∆wij, dipende solo dai pattern di attivazione delle unità i e j, e non richiede la conoscenza di ∆E. Il processo di apprendimento nella macchina di Boltzmann dipende quindi solo dalle correlazioni tra coppie di unità. Tale processo crea nella matrice dei pesi w, corrispondente allo stato stabile di energia minima, una rappresentazione distribuita delle correlazioni esistenti tra i membri dell'insieme dei pattern di input e all'interno di ciascun pattern. In altre parole, una macchina di Boltzmann può formare una rappresentazione che, alla fine, riproduce le relazioni tra le classi di eventi presenti nel suo ambiente. Essa fornisce quindi una possibile soluzione al problema di come costruire tali rappresentazioni ab initio. Più in generale, fornisce un modo per formare rappresentazioni distribuite di simboli astratti, e consente lo studio del ragionamento simbolico tramite reti neurali adattive.
Retropropagazione
La macchina di Boltzmann rappresenta un notevole progresso nell'apprendimento automatico. Tuttavia, usando una variante dell'algoritmo Monte Carlo per trovare i minimi globali, risulta molto lenta. Inoltre una macchina di Boltzmann è una rete di Hopfield, e come tale ha soltanto sinapsi simmetriche. Queste limitazioni furono superate da D.E. Rumelhart e collaboratori (Rumelhart et al., 1986), i quali realizzarono con successo l'algoritmo di correzione dell'errore basato sulla retropropagazione (backpropagation), suggerito originariamente da Rosenblatt. La figura (fig. 18) illustra la struttura della rete. Si tratta essenzialmente di un perceptron a due strati con unità sensoriali (s), unità attuatrici motorie (m) e uno strato intermedio di unità nascoste (h). Le regole per la modificazione delle connessioni derivano però da quelle dell' ADALlNE, sopra descritte. Ricordiamo che in un ADALlNE la regola per le modificazioni dei pesi si ottiene minimizzando la funzione errore E= (1/2)ε(x)Tε(x), con ε(x) = = a(x) - W x, usando la discesa di gradiente nello spazio W. Rumelhart e collaboratori mostrarono che la seguente, semplice estensione di tale regola risolve il problema dell' attribuzione dei meriti. Supponiamo che gli output delle unità motorie e nascoste siano dati, rispettivamente,da
formula, [51]
dove σ(x) è un vettore con i-esima componente uguale a σ(xi) e σ è una funzione sigmoide la cui derivata indicheremo con σ'. Queste equazioni non sono altro che le versioni stazionarie dell'equazione [4]. Modifichiamo la regola di apprendimento dell'ADALlNE per minimizzare E con ε(x) =a(x)-σ[Wx]. Per le unità motorie ne segue:
∆Wm = [σ' · h]{a(s) - σ[Wmσ(WhS)]}T [52]
e per le unità nascoste, l'equazione:
∆Wh =σ'Wmσs{a(s) - σ[Wmσ(WhS)]}T. [53]
Tali cambiamenti dei pesi sono proprio quelli necessari per minimizzare E. In pratica i calcoli si svolgono in due passi. Nel primo passo (in avanti) la rete viene stimolata con un pattern s, e si calcolano i vettori ε(s) e σ'. Nel secondo passo (all'indietro) si usano questi vettori per modificare prima i pesi Wm, quindi i pesi Wh, e così via, da cui il nome di retropropagazione assegnato all'algoritmo. La figura (fig. 19) illustra schematicamente questo procedimento. L'algoritmo di Rumelhart e collaboratori fornisce una soluzione al problema dell'attribuzione dei meriti, e rende i perceptron e gli ADALlNE analogici multistrato strumenti potenti per lo studio dell'apprendimento supervisionato nelle reti neurali adattive. Descriveremo nel seguito alcune applicazioni della retropropagazione.
Il problema x XOR y
Abbiamo sottolineato precedentemente il fallimento dei perceptron elementari (e degli ADALINE) nel valutare la funzione logica x XOR y. Questa funzione, come abbiamo visto, è vera se x è falsa e y è vera (o viceversa), ed è falsa altrimenti. Utilizzando la retropropagazione si ottiene la rete mostrata in figura (fig. 20), dopo un addestramento con 558 passi. I pesi mostrati includono soglie pari a - 2,2 e - 6,3, anch'esse determinate dall'algoritmo, poiché tali soglie si possono considerare semplicemente come pesi (cambiati di segno) di connessioni con unità nascoste sempre attive (tI e t2 in figura). In questo caso sia l'unità nascosta che quella motoria hanno soglie negative, e risultano attive (+ l), a meno che non vengano sufficientemente inibite. L'unità nascosta è attiva se nessuna delle unità sensoriali lo è, e quando è attiva spegne l'unità motoria. Quest'ultima viene disattivata anche quando entrambe le unità sensoriali sono attive.
Il problema T/C
Un altro problema risolto dalla retropropagazione è di natura geometrica, e consiste nel distinguere le lettere T e C indipendentemente da eventuali traslazioni e rotazioni. La figura (fig. 21) mostra i pattem, mentre nella figura seguente (fig. 22) è illustrata l'architettura della rete utilizzata da Rumelhart e collaboratori per risolvere il problema (Rumelhart et al., 1986). Questa struttura è più o meno la stessa che Rosenblatt e molti altri hanno impiegato per problemi simili. È notevole il fatto che le unità nascoste sono connesse solo con piccole porzioni dello strato di unità s, chiamate campi recettivi, mentre le unità motorie sono connesse con molte unità nascoste ben separate. Tale struttura riproduce, in qualche misura, l'architettura delle aree visive. Dopo un numero di presentazioni dei pattem T e C compreso tra 5000 e 10.000, con le relative risposte, la rete impara a svolgere il compito. In questo processo, i campi recettivi delle unità nascoste si adattano in diversi modi al compito da svolgere. La figura (fig. 23) mostra i pattem di pesi per alcuni di tali campi recettivi. Nella figura 23a è mostrato un campo recettivo simile a quello di una cellula gangliare della retina, con centro ON e periferia OFF, che risulta un ottimo rivelatore di T. La figura 23b mostra un campo recettivo simile a quello di un rivelatore corticale di bordi o di barre, con selettività verticale. Anche questo risulta un ottimo rivelatore di T. Anche la figura 23c ricorda un rivelatore corticale di bordi, ma con selettività obliqua. Si può verificare che le unità nascoste che possiedono un campo recettivo simile possono essere attivate da una T in cinque posizioni diverse, ma possono essere attivate da una C in tre sole posizioni. Infine, le unità nascoste con i campi recettivi mostrati in figura 23d non sono attivate né dalle T né dalle C. La C è però una figura più compatta della T, e perciò rende inattivo un numero minore di unità nascoste. L'effetto risultante dei vari campi recettivi è tale da facilitare la distinzione delle T dalle C, mediante un semplice operazione a soglia sulle unità di output. È importante notare che questi campi si formano in modo cooperativo: ognuno è influenzato da tutti gli altri e dalle unità motorie. Il valore ottimale di ogni peso dipende quindi dal valore che assume ogni altro peso della rete.
La rete NETtalk
In un'applicazione anche più sorprendente, T. Sejnowski e C.R. Rosenberg hanno addestrato un'altra rete, simile a quelle descritte, a 'leggere' e a 'pronunciare' un testo in inglese (Sejnowski e Rosenberg, 1986). La loro rete comprende 203 unità recettrici, organizzate in 7 gruppi comprendenti ognuno 29 unità, 80 unità nascoste e 26 unità motorie. All'interno di ogni gruppo di unità s, 26 unità codificano una lettera dell' alfabeto inglese, mentre le restanti 3 servono per i segni di punteggiatura e la separazione tra le parole. Un pattern di stimolo è quindi una stringa di sette caratteri. Le unità motorie codificano i suoni associati alla pronuncia, o fonemi, oltre che l'accento e la delimitazione delle sillabe. La rete è stata addestrata su un certo numero di testi utilizzando la retropropagazione. In un esperimento si è utilizzata la trascrizione fonetica del parlato continuo e informale di un bambino. Da questo corpus sono state estratte circa 1000 parole, e dopo 50.000 presentazioni la rete riusciva a leggere e a pronunciare con un'accuratezza pari a circa il 95%. La figura (fig. 24) mostra il campo recettivo di una delle unità nascoste. È chiaro che questa unità ha una rappresentazione distribuita di molti attributi della stringa di input. In seguito, alla rete è stato presentato un testo di 439 parole (molte delle quali nuove) pronunciate dallo stesso bambino, e la rete lo leggeva e pronunciava con un'accuratezza del 78%. Questo è un esempio di generalizzazione: la rete di Sejnowski e Rosenberg, da loro detta NETtalk, generalizza molto bene. In effetti, gli ADALINE e i perceptron multi strato generalizzano piuttosto bene in diverse applicazioni, proprio come Rosenblatt sosteneva tanti anni fa. Un'altra proprietà della rete NETtalk è la resistenza ai guasti. Una rete NETtalk danneggiata in modo sostanziale è ancora in grado di leggere e pronunciare con un'accuratezza vicina al 40%, e recupera in fretta dopo un nuovo addestramento. Ci si aspetta che queste proprietà si manifestino in tutte le reti con rappresentazione distribuita. Nell'insieme, la rete NETtalk funziona sorprendentemente bene, ma rivela limiti nella capacità di trattare ambiguità sintattiche e semantiche.
Retropropagazione ricorrente
Gli esempi appena esposti riguardano tutti delle semplici reti feedforward (con propagazione in avanti). F.I. Pine da (1987) e R.I. Williams e D. Zipser (1989) sono riusciti a estendere l'algoritmo di retropropagazione a reti ricorrenti. L'algoritmo di Pineda è un'estensione diretta dell'algoritmo di Rumelhart e collaboratori che abbiamo discusso precedentemente; però è necessario attendere che la rete si attesti in uno stato stazionario, prima di effettuare l'aggiornamento. L'algoritmo di Williams e Zipser non soffre di questa limitazione, e si può usare on fine. Poiché le reti ricorrenti sono molto più potenti, dal punto di vista computazionale, rispetto a quelle feedforward, può sembrare che, in linea di principio, le reti neurali analogiche possano essere addestrate a compiere qualsiasi elaborazione realizzabile da macchine finite. L'algoritmo di Williams e Zipser è stato applicato in molti settori, soprattutto in neuroscienza computazionale. Un esempio notevole è fornito dal lavoro di Zipser e collaboratori su modelli della memoria attiva a breve termine (Zipser et al., 1993). Invitiamo il lettore a confrontare tale lavoro con quello di Amit e collaboratori e con le proposte originali di Wilson e Cowan.
Statistica e teoria dell'informazione
Predizione, filtri ed elaborazione del segnale
È chiaro che, per quanto riguarda l'elaborazione dei dati, c'è un'ampia interdisciplinarità tra la statistica e le reti neurali. Questa relazione era già chiara ai primi ricercatori, come Rosenblatt e Widrow, ma è stata formalizzata solo in tempi più recenti. Consideriamo per esempio il problema di predire o filtrare una sequenza di p atte m di input {Xj,X2, ...,XN}. Indichiamo con {y*1,y*2, ... ,y*N} la sequenza corrispondente di output desiderati, o output di addestramento. Questo problema di filtraggio può essere riformulato come un opportuno problema di minimizzazione dell' errore e studiato con metodi simili a quelli usati nella retropropagazione. Il filtro 'ottimale' corrisponde a quello introdotto da Wiener nel suo lavoro pionieristico sulla predizione e il filtraggio, che è noto oggi come filtro di Wiener (Wiener, 1949). In molti casi pratici il filtro voluto si può ottenere in modo adattivo utilizzando l'algoritmo dell'ADALINE, che converge, al crescere di N, alla soluzione del filtro di Wiener. Questo metodo presenta un notevole vantaggio computazionale, quando le quantità necessarie a determinare il filtro di Wiener sono non note o difficili da calcolare. Vi è ormai un consenso generale sulle molte analogie tra tecniche statistiche e reti neurali. La tabella (tab. 3) mette in risalto alcune relazioni tra i due campi di ricerca (Hastie, 1996).
Analisi delle componenti principali
Un altro esempio della relazione tra statistica e reti neurali è fornito dall'applicazione degli algoritmi di apprendimento non supervisionato all'analisi delle componenti principali. Dato un insieme di input {x} con matrice di correlazione R, l'autovettore corrispondente all' auto valore massimo di R individua la prima componente principale della varianza di {x}. Gli autovettori corrispondenti agli altri auto valori, posti in ordine decrescente, corrispondono alle successive componenti principali. È ben noto che per estrarre queste componenti principali bisogna diagonalizzare la matrice R. E. Oja mostrò per primo che una semplice modifica della regola di Hebb consente di estrarre le componenti principali (Oja, 1982). L'evoluzione di una sinapsi alla Hebb si può descrivere mediante l'equazione ∆Wk = ηykxkT, dove Yk = σ(Wkxk) è l'output di un singolo strato di neuroni con input Xk e Wk è la matrice dei pesi all'istante (discreto) k. Nel caso in cui σ sia una funzione lineare, si può riscrivere questa equazione nella forma ∆Wk = ηWkXkXkT. Se ∆Wk è sufficientemente piccolo, si può effettuare una media sulle variazioni di Wk, ricavando l'equazione differenziale:
formula [54]
in cui R= (xxT).
Gli elementi della matrice dei pesi W crescono quindi esponenzialmente con velocità proporzionale alla matrice di correlazione dell'input R. Oja modificò le equazioni di aggiornamento nella forma ∆Wk = ηYk(Xk - WkTYk)T ricavando l'equazione differenziale per variazioni lente di W:
formula. [55]
Si può dimostrare che questa equazione porta a ortogonalizzare la matrice W, e in effetti a diagonalizzare R, e quindi consente l'estrazione delle componenti principali.
Notiamo che la regola di apprendimento di Oja realizza un algoritmo di discesa di gradiente stocastico per la minimizzazione della funzione:
formula, [56]
formula. [57]
Dopo il lavoro di Oja sono apparse molte varianti del suo algoritmo, e sono state sviluppate molte applicazioni per estrarre informazione dagli insiemi di dati.
Infomax
C'è anche una stretta relazione tra gli algoritmi che massimizzano l'informazione o l'entropia di un insieme di dati, e quelli che massimizzano l'informazione mutua tra gli input e gli output di una rete (Linsker, 1990; vedi anche i saggi di J. Hertz, I risultati dell'elaborazione neuronale come fonte dell'informazione, e W. Bialek, Potenzialità e limitazioni nella misura della trasmissione dell'informazione neuronale). Supponiamo che X sia un insieme {x} di variabili casuali, discrete o continue, con distribuzione di probabilità p(x). Seguendo Shannon, definiamo l'informazione, o entropia, H(X) associata a questo insieme come
formula, [58]
e l'informazione mutua tra due insiemi X e Y come
formula. [59]
Ne segue immediatamente che
I(X;Y)=H(X)-H(XIY). [60]
Se Y = Wx, come in molti dei circuiti neurali che stiamo considerando,
formula. [61]
Dunque, dato qualsiasi algoritmo in cui le variazioni dei pesi sono basate sulla discesa di gradi ente, massimizzare l'entropia dell'output è equivalente a massimizzare l'informazione mutua tra input e output. Questa procedura di massimizzazione fu chiamata lnfomax da Linsker, che riuscì a ricavare diverse regole di apprendimento di tipo hebbiano, applicandole poi alla formazione dei campi recettivi e delle mappe di Kohonen.
Riduzione della ridondanza
Esiste una relazione anche tra l'Infomax e la cosiddetta riduzione della ridondanza (Barlow, 1959). Consideriamo il sistema lineare Y = W x in presenza di rumore additivo sia sull'inputx che sull'outputy. Defrniamo il 'vero' input s e il 'vero' output z tramite le formule x=s+nj e z=y+n2, dove nj e n2 indicano rispettivamente il rumore in input e in output. L'informazione mutua tra se z è quindi I(S;Z), e la ridondanza del sistema è data da
formula [62]
dove C(Z) è la capacità di trasmissione di informazione del sistema (Shannon, 1948). Chiaramente, massimizzando l'informazione mutua 1(S;Z) si minimizza la ridondanza R. Un algoritmo per raggiungere questo scopo fu proposto da M.C. Goodall (1960); reintrodotto da Il Atick e A.N. Redlich (1990), tale algoritmo è stato applicato all'elaborazione dei segnali visivi da parte della retina.
Analisi delle componenti indipendenti
Analisi non lineare delle componenti indipendenti. - In alcuni lavori successivi, Oja e collaboratori hanno esteso l'algoritmo di apprendimento per l'analisi lineare delle componenti principali in modo da includere reti non lineari (Oja et al., 1991). Le equazioni di aggiornamento diventano
formula. [63]
Poniamo Zk = WkXk e supponiamo che σ(zk = tanh(zk). Si può dimostrare che l'equazione [63] massimizza la quantità
elemento per elemento. Supponiamo ora che una preelaborazione abbia già diagonalizzato e riscalato i dati, in modo che
(procedimento chiamato sphering). La quantità (f dzktanh(zk) si riduce approssimativamente a - [1 + 1/2k(zk)],
dove
è la curtosi di Zk. Dunque l'equazione [63] minimizza la curtosi. La regola di aggiornamento non lineare di Oja e collaboratori opera quindi una ricerca esplorativa della proiezione (EPP, Exploratory Projection Pursuit): si tratta di un algoritmo statistico che cerca le direzioni interessanti nello spazio degli input, proiettando i vettori di input Xk su alcuni versori Wb cioè formando
nel modo ora descritto. Un valore basso di curtosi corrisponde, per esempio, a una bimodalità di p(x).
Dall'equazione [63] si deduce anche che, all'equilibrio, le Zk sono statisticamente indipendenti. L'algoritmo di Oja e collaboratori trova quindi le componenti indipendenti degli input {x}, pur di averli preventivamente sottoposti al processo di sphering. Ciò suggerisce di adottare un processo per trovare le componenti statisticamente indipendenti che consista in due passi: dapprima viene operato lo sphering degli {xk} per generare le {zk}; successivamente si ricava il vettore dei pesi Ŵk che minimizza la curtosi k(zk). Per il primo stadio si può utilizzare un algoritmo di analisi delle componenti principali modificato, per il secondo l'algoritmo non lineare di Oja e collaboratori che abbiamo descritto.
L'algoritmo E/M. - È chiaro che è semplice estendere l'analisi delle componenti principali e i relativi algoritmi alla rete ricorrente mostrata in figura (fig. 25), la cui funzione è quella di formulare una codifica ottimale degli input x trovando le migliori stime degli output y e delle matrici dei pesi W e U, cioè minimizzando la funzione
J(U,y) = ⟨(x- Uy)T (x- Uy)⟩ [64]
rispetto a U e y.
Dati x e W si può ricavare y, dunque U, e così via (Rao e Ballard, 1997).
Un algoritmo molto simile è stato proposto da R. Neal e P. Dayan per la tecnica statistica chiamata analisi fattoriale (Neal e Dayan, 1996). In questa analisi si spiegano le correlazioni in termini di variabili nascoste, o fattori. Supponiamo di avere n variabili visibili x e k variabili nascoste y, in modo che x = Gy+e, dove e è un rumore gaussiano con componenti indipendenti tra di loro (la matrice di covarianza: (σ2 è diagonale). La matrice dei pesi G viene scelta in modo da minimizzare la funzione di verosimiglianza logaritmica
L(G,y) = (1ogP(xly,G,β)), [65]
dove la media è fatta rispetto alle variabili nascoste y. Nel caso in cui la probabilità condizionale P(xly, G, σ2) sia gaussiana, minimizzando J(G,y) si massimizza L(G,y). Ne segue che sia G sia σ2 si possono far evolvere usando la discesa di gradiente, una volta noti x e y. Ma come si ricavano le y? Facciamo l'ipotesi che siay=Rx+v, dove v è un rumore gaussiano con matrice di covarianza diagonale μ2, e che R e μi2 vengano aggiornati con la discesa di gradi ente, una volta noti y e x. Questo schema di aggiornamento costituisce una variante dell'algoritmo di massimizzazione dell' aspettazione (EM, Expectation Maximization). Si tratta di uno schema iterativo che prevede due passi. Dati i valori osservati x e le stime attuali di G e (J'2 si trovalaP(Ylx, G, (J'2); questo è il passo E (aspettazione). Si ricavano le nuove stime di G e (J'2 che massimizzano il valore aspettato della verosimiglianza logaritmica di x, utilizzando la y ottenuta nel passo E; questo è il passo M (massimizzazione).
Nell'algoritmo di Neal-Dayan il passo E, da x a y, viene chiamato fase di riconoscimento, mentre il passo M, da y a x, viene chiamato fase generativa. Nell'insieme l'algoritrno è una particolare variante del cosiddetto algoritmo di veglia-sonno: la sua realizzazione in termini di reti neurali prende il nome di macchina di Helmholtz (Hinton et al., 1995). L'algoritmo EM è largamente utilizzato in statistica e nelle reti neurali, per diverse applicazioni. Il filtro Kalman-Bucy si può considerare come un caso particolare dell'algoritrno EM.
Conclusioni
È evidente che dal 1943 ci sono stati progressi considerevoli nella teoria e nella pratica delle reti neurali. Il lavoro pionieristico di McCulloch e Pitts, Wiener, Hebb, Beurle, Uttley, Taylor, Rosenblatt, Widrow, Barlow e altri ha stimolato da un lato un'ampia raccolta di algoritrni per l'elaborazione di insiemi di dati reali e di immagini, e dall'altro ha portato a una varietà di equazioni per formulare modelli di diversi aspetti dell'elaborazione dell'informazione nel cervello. Forse lo sviluppo recente più importante consiste nell'aver compreso che le reti neurali e la statistica tradizionale sono argomenti fortemente legati tra loro. È lecito attendersi un'evoluzione ulteriore di questi legami, oltre allo sviluppo di algoritmi nuovi e potenti per la predizione, il filtraggio e l'elaborazione dei segnali.
Bibliografia citata
AMIT, D., BRUNEL, N., TSODYKS, M.V. (1994) Correlations of cortical hebbian reverberations: theory versus experiment. J. Neurosci., 14, 6435-6445.
ANCK, J.J., REDLICH, A.N. (1990) Towards a theory ofearly visual processing. Neural Comput., 2, 308-320.
BARLOW, H.B. (1959) Sensory mechanisms, the reduction of redundancy, and intelligence. In Mechanisation of thought processes, National Physical Laboratory Symposium 10, HMSO, Londra.
BARLOW, H.B. (1972) Single units and sensation: a neuron doctrine for perceptual psychology? Perception l, 371-394.
BAUM, E.B., MOODY, J., WILCZEK, F. (1988) InternaI representations for associative memory. Biol. Cybern. 59, 217-228.
BEURLE, R.L. (1956) Properties of a mass of cells capable of regenerating pulses. Phil. Trans. R. Soc. Lond. B, 240, 55-94.
BEURLE, R.L. (1962) Functional organization in random networks. In Principles of selforganization, Transactions, a c. di von Foerster H., Zopf G.W. Jr., Oxford e New York, Pergamon Press.
COWAN, J.D. (1967) A mathematical theory of centraI nervous activity, Tesi, University of London.
COWAN, J.D. (1968) Statistical mechanics ofnervous nets, In Neural Networks, a c. di Caianiello E.R., Berlino, Springer-Verlag.
COWAN, J.D., FRIEDMAN, A.E. (1991) Simple spin models for the formation of ocular dominance columns and iso-orientation patches. In Advances in neural inJormation processing systems voI. 3, a c. di Lippman et. al., San Mateo, Morgan Kauffman.
CRAGG, B.G., TEMPERLEY, H.N.V. (1954) The organisation of neurones: a cooperative analogy. EEG Clin. Neurophysiol., 6, 85-92.
DURBIN, R., MITCHINSON, G. (1990) A dimension reduction framework for understanding cortical maps. Nature, 343, 644-647.
DURBIN, R., WILLSHAW, D. (1987) An analogue approach to the travelling salesman problem using an elastic net method. Nature, 326, 689-691.
FARLEY, B.G., CLARK, W.A. (1961) Activity in networks of neuron-like elements. Information theory, voI. 4, a c. di Cherry E.C., Londra, Butterworths, pp. 242-251.
GOODALL, M.C. (1960) Performance of a stochastic net. Nature, 185, 557-558.
GREENE, P.H. (1965) Superimposed random coding of stimulusresponse counections. Bull. Math. Biophys. Suppl., 191-202.
GROSSBERG, S. (1969) On learning and energy-entropy dependent in recurrent and nonrecurrent signed networks. J. Statistical Physics, 1, 319-350.
GROSSBERG, S. (1973) Contour enhancement, short term memory, and constancies in reverberating neural networks. Studies in Appl. Math., LII, 3, 213-257.
HASTIE, T. (1996) From traditional statistical models to neural networks, NIPS96 Tutorial.
HAUSSLER, A., MALSBURG, C. VON DER (1983) Development of retinotopic projections: an analytical treatrnent. J. Theoret. Neurobiol., 2, 47-73.
HEBB, D.O. (1949) The organization of behavior, a neuropsychological theory. New York, Wiley.
HINTON, G.E., DAYAN, P., FREY, B.J., NEAL, R.M. (1995) The 'wake-sleep' algorithm for unsupervised neural networks. Science, 268, 1158-1161.
HINTON, G.E., SEINOWSKI, T.J. (1983) Optimal perceptual inference. Proc. IEEE Computer Soc. Con. Computer Vision and Pattern Recognition, Washington, pp. 448-453.
HOPFIELD, J.J. (1982) Neural networks and physical systems with emergent collective computational abilities. Proc. Nat!. Acad. Sci. USA, 79, 2554-2558.
HOPFIELD, J.J. (1984) Neurons with graded response have colle ctive computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA, 81, 3088-3092.
HOPFIELD, J.J., TANK, D.W. (1985) 'Neural' computation of decisions in optimization problems. Biol. Cybern., 52, 141-152.
KIRKPATRICK, S., GELATT, C.D. Jr., VECCHI, M.P. (1983) Optimization by simulated annealing. Science, 229, 671-679.
KOHONEN, T. (1982) Self-organized formation of topologically correct feature maps. Biol. Cybern., 43, 59-70.
LASHLEY, K.S. (1950) In search ofthe engram. Symp. Soc. Expt. Biol., 4, 454-482.
LINSKER, R. (1990) Perceptual neural organization: some approaches based on network models and information theory. Ann. Rev. Neurosci. 13, 257-281.
LITTLE, W.A. (1974) The existence ofpersistent states in the brain. Math. Biosci., 19, 101-120.
LONGUET-HIGGINS, H.C., WILLSHAW, D.J., BUNEMAN, O.P. (1970) Theories of associative recall. Q. Rev. Biophys., 3, 223-244.
MCCULLOCH, W.S. (1961) What is a number, that a man may know it, and a man, that he may know a number? GeneraI Semantics Bull., 26-27, 7-18.
MCCULLOCH, W.S., PITTS, W. (1943) A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys., 5, 115-133.
MARR, D. (1969) A theory of cerebellar cortex. J. Physiol. (Lond.), 202, 437-470.
MINSKY, M., PAPERT, S. (1969) Perceptrons: an introduction to computational geometry, Cambridge, Mass., MIT Press.
MOOERS, C.N. (1949) Application of random codes to the gathering of statistical information. Zator Co. Tech. Bull., 31.
NEAL, R., DAYAN, P. (1996) Factor analysis using delta-mIe wakesleep learning. TR 9607, Departrnent of Statistics, University of Toronto.
NEUMANN, J. VON (1956) Probabilistic logics and the synthesis of reliable organisms from unreliable components. In Automata Studies, a c. di Shannon C.E., McCarthy J., Princeton, N.J., Princeton University Press, pp. 43-98.
OBERMAYER, K, RITTER, H., SCHULTEN, K (1990) A principle for the formation of the spatial stmcture of cortical feature maps. Proc. Natl. Acad. Sci. USA, 87, 8345-8349.
OJA, E. (1982) A simplified neuron model as a principal component analyzeI. J. Mathematical Biology, 15, 267-273.
OJA, E., OGAWA, H., WANGVIWATTANA, J. (1991) Learning in nonlinear constrained Hebbian networks. In Proceedings of the 1991 International conJerence: artificial neural networks, a c. di Kohonen T. et al., Amsterdam-New York, North Holland.
PINEDA, F.J. (1987) Generalization ofbackpropagation to recurrent neural networks. Phys. Rev. Lett., 18, 2229-2232. RAO, R., BALLARD, D.H. (1997) Dynamic model of visual recognition predicts neural response properties in the visual cortex. Neural Comput., 9, 721-763.
RASHEVSKY, N. (1938) Mathematical Biophysics; psychomathematical foundations of biology. Chicago, University of Chicago Press.
RESCORLA, R.A., WAGNER, A.R. (1972) A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement. In Classical conditioning II, a c. di Black A.H., Prokasy W.F., New York, Appleton-CenturyCrofts, pp. 64-99.
ROSENBLATT, F. (1958) The perceptron, a probabilistic model for information storage and organization in the brain. Psych. Rev., 62, 386-408.
RUMELHART, D.E., HINTON, G.E., WILLIAMS, R.J. (1986) Leaming internaI representations by error propagation. In Parallel distributed processing: explorations in the microstructure of cognition, 1, Foundations, a c. di Rumelhart D.E., McClelland J.L., Cambridge, Mass., MIT Press.
SEINOWSKI, T., ROSENBERG, C.R. (1986) NETtalk, a parallel network that learns to read aloud. Technical Report JHU/EECS86/01, Johns Hopkins Univ. EE and Comp. Sci.
SHANNON, C.E. (1948) A mathematical theory of communication. BelI Syst. Tech. J., 27, 379-423; 623-656. SHERRINGTON, D., KIRKPATRICK, S. (1975) Spin glasses. Phys. Rev. Lett., 35, 1972.
STEINBUCH, K (1961) Die Lemmatrix. Kybernetik, l, 36-45.
SWINDALE, N.V. (1980) A model for the formation of ocular dominance stripes, Proc. R. Soc. Lond. B Biol. Sci., 208, 243-264.
SWINDALE, N.V. (1982) A model for the formation of orientation columns. Proc. R. Soc. Lond. B Biol. Sci., 215, 211-230.
TANAKA, S. (1989), Theory of self-organization of cortical maps. In Advances in neural information processing systems, voI. I, a c. di Touretzky D.S., San Mateo, Morgan Kauffman, pp. 451-458.
TAYLOR, W.K. (1956) Electrical simulation of some nervous system functional activities. Information theory, voI. 3, a c. di Cherry E.C., Londra, Butterworths, pp. 314-328.
TURING, A.M. (1952) The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B Biol. Sci .. , 237, 37-72.
UTTLEY, A.M. (1954) The classification of signals in the nervous system. EEG Clin. Neurophysiol., 6, 49.
UTTLEY, A.M. (1956) A theory of the mechanism of leaming based on the computation of conditional probabilities. Proc. 1st Int. Conf. on Cybernetics, Parigi, Namur, Gauthier-Villars.
WIDROW, B., HOFF, M.E. (1960) Adaptive switching circuits. WESCON Convention Record, IV, 96-104.
WIENER, N. (1949) Extrapolation, interpolation and smoothing of stationary time series with engineering applications. Cambridge, Mass., MIT Press.
WILLIAMS, R.J., ZIPSER, D. (1989) A leaming algorithm for continually muning fully recurrent neural networks. Neural Comput., l, 270-280.
WILLSHAW, D.J., LONGUET-HIGGINS, H.C. (1969) The holophonerecent developments. In Machine intelligence 4, a c. di Michie D., Edimburgo, Edinburgh University Press.
WILLSHAW, D.J., MALSBURG, C. VON DER (1976) How pattemed neural counections can be set up by self-organization. Proc. R. Soc. Lond. B Biol. Sci., 194, 431-445.
WILSON, H.R., COWAN, J.D. (1972) Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J., 12, 1-24.
WILSON, H.R., COWAN, J.D. (1973) A mathematical theory ofthe functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13, 55-80.
WINOGRAD, S., COWAN, J.D. (1963) ReliabIe computation in the presence ofnoise. Cambridge, Mass., MIT Press.
ZIPSER, D., KEHOE, B., LITTLEWORT, G., FUSTER, J. (1993) A spiking network model of short-term active memory. J. Neurosci., 13, (8), 3406-3420.
Bibliografia generale
HAYKIN, S. Neural networks: a comprehensive foundation. Upper Saddle River, New York, Prentice Hall, 1999.