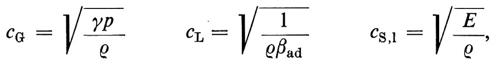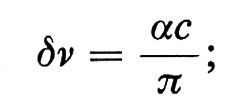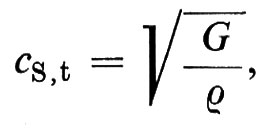Suono

Suono

di Daniele Sette

SOMMARIO: 1. Introduzione. □ 2. La parola. □ 3. L'acustica musicale. □ 4. Il rumore. □ 5. L'acustica architettonica. □ 6. La bioacustica. □ 7. L'acustica fisica: a) la propagazione nei gas; b) la propagazione nei liquidi; c) la propagazione nei solidi; d) l'acustica dei plasmi. □ 8. Gli ultrasuoni di elevata intensità. □ 9. L'acustica elettronica e le onde superficiali. □ 10. L'acustica subacquea. □ 11. Le prove non distruttive. □ 12. La microscopia acustica. □ 13. L'olografia acustica. □ 14. Gli ultrasuoni in medicina. □ Bibliografia.

1. Introduzione.

La parola ‛suono', a rigor di termini, sta a indicare la sensazione acustica; tuttavia, essa è comunemente usata anche per indicare le vibrazioni che possono produrre tale sensazione. Inoltre, essa è stata di frequente, anche se impropriamente, usata per indicare la fenomenologia connessa con queste vibrazioni. In definitiva, il termine suono è divenuto per molti versi sinonimo di ‛acustica'. In questo articolo la parola sarà usata in questa accezione più estesa.

Un'ulteriore estensione del significato di suono, e di acustica, si è resa necessaria in questo secolo da quando si sono potute studiare vibrazioni di natura assai diversa, nei mezzi più vari, oltre i limiti di frequenza e d'intensità propri della sensibilità dell'orecchio umano. Al presente, il significato delle parole suono e acustica si è esteso sino a includere ogni specie di vibrazione meccanica, indipendentemente dal tipo, dalla frequenza e dal mezzo in cui si propaga. Talora si fa uso dei termini ‛infrasuoni', ‛ultrasuoni' e ‛ipersuoni' per indicare rispettivamente vibrazioni di frequenza inferiore ai 40 Hz, compresa tra i 20.000 e i 10⁹ Hz e superiore ai 10⁹ Hz.

Sebbene sia essenzialmente una branca della fisica, tuttavia l'acustica presenta un particolare carattere di scienza veramente interdisciplinare, in virtù dei suoi molteplici e profondi rapporti con altre scienze, con tecnologie di vario genere e con l'arte. Un'immagine suggestiva di tale situazione, fornita da R. B. Lindsay, è mostrata nella fig. 1: un nucleo di fenomeni fisici, che riguardano le vibrazioni meccaniche dei corpi e la radiazione meccanica nei mezzi materiali, dà vita a una vasta serie di effetti distinti connessi con le scienze della vita e della Terra, con l'ingegneria e con l'arte.

Il progresso compiuto in questo secolo sia nell'acustica fondamentale sia in quella applicata è stato enorme.

Alla fine del secolo scorso le ricerche di acustica concernevano i principali fenomeni fisici dei suoni alle tradizionali basse frequenze e la descrizione di questi fenomeni aveva trovato un'eccellente sistemazione fisico-matematica nel lavoro di molti scienziati. Basti qui ricordare The theory of sound di lord Rayleigh, testo fondamentale dell'intera fisica.

Per tutto il XIX secolo sono state fatte molte ricerche sull'anatomia dell'orecchio e le sue proprietà uditive; il rapporto intercorrente tra altezza e frequenza fu stabilito da F. Savart e sono state eseguite varie prove specifiche per determinare i limiti di udibilità con sorgenti quali diapason, barre, ecc. G. Ohm nel 1843 formulò l'ipotesi che tutti i toni in musica dipendessero da vibrazioni armoniche di frequenza definita e che il timbro di un suono musicale fosse dovuto alla combinazione di toni semplici di frequenze commensurabili; ciò portò alle ricerche di importanza fondamentale compiute da H. von Helmholtz, il quale formulò la cosiddetta teoria della risonanza della percezione uditiva, che è stata la base di ultenori ricerche realizzate nel XX secolo.

L'importanza crescente delle comunicazioni telefoniche e le prime applicazioni di registrazione sonora negli ultimi decenni del secolo scorso hanno richiamato l'attenzione sul problema del miglioramento dell'efficienza dei trasduttori elettroacustici, di quei dispositivi, cioè, che convertono l'una nell'altra l'energia elettrica e quella acustica.

Tutto il progresso dell'acustica nel XX secolo è fondato sul successo conseguito coi trasduttori elettromeccanici (elettroacustica), che possono fungere sia da sorgenti sia da ricevitori: l'enorme estensione della gamma di frequenze studiate e lo sviluppo di ricerche in molti settori in cui si richiedono alte sensibilità e fedeltà sono stati possibili grazie ai nuovi mezzi di trasduzione elettroacustica. Alla fine del secolo scorso si svilupparono i microfoni a carbone e i trasduttori elettrici, basati sulle interazioni elettrostatiche, magnetiche o elettromagnetiche tra i corpi. Nel secolo attuale si è assistito a un continuo moltiplicarsi di questi dispositivi, resi anche più efficienti dal contemporaneo sviluppo dell'elettronica e della tecnologia dei circuiti elettrici, e dall'uso di altri effetti di trasduzione elettroacustica: l'effetto magnetostnttivo e quello piezoelettrico.

Di particolare importanza è quest'ultimo effetto, per il quale si producono deformazioni elastiche in una piastra - opportunamente ritagliata da particolari cristalli (tormalina, quarzo, sale di Rochelle, ecc.) o fatta di ceramiche ferroelettriche debitamente trattate (titanato di bario) - come conseguenza di una polarizzazione elettrica e viceversa; una siffatta piastra o lamina vibra fortemente e agisce da sorgente, se sottoposta a un campo elettrico di frequenza opportuna; la stessa lamina posta in vibrazione da un'onda sonora che la investe produce un campo elettrico alternato che permette la rivelazione del suono. Tali trasduttori hanno aperto la strada agli ultrasuoni e allo studio della radiazione sonora in molti nuovi materiali. Si può ricordare che l'uso di trasduttori piezoelettrici di questa specie risale alla prima guerra mondiale e si deve a P. Langevin: lamine tagliate da grossi cristalli naturali di quarzo furono impiegate in sistemi di rilevamento a eco acustica dei sottomarini. Oggi si usano comunemente i trasduttori piezoelettrici per generare e rivelare onde sia longitudinali sia trasversali fino a frequenze dell'ordine dei gigahertz (10⁹ Hz).

Non è qui possibile fornire una descrizione completa dello sviluppo dei vari settori dell'acustica; ci limitiamo pertanto a considerarne solo alcuni, per dare un'idea corretta dei progressi compiuti e della natura dei problemi che si presentano in questo campo. Non tratteremo argomenti importanti, quali la registrazione del suono, i sistemi di riproduzione ad alta fedeltà e i sistemi stereofonici: va comunque messo in evidenza l'enorme interesse culturale e sociale che lo sviluppo in questi settori ha avuto. Le proprietà strutturali e funzionali degli organi della percezione del suono sono ampiamente e specificamente trattate nell'articolo udito.

2. La parola.

Il sistema degli organi che producono la voce umana è costituito dai polmoni, che forniscono la riserva d'aria, dalla laringe con le corde vocali, che sono le sorgenti del movimento di vibrazione, e dalle cavità della gola, della bocca e del naso, che fungono da risonatori. Le corde vocali sono due coppie di protuberanze cartilaginee di forma triangolare (v. fig. 2) le corde della coppia inferiore (T₁, T₂) si chiamano corde tonali, le altre (F₁, F₂) false corde. Le corde vocali di ciascuna coppia distano di pochi decimi di millimetro quando sono in funzione (l'intervallo si chiama glottide). L'aria che proviene dai polmoni attraverso la trachea (un canale di circa 2,5 cm di diametro), premendo contro le corde vocali, ne determina uno spostamento che fa crescere la tensione nelle corde così che queste tornano alla posizione di partenza per iniziare un nuovo ciclo, mantenendosi in vibrazione.

La produzione di un moto di vibrazione continuo delle corde da parte del flusso d'aria unidirezionale è molto simile alla produzione delle vibrazioni di una corda di violino, che prende energia dall'archetto che si muove in un unico verso. La rapidità delle vibrazioni è determinata dalla lunghezza e dalla tensione delle corde: nelle donne e nei bambini le corde sono più sottili e più corte di quelle dell'uomo e producono suoni più alti. La nota prodotta dalle corde vocali (tono laringeo) non è molto musicale e il fascino particolare della voce umana è dato dall'effetto aggiuntivo modulante delle cavità risonanti. Se si lasciano in riposo le corde vocali, l'aria passa attraverso la laringe senza subire praticamente alterazioni di moto e il suono prodotto è dovuto alle vibrazioni naturali delle cavità risonanti: ciò appare ben evidente quando si fischia; la maggior parte delle consonanti (p, s, . . . ) è prodotta in tale maniera.

Il sistema che genera la voce è una sorgente piuttosto complessa rispetto alle lunghezze d'onda dei suoni prodotti (circa 30 cm a 1.000 Hz) le dimensioni della testa sono tali da rendere molto importanti gli effetti di diffrazione; per questo motivo il suono prodotto dalla bocca gira intorno alla testa e può essere udito anche da chi lo emette o da un ascoltatore posto alle spalle di chi parla. La potenza media di chi parla, misurata davanti al volto, può variare da 80 dB, a 15 cm, a 65 dB, a 1 m dalla bocca: questi decibel si intendono relativi al livello standard di 10^-16 W/cm².

I singoli suoni che formano la parola si distinguono in vocali, semivocali (r, l, m, n) e consonanti. La potenza è assai maggiore per le vocali che per le consonanti. Tuttavia l'articolazione e l'intelligibilità della parola dipendono essenzialmente dalle consonanti. Nonostante la gran mole di lavoro svolto recentemente, non si è ancora trovato un modo soddisfacente per analizzare il suono della parola né si è risolto il problema di determinare i parametri che contengono l'informazione e quelli che portano il contenuto semantico. A indicare le difficoltà incontrate basti ricordare che i suoni base (fonemi) combinati in sillabe da chi parla si modificano reciprocamente. Attualmente si stanno svolgendo numerose ricerche in questo campo con l'ausilio di calcolatori di grandi capacità e di tecniche particolari per un'analisi rapida dello spettro del suono, con il proposito di stabilire come rivelare e misurare il contenuto semantico della parola e di sviluppare dei sistemi atti a trasformare automaticamente la parola in scrittura.

3. L'acustica musicale.

L'acustica musicale si occupa dello studio degli strumenti musicali già esistenti e della progettazione di strumenti nuovi. In questo settore dell'acustica, che per molto tempo non ha registrato grandi novità, in questi ultimi anni si stanno prospettando nuovi sviluppi. Le tecniche elettroniche hanno permesso di studiare i transienti e l'evoluzione temporale dei toni prodotti da strumenti tradizionali, fornendo così vigore all'analisi delle prestazioni degli strumenti e a quella degli elementi fisici, fisiologici ed estetici coinvolti negli effetti uditivi suscitati dall'ascolto di un brano musicale eseguito da un particolare solista. Questo studio si avvale inoltre dei nuovi metodi di sintesi dei suoni, che permettono, grazie all'impiego dei calcolatori, di produrre qualunque suono attraverso la sintesi delle sue caratteristiche fisiche: si possono così controllare i risultati dell'analisi dei suoni.

Le forme tradizionali degli strumenti si basano sui sistemi meccanici di risonanza: ciò comporta limitazioni di vario genere nei toni che si possono produrre. Oggigiorno si costruiscono strumenti musicali elettronici nei quali si generano, in circuiti estremamente ‛versatili', delle oscillazioni elettriche, la cui energia viene poi trasformata in energia acustica. Grazie allo sviluppo di apparecchiature a stato solido, che permettono di ridurre in un piccolo spazio complesse strumentazioni, si avrà ben presto una diffusione di nuove tecniche di avanguardia che potranno rivoluzionare la musica tradizionale. L'uso dei calcolatori per queste apparecchiature potrà arricchire di nuovi aspetti le tradizionali caratteristiche estetiche della musica.

4. Il rumore.

Strettamente connessa con le caratteristiche fisiologiche del sistemà uditivo dell'uomo è la risposta di questi al ‛rumore', ove si intenda con questo termine ogni suono non desiderato. Una tale definizione esprime con chiarezza l'importanza preminente dell'aspetto soggettivo (non desiderato) nella reazione dell'ascoltatore allo stimolo fisico (suono): un suono può risultare significativo e gradevole (voce, musica) per un individuo ed essere respinto alla stregua di un rumore da un altro, o anche dallo stesso in condizioni differenti.

La capacità di selezionare e scartare i suoni è un aspetto importante delle caratteristiche fisiologiche e psicologiche dell'udito.

Le sorgenti di rumore possono essere molto varie e finora sono state scarsamente studiate si incontrano problemi particolari allorché si cerca di comprendere il meccanismo d'azione di sorgenti molto intense o le caratteristiche degli effetti non lineari, la generazione di armoniche e subarmoniche e così via. I rumori prodotti da urti, ovvero le vibrazioni dovute a forze impulsive (battimani, macchinari in funzione, treni, automobili, motori a reazione) sono di grande importanza e assai difficili a studiarsi. Particolarmente complesso è il problema della misura, poiché l'obiettivo è valutare aspetti soggettivi, collegati col disturbo prodotto dal rumore, mediante determinazioni fisiche sulle onde sonore sino a oggi non si sono ottenuti risultati soddisfacenti facendo uso delle misure convenzionali, quali la distribuzione dell'energia nelle varie bande di frequenza acustica, la durata delle componenti di diversa frequenza, ecc.

Di recente, nello studio dei problemi connessi col rumore si sono introdotte le tecniche di correlazione, che permettono di studiare le caratteristiche del campo sonoro dal punto di vista della sua evoluzione temporale anziché da quello della composizione spettrale si trattano i segnali forniti da microfoni dislocati in posizioni diverse del campo sonoro al fine di ricavare le informazioni sulle caratteristiche del campo sonoro globale.

Il livello del rumore nell'ambiente in cui si vive dev'essere controllato, non soltanto perché i rumori molto intensi disturbano e impediscono la concentrazione, ma anche perché possono provocare danni permanenti all'orecchio: nella fig. 3 è riportata un'indicazione di massima di livelli di rumore. In seguito allo sviluppo dell'industrializzazione intensiva nelle aree urbane e al vertiginoso aumento del numero di veicoli e di motori (automobili, aerei, ecc.), l'insieme dei suoni ‛non desiderati' nella vita d'oggi ha raggiunto le dimensioni di un fattore di inquinamento, che è tra i maggiori responsabili del danneggiamento dell'ambiente. Si capisce quindi dal momento che il controllo del rumore è ancora a uno stadio assai poco soddisfacente il grande sforzo oggi profuso nella ricerca in questo campo.

La diminuzione del livello di rumore si può ottenere sia mediante un intervento sulle sorgenti, per esempio mediante una migliore progettazione delle macchine e delle strutture, sia mediante provvedimenti atti a proteggere l'ambiente in cui si vive dal suono generato esternamente. Entrambi i metodi possono risultare difficili da praticare, assai costosi e spesso assai poco efficienti.

Connessi con i problemi relativi al rumore sono quelli che riguardano la risposta delle strutture (costruzioni, macchinari, ecc.) agli urti; risposta di cui bisogna tener conto sia per avere un basso livello sonoro nell'ambiente sia per garantire la sicurezza d'esercizio delle strutture stesse. Nel costruire modelli di strutture complesse si incontrano generalmente grandi difficoltà, sia a livello matematico (i calcoli normalmente sono affidati all'elaboratore) sia a livello dei controlli sperimentali.

5. L'acustica architettonica.

Il campo sonoro nel punto di ricezione dipende in maniera determinante sia dalle caratteristiche della sorgente (forma, dimensioni, direttività), sia dagli oggetti presenti nel campo. Le lunghezze d'onda dei suoni udibili (da 8 a 10^-2 m) sono confrontabili con le dimensioni di molti oggetti dell'ambiente, così che la diffrazione risulta essere un fattore fondamentale per la determinazione del campo sonoro per esempio, si deve alla diffrazione la possibilità di udire, all'aperto, una persona che parli da dietro un ostacolo. Solamente nel caso in cui le dimensioni degli ostacoli siano grandi rispetto alle lunghezze d'onda, si può studiare la propagazione facendo ricorso all'approssimazione geometrica, come se l'energia viaggiasse lungo raggi che vengono riflessi e rifratti dalle superfici di separazione tra i diversi mezzi. Un caso di campo acustico di grande importanza pratica si ha allorquando un ambiente è occupato da un certo numero di ascoltatori. Scopo dell'acustica architettonica è far sì che sia assicurata una buona condizione d'ascolto in questi ambienti.

All'epoca dei Greci e dei Romani furono compiute imprese notevoli nella costruzione dei teatri all'aperto, al fine di assicurare una quantità sufficiente di energia a ognuno dei numerosi (sino a 30.000 ascoltatori e l'assenza di concentrazione del suono in certi punti (echi) ciò si otteneva seguendo alcune regole, quali la costruzione a forma di ventaglio del teatro, la disposizione a scala dei posti, la posizione dell'orchestra, la collocazione di superfici riflettenti al di sotto e alle spalle degli attori.

Le proprietà acustiche di luoghi chiusi adibiti a riunioni sono state largamente trascurate sino alla fine del secolo scorso. In epoche precedenti, quando si costruivano luoghi di riunione (chiese, sale da concerto, ecc.), non si consideravano affatto i problemi connessi col suono, cosicché le proprietà acustiche dei diversi ambienti ebbero notevole influenza sullo sviluppo della musica e delle comunicazioni; per esempio, le chiese gotiche posseggono tempi di riverberazione assai lunghi, che sono causa di inintelligibilità dei discorsi e dello sviluppo di particolari canti rituali; sempre gli effetti di riverberazione sono all'origine dello sviluppo della musica per organo; i tempi brevi di riverberazione delle sale da musica dei palazzi, dovuti alla presenza di tappeti e tappezzerie, hanno invece senza dubbio influenzato la composizione della musica da camera.

Le conoscenze dell'acustica incominciarono a essere applicate per la specificazione delle caratteristiche di luoghi chiusi attorno al 1895, da W. C. Sabine; i suoi esperimenti, condotti per lo più in sale di medie dimensioni, misero in evidenza la grande importanza che ha, al fine di caratterizzare l'acustica di un ambiente, il tempo di riverberazione, cioè il tempo che occorre perché il suono decada da una condizione stazionaria fino a esaurirsi o, meglio, fino a ridursi a un milionesimo (−60 dB) della sua intensità iniziale.

A seguito di ipotesi assai restrittive, come quella che la distribuzione sonora nell'ambiente sia uniforme e che tutte le direzioni dei raggi siano equiprobabili, il che comporta una diffusione del suono perfetta, Sabine fu in grado di calcolare un'espressione statistica del tempo di riverberazione (τ) in funzione solamente del volume (V) dell'ambiente e di un coefficiente (A), che rappresenta il potere totale di assorbimento dell'ambiente. Facendo uso delle unità del sistema internazionale, risulta

τ=0,16 V/A,

con A=α₁S₁+α₂S₂+..., dove gli α_i sono i coefficienti di assorbimento delle pareti di area S_i.

Tale formula fu successivamente migliorata da Eyring, il quale considerò più esattamente l'effetto delle riflessioni multiple sulle pareti. Queste formule sono assai utili ma, come successivi esperimenti hanno mostrato, non risolvono completamente il problema dell'acustica architettonica: oggi si pone anche in dubbio il risultato principale della soluzione data da Sabine al problema e cioè che τ non dipenda dalla forma dell'ambiente. Il tempo di riverberazione è certamente un parametro di fondamentale importanza e il suo valore ottimale dipende dall'uso che si intende fare dell'ambiente. Le sale per conferenze richiedono tempi di riverberazione più corti di quelle di eguali dimensioni destinate alla musica: i tempi lunghi di riverberazione provocano la sovrapposizione dei suoni successivi del discorso con una conseguente diminuzione dell'articolazione (misurata dalla percentuale di suoni monosillabici privi di significato pronunciati da chi parla e compresi da chi ascolta) e un peggioramento delle condizioni d'ascolto. Diamo i seguenti valori indicativi per i tempi di riverberazione, alla frequenza di 500 Hz, per sale di circa 10⁴ m³: 1 secondo per discorsi, 1,7 per la musica e 2 per la musica d'organo. Per molto tempo gli studi di progettazione di acustica ambientale si fondarono sull'analisi fatta da Sabine per i tempi di riverberazione; la si integrava con considerazioni sulla propagazione dei raggi, solitamente condotte sulla base di modelli delle sale da costruire, per assicurare l'assenza di echi, una buona distribuzione dell'energia sonora, l'esposizione diretta di ogni ascoltatore al suono proveniente dalla sorgente, ecc., e ci si preoccupava che il rumore nell'ambiente si mantenesse a un livello accettabile.

In relazione a ciò furono costruiti nuovi tipi di materiale assorbente e di dispositivi che migliorano la distribuzione dell'energia acustica nell'ambiente, sull'intero arco di frequenze che interessano: l'introduzione dei sistemi di amplificazione del suono ha offerto nuove possibilità e posto nuovi problemi per il conseguimento di buone condizioni di ascolto. Si è purtuttavia reso manifesto che l'analisi di Sabine è troppo elementare e in particolare che la forma dell'ambiente ha un'influenza considerevole, a parità delle restanti condizioni, sulle proprietà acustiche ambientali. Si può costruire una teoria migliore della distribuzione del suono in una stanza considerando lo spazio limitato alla stregua di una cavità caratterizzata da modi propri di vibrazione che possono esser messi in eccitazione dalla sorgente. La soluzione dell'equazione delle onde acustiche atta a determinare i modi di vibrazione diviene però un problema matematico di complessità notevolissima non appena la forma dell'ambiente, dalla quale dipendono le condizioni al contorno, non è più semplicissima; inoltre, l'assorbimento sulle pareti, che di norma varia con l'angolo di incidenza dell'onda, la presenza di assorbitori nell'ambiente (per esempio gli ascoltatori), la dipendenza dell'assorbimento di tali corpi dalla frequenza rendono l'effettiva situazione non descrivibile secondo una ragionevole approssimazione. A ciò si aggiunga il fatto che l'orecchio è l'ultimo giudice della situazione e che il giudizio, almeno in parte, è determinato da fattori fisiologici e psicologici.

Per questi motivi l'equazione delle onde non può fornire più di qualche criterio qualitativo (spesso assai vantaggioso, in ispecie quando si tratti di ambienti piccoli e di forma regolare) e si deve procedere empiricamente per determinare le proprietà acustiche dell'ambiente. Questo è quel che si fa attualmente. S'è trovato, per esempio, che il suono che raggiunge l'ascoltatore dopo essere stato riflesso da una parete è percepito in maniera diversa a seconda del tempo di ritardo rispetto al suono che giunge direttamente e a seconda della posizione (anteriore, destra, sinistra, posteriore) della superficie riflettente. È ovvio che non è solo il tempo di riverberazione ad avere importanza, ma anche il modo in cui, punto per punto della sala, i vari contributi del suono riflesso si sommano l'uno all'altro e al suono che proviene direttamente, almeno per un certo intervallo di tempo dopo la ricezione del suono diretto (circa 200 ms nelle sale da concerto); sembra anche probabile che le carattenstiche ottimali di sovrapposizione varino con la frequenza. Si comprende la complessità della situazione se si considera, per esempio, il gran numero di attributi soggettivi che nel caso di sale da concerto rientrano nel giudizio sulle qualità acustiche della sala: tra questi vanno compresi la vivacità (che dipende principalmente dal tempo di riverberazione), la ricchezza dei bassi, l'intensità, la chiarezza, il brio, la diffusione, l'equilibrio orchestrale, l'eco, il rumore di fondo, la distorsione, vari effetti di stereofonia spaziale.

Attualmente si stanno conducendo numerosi studi ed esperimenti su modelli reali e simulati al calcolatore, per cercare di migliorare la comprensione del modo in cui intervengono i vari fattori e i singoli effetti.

6. La bioacustica.

Il suono è uno dei tramiti più importanti mediante cui gli animali stabiliscono un rapporto con l'ambiente.

Negli ultimi anni si è dato inizio ad accurate ricerche per analizzare in dettaglio i suoni emessi nell'aria o nell'acqua da molti animali, i modi in cui si sono evoluti e funzionano nelle varie specie i meccanismi di produzione e di ricezione del suono e le funzioni svolte dai suoni prodotti da ciascuna specie per le esigenze vitali del singolo animale. Non ci è possibile qui entrare nei dettagli di questo tipo specializzato di ricerca interdisciplinare e ci limiteremo a poche indicazioni di carattere generale.

L'intervallo di frequenza usato varia ampiamente dagli infrasuoni agli ultrasuoni: è cosa ben nota che l'orecchio del cane è sensibile anche a frequenze di 70 kHz; viceversa i Pesci hanno un'alta sensibilità sui 300-500 Hz, mentre sono sordi alle frequenze di 1.500-2.000 Hz; gli invertebrati marini emettono un rumore con uno spettro contenuto tra i 20 e i 20.000 Hz; gli ultrasuoni emessi dai pipistrelli contengono frequenze attorno ai 50.000 Hz, ecc.

Interessante è l'uso che i pipistrelli fanno del suono: se ne servono per localizzare gli ostacoli attraverso una specie di sistema di rilevazione dell'eco. Il pipistrello emette ultrasuoni fatti di impulsi di 50 kHz circa e localizza gli ostacoli attraverso il tempo di ritardo e la direzione dell'eco; il ritmo di ripetizione degli impulsi è di 5-10 al secondo, quando il pipistrello è fermo, e aumenta fino a 20-30 quando vola in ambiente libero e a 50-60 in vicinanza di un ostacolo. La precisione ottenibile nella localizzazione degli ostacoli con tale sistema è piuttosto alta (la lunghezza d'onda nell'aria di un suono di 50 kHz è di 0,7 cm). Molto interessanti sono i dettagli di questo metodo altamente specializzato e del meccanismo fisiologico che consente di ottenere questi risultati (v. ultrasuoni negli animali).

Analoghi sistemi tipo ‛sonar', di localizzazione per eco, hanno anche le balene e i delfini. In questi casi dei ticchettii di durata inferiore al centesimo di secondo vengono prodotti entro camere d'aria della cavità nasale. Questi ticchettii hanno un contenuto energetico d'alta frequenza con uno spettro che si estende a 100-120 kHz. Il ritmo di ripetizione dipende dalla distanza degli ostacoli e può raggiungere valori di circa 200 impulsi al secondo.

Attualmente si stanno conducendo studi sistematici sui suoni emessi dai vari animali nell'aria e nell'acqua, da cui si ricavano dati che permettono, in molti casi, di distinguere le specie e di determinare talvolta il significato biologico di molti suoni usati dagli animali (comportamento territoriale, allarme, segnali sessuali, comunicazioni, organizzazione sociale, ecc.). Tali risultati sono di importanza considerevole al fine di avere una migliore conoscenza del comportamento animale e, associati a ciò che si sa sui meccanismi di produzione, ricezione e analisi dei suoni, permettono di progredire nello studio dell'evoluzione animale.

Le ricerche di bioacustica marina forniscono importanti contributi alla nostra conoscenza della biomassa oceanica, della sua distribuzione e del suo comportamento. A parte l'interesse intrinseco di questi studi, va tenuto presente che la biomassa oceanica costituisce una potenziale fonte di nutrimento per l'uomo.

7. L'acustica fisica.

Passiamo ora dai fenomeni che in qualche modo riguardano il funzionamento dei meccanismi di ricezione acustica all'esame delle caratteristiche fisiche della propagazione di onde elastiche nei materiali e dei fenomeni da queste indotti nella materia. È chiaro che i suoni udibili costituiscono una porzione assai limitata dell'intero spettro delle onde acustiche, sia per ciò che attiene alle frequenze, sia per i tipi di vibrazione. In particolare, la frequenza può variare con continuità da valori molto bassi (infrasuoni) ai valori dei suoni percepibili, fino a quelli degli ultrasuoni (si sono generati e studiati suoni con frequenze fino a 10¹¹ Hz). Finora, se si eccettua il caso delle onde sismiche nel terreno, il campo degli infrasuoni è stato poco studiato. I suoni di questa importante banda di frequenza sono stati presi in seria considerazione dopo lo sviluppo delle nuove apparecchiature elettroniche d'alta stabilità, con cui si possono eseguire misure che richiedono lunghi intervalli di tempo. Per esempio, s'è visto che l'atmosfera è piena di infrasuoni con periodo di oltre un secondo; ciò è dovuto al fatto che l'assorbimento a queste frequenze è molto basso e che quindi le onde originatesi in un punto dell'atmosfera per via di numerosi fenomeni naturali (temporali, terremoti, ecc.) si propagano per migliaia di chilometri senza un'apprezzabile attenuazione.

Gli ultrasuoni costituiscono sin dal 1920 un fruttuoso campo di ricerche, oggi largamente coltivato per lo studio delle proprietà della materia e per le possibili applicazioni tecnologiche.

Col crescere della frequenza tre proprietà delle onde elastiche divengono rilevanti e determinano le principali caratteristiche degli ultrasuoni: 1) l'energia tende a propagarsi per raggi rettilinei, che subiscono riflessioni e rifrazioni sulle superfici di discontinuità. Nelle figg. 4 e 5 sono mostrati fasci ultrasonori (tracce chiare) prodotti in un liquido da una sorgente di 8 MHz, riflessi da una superficie metallica ed eliminati da un assorbitore (v. fig. 4) o concentrati da una lente (v. fig. 5); 2) la lunghezza d'onda diminuisce, rendendo così possibile, con apparecchiature di laboratorio, l'osservazione del comportamento della materia sottoposta a sforzi elastici; 3) l'energia trasportata dalle onde cresce rapidamente. Nel caso di onde piane longitudinali l'intensità è data dall'espressione ρcA²ω²/2, dove ρ rappresenta la densità del mezzo, c la velocità del suono, A l'ampiezza di vibrazione dell'onda e ω=2πν: per esempio, nell'acqua l'intensità varia da 10^-2 a 10² W/cm² per ampiezze di 0,1 μm quando la frequenza ν passa da 20 kHz a 2 MHz. L'elevata densità di energia provoca vari effetti.

Un esempio degli effetti particolari connessi coi piccoli valori delle lunghezze d'onda è la diffrazione della luce prodotta dalle onde ultrasonore. Quando in un mezzo omogeneo e trasparente si produce un sistema di onde elastiche piane di alta frequenza (progressive o anche stazionarie), densità e indice di rifrazione risultano modulati sinusoidalmente e il mezzo stratificato si comporta approssimativamente come un reticolo di diffrazione per un raggio di luce che lo attraversi in direzione normale a quella del fascio sonoro. L'angolo di deviazione θ−θ₀ tra la direzione della luce diffratta e quella del raggio incidente è dato da una relazione simile a quella dei reticoli ottici: sen θ−sen θ₀=kΛ/λ, dove Λ e λ sono, rispettivamente, la lunghezza d'onda della luce e del suono e k è l'ordine dello spettro di diffrazione. La tav. f. t. mostra una figura di diffrazione della luce emessa da una lampada a incandescenza, prodotta da onde sonore di 8 MHz. La fig. 6 mostra gli spettri di diffrazione ottenuti con cristalli anisotropi la sorgente a quarzo di onde piane è posta su una faccia del cristallo; peraltro onde longitudinali e trasversali si generano in numerose direzioni per effetto della riflessione del suono all'interno del cristallo; ciascuna di tali onde diffrange la luce e provoca una serie di spettri di diffrazione che appaiono nella figura come immagini della sorgente puntiforme di luce.

Gli effetti di diffrazione, che furono scoperti quasi contemporaneamente (1932) da Debye e Sears negli Stati Uniti e da Lucas e Biquard in Francia, sono alla base di molti metodi di studio del campo sonoro e della determinazione della velocità e dell'assorbimento del suono in mezzi trasparenti. La visualizzazione del campo sonoro delle figg. 4 e 5 è stata fatta con il metodo schlieren (v. fig. 7), nel quale l'immagine di un piano del campo sonoro è ottenuta facendo uso della sola luce diffratta; la luce è inviata all'immagine unicamente dai punti del campo sonoro.

La posizione degli spettri di diffrazione e la loro intensità sono legate, rispettivamente, alla velocità e all'assorbimento del suono nel mezzo. Per mezzo della diffrazione della luce da parte del suono si sono anche potute costruire delle celle per la modulazione d'ampiezza o di frequenza della luce la modulazione d'ampiezza della luce diffratta, ovvero di quella non diffratta, si ottiene semplicemente modulando l'intensità del fascio sonoro; la modulazione di frequenza a frequenza 2ν si può facilmente ottenere sul raggio di luce non diffratto mediante l'impiego di un'onda sonora stazionaria di frequenza ν (la perturbazione svanisce 2ν volte al secondo). Tali celle, mediante le quali si può modulare la luce con potenze relativamente basse, sono di corrente applicazione nelle tecniche di modulazione di raggi di luce laser sulla banda di frequenze attorno a qualche megahertz.

Si può avere anche la riflessione alla Bragg, che è stata osservata a frequenze elevate. Di particolare interesse è il caso della riflessione alla Bragg della luce da parte di onde elastiche di origine termica (onde di Debye) presenti in un mezzo (diffusione, o scattering, di Brillouin). Le fluttuazioni adiabatiche della costante dielettrica di un mezzo si possono infatti descrivere mediante uno spettro ampio di onde piane che si propaghino in ogni direzione; l'interazione di un'onda luminosa piana di lunghezza d'onda Λ con un'onda sonora di lunghezza d'onda λ, che agisce da reticolo di diffrazione per via di una variazione sinusoidale dell'indice di rifrazione, porta alla riflessione alla Bragg secondo una direzione che forma un angolo θ_B con la direzione della luce incidente, dato dalla seguente espressione:

2λ sen(θ_B/2)=Λ/n,

in cui n è l'indice di rifrazione del mezzo non disturbato. Inoltre, a causa del movimento del reticolo di diffrazione, la frequenza della luce è variata per effetto Doppler, si che appare un doppietto nella luce diffratta; la variazione di frequenza è uguale alla frequenza dell'onda sonora e la posizione del doppietto ai lati della luce che non ha subito vanazioni dipende dalla velocità del suono. La larghezza totale δν di ciascuna riga del doppietto dipende da quanto l'onda sonora si scosta dalla forma sinusoidale pura, e cioè dall'assorbimento del suono:

α è il coefficiente d'assorbimento acustico per l'ampiezza A (A=A₀ e^-αx se x è scelto coincidente con la direzione di propagazione dell'onda). Nella fig. 8 è riportata l'analisi spettrale della luce diffratta a 90° da benzene a 23 °C (E. R. Pike e J. M. Vaugham). L'analisi è stata eseguita con un interferometro di Fabry-Perot e registrata con un multicanale. La sorgente luminosa era un laser a ioni d'argo (Λ=4.880 Å) a modo singolo.

Si può anche considerare una diffrazione stimolata alla Brillouin, ottenuta mediante gli effetti meccanici (elettrostrizione) prodotti dal campo elettrico dell'onda luminosa; si può dimostrare teoricamente che il campo elettrico della luce incidente deve superare un valore critico di soglia. L'effetto è stato osservato con l'impiego di luce laser. La diffrazione di Brillouin rappresenta un metodo di notevole importanza per la determinazione delle caratteristiche di propagazione (c, α) delle onde acustiche nella regione delle frequenze di 10⁹-10¹⁰ Hz. Ricerche siffatte furono iniziate con le sorgenti termiche tradizionali, ma hanno ricevuto un impulso enorme dall'impiego della luce laser che, grazie alle sue carattenstiche di monocromaticità, di collimazione e di intensità, ha notevolmente migliorato l'accuratezza delle misure.

Lo studio della propagazione del suono nella materia è diventato, a partire dall'ultima guerra mondiale, un potente mezzo d'indagine delle proprietà fondamentali della materia. Un gran numero di effetti particolan può manifestarsi in un mezzo allorché in esso si propaghino onde sonore; essi possono essere rivelati e studiati attraverso la determinazione delle caratteristiche di propagazione. Dobbiamo rammentare che la possibilità di tali studi si deve allo sviluppo di mezzi atti a produrre e rivelare le onde nella banda di frequenza degli ultrasuoni (fino a 10⁹ Hz), e cioè essenzialmente all'efficienza dei trasduttori elettroacustici.

L'impiego degli ultrasuoni è stato di importanza determinante non solamente perché il valore delle lunghezze d'onda (3×10^-4 m, 1,5×10^-3 m, 6×10^-3 m, circa, per frequenze di 1 MHz, rispettivamente in un gas in condizioni normali di pressione, in un liquido e in un solido) ha consentito di sviluppare apparecchiature compatte, ma anche perché ha aperto un campo in cui si possono osservare effetti diversi con tempi caratteristici notevolmente differenti. Le grandezze carattenstiche che si misurano solitamente sono la velocità del suono e il coefficiente di assorbimento. Si può determinare la velocità del suono misurando la lunghezza d'onda e la frequenza (come nel caso degli interferometri, in cui si varia la lunghezza di una colonna di fluido compresa tra sorgente e riflettore piano al fine di stabilire periodicamente le condizioni di stazionarietà), o il tempo di transito di un impulso attraverso un campione di spessore noto, o determinando il valore dell'indice di rifrazione acustico alla superficie di separazione tra due mezzi o la posizione degli spettri di diffrazione nell'interazione di un fascio luminoso con le onde acustiche. In casi particolari si può avere una precisione di 1 parte su 10.000, normalmente quella di 1 su 1.000. Il coefficiente d'assorbimento α si può determinare attraverso i segnali che si ottengono in un interferometro al variare della distanza tra sorgente e riflettore, o misurando l'intensità di luce dello spettro di diffrazione, a distanze diverse (x) dalla sorgente, di onde piane progressive, o misurando la pressione di radiazione esercitata da un'onda su un ostacolo (riflettente o assorbente), per valori diversi di x, o studiando (alle iperfrequenze) la forma delle linee di Brillouin. Il metodo di gran lunga più in uso oggigiorno nella regione dei MHz è quello dell'interferometro a impulsi in una delle sue numerose varianti si raffrontano l'una con l'altra le ampiezze degli echi successivi, mantenendo il riflettore in una posizione fissa, ovvero si segue l'ampiezza di una data eco a mano a mano che il riflettore si muove mantenendosi parallelo alla sorgente.

Il valore della velocità c di propagazione del suono al limite delle basse frequenze è legato alle costanti elastiche e termodinamiche. Valgono, per le onde longitudinali (1), rispettivamente nei gas, nei liquidi e nei solidi omogenei (in mezzi illimitati), le espressioni seguenti:

dove ρ è la densità, p la pressione statica del gas, β_ad la compressibilità adiabatica, E il modulo d'elasticità di estensione (Young). γ=c_p/c_v è il rapporto tra i calori specifici a pressione e a volume costanti e compare per via della natura adiabatica delle compressioni e delle dilatazioni che avvengono nel mezzo quando vi si propagano le onde elastiche. La velocità delle onde trasversali (t) nei solidi omogenei e illimitati è

con G modulo di elasticità di scorrimento.

Nei solidi limitati (per es. sbarre, piastre) la velocità di propagazione dipende non solo dalle carattenstiche elastiche del materiale, ma anche dalla frequenza dello specifico modo di vibrazione. Nel caso di solidi aventi una superficie di separazione con un altro mezzo, è possibile la propagazione di un altro tipo di onde, le onde superficiali (v. cap. 9). Noi qui vogliamo considerare, peraltro, i legami tra caratteristiche di propagazione e struttura dei mezzi.

L'assorbimento del suono è dovuto, alle basse frequenze, alla viscosità di scorrimento e alla conduzione del calore (assorbimento classico). Si capisce quindi come la propagazione di suoni di bassa frequenza possa fornire informazioni importanti sulle proprietà di un materiale in equilibrio termodinamico. Inoltre, se si studiano le caratteristiche elastiche al variare della frequenza, si trova che ciascun mezzo ha solitamente una o più bande in cui la velocità del suono varia (dispersione) e in cui l'assorbimento può essere assai più grande del suo valore classico.

Queste variazioni di solito debbono la propria origine alla presenza di effetti di rilassamento: normalmente, infatti, l'energia può essere presente all'interno di un sistema sotto varie forme e una distribuzione di equilibrio corrisponde a uno stato di equilibrio termodinamico; se questo è alterato da variazioni di pressione o di temperatura prodotte dalle onde elastiche, il mezzo può comportarsi come se possedesse un valore della compressibilità più basso di quello limite per le basse frequenze, e tra le variabili esterne e le condizioni interne può verificarsi un ritardo che determina un ulteriore assorbimento del suono. Gli equilibri presenti in un mezzo e che originano fenomeni di rilassamento possono essere di vari tipi.

a) La propagazione nei gas.

Al fine di illustrare le caratteristiche fondamentali dei processi di rilassamento, facciamo riferimento al più semplice di tali processi, uno di quelli che possono aver luogo nei gas poliatomici. In questi casi, le molecole possono avere energia di traslazione, di rotazione e di vibrazione; l'equilibrio statistico tra le varie forme, proprio di ogni temperatura, è raggiunto attraverso il meccanismo delle collisioni. Si supponga che una data massa di gas poliatomico, contenuta in un recipiente cilindrico dotato di un pistone, sia in equilibrio a pressione p₁, temperatura T₁ e volume V₁; si cambi d'improvviso il volume fino al valore V₂ (v. fig. 9), per esempio con un movimento rapido del pistone; al termine della compressione il gas non è più in equilibrio, cioè pressione e temperatura (p₂, T₂) differiscono da quelle, p₃ e T₃, che si avrebbero in condizioni d'equilibrio. Infatti, le molecole del gas interagiscono col pistone in movimento acquistando energia sotto forma di energia di traslazione (dalla quale dipende la temperatura esterna del gas, quale si può misurare normalmente); il passaggio dell'energia ai gradi di libertà rotazionali e vibrazionali avviene negli urti tra molecole e il conseguimento della distribuzione d'equilibrio dell'energia richiede pertanto un certo intervallo di tempo.

In realtà, la stessa equipartizione dell'energia tra i vari gradi di libertà di traslazione (tre gradi di libertà) avviene mediante le collisioni; ma, poiché per stabilire questo equilibrio bastano poche collisioni, per semplicità si può ritenere che esso si instauri istantaneamente. Volendo illustrare uno soltanto di questi processi di rilassamento, quello relativo al passaggio di energia ai gradi di libertà vibrazionali, supponiamo che si stabilisca assai rapidamente anche l'equilibrio tra gradi di libertà di traslazione e di rotazione e che si possa distinguere tra gradi di libertà esterni (di traslazione e rotazione) e interni (di vibrazione); per carattenzzarne l'energia media istantanea si può anche introdurre una temperatura esterna (T_e) e una interna (T_i); all'equilibrio naturalmente T₃=T_i. Facciamo riferimento al processo illustrato nella fig. 9 la variazione della temperatura esterna subito dopo la compressione (T_e>T_i) è dovuta al passaggio di energia dai gradi di libertà esterni (E_e) ai gradi interni (E_i); il conseguimento dell'equilibrio (T_e=T_i=T₃) richiede mediamente un certo numero di collisioni e cioè un intervallo di tempo caratteristico (τ₀); contemporaneamente si ha il rilassamento della pressione in sovrappiù (p₂−p₃) Il processo si inverte se si considera una rapida espansione. Considerando ora un processo ciclico di compressioni ed espansioni, come avviene durante la propagazione del suono, è ovvio che il comportamento del mezzo dipende fortemente dal rapporto tra il periodo proprio della perturbazione (τ) e il tempo di rilassamento. Se τ≫τ₀, in ogni fase del ciclo il sistema ha tempo sufficiente per raggiungere l'equilibrio; passa quindi attraverso stati termodinamici di quasi equilibrio e il suo comportamento non differisce da quello già esaminato al limite zero della frequenza. Se τ≪τ₀, non c'è tempo sufficiente per lo scambio di energia tra gradi di libertà interni ed esterni: tuttova come se non esistessero gradi di libertà interni (equilibrio congelato); scompare il contributo al calore specifico dei gradi interni; il rapporto γ tra i calori specifici è più grande del valore che esso possiede alle basse frequenze e lo Stesso vale per la velocità del suono (v. fig. 10). Le perdite di energia per ciclo (cioè il prodotto αλ) sono molto basse alle alte frequenze, così come lo sono alle basse. Viceversa, quando τ e τ₀ sono confrontabili, lo scambio di energia tra i gradi di libertà esterni e interni diviene sempre più difficile al crescere della frequenza, l'energia scambiata diminuisce e la temperatura interna ritarda rispetto a quella esterna; ciò porta a un calore specifico relativo ai gradi di libertà interni, C_i, che diminuisce al crescere della frequenza (cioè a una velocità sonora che aumenta) e a un assorbimento per ciclo che raggiunge il valore massimo per τ=τ₀. Nella fig. 10 sono dati gli andamenti tipici della velocità del suono c/c₀, di α/ν² e di αλ nel caso di un unico processo di rilassamento (A=(c_∞−c₀)/c_∞ è la cosiddetta intensità del processo di rilassamento). La fig. 11 fornisce i dati relativi al CO₂ (W. Leonard). Da questa descrizione elementare di un semplice processo di rilassamento si ricavano gli andamenti di c e αλ in funzione della frequenza (Herzfeld-Rice), che, con opportune variazioni, sono validi per tutti i fenomeni di rilassamento, come si può verificare formalmente con la termodinamica dei processi irreversibili, o con la meccanica statistica, o anche con la teoria quantistica delle perturbazioni.

Due sono le grandezze che interessano in un processo di rilassamento la costante che descrive l'ampiezza dell'effetto (nel caso considerato dei gas, il rapporto C_i/C_e dei contributi dei gradi di libertà interni ed esterni al calore specifico a volume costante) e il tempo di rilassamento. Entrambe queste grandezze danno indicazioni sulla struttura della materia. Nel caso di gas poliatomici la prima grandezza permette di stabilire quali stati vibrazionali siano interessati al fenomeno; la fig. 12 si riferisce a un caso (diclorometano) in cui il passaggio di energia ai gradi di libertà vibrazionali della molecola avviene con due distinti tempi caratteristici e in cui si possono riconoscere i modi di vibrazione implicati in ciascun processo. Il tempo di rilassamento dipende strettamente dalle forze intermolecolan durante l'urto e la sua determinazione sperimentale consente di ricavare ulteriori informazioni su tali forze. Analoghi processi di rilassamento hanno luogo in regioni diverse di frequenza (o a pressioni medie p diverse; nei gas, il parametro veramente importante è il rapporto ν/p), per l'equilibrio nella distribuzione di energia tra gradi di libertà di traslazione e di rotazione e tra i tre gradi di libertà di traslazione.

Lo studio sperimentale del comportamento dei gas alle frequenze alle quali il cammino libero medio è grande rispetto alle lunghezze d'onda è di notevole interesse per lo sviluppo di opportune teorie esperienze eseguite fino a frequenze alle quali il cammino libero medio corrisponde a circa 10 lunghezze d'onda mostrano che il coefficiente di assorbimento in questa regione cresce quasi proporzionalmente con la frequenza ν e la velocità si mantiene approssimativamente costante; la teoria basata sull'ipotesi di mezzi continui (la teoria esatta di Navier-Stokes) non si adatta affatto ai risultati.

b) La propagazione nei liquidi.

Nei liquidi, numerose condizioni di equilibrio tra i vari modi in cui l'energia può distribuirsi possono esser perturbate dalle onde acustiche e dar luogo a effetti di rilassamento. Innanzitutto sussiste il medesimo processo osservato nei gas, cioè un effetto di rilassamento termico nella distribuzione dell'energia tra i gradi di libertà interni ed esterni delle molecole; in tal caso sono le variazioni di temperatura prodotte dall'onda che determinano la perturbazione, e il processo può essere descritto con un'espressione del calore specifico che dipenda dalla frequenza. Presentano questo effetto i liquidi che hanno molecole simmetriche, non polari (CCl₄, SO₂), nei quali non vi siano forti associazioni molecolari (liquidi di Kneser, dal nome del fisico che per primo propose una spiegazione per l'assorbimento in eccesso nei liquidi). In molti liquidi vi sono delle associazioni che possono presentarsi sotto forma di strutture quasi cristalline. Tipico è il caso dell'acqua dalle esperienze di Fox e Rock risulta evidente che nel caso dell'acqua il rilassamento termico non costituisce il più importante processo responsabile dell'eccesso di assorbimento, dal momento che questo è presente anche a 4 °C, temperatura alla quale, in conseguenza del caratteristico massimo di densità, la propagazione del suono, secondo la termodinamica, è isoterma e la distribuzione dell'energia tra i gradi di libertà interni ed esterni non viene alterata. In tal caso si deve pensare a un fenomeno di rilassamento strutturale le molecole possono disporsi almeno secondo due strutture caratterizzate da volumi specifici ed energie libere differenti e l'equilibrio è alterato dalle variazioni di pressione prodotte dalle onde sonore. In un tal caso, il processo può essere analizzato mediante un'espressione della compressibilità che dipenda dalla frequenza. Ci sono anche dei liquidi (delle soluzioni, per esempio) in cui avvengono reazioni chimiche il cui equilibrio può essere alterato dalle onde sonore la differenza tra i coefficienti di assorbimento dell'acqua di mare e dell'acqua distillata è dovuta principalmente all'alterazione di un equilibrio al quale partecipa lo ione magnesio.

Si deve notare che in moltissimi liquidi ciascun tipo di rilassamento ha luogo con una distribuzione dei tempi di rilassamento che dipende sia dalla varietà dei modi in cui si possono disporre le molecole, sia dalla complessità delle corrispondenti condizioni di equilibrio alterate dal suono.

Lo studio dell'assorbimento nei liquidi entro una vasta gamma di frequenze ha promosso lo sviluppo di una specie di spettroscopia ultracustica, che è di grande interesse per l'esame della struttura e del comportamento dei liquidi.

Va notato che il coefficiente classico di assorbimento è stato determinato sulla base di un'ipotesi relativa al comportamento dei due coefficienti di viscosità che s'introducono nell'espressione tensoriale degli sforzi. Tale ipotesi è valida soltanto nel caso di gas monoatomici e, se la si lascia cadere, si giunge a un espressione del coefficiente di assorbimento che dipende non solamente dal coefficiente della viscosità di scorrimento, ma anche da quello della viscosità di volume; i processi di rilassamento sopra descritti possono anche esser considerati come modi per determinare il comportamento del coefficiente di viscosità di volume in funzione della frequenza.

Lo studio degli ultrasuoni può esser fatto anche con le onde trasversali (o di scorrimento) e non solamente con quelle longitudinali. L'applicazione degli ultrasuoni ha mostrato che i liquidi, in conseguenza della loro struttura quasi cristallina, posseggono una rigidità di scorrimento (analogamente ai solidi), se gli sforzi sono applicati per un tempo sufficientemente breve.

Le ricerche sulle onde trasversali hanno mostrato che la viscosità di scorrimento è un processo di rilassamento e hanno consentito di determinare i tempi di rilassamento e il modulo di elasticità di scorrimento alle alte frequenze (G_∞): i valori di G_∞ dei liquidi del tipo del glicerolo non differiscono gran che da quelli dei solidi (per il glicerolo circa 1/30 di quello del nichel). La spettroscopia ultracustica nei liquidi può essere perciò estesa al caso delle onde trasversali.

Qui si sono voluti dare solo alcuni esempi dei tipi di processi di rilassamento che avvengono nei liquidi e che possono essere utilizzabili per lo studio della struttura della materia si potrebbero ricordare altri casi di grande importanza nel campo dei processi critici, dei polimeri, dei vetri, ecc.

Prima di concludere queste indicazioni generali sugli studi ultracustici dello stato liquido, si vuole qui ricordare il caso dei moti ondulatori nell'elio liquido, che hanno suscitato un interesse particolare.

I due isotopi stabili ⁴He e ³He obbediscono a statistiche differenti (rispettivamente a quella di Bose-Einstein e a quella di Fermi). L'⁴He liquido può presentare vari tipi di moti ondulatori, cui è stato dato il nome di ‛primo suono', ‛secondo suono', ecc., sebbene alcuni di questi non siano onde sonore nel senso tradizionale del termine. La propagazione isoentropica di un'onda di compressione prende il nome di ‛primo suono' la sua velocità presenta un andamento a cuspide al passaggio della temperatura, fatta variare verso valori sempre più bassi, attraverso il punto λ. Sotto questo punto λ (2,2 °K) l'⁴He si modifica in He II, nel quale è praticamente assente la viscosità e la conducibilità termica (superfluidità) aumenta notevolmente.

Nell'He II si può avere un nuovo tipo di movimento ondulatorio che viene impropriamente detto ‛secondo suono'. In realtà le onde sono onde termiche; il fenomeno è messo in evidenza dal fatto che un impulso di temperatura generato in un punto da un riscaldatore modulato è ricevuto praticamente senza alcun disturbo in un punto diverso del liquido (v. criofisica). La velocità del secondo suono aumenta in maniera complessa dal valore zero a mano a mano che la temperatura viene abbassata al disotto del punto λ. ‛Terzo suono' è detto il modo relativo a onde che si propagano sulla superficie di una pellicola di elio. Il ‛quarto suono' è il modo di un'onda particolare che può propagarsi quando l'He II è contenuto in capillari; nel quarto suono si hanno contemporaneamente cambiamenti di pressione, temperatura, densità ed entropia per unità di massa. Il ‛suono zero' e un modo analogo a quello delle normali onde longitudinali, avente velocità e coefficiente di assorbimento diversi da quelli del suono ordinario, e può presentarsi soltanto a temperature assai basse (da cui il nome) in un sistema che obbedisca alla statistica di Fermi; lo si può notare e studiare nell'³He liquido. Non vi è qui modo di dare ulteriori più approfondite informazioni, ma è manifesto che lo studio della propagazione dei ‛suoni' a varie frequenze nell'elio liquido costituisce un potente mezzo d'indagine delle caratteristiche fondamentali del comportamento di tali sistemi quantici.

c) La propagazione nei solidi.

Se ora passiamo a considerare la propagazione di onde elastiche nei solidi, ci imbattiamo in un gran numero di processi i quali comportano dissipazioni di energia e variazioni di velocità. (V. anche solidi, fisica dei).

In aggiunta alla diffusione, che può divenire una causa importante di perdita di energia acustica qualora siano presenti inomogeneità elastiche (quali gruppi di difetti nei cristalli, precipitati, superfici di confine di grani, pareti di domini magnetici), le perdite più importanti si riscontrano nei processi di rilassamento connessi o con proprietà intrinseche dei solidi, cioè presenti anche nei cristalli perfetti, o con difetti di vario tipo (impurità, dislocazioni, ecc.), propri del campione in esame. Una prima causa di dissipazioni (effetto termoelastico) consiste nel fatto che, ogni qual volta si applica uno sforzo a un materiale, la conseguente deformazione è accompagnata da una variazione di temperatura; in una distribuzione non omogenea di deformazioni, qual è quella prodotta da un'onda sonora, appaiono dei gradienti di temperatura tra regioni di compressione e di rarefazione che provocano la conduzione di calore e quindi l'assorbimento acustico. Zener per primo ha considerato questo tipo di perdite per spiegare il decadimento che si osserva nella vibrazione di piastrine a frequenze relativamente basse (circa 500 Hz). È ovvio che, per vibrazioni molto lente, le trasformazioni di energia meccanica in calore e viceversa avvengono in maniera reversibile e isotermica e non si hanno perdite; lo stesso accade a frequenze molto alte alle quali il trasferimento di calore non ha tempo sufficiente per avvenire e la trasformazione diviene nuovamente reversibile (e adiabatica). Le perdite dovute a trasferimento di calore si verificano tra questi limiti con un tipico meccanismo di rilassamento; il tempo di rilassamento (Zener) dipende dal coefficiente di diffusione termica del materiale e dalle dimensioni della piastrina vibrante.

Un altro effetto termoelastico si ha nei metalli policristallini non cubici, quale conseguenza di disuniformità della distribuzione della temperatura, che insorgono allorquando un'onda sonora si propaga in una struttura a grani aventi assi cristallografici diversamente orientati; anche questo fenomeno comporta perdite per conduzione termica secondo un meccanismo di rilassamento. Altre specie di rilassamenti e di perdite si hanno nelle soluzioni solide, per il fatto che le posizioni preferenziali delle impurità dipendono dalla pressione e che i gradienti di pressione prodotti dalle onde sonore danno origine a un processo di diffusione: i tempi di rilassamento sono piuttosto lunghi, anche a temperature relativamente elevate. Anche nei cristalli chimicamente puri ci sono imperfezioni, quali le dislocazioni, che si muovono se sottoposte a gradienti di pressione; questo processo di diffusione avviene lentamente e il rilassamento corrispondente si osserva solitamente alle basse frequenze e spesso anche a temperature piuttosto elevate. Lo studio di questo e di altri processi ancora (Bordoni, Truell, Granato), che caratterizzano il comportamento delle dislocazioni in un campo acustico, costituisce un potente mezzo d'indagine di importanti proprietà dei solidi. Nel caso in cui un'onda ultrasonora si propaghi in un cristallo ferromagnetico, si verifica un altro processo di rilassamento, dovuto al fatto che le posizioni delle pareti di Block (tra domini magnetici) dipendono dalle deformazioni presenti in seno al materiale: le pareti vibrano, alla frequenza dell'onda sonora, con un ampiezza e una fase che dipendono dalla frequenza e dalle deformazioni; questo movimento periodico delle pareti induce delle correnti parassite e provoca delle perdite nel materiale.

Tutti questi processi hanno tempi caratteristici piuttosto lunghi e sono osservabili alle basse frequenze. Alle alte frequenze si verificano nuovi processi, nei quali si ha uno scambio di energia tra il campo sonoro e il sistema solido: di solito questi fenomeni evidenziano il fatto che la continuità delle onde sonore, ipotizzata nelle trattazioni classiche, è solo un'approssimazione che si dimostra adatta per l'analisi a bassa frequenza, mentre in realtà si deve tener conto della quantizzazione dell'energia acustica (così come di quella elettromagnetica) secondo fononi di energia hν. In questi processi elementari si deve distinguere l'interazione delle onde sonore con portatori liberi da quella con il reticolo cristallino: si possono verificare tutte e due nei metalli e solo la seconda nei dielettrici. Un primo processo che comporta l'assorbimento acustico da parte degli elettroni nei metalli (Bömmel) si può descrivere come dovuto agli urti tra gli elettroni e i fononi che rappresentano le onde sonore di Debye di origine termica. In condizioni di equilibrio gli scambi di energia tra elettroni e fononi non modificano l'energia media posseduta dai due tipi di particelle; se sono gli elettroni a possedere un'energia superiore a quella d'equilibrio, l'energia in eccesso è trasferita alle onde di Debye (effetto Joule); se, viceversa, le onde sonore che si propagano in una direzione hanno energia superiore al valore d'equilibrio, come accade nel caso in cui un'onda è generata nel campione dall'esterno, il trasferimento di energia dal suono agli elettroni prevale sul flusso energetico in verso opposto e di conseguenza si ha un assorbimento del suono. Il processo dipende strettamente dal rapporto tra la lunghezza d'onda acustica e il cammino libero medio degli elettroni: a basse temperature (10 °K) e a 100 MHz (corrispondenti a λ=10^-5 m) il cammino libero degli elettroni, che in metalli molto puri è di circa 10^-3 m, può divenire più piccolo di λ nei metalli non puri. Lo studio di questo effetto in funzione della temperatura si è dimostrato di particolare utilità nei superconduttori, dove ha posto in luce l'esistenza di un intervallo proibito di energia nella distribuzione degli elettroni alla temperatura di transizione alla superconduttività come è indicato dalla teoria di Bardeen-Cooper-Schrieffer e una sua anisotropia nei cristalli. Sono stati fatti calcoli semiclassici e quantistici relativamente all'interazione tra elettroni di conduzione e onde ultrasonore.

Di particolare utilità è lo studio delle interazioni tra gli elettroni liberi e le onde sonore in un cristallo in presenza di un campo magnetico (Morse, Bömmel). Il campo magnetico in primo luogo. incurva la traiettoria degli elettroni e riduce la distanza tra urti successivi nella direzione di propagazione dell'onda; ciò, come si può mostrare, riduce l'assorbimento dell'onda acustica. Questo è il solo effetto che si ha nel caso in cui il cammino libero medio degli elettroni (l_e) sia minore dell'inverso della costante di propagazione (q=2π/λ), cioè nel caso in cui sia ql_e〈1. In tal caso il rapporto α(H)/α(0) tra il coefficiente d'assorbimento in presenza di un campo magnetico H, normale alla propagazione dell'onda, e il coefficiente di assorbimento in assenza di campo dipende dalla frequenza di ciclotrone (ω_c=eH/mv, dove e ed m sono, rispettivamente, la carica e la massa dell'elettrone e v è la velocità della luce), come in un tipico processo di rilassamento, e decresce in maniera monotona con H.

Assai più interessante è tuttavia il caso in cui sia ql_e>1, cioè il caso in cui il cammino libero medio sia più grande della lunghezza d'onda: il coefficiente d'assorbimento riportato in funzione del campo magnetico presenta un comportamento approssimativamente dovuto alla sovrapposizione di oscillazioni smorzate a una diminuzione monotona. Si sono individuate tre specie di oscillazioni.

1. Risonanze geometriche. Si ha un effetto tipo risonanza quando il campo magnetico è tale che le orbite elettroniche, tra un urto e il successivo, siano semicirconferenze di diametro pari a un multiplo intero di lunghezze d'onda del campo acustico; la trattazione quantistica del fenomeno mostra che, per un'onda che si propaghi secondo la direzione x e un campo magnetico orientato in direzione z, l'attenuazione degli ultrasuoni in funzione di 1/H ha andamento periodico con periodo dipendente dalla dimensione della superficie di Fermi nello spazio dei momenti (k) lungo la direzione y (vale a dire k_y) e dalla frequenza acustica.

2. Oscillazioni quantiche. L'origine di questo processo è simile a quella che determina le oscillazioni della suscettività magnetica (effetto de Haas-van Alphen) e della resistività elettrica (effetto Shubnikov-de Haas). Queste oscillazioni si osservano quando un'onda acustica si propaga in una direzione non perpendicolare ad H e danno luogo a un assorbimento periodico in funzione di 1/H che, tuttavia, diversamente dagli effetti 1 e 3, non dipende dalla frequenza del suono. I livelli di energia degli elettroni in presenza di un campo magnetico si separano (livelli di Landau); l'interazione tra elettroni e onde acustiche si ha per gli elettroni della superficie di Fermi e l'attenuazione acustica ha luogo per effetto dell'assorbimento, da parte degli elettroni, di un quanto d'energia dell'onda acustica; le leggi di conservazione dell'energia e della quantità di moto determinano le caratteristiche dell'interazione e si può mostrare che le oscillazioni dell'assorbimento degli ultrasuoni periodiche in 1/H consentono di eseguire la misura di una qualunque sezione della superficie di Fermi normale al campo magnetico (la giacitura di tali sezioni può essere cambiata variando il vettore d'onda q).

3. Risonanze acustiche di ciclotrone. Hanno luogo quando la frequenza acustica è un multiplo intero della frequenza elettronica di ciclotrone; anche in tal caso la periodicità della frequenza acustica dipende da importanti caratteristiche della superficie di Fermi degli elettroni.

Nei solidi non conduttori si deve considerare l'assorbimento dovuto al reticolo cristallino. Un primo tipo di assorbimento è stato osservato nei solidi molecolari (quali il benzene) ed è stato interpretato (Libermann) come dovuto a un lento scambio di energia tra le onde di Debye e le vibrazioni intermolecolari, prodotto da una debole interazione continua che ha origine nei termini di anarmonicità. Una causa più generale di assorbimento dovuto al reticolo risiede nell'interazione tra le onde ultrasonore e le onde termiche, determinata dal comportamento non lineare dei solidi: questo processo non avrebbe ragione d'esistere se le forze interatomiche fossero rigorosamente armoniche; viceversa gli spostamenti degli atomi nei solidi non sono linearmente legati alle forze. Il comportamento anarmonico può essere trattato considerando i termini del terzo ordine o di ordine più elevato nell'espressione dell'energia elastica. Quantisticamente, si debbono considerare processi a fononi multipli (fononi acustici e termici) in cui si conservano quantità di moto ed energia.

Altre interazioni che possono essere studiate con profitto nei solidi, mediante misure di assorbimento acustico, sono quelle con le onde di spin nei cristalli ferromagnetici, con le onde di spin nucleari e con gli spins elettronici dei centri paramagnetici.

Quando un metallo diviene superconduttore, l'assorbimento degli ultrasuoni diminuisce rapidamente al diminuire della temperatura, a causa del venir meno del contributo all'assorbimento da parte degli elettroni di conduzione gli elettroni nello stato superconduttore, infatti, non interagiscono con le onde acustiche. Questo comportamento trova la sua logica spiegazione nella teoria di Bardeen-Cooper-Schrieffer della superconduttività.

Di particolare interesse è lo studio della propagazione delle onde elastiche nei cristalli piezoelettrici, dove le onde elettromagnetiche si accoppiano con le onde sonore così che l'analisi richiede l'uso contemporaneo dell'equazione delle onde elastiche e delle equazioni di Maxwell. Generalmente, l'accoppiamento tra questi due tipi di onde dà origine a tre onde elastiche e due elettromagnetiche: tra queste onde esistono delle differenze sostanziali. Ci sono onde elastiche ‛veloci', la cui velocità di fase s'avvicina a quella delle onde elettromagnetiche e che si possono interpretare come deformazioni meccaniche che accompagnano l'onda elettromagnetica; ci sono onde elettromagnetiche ‛lente', con velocità di fase prossima a quella delle onde elastiche, che si possono interpretare come variazioni di campo elettrico che accompagnano l'onda elastica. La situazione può essere ancor più complessa, come nel caso in cui il cristallo, oltre a essere piezoelettrico, è anche semiconduttore: il legame tra la densità di corrente e il campo elettrico è assai più complicato di quello espresso dalla semplice legge di Ohm, per la presenza di termini di diffusione nella conduttività dovuta ai portatori di cariche. In tal caso l'attenuazione e la dispersione dell'onda elastica possono verificarsi come conseguenza dell'interazione di questa con le correnti e le cariche spaziali generate dal campo elettrico interno dovuto all'effetto piezoelettrico. In un semiconduttore piezoelettrico si può anche ottenere (come si è fatto, per esempio, con il CdS) l'amplificazione delle onde acustiche mediante l'applicazione di un campo elettrico costante in direzione della propagazione, che faccia muovere i portatori di canche con velocità maggiore di quella delle onde acustiche.

Un'onda elastica che si propaghi in un semiconduttore, ovvero in un conduttore che presenti una particolare struttura di bande, può interagire con i portatori di cariche in modo da produrre una differenza di potenziale costante tra le estremità del campione nella direzione della propagazione dell'onda: a questo effetto si dà il nome di ‛effetto acustoelettrico'; esso è essenzialmente dovuto al raggruppamento dei portatori di cariche, prodotto dal potenziale di deformazione, e lo si pone facilmente in evidenza nei semiconduttori, poiché la presenza di due tipi di portatori impedisce la comparsa di cariche spaziali apprezzabili e delle conseguenti forze di repulsione. È stato osservato che l'effetto si può pensare come prodotto dalla pressione di radiazione esercitata dall'onda ultrasonora sui portatori liberi che agiscono da assorbitori.

d) L'acustica dei plasmi.

L'acustica dei plasmi studia alcuni fenomeni dinamici nei gas neutri ionizzati, che dipendono da forze generate da campi elettrici e magnetici esterni e dallo stesso movimento del gas. Tali fenomeni hanno una stretta dipendenza dallo stato di ionizzazione del gas e cioè dal rapporto tra il numero di particelle cariche e il numero di particelle neutre contenute nell'unità di volume. Nei plasmi debolmente ionizzati (10¹⁰ ioni su 10¹⁶ molecole neutre per centimetro cubo) prevale l'effetto del gas neutro e le particelle cariche, in un'onda sonora ordinaria, sono costrette a seguire quelle neutre. Le particelle cariche (elettroni e ioni) traggono però energia dal campo elettrico esterno che sostiene il plasma nel suo stato; parte dell'energia degli elettroni si trasferisce alle particelle neutre (la temperatura degli elettroni è di circa 10⁴÷10⁵ °K, mentre quella del gas neutro si mantiene attorno ai 500 °K). Questo processo può a) provocare un trasferimento di energia elettrica alle onde acustiche, e quindi un'amplificazione dell'onda inviata dall'esterno, se sono soddisfatte opportune condizioni d'accoppiamento; b) condurre a un'eccitazione spontanea dei modi acustici all'interno del recipiente contenente il plasma, in conseguenza di perturbazioni della densità; c) dar origine a un'onda acustica nel gas neutro, se il campo elettrico esterno viene periodicamente variato.

In tutte queste onde che si generano nei gas debolmente ionizzati le particelle neutre, gli ioni e gli elettroni si muovono approssimativamente con la stessa fase e con la stessa ampiezza; l'accoppiamento forte si ha mediante gli urti e la velocità di propagazione è quasi la medesima che si ha nel gas non ionizzato.

Al contrario, nei gas fortemente ionizzati si può trascurare l'effetto delle particelle neutre e i fenomeni che si producono sono dovuti agli elettroni e agli ioni che hanno differenti velocità termiche e, in generale, anche differenti temperature; la temperatura degli elettroni, generalmente, è molto più elevata di quella degli ioni. Sono possibili vari tipi di moti ondulatori. Nella cosiddetta onda acustoionica non c'è separazione di cariche; si possono osservare delle perturbazioni della densità e, corrispondentemente, delle variazioni adiabatiche della temperatura; in questo tipo di moto ondulatorio, gli ioni rappresentano la parte inerziale e agli elettroni spetta il compito di produrre la forza di richiamo. Di importanza maggiore è un altro tipo di moto, longitudinale, le cui caratteristiche essenziali sono la separazione delle cariche e il campo elettrico corrispondente (oscillazioni di plasma). La presenza di un campo magnetico rende il plasma anisotropo e la propagazione di onde diviene considerevolmente più complessa (onde magnetoacustiche).

Tutti questi tipi di onde elastiche sono molto importanti per il comportamento dei plasmi e vengono studiate a fondo nella fisica dei plasmi e in astrofisica.

Dal breve resoconto fatto dei risultati ottenuti negli ultimi decenni nei campi di studio dell'acustica fisica e della struttura della materia si capisce perché le ricerche di ultracustica siano diventate tanto importanti e perché si vadano compiendo intensi sforzi per generare e utilizzare onde acustiche di frequenze elevatissime. Il limite attuale delle frequenze ultrasonore non va oltre 10¹¹ Hz; se si potesse aprire alla ricerca la banda delle frequenze comprese tra 10¹¹ e 10¹⁴ Hz, ne risulterebbero enormemente ampliate le cognizioni sulla struttura della materia. In quella banda, infatti, sono comprese le frequenze di rilassamento dei gas che hanno composizione molecolare semplice, i cui processi di collisione potrebbero essere analizzati teoricamente con più facilità che non quelli dei gas che hanno una complessa molecola poliatomica. Anche nei liquidi i processi di rilassamento presentano tempi dell'ordine di 10^-12 s.

Frequenze dell'ordine di 10¹³÷10¹⁴ Hz corrispondono alle frequenze critiche del reticolo cristallino dei solidi, alle quali l'energia dei fononi (hν=4×10^-4 eV per ν=10¹¹ Hz) diventa adatta a indurre transizioni quantiche negli atomi. Le ricerche in questi campi di frequenza permetterebbero di studiare le interazioni elettrone-fonone, fonone-fonone e altre interazioni quantiche nei solidi.

8. Gli ultrasuoni di elevata intensità.

Come già si è accennato, l'intensità delle onde sonore aumenta proporzionalmente al quadrato della frequenza; con le usuali sorgenti di quarzo si possono generare, a frequenze ultracustiche e in vari mezzi, onde piane aventi intensità sonora di alcuni W/cm² e, ricorrendo a particolari meccanismi di concentrazione, intensità dell'ordine di 10⁵ W/cm² (Rosenberg).

Per dare un'idea grossolana di questi valori, si pensi che l'intensità del suono emesso da un altoparlante in una stanza è dell'ordine di 10^-8 W/cm² e quella dell'onda impulsiva che accompagna l'esplosione di un proiettile è dell'ordine di 10^-3 W/cm². Agli alti valori delle intensità corrispondono pressioni acustiche di qualche centinaio di atmosfere e accelerazioni delle particelle di 10⁷ volte quella di gravità. Tali intensità possono provocare la vaporizzazione del mezzo in cui l'onda si propaga, poiché i meccanismi di dissipazione dell'onda producono enormi quantità di calore. Prima che questi limiti estremi siano raggiunti avvengono svariati altri fenomeni (macroacustici) che spesso possono prestarsi a utili applicazioni. Un fascio ultrasonoro di intensità elevata che colpisca la superficie libera di un liquido produce uno zampillo del liquido che può innalzarsi fino a parecchi centimetri di altezza; in condizioni opportune l'irradiazione di sistemi a due fluidi provoca la formazione di aerosol e di emulsioni; non è ancora chiaro quale sia il meccanismo che presiede a questi processi, ma certamente esso dipende dalle condizioni di flusso idrodinamico prodotte nel fluido e dall'alta pressione che s'origina all'improvvisa implosione delle bolle di cavitazione. L'impiego degli ultrasuoni nei processi di emulsionamento è oggi abituale nell'industria.

Un secondo effetto consiste nella coagulazione delle sospensioni, come i fumi e le nebbie; anche questo effetto dipende strettamente dalle condizioni idrodinamiche create dalle onde di grande intensità le particelle piccole prendono parte alla vibrazione prodotta nel mezzo dal suono di grande intensità, si urtano e si uniscono insieme; ciò provoca la formazione di particelle sempre più grandi che infine si allontanano dal campo. L'applicazione pratica di questo effetto è importante per l'eliminazione delle particelle nocive dai fumi industriali.

La cavitazione per effetto di ultrasuoni è un fenomeno particolare che può verificarsi nei liquidi ogni qual volta l'ampiezza dell'onda superi un valore di soglia proprio del liquido e delle condizioni sperimentali si producono delle cavità che crescono in seno al campo sonoro fino a raggiungere dimensioni di risonanza, oscillano e implodono violentemente. Il processo è assai complesso e molti suoi aspetti attendono ancora una spiegazione. La comparsa delle cavità avviene ad ampiezze di vibrazione tali che la pressione acustica corrispondente, durante la parte negativa del ciclo, raggiunge valori di circa un'atmosfera; questo valore è ben al di sotto della pressione di strappo propria di un liquido (centinaia o migliaia di atmosfere), quindi il processo non consiste in una rottura del liquido. La cavitazione è prodotta dalla crescita, entro il campo acustico, di nuclei che preesistono all'irraggiamento sonoro o che vengono creati durante l'irraggiamento. Queste microcavità, i cui raggi possono raggiungere valori di qualche micron e che agiscono da nuclei, possono esser introdotte nel liquido in un gran numero di modi, per esempio mediante agitazione in presenza di gas o irraggiamento con particelle d'alta energia (Sette); quest'ultimo procedimento ricorda quanto avviene nelle camere a bolle. È stato provato, per esempio, che neutroni di elevata energia presenti nella radiazione cosmica possono cedere a nuclei di ossigeno un'energia sufficiente per produrre nuclei di cavitazione. Tra l'altro, questo processo offre la possibilità di impiegare la cavitazione da ultrasuoni per una spettroscopia di neutroni di alta energia.

I nuclei possono crescere nel campo sonoro per via della cosiddetta diffusione rettificata, dovuta all'asimmetria della diffusione del gas dal liquido alle cavità e viceversa durante il semiperiodo di pressione acustica positiva e il semipenodo opposto, in conseguenza dei valori differenti raggiunti dalla superficie della bolla.

Si debbono distinguere almeno due tipi di cavitazione: 1) la cavitazione gassosa, che ha luogo nei liquidi in cui sono disciolti dei gas; in tal caso le cavità posseggono internamente grandi quantità di gas; 2) la cavitazione di vapore in quei liquidi che praticamente sono privi di gas disciolti; in tal caso, le cavità si riempiono dei vapori del liquido. La soglia di cavitazione è più alta nel secondo caso e la scomparsa implosiva delle bolle dà origine a un'onda d'urto molto intensa. Il processo di cavitazione trasforma la densità di energia relativamente bassa di un campo sonoro in una densità di energia elevata all'interno e intorno alla cavità che implode. Ciò avviene durante un moto non lineare della cavità. L'energia complessiva di una cavità che imploda può essere bassa, ma la sua convergenza in un punto durante l'implosione genera enormi densità di energia: all'interno della bolla si possono raggiungere pressioni e temperature molto elevate, mentre sull'interfaccia vengono prodotte onde d'urto che s'irradiano nel liquido.

La cavitazione acustica può dar luogo a effetti assai vistosi, come la luminescenza, e a reazioni chimiche nel liquido, ovvero all'erosione di materiali solidi presenti nel campo. Quest'ultimo effetto è della stessa natura di quello che avviene sulle pale rotanti delle eliche di un'imbarcazione, a causa della cavitazione che si verifica nella regione ove la pressione statica ha valori negativi.

Il fenomeno della cavitazione ha grande importanza per varie ragioni: in primo luogo presenta un interesse intrinseco, dato che dev'essere ancora chiarito in molti suoi aspetti, e poi si presta a svariate applicazioni, di cui si è già dato qualche esempio (reazioni chimiche, erosioni, emulsioni). Naturalmente, nelle applicazioni dell'acustica subacquea, la cavitazione pone un limite alle densità di potenza che si possono irradiare e alle distanze utili per eventuali collegamenti: non appena la cavitazione ha inizio, l'energia di un fascio ultrasonoro viene notevolmente diffusa.

Un notevole numero di effetti biologici prodotti dagli ultrasuoni è essenzialmente dovuto alla cavitazione: per esempio, la distruzione di protozoi, di eritrociti o anche di piccoli animali e pesci in liquidi irradiati da intensi campi sonori. L'azione distruttiva sui batteri ha trovato un'utile applicazione nella sterilizzazione del latte.

Un altro effetto della cavitazione è la depolimerizzazione di grossi polimeri in soluzione liquida. L'azione pulente di un liquido detergente in cavitazione viene sfruttata nell'industria, in particolar modo per pulire piccoli componenti metallici che presentino superfici interne non accessibili. In odontoiatria si fa ricorso a un procedimento analogo per pulire i denti da depositi induriti.

Quali ulteriori applicazioni industriali degli ultrasuoni ad alta intensità ricordiamo un'apparecchiatura saldatrice, in cui l'energia acustica (alla frequenza di circa 20-30 kHz) viene convertita in calore all'estremità della punta di un ferro saldatore, e un trapano ove un utensile vibra a contatto col materiale da trapanare in presenza di una polvere abrasiva. L'azione di taglio è eseguita dall'abrasivo mosso avanti e indietro dall'utensile; con questo trapano si possono anche forare, secondo forme complesse, materiali di vario genere (metalli, vetri e ceramiche). Questo tipo di trapano è largamente usato nell'industria elettronica. Attrezzature simili si usano anche per lavori di odontoiatria.

9. L'acustica elettronica e le onde superficiali.

La propagazione del suono in mezzi opportunamente progettati trova impiego in un numero sempre crescente di applicazioni, in complesse apparecchiature elettroniche per l'esecuzione di operazioni speciali che, diversamente, richiederebbero circuiti elettronici più elaborati. A fianco dei filtri a quarzo di elevata selettività e delle lamine di cristalli piezoelettrici per stabilizzazione di frequenza nei circuiti d'alta frequenza (1 parte su 10¹⁰), nei quali trova vantaggiosamente impiego la caratteristica d'alto Q di risonanza meccanica di vibratori particolari, vi sono anche applicazioni in cui fasci di radiazioni acustiche si propagano nei dispositivi.

Onde propagantisi nell'interno di solidi consentono la costruzione di linee di ritardo, molto usate, da tempo, nella tecnologia dei radar e dei calcolatori. L'operazione eseguita è la memorizzazione di un segnale per un certo intervallo di tempo (di solito inferiore al millisecondo) e il suo successivo recupero per la rivelazione o per l'impiego in processi di calcolo. Le linee di ritardo normalmente sono dei cilindri di materiale solido (quarzo) o liquido, con due trasduttori uno che invia il segnale, l'altro che lo rivela dopo un percorso (semplice o multiplo) compiuto entro il cilindro. I segnali usati sono impulsi ultracustici della durata del microsecondo con frequenza contenuta nella regione situata intorno al megahertz. Si possono ottenere tempi di ritardo notevolmente più lunghi con solidi poliedrici, facendo riflettere il fascio ultrasonoro varie volte su facce diverse all'interno del solido fra il trasduttore di ingresso e quello di uscita.

Oggi, peraltro, sia per la costruzione di linee di ritardo, sia per effettuare numerose altre operazioni su segnali elettrici, si ricorre sempre più spesso all'impiego di onde superficiali. Si tratta di onde la cui propagazione avviene essenzialmente in un sottile strato superficiale di solidi a contatto con aria. Tali dispositivi hanno numerosi pregi, fra i quali ricorderemo il fatto che le onde che corrispondono a un segnale variabile nel tempo si trovano, a un certo istante, disposte spazialmente sulla superficie del solido rendendo possibili interventi per il prelievo del segnale stesso o per la sua modifica in funzione delle caratteristiche desiderate per il dispositivo. Facendo, inoltre, ricorso come mezzo di propagazione a materiali piezoelettrici o a film piezoelettrici opportunamente depositati su substrati adatti, è possibile realizzare facilmente efficienti trasduttori, come sorgenti e rivelatori, con tecniche fotolitografiche. Le stesse tecniche possono essere usate per costruire guide per onde superficiali. A tutto ciò si associa un uso limitato di materiali pregiati, rispetto al caso di dispositivi a onde di volume. Per tutte queste caratteristiche i dispositivi a onde superficiali trovano un sempre maggiore impiego per frequenze fino all'ordine dei gigahertz.

Non abbiamo qui la possibilità di illustrare i vari tipi di onde superficiali e di modi di vibrazione di superficie in piastre, che si possono avere usando materiali isotropi, anisotropi, piezoelettrici o in sottili strati disposti su un differente substrato. Ci limiteremo, prima di accennare ad alcuni dei più interessanti impieghi delle onde superficiali, a illustrare il presentarsi di questo tipo di onde nel caso più semplice, quello di un solido isotropo a contatto con il vuoto o, quel che è praticamente lo stesso, con un mezzo gassoso, quale l'aria. La velocità di propagazione di onde elastiche in un solido dipende in maniera diretta dalle caratteristiche del mezzo nelle espressioni per la velocità delle onde longitudinali o trasversali interviene il corrispondente modulo di elasticità (E o G). Queste caratteristiche, in ultima analisi, dipendono dalle forze che un singolo atomo scambia con gli altri e sono, in un solido isotropo, costanti fintantoché un atomo è circondato da un gran numero di altri atomi in ogni direzione, come accade ben all'interno del campione; ciò non è più vero in prossimità di una superficie limite (cioè negli ultimi strati atomici). Ne segue che la velocità delle onde longitudinali e trasversali varia (decresce), man mano che dall'interno di un solido isotropo ci si avvicina alla superficie, in uno spessore di pochi strati atomici.

In conseguenza di ciò una perturbazione elastica, originata in superficie, nel propagarsi verso l'interno trova strati successivi caratterizzati da velocità di propagazione (per onde longitudinali e trasversali) gradatamente crescenti e viene rifratta verso la superficie, in maniera analoga a quanto accade per le onde luminose in aria in prossimità della superficie terrestre, quando questa, molto calda, produce il riscaldamento degli strati di aria a essa prossimi (fenomeno del miraggio) la propagazione resta confinata all'interno di un sottile strato superficiale. Si può originare quindi un tipo particolare di perturbazione elastica nella quale si ha un'onda (di Rayleigh) sulla superficie, associata a due onde, una longitudinale e una trasversale, propagantisi nel solido al di sotto della superficie, in direzioni e con intensità relative opportune; la fig. 13 illustra, per un'onda che si propaghi nella direzione x lungo la superficie, i legami che intercorrono fra i vettori d'onda (intensità k=2π/λ) delle onde superficiale, longitudinale e trasversale (z è normale alla superficie verso l'interno del solido) k_s è pari alla proiezione sulla superficie di k₁ e k_t. La teoria mostra come le onde (longitudinali e trasversali) diminuiscano rapidamente in intensità nell'interno del solido: in un materiale isotropo esse sono completamente assorbite in uno spessore di circa 2,5 λ_s. In una tale perturbazione lo spostamento di una particella ha una componente in direzione x parallela alla superficie e una in direzione z normale: ne segue un moto ellittico.

Le caratteristiche delle onde superficiali sono più complesse in materiali anisotropi: la dipendenza delle velocità delle onde di volume dalla direzione di propagazione conduce alla dipendenza delle caratteristiche delle onde superficiali dalla giacitura cristallografica della superficie stessa; si possono originare particolari processi di deviazione o di concentrazione del fascio. Ancora più complessa è l'analisi della propagazione di onde superficiali nel caso di cristalli piezoelettrici, ove alle onde elastiche si accoppiano campi elettrici.

Vogliamo ora accennare al tipo più diffuso di trasduttore per la creazione e per la rivelazione di onde superficiali. Un primo metodo per ottenerlo è quello di produrre mediante fotodeposizione due elettrodi metallici (in genere di Al) a forma di pettini con denti intercalati, sulla superficie, avente opportuna giacitura cristallografica, di un cristallo piezoelettrico (in genere quarzo o niobato di litio, LiNbO₃: v. fig. 14A). Una seconda maniera è quella di depositare gli elettrodi, come nel primo caso, su un substrato non piezoelettrico e di depositarvi sopra, successivamente, uno strato di materiale piezoelettrico (v. fig. 14B). Nella versione più semplice (v. fig. 14C) i denti hanno uguale lunghezza e sono uniformemente spaziati (le distanze mutue fra i denti dei due pettini possono essere dell'ordine di alcune decine di μm per trasduttori da usare per onde superficiali aventi frequenze di centinaia di MHz). Se fra i due elettrodi viene applicata una differenza di potenziale, si origina nel materiale piezoelettrico una distribuzione spaziale di sforzi elastici, e una conseguente distribuzione di deformazioni che si estende al contiguo strato superficiale al di là della zona degli elettrodi; se la differenza di potenziale viene variata, si generano onde superficiali. Per un'eccitazione sinusoidale le onde superficiali sono della stessa frequenza, e possono essere calcolate sommando in un punto sulla superficie le deformazioni dovute all'arrivo delle perturbazioni generate in corrispondenza dei vari elementi del trasduttore, tenendo conto della posizione degli elementi stessi e della velocità di propagazione delle onde (c_s). Per una data geometria (distanza d fra i denti e lunghezza dei denti molto superiore a d), le onde superficiali generate sono piane e sono emesse dalle due parti del trasduttore; l'intensità di tali onde al variare della frequenza di eccitazione (ν) è massima quando la lunghezza d'onda, λ_s=c_s/ν, è pari alla distanza fra due denti contigui di un pettine. È questa la condizione di risonanza del trasduttore; in tal caso i contributi alla perturbazione in un punto della superficie, dovuti alle deformazioni corrispondenti ai vari elementi del trasduttore, si sommano in fase.

Un'ulteriore conseguenza dell'estensione geometrica del trasduttore e della velocità di propagazione finita è l'esistenza di un tempo di salita (o di discesa) dell'ampiezza delle onde in un punto, quando il segnale sinusoidale viene applicato (o tolto) agli elettrodi: occorre che i contributi delle perturbazioni generate dai vari elementi raggiungano il punto in questione e ciò richiede un numero di oscillazioni applicate agli elettrodi pari al numero di coppie di denti del trasduttore (n). La fig. 15 mostra la caratteristica di un trasduttore di questo tipo e riporta l'ampiezza (H) della risposta al variare della frequenza con cui varia la differenza di potenziale applicata: l'ampiezza va a zero per la prima volta per una deviazione Δν dalla frequenza di risonanza (ν₀) pari a ν₀/n.

Il numero di coppie di denti (n) ha interesse anche per il rendimento del trasduttore, cioè per il rapporto fra energia trasferita alle onde superficiali ed energia elettrica data al trasduttore. È possibile vedere che, a causa della presenza di fenomeni di reazione, il valore più opportuno per n dipende dal materiale impiegato; nel caso del niobato di litio è 4-5 coppie. La fig. 16 dà lo schema di impiego di due trasduttori del tipo ora esaminato per realizzare una linea di ritardo.

Un trasduttore interdigitale per onde superficiali è, da un punto di vista circuitale, un elemento che per un segnale elettrico impresso produce in uscita un segnale sotto forma di onde superficiali (da una parte del trasduttore) o viceversa. Per le applicazioni elettroniche esso può essere caratterizzato esaminando la risposta a un segnale impulsivo molto stretto (funzione δ), che, secondo l'analisi armonica, può essere considerato formato dalla sovrapposizione di oscillazioni sinusoidali di frequenze distribuite in uno spettro continuo molto vasto (teoricamente infinito). La fig. 17A presenta, per un trasduttore interdigitale del tipo considerato, la risposta a un impulso δ e la risposta in frequenza. Da tali caratteristiche si vede che l'elemento si comporta come un filtro capace di far ritrovare all'uscita (sotto forma di onde elastiche) solo alcune delle frequenze presenti nel segnale elettrico in ingresso; la larghezza della banda passante è inversamente proporzionale a n.

Le caratteristiche di risposta del trasduttore peraltro possono essere variate cambiando la configurazione geometrica degli elettrodi a pettine, perché in tal modo si cambiano in intensità e fase gli addendi presenti nella deformazione totale in un punto della superficie, derivanti dalle deformazioni in corrispondenza dei vari elementi del trasduttore. Per esempio la fig. 17B mostra la risposta impulsiva e la risposta in frequenza di un trasduttore interdigitale con i pettini opportunamente pesati (apodizzati): esso realizza un filtro passa banda. La fig. 18 mostra un trasduttore usato per la generazione o per la compressione di segnali modulati in frequenza. In tale trasduttore la distanza fra i denti successivi dei pettini varia linearmente. La risposta in frequenza di un tale trasduttore è notevolmente più ampia di quella che esso avrebbe se, pur mantenendo la stessa lunghezza totale, avesse denti ugualmente spaziati: si può pensare che tale banda sia compresa approssimativamente fra le frequenze cui corrispondano lunghezze d'onda pari alle distanze interdigitali agli estremi del trasduttore; inoltre è possibile vedere che, se si invia un segnale complesso in un verso, sono ridotti i tempi di attraversamento del trasduttore per le frequenze più elevate (l'opposto accade nell'altro verso di propagazione). Ciò è del tutto equivalente ad avere un mezzo di propagazione dispersivo per le onde acustiche, nel quale cioè la velocità di propagazione è funzione della frequenza si ha quindi una linea di ritardo (fra ingresso e uscita del segnale) dispersiva. Di conseguenza, se viene inviato in ingresso un segnale modulato linearmente in frequenza si ottiene in uscita un segnale impulsivo (v. fig. 18A). Analogamente se si invia in ingresso un segnale impulsivo si ha all'uscita un segnale modulato linearmente in frequenza (v. fig. 18B).

Diamo ora alcuni altri esempi di impiego delle onde superficiali in dispositivi elettronici. La fig. 19 mostra lo schema di un accoppiatore a strisce multiple le onde superficiali (A₁) generate dal trasduttore interdigitale incidono normalmente su una serie di strisce metalliche depositate sul materiale piezoelettrico, di altezza all'incirca doppia di quella del fascio. In tale maniera si può avere la biforcazione del fascio sonoro: l'energia acustica può essere trasferita lateralmente (fascio B₂), in parte o totalmente. L'effetto si comprende facilmente pensando che le onde incidenti producono campi elettrici sulle strisce metalliche, producendo una sorgente nella regione non investita. La combinazione opportuna delle fasi delle perturbazioni prodotte dalle varie strisce può condurre ad avere irraggiamento nel secondo canale solo nel verso della radiazione incidente nel primo canale e, al variare della lunghezza dell'accoppiatore, ad alterare la ripartizione dell'energia nei due canali emergenti, fino a un suo trasferimento completo nel secondo canale. Si osservi inoltre che, se le strisce metalliche vengono conformate in modo che la parte non investita dalle onde incidenti formi un angolo rispetto alla parte esposta alla radiazione in ingresso, il secondo canale viene emesso in una direzione diversa da quella incidente si può cioè realizzare un deviatore.

La fig. 20 mostra uno schema formato da due trasduttori inderdigitali collegati elettricamente fra loro il dispositivo risuona a ogni frequenza per la quale lo sfasamento totale lungo il circuito è un multiplo intero di 2π; tale sfasamento dipende quindi, a parità di altri elementi, dalla lunghezza i del percorso acustico. Un tale dispositivo può divenire un oscillatore se tra i due trasduttori si inserisce un amplificatore. Con opportuni schemi si possono realizzare oscillatori accordabili od oscillatori di grande stabilità a una determinata frequenza.

L'energia nelle onde superficiali viene mantenuta in fasci che hanno piccolissime sezioni trasversali: è possibile pertanto raggiungere facilmente intensità elevate, alle quali il comportamento dei materiali diviene non lineare. Da ciò si trae profitto per costruire amplificatori, mescolatori di frequenza e dispositivi atti a eseguire operazioni analitiche su segnali, quali invertitori temporali, convolutori e correlatori tra due segnali.

Vogliamo infine accennare alle guide d'onda per onde superficiali, ottenute producendo sulla superficie del solido strisce ove la velocità di propagazione delle onde è inferiore a quella nel resto della superficie di una quantità opportuna, in modo da far sì che, mediante la riflessione ai bordi, onde opportunamente lanciate in esse non possano uscirne. Ciò si può realizzare con varie tecniche. Una prima maniera (v. fig. 21A) è quella di disporre su un substrato una striscia di un materiale avente velocità di propagazione per onde elastiche di volume inferiore a quella del substrato ( per esempio oro su quarzo fuso); un secondo metodo (v. fig. 21B) consiste nel depositare una striscia metallica su un supporto piezoelettrico con l'effetto di cortocircuitare i campi elettrici associati all'onda superficiale sotto la striscia. Un terzo metodo consiste nel configurare le superfici del cristallo con un rilievo emergente dal piano (v. fig. 21C). Un altro metodo (v. fig. 21D) consiste nel produrre variazioni opportune delle proprietà dello strato superficiale lungo una striscia, mediante diffusione di atomi opportuni o mediante impiantazione ionica. Un altro metodo ancora usa fibre di quarzo fuso a sezione circolare (v. fig. 21E) analoghe alle fibre ottiche, nelle quali il materiale del nucleo centrale ha velocità di propagazione più bassa del rivestimento.

L'impiego delle onde superficiali in guida d'onda può essere spesso utile già nella costruzione di componenti dei tipi esaminati in precedenza, in cui un'unica operazione viene affidata alle onde superficiali, con il vantaggio di operare con fasci molto stretti e di poterne variare la direzione a volontà: si pensi alla possibilità di realizzare lunghe linee di ritardo, divisori di potenza (v. fig. 22), ecc. Il loro impiego peraltro consente la costruzione di altri dispositivi, come accoppiatori direzionali e filtri di frequenza, utilizzando le onde evanescenti all'esterno della guida, che accompagnano la propagazione dell'energia nella guida stessa.

Lo sfruttamento delle possibilità offerte dalle guide è solo all'inizio e fa prevedere un rigoglioso sviluppo in applicazioni nuove, quale per esempio la costruzione di dispositivi integrati di piccole dimensioni nei quali varie operazioni vengano successivamente affidate a onde superficiali sul medesimo substrato; la tecnologia corrispondente ha preso il nome di ‛microsuono'.

10. L'acustica subacquea.

Le onde acustiche si sono rivelate un mezzo insostituibile per ricavare informazioni di vario genere su e da oggetti immersi nell'acqua, specialmente nell'acqua del mare, in cui le onde elettromagnetiche non possono essere impiegate a causa dell'elevata attenuazione che vi subiscono. Le applicazioni principali sono la rivelazione di oggetti sommersi e le comunicazioni sottomarine. Un primo metodo per individuare oggetti immersi che producano essi stessi dei suoni (rumori), come i sottomarini, consiste nell'impiego di una serie di microfoni a immersione (idrofoni) i segnali rivelati dagli idrofoni vengono trattati elettronicamente in modo da poter determinare la posizione della sorgente sonora attraverso misure di differenze di fase. Nel caso di un sottomarino, la sorgente può essere lo scafo stesso che vibra come un tutto unico sotto l'effetto del rumore prodotto dai motori (bassa frequenza) o il rumore di cavitazione prodotto dalle eliche (spettro a larga banda). Un secondo metodo, particolarmente indicato per quegli oggetti che non emettono suoni, è simile al ben noto sistema radar e si suol chiamare sonar uno stretto fascio di ultrasuoni è inviato nell'acqua in una certa direzione; ruotando il trasduttore, il fascio spazza la zona circostante e, quando incontra un ostacolo, il trasduttore, che agisce al tempo stesso da emettitore e da ricevitore, rivela un'eco; dalla posizione del trasduttore e dal ritardo dell'eco si deduce con facilità sia la direzione, sia la distanza dell'ostacolo. Le frequenze che si impiegano in questo tipo di applicazioni sono comprese tra i 20 e i 175 kHz e sono scelte di volta in volta come compromesso che soddisfi in modo ottimale le opposte esigenze di una propagazione collimata del fascio (la collimazione migliora al crescere della frequenza) e una buona portata del sonar (la quale diminuisce al crescere della frequenza in conseguenza dell'aumento dell'attenuazione).

Si deve far qui menzione del fatto che, poiché il fascio sonoro incontra nell'acqua diverse inomogeneità (dovute a gradienti termici , a correnti del liquido, a variazioni di salinità, ecc.) che ne provocano la rifrazione, la diffrazione, la diffusione e l'assorbimento, la determinazione precisa della posizione degli ostacoli richiede una valutazione piuttosto complessa delle correzioni. Per chiarire in parte questo punto, nella fig. 23A è riportato un andamento tipico delle variazioni più rilevanti di velocità nell'acqua di mare, in funzione della profondità. Vi si possono distinguere tre strati quello in superficie ha uno spessore che può essere anche di 100 m, ma dipende da vari fattori (la radiazione incidente, il vento, il luogo, il periodo dell'anno, ecc.); i moti del fluido mantengono la temperatura uniforme in questo strato e la velocità del suono aumenta leggermente con la profondità, in conseguenza dell'aumento di pressione. Il secondo strato (termoclino) ha una temperatura che diminuisce rapidamente fino a circa 0-2 °C; questo gradiente di temperatura, nonostante l'effetto contrario della pressione sulla velocità, provoca una diminuzione della velocità con la profondità. Il terzo strato (acqua profonda) presenta una temperatura uniforme e la velocità vi aumenta con la pressione idrostatica. Una distribuzione di velocità di questo tipo provoca un effetto complesso sulla radiazione emessa da una sorgente nella fig. 23B è data l'indicazione del tipico andamento dei raggi.

Ricordiamo qui che il primo impiego dei trasduttori piezoelettrici di Langevin fu la rivelazione, mediante eco, di oggetti posti sott'acqua. Da allora il metodo si è sostanzialmente evoluto e nei moderni sonar l'immagine dell'ostacolo, periodicamente investito dal fascio, è fornita sullo schermo di un tubo a raggi catodici. Lo stesso tipo di equipaggiamento è largamente impiegato nella pesca, per la localizzazione di grossi pesci isolati o di branchi di piccoli pesci, e in oceanografia; in quest'ultimo caso il fondo marino costituisce l'ostacolo e il sonar permette di determinare il profilo del fondo e degli strati di sedimenti presenti lungo la rotta della nave. Le informazioni raccolte in questo modo si stanno dimostrando di fondamentale importanza per l'elaborazione delle teorie riguardanti l'origine e l'evoluzione dei continenti e della crosta terrestre. La fig. 24 illustra un metodo leggermente diverso (il metodo di individuazione del profilo del terreno mediante riflessione continua; Sargent, 1968), che consiste nel registrare la riflessione da parte del fondale roccioso sotto il fondo marino per ricavarne dati sulla sua conformazione. La fig. 25 (Sargent, 1969), che è un'autentica registrazione in acque poco profonde, mostra l'informazione che si può ottenere con questo metodo, malgrado le difficoltà dovute agli echi multipli.

L'impiego di fasci sonori per comunicazioni sottomarine diventa assai complesso quando le distanze superano qualche chilometro. Ricordiamo che in condizioni opportune si è riusciti a rivelare segnali acustici a distanze di circa 20.000 km (tra le Bermude e l'Oceano Indiano). Questo è un esempio della cosiddetta trasmissione in canali di profondità. In corrispondenza della base dello strato termoclino (v. fig. 23), dove la velocità del suono presenta un minimo, i raggi emessi da una sorgente con una piccola inclinazione rispetto al piano orizzontale rimangono confinati in un canale (v. fig. 26); la forma dei fronti d'onda è sferica in vicinanza della sorgente, ma diviene subito pressoché cilindrica.

Tutti i problemi connessi con la trasmissione di segnali sott'acqua sono oggi argomento di attente ricerche. Per progredire su questa linea, è necessario acquisire una conoscenza più profonda di come si propaghino sott'acqua i suoni d'ogni frequenza e intensità in tutte le possibili condizioni fisiche. Il segnale che si può ricevere in un punto che disti dalla sorgente centinaia di volte la profondità media del mare nel tratto tra i due punti è il risultato dei contributi di suoni che hanno percorso cammini differenti in conseguenza delle inomogeneità del mezzo, della presenza del fondo e della superficie libera.

Le inomogeneità del mezzo, come si è già accennato, dipendono dalle distribuzioni stazionarie tridimensionali della temperatura e della pressione, dalle loro fluttuazioni, dalla presenza di particelle diffondenti in sospensione, come bolle e organismi; difficile da calcolare è anche l'effetto della riflessione sulla superficie libera, per via della rugosità sempre variante e del movimento della superficie riflettente.

La trasmissione tra due punti deve essere caratterizzata per mezzo di una trattazione statistica dell'informazione di ampiezza e di fase. Il problema, sebbene più complesso, è per un certo verso simile a quello che si affronta nelle comunicazioni mediante laser attraverso un'atmosfera turbolenta. In questi studi l'uso dei calcolatori sembra dimostrarsi particolarmente interessante. Per un argomento cosi generale diviene molto importante la caratterizzazione statistica del rumore ambientale (spettro di frequenza, tempo, posizione geografica e direttività).

11. Le prove non distruttive.

Il suono è alla base di diversi metodi per saggiare l'integrità di materiali solidi sia prima di usarli per costruire manufatti sia durante il funzionamento di questi. Sebbene si faccia da tempo uso di suoni di frequenze percepibili per le prove d'integrità dei materiali (percuotendo l'oggetto da esaminare, che può essere una ruota di vagone ferroviario, un vetro, un vaso di ceramica, ecc., e analizzando il suono così prodotto), tuttavia, nella maggioranza dei metodi industriali, sono impiegate le frequenze della banda ultracustica. Un importante metodo, che ha molteplici varianti, è simile al sonar, di cui abbiamo già parlato mediante un trasduttore piezoelettrico si invia un fascio sottile di ultrasuoni nel campione e si captano gli echi rinviati dalla superficie limite opposta del pezzo o dagli eventuali difetti del materiale. Il metodo consente di effettuare un esame dei materiali prima di costruire con questi dei manufatti costosi che debbano essere sottoposti a gravose condizioni di esercizio, e di provare i manufatti prodotti; è usato anche largamente, spesso in versioni elaborate e congiuntamente coi calcolatori, in tutte le costruzioni meccaniche d'avanguardia.

In altri metodi di prove non distruttive si fa uso delle onde superficiali per ottenere informazioni sull'omogeneità di uno strato superficiale sottile. Un metodo piuttosto recente, particolarmente adatto per il controllo del materiale in condizioni di impiego di un manufatto,è quello dell'emissione acustica. Il metodo si basa sul fatto che, in molti casi, la crescita di difetti o di rotture e l'annichilazione delle dislocazioni, in un materiale che subisca una deformazione, sono accompagnate dall'emissione di una notevole quantità di energia acustica; pertanto è possibile impiegare questi processi come sorgenti sonore, osservare le onde elastiche mediante opportuni rivelatori e individuare la presenza di difetti e la loro crescita. Le onde elastiche sono solitamente emesse sotto forma di brevi impulsi con spettri di frequenze a banda larga, che comunque si differenziano da caso a caso lo spettro del rumore prodotto dall'annichilazione delle dislocazioni nella regione plastica intorno a un difetto si estende fino a 30 MHz; quello relativo alla comparsa o alla crescita di una rottura ha la maggior parte della propria energia localizzata nella regione delle basse frequenze e non si estende a frequenze così elevate.

Nell'emissione acustica la rivelazione avviene in una banda di frequenze scelta opportunamente (tra i 20 kHz e i 3 MHz). Il metodo ha trovato utili applicazioni nell'analisi di strutture di grandi dimensioni destinate a funzionare in difficili condizioni operative: per esempio, componenti di missili e di veicoli spaziali o camere a pressione di reattori nucleari. In quest'ultimo caso l'ispezione, eseguita durante il funzionamento, è di grande interesse un unico trasduttore fisso dà la possibilità di rivelare danni distanti qualche metro. Si sono anche sviluppati dei metodi piuttosto elaborati di localizzazione dei difetti che impiegano un numero limitato di trasduttori (quattro) e un calcolatore e consentono di ottenere una precisione di 2,5 cm nella localizzazione di difetti in recipienti di 30 m³.

Una seconda versione del metodo dell'emissione acustica per eseguire prove non distruttive permette la verifica di impianti e macchinari in rotazione attraverso l'esame della deviazione dell'ampiezza e della frequenza delle vibrazioni delle varie parti, rispetto ai loro valori normali. Il metodo dell'analisi delle vibrazioni e dell'analisi meccanica impiega gli spettri di frequenza e l'analisi di Fourier e consente di localizzare i guasti di macchinari in rotazione. In un certo senso questo metodo agisce, sia pure a un livello molto più sofisticato, come un buon meccanico, che diagnostica i guasti di un'automobile ascoltando il rumore del motore.

Due altri metodi, di sviluppo recente, in qualche modo connessi con le prove non distruttive, sono quelli della microscopia e dell'olografia.

12. La microscopia acustica.

Una particolare tecnica di analisi delle caratteristiche strutturali di campioni è rappresentata dalla microscopia acustica: un fascio di onde acustiche di elevata frequenza (da qualche centinaio a qualche migliaio di MHz) viene inviato nel campione e ne emerge trasportando le informazioni in completa analogia con quanto accade con le onde luminose nel microscopio ottico. Naturalmente le informazioni si riferiscono a variazioni di caratteristiche elastiche (impendenza acustica, velocità, assorbimento) nelle regioni attraversate dal fascio una tale ispezione risulta in genere complementare all'esame ottico, in quanto fornisce elementi diversi, e diviene di particolare interesse nel caso di oggetti non trasparenti alla luce, quando cioè le informazioni ottiche non sono disponibili. È possibile usare schemi per l'esame di campioni per trasmissione o per riflessione in quest'ultimo caso si utilizza la dipendenza delle riflettività delle onde elastiche dalle proprietà delle superfici stesse e il microscopio consente di avere precise informazioni sulle differenze strutturali esistenti sulle superfici.

A differenza delle prove non distruttive, ove le frequenze usate (1-10 MHz) sono relativamente basse e consentono di avere buone penetrazioni delle onde nei materiali, nel microscopio acustico si usano alte frequenze (e quindi piccole lunghezze d'onda) per avere alta risoluzione; ciò comporta elevati assorbimenti e la necessità di limitare al massimo i percorsi delle onde sonore nel dispositivo. Le lunghezze d'onda sono in genere dell'ordine dei μm e possono raggiungere valori di frazioni di μm, cioè dell'ordine delle lunghezze d'onda della luce.

Sono stati sviluppati due schemi di microscopia acustica; entrambi consentono l'esame del campione con una tecnica analoga a quella del microscopio elettronico a scansione (SEM). Nel primo schema, dovuto a C. F. Quate, chiamato microscopio acustico a scansione (SAM) e indicato nella fig. 27 nella versione a trasmissione, un fascio di onde ultrasonore generato da una sorgente è inviato in una sbarra cilindrica di zaffiro che termina con una superticie sferica, in modo che la radiazione, uscendo dalla sbarra in acqua, venga focalizzata su una piccola regione del campione; un dispositivo simmetrico a quello descritto porta la radiazione emergente dal campione a un rivelatore piezoelettrico, il cui segnale, appositamente trattato, serve a modulare in intensità il pennello elettronico di un tubo catodico per televisione. Il campione viene spostato meccanicamente nelle due direzioni; in sincronismo con tale moto si muove il pennello elettronico del tubo da televisione, consentendo di ricostruire sullo schermo, punto per punto, l'immagine acustica del campione. In realizzazioni di questo tipo si usano frequenze di alcune centinaia di MHz, e si è giunti a frequenze di 3 GHz: in quest'ultimo caso il raggio delle lenti è di solo 40 μm.

Il SAM ha il vantaggio di usare rivelatori piezoelettrici che, come è noto, hanno alta sensibilità; ha però lo svantaggio di richiedere la propagazione nel mezzo (per es. acqua) fra lenti e fuoco per distanze non trascurabili, e inoltre richiede lo spostamento meccanico del campione. Un miglioramento della risoluzione potrebbe essere raggiunto usando l'elio liquido (a bassa temperatura) al posto dell'acqua e ottenendo così, per la stessa frequenza, una lunghezza d'onda più piccola e un assorbimento molto più basso.

Nel secondo schema, il microscopio acustico a scansione laser (SLAM) dovuto ad A. Korpel e L. W. Kessler, un fascio di onde piane generato da una sorgente viene inviato nel campione a essa direttamente accoppiato; nel campione le onde vengono assorbite, diffuse e modificate nella distribuzione di fase secondo le caratteristiche elastiche delle microstrutture presenti; dopo avere attraversato il campione, il fascio d'onde incide ad angolo su una superficie piana e otticamente riflettente (del campione stesso o di uno specchio plastico a esso aderente); tale superficie viene distorta dinamicamente dalla pressione acustica esercitata dall'onda incidente. Un fascio laser riflesso dalla superficie riflettente, corrugata dall'onda acustica, viene opportunamente usato per rivelare punto per punto, con un'opportuna scansione, la deformazione dello specchio e quindi l'ampiezza della pressione acustica. L'immagine è anche qui ricostruita su un tubo da televisione. La frequenza di operazione è fra 100 e 500 MHz; in questo caso, a differenza dello schema SAM, le onde si propagano essenzialmente nel campione e quindi, a seconda delle caratteristiche di propagazione in questo, l'esame può essere compiuto anche in campioni spessi. Si noti inoltre che con questa tecnica si possono usare onde trasversali invece che longitudinali, con il vantaggio di avere lunghezze d'onda più piccole (e quindi risoluzione maggiore) per la stessa frequenza.

Il metodo della microscopia acustica, ancora in via di sviluppo, trova importanti applicazioni in un crescente numero di campi: nella ricerca biomedica permette di distinguere strutture differenziate senza l'impiego di coloranti chimici, come invece si fa di solito quando si usa il microscopio ottico, e può essere applicato anche per l'esame di tessuti vivi, fornendo un potente metodo diagnostico. La fig. 28 mostra le immagim del tessuto di un tumore della mammella ottenute con microscopio acustico, senza coloranti, e con microscopio ottico (600 MHz) da Lemons e Quate.

Nello studio dei materiali il microscopio acustico consente di porre in evidenza variazioni strutturali, fessure, difetti di piccole dimensioni e rende anche possibile lo studio del comportamento di campioni sotto sforzo. Nella versione a riflessione il microscopio acustico si presta all'esame accurato delle saldature e delle irregolarità, per esempio nei componenti elettronici e nei microcircuiti. Infine il microscopio acustico può essere impiegato, con opportune metodologie, per determinazioni quantitative di variazioni delle proprietà elastiche di un campione su scala microscopica e anche delle proprietà di non linearità acustica dei materiali: in tal caso la rivelazione è fatta a frequenze armoniche di quella di eccitazione. La fig. 29 mostra un confronto fra le immagini del tessuto di un rene ottenute a 450 MHz (A) e a 900 MHz (B), con eccitazione alle rispettive frequenze, e (C) l'immagine di seconda armornea ottenuta con eccitazione a 450 MHz e rivelazione a 900 MHz.

13. L'olografia acustica.

L'olografia acustica, che mediante l'impiego di una radiazione sonora coerente consente di ricostruire un'immagine tridimensionale visiva degli oggetti, è analoga all'olografia ottica; tuttavia, mentre con quest'ultima non si possono ricavare dettagli delle parti interne di un oggetto che non sia trasparente alla luce, le immagini ottenute per via di ologrammi acustici possono dare informazioni preziose sulla struttura interna di qualsiasi oggetto, dal momento che le onde sonore vi si possono propagare. Le caratteristiche generali dei metodi olografici sono descritte altrove (v. olografia) a proposito dell'olografia ottica, così che qui ci limitiamo a dare qualche indicazione per il caso acustico. L'olografia è un processo a due stadi. Nel primo l'ologramma viene costruito mediante la registrazione di un sistema di frange d'interferenza prodotte su un piano da due sistemi di onde sonore coerenti, l'uno che proviene dall'oggetto, l'altro che funge da fascio di riferimento (v. fig. 30A). Le onde del primo sistema possono aver origine nell'oggetto stesso, che agisce da sorgente primaria, o possono esser prodotte per diffusione di un fascio che irradi l'oggetto; il più delle volte il mezzo in cui l'oggetto è situato è l'acqua o l'aria.

Il secondo stadio consiste nella ricostruzione del fronte d'onda proprio dell'immagine; se, infatti, si espone l'ologramma già registrato al fascio d'onde di riferimento (v. fig. 30B), esso agisce alla stregua di un reticolo di diffrazione e ricostruisce nel mezzo le onde acustiche così come esse emergevano dall'oggetto; in realtà, se la registrazione dell'ologramma è fatta su una superficie, si producono due immagini acustiche quella vera e la sua coniugata. Si preferisce avere la ricostruzione sotto forma di onde luminose, anziché acustiche, in modo da potere facilmente esaminare la struttura interna dell'oggetto ‛visto' dalle onde sonore, mettendo a fuoco piani differenti dell'immagine ottica, come nell'olografia ottica. Ciò si può fare poiché un ologramma registrato con radiazione coerente di una certa lunghezza d'onda può essere ricostruito con radiazione coerente anche di altro tipo e di altra lunghezza d'onda (a parte qualche distorsione nel caso di lunghezze d'onda molto diverse). Per ottenere questi risultati l'ologramma acustico viene registrato facendone un'immagine ottica su una lastra fotografica, che è successivamente esposta a luce laser per la ricostruzione tridimensionale. L'ologramma cosi ottenuto è costituito da un agglomerato di frange interrotte e di ammassi granulari che non hanno nel loro insieme alcuna rassomiglianza diretta con l'oggetto. La fig. 31 riproduce una di queste registrazioni cui è sovrapposto un disegno a inchiostro di S. Dalì e mostra come essa abbia stimolato la fantasia dell'illustre artista surrealista.

Nella fig. 32 è presentato lo schema di uno dei metodi (‛a deformazione di superficie liquida') più efficienti e semplici di registrazione di un ologramma acustico: la pressione di radiazione prodotta dalle onde acustiche sulla superficie libera del liquido (acqua) deforma la superficie piana secondo la figura d'interferenza, poi visualizzata mediante luce collimata e registrata su lastra fotografica. Normalmente, nella zona della superficie libera del liquido in cui si forma l'ologramma, l'acqua (che è contenuta nel recipiente) è sostituita da una pellicola d'olio o di soluzione di un agente tensioattivo che riduce la tensione superficiale; ciò è ottenuto interponendo una sottile membrana trasparente tra l'acqua e lo strato, spesso pochi millimetri, di liquido più leggero. Con tale sistema si sono registrati ologrammi fatti con onde sonore, con frequenze contenute nella regione dei MHz e con essi si sono posti in netta evidenza cavità, difetti, rotture di dimensioni dell'ordine di λ in solidi o in organi interni di animali viventi. L'olografia acustica apre nuove possibilità nei settori delle prove non distruttive, della diagnostica medica, della visualizzazione di oggetti posti sott'acqua o di strati sotterranei, grazie alla sua caratteristica di rivelare le discontinuità presenti nella struttura interna degli oggetti esaminati. Naturalmente, ciò si può ottenere anche con altri metodi acustici di ispezione, con il sonar, per esempio; l'olografia però offre il vantaggio di fornire immagini tridimensionali.

14. Gli ultrasuoni in medicina.

Gli ultrasuoni vengono usati sempre più estesamente a scopi diagnostici e terapeutici. Per quanto riguarda l'impiego diagnostico, gli ultrasuoni forniscono un potente mezzo di indagine, che può completare e a volte sostituire con vantaggio l'impiego dei raggi X, rispetto ai quali presentano il notevole pregio di non essere ionizzanti; essi pertanto possono essere usati ripetutamente e a lungo, anche durante interventi operatori, senza alcun danno per il paziente; naturalmente le intensità dei fasci vengono tenute basse, ben al di sotto dei valori che potrebbero produrre danni nei tessuti.

Mentre i raggi X consentono l'esame dell'assorbimento della radiazione elettromagnetica nelle regioni del corpo attraversate, la propagazione degli ultrasuoni è influenzata da alcune proprietà meccaniche dei tessuti, in particolare dalle vanazioni di densità ρ, di velocità di propagazione del suono c (e quindi di impedenza acustica ρc) e del coefficiente di assorbimento. Gli ultrasuoni quindi possono fornire informazioni su organi a tessuto molle, vasi sanguigni, tumori (in quest'ultimo caso anche quando, invece, i raggi X non sono in grado di rilevarne la presenza): i vari tessuti nei Mammiferi hanno impedenze acustiche spesso sufficientemente diverse per produrre riflessioni (e quindi echi) quando un fascio di onde elastiche investe le superfici limiti degli organi. Inoltre lo stesso tessuto può avere coefficienti di assorbimento diversi in condizioni diverse; per esempio la curva del coefficiente di assorbimento in funzione della frequenza è decisamente più bassa per il tessuto cerebrale in condizioni normali che per lo stesso tessuto in condizioni tumorali o per un edema cerebrale postoperatorio o durante anestesia generale.

Il metodo più diffuso per l'esame di organi o formazioni all'interno del corpo è quello dell'eco di impulsi, simile a quello in uso nelle prove non distruttive; le frequenze impiegate sono comprese nella regione di qualche MHz e sono scelte in modo da conciliare le opposte esigenze di ottenere un fascio stretto e al tempo stesso un assorbimento non elevato.

Con questa tecnica è possibile eseguire un'encefalografia, la quale è di grande aiuto per la localizzazione di tumori e alterazioni traumatiche. Le tecniche a eco di impulsi acustici sono utilizzate anche per altre zone del corpo, per la localizzazione di carcinomi ovarici, di cisti di grosse dimensioni, di calcoli epatici, ecc. La fig. 33 mostra i risultati dell'esame a 5 MHz di una mammella normale, mentre la fig. 34 si riferisce a una mammella affetta da cancro. Le stesse tecniche vengono anche usate per l'esame di scheletri fetali e consentono di vedere lo scheletro molte settimane prima di quanto non sia possibile per via radiografica. Le figg. 35 e 36 danno i risultati dell'esame di un utero dopo 10 e, rispettivamente, 38 settimane di gravidanza.

L'applicazione degli ultrasuoni all'esame dell'occhio è particolarmente felice per la struttura a strati di differenti proprietà acustiche propria dell'occhio. La tecnica a eco si impiega anche per l'esame di strutture di tessuti in movimento (valvole cardiache, linea mediana del cervello durante sistole cardiaca, intestino in peristalsi, ventricoli durante attacchi di epilessia). Per questi casi si sono perfezionati dei metodi a irraggiamento continuo del suono, coi quali si determina la velocita del tessuto in movimento (v) mediante la variazione di frequenza (Δν) subita dall'onda riflessa per effetto Doppler: v=Δνc/2ν cos θ, essendo c la velocità del suono nel mezzo, ν la frequenza degli ultrasuoni usati e θ l'angolo tra il fascio sonoro e il vettore velocità. Metodi analoghi vengono usati per la determinazione della velocità del sangue nei vasi: in questo caso sono i globuli rossi in moto che diffondono indietro la radiazione.

In tutte queste applicazioni un notevole miglioramento dei metodi e delle prestazioni delle apparecchiature si sta ottenendo mediante l'associazione dell'indagine ultrasonora con elaboratori elettronici. La tecnica più avanzata in questo settore è la tomografla acustica (ricostruzione dell'immagine mediante elaborazione delle informazioni al calcolatore), analoga alla tomografia a raggi X. In tal caso una stessa sezione trasversale di una parte del corpo (per es. cervello, addome) viene esaminata varie volte di seguito dal fascio emesso da una sorgente che ogni volta è posta in una posizione diversa, intorno alla sezione stessa; le informazioni relative ai fasci emergenti dopo l'attraversamento vengono immagazzinate in un calcolatore e quindi elaborate per costruire punto per punto l'immagine dei parametri meccanici (velocità, assorbimento) nella sezione, che hanno determinato l'insieme delle informazioni. Si ottiene così una riproduzione dei dettagli morfologici della sezione stessa.

Per gli usi terapeutici del suono, si pone una sonda acustica in contatto con la superficie del corpo in modo da inviare nei tessuti una quantità controllata di energia sonora per accelerare il processo curativo. Vari sono i meccanismi attraverso i quali si ottiene questo risultato: riscaldamento locale, micromassaggio e aumento delle velocità di diffusione attraverso le membrane.

Le applicazioni terapeutiche degli ultrasuoni sono state effettuate in tre casi principali a) malattie del sistema nervoso periferico (neuriti e nevralgie); b) malattie del sistema muscolare (spondiliti, artriti, mialgie); c) malattie della pelle (ulcere e scheloderma).

Nei vari casi si sono trovate delle regole empiriche per determinare la frequenza (di solito scelta nella regione dei MHz), l'intensità del fascio (dell'ordine di qualche W/cm²), il punto di concentrazione del fascio e la durata dell'irraggiamento. Il problema del dosaggio in questi casi è piuttosto serio e richiede ancora molta ricerca.

Una concentrazione intensa di ultrasuoni si è usata talvolta per scopi chirurgici, per esempio per distruggere tessuti nervosi di una zona ben localizzata, mediante le azioni combinate del calore e delle forze meccaniche prodotte dalle vibrazioni ad alta frequenza e di opportuna intensità. I rischi di questi tipi di impiego sono però spesso ancora piuttosto notevoli.

Bibliografia.

Barone, A., Generation, detection and measurement of ultrasound, in Encyclopedia of physics (a cura di S. Flügge), vol. XI, t. 2, Acoustics II, Berlin 1962, pp. 74-152.

Békésy, G. von, Experiments in hearing, New York 1960.

Beranek, L. L., Acoustics, New York 1954.

Beranek, L. L., Noise reduction, New York 1960.

Beranek, L. L., Acoustic measurements, New York 1962.

Bergmann, L., Der Ultraschall und seine Anwendung in Wissenschaft und Technik, Berlin 1954.

Brillouin, L., Wave propagation and group velocity, New York 1960.

Busnel, R. G., Animal sonar systems. Biology and bionics, Nato Advanced Study Institute, Laboratoire de physique acoustique, Joug-en-Jasos 1966.

Flanagan, J. L., Speech analysis, synthesis and perception, Berlin 1967.

Fletcher, H., Speech and hearing, New York 1936.

Helmholtz, H. L. F. von, Die Lehre von Tonempfindungen als physiologische Grundlage für die Theorie der Musik, Brunswick 1863.

Hueter, T. F., Bolt, R. H., Sonics, New York 1962.

Hunt, F. V., Electroacoustics, New York 1954.

Knudsen, V. O., Harris, C. M., Acoustical designing in architecture, New York 1950.

Lindsay, R. B., Mechanical radiation, New York 1960.

Mason, W. P., Electromechanical transducers and wave filters, New York 1942.

Mason, W. P., Piezoelectric crystals and their application to ultrasonics, New York 1950.

Mason, W. P., Physical acoustics, principles and methods, voll. I-VII, New York 1964-1970.

Morse, P. M., Vibration and sound, New York 1948.

Olson, H. F., Elements of acoustical engineering, New York 1948.

Rayleigh, J. W. S., The theory of sound, 2 voll., London 1929-1937², New York 1960.

Sabine, W. C., Collected papers on acoustics, Cambridge, Mass., 1927.

Stephens, R. W., Bate, A. E., Acoustics and vibrational physics, London 1966.

Tobias, J. V., Foundation of modern auditory theory, New York 1970.