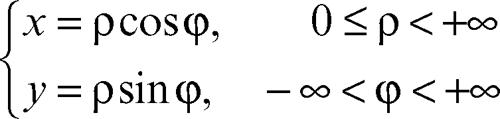Riemann, superficie di

Enciclopedia della Matematica (2013)

Riemann, superficie di


Riemann, superficie di ente geometrico ideato da B. Riemann per rendere monodroma una funzione polidroma complessa, di variabile complessa, w = ƒ(z), in modo da poter mettere i suoi valori in corrispondenza biunivoca con i punti del piano complesso. L’idea risolutiva di Riemann fu quella di operare nel piano complesso dei tagli che uniscono punti di diramazione. Per punto di diramazione si intende un punto isolato P tale che, considerato un punto A del piano complesso, è possibile determinare nell’insieme dei valori assunti da w almeno un percorso chiuso intorno a P al termine del quale il valore di w in A è cambiato; un tale punto A, controimmagine dei punti di diramazione, è a sua volta detto punto di ramificazione. Operando tali tagli si impedisce alla funzione di assumere valori diversi in uno stesso punto e, pertanto, i valori assunti da w possono essere messi in corrispondenza biunivoca con i punti del piano complesso. In questo modo, però, sul piano così tagliato risulta definito solo un ramo della funzione. Riemann considerò allora tanti diversi piani complessi tagliati, detti fogli, uno per ciascun ramo, da connettere opportunamente: il numero di tali fogli è anche detto indice di ramificazione. In tal modo, i punti della superficie composta dai diversi fogli, possono essere messi in corrispondenza biunivoca e continua con tutti i valori w assunti dalla funzione polidroma (tale procedura è detta fogliettamento o foliazione). Per esempio, la superficie di Riemann della funzione logaritmo si può ottenere saldando insieme le superfici corrispondenti alle infinite funzioni olomorfe ln|z| + iArgz + 2kπi, con k intero arbitrario, ciascuna delle quali si riduce al campo in cui la funzione risulta appunto olomorfa: ciò si ottiene prendendo, per ogni k, il piano complesso Ck* privato dell’origine, tagliandolo lungo il semiasse reale negativo e collegandolo col piano di indice k + 1 in modo che il margine inferiore del taglio del primo venga identificato punto per punto con il margine superiore del taglio del secondo. La superficie ottenuta, della quale una rappresentazione parametrica è fornita da

formula

è a «infiniti fogli», con un punto di diramazione in O; essa ricopre infinite volte il piano complesso, con eccezione per l’origine. Le proprietà delle superfici di Riemann hanno numerose connessioni con quelle delle curve algebriche: per esempio, il genere di una curva algebrica piana è il massimo numero di curve regolari chiuse che si possono tracciare sulla relativa superficie di Riemann.

Una superficie di Riemann è una → varietà complessa di dimensione 1, localmente omeomorfa ad aperti del piano complesso.

Vedi anche
Eugenio Bertini Matematico italiano (Forlì 1846 - Pisa 1933). Volontario nella guerra del 1866, allievo a Bologna di L. Cremona, poi a Pisa di E. Betti e U. Dini; prof. nelle univ. di Pavia e di Pisa, dove si stabilì definitivamente nel 1892; socio nazionale dei Lincei (1904). Il B. si pose per primo il problema della ... omeomorfismo In matematica, corrispondenza biunivoca e bicontinua tra due spazi topologici S e S′, tale cioè che: a) a ogni punto P di S associ uno e un sol punto P′ di S′ e viceversa (corrispondenza biunivoca); b) fissato a piacere un intorno I′ di un qualunque punto P′ di S′, esista un intorno I del punto P corrispondente ... punto isolato In matematica, il punto i. di un insieme A è un punto P appartenente ad A ma non al derivato di A; in altre parole, è un punto di A tale che esista un suo intorno, il quale non contenga alcun punto di A diverso da P stesso. In particolare, punto doppio i. di una curva algebrica piana è un punto doppio ... sottogruppo In matematica, insieme H di elementi di un gruppo G, tale che, mediante l’operazione di composizione definita in G, costituisce a sua volta un gruppo. In altre parole, H è s. di G se il ‘prodotto’ di due elementi qualunque di H, eseguito con la regola valida in G, è un elemento di H e se, insieme con ...
Tag
Vocabolario
riemanniano
riemanniano 〈rim–〉 agg. – Relativo al matematico ted. Bernhard Riemann 〈rìiman〉 (1826-1866): geometria r. (o di Riemann o ellittica), tipo di geometria non euclidea nella quale non esistono rette parallele e, rispetto alla geometria euclidea,...
superfìcie
superficie superfìcie (meno com. superfice) s. f. [dal lat. superficies, comp. di super- e facies «faccia»] (pl. -ci, disus. -cie). – 1. Il contorno di un corpo come elemento di separazione della regione dello spazio occupata dal corpo...