Cerca in:
Haar, misura di
Enciclopedia della Matematica (2013)
Haar, misura di
Haar, misura di per un gruppo topologico compatto e abeliano G(⋅), è una misura di Borel μ che soddisfa le seguenti condizioni:
• μ(x ⋅ S) = μ(S ⋅ x) = μ(S) per ogni x ∈ G e ogni sottoinsieme [...] ; 0 per ogni sottoinsieme aperto e non vuoto A ⊆ G;
• μ(E) < ∞ per ogni sottoinsieme compatto E ⊆ G.
Per esempio, la misura di Lebesgue è una misura di Haar sul gruppo moltiplicativo dei reali non nulli (→ Borel, misura di; → Lebesgue, misura di). ...
Leggi Tutto
Haar, Alfred
Enciclopedia on line
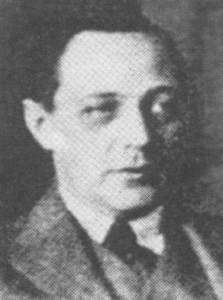Matematico ungherese (Budapest 1885 - Szeged 1933), allievo di D. Hilbert, prof. di fisica-matematica a Kolozsvár (1912) e quindi (dal 1920) di matematica a Szeged. I suoi contributi scientifici vanno [...] compatti che generalizza una nozione già nota per i gruppi di Lie e che è ora nota come misura di Haar: essa ha reso possibili notevoli progressi nella teoria dei caratteri dei gruppi (soprattutto per opera di I. Schur e H. Weyl) e ha consentito a J ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
Misura e integrazione
Enciclopedia del Novecento (1979)
Misura e integrazione
M. Evans Munroe
Introduzione
La nozione di integrale viene spesso introdotta considerando il problema di determinare l'area racchiusa da una curva, prendendo un limite di somme [...] compatta, poniamo per definizione
τ(G)=sup{τ0(C)∣C⊂G; C compatto}.
Utilizzando ϑ e τ nel solito modo, si ottiene una misura di Haar invariante a sinistra.
Uno spazio di misura è una terna (X, Σ, μ) costituita da un insieme X, da una σ-algebra Σ ...
Leggi Tutto
CATEGORIA:
ANALISI MATEMATICA
SISTEMI DINAMICI
Enciclopedia Italiana - VI Appendice (2000)
Sistemi dinamici
Franco Magri
Dmitrij Anosov
Il concetto di sistema è presente nel dibattito scientifico degli ultimi decenni nelle più diverse discipline: dall'idea di sistema fisico a quella di ecosistema, [...] (la quale sia finita sui compatti) è concentrata su qualche sottospazio di quel tipo e ammette una semplice descrizione algebrica, che deriva dalla misura di Haar sul sottogruppo, al quale è associato il sottospazio omogeneo. Nella dimostrazione ...
Leggi Tutto
Gruppi
Enciclopedia del Novecento (1978)
Gruppi
GGeorge W. Mackey
di George W. Mackey
SOMMARIO: 1. Introduzione e storia. □ 2. Concetti fondamentali. □ 3. Anelli di endomorfismi e gruppi lineari. □ 4. La struttura dei gruppi finiti. □ 5. Gruppi [...] può essere scelta in guisa tale che la misura di Haar di un intervallo sia esattamente la lunghezza di quell'intervallo; la misura di Haar si riduce così alla misura di Lebesgue. La teoria di Lebesgue dell'integrazione fu estesa agli spazi astratti ...
Leggi Tutto
La seconda rivoluzione scientifica: matematica e logica. Il Bourbakismo
Storia della Scienza (2004)
La seconda rivoluzione scientifica: matematica e logica. Il Bourbakismo
Jean-Paul Pier
Il Bourbakismo
L'avvento e l'influenza di Bourbaki costituiscono uno dei fenomeni più sorprendenti nella matematica [...] a∈G, f∈L1(G,μ). D'altra parte si esamina l'esistenza di misure quasi invarianti e di misure invarianti in uno spazio omogeneo. Si esplicita la misura di Haar su uno spazio quoziente; vengono trattati numerosi esempi e applicazioni.
L'ottavo capitolo ...
Leggi Tutto
Analisi matematica
Enciclopedia della Scienza e della Tecnica (2007)
Analisi matematica
Jean A. Dieudonné
Alcune delle idee fondamentali che sono alla base del calcolo risalgono ai Greci, ma il loro sviluppo sistematico iniziò soltanto nel XVII secolo. Alla fine di quel [...] che
[23] formula
per ogni f∈B, e tale uguaglianza si può anche scrivere
[24] formula
dove χ è il carattere f →f(0) su B, X=U e dμ(θ) è la misura di Haar normalizzata (1/2π) dθ su U. In generale, dato un carattere χ su A si dice che μ è una ...
Leggi Tutto
CATEGORIA:
ANALISI MATEMATICA
La seconda rivoluzione scientifica: matematica e logica. La teoria della misura
Storia della Scienza (2004)
La seconda rivoluzione scientifica: matematica e logica. La teoria della misura
Maurice Sion
La teoria della misura
Con la nozione matematica di misura si vogliono analizzare concetti che si riferiscono [...] fu successivamente estesa a ogni gruppo localmente compatto. Tale misura, nota come 'misura di Haar', costituisce oggi le fondamenta della teoria. I coefficienti di Fourier di una funzione hanno dato origine nella teoria moderna alla trasformata ...
Leggi Tutto
CATEGORIA:
STORIA DELLA MATEMATICA
ORSATTI, Adalberto
Dizionario Biografico degli Italiani (2013)
ORSATTI, Adalberto. – Nacque a Chieti il 15 marzo 1937, da Nicola, militare di carriera, e da Maria Gagliardi.
Allievo della scuola militare della Nunziatella a Napoli tra il 1952 e il 1955, si trasferì [...] legati alla teoria dei gruppi abeliani, in cui vennero trattati i gruppi compatti, la misura di Haar, il teorema di Peter Weyl e la dualità di Pontryagin.
Un altro argomento di rilievo cui Orsatti diede un importante contributo fu quello degli anelli ...
Leggi Tutto
FIBRE TESSILI
Enciclopedia Italiana (1932)
Con questo nome sono indicati tutti quei prodotti fibrosi, di origine naturale o artificiale che possono essere trasformati in filati e in tessuti. Questa definizione esclude dal novero delle fibre tessili [...] possibilità d'uso di una materia fibrosa per scopi tessili presuppone la coesistenza in una certa misura di alcune proprietà della Berlino 1929; C. Kronacher e G. Lodemann, Technik der Haar- und Wolleuntersuchung, Vienna 1930; C. Pertusi, Le fibre ...
Leggi Tutto