tautologia

tautologia

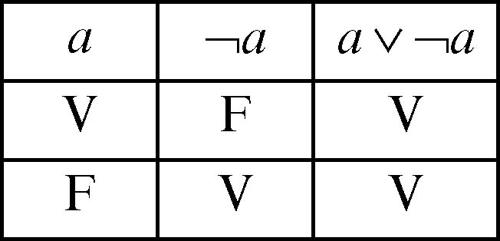
tautologia (dal greco tautós, «stesso, identico» e lógos, «ragionamento») in logica matematica, proposizione che risulta vera indipendentemente dal valore di verità delle singole parti che la compongono. Tale è, per esempio, l’enunciato a ∨ ￢a, (da interpretarsi e leggere come «a o non a» come si evince dalla seguente tavola di verità:

La tautologia a ∨ ￢a è anche nota sotto il nome di principio del terzo escluso o tertium non datur.

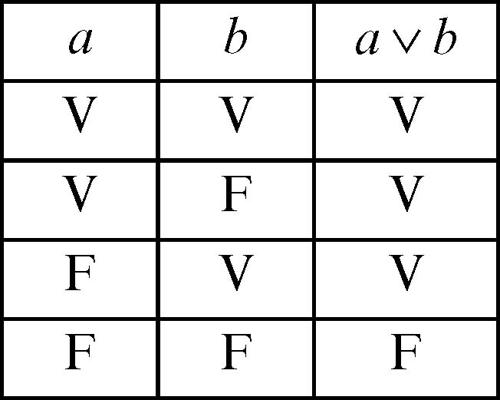
Non è invece una tautologia un enunciato che non risulti sempre vero a seconda dei valori di verità degli enunciati componenti, quale per esempio il seguente:

Una tautologia esprime quindi una verità formale e sintattica, indipendentemente da qualunque interpretazione.

Altri esempi di tautologie sono le seguenti forme:

• A ⇒ (B ⇒ A) (legge dell’’«a fortiori»)

• ￢(A ∧ ￢A) (principio di non contraddizione)

• ￢￢A ⇔ A (doppia negazione)

• A ⇔ A (riflessività della doppia implicazione)

• (A ⇔ B) ⇔ (B ⇔ A) (simmetria della doppia implicazione)

• ((A ⇔ B) ∧ (B ⇔ C)) ⇔ (A ⇔ C) (transitività della doppia implicazione)

Nel linguaggio argomentativo il termine tautologia ha un’accezione negativa poiché indica una espressione che, pur proponendosi di definire qualcosa, ripete in realtà nel predicato quanto già detto nel soggetto: «Questa non è una spiegazione perché è soltanto una tautologia» è una tipica espressione che utilizza il termine tautologia in accezione negativa.