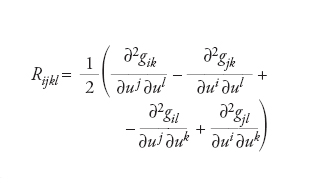tensore di curvatura

tensore di curvatura

Sia M una varietà riemanniana e indichiamo con g_ij le componenti della metrica in un fissato sistema di coordinate locali. Il tensore di curvatura valuta la curvatura della varietà. Le sue componenti R_ijkl si esprimono in termini dei coefficienti della metrica riemanniana nel modo seguente:

Le componenti del tensore di curvatura possono essere espresse in termini dei simboli di Christoffel e delle loro derivate. Le simmetrie che emergono dalla formula precedente possono essere usate per dimostrare che le funzioni R_ijkl sono determinate esattamente da n²(n²−1)/12 numeri. Nel caso di una superficie, quando n=2, il tensore è determinato da un solo numero che prende il nome di curvatura gaussiana della superficie.

→ Matematica: problemi aperti