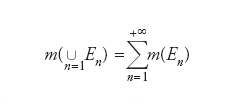teoria della misura
teoria della misura
Una misura è una funzione non negativa sui sottoinsiemi di uno spazio soddisfacente la proprietà di completa additività: la misura di un’unione numerabile di insiemi disgiunti (cioè con intersezione vuota) è pari alla somma delle misure degli insiemi stessi. Il concetto di misura è stato introdotto come astrazione e generalizzazione di quelli di lunghezza, area e volume (grandezze completamente additive), ma anche di densità o distribuzione di probabilità. La teoria della misura è la teoria di questa generalizzazione e costituisce la base per la teoria dell’integrazione. Insieme, esse hanno un ruolo fondamentale nella matematica contemporanea, particolarmente in analisi, analisi funzionale e teoria della probabilità. Alla base del concetto di misura troviamo quello di σ-algebra, una famiglia di sottoinsiemi di uno spazio arbitrario X chiusa rispetto alle unioni numerabili e all’operazione di complementazione (il complementare Ac di A∈X è costituito da tutti gli elementi di X che non appartengono ad A). Uno spazio X dotato di una σ-algebra B è detto spazio misurabile ed è indicato con il simbolo (X,B). Se X è poi uno spazio topologico, la σ-algebra generata dagli insiemi aperti è detta boreliana. Solo una volta che si disponga di una σ-algebra B su uno spazio X è possibile definire una misura m, ovvero una funzione a valori reali su B che soddisfi: (a) 0≤m(E)≤+∞, m(∅)=0 (E∈B, ∅ indica l’insieme vuoto); En∈B (n=1,2,...) e Ei∩Ej=∅ (ifij) implicano
(completa additività). La tripla (X,B,m) è detta allora spazio di misura o misurabile. Se m(X)〈+∞, m è detta misura finita, σ-finita se esiste una successione Xn con ∪n Xn=X e m(Xn)〈0. La più semplice misura finita è ottenuta definendo m(A)=1 se a∈A e m(A)=0 se a∉A, con A∈X: si parla allora di misura (delta) di Dirac in a. Una misura definita sulla σ-algebra degli insiemi boreliani di uno spazio topologico è detta misura boreliana. La teoria della misura è stata sviluppata soprattutto da Henri Léon Lebesgue, che ha inoltre costruito l’importante misura sulla retta reale ℝ che porta il suo nome. Lebesgue parte dalla lunghezza ordinaria degli intervalli e la estende alla σ-algebra boreliana da essi generata. Introduce poi il concetto di funzione misurabile, alla base della sua teoria dell’integrazione.